1 Introduction

The flexible marine riser is the connection between the well head in the sea bed and the platform/vessel on sea surface for transporting the crude oil and natural gas. With the trend of extracting natural resources in deep ocean environment growing [1], the riser plays a crucial role. The riser is mainly subjected to environmental disturbance (waves, wind and ocean currents) and its internal forces. These may cause the vibration and deformation of the riser, which produce the premature fatigue problems. Besides, the American Petroleum Institute requires that maximum non-drilling angles should be limited to \(4^{\circ }\) [2]. Therefore, it is necessary to give an effective control to suppress vibration and prevent the violation of the angle constraints for the riser system.

The dynamics of the riser is generally described by the model of an Euler–Bernoulli beam, which is a distributed parameter system (DPS) [3–9]. The main challenge for solving the control problem of DPS is to control the infinite-dimensional state space using finite sensors and actuators [10–13, 13, 14]. Common methods to use the finite-dimensional techniques are finite element method [15, 16], Galerkin’s method [17, 18] and assumed modes method [19–21]. In these methods, only some critical modes are considered. It would happen that the controller does not stabilize the original infinite-dimensional system, which was documented by Balas in [22] and termed as the “spillover” effect.

Boundary control gains increasingly attention recently due to its practicality in implementation [23–25, 25–29]. Since actuators [30–33] and sensors [34–36] are applied at the boundary of the flexible structure, the dynamics of the system will not be influenced. Then, boundary control can be designed based on the original infinite-dimensional model, and then, the spillover problem is avoided. Lastly, in this paper, novel barrier terms are proposed in the boundary control laws. These terms can ensure the constraints of the joint angles. Without these barrier terms, the constraints would be violated. Therefore, boundary control is widely used in the control design for DPSs [37–43]. In [44], a static output feedback control is designed via the Euler–Bernoulli beam boundary and ODE measurements. Using the proposed control, the closed-loop system is proved to be exponentially stable by the Lyapunov’s direct method. In [45], the vessel dynamics is taken into consideration when modeling. In [46], an actuator at the upper riser is designed to control the transverse deflection of the riser with input saturation. The control problem for a flexible air-breathing hypersonic vehicle (FAHV) is addressed by boundary output feedback control in [47], where a coupled system including both PDEs and ODEs is used to model the FAHV. In [48], boundary and adaptive control laws are designed for a moving beam system.

In practical application and industrial environment, constrained problems [49, 50] are commonly existing in physical stoppages, saturation and safety specifications. The barrier Lyapunov function [51–55] is an effective method to handle constraints.

In this paper, boundary control is designed to suppress the vibration of the marine riser system by three actuators at the top end. In case of lager vibrations, the control system restricts the joint angles within given ranges via the feedback signals. The stability of the riser systems is obtained by using integral-barrier Lyapunov function. The boundary control is directly designed for the original infinite-dimensional riser system, without any model discretization. Thus, the spillover problem can be eliminated entirely. The main contributions of this paper are summarized as follows:

  1. (i)

    To be more precise, the distributed disturbances along the riser are considered. Under the distributed disturbances, the governing equations of the flexible riser are descried by three nonlinear non-homogeneous PDEs, making the dynamic model more complex. Therefore, the control methods based on the homogeneous PDEs cannot be applied directly.

  2. (ii)

    A novel Lyapunov function including an integral Lyapunov term and a barrier Lyapunov term is constructed to guarantee the stability of the system, and the constraints of the joint angles are not violated. The construction of the integral Lyapunov term is based on the mechanical energy \(E_\mathrm{k}(t)\) and \(E_\mathrm{p}(t)\) shown in Sect. 2.

2 Dynamics and preliminaries

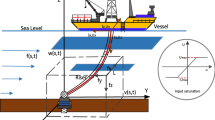
Figure 1 shows a three-dimensional marine riser with its end fixed on at origin and tip clamped with a payload (vessel). The control is implemented at the tip by the actuator. In this paper, the effect of gravity is ignored. Let s and t be the independent spatial and time variables, respectively. For clarification, the notations \((\dot{*})=\partial (*)/\partial t, (*)^{\prime }=\partial (*)/\partial s\) are used throughout this paper.

Fig. 1
figure 1

A nonlinear three-dimensional marine riser

Full size image

2.1 Dynamics analysis

The kinetic energy \(E_\mathrm{k}(t)\) and the potential energy \(E_\mathrm{p}(t)\) of the riser system can be represented as

$$\begin{aligned} E_\mathrm{k}(t)= & {} \frac{1}{2} M[(\dot{x}_L)^2+(\dot{y}_L)^2+(\dot{z}_L)^2]\nonumber \\&+\,\frac{1}{2} \rho \int ^L_0 [(\dot{x})^2+(\dot{y})^2+(\dot{z})^2]ds \end{aligned}$$
(1)
$$\begin{aligned} E_p(t)= & {} \frac{1}{2} T\int ^L_0[(x^{\prime })^2+(y^{\prime })^2]ds\nonumber \\&+\frac{1}{2} EI\int ^L_0[(x^{\prime \prime })^2+(y^{\prime \prime })^2]ds\nonumber \\&+\frac{1}{2} EA\int ^L_0[z^{\prime }+\frac{1}{2} (x^{\prime })^2+\frac{1}{2} (y^{\prime })^2]^2ds \end{aligned}$$
(2)

where \(\dot{x}=\dot{x}(s,t)\), \(x^{\prime }=x^{\prime }(s,t)\), \(x^{\prime \prime }=x^{\prime \prime }(s,t)\) and \(\dot{x}_L=\dot{x}(L,t)\) have been used, and similar abbreviations are used in the sequel.

The virtual work done by external distributed disturbances \(f_x(s,t), f_y(s,t), f_z(s,t)\) on the riser and boundary disturbances \(\mathrm{d}_x(t),\mathrm{d}_y(t), \mathrm{d}_z(t)\) on the tip payload is given by

$$\begin{aligned} \delta W_f(t)=&\int ^L_0 (f_x\delta x+f_y\delta y+f_z\delta z)ds\nonumber \\&+\mathrm{d}_x\delta x_L+\mathrm{d}_y\delta y_L+d_z\delta z_L \end{aligned}$$
(3)

The virtual work done by the control force \(u_x(t),u_y(t),u_z(t)\) to suppress vibration and prevent angle constraint violation can be represented as

$$\begin{aligned} \delta W_m(t)=u_x\delta x_L+u_y\delta y_L+u_z\delta z_L \end{aligned}$$
(4)

Therefore, the virtual work \(\delta W\) done on the system can be represented as

$$\begin{aligned} \delta W(t)=\delta W_f(t)+\delta W_m(t) \end{aligned}$$
(5)

Using the Hamilton’s principle \(\int ^{t_2}_{t_1} \delta [E_\mathrm{k}-E_\mathrm{p}+W]\mathrm{d}t=0\) [56], we can obtain the following governing equations

$$\begin{aligned} \rho \ddot{x}&=Tx^{\prime \prime }+EA(z^{\prime \prime }x^{\prime }+x^{\prime \prime }z^{\prime })+\frac{3}{2} EA(x^{\prime })^{2x\prime \prime }\nonumber \\&\ \quad +\frac{1}{2} EA[x^{\prime \prime }(y^{\prime })^2+2x^{\prime }y^{\prime }y^{\prime \prime }]-EIx^{\prime \prime \prime \prime }+f_x \end{aligned}$$
(6)
$$\begin{aligned} \rho \ddot{y}&=Ty^{\prime \prime }+EA(z^{\prime \prime }y^{\prime }+y^{\prime \prime }z^{\prime })+\frac{3}{2} EA(y^{\prime })^2y^{\prime \prime }\nonumber \\&\ \quad +\frac{1}{2} EA[y^{\prime \prime }(x^{\prime })^2+2y^{\prime }x^{\prime }x^{\prime \prime }]-EIy^{\prime \prime \prime }+f_y \end{aligned}$$
(7)
$$\begin{aligned} \rho \ddot{z}&=EAz^{\prime \prime }+EAx^{\prime }x^{\prime \prime }+EAy^{\prime }y^{\prime \prime }+f_z \end{aligned}$$
(8)

\(\forall (s,t)\in [0,L]\times [0,\infty )\), and the boundary conditions as follows

$$\begin{aligned}&x_0=y_0=z_0=0 \end{aligned}$$
(9)
$$\begin{aligned}&x_0^{\prime \prime }=y_0^{\prime \prime }=z_0^{\prime \prime }=0 \end{aligned}$$
(10)
$$\begin{aligned}&x_L^{\prime \prime }=y_L^{\prime \prime }=z_L^{\prime \prime }=0 \end{aligned}$$
(11)
$$\begin{aligned}&u_x+d_x=M\ddot{x}_L+Tx_L^{\prime }+\frac{1}{2} EA(x_L^{\prime })^3+EAx_L^{\prime }z_L^{\prime }\nonumber \\&\quad +\frac{1}{2} EAx_L^{\prime }(y_L^{\prime })^2-EIx_L^{\prime \prime \prime } \end{aligned}$$
(12)
$$\begin{aligned}&u_y+d_y=M\ddot{y}_L+Ty_L^{\prime }+\frac{1}{2} EA(y_L^{\prime })^3+EAy_L^{\prime }z_L^{\prime }\nonumber \\&\quad +\frac{1}{2} EAy_L^{\prime }(x_L^{\prime })^2-EIy_L^{\prime \prime \prime } \end{aligned}$$
(13)
$$\begin{aligned}&u_z+d_z=M\ddot{z}_L+EAz_L^{\prime }+\frac{1}{2} EA(x_L^{\prime })^2+\frac{1}{2} EA(y_L^{\prime })^2 \end{aligned}$$
(14)

\(\forall t\in [0,\infty )\).

Remark 1

The joint angles of the riser are given as \(\arctan x^{\prime }_L\), \(\arctan y^{\prime }_L\) and \(\arctan z^{\prime }_L\). Except for the vibration suppression, the control laws are designed to constrain the joint angles in given regions, i.e., \(|\arctan x^{\prime }_L|<A_x\), \(|\arctan y^{\prime }_L|<A_y\) and \(|\arctan z^{\prime }_L|<A_z\), where \(A_x, A_y, A_z>0\). In this paper, the constraints of the joint angles are satisfied via the constraints of the boundary slopes, i.e., the boundary slopes of the riser should satisfy \(|x^{\prime }_L|<C_x\), \(|y^{\prime }_L|<C_y\) and \(|z^{\prime }_L|<C_z\), where \(C_x, C_y, C_z>0\) and \(\arctan C_x=A_x\), \(\arctan C_y=A_y\) and \(\arctan C_z=A_z\).

2.2 Preliminaries

Definition 1

[51] A barrier Lyapunov function (BLF) is a scalar function V(x) defined with respect to the system \(\dot{x}=f(x)\) on an open region \({\mathcal {D}}\) containing the origin, which is continuous, positive definite, has continuous first-order partial derivatives at every point of \({\mathcal {D}}\), has the property \(V(x)\rightarrow \infty \) as x approaches the boundary of \({\mathcal {D}}\) and satisfies \(V(x(t))\le b, \forall t\ge 0\) along the solutions of \(\dot{x}=f(x)\) for \(x(0) \in {\mathcal {D}}\) and a positive constant b.

The schematic illustration of a barrier Lyapunov function is shown in Fig. 2.

Fig. 2
figure 2

Schematic illustration of a barrier Lyapunov function

Full size image

Property 1

[57] If the kinetic energy of the system (6)–(14), given by (1), is bounded, then functions \(\dot{x}^{\prime }(s,t), \dot{x}^{\prime \prime }(s,t), \dot{y}^{\prime }(s,t), \dot{y}^{\prime \prime }(s,t), \dot{z}^{\prime }(s,t)\) and \(\dot{z}^{\prime \prime }(s,t)\) are bounded \(\forall (s,t)\in [0,L]\times [0,\infty )\).

Property 2

[57] If the potential energy of the system (6)–(14), given by (2), is bounded, then functions \(x^{\prime \prime }(s,t), x^{\prime \prime \prime }(s,t), x^{\prime \prime \prime \prime }(s,t), y^{\prime \prime }(s,t), y^{\prime \prime \prime }(s,t), y^{\prime \prime \prime \prime }(s,t)\) and \(z^{\prime \prime }(s,t)\) are bounded \(\forall (s,t)\in [0,L]\times [0,\infty )\).

Assumption 1

For the unknown distributed disturbances \(f_x(s,t), f_y(s,t), f_z(s,t)\) and unknown boundary disturbances \(\mathrm{d}_x(t),\mathrm{d}_y(t), \mathrm{d}_z(t)\), we assume that there exist constants \(\bar{f_x}, \bar{f_y}, \bar{f_z}, \bar{\mathrm{d}_x}, \bar{\mathrm{d}_y}, \bar{\mathrm{d}_z}\in R^+\), such that \(f_x(s,t)\le \bar{f_x},f_y(s,t)\le \bar{f_y}, f_z(s,t)\le \bar{f_z}, \forall [s,t]\in [0,L]\times [0,\infty )\) and \(d_x(t)\le \bar{\mathrm{d}_x}, \mathrm{d}_y(t)\le \bar{\mathrm{d}_y}, \mathrm{d}_z(t)\le \bar{d_z}, \forall t\in [0,\infty ) \). This is a reasonable assumption as the disturbances \(f_x(s,t), f_y(s,t), f_z(s,t), \mathrm{d}_x(t), \mathrm{d}_y(t)\) and \(\mathrm{d}_z(t)\) have finite energy and hence are bounded, i.e., \(f_x(s,t), f_y(s,t), f_z(s,t), \mathrm{d}_x(t), \mathrm{d}_y(t), \mathrm{d}_z(t)\in {\mathcal {L}}_{\infty }\). The knowledge of exact values of the disturbances is not required.

3 Control design

The control objectives are to suppress the vibration of the riser in three-dimensional space and guarantee that the joint angles of the marine riser remain in constrained ranges in the presence of environment disturbances. The IBLF-based method is used to construct the control inputs \(u_x, u_y, u_z\) and analyze the stability of the closed-loop system.

For the system given by the governing Eqs. (6)–(8) and boundary conditions (9)–(14), we propose the following control laws:

$$\begin{aligned} u_x&=-{\mathrm {sgn}}(\dot{x}_L+\beta Lx_L^{\prime })\bar{\mathrm{d}}_x+\tau _x(t)\nonumber \\&\quad \ -\,M\beta L\dot{x}_L^{\prime }-k_{1x}(\dot{x}_L+\beta Lx_L^{\prime })- (\dot{x}_L-\beta Lx_L^{\prime })\nonumber \\&\ \quad \times \left( k_{2x}+M\frac{x_L^{\prime }\dot{x}^{\prime }_L}{C^{2}-x_L^{\prime {2}}}\right) /A -\tau _x(t)/A \end{aligned}$$
(15)
$$\begin{aligned} u_y&=-{\mathrm {sgn}}(\dot{y}_L+\beta Ly_L^{\prime })\bar{\mathrm{d}}_y+\tau _y(t)\nonumber \\&\ \quad -\,M\beta L\dot{y}_L^{\prime }-k_{1y}(\dot{y}_L+\beta Ly_L^{\prime })- (\dot{y}_L-\beta Ly_L^{\prime })\nonumber \\&\ \quad \times \left( k_{2y}+M\frac{y_L^{\prime }\dot{y}^{\prime }_L}{C^{2}-y_L^{\prime {2}}}\right) /B -\tau _y(t)/B \end{aligned}$$
(16)
$$\begin{aligned} u_z&=-{\mathrm {sgn}}(\dot{z}_L+\beta Lz_L^{\prime })\bar{\mathrm{d}}_z+\tau _z(t)\nonumber \\&\quad \ -M\beta L\dot{z}_L^{\prime }-k_{1z}(\dot{z}_L+\beta Lz_L^{\prime })-(\dot{z}_L-\beta Lz_L^{\prime })\nonumber \\&\quad \ \times \left( k_{2z}+M\frac{z_L^{\prime }\dot{z}^{\prime }_L}{C^{2}-z_L^{\prime {2}}}\right) /C -\tau _z(t)/C \end{aligned}$$
(17)

where \(k_{1x}, k_{2x}, k_{1y}, k_{2y}, k_{1z}, k_{2z}\) are the positive control gains, and \({\mathrm {sgn}}(\cdot )\) denotes the signum function, \(\tau _x(t), \tau _y(t), \tau _z(t)\) are defined as

$$\begin{aligned} \tau _x(t)&=Tx_L^{\prime }+\frac{1}{2} EA(x_L^{\prime })^3+EAx_L^{\prime }z_L^{\prime }\nonumber \\&\ \quad +\frac{1}{2} EAx_L^{\prime }(y_L^{\prime })^2-EIx_L^{\prime \prime \prime } \end{aligned}$$
(18)
$$\begin{aligned} \tau _y(t)&=Ty_L^{\prime }+\frac{1}{2} EA(y_L^{\prime })^3+EAy_L^{\prime }z_L^{\prime }\nonumber \\&\ \quad +\frac{1}{2} EAy_L^{\prime }(x_L^{\prime })^2-EIy_L^{\prime \prime \prime } \end{aligned}$$
(19)
$$\begin{aligned} \tau _z(t)&=EAz_L^{\prime }+\frac{1}{2} EA(x_L^{\prime })^2+\frac{1}{2} EA(y_L^{\prime })^2 \end{aligned}$$
(20)

and the barrier terms A, B and C are given as

$$\begin{aligned} A= & {} \ln {\frac{2C_x^2}{C_x^2-x_L^{\prime {2}}}}, ~~~~B=\ln {\frac{2C_y^2}{C_y^2-y_L^{\prime {2}}}},\nonumber \\ C= & {} \ln {\frac{2C_z^2}{C_z^2-z_L^{\prime {2}}}} \end{aligned}$$
(21)

Consider the Lyapunov function candidate as

$$\begin{aligned} V(t)=V_1(t)+V_2(t)+V_3(t) \end{aligned}$$
(22)

where

$$\begin{aligned} V_1(t)&=\frac{1}{2} \rho \int ^L_0[(\dot{x})^2+(\dot{y})^2+(\dot{z})^2]ds\nonumber \\&\quad \ +\frac{1}{2} EA\int ^L_0[z^{\prime }+\frac{1}{2} (x^{\prime })^2+\frac{1}{2} (y^{\prime })^2]^2ds \nonumber \\&\quad \ +\frac{1}{2} EI\int ^L_0[(x^{\prime \prime })^2+(y^{\prime \prime })^2]ds\nonumber \\&\quad \ +\frac{1}{2} T\int ^L_0[(x^{\prime })^2+(y^{\prime })^2]ds \end{aligned}$$
(23)
$$\begin{aligned} V_2(t)&=\frac{1}{2} M(\dot{x}_L+\beta Lx_L^{\prime })^2A+\frac{1}{2} M(\dot{y}_L\nonumber \\&\quad \ +\beta Ly_L^{\prime })^2B +\frac{1}{2} M(\dot{z}_L+\beta Lz_L^{\prime })^2C \end{aligned}$$
(24)
$$\begin{aligned} V_3(t)&=\beta \rho \int ^L_0s(\dot{x}x^{\prime }+\dot{y}y^{\prime }+\dot{z}z^{\prime })ds \end{aligned}$$
(25)

where \(\beta \) is a positive constant, \(V_1(t)\) is designed based on the mechanical energy \(E_k(t)\) and \(E_p(t)\), called the energy term, the auxiliary term \(V_2(t)\) is related to the payload, and the crossing term \(V_3(t)\) is designed to facilitate the stability analysis.

Lemma 1

The Lyapunov candidate function given by (22) is positive definite as

$$\begin{aligned} \lambda _1(\zeta (t)+V_2(t))\le V(t) \le \lambda _2(\zeta (t)+V_2(t)) \end{aligned}$$
(26)

where \(\lambda _1\) and \(\lambda _2\) are two positive constants and

$$\begin{aligned} \zeta (t)&=\int ^L_0[(\dot{x})^2+(x^{\prime })^2+(\dot{y})^2+(y^{\prime })^2 +(\dot{z})^2+(z^{\prime })^2\nonumber \\&\quad \ +\,(x^{\prime })^4+(y^{\prime })^4+(x^{\prime }y^{\prime })^2+(x^{\prime \prime })^2+(y^{\prime \prime })^2]ds \end{aligned}$$
(27)

Proof

According to generalized Young’s inequality [57], let \(\delta \) satisfy \(T-\frac{EA}{2\delta }\ge 0\) and \(\frac{1}{4}-\delta \ge 0\), where \(\delta \) is a positive constant, we have

$$\begin{aligned} 0\le \eta _1\zeta (t)\le V_1(t)\le \eta _2\zeta (t) \end{aligned}$$
(28)

where \(\eta _1\) and \(\eta _2\) are defined as

$$\begin{aligned}&\eta _1=\frac{1}{2} \min \left[ \rho ,T-\frac{EA}{2\delta },\frac{1}{2} EA,EA\left( \frac{1}{4}-\delta \right) , EI\right] \end{aligned}$$
(29)
$$\begin{aligned}&\eta _2=\frac{1}{2} \max \left[ \rho ,T+\frac{EA}{2\delta },\frac{1}{2} EA, EA \left( \frac{1}{4}+\delta \right) ,EI \right] \end{aligned}$$
(30)

Similarly, we can obtain

$$\begin{aligned} |V_3(t)|&\le \beta \rho L\int ^L_0[(\dot{x})^2+(x^{\prime })^2+(\dot{y})^2+(y^{\prime })^2\nonumber \\&\quad +\, (\dot{z})^2+(z^{\prime })^2]ds\le \beta \rho L\zeta (t) \end{aligned}$$
(31)

Let \(\beta \) satisfy \(\beta \rho L<\eta _1\), we have \(0<\beta \rho L<\zeta _1\). Let \(\xi _1=\eta _1-\beta \rho L,\xi _2=\eta _2+\beta \rho L\), we further have

$$\begin{aligned} 0\le \xi _1V_1(t)\le V_1(t)+V_3(t)\le \xi _2V_1(t). \end{aligned}$$
(32)

Therefore, we have

$$\begin{aligned} 0\le \lambda _1[(\zeta (t)+V_2(t))\le V(t)\le \lambda _2(\zeta (t)+V_2(t)), \end{aligned}$$
(33)

where \(\lambda _1=\min (\xi _1,1)\) and \(\lambda _2=\max (\xi _2,1)\) are two positive constants. \(\square \)

Lemma 2

The time derivative of the Lyapunov candidate function in (22) is given as

$$\begin{aligned} \dot{V}(t)\le -\lambda V(t)+\varepsilon , \end{aligned}$$
(34)

where \(\lambda \) and \(\varepsilon \) are two positive constants.

Proof

Differentiating \(V_1(t)\) by parts and applying generalized Young’s inequality [57], we have

$$\begin{aligned} \dot{V}_1(t)&\le \delta _1\int ^L_0f_x^2ds+\delta _2\int ^L_0f_y^2ds+\delta _3\int ^L_0f_z^2ds\nonumber \\&\quad \ +\frac{1}{\delta _1}\int ^L_0(\dot{x})^2ds +\frac{1}{\delta _2}\int ^L_0(\dot{y})^2ds\nonumber \\&\quad \ +\frac{1}{\delta _3}\int ^L_0(\dot{z})^2ds+\Delta _1 \end{aligned}$$
(35)

where \(\delta _1\)–\(\delta _3\) are positive constants, and \(\Delta _1\) is the sum of the boundary terms in \(\dot{V}_1(t)\). Substituting boundary conditions (9)–(14) to \(\Delta _1\), we obtain

$$\begin{aligned} \Delta _1 =\tau _x(t)\dot{x}_L+\tau _y(t)\dot{y}_L+\tau _z(t)\dot{z}_L \end{aligned}$$
(36)

The differentiation of \(V_2(t)\) and substitution of the control laws (15)–(17) yield

$$\begin{aligned} \dot{V}_2(t)&\le -k_{1x}(\dot{x}_L+\beta Lx_L^{\prime })^2A-k_{2x}(\dot{x}_L)^2\nonumber \\&\ \quad +\,k_{2x}\beta ^2 L^2(x_L^{\prime })^2- \tau _x(t)(\dot{x}_L+\beta Lx_L^{\prime })\nonumber \\&\ \quad -\, k_{1y}(\dot{y}_L+\beta Ly_L^{\prime })^2B-k_{2y}(\dot{y}_L)^2\nonumber \\&\ \quad +k_{2y}\beta ^2 L^2(y_L^{\prime })^2-\tau _y(t)(\dot{y}_L+\beta Ly_L^{\prime })\nonumber \\&\ \quad -k_{1z}(\dot{z}_L+\beta Lz_L^{\prime })^2C-k_{2z}(\dot{z}_L)^2\nonumber \\&\ \quad +k_{2z}\beta ^2 L^2(z_L^{\prime })^2-\tau _z(t)(\dot{z}_L+\beta Lz_L^{\prime }) \end{aligned}$$
(37)

Time derivative of \(V_3(t)\) is given as

$$\begin{aligned} \dot{V}_3(t)=&-\frac{1}{2} \beta \rho \int ^L_0 (\dot{x})^2ds-\frac{1}{2} \beta \rho \int ^L_0(\dot{y})^2ds\nonumber \\&-\frac{1}{2} \beta \rho \int ^L_0 (\dot{z})^2ds-\frac{1}{2}\beta EA\int ^L_0(z^{\prime })^2ds\nonumber \\&-\frac{3}{8} \beta EA\int ^L_0(x^{\prime })^4ds-\frac{3}{8} \beta EA\int ^L_0(y^{\prime })^4ds\nonumber \\&-\beta EA\int ^L_0(x^{\prime })^2z^{\prime }ds-\beta EA\int ^L_0(y^{\prime })^2z^{\prime }ds\nonumber \\&-\frac{3}{4} \beta EA\int ^L_0(x^{\prime }y^{\prime })^2ds-\frac{1}{2} \beta EI\int ^L_0(x^{\prime \prime })^2ds\nonumber \\&-\frac{1}{2} \beta EI\int ^L_0(y^{\prime \prime })^2ds-\frac{1}{2} \beta T\int ^L_0(x^{\prime })^2ds\nonumber \\&- \frac{1}{2} \beta T\int ^L_0(y^{\prime })^2ds+\beta \int ^L_0s(f_x x^{\prime }\nonumber \\&+f_y y^{\prime }+f_z z^{\prime })ds+\Delta _2 \end{aligned}$$
(38)

where \(\Delta _2\) is the sum of the boundary terms in \(\dot{V}_3(t)\). Substituting the boundary conditions (9)–(14) to \(\Delta _2\), we have

$$\begin{aligned} \Delta _2&=\frac{1}{2} \beta \rho L(\dot{x}_L)^2 +\frac{1}{2} \beta \rho L(\dot{y}_L)^2+ \frac{1}{2} \beta \rho L(\dot{z}_L)^2\nonumber \\&\quad +\,\tau _x(t)\beta Lx_L^{\prime }+\tau _y(t)\beta Ly_L^{\prime } +\tau _z(t)\beta Lz_L^{\prime }\nonumber \\&\quad -\, \frac{1}{2} \beta \mathrm{TL}(x_L^{\prime })^2-\frac{1}{2} \beta \mathrm{TL}(y_L^{\prime })^2\nonumber \\&\quad -\,\frac{1}{2} \beta EAL\left[ \frac{1}{2}(x_L^{\prime })^2+\frac{1}{2}(y_L^{\prime })^2+z_L^{\prime }\right] ^2 \end{aligned}$$
(39)

Then, we can further have

$$\begin{aligned} \dot{V}(t)&\le -\left( \frac{1}{2}\beta \rho -\frac{1}{\delta _1}\right) \int ^L_0(\dot{x})^2ds\nonumber \\&\quad \ -\,\left( \frac{1}{2}\beta \rho -\frac{1}{\delta _2}\right) \int ^L_0(\dot{y})^2ds\nonumber \\&\quad \ -\,\left( \frac{1}{2}\beta \rho -\frac{1}{\delta _3}\right) \int ^L_0(\dot{z})^2ds\nonumber \\&\quad \ -\, \left( \frac{1}{2}\beta EA-\beta L\delta _6\right) \int ^L_0(z^{\prime })^2ds\nonumber \\&\quad \ -\,\frac{3}{8} \beta EA\int ^L_0(x^{\prime })^4ds - \frac{3}{8} \beta EA\int ^L_0(y^{\prime })^4ds\nonumber \\&\quad -\, \beta EA\int ^L_0(x^{\prime })^2z^{\prime }ds-\beta EA\int ^L_0(y^{\prime })^2z^{\prime }ds\nonumber \\&\quad \ -\,\frac{3}{4} \beta EA\int ^L_0(x^{\prime }y^{\prime })^2ds - \frac{1}{2} \beta EI\int ^L_0(x^{\prime \prime })^2ds\nonumber \\&\quad \ -\, \frac{1}{2} \beta EI\int ^L_0(y^{\prime \prime })^2ds\nonumber \\&\quad \ -\,\left( \frac{1}{2} \beta T-\beta L\delta _4\right) \int ^L_0(x^{\prime })^2ds\nonumber \\&\quad \ -\, \left( \frac{1}{2} \beta T-\beta L\delta _5\right) \int ^L_0(y^{\prime })^2ds\nonumber \\&\quad + \,\left( \delta _1+\frac{\beta L}{\delta _4}\right) \int ^L_0 f_x^2ds\nonumber \\&\quad +\,\left( \delta _2+\frac{\beta L}{\delta _5}\right) \int ^L_0 f_y^2ds\nonumber \\&\quad \ +\,\Big (\delta _3+\frac{\beta L}{\delta _6}\Big )\int ^L_0 f_z^2ds\nonumber \\&\quad \ -\,k_{1x}M(\dot{x}_L+\beta Lx_L^{\prime })^2A\nonumber \\&\quad \ -\,k_{1y}M(\dot{y}_L+\beta Ly_L^{\prime })^2B\nonumber \\&\quad \ -\, k_{1z}M(\dot{z}_L+\beta Lz_L^{\prime })^2C\nonumber \\&\quad \ -\,\left( k_{2x}-\frac{1}{2}\beta \rho L\right) \dot{x}_L^2-\left( k_{2y} -\frac{1}{2}\beta \rho L\right) \dot{y}_L^2\nonumber \\&\quad \ -\,\left( k_{2z}-\frac{1}{2}\beta \rho L\right) \dot{z}_L^2\nonumber \\&\quad \ -\, [2\beta TL-\beta ^2L^2(2k_{2x}+2k_{2y}+k_{2z})]z_L^{\prime {2}}\nonumber \\&\quad -\,\frac{1}{2} \beta EAL\left[ \frac{1}{2}(x_L^{\prime })^2+\frac{1}{2}(y_L^{\prime })^2+z_L^{\prime }\right] ^2\nonumber \\&\le -\lambda _3[\zeta (t)+V_2(t)]+\varepsilon \end{aligned}$$
(40)

where \(\delta _4\)–\(\delta _6\) are positive constants, and

$$\begin{aligned} \lambda _3&=\min \Big \{\frac{1}{2}\beta \rho -\frac{1}{\delta _1}, \frac{1}{2}\beta \rho -\frac{1}{\delta _2}, \frac{1}{2}\beta \rho \nonumber \\&\quad \ -\frac{1}{\delta _3}, \frac{1}{2}\beta EA-\beta L\delta _6, \frac{3\beta }{8}, \frac{1}{2} \beta T\nonumber \\&\quad \ -\beta L\delta _4, \frac{1}{2} \beta T-\beta L\delta _5, \frac{2k_{1x}}{M},\frac{2k_{1y}}{M},\frac{2k_{1z}}{M} \Big \} \end{aligned}$$
(41)
$$\begin{aligned} \varepsilon&=\left( \alpha \delta _1+\frac{\beta L}{\delta _4}\right) \int ^L_0 f_x^2ds+\left( \alpha \delta _2+\frac{\beta L}{\delta _5}\right) \nonumber \\&\ \quad \times \int ^L_0 f_y^2ds +\left( \alpha \delta _3+\frac{\beta L}{\delta _6}\right) \int ^L_0 f_z^2ds\nonumber \\&\le \left( \alpha \delta _1+\frac{\beta L}{\delta _4}\right) \bar{f_x} +\left( \alpha \delta _2+\frac{\beta L}{\delta _5}\right) \bar{f_x}\nonumber \\&\quad \ +\left( \alpha \delta _3+\frac{\beta L}{\delta _6}\right) \bar{f_x}\in {\mathcal {L}}_{\infty } \end{aligned}$$
(42)

Choosing \(2 k_{2x}\ge \beta \rho L, 2k_{2y}\ge \beta \rho L, 2k_{2z} \ge \beta \rho L\), and the designed parameters \(\beta \), \(\delta _1\)–\(\delta _6\) are selected to satisfy the following conditions:

$$\begin{aligned}&\frac{1}{2}\beta \rho -\frac{1}{\delta _1}\ge 0 \end{aligned}$$
(43)
$$\begin{aligned}&\frac{1}{2}\beta \rho -\frac{1}{\delta _2}\ge 0 \end{aligned}$$
(44)
$$\begin{aligned}&\frac{1}{2}\beta \rho -\frac{1}{\delta _3}\ge 0 \end{aligned}$$
(45)
$$\begin{aligned}&EA- 2L\delta _6 \ge 0 \end{aligned}$$
(46)
$$\begin{aligned}&T- 2L\delta _4 \ge 0 \end{aligned}$$
(47)
$$\begin{aligned}&T- 2L\delta _5 \ge 0 \end{aligned}$$
(48)
$$\begin{aligned}&2 TL-\beta L^2(2k_{2x}+2k_{2y}+k_{2z})\ge 0 \end{aligned}$$
(49)

Combining (26) and (40), we have

$$\begin{aligned} \dot{V}(t)\le -\lambda V(t)+\varepsilon , \end{aligned}$$
(50)

where \(\lambda =\lambda _3/\lambda _2\) and \(\varepsilon >0\). \(\square \)

Theorem 1

For the system described by (6)–(8) and boundary conditions (9)–(14), under Assumption 1, and the control laws (15)–(17), given that the initial conditions are bounded, we can conclude that:

  1. (i)

    the states of the system x(s, t), y(s, t) and z(s, t) will remain in the compact set \(\Omega _1\) defined by

    $$\begin{aligned} \Omega _1&:=\{x(s,t),y(s,t),z(s,t)\nonumber \\&\quad \ \in R |~|x(s,t)|,|y(s,t)|,|z(s,t)|\nonumber \\&\le D_1,\forall (s,t)\in [0,L]\times [0,\infty )\} \end{aligned}$$
    (51)

    where the constant \(D_1=\sqrt{\frac{L}{\lambda _1}\Big (V(0)+\frac{\varepsilon }{\lambda }\Big )}\).

  2. (ii)

    the states of the system x(s, t), y(s, t) and z(s, t) will eventually converge to the compact \(\Omega _2\) defined by

    $$\begin{aligned} \Omega _2&:=\{x(s,t),y(s,t),z(s,t)\in R |~\lim _{t\rightarrow \infty }|x(s,t)|,\nonumber \\&\quad \ \lim _{t\rightarrow \infty }|y(s,t)|,\lim _{t\rightarrow \infty }|z(s,t)|\nonumber \\&\le D_2,\forall t\in [0,\infty )\} \end{aligned}$$
    (52)

    where the constant \(D_2=\sqrt{\frac{L\varepsilon }{\lambda _1\lambda }}\).

Proof

Multiplying (34) by \(e^{\lambda t}\) yields

$$\begin{aligned} \frac{\partial }{\partial t}(Ve^{\lambda t})\le \varepsilon e^{\lambda t} \end{aligned}$$
(53)

Integration of the above inequality, we obtain

$$\begin{aligned} V(t)&\le \left( V(0)-\frac{\varepsilon }{\lambda }\right) e^{-\lambda t}+\frac{\varepsilon }{\lambda }\le V(0)e^{-\lambda t}\nonumber \\&\quad \ +\frac{\varepsilon }{\lambda }\in {\mathcal {L}}_{\infty } \end{aligned}$$
(54)

which implies V(t) is bounded. Utilizing Wirtinger’s inequality (or Poincaŕe) [57] and (26), we obtain

$$\begin{aligned} \frac{1}{L} [x(s,t)]^2&\le \int ^L_0[x^{\prime }(s,t)]^2ds\le \zeta (t)\nonumber \\ {}&\le \frac{1}{\lambda _1}V(t)\in {\mathcal {L}}_{\infty } \end{aligned}$$
(55)
$$\begin{aligned} \frac{1}{L} [y(s,t)]^2&\le \int ^L_0[y^{\prime }(s,t)]^2ds\le \zeta (t)\nonumber \\ {}&\le \frac{1}{\lambda _1}V(t)\in {\mathcal {L}}_{\infty } \end{aligned}$$
(56)
$$\begin{aligned} \frac{1}{L} [z(s,t)]^2&\le \int ^L_0[z^{\prime }(s,t)]^2ds\le \zeta (t)\nonumber \\ {}&\le \frac{1}{\lambda _1}V(t)\in {\mathcal {L}}_{\infty } \end{aligned}$$
(57)

Rearranging the terms of the above three inequalities, we can obtain

$$\begin{aligned}&|x(s,t)|,|y(s,t)|,|z(s,t)|\le \sqrt{\frac{L}{\lambda _1}\left( V(0)e^{-\lambda t}+\frac{\varepsilon }{\lambda }\right) }\nonumber \\&\quad \le \sqrt{\frac{L}{\lambda _1}\left( V(0)+\frac{\varepsilon }{\lambda }\right) },\forall (s,t)\in [0,L]\times [0,\infty ) \end{aligned}$$
(58)

Furthermore, from (58), we can obtain

$$\begin{aligned} \lim _{t\rightarrow \infty }|x(s,t)|&\le \sqrt{\frac{L\varepsilon }{\lambda _1\lambda }},\forall s\in [0,L] \end{aligned}$$
(59)
$$\begin{aligned} \lim _{t\rightarrow \infty }|y(s,t)|&\le \sqrt{\frac{L\varepsilon }{\lambda _1\lambda }},\forall s\in [0,L] \end{aligned}$$
(60)
$$\begin{aligned} \lim _{t\rightarrow \infty }|z(s,t)|&\le \sqrt{\frac{L\varepsilon }{\lambda _1\lambda }},\forall s\in [0,L] \end{aligned}$$
(61)

\(\square \)

Remark 2

By proposing the barrier Lyapunov function bounded in a symmetrical region shown in Fig. 2, it is thus guaranteed that the barriers are not transgressed. From Ineqs. (54) and (55), we know that V(t) is bounded and \(\zeta (t)\le \frac{1}{\lambda _1}V(t)\) is also bounded \(\forall t \in [0,\infty )\). Furthermore, from Ineq. (26) in Lemma 1 and the fact that \(V_2(t)\) and \(\zeta (t)\) are positive functions, we have that \(V_2(t)\) is also bounded \(\forall t \in [0,\infty )\). From the definition of barrier Lyapunov function, we know that \(V_2(t)\rightarrow \infty \), as \(|x^{\prime }_L|\rightarrow C_x, |y^{\prime }_L|\rightarrow C_y, |z^{\prime }_L|\rightarrow C_z\). Consequently, we know that \(x^{\prime }_L\ne C_x\), \(y^{\prime }_L \ne C_y\) and \(z^{\prime }_L \ne C_z\). Given that \(|x^{\prime }(L,0)|<C_x\), \(|y^{\prime }(L,0)|<C_y\) and \(|z^{\prime }(L,0)|<C_z\), from Fig. 2, we can further infer that \(|x^{\prime }_L|, |y^{\prime }_L|, |z^{\prime }_L|\) remain in the sets \(|x^{\prime }_L|<C_x\), \(|y^{\prime }_L|<C_y\) and \(|z^{\prime }_L|<C_z\), \(\forall t \in [0,\infty )\). Therefore, we have \(|\arctan x^{\prime }_L|<\arctan C_x\), \(|\arctan y^{\prime }_L|<\arctan C_y\) and \(|\arctan z^{\prime }_L|<\arctan C_z\), \(\forall t \in [0,\infty )\), namely the joint angles are constrained in the given angle regions.

Fig. 3
figure 3

Boundary disturbances: (a) \(\mathrm{d}_x(t)\) and \(\mathrm{d}_y(t)\); (b) \(d_z(s,t)\)

Full size image
Fig. 4
figure 4

Displacements of the riser without control: a x(s, t); b y(s, t); c z(s, t)

Full size image

Remark 3

According to (28) and (55), we can state that \(\zeta (t)\) and \(V_1(t)\) are bounded \(\forall t\in [0,\infty )\). Since \(V_1(t)\) is bounded, \(\dot{x}(s,t), x^{\prime }(s,t), x^{\prime \prime }(s,t), \dot{y}(s,t), y^{\prime }(s,t), y^{\prime \prime }(s,t), \dot{z}(s,t)\) and \(z^{\prime }(s,t)\) are bounded \(\forall (s,t)\in [0,L]\times [0,\infty )\). From (1), the kinetic energy of the system is bounded and using Property 1, we can know that \(\dot{x}^{\prime }(s,t)\) and \(\dot{y}^{\prime }(s,t)\) are bounded \(\forall (s,t)\in [0,L]\times [0,\infty )\). From the boundedness of the potential energy (2), we can use Property 2 to conclude that \(z^{\prime \prime }(s,t)\) is bounded, \(\forall (s,t)\in [0,L]\times [0,\infty )\). Finally, using Assumption 1, (6)–(8) through (9)–(14) and the above statements, we can conclude that \(\ddot{x}(s,t), \ddot{y}(s,t)\) and \(\ddot{z}(s,t)\) are also bounded, \(\forall (s,t)\in [0,L]\times [0,\infty )\). From Lemma 3 and the above proof, it is shown the deflection x(s, t), y(s, t) and z(s, t) is uniformly bounded \(\forall (s,t)\in [0,L]\times [0,\infty )\). And we can conclude that the control inputs \(u_x, u_y\) and \(u_z\) are bounded \(\forall (s,t)\in [0,L]\times [0,\infty )\).

Remark 4

The limitation for the proposed control is that there is no term introduced to deal with the effect of \(f_x(s,t), f_y(s,t), f_z(s,t)\). Therefore, only bounded stability can be ensured due to the term \(\varepsilon \). When the upper bounds of the distributed disturbance are large, the control performance would be affected. However, a better control performance can also be obtained by tuning the designed parameters. From Ineqs. (41), (59)–(61), by adjusting the designed parameters, such as increasing \(k_{1x}\), \(k_{1y}\), \(k_{1z}\) will bring a larger \(\lambda _3\). Then, the value of \(\lambda \) will increase, which will produce a better vibration suppression performance. However, increasing in the control gains would bring a high gain control scheme. Therefore, in practical applications, the designed parameters should be adjusted carefully for achieving suitable transient performance and control action.

4 Simulation

In this section, in order to demonstrate the effectiveness and practicability of the proposed control laws (15)–(17), we choose the infinite difference method to carry out the numerical simulation. The initial conditions of the system are given as: \(x(s,t)=\dot{x}(s,t)=y(s,t)=\dot{y}(s,t)=z(s,t)=\dot{z}(s,t)=0\).

In this paper, for simulation purposes, the external distributed disturbances are simulated with several sinusoids signals with different frequencies, which can be used to model the ocean disturbances in offshore engineering. The reader can refer to [58] for the detailed parameters of distributed disturbances on the riser. The external boundary disturbances are generated by the following equations

$$\begin{aligned} \mathrm{d}_x(t)= & {} \mathrm{d}_y(t) = ( 3+0.8\sin (0.7t)+0.2\sin (0.5t)\nonumber \\&+\,0.2\sin (0.9t) )\times 10^5\end{aligned}$$
(62)
$$\begin{aligned} d_z(t)= & {} (3+0.2\sin (0.5t))\times 10^4 \end{aligned}$$
(63)

From (62) and (63), the periods of boundary disturbances are \(T_x=T_y=20\pi \)s, \(T_z=4\pi \)s, the frequencies of boundary disturbances are \(f_x=f_y=0.016\)Hz, \(f_z=0.08Hz\) and the amplitudes of boundary disturbances are \(A_x=A_y=4.2\times 10^5\), \(A_z=3.2\times 10^4\), respectively. The simulations for boundary disturbances are shown in Fig. 3.

Table 1 Parameters of the system
Full size table
Fig. 5
figure 5

Displacements of the riser with the proposed control: a x(s, t); b y(s, t); c z(s, t)

Full size image
Fig. 6
figure 6

Displacements of the riser with the PD control: a x(s, t); b y(s, t); c z(s, t)

Full size image

Parameters of the riser system are given in Table 1.

The length of simulation time is \(500\,\hbox {s}\).

4.1 Comparison with the PD control

In this subsection, the simulation results have been discussed thoroughly by comparing with the traditional PD control. The dynamic responses of the flexible riser are simulated in the following cases:

(i) Without control: The flexible riser is simulated without control, and the spatial time representations are shown in Fig. 4. From the simulation results shown in Fig. 4, it can be observed that when there is no control input, there are large vibrations along the riser subjected to the external disturbances. For example, we can obtain \(\max |z(x,t)|=4.4\,\mathrm{m}\).

(ii) With the proposed boundary control force: The boundary control laws (15)–(17) developed by using integral-barrier Lyapunov function is simulated with the control parameters \(k_{1x}=2\times 10^3\), \(k_{2x}=8\times 10^5\),\(k_{1y}=3\times 10^3\),\(k_{2y}=4\times 10^5\),\(k_{1z}=5\times 10^3\) and \(k_{2z}=10^6\). The spatial time representations are shown in Fig. 5. When the proposed control laws applied, we can see that the proposed boundary laws (15)–(17) could suppress the vibrations in all three directions. In addition, in the z direction, the displacement magnitude is regulated to around 0 at the top end of the riser, illustrating that good control performance is ensured with the proposed control.

Fig. 7
figure 7

Boundary displacement of the riser without control: a x(L, t); b y(L, t); c z(L, t)

Full size image
Fig. 8
figure 8

Boundary displacement of the riser with the proposed control: a x(L, t); b y(L, t); c z(L, t)

Full size image
Fig. 9
figure 9

Boundary displacement of the riser with the PD control: a x(L, t); b y(L, t); c z(L, t)

Full size image
Fig. 10
figure 10

Boundary slopes of the riser without control: a \(x^{\prime }(L,t)\); b \(y^{\prime }(L,t)\); c \(z^{\prime }(L,t)\)

Full size image

(iii) With the PD control: The flexible riser system is analyzed with the traditional PD control \(u_1(t)=-k_{p1}w(L,t) - k_{d1}\dot{w}(L,t)\), \(u_2(t)=-k_{p2}y(L,t) - k_{d2}\dot{y}(L,t)\) and \(u_3(t)=-k_{p3}z(L,t) - k_{d3}\dot{z}(L,t)\) by choosing \(k_{p1}=k_{p2}=k_{p3}=5\times 10^5\) and \(k_{d1}=k_{d2}=8\times 10^5\), \(k_{d3}=10^6\). The displacements of the riser under the PD control are shown in Fig. 6. We can observe that the vibration can also be suppressed by the PD control.

Fig. 11
figure 11

Boundary slopes of the riser with the proposed control: a \(x^{\prime }(L,t)\); b \(y^{\prime }(L,t)\); c \(z^{\prime }(L,t)\)

Full size image

The end-point deflection has also been presented to show the advantages of the proposed method. Figures 7, 8 and 9 show the displacements of the riser at \(x=L\). From Figs. 7, 9, we can conclude that both the proposed control and the PD control are effective in regulating w(L, t), y(L, t) and z(L, t). However, obviously, the response of the proposed control is faster than that of the PD control.

Fig. 12
figure 12

Boundary slopes of the riser with the PD control: (a) \(x^{\prime }(L,t)\); (b) \(y^{\prime }(L,t)\); (c) \(z^{\prime }(L,t)\)

Full size image

Additional, boundary slopes of the riser are simulated in Figs. 10, 11 and 12. As shown in Fig. 12, with the PD control, the constraints for boundary slopes of the riser are violated. However, the proposed control laws ensure that the boundary slopes of the riser \(|x^{\prime }_L|\le C_x\), \(|y^{\prime }_L|\le C_y\) and \(|z^{\prime }_L|\le C_z\) are due to the existence of the barrier Lyapunov functions.

Although both the proposed control and the PD control are able to stabilize the riser at the small neighborhood of its equilibrium position. However, compared with PD control, the performance of the proposed boundary control exhibits smaller vibration and the states converge faster. And only the proposed boundary control can guarantee the joint angles that remain in the given regions. In addition, the control gains for the PD control are larger than that of the proposed control. From the comparison, we can conclude that we obtain a better control performance by using the proposed control. The control inputs are given in Fig. 13.

Fig. 13
figure 13

Boundary control inputs \(u_x(t)\), \(u_y(t)\) and \(u_z(t)\)

Full size image

4.2 Comparison with different boundary disturbances

In order to test the effects of the frequency and amplitude of the periodic disturbances on the control performance, we have used different boundary disturbances in the simulations. The dynamic responses of the flexible riser are simulated in the following cases:

(i) Changing the frequency of the external disturbances: For this case, with the amplitude of the external disturbances unchanged, we change the frequency of the external disturbances as

$$\begin{aligned} \mathrm{d}_{x_{1}}(t)= & {} \mathrm{d}_{y_{1}}(t)=( 3+0.8\sin (7 t)+ 0.2\sin (5 t)\nonumber \\&+\,0.2\sin (9 t) )\times 10^5 \end{aligned}$$
(64)
$$\begin{aligned} \mathrm{d}_{z_{1}}(t)= & {} ( 3+0.2\sin (5 t) )\times 10^4 \end{aligned}$$
(65)

For boundary disturbances (64) and (65), the periods are \(T_{x1}=T_{y1}=2\pi \hbox {s}\), \(T_{z1}=0.4\pi \hbox {s}\), and the frequencies are \(f_{x1}=f_{y1}=0.16\,\hbox {Hz}\), \(f_{z1}=0.8\,\hbox {Hz}\).

The simulation results are exactly the same with Figs. 5, 8 and 11 by using the same control gains, i.e., \(k_{1x}=2\times 10^3\), \(k_{2x}=8\times 10^5\),\(k_{1y}=3\times 10^3\), \(k_{2y}=4\times 10^5\),\(k_{1z}=5\times 10^3\) and \(k_{2z}=10^6\). From the simulation results, we can observe that changing the frequencies of the disturbances will not affect the control performance.

Fig. 14
figure 14

Displacements of the riser with the proposed control under new disturbances (68) and (69): a x(s, t); b y(s, t); c z(s, t)

Full size image
Fig. 15
figure 15

Boundary displacement of the riser with the proposed control under new disturbances (68) and (69): a x(L, t); b y(L, t); c z(L, t)

Full size image
Fig. 16
figure 16

Boundary slopes of the riser with the proposed control under new disturbances (68) and (69): a \(x^{\prime }(L,t)\); b \(y^{\prime }(L,t)\); c \(z^{\prime }(L,t)\)

Full size image

(ii) Changing the amplitude of the external disturbances: For this case, with the frequency of the external disturbances unchanged, we change the amplitude of the external disturbances as

$$\begin{aligned} d_{x_{2}}(t)= & {} d_{y_{2}}(t)=( 5+0.8\sin (0.7 t)+0.2\sin (0.5 t)\nonumber \\&+\,0.2\sin (0.9 t) )\times 10^6 \end{aligned}$$
(66)
$$\begin{aligned} d_{z_{2}}(t)= & {} ( 5+0.2\sin (0.5 t) )\times 10^5 \end{aligned}$$
(67)

The amplitudes of boundary disturbances (66) and (67) are \(A_{x2}=A_{y2}=6.2\times 10^6\), \(A_{z2}=5.2\times 10^5\).

The simulation results are shown in Figs. 14, 15 and 16. The control gains are chosen as \(k_{1x}=8\times 10^3\), \(k_{2x}=8\times 10^5\), \(k_{1y}=8\times 10^3\), \(k_{2y}=10^6\), \(k_{1z}=3\times 10^5\) and \(k_{2z}=2\times 10^6\).

From the simulation results, it can be observed that when we increase the amplitudes of the external disturbances, the proposed control can still suppress the vibration of the riser in three directions. In addition, the proposed control laws can also ensure the boundary slopes of the riser \(|x^{\prime }_L|\le C_x\), \(|y^{\prime }_L|\le C_y\) and \(|z^{\prime }_L|\le C_z\). However, the control gains become larger.

In addition, we have investigated the settling time for boundary displacements, i.e., the time required for the response of boundary displacements x(L, t), y(L, t) and z(L, t) to settle within \(5~\%\) of their final values. The results are listed in Table 2.

Table 2 Settling time for different disturbances
Full size table

From Table 2, we can see that the settling time for disturbances (64) and (65) are exactly the same with the settling time for disturbances (62) and (63), illustrating that changing the frequency of the disturbances will not affect the converging speed. However, increasing the amplitudes of the disturbances, all boundary displacements x(L, t), y(L, t) and z(L, t) converge slower.

5 Conclusion

This paper has presented the boundary control design for a flexible marine riser system subjected to the environmental disturbances. With the proposed control, the vibration of the riser has been suppressed and the constraints of the joint angles have been handled. The bounded stability has been proved based on the Lyapunov’s direct method. The numerical simulations have been carried out to illustrate the performance of the controlled system. In this paper, effects of internal flow have been neglected for simplicity. In the future, we will discuss the model analysis and the control design of a flexible riser system with internal flow in three-dimensional space, which includes a more complicated dynamic model. In addition, the input nonlinearities will be under consideration for the riser system.