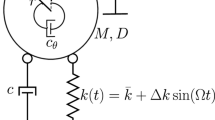Nonlinear energy sink to control vibrations of an internally nonresonant elastic string

Abstract

A nonlinear elastic string is considered here as a main structure to be passively controlled using a Nonlinear Energy Sink (NES). The string is internally nonresonant due to a point mass and an elastic spring applied at a free tip, and a distributed force with harmonic time-law is assumed. The Multiple Scale/Harmonic Balance method, already introduced for finite degree of freedom systems, is extended here in direct approach, being applied to the partial differential equations ruling the dynamics of the system. Amplitude modulation equations are obtained and discussion of some solutions, where the beneficial effect of the NES is evident, are made.

1 Introduction

Nonlinear energy sinks (NES) are strongly nonlinear oscillators attached to a primary structure, used to act as passive control device. An extensive background on characteristics and applications of NES is reported in [23]. Generally, the mass of the attached oscillator is small compared to that of the primary system to be controlled, and the essentially nonlinear stiffness induces one-way mechanical energy transfer from the primary structure to the NES. The nonlinearizable nature of NES makes difficult the application of standard perturbation techniques to systems describing the dynamics of structures where they are attached as control devices. In particular, NES do not have a natural linear frequency and, as a consequence, in principle they turn out to get resonant at any frequencies with the main structure, so that large band tuning with it is involved. Moreover, the best performance of the NES is reached when relaxation oscillations and strongly modulated responses are triggered, which are typical responses of singular perturbation problems, where transitions from slow to fast dynamics, and back, are induced [10].

The use of the NES as passive control devices has received great attention in the literature, and here just some of the large amount of papers dedicated to the topic are cited. In [6], a NES is applied to a main linear oscillator harmonically excited by a 1:1 resonant force. In [22] a NES is applied to harmonically forced two d.o.f. system in internal resonance. In [12] a NES is coupled to a Bouc-Wen type oscillator, while in [24] a NES is used to control the flutter oscillations of a long-span bridge. In [7, 23], NES is used to suppress aeroelastic instabilities on a class of rigid airfoils, modeled as a two d.o.f. section-model, under stationary wind in the quasi-steady hypothesis. In [8, 20] NES are applied to suppress vibrations of continuous beams.

Some drawbacks on the use of NES are reported in the literature too [15, 17]. They are mostly concerned on the possible occurrence of multiple coexisting solutions, which can even thwart the beneficial effects of the NES.

Due to the fact that the equations of NES are nonlinearizable, standard perturbation techniques are not directly applicable. Accordingly, the study of the slow-flow dynamics can be approached by means of the complexification averaging (referred as CX-A) proposed by Manevitch [16] and, only as a further step, the Multiple Scale Method [18].

Regular perturbation theory is used in [2, 3, 5] to deal with various classes of coupled linear and (essentially) nonlinear oscillators, and conditions to trigger energy transfer are found. There, the assumption of working in finite time intervals is always given.

Recently a new perturbation algorithm, based on a merging of Multiple Scale Method and Harmonic Balance (and referred as MSHBM), has been proposed to study multi-d.o.f. dynamical systems equipped with NES, under harmonic external force [13] as well as aero-elastic effects [14]. In [9] the same algorithm is used to study the effect of the NES to control the chatter in the turning process and in [1] to evaluate the attenuation of lateral vibrations of a rotor via NES. The algorithm allows one to skip the initial complexification and, moreover it produces the set of equations in normal form.

On the other hand, out of the context of systems provided with NES, the Multiple Scale Method can be applied in direct approach to continuous structures, where the number of d.o.f. reaches infinite (see e.g. [11, 18, 19, 21]). In those cases both qualitative and quantitative differences are found if the method is, in contrast, applied to a classical low-order Galerkin model.

In this paper the direct form of the MSHBM is presented, being the method extended to cases of infinite number of d.o.f., when internal resonances are not present. In particular a nonlinear taut elastic string, under the action of external harmonic force, and provided with NES is considered here. The string is made internally nonresonant (at least for the first few transverse modes) by applying a supplementary point mass and a linear elastic spring at the tip. A NES is applied at a specific abscissa to act as control device. The continuum dynamical problem is obtained, when the external force is 1:1 resonant with a generic mode of the string. The MSHBM is specialized for that system, being applied to the partial differential equations of motion, in order to analyze the response and provide a tool to optimize the position and the constitutive parameters of the NES. Numerical results are compared to those obtained through direct numerical integration of an approximated system of ordinary differential equations, drawn by means of a multi-mode Galerkin projection of the main partial differential equations.

2 The model

A nonlinear extensible elastic string $AB$ is considered (see Fig. 1). The string is restrained at $A$, while a concentrated mass $m_B$ and a vertical elastic spring of linear stiffness $k_B$ are applied at $B$. In particular, they simulate in a rough way (through a 1 d.o.f. linear oscillator) a flexible branched tower, working as right support of a small sag-to-span electric transmission cable, which in turn is approximated by a taut string. The string is supposed of initial length $\ell$ and prestress tensile force $N$. An external, distributed, harmonically time-dependent, force $p(x)\cos (\Omega t)$ is supposed to be applied to the string ($x$ being the abscissa measured in the prestressed configuration and $t$ the time). The mass per unit length of the string is $\rho$ and its longitudinal stiffness $EA$. A NES characterized by a mass $m$, cubic stiffness coefficient $k$ and linear damping coefficient $c$, is linked to the string at point $C$, corresponding to the abscissa $x_C$. Denoting by $v(x,t)$ the in-plane transverse displacement of a generic point of the string and by $y(t)$ the displacement of the NES, the nonlinear equations of motion, up to the cubic order, read (see [18, 19] for the equations of motion of the string, obtained after the classic condensation procedure of the longitudinal displacement and valid under the hypothesis of large ratio between the celerity of longitudinal vs. transverse waves)

$$\begin{aligned}&{N}v''(x,t)+\frac{EA}{\ell }v''(x,t)\left[ \int _0^{\ell }\!\!\frac{v'^2(x,t)}{2}dx\right] -\rho \ddot{v}(x,t)\\&\quad +p(x)\cos (\varOmega t)-\left[ k(v(x,t)-y(t))^3\right. \\&\quad \left. +c(\dot{v}(x,t)-\dot{y}(t))\right] \delta (x-x_C)=0\\&m\ddot{y}(t)-\left[ k(v(x_C,t)-y(t))^3\right. \\&\quad \left. +c(\dot{v}(x_C,t)-\dot{y}(t))\right] =0 \end{aligned}$$

(1)

where $\delta (x)$ is the Dirac delta, the dot indicates time-derivative and the prime space-derivative.

Fig. 1

String equipped with a NES

The geometric boundary condition at $A$ states that $v(0, t)=0$, while the mechanical boundary condition, to be applied at $B$, reads

$${N}v'(\ell ,t)+\frac{EA}{\ell }v'(\ell ,t)\left[ \int _0^{\ell }\!\!\frac{v'^2(x,t)}{2}dx\right] = -k_B v(\ell ,t)-m_B\ddot{v}(\ell ,t)$$

(2)

which describes the balance of forces at the boundary: the linear geometrical stiffness and the nonlinear elastic one, at the left side of Eq. (2), provide forces which are balanced by inertia and elastic forces of the mass-spring system. Relevant initial conditions must be added too.

Defining nondimensional quantities, namely

$$\begin{aligned}\tilde{x}&=\frac{x}{\ell},\;\tilde{t}=\bar{\omega} t,\; \tilde{y}=\frac{y}{\ell},\; \tilde{v}=\frac{v}{\ell},\;\tilde{u}=\frac{u}{\ell},\;\tilde{x}_C=\frac{x_C}{\ell},\\\tilde{\delta}&=\ell\delta,\;\eta=\frac{EA}{N},\;\kappa=\frac{k\ell^3}{N},\;\xi=\frac{c\bar{\omega}\ell}{N},\;\tilde{m}=\frac{m}{\rho\ell},\\\tilde{p}&=\frac{p\ell}{N},\;\tilde{\Omega}=\frac{\Omega}{\bar{\omega}},\;\tilde{k}_B=\frac{k_B\ell}{N},\;\tilde{m}_B=\frac{\bar{\omega}^2m_B\ell}{N},\;\bar{\omega}=\frac{1}{\ell}\sqrt{\frac{N}{\rho}}\end{aligned}$$

(3)

Eq. (1) become, in nondimensional form (omitting the tilde) and after inclusion of the contribution of linear structural damping ($\zeta \dot{v}(x,t)$, where $\zeta$ is the damping coefficient):

$$\begin{aligned}&\ddot{v}+\zeta \dot{v}-v''-\eta v''\left[ \int _0^{1}\!\!\frac{v'^2}{2}dx\right] +\left[ \kappa (v-y)^3\right. \\&\quad \bigl .+\xi (\dot{v}-\dot{y})\bigr ]\delta (x-x_C)=p\cos (\varOmega t) \\&m\ddot{y}-\left[ \kappa (v_C-y)^3+\xi (\dot{v}_C-\dot{y})\right] =0 \end{aligned}$$

(4)

where $v_C(t){\mathrel{\mathop :}}=v(x_C,t)$, and the boundary conditions

$$\begin{aligned}&v(0,t)=0 \\&v'(1,t)+\eta v'(1,t)\left[ \int _0^{1}\!\!\frac{v'^2}{2}dx\right] \\&\quad= -k_B v(1,t)-m_B \ddot{v}(1,t) \end{aligned}$$

(5)

Now the dot and the prime indicate derivative with respect to the nondimensional time and abscissa, respectively.

It is convenient to introduce the relative displacement function between the main structure at point $C$ and NES: $z(t){\mathrel{\mathop :}}=v(x_C,\,t)-y(t)$. Therefore equations (4) become:

$$\begin{aligned}&\ddot{v}+\zeta \dot{v}-v''-\eta v''\left[ \int _0^{1}\!\!\frac{v'^2}{2}dx\right] \\&\quad +\left[ \kappa z^3+\xi \dot{z}\right] \delta (x-x_C)=p\cos (\varOmega t) \\&m(\ddot{z} -\ddot{v}_C)+\kappa z ^3+\xi \dot{z} =0 \end{aligned}$$

(6)

3 The multiple scale/harmonic balance method

The dependent variables are rescaled through a nondimensional small parameter $\epsilon$ such that $0<\epsilon \ll 1$, as $(v,z){\mathrel{\mathop :}}=\epsilon ^{1/2}( \tilde{v},\tilde{z})$, consistently with the presence of cubic nonlinearity. The damping is rescaled as $\zeta =\epsilon \tilde{\zeta }$ and the external force as $p=\epsilon ^{3/2}\tilde{p}$, consistently with the idea to order both damping and excitation at the same level of the nonlinearity. It is assumed that the external excitation is 1:1 resonant with one of the linear modes (the $j$-th mode of frequency $\omega_j$) of the string (with NES disengaged), and no other resonance combinations are possible. A detuning parameter $\sigma$ is therefore introduced for the external excitation, as $\Omega=\omega_j+\sigma$; it is rescaled as $\sigma =\epsilon \tilde{\sigma }$. The parameters of the NES are rescaled too, since both its mass and damping are assumed small: $(m,\xi ){\mathrel{\mathop :}}=\epsilon ( \tilde{m},\tilde{\xi })$. The rescaling leads to the following equations, after omission of tilde and division by $\epsilon ^{1/2}$:

$$\begin{aligned}&\ddot{v}-v''+\epsilon \biggl [\zeta \dot{v}-\eta v''\left[ \int _0^{1}\!\!\frac{v'^2}{2}dx\right] \\&\quad +\left[ \kappa z^3+\xi \dot{z}\right] \delta (x-x_C)-p\cos (\varOmega t)\biggr ]=0 \\&\epsilon \left[ m(\ddot{z} -\ddot{v}_C)+\kappa z ^3+\xi \dot{z} \right] =0 \end{aligned}$$

(7)

with boundary conditions:

$$\begin{aligned}&v(0,t)=0 \\&v'(1,t)+k_B v(1,t)+m_B \ddot{v}(1,t) \\&\quad +\epsilon \eta v'(1,t)\left[ \int _0^{1}\!\!\frac{v'^2}{2}dx\right] =0 \end{aligned}$$

(8)

According to the Multiple Scale Method, independent time scales $t_0:=t, t_1:=\epsilon t, t_2=\epsilon ^2t,\ldots$ are introduced and, consistently, the time derivatives expressed as $\frac{\partial }{\partial t}=d_0+\epsilon d_1+\epsilon ^2 d_2+\ldots$ and $\frac{\partial ^2}{\partial t^2}=d_0^2+2\epsilon d_0 d_1+\epsilon ^2(d_1^2+2d_0d_1)+\ldots$, where $d_j{\mathrel{\mathop :}}=\partial /\partial t_j$, for $j=0,1,2,\ldots$. Moreover, the dependent variables are expanded in series as:

$$\begin{aligned} \left\{\begin{matrix} v \\ z \end{matrix}\right\}=\left\{\begin{matrix} v_0\\ z_0 \end{matrix}\right\}+\epsilon \left\{\begin{matrix} v_1\\ z_1 \end{matrix}\right\}+\epsilon^2\left\{\begin{matrix} v_2\\ z_2 \end{matrix}\right\}+\ldots \end{aligned}$$

(9)

Substituting in Eqs. (7) and (8) and collecting terms of the same order in $\epsilon$, lead to the following perturbation equations:

$$\begin{aligned} order\;\epsilon ^0: \\ d_0^2&v_0-v''_0=0\end{aligned}$$

(10)

$$\begin{aligned} order\;\epsilon ^1: \\ d_0^2v_1-v''_1=-2 d_0d_1v_0-\zeta d_0v_0+p\cos (\varOmega t_0) \\&-(\xi d_0z_0+\kappa z_0^3)\delta (x-x_C)+\eta v_0''\left[ \int _0^{1}\!\!\frac{v_0'^2}{2}dx\right] \end{aligned}$$

(11)

$$\begin{aligned} m&(d_0^2z_{0}-d_0^2v_{C_0})+\xi d_0 z_{0} +\kappa z_{0}^3 =0\end{aligned}$$

(12)

$$\begin{aligned} order\;\epsilon ^2: \\ d_0^2v_2-v''_2=- (d_1^2v_0+2 d_0d_2v_0+2d_0d_1v_1) \\&-\zeta (d_2v_0+d_1v_1)-\left[ \xi (d_0z_1+d_1z_0)\right. \\&\left. +3\kappa z_0^2z_1\right] \delta (x-x_C)+\eta v_1''\left[ \int _0^{1}\!\!\frac{v_0'^2}{2}dx\right] \\&+\eta v_0''\left[ \int _0^{1}\!\!v'_0v_1'dx\right] \end{aligned}$$

(13)

$$\begin{aligned} m(&d_0^2 z_{1}-d_0^2v_{C_1})+\xi d_0 z_{1} +3\kappa z_{0}^2z_{1}= \\&-2m(d_0d_1z_{0}-d_0d_1v_{C_0})-\xi d_1z_{0} \end{aligned}$$

(14)

and relevant boundary conditions:

$$\begin{aligned} order\;\epsilon ^0: \\ v_0&(0,t_0,t_1,\ldots )=0, \\ v_0'&(1,t_0,t_1,\ldots )+k_B v_0(1,t_0,t_1,\ldots ) \\&+m_B d_0^2v_0(1,t_0,t_1,\ldots )=0\end{aligned}$$

(15)

$$\begin{aligned} order\;\epsilon ^1: \\ v_1&(0,t_0,t_1,\ldots )=0, \\ v_1'&(1,t_0,t_1,\ldots )+k_B v_1(1,t_0,t_1,\ldots ) \\&+m_B d_0^2v_1(1,t_0,t_1,\ldots )= \\&-\eta v_0'(1,t_0,t_1,\ldots )\left[ \int _0^{1}\!\!\frac{v_0'^2}{2}dx\right] \\&-2m_Bd_0d_1v_0(1,t_0,t_1,\ldots )\end{aligned}$$

(16)

$$\begin{aligned} order\;\epsilon ^2: \\ v_2&(0,t_0,t_1,\ldots )=0, \\ v_2'&(1,t_0,t_1,\ldots )+k_B v_2(1,t_0,t_1,\ldots ) \\&+m_B d_0^2v_2(1,t_0,t_1,\ldots )= \\&-\eta v_1'(1,t_0,t_1,\ldots )\left[ \int _0^{1}\!\!\frac{v_0'^2}{2}dx\right] \\&-\eta v_0'(1,t_0,t_1,\ldots )\left[ \int _0^{1}\!\!v_0'v_1'dx\right] \\&-m_B(d_1^2v_0(1,t_0,t_1,\ldots )+2d_0d_2v_0(1,t_0,t_1,\ldots ) \\&+2d_0d_1v_1(1,t_0,t_1,\ldots )) \end{aligned}$$

(17)

The small values of mass and damping of the NES, as well as the lack of its linear stiffness, cause that no equation relevant to the NES appears at order $\epsilon ^0$, where just the linearized problem of the string (with NES disengaged) is obtained. Moreover, as a consequence of both the 1:1 external resonance with one of the linear modes of the string, and the presence of damping, all the other (nonresonant) modes cause a higher-order contribution to the response. In this respect, the contribution of the resonant mode is retained only, so that the (generating) solution of Eqs. (10),(15) is:

$$\begin{aligned} v_0(x,t_0,t_1,\ldots )= A(t_1,\ldots )\varphi (x) e^{i\omega t_0} +cc \end{aligned}$$

(18)

where: $A(t_1,\ldots )$ is a complex modal amplitude to be evaluated, depending on the slower time-scales; $i$ is the imaginary unit; $\omega\mathrel{\mathop :}=\omega_j$ and $\varphi(x)\mathrel{\mathop :}=\varphi_j(x)$ are the ($j$-th) resonant eigenvalue and (real) eigenfunction of the problem with NES disengaged; $cc$ stands for complex conjugate. In particular, the natural frequency $\omega$ is the $j$-th root of the characteristic equation

$$\begin{aligned} \tan \omega =\frac{\omega }{\omega ^2 m_B-k_B} \end{aligned}$$

(19)

and the relevant eigenfunction is $\varphi (x)=\sin (\omega x)$.

When passing to the $\epsilon$ order, the NES equation (12) is first considered, and the Harmonic Balance method [18] is applied after supposing the solution as:

$$\begin{aligned} z_0(t_0,t_1,\ldots )= \sum _{k=1}^{+\infty }B_{0_k}(t_1,\ldots )e^{i k \omega t_0} +cc \end{aligned}$$

(20)

where $B_{0_k}(t_1,\ldots )$ are complex amplitudes depending on slow time, to be evaluated. After substitution of Eq. (18) and (20) in Eq. (12) and balance of frequency $\omega$ (other frequencies are neglected, as well as just $B_0{\mathop{\mathrel :}}=B_{0_k}$ is retained, coherently with [13]), the following algebraic equation is obtained:

$$\begin{aligned} -m\omega ^2(B_0- A\varphi (x_c))+i\xi \omega B_0+3\kappa B_0^2\bar{B}_0=0 \end{aligned}$$

(21)

describing the manifold which constrains the steady value of the string amplitude of oscillation to that of the NES (the overbar here stands for complex conjugate). In fact, if a polar transformation is introduced for both $A$ and $B_0$ (namely $A{\mathrel{\mathop :}}=\frac{1}{2}ae^{i\alpha }$ and $B_0{\mathrel{\mathop :}}=\frac{1}{2}be^{i\beta }$), manipulations on Eq. (21) give the equation for the manifold:

$$\begin{aligned} m^2\omega ^4 \varphi (x_c)^2 a^2=(m\omega ^2 b-\frac{3}{4}\kappa b^3)^2+\xi ^2\omega ^2 b^2 \end{aligned}$$

(22)

To catch the dynamics out of manifold (22), Eqs. (11), (16) must be tackled. In particular, the solution of Eq. (11) is sought in the form

$$\begin{aligned} v_1(x,t_1,t_2)=\psi _1(x,t_1,t_2)e^{i\omega t_0}+\psi _3(x,t_1,t_2)e^{3i\omega t_0}+cc \end{aligned}$$

(23)

where $\psi _1(x,t_1,t_2),\psi _3(x,t_1,t_2)$ are complex functions to be determined. This expression for $v_1$ in Eq. (23) is suggested by the presence of cubic nonlinear terms in Eq. (11). Then Eq. (23) is substituted in Eqs. (11) and (16), and terms multiplying $\exp (i\omega t_0)$ and $\exp (3i\omega t_0)$ are mutually separated, giving two ordinary differential equations with relevant boundary conditions, respectively. The first one is:

$$\begin{aligned} \psi _1''+\omega ^2\psi _1=-f_1(x,t_1,t_2) \end{aligned}$$

(24)

with boundary conditions

$$\begin{aligned}&\psi _1(0,t_1,t_2)=0 \\&-\psi '_1(1,t_1,t_2)-(k_B-\omega ^2m_B)\psi _1(1,t_1,t_2)= \\&\quad 2i m_B\omega \varphi (1)d_1A+3\eta \nu \varphi '(1)A^2\bar{A} \end{aligned}$$

(25)

where

$$\begin{aligned}&f_1(x,t_1,t_2){\mathrel{\mathop :}}=-2i\omega \varphi (x) d_1A \\&\quad -i\zeta \omega \varphi (x) A-(i\omega \xi B_0+3\kappa B_0^2\bar{B}_0)\delta (x-x_C) \\&\quad +3\eta \nu \varphi ''(x)A^2\bar{A}+\frac{p(x)}{2}e^{i\sigma t_1} \end{aligned}$$

(26)

and $\nu =\int _0^1\!\!\varphi '(x)^2dx/2=(\omega +\sin \omega \cos \omega )\omega /4$.

The second one is:

$$\begin{aligned} \psi _3''+9\omega ^2\psi _3=-f_3(x,t_1,t_2) \end{aligned}$$

(27)

with boundary conditions

$$\begin{aligned}&\psi _3(0,t_1,t_2)=0 \\&-\psi '_3(1,t_1,t_2)-(k_B-9\omega ^2m_B)\psi _3(1,t_1,t_2)= \\&\quad \eta \nu \varphi '(1)A^3 \end{aligned}$$

(28)

where

$$\begin{aligned} f_3(x,t_1,t_2){\mathrel{\mathop :}}=-\kappa B_0^3 \delta (x-x_c)+\eta \nu \varphi ''(x)A^3 \end{aligned}$$

(29)

In order to get a solution from Eqs. (24),(25), the solvability condition must be enforced on them, which reads:

$$\begin{aligned}&-\int _0^1\!\!f_1(x,t_1,t_2)\varphi (x)dx \\&\qquad +2i m_B\omega \varphi (1)^2d_1A+2\eta \nu \varphi '(1)\varphi (1)A^2\bar{A}=0 \end{aligned}$$

(30)

Substitution of Eq. (26) in Eq. (30) provides:

$$\begin{aligned} d_1A= c_1 A+c_2 B_0+ic_3 B_0^2\bar{B}_0+ic_4 A_1^2\bar{A}_1+ i c_5 p_j e^{i\sigma t_1} \end{aligned}$$

(31)

where $p_j=\int _0^1\!\!p(x)\varphi (x)dx$ and the expressions of the coefficients $c_j$ are given in Appendix 1. The substitution of Eq. (31) in Eq. (24) and (25) allows one to obtain a solution for this system (see details in Appendix 2), which reads:

$$\begin{aligned} \psi _1(x,t_1,t_2)&= iAw_1(x)+iB_0w_2(x)+B_0^2\bar{B}_0w_3(x) \\&\quad +A^2\bar{A}w_4(x)+ w_5(x)e^{i\sigma t_1} \end{aligned}$$

(32)

In Eq. (32) the normalization condition consisting in a vanishing amplitude for the complementary solution is assumed.

On the other hand, system (27),(28) is not singular and admits the following solution:

$$\begin{aligned} \psi _3(x,t_1,t_2)&= \varGamma (t_1,t_2)\sin (3\omega x) \\&\quad +B_0^3w_6(x)+A^3w_7(x) \end{aligned}$$

(33)

where $w_k(x), (k=1,\ldots ,7)$ and $\varGamma (t_1,t_2)$ are defined in Appendix 1.

Equation (14) is considered and a further harmonic balance is applied to it, assuming the following expression for $z_1$:

$$\begin{aligned} z_1(t_0,t_1,\ldots )= \sum _{k=1}^{+\infty }B_{1_k }(t_1,\ldots )e^{i k \omega t_0} +cc \end{aligned}$$

(34)

Retaining only the first term $(B_1{\mathop{\mathrel :}}=B_{1_k})$, substituting Eqs. (18), (20) and (23) in Eq. (14) and balancing the $\omega$-frequency terms, the following equation is obtained:

$$\begin{aligned}&-m\omega ^2 B_1+i\xi \omega B_1+3\kappa B_0^2\bar{B}_1+6\kappa B_0\bar{B}_0B_1 \\&\qquad +(\xi +2im\omega )d_1B_0 -2im\omega \varphi (x_C) d_1A \\&\qquad +m\omega ^2(iA w_{C_1}+iB_0w_{C_2}+B_0^2\bar{B}_0w_{C_3} \\&\qquad +A^2\bar{A}w_{C_4})+m\omega ^2w_{C_5}e^{i\sigma t_1}=0 \end{aligned}$$

(35)

where $w_{C_k}{\mathop{\mathrel :}}=w_k(x_C), k=1,\ldots ,5$. Equations (21) and (35) can be reconstituted, using the definition $B{\mathrel{\mathop :}}= B_0+\epsilon B_1$: coming back to the true time and reabsorbing $\epsilon$ one obtains:

$$\begin{aligned}&(\xi +2im\omega )\dot{B}-2im\omega \varphi (x_C) \dot{A}=(m\omega ^2(1-iw_{C_2}) \\&\quad -i\xi \omega )B-(3\kappa +m\omega ^2w_{C_3}) B^2\bar{B} -m\omega ^2 (\varphi (x_C) \\&\quad +iw_{C_1})A-m\omega ^2w_{C_4}A^2\bar{A}-m\omega ^2w_{C_5}e^{i\sigma t} \end{aligned}$$

(36)

Equation (36) describes the dynamics of the amplitude $B$, allowing to both the variables $A$ and $B$ to evolve out of the manifold described by Eq. (21). The derivatives of $B$ and $A$ have been obtained just at the second-order, being multiplied by small coefficients $\xi$ and $m$, which cause singular perturbation.

In a similar way, Eq. (31) can be written in the true time, becoming:

$$\begin{aligned} \dot{A}=c_1 A+c_2 B+ic_3 B^2\bar{B}+ic_4 A^2\bar{A}+ i c_5 p_j e^{i\sigma t} \end{aligned}$$

(37)

Eqs. (37) and (36) are the complex Amplitude modulation equations (AME) ruling the slow dynamics of the string and NES. They can be written in real form after applying the polar transformation $A(t){\mathrel{\mathop :}}=\frac{1}{2}a(t)e^{i\alpha (t)}$ and $B(t){\mathrel{\mathop :}}=\frac{1}{2}b(t)e^{i\beta(t)}$, separating real and imaginary parts, defining phase differences as $\gamma (t){\mathrel{\mathop :}}=\alpha (t)-\beta (t)$ and $\vartheta (t){\mathrel{\mathop :}}=\alpha (t)-\sigma t$, and combining the obtained equations. They read

$$\begin{aligned} \dot{a}&= {{\mathcal{F}}_1(a,b,\gamma ,\vartheta)} \\ \dot{b}&= {{\mathcal{F}}_2(a,b,\gamma ,\vartheta )} \\ \dot{\gamma }&= {{\mathcal{F}}_3(a,b,\gamma ,\vartheta )} \\ \dot{\vartheta }&= {{\mathcal{F}}_4(a,b,\gamma ,\vartheta)}\end{aligned} $$

(38)

valid for $a\neq 0$ and $b\neq 0,$where the nonlinear functions ${{\mathcal{F}}_k}$ ($k=1,\ldots ,4$) are not reported for brevity.

Equilibrium points of system (38), which correspond to periodic motions of both the string and NES, can be computed by solving it for $\dot{a}=\dot{b}=\dot{\gamma }=\dot{\vartheta }=0$. Their stability is analyzed evaluating the eigenvalues of the relevant Jacobian matrix; moreover the stability of periodic solutions of Eq. (38), which correspond to quasi-periodic motions of the string and NES, is evaluated by analysis of the Floquet multipliers of the monodromy matrix. In the following section, all those computations are carried out by means of the softwares Auto [4] and Mathematica [25].

4 Numerical results

Numerical results are obtained for a case-study, which corresponds to a string whose nonlinear coefficient is $\eta =2.825$; moreover $m_B=0.3167$ and $k_B=3.9\times 10^{-3}$ are assumed for the tip mass and spring, respectively. The external force is considered as uniform $(p(x)\equiv p)$ and the damping coefficient of the string is $\zeta =1.557\%$. The nondimensional parameters of the NES are $m=0.05, \kappa =400, \xi =0.01$.

First, the two members of the characteristic equation (19) are plotted in Fig. 2a, where the intersections of the two graphs (blue and magenta lines), denoted by the red dots, represent the roots of the equation; in particular, the first four roots are $\omega _1=1.208, \omega _2=3.831, \omega _3=6.722 , \omega _4=9.738$. The relevant eigenfunctions are shown in Fig. 2b.

Fig. 2

Natural frequencies and modes: (a) Plot of the two members of the characteristic equation (19) (left member: blue line; right member: magenta line) and highlighting of the natural frequencies (red points); (b) natural modes corresponding to the first (blue), second (magenta), third (brown) and fourth (green) eigenvalues

If not differently stated, from now on the external force is assumed to be resonant to the second mode, therefore $\omega {\mathrel{\mathop :}}=\omega _2$ and $\varphi (x){\mathrel{\mathop :}}=\varphi _2(x)$.

It is interesting to look at the invariant manifold (22) if the position of the NES is changed along the span of string: when it is attached to the abscissa corresponding to the mode antinode (red point in Fig. 3a), it is expected that the maximum amount of energy transfer is obtained, whereas if it is applied to the tip (blue point in Fig. 3a) or, worse, close to the mode node (black point in Fig. 3a), less energy transfer is predicted. In fact the corresponding invariant manifolds, shown in Fig. 3b, denote that for fixed NES oscillation amplitude $b$, smaller string oscillations $a$ are involved when the NES is placed at the antinode (red line) than at tip (blue line) or close to the node (black line), where the contribution of the NES is very low.

Fig. 3

Position of the NES on the span and second mode (a); corresponding invariant manifolds (b)

Amplitude of periodic motions of both the string and NES, for force amplitude value $p=0.007$, are shown in Fig. 4 in terms of frequency detuning $\sigma$. In particular, in Fig. 4a, the frequency-response curve obtained for disengaged NES (black curve) is superimposed to the corresponding curve obtained when NES is engaged (red line). In Fig. 4b, the amplitude of oscillation $b$ of the NES is shown. Blue points represent Hopf bifurcations. It is evident the beneficial effect of the NES, whose presence reduces the peak of the string amplitude of oscillations $a$.

Fig. 4

Frequency-response curves of the string (a) and NES (b), for $p=0.007$. Red line: response with NES at the antinode; black line response with NES disengaged. Blue points indicate Hopf bifurcations. Continuous line stable; dashed line unstable

In Fig. 5, the periodic time-evolutions of the vertical displacement of the mid-span of the string ($v_m{\mathrel{\mathop :}}=v(1/2,t)$) and of the NES ($z(t)$) are shown for $\sigma =0.02$, with NES at the antinode. They are superimposed to the corresponding evolutions (dotted line) obtained by time-integration of an approximated system of ODE, which is drawn after a Galerkin projection of Eqs. (6),(5) on a basis constituted by the eight first natural modes of the string. They show a very good agreement.

In Fig. 6, a more detailed zoom of Fig. 4 is shown, where the branches of periodic motions in $a$ and $b$ arising from the Hopf bifurcation points are highlighted. In particular, from the left Hopf bifurcation point, occurring at about $\sigma =0.05$, a stable branch of periodic motions in $a$ and $b$ arises, giving rise to weakly modulation responses (WMR, which correspond to quasi-periodic oscillations of string and NES). Filled regions describe amplitude of the corresponding limit cycles, and blue lines indicate the maximum and minimum of the oscillations. The branch suddenly becomes unstable (lightly filled regions), and Strongly Modulated Responses are induced after a cascade of Period Doubling bifurcations (not shown in the Figure). Then, after a fold, the branch dies on the right Hopf bifurcation point, at about $\sigma =0.127$.

Fig. 5

Periodic time-evolution of the string mid-span (a) and NES (b), for $p=0.007$ and $\sigma =0.02$. Continuous line reconstituted functions from MSHBM; dotted line reconstituted functions from a discrete Galerkin model

In Fig. 7a and 7b, the WMR (for $\sigma =0.064$) and SMR (for $\sigma =0.070$) are superimposed to the invariant manifold, respectively. The first one develops itself close to the fold of the invariant manifold, while the second one describes relaxation oscillations around it. In Fig. 8, the time-evolutions of both $a$ and $b$ are shown for the same SMR. For the same case, the time-evolutions of the vertical displacement of the mid-span of the string and of the NES are shown in Fig. 9a and 9b, respectively, compared to the corresponding response provided by direct integration of the Galerkin model (Fig. 9c and 9d), still showing good agreement. As said, they describe relaxation oscillations, which are one of the typical features of singular perturbed systems. Moreover, those (quasi-periodic) oscillations are found to be, for any value of $\sigma$, significantly smaller than the (periodic) oscillations experienced by the string without NES, proving the beneficial effect of the NES.

As a further analysis, the effect of the same NES engaged at the same position is verified in case of external force which is resonant to the first mode. It is worth noticing that, in this case, the position of the NES is not optimized, since it is not applied in correspondence of the antinode of the mode (see Fig. 3). This analysis is performed for the external force amplitude $p=0.0005$. The corresponding frequency-response curves are shown in Fig. 10, where the black line is relevant to the string without NES, while the red line to the system with NES engaged. The significant reduction of the resonance peak is evident. Moreover, Hopf bifurcations (blue points in Fig. 10), as well as SMR, are obtained too. In particular, the SMR are shown in Fig. 11 (black line) for $\sigma =0$, superimposed to the invariant manifold (red line), and in Fig. 12 versus time. The corresponding displacement of the mid-span of the string and of the NES are shown in Fig. 13a,b, respectively, in good agreement with those obtained with integration of the discrete Galerkin system (Fig. 13c,d). Still in this case the quasi-periodic evolution of $v_m$ shows amplitudes which are significantly smaller than those experienced without NES. Therefore, it is worth pointing out that the beneficial effect is proved in this case too, except perhaps for a very narrow region of frequencies at the left of the first resonance peak $(\sigma \in [-0.012,-0.011])$, where some SMR can lightly overtake the periodic motion of the system without NES, for the same frequency. On the other hand, the remarkable lowering of the resonance peak can generally overcome this drawback. Different behavior can be obtained for larger values of $p$, where sometimes the NES may induce oscillations which can be significantly larger than those experienced without it.

Fig. 6

Detail of the frequency-response function with NES at the antinode (red line), for $p=0.007$. Blue points indicate Hopf bifurcations; blue line and filled region indicate limit cycles in $a$ and $b$. Continuous line stable; dashed line unstable

Fig. 7

Weakly Modulated Response ($\sigma =0.064$, blue line (a)) and Strongly Modulated Response ($\sigma =0.070$, black line (b)) with NES at the antinode, for $p=0.007$; red line invariant manifold. Continuous line stable; dashed line unstable

Fig. 8

Time evolutions of the Strongly Modulated Responses for $p=0.007$ and $\sigma =0.070$: (a) string oscillation amplitude $a$; (b) NES oscillation amplitude $b$

Fig. 9

Quasi-periodic time-evolution of the string mid-span and NES displacement, for $p=0.007$ and $\sigma =0.02$. String mid-span (a) and NES displacement (b) as reconstituted from MSHBM; string mid-span (c) and NES displacement (d) as reconstituted from the discrete Galerkin model

Fig. 10

Frequency-response curves of the string (a) and NES (b), when the force is resonant to the first mode, for $p=0.0005$. Red line: response with NES engaged; black line response with NES disengaged. Blue points indicate Hopf bifurcations. Continuous line stable; dashed line unstable

Fig. 11

Strongly Modulated Response for $\sigma =0$ for $p=0.0005$ resonant to the first mode; red line: invariant manifold. Continuous line stable; dashed line unstable

Fig. 12

Time evolutions of the Strongly Modulated Responses for $p=0.0005$ and $\sigma =0$, resonant to the first mode: (a) string oscillation amplitude $a$; (b) NES oscillation amplitude $b$

Fig. 13

Quasi-periodic time-evolution of the string mid-span and NES displacement, for $p = 0.0005$ and $\sigma =0$ resonant to the first mode. String mid-span (a) and NES displacement (b) as reconstituted from MSHBM; string mid-span (c) and NES displacement (d) as reconstituted from the discrete Galerkin model

5 Conclusions

The Multiple Scale/Harmonic Balance Method (MSHBM) is a perturbation method suitable to determine the equations which rule the slow/fast dynamics of systems provided with Nonlinear Energy Sink as control device. Here the MSHBM has been applied in direct form to an infinite dimensional structure, constituted by an internally nonresonant string excited by a 1:1 resonant harmonic force, with NES applied. The relevant AME have been obtained and their singular perturbation nature has been observed, due to the small mass and damping of the NES.

Numerical results have been shown in terms of invariant manifold, frequency-response plots as well as time-series, for periodic, Weakly and Strongly Modulated Responses. They denote the beneficial effect of the same NES to reduce the amplitude of oscillation of the string, once external force has moderate amplitude and it is resonant to the second or first mode. Results are in good agreement with those provided by a discrete, approximated, system of ordinary differential equations obtained by means of a Galerkin projection of the infinite dimensional problem.

Appendices

Coefficients of the equations

The expression of the coefficients of Eq. (31) are:

$$\begin{aligned} c&= \int _0^1\!\!\varphi (x)^2dx+m_B\varphi (1)^2,\; c_1=-\frac{\zeta }{2c}\int _0^1\!\!\varphi (x)^2dx, \\ c_2&= -\frac{\xi }{2c}\varphi (x_C),\;c_3=\frac{3\kappa }{2\omega c}\varphi (x_C),\; c_5=-\frac{1}{4\omega c}, \\ c_4&= -\frac{3\eta \nu }{2\omega c}\left[ \int _0^1\!\!\varphi ''(x)\varphi (x)dx-\varphi '(1)\varphi (1)\right] \end{aligned}$$

(39)

In order to write the expressions of the coefficients of Eq. (32) and (33), first the following definitions are introduced:

$$\begin{aligned} I_1(x,x_C)&= \frac{1}{\omega }\sin (\omega (x-x_C))H(x-x_C) \\ J_1(x)&= \frac{1}{\omega }\int _0^x\!\!\varphi (s)\sin (\omega (x-s))ds \\&= \frac{1}{2\omega ^2}(\sin (\omega x)-\omega x \cos (\omega x)) \\ P(x)&= \frac{1}{\omega }\int _0^x\!\!p(s)\sin (\omega (x-s))ds \\ I_3(x,x_C)&= \frac{1}{3\omega }\sin (3\omega (x-x_C))H(x-x_C) \\ J_3(x)&= \frac{1}{3\omega }\int _0^x\!\!\varphi (s)\sin (3\omega (x-s))ds=\frac{\sin (\omega x)^3}{6\omega ^2} \end{aligned}$$

(40)

where $H(x)$ is the Heaviside step (here the Dirac delta and Heaviside step are considered in the sense of distributions). In particular, the expressions of $I_1(x, x_C)$ and $I_3(x, x_C)$ are obtained as solution of the linear ordinary differential equations

$$\begin{aligned} y''(x)+\omega ^2y(x)=\delta (x-x_C) \end{aligned}$$

(41)

and

$$\begin{aligned} y''(x)+9\omega ^2y(x)=\delta (x-x_C) \end{aligned}$$

(42)

to vanishing initial conditions, respectively. Then the following expressions are obtained:

$$\begin{aligned} w_1(x)&= (\zeta \omega +2\omega c_1)J_1(x) \\ w_2(x)&= 2\omega c_2J_1(x)+\xi \omega I_1(x, x_c) \\ w_3(x)&= -2\omega c_3J_1(x)+3\kappa I_1(x,x_c) \\ w_4(x)&= (3\eta \nu \omega ^2-2\omega c_4)J_1(x) \\ w_5(x)&= -\frac{1}{2}P(x)-2\omega c_5 p_jJ_1(x) \\ w_6(x)&= \kappa I_3(x,x_c) \\ w_7(x)&= -\eta \nu \omega ^2J_3(x) \end{aligned}$$

(43)

and

$$\begin{aligned}&\varGamma (t_1,t_2)=-\frac{1}{3\omega \cos (3\omega )+(k_B-9\omega ^2 m_B)\sin (3\omega )} \\&\quad [(w_6'(1)+(k_B-9\omega ^2 m_B)w_6(1))B_0^3 \\&\quad +(w_7'(1)+(k_B-9\omega ^2 m_B)w_7(1)+\eta \nu \varphi '(1))A^3] \end{aligned}$$

(44)

Details on the solution of Eq. (24)

After the application of the solvability condition (31) on the boundary value problem (24),(25), it becomes

$$\begin{aligned}&\psi _1''+\omega ^2\psi _1=i\omega (\zeta +2 c_1)\varphi (x)A+i\omega (\xi \delta (x-x_C) \\&\quad +2c_2\varphi (x))B_0+(3\kappa \delta (x-x_C)+2\omega c_3\varphi (x))B_0^2\bar{B}_0 \\&\quad -(3\eta \nu \varphi ''(x)+2\omega c_4\varphi (x))A^2\bar{A} \\&\quad -(p(x)/2+2\omega p_j c_5\varphi (x))e^{i\omega t_1} \end{aligned}$$

(45)

with boundary conditions

$$\begin{aligned}&\psi _1(0)=0 \\&-\psi _1'(1)-(k_B-\omega ^2 m_B)\psi _1(1)=2m_bi\omega c_1\varphi (1)A \\&-(3\eta \nu \varphi '(1)-2m_B\omega c_4\varphi (1))A^2\bar{A} \\&+2m_Bi\omega c_2\varphi (1)B_0-2m_B\omega c_3\varphi (1)B_0^2\bar{B}_0 \\&-2m_B\omega c_5\varphi (1) p_j e^{i\sigma t_1} \end{aligned}$$

(46)

The solution of Eq. (45) is

$$\begin{aligned} \psi _1(x,t_1,t_2)&= \Lambda _1(t_1,t_2)\cos (\omega x)+\Lambda _2(t_1,t_2)\sin (\omega x) \\&\quad +iAw_1(x)+iB_0w_2(x)+B_0^2\bar{B}_0w_3(x) \\&\quad +A^2\bar{A}w_4(x)+ w_5(x)e^{i\sigma t_1} \end{aligned}$$

(47)

where $w_k(x)$ ($k=1,\ldots ,5$) are given in Eq. (43) whereas the coefficients $\Lambda _{1,2}$ of the complementary solution are undetermined so far; they should be evaluated by means of the boundary conditions (46), which however lead to the following singular algebraic system in the variables $\Lambda _{1,2}$:

$$\left[\begin{array}{ll} 1 & 0 \\ 1 & 0 \end{array}\right]\left(\begin{array}{l} \Lambda _1\\ \Lambda _2 \end{array}\right)= \left(\begin{array}{l} 0\\ 0 \end{array}\right)$$

(48)

the solution of which can be taken as $\Lambda _{1,2}=0$ (after having imposed a normalization condition).