Intermittent synchronization of reaction–diffusion neural networks with mixed delays via Razumikhin technique

Abstract

This paper revisits the exponential synchronization problem of two identical reaction–diffusion neural networks with Dirichlet boundary conditions and mixed delays via periodically intermittent control. The focus is on developing a new Lyapunov–Razumikhin method such that the overdesign that stems from the existing Lyapunov functional method can be reduced. The novelty of the proposed Lyapunov–Razumikhin method is the ability to provide better estimates on the state variables of the synchronization error system and impose no restriction on delay derivatives. By exploring the reaction–diffusion effect using the extended Wirtinger’s inequality, an improved result on intermittent synchronization is derived. The problem of designing optimal intermittent synchronization controllers is addressed, and an easily computable method to determine the controller gain with minimal norm is presented. Finally, two illustrative examples are presented to show the validity of the obtained results and the superiority over the existing ones.

1 Introduction

Nowadays, artificial neural networks are being widely applied to a lot of fields, such as image analysis, signal processing, pattern recognition, associative memory, optimization, cryptography, and model identification. These applications rely crucially on the dynamical properties of the designed neural networks. For this reason, the study of dynamical properties of neural networks has attracted much interest. Most previous studies have largely concentrated on the neural networks modeled by ordinary differential equations (ODEs) [1–5] in which the neurons are assumed to be evenly distributed. These ODE models ignore both the spatial detail and the diffusing behavior observed in natural and artificial neural networks. In fact, in implementation of neural networks, the electrons transportation through a nonuniform electromagnetic field generally produces the diffusion phenomena. Therefore, it is necessary to introduce the reaction–diffusion terms in neural network models for achieving good approximation of the spatiotemporal actions and interactions of real-world neurons. The reaction–diffusion neural networks can be modeled by partial differential equations (PDEs) of diffusion type. It is worth mentioning that the PDEs describing the reaction–diffusion neural networks cause some difficulties, since both existence and qualitative properties of the solutions are more difficult to be established. In recent years, the problems of stability, periodicity, and Hopf bifurcation for reaction–diffusion neural networks have been addressed, and several important results have been reported, see [6–12] and the references therein.

On the other hand, a large attention has been taken to the research on collective behaviors of coupled oscillators. A review about collective behaviors of coupled neurons and pattern transition can be found in [13]. In [14], the emergence of emitting wave induced by autapse (in electrical type) with negative feedback was investigated. In [15], collision between emitting waves from different local areas driven by electric autapses under different time delays was observed. As the major collective behavior, synchronization of coupled oscillators has been observed in physical, biological, and social systems. In particular, synchronization of chaotic dynamics has attracted significant research interest during the last decades due to its important role in understanding the synchronization mechanism of coupled nonlinear systems [16, 17] and its potential applications in various engineering fields [18, 19]. In [20], a general method for synchronizing coupled PDEs with spatiotemporal chaotic dynamics was described. Meanwhile, several control strategies have been proposed to synchronize coupled reaction–diffusion neural networks. In [21–23], complete synchronization of coupled delayed reaction–diffusion neural networks was studied, in which continuous linear state-feedback control was suggested. In [24, 25], adaptive control was used to synchronize the coupled reaction–diffusion neural networks with delays. In [26], the synchronization problem for reaction–diffusion neural networks was investigated under the stochastic sampled-data control.

Recently, the discontinuous feedback synchronization schemes, including impulsive synchronization [27–29] and intermittent synchronization [30–32], have been applied to synchronization problem of coupled reaction–diffusion neural networks. Compared with continuous feedback synchronization, these discontinuous feedback synchronization schemes can efficiently reduce bandwidth usage due to the decreased amount of synchronization information transmitted from the drive system to the response system, so they are practical and effective in many areas, especially for secure communications systems. Note that in the impulsive synchronization framework, the updates given to the state of the response system are performed in instantaneous fashion. But with intermittent synchronization, the response system is kept in update mode for nonzero time intervals. So, intermittent synchronization fills the gap between the two extremes of continuous and impulsive synchronization and thus can give more flexibility to the designer. Intermittent stabilization and synchronization for delayed neural networks governed by ODEs have been studied in [33–42]. In [30], for the first time, periodically intermittent synchronization for two identical reaction–diffusion neural networks with mixed delays was developed. Using exponential-type Lyapunov functionals, sufficient conditions for exponential synchronization were derived. By considering stochastic disturbance, similar work concerning intermittent synchronization of delayed stochastic neural networks with reaction–diffusion terms can be found in [31, 32]. It should be pointed out that the intermittently controlled time-delay system is a switched time-delay system in which a stable mode and an unstable mode run alternately, and thus, its stability depends on whether the decay degree of the stable mode can suppress the growth degree of the unstable mode. Therefore, the accuracy of estimating the decay/growth rate of solutions of the stable/unstable mode affects the conservatism of the derived synchronization criterion seriously. The exponential estimates presented in [30–32] were performed by means of quadratic Lyapunov functionals. Due to the finiteness of the activation intervals, the quadratic integral terms in these Lyapunov functionals may lead to overdesign in estimating the decay/growth rate of solutions of the stable/unstable mode, which brings some conservatism. Moreover, applying the quadratic integra terms for handling the delayed terms of the state equation imposes strict restriction on delay derivative, which, in turn, limits the application scope of the derived results. The above observations indicate that the developed intermittent synchronization conditions for coupled delayed reaction–diffusion neural networks are, however, too restrictive for some applications. One will naturally raise a question: Whether the conservatism of these intermittent synchronization conditions could be further reduced if we adopt Lyapunov–Razumikhin technique other than Lyapunov functional method as described in [30–32]?

In this paper, motivated by the above observations, we propose a Lyapunov–Razumikhin method for intermittent synchronization analysis of coupled reaction–diffusion neural networks with mixed delays. By developing a Razumikhin technique for exploring the effect of the relation between the delay and the control width on the dynamical behavior of the synchronization error system, a less conservative criterion for intermittent synchronization without any restriction on delay derivatives is derived. In relation to intermittent synchronization, the design of state-feedback intermittent synchronization controllers is also studied. The intermittent gain matrices can be obtained by solving a set of linear matrix inequalities. The main contributions of this paper are threefold. (1) We show how the Razumikhin technique is utilized for getting a better estimate on the decay/growth rate of the solutions of stable/unstable mode. (2) We show how the reaction–diffusion effect can be further explored with the extended Wirtingers inequality. (3) We show how the intermittent synchronization controller with minimized feedback gain can be designed in the framework of linear matrix inequalities.

The rest of this paper is structured as follows: Next section formulates the problem. A new periodically intermittent synchronization result is presented in Sect. 3. Section 4 provides a sufficient condition for designing periodically intermittent synchronization controllers. In Sect. 5, two reaction–diffusion chaotic neural networks are simulated to verify the effectiveness of the theoretical results. Finally, the paper is concluded in Sect. 6.

2 System description and preliminaries

In the sequel, if not explicitly, matrices are assumed to have compatible dimensions. The notation $P>(\ge ,{<}, \le )\,0$ is used to denote a symmetric positive-definite (positive-semidefinite, negative, negative-semidefinite) matrix. I and $I_n$ denote an identity matrix of suitable dimension and an identity matrix of size $n\times n$, respectively. $\mathbb {N}_0$ represents the set of nonnegative integers, that is, $\mathbb {N}_0=\{0,1,2,\ldots \}$.

Consider the following reaction–diffusion neural networks with discrete and finite distributed delays:

$$\begin{aligned} \frac{\partial z(t,x)}{\partial t}&=\;\sum \limits _{q = 1}^m \frac{\partial }{\partial x_q}\left( D_q\frac{\partial z(t,x)}{\partial x_q}\right) \nonumber \\&\quad -\,Az(t,x)+W_0f(z(t,x))\nonumber \\&\quad +\,W_1f(z(t-\tau (t),x))\nonumber \\&\quad +\,W_2 \int _{t - \sigma (t) }^t f(z(s,x))\mathrm{d}s+J,\nonumber \\&\quad \, (t,x)\in \mathbb {R}_+\times \varOmega , \end{aligned}$$

(1)

where $\varOmega = \{(x_1,x_2,\ldots ,x_m)^\mathrm{T}{:}\ |x_q|\le l_q,\ q = 1,2,\ldots ,m\}$ with $\partial \varOmega$ being its boundary; $z(t,x) = \left( z_1(t,x),z_2(t,x),\ldots ,z_n(t,x)\right)$ is the neuron state vector at time t and in space x; $D_q=\mathrm{diag}\big (d_{q1},d_{q2},\ldots ,d_{qn}\big )$ with $d_{qi}\ge 0$, $q=1,2,\ldots ,m$, $i=1,2,\ldots ,n$, are the transmission diffusion coefficients; $A = \mathrm{diag}\left( a_1,a_2,\ldots ,a_n\right)$ with $a_i>0$ representing the reset rate of the ith neuron is the self-feedback term; $W_0,W_1,W_2\in {R^{n \times n}}$ denote the connection weight matrix, the delayed connection weigh matrix, the distributively delayed connection weight matrix, respectively; the time-varying functions $\tau (t)$ and $\sigma (t)$ denote the transmission discrete delay and distributed delay, respectively, and satisfy $\underline{\tau } \le \tau (t) \le \overline{\tau }$ and $0\le \sigma (t)\le \overline{\sigma }$; $J\in \mathbb {R}^n$ is the external input vector; $f(z) =\left( f_1(z_1),f_2(z_2),\ldots ,f_n(z_n)\right)$ with $f_i(\cdot )$ being the activation function of the ith neuron satisfies the following assumption:

(H) For each $i\in \{1,2,\ldots ,n\}$, there exist scalars $F_i$ and $G_i$ such that

$$\begin{aligned} { G_i \le \frac{f_i(z_1) - f_i(z_2)}{z_1 - z_2} \le F_i,\quad \forall z_1,z_2\in \mathbb {R},\quad z_1\ne z_2}. \end{aligned}$$

The initial value and boundary value conditions associated with neural network (1) are given by

$$\begin{aligned} z(s,x)&= \phi (s,x),\quad (s,x) \in [ - r,0] \times \varOmega ,\\ z(t,x)&= 0,\quad (t,x) \in [- r, + \infty ) \times \partial \varOmega , \end{aligned}$$

where $r=\max \{\overline{\tau },\overline{\sigma }\}$, and $\phi (s,x)\in C([-r,0] \times \varOmega ,\mathbb {R}^n)$.

We consider system (1) as the drive system. The corresponding response system is

$$\begin{aligned} \frac{\partial \hat{z}(t,x)}{\partial t}&= \sum \limits _{q = 1}^m \frac{\partial }{\partial x_q}\left( D_q\frac{\partial \hat{z}(t,x)}{\partial x_q}\right) - A\hat{z}(t,x)\nonumber \\&\quad +\,{W_0}f(\hat{z}(t,x))+{W_1}f(\hat{z}(t - \tau (t),x))\nonumber \\&\quad +\,W_{2}\int _{t - \sigma (t) }^t f(\hat{z}(s,x))\mathrm{d}s+J+Bu(t),\nonumber \\&\quad \,(t,x)\in \mathbb {R}_+\times \varOmega , \end{aligned}$$

(2)

with the initial value and boundary value conditions

$$\begin{aligned} \hat{z}(s,x)&= \hat{\phi }(s,x),\quad (s,x) \in [ - r,0] \times \varOmega ,\\ \hat{z}(t,x)&= 0,\quad (t,x) \in [ - r, + \infty ) \times \partial \varOmega , \end{aligned}$$

where $\hat{z}(t,x)\in \mathbb {R}^n$ is the state vector of the response system, $B\in \mathbb {R}^{n\times n_c}$ is the input matrix, $u(t)\in \mathbb {R}^{n_c}$ is the control input vector, and $\hat{\phi }(s,x)\in C([-r,0] \times \varOmega ,\mathbb {R}^n)$.

The objective of this paper is to design periodically intermittent controllers such that the complete synchronization between system (1) and system (2) is achieved. The periodically intermittent state-feedback controller has the form

$$\begin{aligned} u(t)=K(t)\left( z(t,x)-\hat{z}(t,x)\right) , \end{aligned}$$

(3)

in which

$$\begin{aligned} K(t) = \left\{ \begin{array}{lll} K, &{}\quad t\in [kT, kT + \delta _k)\\ 0, &{}\quad t\in [kT + \delta _k, (k + 1)T)\end{array}\right. ,\quad k \in \mathbb {N}_0. \end{aligned}$$

In the above, $K\in \mathbb {R}^{n_c\times n}$ is the intermittent feedback gain to be designed, $T>0$ denotes the control period, and $\delta _k\in [\underline{\delta },\overline{\delta }]$ with $0<\underline{\delta }\le \overline{\delta }<T$ denotes the width of control window.

Define the synchronization error $e(t,x) = \hat{z}(t,x) - z(t,x)$. From (1)–(3), the synchronization error system is

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial e(t,x)}{\partial t} &{}=\sum \limits _{q = 1}^m \frac{\partial }{\partial x_q}\left( D_q\frac{\partial e(t,x)}{\partial x_q}\right) - (A+ BK )e(t,x)\\ &{}\quad +\, {W_0}g(e(t,x))+W_1g(e(t - \tau (t),x))\\ &{}\quad +\, W_{2}\int _{t - \sigma (t)}^tg(e(s,x))\mathrm{d}s,\nonumber \\ &{}\quad (t,x)\in [kT, kT + \delta )\times \varOmega \\ \frac{\partial e(t,x)}{\partial t} &{}=\sum \limits _{q = 1}^m \frac{ \partial }{\partial x_q}\left( D_q\frac{\partial e(t,x)}{\partial x_q}\right) - Ae(t,x)\\ &{}\quad +\,W_0g(e(t,x)) +W_1g\left( e(t - \tau (t),x)\right) \\ &{}\quad +\, W_2\int _{t - \sigma (t)}^t g(e(s,x))\mathrm{d}s,\nonumber \\ &{}\quad (t,x)\in [kT + \delta ,(k + 1)T)\times \varOmega \\ e(s,x) &{}= e_0(s,x)\triangleq \hat{\phi }(s,x)-\phi (s,x),\\ &{}\quad (s,x) \in [ - r,0] \times \varOmega \nonumber \\ e(t,x) &{}= 0,\ (t,x) \in [ - r, + \infty ) \times \partial \varOmega \nonumber \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(4)

where $g(e(t,x))=f(\hat{z}(t,x))-f(z(t,x))$. From (H), we have

$$\begin{aligned} G_i\le \frac{g_i(e_i)}{e_i}\le F_i,\quad \forall e_i\in \mathbb {R}-{0},\quad i=1,2,\ldots ,n. \end{aligned}$$

(5)

For $z(t,x)\in C([-r,b]\times \varOmega ,\mathbb {R}^n)$ with $b\ge 0$, define

$$\begin{aligned} \Vert z(t,\cdot )\Vert _2 =\left( \int _\varOmega z^\mathrm{T}(t,x)z(t,x) \mathrm{d}x\right) ^{1/2}, \end{aligned}$$

and for $\phi (\theta ,x)\in C([-r,0]\times \varOmega ,\mathbb {R}^n)$, define

$$\begin{aligned} \Vert \phi \Vert _C=\max \limits _{\theta \in [-r,0]}\Vert \phi (\theta ,\cdot )\Vert _2. \end{aligned}$$

Throughout the paper, we use the following stability concept for the synchronization error system (4).

Definition 1

The synchronization error system (4) is said to be globally exponentially stable, if there exist two positive constants $\gamma$ and M, such that $\Vert e(t,x)\Vert _2\le M\Vert e_0\Vert _C\mathrm{e}^{ - \gamma t}$, for all $t\ge 0$.

Now, the synchronization problem is reduced to the problem of designing a gain matrix K such that the synchronization error system (4) is globally exponentially stable.

The following lemmas will be needed in proving our results.

Lemma 1

For any compatible vectors x and y, matrix $M>0$, the following inequality holds

$$\begin{aligned} 2{x^T}y \le {x^T}Mx + {y^T}{M^{ - 1}}y. \end{aligned}$$

Lemma 2

Let $S{:}\,\varOmega \rightarrow {R^n}$ be a vector function belonging to $C^1(\varOmega )$, which vanishes on boundary $\partial \varOmega$ of $\varOmega$, i.e., $S(x)|_{\partial \varOmega } = 0$. Then, for any $q\in {1,2,\ldots ,m}$, for any $n \times n$ matrix $R\ge 0$, the following inequality holds

$$\begin{aligned} \int _\varOmega S^\mathrm{T}(x) RS (x)\mathrm{d}x \le \frac{4l_q^2}{\pi ^2}\int _\varOmega \left( \frac{\partial S}{\partial x_q}\right) ^\mathrm{T}R\frac{\partial S}{\partial x_q}\mathrm{d}x. \end{aligned}$$

(6)

Proof

Fix $q\in {1,2,\ldots ,m}$, from Wirtinger’s inequality [43], for any $R>0$, we have

$$\begin{aligned} \int _{ - l_q}^{l_q}S^\mathrm{T}(x) RS (x)\mathrm{d}x_{q} \le \frac{4L_{q}^2}{\pi ^2}\int _{ - l_q}^{l_q}\left( \frac{\partial S}{\partial x_q}\right) ^\mathrm{T}R\frac{\partial S}{\partial x_q}\mathrm{d}x_{q}. \end{aligned}$$

Then, integrating both sides of the above inequality from $- {l_i}$ to $l_i$ for $i\in \{1,2,\ldots ,m\}$ and $i\ne q$, we get (6).

Lemma 3

[44] Let $z{:}\, [-r,a)\rightarrow \mathbb {R}^n$ be continuously differentiable on (0, a) and continuous on $[-r,a)$, where $r,\,a>0$. Define $\Vert z_t\Vert _r=\max \nolimits _{\theta \in [-r,0]}\Vert z(t+\theta )\Vert$. For any $t\ge 0$, if $\Vert z(t)\Vert <\Vert z_t\Vert _r$, then $D^+\Vert z_t\Vert _r\le 0$; if $\Vert z(t)\Vert =\Vert z_t\Vert _r$, then $D^+\Vert z_t\Vert _r=\mathrm{max}\{0,D^+|z(t)|\}$.

3 Intermittent synchronization analysis

In this section, we first develop a Razumikhin-type technique for achieving an exponential estimate of the solutions of error system (4) in the closed-loop mode. For $k\in \mathbb {N}_0$, define $t_{ik}=\left\{ \begin{array}{lll}kT, &{}\quad i=1\\ kT+{\delta _k}, &{}\quad i=2\end{array}\right.$. Set $\varDelta _{ik}=[t_{ik},t_{3-i,k+i-1})$, and $\overline{\varDelta }_{ik}=[t_{ik},t_{3-i,k+i-1}]$, $i=1,2$.

Lemma 4

Given ${n_c}\times n$ matrix K, the control period T, and the control width $\delta _k\in [\underline{\delta },\overline{\delta }]$ with $0<\underline{\delta }\le \overline{\delta }<T$, consider the synchronization error system (4) satisfying (H). If for some prescribed scalars $\epsilon \ge 0$, $\beta _1\ge 0$, and $\alpha _{1i}>0$, $i=1,2$, there exist a $n\times n$ matrix $P_{1}> 0$, and $n\times n$ positive diagonal matrices $\varLambda _{1h}$, $h=0,1,2$, such that the following linear matrix inequalities (LMIs) hold:

$$\begin{aligned}&P_1D_q+D_qP_1\ge 0,\quad q=1,2,\ldots ,m, \end{aligned}$$

(7)

$$\begin{aligned}&\varXi _1 \triangleq \left[ \begin{array}{lllll} {\varGamma _1} &{}0 &{}P_1W_0 + L_2\varLambda _{10} &{}P_1W_1 &{}\overline{\sigma } P_1W_{2}\\ {*} &{}-\alpha _{11}P_1+L_1\varLambda _{11} &{}0 &{}L_2\varLambda _{11} &{}0\\ {*} &{}{*} &{}-\varLambda _{10} &{}0 &{}0\\ {*} &{}{*} &{}{*} &{}-\varLambda _{11} &{}0\\ {*} &{}{*} &{}{*} &{}{*} &{}-\overline{\sigma } \varLambda _{12} \end{array} \right] <0 \nonumber \\\end{aligned}$$

(8)

$$\begin{aligned}&\tilde{L}\varLambda _{12} \le \alpha _{12}P_1 \end{aligned}$$

(9)

where

$$\begin{aligned} \varGamma _1&= \left( \epsilon +\beta _1 +\alpha _{11}\mathrm{e}^{(\beta _1+\epsilon )\overline{\tau }} +\frac{\alpha _{12}}{\beta _1 + \epsilon }\left( \mathrm{e}^{\overline{\sigma }(\beta _1+\epsilon )}-1\right) \right) P_1 \\&\quad -\,\sum \limits _{q = 1}^m \frac{\pi ^2}{4l_q^2}\left( P_1 D_q+D_qP_1\right) \\&\quad -\,P_1(A+ BK ) - (A+ BK )^\mathrm{T}P_1+L_1\varLambda _{10},\\ L_1&=-\mathrm{diag}\left( G_1F_1,G_2F_2,\ldots ,G_nF_n\right) ,\\ L_2&=\frac{1}{2}\mathrm{diag}\left( G_1+F_1,G_2+F_2,\ldots ,G_n+F_n\right) ,\\ \tilde{L}&=\mathrm{diag}\left( \max \{|G_1|^2,|F_1|^2\},\max \{|G_2|^2,|F_2|^2\},\right. \\&\quad \left. \ldots ,\max \{|G_n|^2,|F_n|^2\}\right) , \end{aligned}$$

then,

$$\begin{aligned} V_1(t) \le \overline{V}_1 (t_{1k})\mathrm{e}^{ - {\beta _1}(t - kT )},\quad t \in \overline{\varDelta }_{1k},\quad k \in \mathbb {N}_0, \end{aligned}$$

(10)

and

$$\begin{aligned} \overline{V}_1(t_{2k})\le \mathcal{H}_1(\beta _1)\overline{V}_1(t_{1k}),\quad k\in \mathbb {N}_0, \end{aligned}$$

(11)

where $V_1(t) = \mathrm{e}^{\epsilon t}\int _\varOmega e^\mathrm{T}(t,x)P_1e(t,x)\mathrm{d}x,\,\overline{V}_1 (t) = \mathop {\max }\nolimits _{-r\le \theta \le 0} {V_1}(t + \theta )$, and $\mathcal{H}_1(\beta _1){=}\min \{1,\mathrm{e}^{-\beta _1({\underline{\delta }}\,-r)}\}$.

Proof

For any given $k\in \mathbb {N}_0$, set $U_{1}(t){=}\mathrm{e}^{\beta _1(t-t_{1k} )}V_{1}(t)$, $t\in [t_{1k}- r, t_{2k}]$. We prove that for any given $\varepsilon >0$, $U_{1}(t)$ satisfies

$$\begin{aligned} U_1(t) < (1 + \varepsilon )\overline{V}_{1}(t_{1k}),\quad t \in {\varDelta _{1k}}. \end{aligned}$$

(12)

By the contrary, there exists at least one $t\in \varDelta _{1k}$ such that $U_{1}(t)\ge (1+\varepsilon )\overline{V}_{1}(kT)$. Let ${t^*} = \inf \{ t \in \varDelta _{1k};{U_1}(t)\ge (1 + \varepsilon )\overline{V}_1(t_{1k})\}$. Note that

$$\begin{aligned}&U_{1}(t_{1k}+\theta )=\mathrm{e}^{\beta _1{\theta } }V_{1}(t_{1k}+\theta )<(1 + \varepsilon )\overline{V}_{1}(t_{1k}),\nonumber \\&\quad \theta \in [-r,0]. \end{aligned}$$

It follows that ${t^*} \in (t_{1k},t_{2k} )$. Moreover,

$$\begin{aligned} {U_1}({t^*})= & {} (1 + \varepsilon )\overline{V}_1 (kT ),{U_1}(t) < (1 + \varepsilon )\overline{V}_1 (kT ),\nonumber \\&\quad \forall t \in [t_{1k} - r,{t^*}), \end{aligned}$$

(13)

and

$$\begin{aligned} {\dot{U}_1}({t^*}) \ge 0. \end{aligned}$$

(14)

The relation (13) implies that

$$\begin{aligned} U_1({t^*}) \ge U_1\left( {t^*} - \tau ({t^*})\right) , \end{aligned}$$

which further implies

$$\begin{aligned} 0&\le \alpha _{11}\left( \mathrm{e}^{(\beta _1 + \epsilon )\overline{\tau }}\int _\varOmega e^\mathrm{T}(t^*,x)P_1e(t^*,x)\mathrm{d}x \right. \nonumber \\&\quad \left. - \int _\varOmega e^\mathrm{T}(t^* - \tau (t^*),x)P_1e(t^* - \tau (t^*),x)\mathrm{d}x\right) . \end{aligned}$$

(15)

The relation (13) also implies that

$$\begin{aligned} U_1({t^*}) \ge U_1(s),\quad s\in [t^*-r,t^*]. \end{aligned}$$

It follows that

$$\begin{aligned}&\mathrm{e}^{(\beta _1+\epsilon )(t^{*}-s)}\int _\varOmega e^\mathrm{T}(t^*,x)P_1e(t^*,x)\mathrm{d}x\\&\quad \ge \int _\varOmega e^\mathrm{T}(s,x)P_1e(s,x)\mathrm{d}x,\quad s\in [t^*-r,t^*]. \end{aligned}$$

Integrating the above inequality from $t^{*}-\sigma (t^{*})$ to $t^{*}$ yields

$$\begin{aligned}&\frac{1}{\beta _1+\epsilon }\left( \mathrm{e}^{(\beta _1+\epsilon )\overline{\sigma }}-1\right) \int _\varOmega e^\mathrm{T}(t^*,x)P_1e(t^*,x)\mathrm{d}x\nonumber \\&\quad \ge \int _\varOmega \int _{t^*-\sigma (t^{*})}^{t^*} e^\mathrm{T}(s,x)P_1e(s,x)\mathrm{d}s\mathrm{d}x. \end{aligned}$$

(16)

For $t\in (t_{1k},t_{2k})$, the derivative of ${U_1}(t)$ along the solutions of error system (4) is

$$\begin{aligned} {{\dot{U}}_1}(t)&= \mathrm{e}^{\beta _1(t-t_{1k})+\epsilon t}\int _\varOmega \bigg \{e^\mathrm{T}(t,x)\big [(\beta _1+\epsilon )P_1\nonumber \\&\quad -P_1(A+ BK ) -\,(A+ BK )^\mathrm{T}P_1\big ]e(t,x)\nonumber \\&\quad + 2e^\mathrm{T}(t,x)P_1\sum \limits _{q=1}^m\frac{\partial }{\partial x_q}\left( D_q \frac{\partial e(t,x)}{\partial x_q}\right) \nonumber \\&\quad +\,2e^\mathrm{T}(t,x)P_1W_0g(e(t,x))+ 2e^\mathrm{T}(t,x)\nonumber \\&\quad \times \, P_1W_1g(e(t-\tau (t),x))+\,2e^\mathrm{T}(t,x)\nonumber \\&\quad \times P_1W_{2}\int _{t - \sigma (t) }^t g(e(s,x))\mathrm{d}s\bigg \} \mathrm{d}x. \end{aligned}$$

(17)

Denoting $P_{1}=(p_{ij})_{n\times n}$, integration by parts and application of the Dirichlet boundary condition lead to

$$\begin{aligned}&2\int _\varOmega e^\mathrm{T}(t,x)P_1\sum \limits _{q=1}^m\frac{\partial }{\partial x_q}\left( D_q \frac{\partial e(t,x)}{\partial x_q}\right) \nonumber \\&\quad = \sum \limits _{q = 1}^m \sum \limits _{i,j = 1}^n2\int _\varOmega e_i(t,x)p_{ij}\frac{\partial }{\partial x_q}\left( d_{qj}\frac{\partial e_j(t,x)}{\partial x_q}\right) \mathrm{d}x\nonumber \\&\quad = -\,\sum \limits _{q = 1}^m 2\int _\varOmega \sum \limits _{i,j = 1}^n \frac{\partial }{\partial x_q}e_i(t,x)p_{ij}d_{qj}\frac{\partial e_j(t,x)}{\partial x_q}\mathrm{d}x\nonumber \\&\quad = -\,\sum \limits _{q = 1}^m \int _\varOmega \frac{\partial e^\mathrm{T}(t,x)}{\partial x_q} (P_1D_q+D_qP_1)\frac{\partial e(t,x)}{\partial x_q}\mathrm{d}x.\nonumber \end{aligned}$$

(18)

Recalling condition (7), application of the inequality (6) in Lemma 2 yields

$$\begin{aligned}&\int _\varOmega e^\mathrm{T}(t,x)P_1\sum \limits _{q = 1}^m \frac{\partial }{\partial x_q}\left( D_q\frac{\partial e(t,x)}{\partial x_q}\right) \mathrm{d}x \nonumber \\&\quad \le - \sum \limits _{q = 1}^m \frac{\pi ^2}{4l_q^2}\int _\varOmega e^\mathrm{T}(t,x) P_1D_qe(t,x)\mathrm{d}x. \end{aligned}$$

(19)

Using the inequality in Lemma 1 and considering the relation (5), we have

$$\begin{aligned}&2\int _\varOmega e^\mathrm{T}(t,x)P_1 W_{2}\int _{t-\sigma (t)}^t g(e(s,x))\mathrm{d}s\mathrm{d}x\\&\quad \le \int _\varOmega \int _{t - \sigma (t) }^{t}\big [e^\mathrm{T}(t,x)P_1W_{2}\varLambda _{12}^{-1}W_2^\mathrm{T}P_1\mathrm{d}s\mathrm{d}x \\&\qquad + g(e(s,x))\varLambda _{12}g(e(s,x))\big ]\mathrm{d}s\mathrm{d}x \\&\quad \le \int _\varOmega \overline{\sigma } e^\mathrm{T}(t,x)P_1W_2\varLambda _{12}^{- 1}W_2^\mathrm{T}P_1e(t,x)\mathrm{d}x \\&\qquad + \int _\varOmega \int _{t - \sigma (t) }^{t}e^\mathrm{T}(s,x)\tilde{L}\varLambda _{12}e(s,x)\mathrm{d}s\mathrm{d}x. \end{aligned}$$

It follows from condition (9) and relation (16) that

$$\begin{aligned}&2\int _\varOmega e^\mathrm{T}(t^*,x)P_1 W_{2}\int _{t^*-\sigma (t^*)}^{t^*}g(e(s,x))\mathrm{d}s\mathrm{d}x\nonumber \\&\quad \le \int _\varOmega \overline{\sigma } e^\mathrm{T}(t^*,x)P_1W_2\varLambda _{12}^{- 1}W_2^\mathrm{T}P_1e(t^*,x)\mathrm{d}x \nonumber \\&\qquad +\,\alpha _{12}\int _\varOmega \int _{t^* - \sigma (t^*) }^{t^*}e^\mathrm{T}(s,x)P_1e(s,x)\mathrm{d}s\mathrm{d}x\nonumber \\&\quad \le \int _\varOmega e^\mathrm{T}(t^*,x)\bigg (\overline{\sigma } P_1W_2\varLambda _{12}^{- 1}W_2^\mathrm{T}P_1+\frac{\alpha _{12}}{\beta _1+\epsilon }\nonumber \\&\qquad \times \,\left( \mathrm{e}^{(\beta _1+\epsilon )\overline{\sigma }}-1\right) P_1\bigg )e(t^*,x)\mathrm{d}x. \end{aligned}$$

(20)

On the other hand, by the relation (5),

$$\begin{aligned}&0\le (F_ie_i-g_i(e_i))(g_i(e_i)-G_ie_i),\ \mathrm{for\ any} \nonumber \\&\quad e_i\in \mathbb {R},\quad i=1,2,\ldots ,n. \end{aligned}$$

Set $\varLambda _{1h} = \mathrm{diag}\{ \lambda _{1h1},\lambda _{1h2},\ldots ,\lambda _{1hn}\}$, $h=0,1$. It follows from the above inequalities that

$$\begin{aligned}&0 \le \sum \limits _{i = 1}^n \lambda _{10i}\left( F_i e_i(t,x) - g_{i}(e_i(t,x))\right) \nonumber \\&\qquad \big ( g_{i}(e_i(t,x)) - G_i e_i(t,x)\big )\nonumber \\&\qquad +\,\sum \limits _{i = 1}^n \lambda _{11i}\left( F_i e_i(t-\tau _{i}(t),x) \right. \nonumber \\&\qquad \left. - g_{i}(e_i(t-\tau _{i}(t),x)\right) \big (g_{i}e_i(t-\tau _{i}(t),x)\nonumber \\&\qquad -\,G_ie_i(t-\tau _{i}(t),x)\big )\nonumber \\&\quad =\eta ^\mathrm{T}(t,x)\left[ \begin{array}{llll} L_1\varLambda _{10} &{}\quad 0 &{}\quad L_2\varLambda _{10} &{}\quad 0\\ {*} &{}\quad L_1\varLambda _{11} &{}\quad 0 &{}\quad L_2\varLambda _{11}\\ {*} &{}\quad {*} &{}\quad -\varLambda _{10} &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad -\varLambda _{11} \end{array} \right] \nonumber \\&\qquad \times \,\eta (t,x), \end{aligned}$$

(21)

where $\eta (t,x)=\mathrm{col}(e(t,x),e(t-\tau (t),x),g(e(t,x)),g(e(t-\tau (t),x)))$.

Substituting (18) and (19) into (17) with $t=t^{*}$ and using (15) and (20) yields

$$\begin{aligned} \dot{U}_1(t^*) \le \mathrm{e}^{\beta _1(t-t_{1k})+\epsilon t}\int _\varOmega \eta ^\mathrm{T}(t^{*},x)\tilde{\Xi } _{1}\eta (t^{*},x)\mathrm{d}x, \end{aligned}$$

(22)

where

$$\begin{aligned} \tilde{\Xi } _{1} = \left[ \begin{array}{llll} \tilde{\varGamma }_1 &{}\quad 0 &{}\quad P_1W_0 + L_2\varLambda _{10} &{}\quad P_1W_1\\ 0 &{}\quad -\alpha _{11}P_1+L_1\varLambda _{11} &{}\quad 0 &{}\quad L_2\varLambda _{11}\\ {*} &{}\quad {*} &{}\quad -\varLambda _{10} &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad -\varLambda _{11} \end{array} \right] , \end{aligned}$$

in which $\tilde{\varGamma }_1=\varGamma _1+\overline{\sigma } P_1W_2\varLambda _{12}^{-1}W_2^\mathrm{T}P_1$.

Application of Schur complement to (8) leads to $\varXi _{1}<0$. Then coming back to (21), we obtain $\dot{U}_1(t^*)<0$, which contradicts (14). Thus, (12) holds. Let $\varepsilon \rightarrow {0^ + }$, we arrive at (10). Note that for given $\theta \in [-r,0]$, the claim (10) implies that

$$\begin{aligned} V_1(t_{2k}+\theta )\le \overline{V}_1(t_{1k}),\quad \mathrm{for}\ t_{2k}+\theta \le t_{1k}, \end{aligned}$$

(23)

and

$$\begin{aligned} V_1(t_{2k}+\theta )\le \overline{V}_1(t_{1k})\mathrm{e}^{-\beta _1(\delta _k+\theta )},\quad \mathrm{for}\ t_{2k}+\theta >t_{1k}. \end{aligned}$$

(24)

Putting (22)–(23) together yields (11). This completes the proof.

Next, we use a slightly different technique to estimate the solutions of error system (4) in the open-loop mode.

Lemma 5

Given ${n_c}\times n$ matrix K, the control period T, and the control width $\delta _k\in [\underline{\delta },\overline{\delta }]$ with $0<\underline{\delta }\le \overline{\delta }<T$, consider the synchronization error system (4) satisfying (H). If for some prescribed scalars $\epsilon \ge 0$, $\beta _{i}\ge 0$, $\alpha _{ij}>0$, $i=2,3$, $j=1,2$, satisfying $\beta _2\ge \beta _3$, there exist a $n\times n$ matrix $P_{2}> 0$, and $n\times n$ positive diagonal matrices $\varLambda _{ih}$, $i=2,3$, $h=0,1,2$, such that the following LMIs hold:

$$\begin{aligned}&P_2D_q+D_qP_2\ge 0,\quad q=1,2,\ldots ,m, \end{aligned}$$

(25)

$$\begin{aligned}&\left[ \begin{array}{lllll} \varGamma _{i} &{}\quad 0 &{}\quad P_2W_0 + L_2\varLambda _{i0} &{}\quad P_2W_1 &{}\quad \overline{\sigma } P_2W_2\\ {*} &{}\quad -\alpha _{i1}P_2+L_1\varLambda _{i1} &{}\quad 0 &{}\quad L_2\varLambda _{i1} &{}\quad 0\\ {*} &{}\quad {*} &{}\quad -\varLambda _{i0} &{}\quad 0 &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad -\varLambda _{i1} &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad 0 &{}\quad -\overline{\sigma }\varLambda _{i2} \end{array} \right] \nonumber \\&\quad <0,\quad i=2,3 \end{aligned}$$

(26)

$$\begin{aligned}&\tilde{L}\varLambda _{i2} \le \alpha _{i2}P_2,\ i=2,3, \end{aligned}$$

(27)

where

$$\begin{aligned} \varGamma _2&=\left( \epsilon -\beta _2 +\alpha _{21}\mathrm{e}^{\epsilon \overline{\tau }}+ \frac{\alpha _{22}}{\epsilon }\left( \mathrm{e}^{\epsilon \overline{\sigma } }-1\right) \right) \\&\quad P_2 - \sum \limits _{q = 1}^m \frac{\pi ^2}{4l_q^2}\left( P_2 D_q+D_qP_2\right) \\&\quad -\,P_2A - A^\mathrm{T}P_2+L_1\varLambda _{20},\\ \varGamma _3&=\left( \epsilon -\beta _3 +\alpha _{31}H(\beta _3,\epsilon )+ \frac{\alpha _{32}}{\epsilon -\beta _3}\right. \nonumber \\&\left. \quad \left( \mathrm{e}^{(\epsilon -\beta _3)\overline{\sigma } }-1\right) \right) P_2\\&\quad -\,\sum \limits _{q = 1}^m \frac{\pi ^2}{4l_q^2}\left( P_2 D_q+D_qP_2\right) \nonumber \\&\quad - P_2A - A^\mathrm{T}P_2+L_1\varLambda _{30}, \end{aligned}$$

in which

$$\begin{aligned} H(\beta _3,\epsilon )=\left\{ \begin{array}{ll}\mathrm{e}^{(\epsilon -\beta _3)\underline{\tau }}, &{}\quad \beta _3\ge \epsilon \\ \mathrm{e}^{(\epsilon -\beta _3)\overline{\tau }}, &{}\quad \beta _3< \epsilon \end{array}\right. , \end{aligned}$$

(28)

Then,

$$\begin{aligned} \overline{V}_2(t) \le \overline{V}_2(t_{2k})\mathcal{H}_2(\beta _2,\beta _3),\ t\in \overline{\varDelta }_{2k},\ k \in \mathbb {N}_0, \end{aligned}$$

(29)

where $V_2(t) = \mathrm{e}^{\epsilon t}\int _\varOmega e^\mathrm{T}(t,x)P_2e(t,x)\mathrm{d}x$, $\overline{V}_2(t) = \mathop {\max }\nolimits _{ - r \le \theta \le 0} {V_2}(t+\theta )$, and

$$\begin{aligned} \mathcal{H}_2(\beta _2,\beta _3)=\mathrm{e}^{(\beta _2-\beta _3)\min \{T-{\underline{\delta }},r\}+\beta _3(T-{\underline{\delta }})}. \end{aligned}$$

Proof

Fix $k\in \mathbb {N}_0$. We start by showing that

$$\begin{aligned} D^+\overline{V}_2(t)\le \beta _2\overline{V}_2(t),\quad \forall \, t\in \varDelta _{2k}. \end{aligned}$$

(30)

For any given $t\in \varDelta _{2k}$, at least one of the following two cases holds: (1) $V_2(t)<\overline{V}_2(t)$; (2) $V_2(t)=\overline{V}_2(t)$. If case (1) holds, then by Lemma 3, we have $D^+\overline{V}_2(t)\le 0$, i.e., (29) holds.

If case (2) holds, it follows that $V_2(t)\ge V_2(s)$, $s\in [t-r,t]$. Then, similar to the proofs of (15) and (19), we can obtain from condition (26) with $i=2$ that

$$\begin{aligned}&\alpha _{21}\left( \mathrm{e}^{\epsilon \overline{\tau }}\int _\varOmega e^\mathrm{T}(t,x)P_2e(t,x)\mathrm{d}x \right. \nonumber \\&\quad \left. - \int _\varOmega e^\mathrm{T}(t - \tau (t),x)P_2e(t - \tau (t),x)\mathrm{d}x\right) \ge 0,\nonumber \\ \end{aligned}$$

(31)

and

$$\begin{aligned}&2\int _\varOmega e^\mathrm{T}(t,x)P_2 W_{2}\int _{t-\sigma (t)}^{t}g(e(s,x))\mathrm{d}s\mathrm{d}x\nonumber \\&\quad \le \int _\varOmega e^\mathrm{T}(t,x)\bigg (\overline{\sigma } P_2W_2\varLambda _{22}^{- 1}W_2^\mathrm{T}P_2\nonumber \\&\qquad +\frac{\alpha _{22}}{\epsilon }\left( \mathrm{e}^{\epsilon \overline{\sigma }}-1\right) P_2\bigg )e(t,x)\mathrm{d}x. \end{aligned}$$

(32)

The relation (5) implies

$$\begin{aligned}&0\le \eta ^\mathrm{T}(t,x)\nonumber \\&\quad \left[ \begin{array}{llll} L_1\varLambda _{i0} &{}\quad 0 &{}\quad L_2\varLambda _{i0} &{}\quad 0\\ {*} &{}\quad L_1\varLambda _{i1} &{}\quad 0 &{}\quad L_2\varLambda _{i1}\\ {*} &{}\quad {*} &{}\quad -\varLambda _{i0} &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad -\varLambda _{i1} \end{array} \right] \nonumber \\&\eta (t,x),\quad i=2,3. \end{aligned}$$

(33)

The derivative of $V_2(t)$ along the solutions of error system (4) on $(t_{2k},t_{1,k+1})$ is

$$\begin{aligned} {\dot{V}}_2(t)&= \mathrm{e}^{\epsilon t}\int _\varOmega \bigg \{e^\mathrm{T}(t,x) \nonumber \\&\quad \big [\epsilon P_2-P_2A-A^\mathrm{T}P_2\big ]e(t,x)+ 2e^\mathrm{T}(t,x)P_2 \nonumber \\&\quad \times \,\sum \limits _{q=1}^m\frac{\partial }{\partial x_q}\left( D_q \frac{\partial e(t,x)}{\partial x_q}\right) + 2e^\mathrm{T}(t,x)\nonumber \\&\quad P_2W_0g(e(t,x))+\,2e^\mathrm{T}(t,x)P_2W_1\nonumber \\&\quad \times \,g(e(t-\tau (t),x)) + 2e^\mathrm{T}(t,x)\nonumber \\&\quad P_2W_{2}\int _{t - \sigma (t) }^t g(e(s,x))ds\bigg \} \mathrm{d}x. \end{aligned}$$

(34)

Applying the inequality (18) with $P_2$ instead of $P_1$ and the inequalities (30)–(32) to (33) leads to

$$\begin{aligned} {\dot{V}}_2(t)\le \beta _2V_2(t)+\mathrm{e}^{\epsilon t}\int _\varOmega \eta ^\mathrm{T}(t,x)\varXi _2\eta (t,x)\mathrm{d}x, \end{aligned}$$

(35)

where

$$\begin{aligned} \varXi _{2} = \left[ \begin{array}{llll} \tilde{\varGamma }_2 &{}\quad 0 &{}\quad P_2W_0 + L_2\varLambda _{20} &{}\quad P_2W_1\\ 0 &{}\quad -\alpha _{21}P_2+L_1\varLambda _{21} &{}\quad 0 &{}\quad L_2\varLambda _{21}\\ {*} &{}\quad {*} &{}\quad -\varLambda _{20} &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad -\varLambda _{21} \end{array} \right] , \end{aligned}$$

in which $\tilde{\varGamma }_2=\varGamma _2+\overline{\sigma } P_2W_2\varLambda _{22}^{-1}W_2^\mathrm{T}P_2$. Note that condition (25) with $i=2$ is equivalent to $\varXi _{2}<0$. It follows from (34) that ${\dot{V}}_2(t)\le \beta _2V_2(t)$. Then by Lemma 3, we obtain $D^+\overline{V}_2(t)\le \beta _2V_2(t)=\beta _2\overline{V}_2(t)$. Therefore, (29) holds.

From (29), we obtain

$$\begin{aligned} V_2(t)\le \overline{V}_2(t)\le \overline{V}_2(t_{2k})\mathrm{e}^{\beta _2(t-t_{2k})},\ t\in \overline{\varDelta }_{2k}. \end{aligned}$$

(36)

Next, we proceed to show that for the case where $r<T-{\delta _k}$, the estimate (35) on $[t_{2k}+r,t_{1,k+1}]$ can be improved as follows

$$\begin{aligned}&V_2(t)\le \overline{V}_2(t_{2k})\mathrm{e}^{(\beta _2-\beta _3)r}\mathrm{e}^{\beta _3(t-t_{2k})},\nonumber \\&\quad t\in [t_{2k}+r,t_{1,k+1}]. \end{aligned}$$

(37)

Set $U_2(t)=V_2(t)\mathrm{e}^{-\beta _3(t-t_{2k})}$. We have to only prove that for any given $\varepsilon >0$, it holds that

$$\begin{aligned} U_2(t)<(1+\varepsilon ) \overline{V}_2(t_{2k})\mathrm{e}^{(\beta _2-\beta _3)r},\quad t\in [t_{2k}+r,t_{1,k+1}]. \end{aligned}$$

(38)

According to (35), (37) is true for $t=t_{2k}+r$. Suppose on the contrary that (37) does not hold, then it follows from (35) that there exists a $t^{*}\in (t_{2k}+r,t_{1,k+1})$ such that

$$\begin{aligned}&U_2(t)\le \overline{V}_2(t_{2k})\mathrm{e}^{(\beta _2-\beta _3)(t-t_{2k})},\quad t\in [t_{2k},t_{2k}+r],\nonumber \\ \end{aligned}$$

(39)

$$\begin{aligned}&U_2(t)\le (1+\varepsilon )\overline{V}_2(t_{2k})\mathrm{e}^{(\beta _2-\beta _3)r},\quad t\in [t_{2k}+r,t^{*}),\nonumber \\ \end{aligned}$$

(40)

$$\begin{aligned}&U_2(t^{*})= (1+\varepsilon )\overline{V}_2(t_{2k})\mathrm{e}^{(\beta _2-\beta _3)r}. \end{aligned}$$

(41)

and

$$\begin{aligned} \dot{U}_2(t^{*})\ge 0. \end{aligned}$$

(42)

The relations (38)–(40) imply that $U_2(t^{*})\ge U_2(s)$, $s\in [t^{*}-r,t^{*}]$. It follows that

$$\begin{aligned} 0&\le \alpha _{31}\left( H(\beta _3,\epsilon )\int _\varOmega e^\mathrm{T}(t^{*},x)P_2e(t^{*},x)\mathrm{d}x\right. \nonumber \\&\quad \left. - \int _\varOmega e^\mathrm{T}(t^{*} - \tau (t^{*}),x)P_2e(t^{*} - \tau (t^{*}),x)\mathrm{d}x\right) , \end{aligned}$$

(43)

and

$$\begin{aligned}&2\int _\varOmega e^\mathrm{T}(t^{*},x)P_2 W_{2}\int _{t^{*}-\sigma (t^{*})}^{t^{*}}g(e(s,x))\mathrm{d}s\mathrm{d}x\nonumber \\&\quad \le \int _\varOmega e^\mathrm{T}(t^{*},x)\bigg (\overline{\sigma } P_2W_2\varLambda _{32}^{- 1}W_2^\mathrm{T}P_2\nonumber \\&\qquad +\frac{\alpha _{32}}{\epsilon -\beta _3}\left( \mathrm{e}^{(\epsilon -\beta _3)\overline{\sigma }}-1\right) P_2\bigg )e(t^{*},x)\mathrm{d}x. \end{aligned}$$

(44)

The derivative of $U_2(t)$ along the solutions of error system (4) on $(t_{2k},t_{1,k+1})$ is given by

$$\begin{aligned} {\dot{U}}_2(t)&= \mathrm{e}^{-\beta _3 (t-t_{2k})}\mathrm{e}^{\epsilon t}\int _\varOmega \bigg \{e^\mathrm{T}(t,x)\big [(\epsilon -\beta _3) P_2\nonumber \\&\qquad -P_2A-A^\mathrm{T}P_2\big ]e(t,x) \nonumber \\&\quad +\,2e^\mathrm{T}(t,x)P_2\sum \limits _{q=1}^m\frac{\partial }{\partial x_q}\left( D_q \frac{\partial e(t,x)}{\partial x_q}\right) \nonumber \\&\quad +\,2e^\mathrm{T}(t,x)P_2W_0g(e(t,x))\nonumber \\&\quad +\,2e^\mathrm{T}(t,x)P_2 W_1g(e(t-\tau (t),x))\nonumber \\&\quad +\,2e^\mathrm{T}(t,x)P_2W_{2}\int _{t - \sigma (t) }^t g(e(s,x))\mathrm{d}s\bigg \} \mathrm{d}x. \end{aligned}$$

(45)

Putting the inequalities (42), (43), and (32) with $i=3$ together into (44), and considering the inequality (18) with $P_2$ instead of $P_1$, we get

$$\begin{aligned} {\dot{U}}_2(t^{*}) \le \mathrm{e}^{-\beta _3 (t^{*}-t_{2k})}\mathrm{e}^{\epsilon t^{*}}\int _\varOmega \eta ^\mathrm{T}(t^{*},x)\varXi _3\eta (t^{*},x)\mathrm{d}x, \end{aligned}$$

(46)

where

$$\begin{aligned} \varXi _3=\left[ \begin{array}{llll} \tilde{\varGamma }_3 &{}\quad 0 &{}\quad P_2W_0 + L_2\varLambda _{30} &{}\quad P_2W_1\\ 0 &{}\quad -\alpha _{31}P_2+L_1\varLambda _{31} &{}\quad 0 &{}\quad L_2\varLambda _{31}\\ {*} &{}\quad {*} &{}\quad -\varLambda _{30} &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad -\varLambda _{31} \end{array} \right] , \end{aligned}$$

in which $\tilde{\varGamma }_3=\varGamma _3+\overline{\sigma } P_2W_2\varLambda _{32}^{-1}W_2^\mathrm{T}P_2$. It is easy to verify that condition (25) with $i=3$ is equivalent to $\varXi _3<0$. It follows from (45) that ${\dot{U}}_2(t^{*})<0$, which contradicts (41). Hence, we have proven (37). Letting $\varepsilon \rightarrow 0$ in (37), we obtain (36). Then, combining (35) and (36) together yields

$$\begin{aligned}&\overline{V}_2(t) \le \overline{V}_2(t_{2k})\mathrm{e}^{(\beta _2-\beta _3)\min \{T-\delta _k,r\}+\beta _3(T-\delta _k)},\\&\quad t\in \overline{\varDelta }_{2k},\quad k \in \mathbb {N}_0. \end{aligned}$$

Recalling $\delta _k\ge \underline{\delta }$ and $\beta _2\ge \beta _3$, the inequality (28) is immediately derived, which completes the proof.

Remark 1

The closed-loop and open-loop modes have different dynamical behaviors. So we introduce different techniques to estimate $V_1(t)$ and $V_2(t)$. In the closed-loop mode, a helpful trick is the introduction of the parameter $\beta _1$ for estimating the decay rate of $V_1(t)$. It can be seen from (11) that the parameter ${\beta _1}$ can lead to a tighter estimate on $\overline{V}_1(t_{2k})$ for the case of $r<{\underline{\delta }}\,$. In the open-loop mode, in order to reduce the conservatism of the estimation analysis for the case of $r<T-{\delta _k}$, we divide the estimation into two steps. It can be seen from (28) that for the case of $r<T-{\delta _k}$, the two-step estimation is less conservative than the single-step estimation. We note that the special dynamical characteristics of synchronization error system (4) for the case of $r<{\delta _k}$ and for the case of $r<T-{\delta _k}$ cannot be captured by the Lyapunov functional method proposed in [30–32].

Based on the above Lemmas 4–5, we are in a position to state our stability criterion for synchronization error system (4).

Theorem 1

Given ${n_c}\times n$ matrix K, the control period T, and the control width $\delta _k\in [\underline{\delta },\overline{\delta }]$ with $0<\underline{\delta }\le \overline{\delta }<T$, consider the drive system (1) and the periodically intermittently controlled response system (2), in which the activation function f satisfies (H). If for some prescribed scalars $\epsilon \ge 0$, $\mu _1>0$, $\beta _{i}\ge 0$, $\alpha _{ij}>0$, $i=1,2,3$, $j=1,2$, satisfying $\beta _2\ge \beta _3$, there exist $n\times n$ matrices $P_{i}> 0$, $i=1,2$, and $n\times n$ positive diagonal matrices $\varLambda _{hi}$, $i=1,2,3$, $h=0,1,2$, such that (7), (8), (9), (24), (25), (26), and the following LMIs hold:

$$\begin{aligned} P_1 \le \mu _2P_2,\ P_2 \le \mu _1P_1, \end{aligned}$$

(47)

where

$$\begin{aligned} \mu _2=\frac{\mathrm{e}^{\epsilon T}}{\mu _1\mathcal{H}_1(\beta _1)\mathcal{H}_2(\beta _2,\beta _3)}, \end{aligned}$$

(48)

then the response system (2) and the drive system (1) are completely synchronized.

Proof

Assume that the LMIs (8), (9), (25), (26), and (46) are feasible, then there exists a positive scalar $\hat{\epsilon }>\varepsilon$ such that the LMIs (8) with $\hat{\epsilon }$ instead of $\epsilon$, (9), (25) with $\hat{\varepsilon }$ instead of $\epsilon$, (26), and (46) still hold. For $t \ge - r$, define $\omega _i(t) = \mathrm{e}^{\hat{\epsilon } t}\int _\varOmega e^\mathrm{T}(t,x)P_ie(t,x)\mathrm{d}x$. Set $\overline{\omega }_i (t) = \mathop {\max }\nolimits _{ - r \le \theta \le 0} \omega _i(t + \theta )$, $i=1,2$, for $t\ge 0$. According to Lemmas 4–5, we have

$$\begin{aligned}&\overline{\omega }_1(t) \le \overline{\omega }_1 (t_{1k}),\quad t \in \overline{\varDelta }_{1k},\quad k \in \mathbb {N}_0, \end{aligned}$$

(49)

$$\begin{aligned}&\overline{\omega }_1(t_{2k})\le \mathcal{H}_1(\beta _1)\overline{\omega }_1(t_{1k}),\quad k\in \mathbb {N}_0,\quad k \in \mathbb {N}_0, \end{aligned}$$

(50)

and

$$\begin{aligned} \overline{\omega }_2(t) \le \overline{\omega }_2 (t_{2k})\mathcal{H}_2(\beta _2,\beta _3),\ t\in \overline{\varDelta }_{2k},\ k \in \mathbb {N}_0, \end{aligned}$$

(51)

Moreover, condition (46) implies that

$$\begin{aligned} \overline{\omega }_1(t) \le \mu _2\overline{\omega }_2(t), \mathrm{and}\ \overline{\omega }_2(t) \le \mu _1\overline{\omega }_1(t), \mathrm{for}\ t \ge 0. \end{aligned}$$

(52)

By virtue of (49)–(51), we deduce that

$$\begin{aligned}&\overline{\omega }_2(t_{1,k+1})\le \overline{\omega }_2(t_{2k})\mathcal{H}_2(\beta _2,\beta _3)\\&\le \mu _1\mathcal{H}_1(\beta _1)\mathcal{H}_2(\beta _2,\beta _3)\overline{\omega }_1(t_{1k}) \end{aligned}$$

It follows from (47) that

$$\begin{aligned}&\overline{\omega }_1(t_{1,k+1})\le \mu _1\mu _2\mathcal{H}_1(\beta _1)\mathcal{H}_2(\beta _2,\beta _3)\overline{\omega }_1(t_{1k})\\&\quad =\mathrm{e}^{\epsilon T}\overline{\omega }_1(t_{1k}), \end{aligned}$$

which implies

$$\begin{aligned} \overline{\omega }_1(t_{1k})\le \mathrm{e}^{k\epsilon T}\overline{\omega }_1(t_{10}),\ k\in \mathbb {N}_0. \end{aligned}$$

(53)

For any given $t\ge 0$, there exists $k\in \mathbb {N}_0$ such that $t\in \varDelta _{1k}$ or $t\in \varDelta _{2k}$. If $t\in \varDelta _{1k}$, it follows from (48) and (52) that

$$\begin{aligned} \overline{\omega }_1(t)\le \mathrm{e}^{k\epsilon T}\overline{\omega }_1(t_{10})\le \mathrm{e}^{\epsilon t}\overline{\omega }_1(t_{10}). \end{aligned}$$

(54)

If $t\in \varDelta _{2k}$, it follows from (48) and (52) that

$$\begin{aligned}&\overline{\omega }_2(t)\le \overline{\omega }_2(t_{2k})\mathcal{H}_2(\beta _2,\beta _3)\le \frac{1}{\mu _2}\mathrm{e}^{(k+1)\epsilon T}\overline{\omega }_1(t_{10})\nonumber \\&\quad \le \frac{\mathrm{e}^{\epsilon (T-\underline{\delta })}}{\mu _2}\mathrm{e}^{\epsilon t}\overline{\omega }_1(t_{10}). \end{aligned}$$

(55)

Set $\lambda _1=\min \nolimits _{i=1,2}\{\lambda _{\min }(P_i)\}$, and $\lambda _2=\lambda _{\max }(P_2)$. Combining with inequalities (53) and (54), we have

$$\begin{aligned} \Vert e(t,x)\Vert _2\le M\mathrm{e}^{-\frac{\hat{\epsilon }-\epsilon }{2}t}\Vert e_0\Vert _C, \end{aligned}$$

where $M=\sqrt{\lambda _2/\lambda _1\max \{1,(1/\mu _2)\mathrm{e}^{\epsilon (T-\underline{\delta })}\}}$. Therefore, we can conclude that synchronization error system (4) is globally exponentially stable.

Remark 2

Unlike [30], the stability analysis of synchronization error system (4) is performed by using a Razumikhin-type estimation technique. Compared with the Lyapunov functional-based analysis method proposed in [30], an attractive feature of our method is that there is no restriction on the derivatives of $\tau (t)$ and $\sigma (t)$, and more information on the bounds of the discrete delay $\tau (t)$ is taken into account. Therefore, our synchronization criterion is suitable for a wider class of delayed reaction–diffusion neural networks.

4 Intermittent controller design

In this section, under the assumption that

$$\begin{aligned} G_i\le 0 \le F_i,\quad \mathrm{for}\,\,i=1,2,\ldots ,n, \end{aligned}$$

(56)

we will present solutions to the exponential synchronization problem of the drive system (1) and the intermittently controlled response system (2). For this purpose, we set $\overline{L}_1=L_1^{\frac{1}{2}}$. Based on Theorem 1, we are ready to address the issue of periodically intermittent controller design.

Theorem 2

Given the control period T and the control width $\delta _k\in [\underline{\delta },\overline{\delta }]$ with $0<\underline{\delta }\le \overline{\delta }<T$, consider the drive system (1) and the periodically intermittently controlled response system (2), in which the activation function f satisfies (H). If for some prescribed positive scalars $\epsilon$, $\mu _1$, $\beta _i$, $\alpha _{ij}$, $i = 1,2,3, j=1,2$ satisfying $\beta _2 \ge \beta _3$, there exist $n\times n$ matrices $X_i>0$, $i = 1,2$, $n\times n$ positive diagonal matrices $\bar{\varLambda }_{ih}$, $i=1,2,3$, $h=0,1,2$, and a $n_c \times n$ matrix $\bar{K}$, such that the following LMIs hold:

$$\begin{aligned}&D_q X_i+X_iD_q\ge 0,\ i=1,2,\quad q=1,2,\ldots ,m, \end{aligned}$$

(57)

$$\begin{aligned}&\left[ {\begin{array}{*{20}{l}} {\Upsilon _i} &{}\quad 0 &{}\quad W_0\bar{\varLambda }_{i0}+X_iL_2 &{}\quad W_1\bar{\varLambda }_{i1} &{}\quad \overline{\sigma }W_2\bar{\varLambda }_{i2} &{}\quad 0 &{}\quad X_i{\overline{L}}_1\\ {*} &{}\quad -\alpha _{i1}X_i &{}\quad 0 &{}\quad X_iL_2 &{}\quad 0 &{}\quad X_i{\overline{L} }_1 &{}\quad 0\\ {*} &{}\quad {*} &{}\quad -\bar{\varLambda }_{i0} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad -\bar{\varLambda }_{i1} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad {*} &{}\quad -\overline{\sigma }\bar{\varLambda }_{i2} &{}\quad 0 &{}\quad 0\\ {*} &{}\quad {*} &{}\quad {*} &{}\quad {*} &{}\quad {*} &{}\quad -\bar{\varLambda }_{i1} &{}\quad 0 \\ {*} &{}\quad {*} &{}\quad {*} &{}\quad {*} &{}\quad {*} &{}\quad {*} &{}\quad -\bar{\varLambda }_{i0} \end{array}} \right] < 0,\quad i=1,2,3, \end{aligned}$$

(58)

$$\begin{aligned}&X_i\le \alpha _{i2}\tilde{L}^{-1}\bar{\varLambda }_{i2},\quad i=1,2,3 \end{aligned}$$

(59)

$$\begin{aligned}&X_2\le \mu _2X_1,\quad X_1\le \mu _1X_2 \end{aligned}$$

(60)

where $X_3=X_2$, $\mu _2$ is defined in (47), and

$$\begin{aligned} \Upsilon _1&= \left( \epsilon +\beta _1 +\alpha _{11}\mathrm{e}^{(\beta _1+\epsilon )\overline{\tau }} +\frac{\alpha _{12}}{\beta _1 + \epsilon }\left( \mathrm{e}^{\overline{\sigma }(\beta _1+\epsilon )}-1\right) \right) X_1\\&\quad -\,\sum \limits _{q = 1}^m \frac{\pi ^2}{4l_q^2}\big (D_q X_1 +\,X_1D_q\big )- AX_1 - X_1{A}^\mathrm{T}-B \overline{K}-(B \overline{K})^\mathrm{T},\\ \Upsilon _2&=\left( \epsilon -\beta _2 +\alpha _{21}\mathrm{e}^{\epsilon \overline{\tau }}+ \frac{\alpha _{22}}{\epsilon }\left( \mathrm{e}^{\epsilon \overline{\sigma } }-1\right) \right) X_2\\&\quad -\,\sum \limits _{q = 1}^m \frac{\pi ^2}{2l_q^2}\left( D_q X_2+X_2D_q\right) -\,AX_2 - X_2A^\mathrm{T},\\ \Upsilon _3&=\left( \epsilon -\beta _3 +\alpha _{31}H(\beta _3,\epsilon )+ \frac{\alpha _{32}}{\epsilon -\beta _3}\left( \mathrm{e}^{(\epsilon -\beta _3)\overline{\sigma } }-1\right) \right) X_2\\&\quad -\,\sum \limits _{q = 1}^m \frac{\pi ^2}{2l_q^2}\big (D_q X_2 +\,X_2D_q\big )- A X_2- X_2A^\mathrm{T}, \end{aligned}$$

then $K=\bar{K}X_1^{-1}$,the response system (2) and the drive system (1) are completely synchronized.

Proof

Define $P_i=X_i^{-1},\ i=1,2$, $\bar{\varLambda }_{jh}=\varLambda _{jh}^{-1},\ j=1,2,3,\ h=0,1,2$, and $K=\bar{K}X_1^{-1}$. It is easy to see that the matrix inequalities (56), (58), and (59) are equivalent to (7) and (24), (9) and (26), and (46), respectively. Set $P_3=P_2$. Pre- and post-multiplying (57) by diag$\{P_i,P_i,\varLambda _{i0},\varLambda _{i1},\varLambda _{i2},\varLambda _{i1},\varLambda _{i0}\}$, $i=1,2,3$, and using Schur complement, we obtain (8) and (25). Thus, the condition of Theorem 1 is satisfied. This means that the control gain K renders the synchronization error system (4) to be globally exponentially stable.

Remark 3

The results in [30–32] are only concerned with deriving some sufficient conditions for periodically intermittent synchronization. Since these sufficient conditions are related to the solutions to some transcendental equations, it is difficult to apply these sufficient conditions for designing synchronization controllers. The synchronization criterion presented in Theorem 1, however, is expressed in the form of matrix inequalities. By using matrix transformation technique, the design problem of synchronization controllers is reduced to a feasibility problem of the LMIs given in Theorem 2.

Table 1 Values of the tuning parameters for various T

Table 2 The minimum rates of control time for various T

Remark 4

From a practical point of view, it is desirable to design a controller with small gain. This is because the designed controllers with small gains will reduce the energy consumption. Therefore, we propose the following optimization problem to limit the norm of gain matrix K.

$$\begin{aligned} \begin{aligned} \text {minimize}&\quad \nu \\ \text {subject to}&\; \begin{bmatrix} X_1&\quad {\bar{K}}^\mathrm{T} \\ *&\quad -\eta _0\nu ^2 \\ \end{bmatrix}<0, \\&\; X_1\ge \eta _0I, (56)-(59). \end{aligned} \end{aligned}$$

(61)

The optimization problem (60) can be solved by using the following algorithm.

Algorithm 1. (Intermittent synchronization controller design algorithm)

Step 1: Set initial $\nu$ and step length h.

Step 2: Solving the LMIs in the constraint condition of the optimization problem (60) to obtain $\bar{K}$.

Step 3: If Step 2 gives a feasible solution, set $\nu =\nu -h$ and return to Step 2. Otherwise, stop.

If $\nu _{\min }$ is the minimum value of the optimization problem (60), then the spectral norm of gain matrix K satisfies $\Vert F\Vert \le \nu _{\min }$.

5 Numerical examples

In this section, the applicability of the derived synchronization results is illustrated through two numerical examples.

Example 1

In order to show the less conservatism of our result, we consider the example given in [30] for comparison. The drive system of the example is a two-dimensional delayed reaction–diffusion neural network with the form of (1), in which $\varOmega =[-5,5]$ and $m=1$, and the system parameters are as follows:

$$\begin{aligned} D_1= & {} 0.1I_2,\ A=I_2,\ W_0=\left[ \begin{array}{lll} 1.8 &{}\quad -0.15 \\ -5.2 &{}\quad 3.5 \end{array}\right] ,\\&W_1=\left[ \begin{array}{lll} -1.7 &{}\quad -0.12 \\ -0.26 &{}\quad -2.5 \end{array}\right] , W_2=\left[ \begin{array}{lll} 0.6 &{}\quad 0.15 \\ -2 &{}\quad -0.1 \end{array}\right] ,\\&\quad J=0,\quad \tau _i(t)=\frac{e^t}{e^t+1},\ i=1,2,\ \sigma (t)=1,\ \end{aligned}$$

and the activation functions are given by $f_i(s)=\tanh (s),\ \mathrm{for}\ s\in \mathbb {R},\ i=1,2$, the corresponding intermittently controlled response system is described by (2) and (3) with $BK =\mathrm{diag}(6,16)$.

It is easy to verify that $\underline{\tau }=0.5$, $\overline{\tau }=1$, $\overline{\sigma }=1$, $L_1=0$, $L_2=0.5I_2$, and $\tilde{L}=I_2$. To compare our result with the result of [30], we assume that the control width $\delta _k$ is constant, i.e., $\delta _k=\delta$ for all $k\in \mathbb {N}_0$. Now, for given control period T, we apply our Theorem 1 to find the minimum rate of control time defined by $\kappa =\delta /T$, which guarantee the complete synchronization of the drive and response system. When the control period T is selected as $T= 0.5,\, 1,\, 2,\, 3,\, 5$ and 10 successively, by solving the LMIs of Theorem 1 with the choice of the corresponding values of parameter vector $(\epsilon ,\mu _1,\beta _1,\beta _2,\beta _3,\alpha _{11},\alpha _{12},\alpha _{21},\alpha _{22},\alpha _{31},\alpha _{32})$ given in Table 1, the obtained maximum rates of control times for different control period T are listed in Table 2. The calculation results in Table 2 show that the rate of control time actually decreases as we increase the value of control period T.

For this example, both the results of [31, 32] fail to verify the stability of the synchronization error system. The synchronization condition given in [30] relies on the discrete-delay derivative $\dot{\tau }_i(t)$, $i=1,2$. It is easy to that $s_i\triangleq \inf \nolimits _{t\ge 0}\{1-\dot{\tau }(t)\}=0.75$. However, in [30], the values of $s_i$, $i=1,2$, are taken as $s_i=1$, $i=1,2$. Moreover, according to Corollary 3 of [30], the synchronization criterion given in Corollaries 4–5 of [30] is incorrect. By applying the synchronization criterion of Corollary 3 in [30] with $s_i=0.75$, $=1,2$, the minimum value of $\kappa$ for any control period T is 0.994. Clearly, the calculations show that our method improves the corresponding one in [30–32].

For simulation studies, the initial value and boundary value conditions of the drive system are chosen as

$$\begin{aligned} z(s,x)&=\left( \sin ^{2}(\pi x),2\sin ^{2}\left( \frac{\pi x}{5}\right) \right) ^\mathrm{T},\nonumber \\&(s,x)\in [-1,0]\times \varOmega , \\ z(t,x)&=0,\ (t,x)\in [-1,+\infty )\times \partial \varOmega , \end{aligned}$$

(62)

The temporal evolution of the drive system with the initial condition (61) and the boundary value condition (62) is depicted in Fig. 1. In this situation, the drive system exhibits spatiotemporal chaotic behavior. To illustrate the effectiveness of our intermittent synchronization criterion, we choose $T=0.5$ and $\delta =0.4669$. Then, $\kappa =0.9338$. According to Table 2, the complete synchronization of the intermittently coupled neural networks can be achieved. Since $0.9338<0.994$, the synchronization criterion given in [30] fails to work. We assume that the initial value and boundary value conditions of the intermittently controlled response system are given by

$$\begin{aligned} \hat{z}(s,x)&=\left( -0.7\sin ^{2}(\pi x),1.4\sin ^{2}\left( \frac{\pi x}{5}\right) \right) ^\mathrm{T},\\&\quad (s,x)\in [-1,0]\times \varOmega ,\\ \hat{z}(t,x)&=0,\quad (t,x)\in [-1,+\infty )\times \partial \varOmega , \end{aligned}$$

The spatiotemporal evolution of synchronization error e(t, x) is depicted in Fig. 2. Referring to this figure, it can seen that the synchronization error becomes sufficiently small for $t>2$ s, which indicates that the synchronization is successfully achieved.

Fig. 1

Spatiotemporal chaotic behavior of the neural network described in Example 1

Fig. 2

Spatiotemporal evolution of synchronization error e(t, x) for Example 1

Example 2

Consider a delayed reaction–diffusion neural network to be the drive system (1) with the following parameters:

$$\begin{aligned} \begin{aligned} {D_1}&= {10^{ - 4}}I,A = {\text {I}},m = 1, \\ \varOmega&= [ - 0.5,0.5],\tau (t) = 0.9,\sigma (t) = 0.1. \\ W_0&= \left[ {\begin{array}{*{20}{l}} 1+\frac{\pi }{4} &{}\quad 20 &{}\quad 0.001 \\ 0.1 &{}\quad 1+\frac{\pi }{4} &{}\quad 0.001 \\ 3 &{}\quad -0.56 &{}\quad -0.12 \end{array}} \right] , \\ W_1&= \left[ {\begin{array}{*{20}{l}} -1.3\sqrt{2}\frac{\pi }{4} &{}\quad 0.1 &{}\quad -0.001 \\ 0.1 &{}\quad -1.3\sqrt{2}\frac{\pi }{4} &{}\quad 0.01 \\ 2 &{}\quad -0.85 &{}\quad -0.02 \end{array}} \right] ,\\ W_2&= \left[ {\begin{array}{*{20}{l}} 0.06 &{}\quad 0.15 &{}\quad 0 \\ -0.2 &{}\quad -0.01 &{}\quad 0.01 \\ 0 &{}\quad 0.02 &{}\quad 0.03 \end{array}} \right] ,\quad J = \left[ {\begin{array}{*{20}{l}} 0 \\ 0 \\ 0 \end{array}} \right] ,\\ \end{aligned} \end{aligned}$$

and the activation functions are given by ${f_i}(x) = \frac{{|x + 1| - |x - 1|}}{2},i = 1,2,3$. The corresponding intermittently controlled response system is described by (2) with $B^\mathrm{T} =\left[ \begin{array}{lll}1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0\end{array}\right] ^\mathrm{T}$.

One can verify that the assumption (H) is satisfied. Moreover, $\underline{\tau }=\overline{\tau }=0.9$, $\overline{\sigma }=0.1$, $L_1=0$, $L_2=0.5I_3$, and $\tilde{L}=I_3$. For given control period $T=2$, and the control width $\delta _k\in [1.86,1.9]$, solving the optimization problem (60) with the choice of

$$\begin{aligned}&\left( \epsilon ,\mu _1,\beta _1,\beta _2,\beta _3,\alpha _{11},\alpha _{12},\alpha _{21},\alpha _{22},\alpha _{31},\alpha _{32}\right) \\&\quad =(0.18,1.74,0.98,8.99,7.88,0.24,0.03,1.23,\\&\quad 0.93,2.66,1.01), \end{aligned}$$

the obtained minimum value of $\nu$ is $\nu =31.79$. The corresponding intermittent synchronization gain is given by $K = \left[ {\begin{array}{lll} 6.0933 &{}\quad 1.2837 &{}\quad -0.0658\\ -0.2258 &{}\quad 31.6819 &{}\quad 0.0126 \end{array}} \right]$. For simulation studies, the initial conditions of the drive system and the response system are set to

$$\begin{aligned} \phi (s,x)= & {} \left( \cos ^{2}(\pi x),\sin ^{2}(2\pi x),\frac{1}{2}\cos ^{2}(\pi x)\right) ^\mathrm{T},\nonumber \\&\quad (s,x)\in [-0.9,0]\times \varOmega , \end{aligned}$$

(63)

and

$$\begin{aligned} \hat{\phi }(s,x)= & {} \left( \cos (\pi x)\sin ^2(2\pi x),\frac{3}{2}\cos (\pi x),2\sin ^{2}(4\pi x)\right) ^\mathrm{T},\\&\quad (s,x)\in [-0.9,0]\times \varOmega , \end{aligned}$$

respectively. Moreover, the drive system and the response system are supplemented with the following Dirichlet boundary value conditions:

$$\begin{aligned} z(t,x)=\hat{z}(t,x)=0,\quad (t,x)\in [-0.9,+\infty )\times \partial \varOmega . \end{aligned}$$

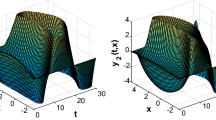
With the initial condition (63) and the Dirichlet boundary value condition, the drive system exhibits a chaotic behavior as shown in Fig. 3a–c. To illustrate the effect of intermittent feedback on the synchronization performance, we assume that the control width $\delta _k$ is generated randomly with the constraint that $1.86\le \delta _k\le 1.9$. The spatiotemporal evolution of the synchronization error e(t, x) is depicted in Fig. 4a–c. Referring to this figure, it can be seen that the synchronization is achieved for $t>8\,\mathrm{s}$, showing the effectiveness of the proposed intermittent synchronization controller design method.

Fig. 3

Spatiotemporal chaotic behavior of the neural network described in Example 2

Fig. 4

Spatiotemporal evolution of synchronization error e(t, x) for Example 2

6 Conclusions

The periodically intermittent synchronization problem for coupled reaction–diffusion neural networks with mixed delays has been revisited. A novel piecewise exponential-type Lyapunov function-based method has been introduced to analyze the stability of the synchronization error system. The new method is based on the subtle estimates on the decay/divergent rate of solutions during closed-/open-loop mode. Consequently, an improved synchronization result has been derived, which can provide smaller rate of control time than the previous results. Based on the established synchronization criterion, a LMI-based sufficient condition for designing desired synchronization controllers has been presented. Two numerical examples have shown the effectiveness of the proposed results. The idea behind this paper may be further extended to the intermittent synchronization problem of complex dynamical networks governed by coupled parabolic partial differential equations with time delays. It is worth mentioning that in comparison with continuous synchronization method, the proposed intermittent synchronization scheme can greatly reduce the amount of information required to be transmitted to achieve synchronization of transmitter and receiver. Furthermore, the spatiotemporal chaos model has greater volume keys and key space than the time chaos model and thus can improve additionally security. Theses characteristics are important for secure communication and encryption schemes. The applications of the proposed intermittent synchronization scheme to secure communication would be discussed in the follow-up work.