1 Introduction

Many systems encountered in practice involve a jump between many continuous or discrete dynamics systems, which be called switched system [1–3]. As a special class of hybrid system, it consists of a finite number of modes, which may jump from one to another according to a switching rule, has become a popular subject, since it is successfully applied to many real life, e.g., a valve or a power switch opening and closing, a thermostat turning the heat on and off, and a server switching between buffers in a queueing network. At the same time, it has been widely studied to many fields such as air traffic control, robotics, automotive industry, aircraft, and power systems. Therefore, the stability and synchronization problem of switched networks [4] with control or without control have gained scholars’ attentions. The recent paper [5] considered mode-dependent impulsive effects to coupled switched neural networks, the impulsive effects can exist not only at the instants coinciding with the system switching but also at the instants when there is no system switching. On the other hand, due to finite switching speed of amplifies and communication speed between the neurons, time delays often exist in the electronic implementations of neural networks, which may lead to exhibit oscillation or other unstable behaviors. Taking factors of modeling error, external perturbation, and parameter fluctuation into consideration, robust stability analysis of neural networks with time delay has been widely studied [6]. However, there are mainly two forms of uncertainties: interval uncertainty and norm-bounded uncertainty. Up to now, the dynamical behavior of switched interval coupled networks with time-varying delay has a few results, despite its practical importance. Hence, it is of great importance to study synchronization of switched delay networks with interval parameters uncertainty.

Generally speaking, large scale networks cannot synchronize by itself, to reach the synchronization, Heagy et al. [7] proposed the drive-response concept to reach the synchronization of coupled chaotic systems, synchronization control problem of complex networks attracts more and more researchers’ attentions. So far, kinds of effective control approaches and techniques have been proposed for synchronization of complex systems including linear feedback control [8], switching control [9], impulsive control [10], Pinning control [11, 12], intermittent control [13–16], and others. As a special discontinuous feedback control, intermittent control is activated during some intervals and does not work over the other intervals, it can reduce the control time and control cost and has been extensively used in engineering control. In [15], by using Lyapunov stability theory and intermittent control technique, the intermittent controllers and corresponding parameter updating rules were designed to obtain lag synchronization of coupled systems with parameter mismatch, and then the error bound of lag synchronization was estimated in accordance with the parameter mismatch. Moreover, the error level can be smaller than existing results. Authors studied the exponential stochastic synchronization problem for coupled neural networks with stochastic noise perturbations. Based on Lyapunov stability theory, inequality techniques, the properties of Weiner process, and added different intermittent controllers, several sufficient conditions were obtained to ensure exponential stochastic synchronization of coupled neural networks with or without coupling delays under stochastic perturbations. Moreover, the results of this letter were applicable to both directed and undirected weighted networks [16]. A brief review on previous resulting reveals that what these approaches focused on the synchronization or stability of switched neural networks under arbitrary switching rule by using common Lyapunov function method. As we all know, Lyapunov function method requires all the subsystems of the switched system to share a positive definite common Lyapunov function, this requirement is difficult to achieve. These motivate us to develop some procedures to solve the synchronization problem for switched systems.

Matrix measure approach has been proposed to deal with synchronization problem for neural networks [17–20], without constructing Lyapunov function, it is an effective method to obtain synchronization criteria for switched systems. In [18], authors investigated matrix measure \(\mu _{\infty }\) to study exponential synchronization of chaotic neural networks, neither symmetry nor negative (positive) definiteness of the coupling matrix was required, the proposed sufficient conditions for exponential synchronization were easy to verify.

Motivated by the preceding discussion, the main purpose is to study the global exponential drive-response synchronization problem for a class of switched interval delay networks with intermittent and feedback control, different to \(1\)-measure, we will first introduce the \(\omega \)-measure [21] to switched interval networks, combining Halanay inequality technique, designing the coupling control gain matrix, several synchronization criteria are presented for switched interval networks under the arbitrary switching rule, which are easy to verify in practice. Furthermore, simulations show switched systems can be reached to synchronization when all subsystems are chaotic neural networks [22]. The main contributions of this paper can be highlighted as follows: (1) consider the interval parameters fluctuation, a new mathematical model of the switched coupled networks with parameters in interval is established, which presents more practical significance of our current research. (2) Firstly introduce \(\omega \)-measure to switched system, proposed results are easy to verify and generalize the previous results. (3) The obtained criteria can be applied to chaotic system. (4) Moreover, the switched interval networks change as interval networks when \(N=1\), the synchronization criteria for interval networks can be seen as a special case of our main results.

The rest of this paper is organized as follows. In Sect. 2, the model description and preliminaries are given. Section 3 treats of global exponential synchronization problems for switched interval networks with intermittent control. In Sect. 4, synchronization criteria for switched interval networks with feedback control are developed. Two examples are given to demonstrate the validity of the proposed results in Sect. 5. Some conclusions are drawn in Sect. 6.

Notations: Throughout this paper, for any matrix \(A\), \(A>0\) ((\(A<0\))) means that \(A\) is positive definite ( negative definite), \(A^{T}\) denotes the transpose of \(A\). \(\lambda _{\max }(A)\) and \(\lambda _{\min }(A)\) denote the maximum and minimum eigenvalue of \(A\), respectively. \(E\) is the identity matrix. The norm of piecewise right continuous function \(\eta (t)\) is denoted by \(\Vert \eta \Vert _{\tau }=\sup \nolimits _{t_{0}-\tau \le s\le t_{0}}\Vert \eta (t+s)\Vert _{\omega }\). Matrices, if their dimensions not explicitly stated, are assumed to have compatible dimensions for algebraic operations.

2 Model description and preliminaries

Consider a general class of interval networks with discrete time-varying delay described by the following

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)=-Ax(t)+B_{1}g_{1}(x(t))+\,B_{2}g_{2}(x(t\\ -\tau (t)))+J,\\ A\in {A_{l}},\quad B_{k}\in {B_{l}^{(k)}},\quad k=1,2, \end{array}\right. } \end{aligned}$$
(1)

where \(x(t)=\left( x_{1}(t), \ldots , x_{n}(t)\right) ^{T}\in R^{n}\) is the vector of neuron states; \(g_{i}(x)=\left( g_{i1}(x_{1}), \ldots , g_{in}(x_{n}\right) )^{T}: R^{n}\rightarrow R^{n}, i=1,\ 2\) are the vector-valued neuron activation functions; \(\tau (t)\) is the transmission time-varying delay; \(J=\left( J_{1}, \ldots , J_{n}\right) ^{T}\) is a constant external input vector. \(A=\text {diag}(a_{1}, \ldots , a_{n})\) is an \(n\times n\) constant diagonal matrices, \(a_{i}>0, \ i=1, \ldots , n\), are the neural self-inhibitions; \(B_{k}=(b_{ij}^{(k)})\in R^{n\times n}, k=1,\ 2\), are the connection weight matrices, and \(A_{l}=[\underline{A},\overline{A}]= \{A=\text {diag}(a_{i}):\ 0< \underline{a}_{i} \le a_{i} \le \overline{a}_{i}, i=1 , 2, \ldots , n\}\), \(B_{l}^{(k)}=\left[ \underline{B}_{k}, \overline{B}_{k} \right] =\big \{B_{k}=\big (b_{ij}^{(k)}\big ): \underline{b}_{ij}^{(k)} \le b_{ij}^{(k)} \le \overline{b}_{ij}^{(k)}, \ i, j=1, 2, \ldots , n\big \}\) with \(\underline{A}=\text {diag}(\underline{a}_{1}, \underline{a}_{2}, \ldots , \underline{a}_{n}), \overline{A}=\text {diag}(\overline{a}_{1}, \overline{a}_{2}, \ldots , \overline{a}_{n}), \underline{B}_{k}=\big (\underline{b}_{ij}^{(k)}\big )_{n\times n}, \overline{B}_{k}=\big (\overline{b}_{ij}^{(k)}\big )_{n\times n}\).

Throughout this paper, the following assumptions are made on \(g_{i}(\cdot ),i=1,2\) and \(\tau (t)\):

\((\mathcal {H}_{1})\): For any two different \(s,\ t\in R\), there exist constants \(l_{ij}>0\), \(i=1,2,\ j=1,2,\ldots ,n\), such that

$$\begin{aligned} |g_{ij}(s)-g_{ij}(t)| \le l_{ij}|s-t| ,\ i=1, 2,\ j=1, \ldots , n \end{aligned}$$

\((\mathcal {H}_{2})\): Time-varying delay \(\tau (t)\) satisfies

$$\begin{aligned} 0\le \tau (t)\le \tau , \end{aligned}$$

where \(\tau \) is a positive constant.

To reach synchronization of system (1) by periodically intermittent control, the response (slave) system can be designed as

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\dot{y}(t)=-Ay(t)+B_{1}g_{1}(y(t))\\ &{}\qquad \qquad +B_{2}g_{2}(y(t-\tau (t)))+J+U(t),\\ &{} A\in {A_{l}},\quad B_{k}\in {B_{l}^{(k)}},\quad k=1,2, \end{array}\right. } \end{aligned}$$
(2)

where \(y(t)=\left( y_{1}(t), \ldots , y_{n}(t)\right) ^{T}\) is the neuron state of response system. We choose intermittent strategy as follows:

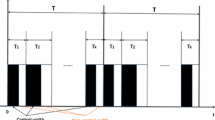
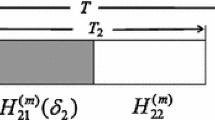
$$\begin{aligned} U(t) = \left\{ {\begin{array}{*{20}l} {K(y(t) - x(t)),} &{}\quad {lT \le t \le lT + \delta ;} \\ {0,} &{}\quad {lT + \delta \le t \le (l + 1)T,} \\ \end{array} } \right. \end{aligned}$$

where matrix \(K\in R^{n\times n}\) is the constant intermittent control gain to be designed, \(T >0\), \(\delta >0\) are the control period and the control width, respectively, and \(l=0,\ 1\ ,2\ \ldots \).

Let error state \(e(t)=y(t)-x(t)\), then error dynamical system between the states of drive system (1) and response system (2) can be derived:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{e}(t)&{}=-Ae(t)+B_{1}f_{1}(e(t))+B_{2}f_{2}(e(t-\tau (t)))\\ &{}\quad \;+Ke(t),\quad l T\le t\le l T+\delta ,\\ \dot{e}(t)&{}=-Ae(t)+B_{1}f_{1}(e(t))+B_{2}f_{2}(e(t-\tau (t))),\\ &{}\qquad l T+\delta \le t\le (l+1)T,\\ &{} A\in {A_{l}},\quad B_{k}\in {B_{l}^{(k)}},\quad k=1,2, \end{array}\right. } \end{aligned}$$
(3)

where \(e(t)=\left( e_{1}(t), \ldots , e_{n}(t)\right) ^{T}\), \(f_{1}(e(t))=g_{1}(e(t)+x(t))-g_{1}(x(t))\), \(f_{2}(e(t-\tau (t)))=g_{2}(e(t-\tau (t))+x(t- \tau (t)))-g_{2}(x(t-\tau (t)))\).

Based on some transformations [23], the interval error system (3) can be equivalently written as

$$\begin{aligned} \begin{aligned} \dot{e}(t)&=-[A_{0}+E_{A}\Sigma _{A}F_{A}]e(t)+[B_{10} +E_{1}\Sigma _{1}F_{1}]\\&\quad \;\times f_{1}(e(t))+[B_{20}+E_{2}\Sigma _{2}F_{2}]f_{2}(e(t-\tau (t)))\\&\quad \;+Ke(t),\quad l T\le t\le l T+\delta ,\\ \dot{e}(t)&=-[A_{0}+E_{A}\Sigma _{A}F_{A}]e(t)+[B_{10} +E_{1}\Sigma _{1}\\&\quad \; F_{1}]f_{1}(e(t))+[B_{20}+E_{2}\Sigma _{2}F_{2}]f_{2}(e(t-\tau (t))),\\&\qquad l T+\delta \le t\le (l+1)T, \end{aligned} \end{aligned}$$
(4)

where \(\Sigma _{A}\in \Sigma ,\ \Sigma _{k}\in \Sigma ,\ k=1,2\).

$$\begin{aligned}&\!\!\!\Sigma =\{\text {diag}[\delta _{11},\ldots ,\delta _{1n},\ldots ,\delta _{n1},\ldots ,\\&\!\!\!\delta _{nn}]\in R^{n^{2}\times n^{2}}: | \delta _{ij}|\le 1,\ i,j=1,2,\ldots ,n\}.\\&\!\!\!A_{0}=\frac{\overline{A}+\underline{A}}{2},\quad H_{A} =[\alpha _{ij}]_{n\times n}=\frac{\overline{A}- \underline{A}}{2}.\\&\!\!\!B_{k0}=\frac{\overline{B}_{k}+ \underline{B}_{k}}{2},\quad H_{B}^{(k)}=[\beta _{ij}]_{n\times n}=\frac{\overline{B}_{k}-\underline{B}_{k}}{2}.\\&\!\!\!E_{A}=\Big [\sqrt{\alpha _{11}}e_{1},\ldots ,\sqrt{ \alpha _{1n}}e_{1},\ldots ,\\&\quad \quad \quad \sqrt{\alpha _{n1}}e_{n},\ldots , \sqrt{\alpha _{nn}}e_{n}\Big ]_{n\times n^{2}},\\&\!\!\!F_{A}=\Big [\sqrt{\alpha _{11}}e_{1},\ldots ,\sqrt{\alpha _{1n}}e_{n},\ldots ,\\&\quad \quad \quad \sqrt{\alpha _{n1}}e_{1},\ldots ,\sqrt{ \alpha _{nn}}e_{n}\Big ]_{n^{2}\times n}^{T},\\&\!\!\!E_{k}=\Big [\sqrt{\beta _{11}^{(k)}}e_{1},\ldots ,\sqrt{ \beta _{1n}^{(k)}}e_{1}, \ldots ,\\&\quad \quad \quad \sqrt{\beta _{n1}^{(k)}}e_{n}, \ldots ,\sqrt{\beta _{nn}^{(k)}}e_{n}\Big ]_{n\times n^{2}},\\&\!\!\!F_{k}=\Big [\sqrt{\beta _{11}^{(k)}}e_{1},\ldots ,\sqrt{ \beta _{1n}^{(k)}}e_{n}, \ldots ,\\&\quad \quad \quad \sqrt{\beta _{n1}^{(k)}}e_{1}, \ldots ,\sqrt{\beta _{nn}^{(k)}}e_{n}\Big ]_{n^{2}\times n}^{T}, \end{aligned}$$

where \(e_{i}\in R^{n}\) denotes the column vector with \(ith\) element to be \(1\) and others to be \(0\).

System (4) has an equivalent form by the following

$$\begin{aligned} \begin{aligned} \dot{e}(t)=&-A_{0}e(t)+B_{10}f_{1}(e(t))+B_{20}f_{2}\\&\quad (e(t-\tau (t)))+E\Delta (t)+Ke(t),\\&\qquad \qquad \qquad l T\le t\le l T+\delta ,\\ \dot{e}(t)=&-A_{0}e(t)+B_{10}f_{1}(e(t))\\&\quad +B_{20}f_{2}(e(t-\tau (t)))+E\Delta (t),\\&\qquad \qquad \qquad l T+\delta \le t\le (l+1)T, \end{aligned} \end{aligned}$$
(5)

where \(E=[E_{A},E_{1},E_{2}]\),

$$\begin{aligned} \Delta (t)&=\left[ \begin{array}{ccc} -\Sigma _{A}F_{A}e(t)\\ \Sigma _{1}F_{1}f_{1}(e(t)) \\ \Sigma _{2}F_{2}f_{2}(e(t-\tau (t))) \end{array} \right] \\&=\text {diag}\{\Sigma _{A},\Sigma _{1},\Sigma _{2}\} \left[ \begin{array}{ccc} -F_{A}e(t)\\ F_{1}f_{1}(e(t)) \\ F_{2}f_{2}(e(t-\tau (t))) \end{array}\right] , \end{aligned}$$

and \( \Delta (t)\) satisfies the following matrix quadratic inequality:

$$\begin{aligned}&\Delta ^{T}(t)\Delta (t)\le \left[ \begin{array}{ccc} e(t)\\ f_{1}(e(t)) \\ f_{2}(e(t-\tau (t))) \end{array}\right] ^{T}\left[ \begin{array}{ccc} F_{A}^{T}\\ F_{1}^{T}\\ F_{2}^{T} \end{array}\right] \nonumber \\&\quad \left[ \begin{array}{ccc} F_{A}^{T}\\ F_{1}^{T}\\ F_{2}^{T} \end{array}\right] ^{T}\left[ \begin{array}{ccc} e(t)\\ f_{1}(e(t)) \\ f_{2}(e(t-\tau (t))) \end{array}\right] . \end{aligned}$$
(6)

The switched interval networks with time-varying delay consist of a set of interval networks with discrete time-varying delay and a switching rule [24]. Each of the interval networks regarded as an individual subsystem. The operation mode of the switched networks is determined by the switching signal. According to (1), the switched interval networks with discrete time-varying delay can be represented as follows:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} &{}\dot{x}(t)=-A_{\sigma (t)}x(t)+B_{1_{ \sigma (t)}}g_{1}(x(t))\\ &{}\qquad \qquad +B_{2_{\sigma (t)}}g_{2}(x(t-\tau (t)))+J,\\ &{}A_{\sigma (t)}\in {A_{l_{\sigma (t)}}},\quad B_{k_{\sigma (t)}}\in {B_{l_{\sigma (t)}}^{(k)}},\quad k=1,2, \end{array}\right. } \end{aligned} \end{aligned}$$
(7)

where \(A_{l_{\sigma (t)}}=[\underline{A}_{\sigma (t)}, \overline{A}_{\sigma (t)}]= \{A_{\sigma (t)}=\text {diag}(a_{i_{\sigma (t)}}):\) \(\ 0<\underline{a}_{i_{\sigma (t)}}\le a_{i_{\sigma (t)}}\le \overline{a}_{i_{\sigma (t)}},i=1,2,\ldots ,n\},\) \(B_{l_{\sigma (t)}}^{(k)}=\left[ \underline{B}_{k_{\sigma (t)}}, \overline{B}_{k_{\sigma (t)}}\right] =\{B_{k_{\sigma (t)}}= [b_{ij_{\sigma (t)}}^{(k)}]: \) \(0<\underline{b}_{ij_{ \sigma (t)}}^{(k)}\le b_{ij_{\sigma (t)}}^{(k)}\le \overline{b}_{ij_{\sigma (t)}}^{(k)},\ i, j=1,2,\ldots ,n\}\) with

$$\begin{aligned} \underline{A}_{\sigma (t)}&=\text {diag}(\underline{a}_{1_{\sigma (t)}}, \underline{a}_{2_{\sigma (t)}},\ldots ,\underline{a}_{n_{\sigma (t)}}),\\ \overline{A}_{\sigma (t)}&=\text {diag}(\overline{a}_{1_{\sigma (t)}}, \overline{a}_{2_{\sigma (t)}},\ldots ,\overline{a}_{n_{\sigma (t)}}),\\ \underline{B}_{k_{\sigma (t)}}&=[\underline{b}_{ij_{ \sigma (t)}}^{(k)}]_{n\times n},\quad \overline{B}_{k_{\sigma (t)}}=[\overline{b}_{ij_{ \sigma (t)}}^{(k)}]_{n\times n}.\\ A_{0_{\sigma (t)}}&=\frac{\overline{A}_{\sigma (t)}+ \underline{A}_{\sigma (t)}}{2},\quad H_{A_{\sigma (t)}}=[\alpha _{ij_{\sigma (t)}}]_{n\times n}\\&=\frac{\overline{A}_{\sigma (t)}-\underline{A}_{\sigma (t)}}{2}.\\ B_{k0_{\sigma (t)}}&=\frac{\overline{B}_{k_{\sigma (t)}}+ \underline{B}_{k_{\sigma (t)}}}{2}, H_{B_{\sigma (t)}}^{(k)}\\&=[\beta _{ij_{\sigma (t)}}]_{n\times n}=\frac{\overline{B}_{k_{\sigma (t)}}- \underline{B}_{k_{\sigma (t)}}}{2}.\\ E_{A_{\sigma (t)}}&=\big [\sqrt{\alpha _{11_{\sigma (t)}}}e_{1}, \ldots ,\sqrt{\alpha _{1n_{\sigma (t)}}}e_{1},\ldots ,\\&\quad \sqrt{\alpha _{n1_{\sigma (t)}}}e_{n},\ldots ,\sqrt{ \alpha _{nn_{\sigma (t)}}}e_{n}\big ]_{n\times n^{2}}.\\ F_{A_{\sigma (t)}}&=\big [\sqrt{\alpha _{11_{\sigma (t)}}}e_{1}, \ldots ,\sqrt{\alpha _{1n_{\sigma (t)}}}e_{n},\ldots ,\\&\quad \sqrt{\alpha _{n1_{\sigma (t)}}}e_{1},\ldots , \sqrt{\alpha _{nn_{\sigma (t)}}}e_{n}\big ]_{n^{2}\times n}^{T}. E_{k_{\sigma (t)}}\\&\quad =\left[ \sqrt{\beta _{11_{\sigma (t)}}^{(k)}}e_{1},\ldots ,\right. \\&\quad \sqrt{\beta _{1n_{\sigma (t)}}^{(k)}}e_{1}, \ldots ,\sqrt{\beta _{n1_{\sigma (t)}}^{(k)}}e_{n},\ldots ,\\&\quad \left. \sqrt{\beta _{nn_{\sigma (t)}}^{(k)}}e_{n}\right] _{n\times n^{2}}.\\ F_{k_{\sigma (t)}}&=\left[ \sqrt{\beta _{11_{\sigma (t)}}^{(k)}}e_{1},\ldots ,\sqrt{\beta _{1n_{\sigma (t)}}^{(k)}}e_{n}, \ldots ,\right. \\&\quad \left. \sqrt{\beta _{n1_{\sigma (t)}}^{(k)}}e_{1},\ldots ,\sqrt{\beta _{nn_{\sigma (t)}}^{(k)}}e_{n}\right] _{n^{2}\times n}^{T}. \end{aligned}$$

\(\sigma (t):[0,+\infty )\rightarrow \Gamma =\{1, 2, \ldots ,N\}\) is the switching signal, which is a piecewise constant function of time. For any \(i\in \{1, 2, \ldots ,N\}\), \(A_{i}=A_{0_{i}}+E_{A_{i}}\Sigma _{A_{i}}F_{A_{i}}\), \(B_{k_{i}}=B_{k0_{i}}+E_{k_{i}}\Sigma _{k_{i}}F_{k_{i}}\), and \(\Sigma _{A_i}\in \Sigma ,\ \Sigma _{k_i}\in \Sigma ,\ k=1,2\). This means that the matrices \((A_{\sigma (t)},B_{1_{\sigma (t)}},B_{2_{\sigma (t)}})\) are allowed to take values, at an arbitrary time, in the finite set \(\{(A_{1},B_{1_{1}},B_{2_{1}}), (A_{2},B_{1_{2}},B_{2_{2}}), \ldots , (A_{N},B_{1_{N}},B_{2_{N}})\}\). In this paper, it is assumed that the switching rule \(\sigma \) is not known a priori and its instantaneous value is available in real time.

Analogously, slave (response) system [25] of switched interval networks should be defined as

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} &{}\dot{y}(t)=-A_{\sigma (t)}y(t)+B_{1_{\sigma (t)}}g_{1} (y(t))\\ &{}\qquad \qquad +\,B_{2_{\sigma (t)}}g_{2}(y(t-\tau (t)))+J+U(t),\\ &{}A_{\sigma (t)}\in {A_{l_{\sigma (t)}}},\ \ \ B_{k_{\sigma (t)}}\in {B_{l_{\sigma (t)}}^{(k)}},\quad k=1,2, \end{array}\right. } \end{aligned} \end{aligned}$$
(8)

From Eq. (5), we have the switched interval drive-response error dynamical system as follows:

$$\begin{aligned} \begin{aligned} \dot{e}(t)=&-A_{0_{\sigma (t)}}e(t)+B_{10_{\sigma (t)}} f_{1}(e(t))\\&+B_{20_{\sigma (t)}}f_{2}(e(t-\tau (t))) +E_{\sigma (t)}\Delta _{\sigma (t)}(t)\\&+K_{\sigma (t)}e(t),\quad l T\le t\le l T+\delta ,\\ \dot{e}(t)=&-A_{0_{\sigma (t)}}e(t)+B_{10_{\sigma (t)}}f_{1}(e(t))\\&+B_{20_{\sigma (t)}}f_{2}(e(t-\tau (t))) +E_{\sigma (t)}\Delta _{\sigma (t)}(t), \\&l T+\delta \le t\le (l+1)T, \end{aligned} \end{aligned}$$
(9)

where \(E_{\sigma }(t)=[E_{A_{\sigma }(t)},E_{1_{\sigma }(t)},E_{2_{\sigma }(t)}]\), and \( \Delta _{\sigma }(t)\) satisfies the following quadratic inequality:

$$\begin{aligned}&\Delta ^{T}_{\sigma }(t)\Delta _{\sigma }(t)\nonumber \\&\quad \le \left[ \begin{array}{ccc} e(t)\\ f_{1}(e(t)) \\ f_{2}(e(t-\tau (t))) \end{array}\right] ^{T}\left[ \begin{array}{ccc} F^{T}_{A_{\sigma }(t)}\\ F^{T}_{1_{\sigma }(t)} \\ F^{T}_{2_{\sigma }(t)} \end{array}\right] \left[ \begin{array}{ccc} F^{T}_{A_{\sigma }(t)}\\ F^{T}_{1_{\sigma }(t)}\\ F^{T}_{2_{\sigma }(t)} \end{array}\right] ^{T}\nonumber \\&\quad \times \left[ \begin{array}{ccc} e(t)\\ f_{1}(e(t)) \\ f_{2}(e(t-\tau (t))) \end{array}\right] . \end{aligned}$$
(10)

Define the indicator function \(\xi (t)=[\xi _{1}(t),\xi _{2}(t),\ldots ,\xi _{N}(t)]^{T}\), where

$$\begin{aligned} \xi _{i}(t)= {\left\{ \begin{array}{ll} 1,\ &{}\text {when the switched system is described }\\ &{}\text { by the } ith \ \text {mode}\ \\ &{}A_{0_i}, B_{k0_i}, k=1, 2, E_{i}, K_{i}\\ 0,\ &{}\ \text {otherwise}. \end{array}\right. } \end{aligned}$$

where \(i=1, 2, \ldots , N\). Therefore, the switched interval error system (9) can also be represented as

$$\begin{aligned}&\dot{e}(t)=\sum _{i=1}^{N}\xi _{i}(t)\{-A_{0_{i}} e(t)+B_{10_{i}}f_{1}(e(t))\nonumber \\&\qquad \qquad +B_{20_{i}}f_{2}(e(t-\tau (t)))\nonumber \\&\qquad \qquad +E_{i}\Delta _{i}(t)+K_{i}e(t)\},\quad l T\le t\le l T+\delta ,\nonumber \\&\dot{e}(t)=\sum _{i=1}^{N}\xi _{i}(t)\{-A_{0_{i}}e(t) +B_{10_{i}}f_{1}(e(t))\nonumber \\&\qquad \qquad +\,B_{20_{i}}f_{2}(e(t-\tau (t)))\nonumber \\&\quad \qquad \quad +\,E_{i}\Delta _{i}(t)\}, \quad l T+\delta \le t\le (l+1)T, \end{aligned}$$
(11)

where \(\sum _{i=1}^{N}\xi _{i}(t)=1\) is satisfied under any switching rules, and the initial value associated with the switched interval error network is assumed to be \(e(s)=\varphi (s)\), \(\varphi (s)\in C([t_{0}-\tau ,t_{0}];R^{n})\).

To obtain the main results of this paper, the following definitions and lemmas are introduced.

Definition 1

For the switched error-state system (11) is said to be globally exponentially stable if there exist positive scalars \(\alpha >0\) and \(\beta >0\) such that

$$\begin{aligned} \Vert e(t)\Vert _{\omega }\le \alpha \Vert \varphi \Vert _{\tau }^{-\beta (t-t_{0})},\ \quad t\ge t_{0}. \end{aligned}$$

Definition 2

([21]) The matrix \(\omega -\)measure of a real square matrix \(W =(w_{ij})_{n\times n}\) is denoted as follows:

$$\begin{aligned} \mu _{\omega }(W)=\lim _{\varepsilon \longrightarrow 0^{+}}\frac{\Vert E_{n}+\varepsilon W\Vert _{\omega }-1}{\varepsilon }, \end{aligned}$$

where \(\Vert W\Vert _{\omega }=\max \nolimits _{j}\sum \nolimits ^{n}_{i=1}\frac{\omega _{i}}{\omega _{j}}|w_{ij}|\) is induced \(\omega -\)norm of matrix \(W\), and the corresponding \(\omega -\)measure is

$$\begin{aligned} \mu _{\omega }(W)=\max \limits _{j}\left\{ w_{jj}+\sum \limits ^{n}_{i=1, i \ne j}\frac{\omega _{i}}{\omega _{j}}|w_{ij}|\right\} . \end{aligned}$$

Remark 1

It should be noted that several results have been given by using matrix measure with \(\mu _{1}(W) (\mu _{1}(W)=\max \nolimits _{j}\{w_{jj}+\sum \nolimits ^{n}_{i=1, i \ne j}|w_{ij}|\})\). However, there is few result in \(\omega -\)measure, and \(\mu _{1}(W)\) can be a special case of our results, since \(\mu _{\omega }(W)\) is degenerated as \(\mu _{1}(W)\) when \(\omega _{i}=const(1, 2, \ldots , n)\).

Lemma 1

The matrix measure \(\mu _{\omega }(\cdot )\) has the following basic properties:

\((i)\) \(-\Vert A\Vert _{\omega }\le \mu _{\omega }(A)\le \Vert A\Vert _{\omega },\quad \forall A\in R^{n\times n};\)

\((ii)\) \(\mu _{\omega }(\alpha A)=\alpha \mu _{\omega }(A),\quad \forall \alpha >0,\; A\in R^{n\times n};\)

\((iii)\) \(\mu _{\omega }(A+B)\le \mu _{\omega }(A)+\mu _{\omega }(B),\quad \forall A, B\in R^{n\times n}.\)

Lemma 2

(Halanay inequality [26]) Let \(s(t):[t_{0}-\tau ,\infty ) \rightarrow [0,\infty )\) be a continuous function, and for all \(t\ge t_{0}\), we have

$$\begin{aligned} D^{+}s(t) \le -a s(t) + b\sup _{t-\tau \le \theta \le t}s(\theta ), \end{aligned}$$

If \(a>b>0\), then

$$\begin{aligned} s(t) \le \sup _{t_0-\tau \le \theta \le t_0}s(\theta )e^{-\lambda (t-t_0)}, \ t\ge t_0, \end{aligned}$$

where \(\lambda >0\) is the unique positive solution of the equation \(\lambda -a+be^{\lambda \tau }=0\).

Lemma 3

Let \(s(t):[t_{0}-\tau ,\infty ) \rightarrow [0,\infty )\) be a continuous function, and for all \(t\ge t_{0}\), we have

$$\begin{aligned} D^{+}s(t) \le a s(t) + b\sup _{t-\tau \le \theta \le t}s(\theta ), \end{aligned}$$

If \(a>0, b>0\), then

$$\begin{aligned} s(t)&\le \sup _{t-\tau \le \theta \le t}s(\theta ) \le \sup _{t_0-\tau \le \theta \le t_0}s(\theta )e^{(a+b)(t-t_0)},\\ t&\ge t_0. \end{aligned}$$

3 Synchronization criteria for switched interval networks with intermittent control

In this section, we will consider the global exponential synchronization of switched interval networks (7) by using intermittent control technique, without constructing Lyapunov-Krasovskii functional, by using matrix measure and Halanay inequality, designing suitable intermittent control gain matrix \(K_{i}\), global exponential stability criteria for switched interval drive-response error system (11) under any arbitrary switched rule are derived , that is to say, the switched interval networks (7) synchronize with the response system (8).

Theorem 1

Under Assumptions \((\mathcal {H}_1)\) and \((\mathcal {H}_2)\), and suppose \(\tau \le \delta \), \(T-\tau \ge \delta \), the switched interval networks (7) will globally exponentially synchronize with the response system (8) under arbitrary switched rule, if intermittent control gain matrices \(K_{i}\) satisfy

$$\begin{aligned}&\!\!\!(a) -\mu _{\omega }(-A_{0_{i}}+K_{i})\nonumber \\&\qquad -l\Vert B_{10_{i}}\Vert _{ \omega }-l\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }-l \Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}}\Vert _{\omega }\nonumber \\&\quad \ge l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega } \Vert F_{2_{i}}\Vert _{\omega }>0\nonumber \\&\!\!\!(b) -\mu _{\omega }(-A_{0_{i}})+l\Vert B_{10_{i}}\Vert _{\omega }\nonumber \\&\quad \quad +\, l\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{ \omega }\Vert F_{1_{i}}\Vert _{\omega }>0\nonumber \\&\!\!\!(c) \rho =r_{1}(\delta -\tau )-r_{2}(T-\delta )>0 \end{aligned}$$
(12)

where \(i=1,\ 2,\,\ldots \, N\), \(l=\max \limits _{1\le j\le n}\{l_{kj}\}\), \(k=1,\ 2\).

Proof

Calculating the time derivative of \(\Vert e(t)\Vert _{\omega }\) along the solution of the system (11), it can follow that when \(lT\le t\le l T+\delta ,\ \ l=0, 1, \ldots \),

$$\begin{aligned}&\!\!\!\displaystyle \lim \limits _{h\rightarrow 0^{+}}\frac{\Vert e(t+h) \Vert _{\omega }-\Vert e(t)\Vert _{\omega }}{h}\nonumber \\&\quad \displaystyle =\lim \limits _{h\rightarrow 0^{+}}\frac{\Vert e(t)+ h\dot{e}(t)+o(h)\Vert _{\omega }-\Vert e(t)\Vert _{\omega }}{h}\nonumber \\&\quad \displaystyle =\lim \limits _{h\rightarrow 0^{+}}\frac{1}{h} \left\{ \Vert e(t)+h\left( \sum _{i=1}^{N}\xi _{i}(t)[-A_{0_{i}}e(t)\right. \right. \nonumber \\&\quad \quad +\,B_{10_{i}}f_{1}(e(t))+B_{20_{i}}f_{2}(e(t-\tau (t)))\nonumber \\&\quad \quad \left. \left. +\,E_{i}\Delta _{i}(t)+K_{i}e(t)]\right) +o(h)\Vert _{\omega }-\Vert e(t)\Vert _{\omega }\right\} \nonumber \\&\quad \displaystyle \le \lim \limits _{h\rightarrow 0^{+}}\sum _{i=1}^{N} \xi _{i}(t)\left\{ \frac{\Vert I+h(-A_{0_{i}} +K_{i})\Vert _{\omega }-1}{h} \right. \nonumber \\&\quad \quad \Vert e(t)\Vert _{\omega }+\Vert B_{10_{i}}\Vert _{\omega }\Vert f_{1}(e(t))\Vert _{\omega }\nonumber \\&\quad \quad +\Vert B_{20_{i}}\Vert _{\omega }\Vert f_{2}(e(t-\tau (t)))\Vert _{\omega }\nonumber \\&\quad \quad \left. +\,\Vert E_{i}\Vert _{\omega }\Vert \Delta _{i}(t)\Vert _{\omega }\right\} \end{aligned}$$
(13)

Using Assumption \((\mathcal {H}_1)\), we have

$$\begin{aligned}&\Vert f_{1}(e(t))\Vert _{\omega }\le l\Vert e(t)\Vert _{\omega },\nonumber \\&\Vert f_{2}(e(t-\tau (t)))\Vert _{\omega } \le l\Vert e(t-\tau (t)))\Vert _{\omega }\nonumber \\&\Vert \Delta _{i}(t)\Vert _{\omega } \le \Vert F_{A_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega }\nonumber \\&\quad +\,\Vert F_{1_{i}}\Vert _{\omega } \Vert f_{1}(e(t))\Vert _{\omega }+\Vert F_{2_{i}}\Vert _{\omega }\Vert f_{2}(e(t- \tau (t)))\Vert _{\omega }\nonumber \\&\quad \le \Vert F_{A_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega }+l\Vert F_{1_{i}} \Vert _{\omega }\Vert e(t)\Vert _{\omega }\nonumber \\&\qquad +\,l\Vert F_{2_{i}}\Vert _{\omega }\Vert e(t-\tau (t)) \Vert _{\omega } \end{aligned}$$
(14)

In the light of (13)–(14), for any \(i=1, 2,\ldots , N\), we obtain that

$$\begin{aligned}&\displaystyle \lim \limits _{h\rightarrow 0^{+}}\frac{ \Vert e(t+h)\Vert _{\omega }-\Vert e(t)\Vert _{\omega }}{h}\\&\quad \displaystyle \le \lim \limits _{h\rightarrow 0^{+}} \sum _{i=1}^{N}\xi _{i}(t)\left\{ \frac{\Vert I+h(-A_{0_{i}}+K_{i}) \Vert _{\omega }-1}{h}\right. \\&\quad \quad \Vert e(t)\Vert _{\omega } + \Vert B_{10_{i}}\Vert _{\omega } \Vert f_{1}(e(t))\Vert _{\omega }\\&\quad \quad \left. +\Vert B_{20_{i}}\Vert _{\omega }\Vert f_{2}(e(t-\tau (t)))\Vert _{ \omega }+\Vert E_{i}\Vert _{\omega }\Vert \Delta _{i}(t)\Vert _{\omega }\!\right\} \\&\quad \displaystyle \le \sum _{i=1}^{N}\xi _{i}(t)\{\mu _{\omega }(-A_{0_{i}}+K_{i}) \Vert e(t)\Vert _{\omega }\\&\quad \quad +\,l\Vert B_{10_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega }+l\Vert B_{20_{i}}\Vert _{\omega }\Vert e(t-\tau (t)))\Vert _{\omega }\\&\qquad +\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega } +l\Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega }\\&\quad \quad +l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}}\Vert _{\omega }\Vert e(t-\tau (t))\Vert _{\omega }\}\\&\quad \displaystyle \le \sum _{i=1}^{N}\xi _{i}(t)\{(\mu _{\omega }(-A_{0_{i}}+K_{i})\\&\quad \quad +l\Vert B_{10_{i}}\Vert _{\omega }+\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}} \Vert _{\omega }\\&\quad \quad +\,l\Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}} \Vert _{\omega })\Vert e(t)\Vert _{\omega }\\&\quad \quad +(l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}} \Vert _{\omega })\Vert e(t-\tau (t))\Vert _{\omega }\}\\&\quad \displaystyle \le (\mu _{\omega }(-A_{0_{i}}+K_{i})+l\Vert B_{10_{i}}\Vert _{\omega } +\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }\\&\quad \quad +l\Vert E_{i}\Vert _{\omega } \Vert F_{1_{i}}\Vert _{\omega })\Vert e(t)\Vert _{\omega }\\&\quad \quad +(l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}} \Vert _{\omega })\Vert e(t-\tau (t))\Vert _{\omega } \end{aligned}$$

According to definition of upper-right Dini derivative, we yield

$$\begin{aligned} \begin{array}{ll} &{}\!\!\!\displaystyle D^{+}\Vert e(t)\Vert _{\omega } \le (\mu _{ \omega }(-A_{0_{i}}+K_{i})+l\Vert B_{10_{i}}\Vert _{\omega }\\ &{}\quad +\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega } \Vert F_{1_{i}}\Vert _{\omega })\Vert e(t)\Vert _{\omega }\\ &{}\quad +(l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}} \Vert _{\omega })\sup \limits _{t-\tau \le s \le t} \Vert e(s)\Vert _{\omega } \end{array} \end{aligned}$$

Let \(a=-\mu _{\omega }(-A_{0_{i}}+K_{i})-l\Vert B_{10_{i}}\Vert _{\omega }-\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }-l\Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}}\Vert _{\omega }\) and \(b=l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}}\Vert _{\omega }\) from condition (12) and Lemma 2.2, one can obtain

$$\begin{aligned} \Vert e(t)\Vert _{\omega }\le \sup _{lT-\tau \le s \le lT} \Vert e(s)\Vert _{\omega }e^{-r_{1}(t-lT)}, \end{aligned}$$
(15)

where \(r_{1}>0\) is the unique positive solution of the equation \(r_{1}-a+be^{r_{1}\tau }=0\).

Similarly, when \(l T+\delta \le t\le (l+1)T,\ \ l=0, 1, \ldots \), we get

$$\begin{aligned}&\!\!\!\displaystyle D^{+}\Vert e(t)\Vert _{\omega } \le (\mu _{\omega } (-A_{0_{i}})+l\Vert B_{10_{i}}\Vert _{\omega }\\&\quad +\Vert E_{i}\Vert _{\omega } \Vert F_{A_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}} \Vert _{\omega })\Vert e(t)\Vert _{\omega }\\&\quad +(l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}} \Vert _{\omega })\sup \limits _{t-\tau \le s \le t} \Vert e(s)\Vert _{\omega } \end{aligned}$$

Let \(a'=\mu _{\omega }(-A_{0_{i}})+l\Vert B_{10_{i}}\Vert _{\omega }+\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}}\Vert _{\omega }\) from condition (12) and Lemma 2.3, one has

$$\begin{aligned} \Vert e(t)\Vert _{\omega }\le \sup _{lT+\delta -\tau \le s \le lT+\delta } \Vert e(s)\Vert _{\omega }e^{-r_{2}(t-lT-\delta )}, \end{aligned}$$
(16)

where \(r_{2}=a'+b>0\).

In the following, we will estimate \(\Vert e(t)\Vert _{\omega }\) by (15) and (16),

$$\begin{aligned} \Vert e(t)\Vert _{\omega }\le \Vert e(0)\Vert _{\tau }e^{-r_{1}t}\quad 0 \le t \le \delta , \end{aligned}$$

For \(\delta \le t \le T\),

$$\begin{aligned} \Vert e(t)\Vert _{\omega }&\le \Vert e(\delta )\Vert _{\tau }e^{r_{2}(t-\delta )}\\&=\sup _{\delta -\tau \le t \le \delta }\Vert e(t)\Vert _{\omega }e^{r_{2}(t-\delta )}\\&\le \Vert e(0)\Vert _{\tau }e^{-r_{1}(\delta -\tau )}e^{r_{2}(t-\delta )}, \end{aligned}$$

Since \(T-\tau \ge \delta \), then

$$\begin{aligned} \Vert e(\omega )\Vert _{\tau }&=\sup _{T-\tau \le t \le T}\Vert e(t)\Vert _{\omega }\\&\le \sup _{T-\tau \le t \le T}\{\Vert e(0)\Vert _{\tau }e^{-r_{1}(\delta -\tau )}e^{r_{2}(t-\delta )}\}\\&=\Vert e(0)\Vert _{\tau }e^{-r_{1}(\delta -\tau )}e^{r_{2}(T-\delta )}\\&=\Vert e(0)\Vert _{\tau }e^{-\rho }. \end{aligned}$$

By mathematical induction, we can prove, for any positive integer \(l\),

$$\begin{aligned} \Vert e(lT)\Vert _{\tau }\le \Vert e(0)\Vert _{\tau }e^{-l\rho }, \end{aligned}$$
(17)

Suppose inequality \((17)\) holds when \(l\le k\). Now, we prove \((17)\) is true when \(l=k+1\).

Firstly, we have

$$\begin{aligned} \Vert e(kT)\Vert _{\tau }\le \Vert e(0)\Vert _{\tau }e^{-k\rho }, \end{aligned}$$

For \(kT \le t \le kT+\delta \),

$$\begin{aligned} \Vert e(t)\Vert _{\omega }&\le \Vert e(kT)\Vert _{\tau }e^{-r_{1}(t-kT)}\nonumber \\&\le \Vert e(0)\Vert _{\tau }e^{-k\rho }e^{-r_{1}(t-kT)}, \end{aligned}$$
(18)

For \(kT+\delta \le t \le (k+1)T\),

$$\begin{aligned} \Vert e(t)\Vert _{\omega }&\le \Vert e(kT+\delta )\Vert _{\tau }e^{r_{2}(t-kT-\delta )}\nonumber \\&= \sup _{kT+\delta -\tau \le t \le kT+\delta }\Vert e(t)\Vert _{\omega }e^{r_{2}(t-kT-\delta )}\nonumber \\&\le \sup _{kT+\delta -\tau \le t \le kT+\delta }\Vert e(0)\Vert \nonumber \\&_{\tau }e^{-k\rho }e^{-r_{1}(t-kT)} e^{r_{2}(t-kT-\delta )}\nonumber \\&\le \Vert e(0)\Vert _{\tau }e^{-k\rho }e^{-r_{1}(\delta -\tau )} e^{r_{2}(t-kT-\delta )} \end{aligned}$$
(19)

Based on (18) and (19), it is easy to see when \(l=k+1\),

$$\begin{aligned} \Vert e((k+1)T)\Vert _{\tau }&= \sup _{(k+1)T-\tau \le t \le (k+1)T}\Vert e(t)\Vert _{\omega }\nonumber \\&\le \sup _{(k+1)T-\tau \le t\le (k+1)T}\{\Vert e(0)\Vert \nonumber \\&_{\tau }e^{-k\rho }e^{-r_{1}(\delta - \tau )}e^{r_{2}(t-kT-\delta )}\}\nonumber \\&= \Vert e(0)\Vert _{\tau }e^{-k\rho }e^{-r_{1}(\delta - \tau )}e^{r_{2}(T-\delta )}\nonumber \\&= \Vert e(0)\Vert _{\tau }e^{-(k+1)\rho } \end{aligned}$$
(20)

Thus, it is clear that (17) holds for all positive integers \(l\).

For any \(t>0\), there exists a constant \(n_{0}>0\), such that \(n_{0} T \le t\le (n_{0}+1)T\). From the above inequality, we have the following:

$$\begin{aligned} \Vert e(t)\Vert _{\omega }&\le \Vert e(n_{0}T)\Vert _{\tau } e^{r_{2}(t-n_{0}T)}\nonumber \\&\le \Vert e(0)\Vert _{\tau }e^{-n_{0}\rho }e^{r_{2}T}\nonumber \\&\le \Vert e(0)\Vert _{\tau }e^{r_{2}T+\rho }e^{-\frac{\rho }{T}t}, \end{aligned}$$
(21)

From Definition 2.1, the error state \(e(t)\) converges exponentially to zero, it implies that every trajectory \(y_{i}(t)\) of (8) will globally exponentially synchronize with the \(x_{i}(t)\) under arbitrary switched rule, this completes the proof.

4 Synchronization criteria for switched interval networks with coupling feedback control

In this section, we will consider switched interval networks with coupling feedback control, when control width \(\delta \) equals the control period \(T\), then the controller is activated at any time, intermittent controller in (2) is changed as coupling feedback controller \(U(t)=K(y(t)-x(t)), \ \forall t\ge 0\), where \(K\in R^{n\times n}\) is the feedback control gain matrix, therefore, switched interval error system (11) changed as

$$\begin{aligned} \dot{e}(t)&= \sum _{i=1}^{N}\xi _{i}(t)\{-A_{0_{i}}e(t) +B_{10_{i}}f_{1}(e(t))\nonumber \\&+\,B_{20_{i}}f_{2}(e(t-\tau (t)))\nonumber \\&+\,E_{i}\Delta _{i}(t)+K_{i}e(t)\}, \end{aligned}$$
(22)

where \(\sum _{i=1}^{N}\xi _{i}(t)=1\) is satisfied under any switching rules, and the initial value associated with the switched interval error network is assumed to be \(e(s)=\varphi (s)\), \(\varphi (s)\in C([t_{0}-\tau ,t_{0}];R^{n})\).

Theorem 2

Under the Assumptions \((\mathcal {H}_1)\) and \((\mathcal {H}_2)\), the switched interval networks (7) will globally exponentially synchronize with the response system (8) by using coupling controller under arbitrary switched rule, if coupling control gain matrix \(K_{i}\) satisfies

$$\begin{aligned}&\!\!\!-\mu _{\omega }(-A_{0_{i}}+K_{i})-l\Vert B_{10_{i}}\Vert _{ \omega }\nonumber \\&\qquad -\,l\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{ \omega }-l\Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}}\Vert _{\omega }\nonumber \\&\qquad \ge l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}}\Vert _{\omega }>0 \end{aligned}$$
(23)

where \(i=1,\ 2,\ \ldots N\),   \(l=\max \limits _{1\le j\le n}\{l_{kj}\}\),   \(k=1,\ 2\).

Proof

Calculating the time derivative of \(\Vert e(t)\Vert _{\omega }\) along the solution of the system (22), it can follow that

$$\begin{aligned}&\!\!\!\displaystyle \lim \limits _{h\rightarrow 0^{+}}\frac{ \Vert e(t+h)\Vert _{\omega }-\Vert e(t)\Vert _{\omega }}{h}\nonumber \\&\quad \displaystyle =\lim \limits _{h\rightarrow 0^{+}}\frac{ \Vert e(t)+h\dot{e}(t)+o(h)\Vert _{\omega }-\Vert e(t)\Vert _{\omega }}{h}\nonumber \\&\quad \displaystyle =\lim \limits _{h\rightarrow 0^{+}}\frac{1}{h}\left\{ \Vert e(t)+h\left( \sum _{i=1}^{N}\xi _{i}(t)[-A_{0_{i}}e(t)\right. \right. \nonumber \\&\quad \quad +\,B_{10_{i}} f_{1}(e(t))+B_{20_{i}}f_{2}(e(t-\tau (t)))\nonumber \\&\left. \left. \quad \quad +\,E_{i}\Delta _{i}(t)+K_{i}e(t)]\right) +o(h)\Vert _{\omega }-\Vert e(t)\Vert _{\omega }\right\} \nonumber \\&\quad \displaystyle \le \lim \limits _{h\rightarrow 0^{+}}\sum _{i=1}^{N}\xi _{i}(t) \left\{ \frac{\Vert I+h(-A_{0_{i}}+K_{i})\Vert _{\omega }-1}{h}\right. \nonumber \\&\quad \quad \Vert e(t)\Vert _{\omega } +\Vert B_{10_{i}}\Vert _{\omega }\Vert f_{1}(e(t))\Vert _{\omega }\nonumber \\&\quad \quad +\,\Vert B_{20_{i}}\Vert _{\omega }\Vert f_{2}(e(t-\tau (t)))\Vert _{\omega }\nonumber \\&\left. \qquad +\,\Vert E_{i}\Vert _{\omega }\Vert \Delta _{i}(t)\Vert _{\omega }\right\} \end{aligned}$$
(24)

Using Assumption \((\mathcal {H}_1)\), we yield

$$\begin{aligned}&\!\!\!\Vert f_{1}(e(t))\Vert _{\omega }\le l\Vert e(t)\Vert _{\omega },\nonumber \\&\!\!\!\Vert f_{2}(e(t-\tau (t)))\Vert _{\omega } \le l\Vert e(t-\tau (t)))\Vert _{\omega }\nonumber \\&\!\!\!\Vert \Delta _{i}(t)\Vert _{\omega } \le \Vert F_{A_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega } +\,\Vert F_{1_{i}}\Vert _{\omega } \Vert f_{1}(e(t))\Vert _{\omega }\nonumber \\&\qquad +\,\Vert F_{2_{i}}\Vert _{\omega }\Vert f_{2} (e(t-\tau (t)))\Vert _{\omega }\nonumber \\&\quad \le \Vert F_{A_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega }+l\Vert F_{1_{i}} \Vert _{\omega }\Vert e(t)\Vert _{\omega }\nonumber \\&\qquad +\,l\Vert F_{2_{i}}\Vert _{\omega }\Vert e(t-\tau (t)) \Vert _{\omega } \end{aligned}$$
(25)

In the light of (24)–(25), for any \(i=1, 2,\ldots , N\), we obtain

$$\begin{aligned}&\!\!\!\displaystyle \lim \limits _{h\rightarrow 0^{+}}\frac{\Vert e(t+h) \Vert _{\omega }-\Vert e(t)\Vert _{\omega }}{h}\nonumber \\&\quad \displaystyle \le \lim \limits _{h\rightarrow 0^{+}}\sum _{i=1}^{N} \xi _{i}(t)\left\{ \frac{\Vert I+h(-A_{0_{i}}+K_{i})\Vert _{\omega }-1}{h}\right. \nonumber \\&\quad \quad \Vert e(t)\Vert _{\omega } +\Vert B_{10_{i}}\Vert _{\omega }\Vert f_{1}(e(t))\Vert _{\omega }\nonumber \\&\quad \quad +\Vert B_{20_{i}}\Vert _{\omega }\Vert f_{2}(e(t-\tau (t)))\Vert _{\omega }\nonumber \\&\left. \qquad +\,\Vert E_{i} \Vert _{\omega }\Vert \Delta _{i}(t)\Vert _{\omega }\right\} \nonumber \\&\quad \displaystyle \le \sum _{i=1}^{N}\xi _{i}(t)\{\mu _{\omega }(-A_{0_{i}}+K_{i}) \Vert e(t)\Vert _{\omega }\nonumber \\&\quad \quad +l\Vert B_{10_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega }+l \Vert B_{20_{i}}\Vert _{\omega }\Vert e(t-\tau (t)))\Vert _{\omega }\nonumber \\&\qquad +\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega }+l \Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}}\Vert _{\omega }\Vert e(t)\Vert _{\omega }\nonumber \\&\quad \quad +l \Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}}\Vert _{\omega }\Vert e(t-\tau (t))\Vert _{\omega }\}\nonumber \\&\quad \displaystyle \le \sum _{i=1}^{N}\xi _{i}(t)\{(\mu _{\omega }(-A_{0_{i}}+K_{i})+l \Vert B_{10_{i}}\Vert _{\omega }\nonumber \\&\quad \quad +\,\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{ \omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}}\Vert _{\omega })\Vert e(t)\Vert _{\omega }\nonumber \\&\quad \quad +(l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}} \Vert _{\omega })\Vert e(t-\tau (t))\Vert _{\omega }\} \nonumber \\&\quad \displaystyle \le (\mu _{\omega }(-A_{0_{i}}+K_{i})+l\Vert B_{10_{i}}\Vert _{\omega }+ \Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }\nonumber \\&\quad \quad +\,l\Vert E_{i}\Vert _{\omega } \Vert F_{1_{i}}\Vert _{\omega })\Vert e(t)\Vert _{\omega }\nonumber \\&\quad \quad +\,(l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}} \Vert _{\omega })\Vert e(t-\tau (t))\Vert _{\omega }\nonumber \\ \end{aligned}$$
(26)

According to Definition of upper-right Dini derivative, we have

$$\begin{aligned}&\!\!\!\displaystyle D^{+}\Vert e(t)\Vert _{\omega } \le (\mu _{\omega } (-A_{0_{i}}+K_{i})+l\Vert B_{10_{i}}\Vert _{\omega }\nonumber \\&\quad +\,\Vert E_{i}\Vert _{ \omega }\Vert F_{A_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}} \Vert _{\omega })\Vert e(t)\Vert _{\omega }\nonumber \\&\quad +\,(l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}} \Vert _{\omega })\nonumber \\&\quad \quad \sup \limits _{t-\tau \le s \le t} \Vert e(s)\Vert _{\omega } \end{aligned}$$
(27)

Let \(a=-\mu _{\omega }(-A_{0_{i}}+K_{i})-l\Vert B_{10_{i}}\Vert _{\omega }-\Vert E_{i}\Vert _{\omega }\Vert F_{A_{i}}\Vert _{\omega }-l\Vert E_{i}\Vert _{\omega }\Vert F_{1_{i}}\Vert _{\omega }\) and \(b=l\Vert B_{20_{i}}\Vert _{\omega }+l\Vert E_{i}\Vert _{\omega }\Vert F_{2_{i}}\Vert _{\omega }\), from condition (23) and Lemma 2.2, one can obtain

$$\begin{aligned} \Vert e(t)\Vert _{\omega }\le \sup _{t_{0}-\tau \le s \le t_{0}} \Vert e(s)\Vert _{\omega }e^{-r_{1}(t-t_{0})},\ \ \ \ \ \ t\ge t_{0}\nonumber \\ \end{aligned}$$
(28)

where \(r_{1}>0\) is the unique positive solution of the equation \(r_{1}-a+be^{r_{1}\tau }=0\).

Therefore, \(e(t)\) converges exponentially to zero with a convergence rate of \(r_{1}\), this completes the proof of theorem 2.

Remark 2

Without constructing complex Lyapunov function, matrix measure method [27] is a very useful tool to deal with the stability and synchronization problems of networks; the derived results by using matrix measure and Halanay inequality are very easy to verify and more general, since matrix measure can have positive values as well as negative values.

Remark 3

Most of existing results deal with synchronization problem of complex networks via adopting \(p\)-measure (\(p=1, 2, \infty \)), it is easy to see that \(\omega \)-measure is replaced by \(p\)-measure in proposed criteria are always true, and \(1\)-measure is a special case of \(\omega \)-measure, hence, synchronization criteria in this paper are different from the previous criteria and improve the existing results.

5 Numerical simulations

In this section, two examples are presented to illustrate the effectiveness of our results obtained in Theorems 1 and 2. It is interesting that Example 2 shows that the switched networks can be reached to synchronization by using obtained synchronization criteria even when each subsystem is chaotic neural networks.

Example 1

Consider the second-order switched interval networks with discrete delay:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} &{}\dot{x}_{i}(t)=-a_{i_{\sigma (t)}}x_{i}(t)+ \sum _{j=1}^{2}b^{(1)}_{ij_{\sigma (t)}}g_{1j}(x_{j}(t))\\ &{}\qquad \qquad +\sum _{j=1}^{2}b^{(2)}_{ij_{\sigma (t)}}g_{2j}(x_{j}(t-\tau (t))\\ &{}\ \ \ \ a_{i_{\sigma (t)}}\in {[\underline{a}_{i_{\sigma (t)}}, \overline{a}_{i_{\sigma (t)}}]},\quad b^{(k)}_{ij_{\sigma (t)}}\in {[\underline{b}^{(k)}_{ij_{\sigma (t)}}, \overline{b}^{(k)}_{ij_{\sigma (t)}}]},\\ &{}\qquad \qquad k=1,2\\ &{}x_{i}(t)=\psi _{i}(t),\quad t\in [-\tau ,0],\quad i, j=1,2. \end{array}\right. } \end{aligned} \end{aligned}$$

\(\sigma (t):[0,+\infty )\rightarrow \Gamma =\{1, 2\}\), \( g_i(x)=tanh(x),\ i=1,2\), \(\tau (t)=1\). Obviously, Assumptions \(\mathcal {H}_1\) are satisfied with \(l=1\). The networks system parameters are defined as

$$\begin{aligned}&\underline{A}_{1}= \begin{pmatrix} 0.99&{}\quad -0.01\\ -0.01&{}\quad 0.99 \end{pmatrix}, \overline{A}_{1}= \begin{pmatrix} 1.01&{}\quad 0.01\\ 0.01&{}\quad 1.01 \end{pmatrix},\\&\quad \underline{B}_{11}= \begin{pmatrix} -2.01&{}\quad 0.99\\ 0.99&{}\quad -1.51 \end{pmatrix},\\&\overline{B}_{11}= \begin{pmatrix} -1.99&{}\quad 1.01\\ 1.01&{}\quad -1.49 \end{pmatrix}, \underline{B}_{21}= \begin{pmatrix} -1.01&{}\quad 1.99\\ 0.49&{}\quad -1.01 \end{pmatrix},\\&\overline{B}_{21}= \begin{pmatrix} -0.99&{}\quad 2.01\\ 0.51&{}\quad -0.99 \end{pmatrix},\\&\underline{A}_{2}= \begin{pmatrix} 0.99&{}\quad -0.01\\ -0.01&{}\quad 0.99 \end{pmatrix}, \overline{A}_{2}= \begin{pmatrix} 1.01&{}\quad 0.01\\ 0.01&{}\quad 1.01 \end{pmatrix},\\&\underline{B}_{12}= \begin{pmatrix} 0.99&{}\quad 2.99\\ -0.51&{}\quad -2.51 \end{pmatrix},\\&\overline{B}_{12}= \begin{pmatrix} 1.01&{}\quad 3.01\\ -0.49&{}\quad -2.49 \end{pmatrix}, \underline{B}_{22}= \begin{pmatrix} -2.01&{}\quad -4.04\\ 0.99&{}\quad 2.99 \end{pmatrix},\\&\overline{B}_{22}= \begin{pmatrix} -1.99&{}\quad -3.99\\ 1.01&{}\quad 3.01\end{pmatrix}, \end{aligned}$$

We choose intermittent strategy as follows:

$$\begin{aligned} \begin{aligned} U(t)= {\left\{ \begin{array}{ll} K_{i}(e(t)),\quad l T\le t\le l T+\delta ;\\ 0, \quad l T+\delta \le t\le (l+1)T, \\ \end{array}\right. } \end{aligned} \end{aligned}$$

where the control period \(T=3\), control width \(\delta =1.8\), and intermittent feedback control gain matrices \(K_{i}(i=1, 2)\) defined as the following:

$$\begin{aligned} K_{1}= \begin{pmatrix} -8&{}\quad -1\\ 0.5&{}\quad -7 \end{pmatrix},\qquad K_{2}= \begin{pmatrix} -10&{}\quad 1\\ -0.5&{}\quad -11\end{pmatrix}. \end{aligned}$$

Let \(\omega _{1}=1\), \(\omega _{2}=2\), by calculating, we have \(-\mu _{\omega }(-A_{0_{1}}+K_{1})-l\Vert B_{10_{1}}\Vert _{\omega }-l\Vert E_{1}\Vert _{\omega }\Vert F_{A_{1}}\Vert _{\omega }-l\Vert E_{1}\Vert _{\omega }\Vert F_{1_{1}}\Vert _{\omega }=2.98 \!\ge \! l\Vert B_{20_{1}}\Vert _{\omega }+l\Vert E_{1}\Vert _{\omega }\Vert F_{2_{1}}\Vert _{\omega }\!=\!2.01\), \(-\mu _{\omega }(-A_{0_{2}}+K_{2})-l\Vert B_{10_{2}}\Vert _{\omega }-l\Vert E_{2}\Vert _{\omega }\Vert F_{A_{2}}\Vert _{\omega }-l\Vert E_{2}\Vert _{\omega }\Vert F_{1_{2}}\Vert _{\omega }=5.98 \ge l\Vert B_{20_{2}}\Vert _{\omega }+l\Vert E_{2}\Vert _{\omega }\Vert F_{2_{2}}\Vert _{\omega }=5.01\), and all conditions in Theorem 1 hold; therefore, switched interval system in this example synchronizes exponentially toward with corresponding its response system under any switching rules. However, in view of \(1\)-measure, it is easy to see that \(-\mu _{1}(-A_{0_{1}}+K_{1})-l\Vert B_{10_{1}}\Vert _{1}-l\Vert E_{1}\Vert _{1}\Vert F_{A_{1}}\Vert _{1}-l\Vert E_{1}\Vert _{1}\Vert F_{1_{1}}\Vert _{1}=2.98 < l\Vert B_{20_{1}}\Vert _{1}+l\Vert E_{1}\Vert _{1}\Vert F_{2_{1}}\Vert _{1}=3.01\), \(-\mu _{1}(-A_{0_{2}}+K_{2})-l\Vert B_{10_{2}}\Vert _{1}-l\Vert E_{2}\Vert _{1}\Vert F_{A_{2}}\Vert _{1}-l\Vert E_{2}\Vert _{1}\Vert F_{1_{2}}\Vert _{1}=4.98 < l\Vert B_{20_{2}}\Vert _{1}+l\Vert E_{2}\Vert _{1}\Vert F_{2_{2}}\Vert _{1}=7.01\); hence, \(\omega \)-measure is more general than \(1\)-measure, the proposed results are less restrictive.

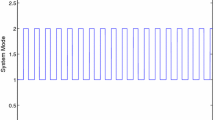
For numerical simulations, let \(A_1=\underline{A}_1, B_{11}=\underline{B}_{11}, B_{21}=\underline{B}_{21}\), and \(A_2=\underline{A}_2, B_{12}=\underline{B}_{12}, B_{22}=\underline{B}_{22}\). Assume that the two subsystems are switched every one second, and the switching rule is shown in Fig. 1. Figure 2 shows the state trajectories of \(e_{1}(t)\) and \(e_{2}(t)\) from random constant initial states in the set \([-1, 1]\times [-1, 1]\) with step \(h=0.01\), it reveals that the trajectory of the switched interval error-state system global exponentially converges to a unique equilibrium \(e^{*}=(0, 0)^{T}\). This is in accordance with the conclusion of Theorem 1.

Fig. 1
figure 1

The switching signal

Full size image
Fig. 2
figure 2

The state trajectories of state variables \(e_{1}\) and \(e_{2}\) of switched error-state system

Full size image

Example 2

Consider the following switched interval networks with discrete delay as a drive system

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} &{}\dot{x}_{i}(t)=-a_{i_{\sigma (t)}}x_{i}(t)+ \sum _{j=1}^{2}b^{(1)}_{ij_{\sigma (t)}}g_{1j}(x_{j}(t))\\ &{}\qquad \qquad +\sum _{j=1}^{2}b^{(2)}_{ij_{\sigma (t)}}g_{2j}(x_{j}(t-\tau (t))\\ &{}\ \ a_{i_{\sigma (t)}}\in {[\underline{a}_{i_{\sigma (t)}}, \overline{a}_{i_{\sigma (t)}}]},\ \ \ b^{(k)}_{ij_{\sigma (t)}}\in {[\underline{b}^{(k)}_{ij_{\sigma (t)}}, \overline{b}^{(k)}_{ij_{\sigma (t)}}]},\\ &{}\qquad \quad k=1,2\\ &{}x_{i}(t)=\varphi _{i}(t),\quad t\in [-\tau ,0],\quad i, j=1,2. \end{array}\right. } \end{aligned} \end{aligned}$$

\(\sigma (t):[0,+\infty )\rightarrow \Gamma =\{1, 2\}\), \( g_i(x)=tanh(x),\ i=1,2\), \(\tau (t)=1\). Choose networks system parameters as

$$\begin{aligned}&\!\!\!\underline{A}_{1}= \begin{pmatrix} 1.00&{}\quad 0.00\\ 0.00&{}\quad 1.00 \end{pmatrix}, \overline{A}_{1}= \begin{pmatrix} 1.02&{}\quad 0.00\\ 0.00&{}\quad 1.02 \end{pmatrix},\\&\!\!\!\underline{B}_{11}= \begin{pmatrix} 2.00&{}\quad -0.10\\ -5.00&{}\quad 4.50 \end{pmatrix},\\&\!\!\!\overline{B}_{11}= \begin{pmatrix} 2.02&{}\quad -0.98\\ -4.98&{}\quad 4.52 \end{pmatrix},\\&\!\!\!\underline{B}_{21}= \begin{pmatrix} -1.50&{}\quad -0.10\\ -0.20&{}\quad -4.00 \end{pmatrix},\\&\!\!\!\overline{B}_{21}= \begin{pmatrix} -1.48&{}\quad -0.98\\ -0.18&{}\quad -3.98 \end{pmatrix},\\&\!\!\!\underline{A}_{2}= \begin{pmatrix} 1.00&{}\quad 0.00\\ 0.00&{}\quad 1.00 \end{pmatrix}, \overline{A}_{2}= \begin{pmatrix} 1.02&{}\quad 0.00\\ 0.00&{}\quad 1.02 \end{pmatrix},\\&\!\!\!\underline{B}_{12}=\begin{pmatrix} 3.00&{}\quad 5.00\\ 0.10&{}\quad 2.00\end{pmatrix},\\&\!\!\!\overline{B}_{12}=\begin{pmatrix} 3.02&{}\quad 5.02\\ 0.12&{}\quad 2.02\end{pmatrix}, \underline{B}_{22}= \begin{pmatrix}-2.50&{}\quad 0.20\\ 0.10&{}\quad -1.50 \end{pmatrix}, \end{aligned}$$

In the following, we will design intermittent control gain matrices \(K_{i}(i=1, 2)\) for the switched interval networks in this example, choose as

$$\begin{aligned} K_{1}=\begin{pmatrix}-12&{}4\\ 4&{}-20\end{pmatrix},\ \ \ K_{2}=\begin{pmatrix}-14&{}6\\ 6&{}-26\end{pmatrix}. \end{aligned}$$

Let \(\omega _{1}=\omega _{2}=1\), by calculating, we have \(-\mu _{\omega }(-A_{0_{1}}+K_{1})-l\Vert B_{10_{1}}\Vert _{\omega }-l\Vert E_{1}\Vert _{\omega }\Vert F_{A_{1}}\Vert _{\omega }-l\Vert E_{1}\Vert _{\omega }\Vert F_{1_{1}}\Vert _{\omega }=4.3132 \ge l\Vert B_{20_{1}}\Vert _{\omega }+l\Vert E_{1}\Vert _{\omega }\Vert F_{2_{1}}\Vert _{\omega }=4.0694\), \(-\mu _{\omega }(-A_{0_{2}}+K_{2})-l\Vert B_{10_{2}}\Vert _{\omega }-l\Vert E_{2}\Vert _{\omega }\Vert F_{A_{2}}\Vert _{\omega }-l\Vert E_{2}\Vert _{\omega }\Vert F_{1_{2}}\Vert _{\omega }=6.2811 \ge l\Vert B_{20_{2}}\Vert _{\omega }+l\Vert E_{2}\Vert _{\omega }\Vert F_{2_{2}}\Vert _{\omega }=5.0638\). All the assumptions of Theorem 2 hold; therefore, switched drive system synchronizes exponentially toward with response system under any switching rules.

For numerical simulations, let \(A_1=\underline{A}_1, B_{11}=\underline{B}_{11}, B_{21}=\underline{B}_{21}\), and \(A_2=\underline{A}_2, B_{12}=\underline{B}_{12}, B_{22}=\underline{B}_{22}\). In this case, the two subsystems are all chaotic neural networks [28]. Assume that the two subsystems are switched every one second, switching signal is shown in Figs. 1, 3 displays two chaotic attractors with the initial conditions \((x_{11}(t), x_{12}(t))^{T}=(0.1, 0.1)^{T}, (x_{21}(t), x_{22}(t)))^T=(2.3, 0.3)^T\), respectively; Fig. 4 depicts the time responses of state variables \(e_{1}(t)\) and \(e_{2}(t)\) from random constant initial states in the set \([-1, 1]\times [-1, 1]\) with step \(h=0.01\), it reveals that the trajectory of the switched interval error-state system global exponentially converges to a unique equilibrium \(e^{*}=(0, 0)^{T}\).

Fig. 3
figure 3

Chaotic attractors of two subsystems of switched networks

Full size image
Fig. 4
figure 4

Time responses of state variables \(e_{1}\) and \(e_{2}\) of switched error-state system

Full size image

6 Conclusion

In this paper, a new matrix measure theory has been proposed to deal with synchronization problem of switched interval delayed networks under the arbitrary switching rule, the intermittent and feedback control gain matrices \(K_{i}\) have been designed, and the proposed synchronization criteria are easy to test. Moreover, the obtained results are more general, it can be promoted to the traditional \(p\)-measure (\(p=1, 2, \infty \))directly, furthermore, the final examples have shown that the \(\omega \)-measure is superior to \(1\)-measure, which can be seen a special case of \(\omega \)-measure.