On the Dynamics of Chua’s oscillator with a smooth cubic nonlinearity: occurrence of multiple attractors

Abstract

Chua’s circuit is one of the well-known nonlinear circuits which have been used to study a rich variety of nonlinear dynamic behaviors such as bifurcation, chaos, and routes to chaos. In this work, I consider the dynamics of Chua’s circuit with a smooth cubic nonlinearity. The dynamics of the model is investigated using standard nonlinear analysis techniques including time series, bifurcation diagrams, phase space trajectories plots, Lyapunov exponents, and basins of attraction. Both period-doubling and crisis routes to chaos are reported. One of the major results of this work is the numerical finding of a parameter region in which Chua’s circuit experiences multiple attractors’ behavior (i.e., coexistence of four different periodic and chaotic attractors). This phenomenon was not reported previously in the Chua’s circuit (despite the huge amount of related research works) and thus represents an enriching contribution to the understanding of the dynamics of Chua’s oscillator. Basins of attraction of various coexisting attractors are depicted showing complex basin boundaries. The results obtained in this work let us conjecture that there are still some unknown and striking behaviors of Chua’s oscillator (e.g., the phenomenon of extreme multistability, i.e., infinitely many attractors) that need to be uncovered.

1 Introduction

It is well known that nonlinear dynamical systems can experience various types of complexity such as bifurcation, chaos, and intermittency, just to name a few. The occurrence of two or more asymptotically stable equilibrium points or attracting sets (e.g., period-n limit cycle, torus, chaotic attractor) as the system parameters are being varied represents another striking and complex behavior observed in nonlinear systems. In a system developing coexisting attractors, the trajectories selectively converge on either of the attracting sets depending on the initial state of the system. Correspondingly, the basin of attraction of an attractive set is defined as the set of initial points whose trajectories converge on the given attractor. The boundary separating each basin of attraction can be a smooth boundary or riddled basin with no clear demarcation (i.e., fractal). This striking and interesting phenomenon has been reported in various nonlinear systems including laser [1], biological systems [2, 3], chemical reactions [4], Lorenz system [5], Newton–Leipnik system [6], and electrical circuits [7–11]. Such a phenomenon is mostly connected to the system symmetry and may be accompanied by some special effects including for instance, symmetry-breaking bifurcation, symmetry restoring crisis, coexisting bifurcations, and hysteresis [12–15]. In practice, the coexistence of multiple attractors implies that an attractor may suddenly jump to a different attractor; the situation in which coexisting attractors possess fractal or intermingled basin of attraction being the most intriguing. In this case, due to noise, the observed signal may be the result of random switching of the system trajectory between two or more coexisting attractors.

In the present work, we consider the dynamics of Chua’s oscillator  [16–20] (with a smooth cubic nonlinearity) with emphasis on the occurrence of multiple attractors. Briefly recall that Chua’s oscillator is a well known and widely studied chaotic oscillator that has been used to demonstrate various types of nonlinear phenomena encountered in nonlinear dynamical systems in general. The occurrence of multiple (more than two) attractors was previously reported in Chua’s circuit by Lozi and Ushiki  [21]. They reported the numerical observation of the co-existence of three distinct chaotic attractors for a least one choice of parameters in Chua’s circuit. Later on, in the review work of Pivka et al. [9], the coexistence of two points attractors, two chaotic attractors and a periodic attractor was also reported. However, to the best of the author’s knowledge, a situation involving the coexistence of four non-static (i.e., oscillatory) attractors in Chua’s circuit is not reported so far in the relevant literature. However, recent results clearly underline the possibility of four distinct/disconnected (oscillatory) attractors in some simple chaotic oscillators such as the jerk circuit [11], the autonomous Duffing Holmes type oscillator  [22], and the memristor-based Shinriki’s circuit [23], just to name a few. Motivated by the above-mentioned results, and provided the universality of Chua’s oscillator, this paper focuses on the dynamics of Chua’s oscillator (with a smooth cubic nonlinearity for Chua’s diode) with particular emphasis on the occurrence of multiple attractors. A window in the parameter space is found in which four distinct non-static coexisting attractors is reported.

The rest of the paper is structured as follows. Section 2 deals with the modeling process. The electronic structure of the Chua’s circuit is presented as well as the corresponding mathematical model with emphasis on the cubic nonlinearity. Some basic properties of the model are underlined. The stability of the equilibrium points is analyzed yielding to the possibility of self-excited oscillations in the oscillator. In Sect. 3, the bifurcation structures of the system are investigated numerically showing period-doubling and symmetry recovering crisis phenomena. A window (in the parameter space) corresponding to the occurrence of multiple coexisting attractors is revealed. Correspondingly, basins of attraction of various coexisting solutions are computed showing complex basin boundaries. Finally, some concluding remarks and proposals for future work are drawn in Sect. 4.

Fig. 1

Schematic diagram of Chua’s oscillator

2 Description and analysis of the model

2.1 The model

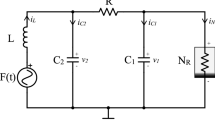
The schematic diagram of Chua’s oscillator is shown in Fig. 1. It consists of a pair of capacitors $\left( {C_1 ,C_2 } \right)$, a pair of resistors $\left( {R_0 ,R} \right)$, a single inductor L and a nonlinear resistor $N_R$. This oscillator is obtained by adding a linear resistor in series with the inductor in the original Chua’s circuit [16–19]. The circuit is described by the following third-order nonlinear system (also referred to as Chua’s equation):

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\hbox {d}\upsilon _1 }{\hbox {d}t}=\frac{1}{C_1 }\left[ {G\left( {\upsilon _2 -\upsilon _1 } \right) -g\left( {\upsilon _1 } \right) } \right] \\ \frac{\hbox {d}\upsilon _2 }{\hbox {d}t}=\frac{1}{C_2 }\left[ {G\left( {\upsilon _2 -\upsilon _1 } \right) +i_3 } \right] \\ \frac{\hbox {d}i_3 }{\hbox {d}t}=-\frac{1}{L}\left( {\upsilon _2 +R_0 i_3 } \right) \\ \end{array}} \right. \end{aligned}$$

(1)

where $g\left( . \right)$ is the $\upsilon -i$ characteristic of the nonlinear resistor (Chua’s diode) $N_R$ which typical $\upsilon -i$ characteristic is given by a piecewise-linear function:

$$\begin{aligned} g\left( {\upsilon _1 } \right) =G_b \upsilon _1 +\frac{1}{2}\left( {G_a -G_b } \right) \left\{ {\left| {\upsilon _1 +E} \right| -\left| {\upsilon _1 -E} \right| } \right\} \nonumber \\ \end{aligned}$$

(2)

With the following change of variables and parameters,

$$\begin{aligned} x= & {} \frac{\upsilon _1 }{E}, \quad y=\frac{\upsilon _2 }{E}, \quad z=i_3 \frac{R}{E}, \quad \alpha =\frac{C_2 }{C_1 }, \quad \beta =\frac{R^{2}C_2 }{L},\nonumber \\ \gamma= & {} \frac{RR_0 C_2 }{L}, \quad m_0 =RG_a , \quad m_1 =RG_b\nonumber \\ k= & {} 1 \quad \hbox {if}\quad RC_2 >0; k=-1\quad \hbox {if}\quad RC_2 <0 \end{aligned}$$

(3)

the following dimensionless version of Chua’s equation is obtained:

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\hbox {d}x}{\hbox {d}t}=k\alpha \left( {y-x-f\left( x \right) } \right) \\ \frac{\hbox {d}y}{\hbox {d}t}=k\left( {x-y+z} \right) \\ \frac{\hbox {d}z}{\hbox {d}t}=k\left( {-\beta y-\gamma z} \right) \\ \end{array}} \right. \end{aligned}$$

(4)

where the nonlinear function $f\left( . \right)$ is defined as:

$$\begin{aligned} f\left( x \right) =m_1 x+\frac{1}{2}\left( {m_0 -m_1 } \right) \left( {\left| {x+1} \right| -\left| {x-1} \right| } \right) \end{aligned}$$

(5)

Briefly recall that Chua’s oscillator can produce an immensely rich variety of chaotic attractors and bifurcation scenarios and is structurally the simplest, but the most complex member of the Chua’s circuit family from a dynamical view point. As previously mentioned, the unique nonlinearity in Chua’s oscillator is the Chua’s diode whose characteristic is mostly assumed piecewise-linear. The piecewise-linear nonlinearity has some advantages with respect to a rigorous mathematical analysis and many works have focussed on the realization of Chua’s diode with the piecewise-linear nonlinearity by real circuits. It should also be mentioned that the only known rigorous proof that Chua’s circuit has a chaotic attractor depends crucially on the choice of a piecewise-linear function. However, the characteristics of nonlinear resistors in real circuits are always smooth [18, 19]. Thus, it is interesting to consider the dynamics of Chua’s oscillator with a smooth nonlinearity  [17–20]. One of the smooth function candidates (among many others) similar to the original three-segment piecewise-linear nonlinearity is a cubic polynomial. In this work, we consider the Chua’s equation (4) where the original piecewise-linear nonlinearity is replaced with a cubic nonlinearity defined by:

$$\begin{aligned} f\left( x \right) =ax^{3}+bx \end{aligned}$$

(6)

In the mathematical model considered throughout this paper [(Chua’s equations (4) and (6)], six parameters can be identified. However, to better concentrate on the phenomenon of multiple attractors experienced by the Chua’s oscillator, five of them will be kept constant (inspired by Ref. [19]) during all the numerical analysis: $k=-1, \beta =53.612186, \gamma =-0.75087096, a=-0.0375582129, b=-0.8415410391$. Therefore, unless otherwise mentioned, the bifurcation analysis of the model will be carried out in terms of the single control parameter $\alpha$.

Fig. 2

Eigenvalues locus (a) related to the origin $E_0 \left( {0,0,0} \right)$ [(resp. (b) to the nontrivial equilibria $E_{1,2} ]$ obtained with $1\le \alpha \le 20$. it can be seen that there is always at least a branch of eigenvalues with positive real part, thus both three equilibria are unstable suggesting the possibility of self-excited oscillations in the system

2.2 Symmetry

System (4) is invariant under the transformation: $\left( {x,y,z} \right) \Leftrightarrow \left( {-x,-y,-z} \right)$. Thus, if $\left( {x,y,z} \right)$ is a solution of system (4) for a fixed set of parameters values, then $\left( {-x,-y,-z} \right)$ is also a solution for the same parameters set. A solution of (4) that is invariant under the above transformation is referred to as symmetric solution; otherwise, it is called an asymmetric solution. The equilibrium point $E_0 \left( {0,0,0} \right)$ is a trivial symmetric static solution. Consequently, attractors in state space have to be symmetric by inversion with respect to the origin; otherwise, they must appear in pairs, to restore the exact symmetry of the model equations. This exact symmetry could be exploited to explain the occurrence of multiple co-existing attractors in state space. Furthermore, it may be helpful to check the integration scheme (i.e., algorithm) used for numerical calculations.

2.3 Fixed point analysis

It is well known that the equilibrium points play a crucial role on the dynamics of a nonlinear system [24–26]. By setting the right hand side of system (4) to zero, it can easily be shown that there are three fixed points: $E_0 =(0,0,0)$ and $E_{1,2} =\left( {\pm \eta ,\frac{\pm \eta \gamma }{\beta +\gamma },\frac{\mp \eta \beta }{\beta +\gamma }} \right)$ with $\eta$ expressed as follows $\eta =\sqrt{\frac{1}{a}\left( {\frac{\gamma }{\beta +\gamma }-1-b} \right) }$. Note that $E_1$ and $E_2$ are symmetric with respect to the origin; consequently, they share the same stability properties. It should also be mentioned that the location in state space of the three fixed points is independent of the control parameter $\alpha$. The Jacobian matrix of system (4) evaluated at any equilibrium point $\left( {\bar{{x}},\bar{{y}},\bar{{z}}} \right)$ is expressed as follows:

$$\begin{aligned} M_J =\left[ {{\begin{array}{lll} {\alpha \left( {1+b+3a\bar{{x}}^{2}} \right) }&{}\quad {-\alpha }&{}\quad 0 \\ {-1}&{}\quad 1&{}\quad {-1} \\ 0&{}\quad \beta &{}\quad \gamma \\ \end{array} }} \right] \end{aligned}$$

(7)

Fig. 3

Bifurcation diagram (a) showing local maxima of the coordinate x versus $\alpha$ and the corresponding graph (b) of largest Lyapunov exponent $(\lambda _{\max } )$ plotted in the range $15\le \alpha \le 20$

The eigenvalues related to the above matrix can be obtained by solving the following characteristic equation ($\det (M_J -\lambda I_d )=0)$:

$$\begin{aligned}&\lambda ^{3}+c_2 \lambda ^{2}+c_1 \lambda +c_0 =0 \end{aligned}$$

(8a)

$$\begin{aligned}&c_2 =-1-\gamma -\alpha \left( {1+b+3a\bar{{x}}^{2}} \right) \end{aligned}$$

(8b)

$$\begin{aligned}&c_1 =\beta -\alpha +\gamma +\alpha \left( {1+\gamma } \right) \left( {1+b+3a\bar{{x}}^{2}} \right) \end{aligned}$$

(8c)

$$\begin{aligned}&c_0 =\alpha \gamma -\alpha \left( {\beta +\gamma } \right) \left( {1+b+3a\bar{{x}}^{2}} \right) \end{aligned}$$

(8d)

where $I_d$ is the $3\times 3$ identity matrix. Following the Routh–Hurwitz stability criterion [26], we have found that any equilibrium point $\left( {\bar{{x}},\bar{{y}},\bar{{z}}} \right)$ is stable if the following inequalities are satisfied:

$$\begin{aligned} c_i>0\left( {i=0,1,2} \right) , \quad c_1 c_2 -c_0 >0 \end{aligned}$$

(9)

Fig. 4

Phase space trajectories (left) and corresponding frequency spectra (right) showing routes to chaos in the system for varying$\alpha$: a Period-1 for $\alpha =15$, b period-2 for $\alpha =16.4$, c period-4 for $\alpha =16.65$, d single band spiraling chaos for $\alpha =17$, e period-5 cycle for $\alpha =18.50$, f double-band chaotic attractor for $\alpha =20$. Pairs of asymmetric attractors are obtained using (non-critical) initial conditions $\left( x\left( 0 \right) \right.$, $y\left( 0 \right)$, $\left. z\left( 0 \right) \right) =\left( {\pm 2,0,0} \right)$

Fig. 5

Two-dimensional projections of the double-band chaotic attractor (a–c) illustrating the complexity of the system and corresponding double-sided Poincaré section (d) in the plane$z=0$. Parameters are those in Fig. 4f

With the parameters’ setting defined above, we have plotted the eigenvalues locus (see Fig. 2a, b) related to the trivial equilibrium point $E_0 \left( {0,0,0} \right)$ (resp. the nontrivial equilibria $E_{1,2}$) when the control parameter $\alpha$ is varied in the range $1\le \alpha \le 20$. In light of the graphs in Fig. 2, it can be noted that there is always at least a branch of eigenvalues with positive real part, thus both three equilibria are unstable and the system generates self-excited oscillations [27, 28]. For instance, considering the particular case of $\alpha =16.615$ for which the system develops four distinct (chaotic and periodic) attractors (see Sect. 4) the eigenvalues evaluated at $E_0$ are $\lambda _1 =3.7684, \lambda _{2,3} =-0.4432\pm j6.3282$, whereas those at $E_{1,2}$ are $\lambda _1 =-6.9752, \lambda _{2,3} =0.6254\pm j6.5644$. This clearly shows that the three fixed points are all unstable (presence of eigenvalues with positive real part) in the regime of multiple attractors, which is typical of self-excited oscillations  [27, 28].

Fig. 6

Bifurcation diagrams (a, b) showing local maxima of the coordinate x obtained respectively for varying $\beta$ and $\gamma$: a $\alpha =20, \gamma =-0.75087096$, b $\alpha =20, \beta =53.612186$. Both diagrams show period-doubling phenomenon, periodic windows, and symmetry restoring crisis scenarios

Fig. 7

Enlargement of the bifurcation diagram of Fig. 3 showing the region in which the model develops multiple coexisting attractors. This region corresponds to values of $\alpha$ in the ranges $16.375\le \alpha \le 17$ and $16.91\le \alpha \le 16.92$. Two sets of data corresponding respectively to increasing (magenta) and decreasing (blue) values of the bifurcation control parameter $\alpha$ are superimposed. (Color figure online)

3 Numerical study

3.1 Computational methods

To explore the rich variety of bifurcation modes that can be observed in our model, we solve numerically system (4) using the classical fourth-order Runge–Kutta integration scheme. For each set of parameters used in this work, the time grid is always fixed to $\Delta t=2\times 10^{-3}$, the system is integrated for a sufficiently long time and the transient is discarded. Two main indicators are substantially exploited to highlight the type of scenario leading to chaos. The bifurcation diagram represents the first indicator, the second indicator consisting of the graph of largest one-dimensional Lyapunov exponent ($\lambda _{\max } )$. Following the latter indicator, the behavior of the system is categorized based on its Lyapunov exponent which is computed numerically by using the reliable algorithm proposed by Wolf et al. [29]. In particular, the sign of the largest Lyapunov exponent determines the growth rate of almost all small perturbations to the system’s state, and thus, the nature of the underlined attractor. For $\lambda _{\max } <0$ all perturbations vanish and trajectories starting sufficiently close to each other converge to the same stable fixed point in state space; for $\lambda _{\max } =0$, initially close orbits remain close but distinct, corresponding to oscillatory motions on a limit cycle or torus; and finally for $\lambda _{\max } >0$, small perturbations grow exponentially, and the system behaves chaotically within the folded space of a strange attractor. To gain further insight about the complex behavior of the Chua’s oscillator with cubic nonlinearity, we plot the Poincaré sections of attractors as well as basins of attraction in case of coexisting solutions. In the parameters’ space, both forward and backward bifurcations diagrams are produced to localize windows of co-existing multiple attractors (i.e., coexisting bifurcations).

Fig. 8

Coexistence of four different attractors (a pair of period-2 limit cycles and a pair of period-3 attractors) for $\alpha =16.38$. Initial conditions (x(0), y(0), z(0)) are $\left( {\pm 0.01,\pm 0.01,\pm 0.01} \right)$ and $\left( {\pm 0.1,\pm 0.1,\pm 0.1} \right)$ respectively

Fig. 9

Coexistence of four different attractors (a pair of period-4 limit cycles and a pair of chaotic attractors) for $\alpha =16.615$. Initial conditions (x(0), y(0), z(0)) are $\left( {\pm 0.01,\pm 0.01,\pm 0.01} \right)$ and $\left( {\pm 0.1,\pm 0.1,\pm 0.1} \right)$ respectively

3.2 Route to chaos

As earlier mentioned, parameter $\alpha$ serves as the main bifurcation control parameter for the Chua’s equation, the rest of parameters being fixed as in Sect. 2. The range $0\le \alpha \le 20.0$ is considered. It is found that the Chua’s oscillator under investigation can experience very rich and striking bifurcation structures when slowly monitoring the bifurcation parameter. Sample results showing the bifurcation diagram for varying $\alpha$ and the corresponding graph of largest 1D Lyapunov exponent are depicted in Fig. (3a, b), respectively. The bifurcation diagram is constructed by plotting local maxima of the coordinate $x\left( \tau \right)$ in terms of the bifurcation control parameter that is increased (or decreased) in small steps in the range $1.0\le \alpha \le 20.0$. The final state at each iteration of the bifurcation control parameter serves as the initial state for the next iteration. This strategy represents a simple way to identify the domain/zone in which Chua’s oscillator develops multiple coexisting attractors (see Sect. 4). In light of the graphs in Fig. (3a, b), the following bifurcation scenarios can be captured when the bifurcation control parameter $\alpha$ is increased in tiny steps. First, for values of $\alpha$ lower than the critical values $\alpha _\mathrm{cr1} =15.90$, the system displays a limit cycle motion. When increasing the control parameter $\alpha$ past this critical value, the stable period-1 limit cycle undergoes a series of period-doubling bifurcations culminating to a single-scroll spiraling chaotic attractor. Further increasing $\alpha$ up to $\alpha _\mathrm{cr2} \approx 17.95$, the spiraling chaotic attractor suddenly collapses, giving rise to a period-5 limit cycle. The period-5 window lies in the range $17.95\le \alpha \le 18.91$. Past the critical value $\alpha _\mathrm{cr3} \approx 18.91$, the period-5 limit cycle suddenly converts to a double-scroll chaotic attractor. A very good coincidence can be captured between the bifurcation diagram and the graph of the largest Lyapunov exponent ($\lambda _{\max } )$. Using the same set of parameters in Fig. 3, some sample numerical phase portraits as well as corresponding time waveforms were computed to confirm different bifurcation sequences observed previously (see Fig. 4). Asymmetric attractors pairs are observed in Fig. 4a(i)–e(i), while a double-scroll strange attractor is depicted in Fig. 4f(i). To gain more insight about the complexity of the attractor depicted in Fig. 4f(i), some two-dimensional projections are shown in Fig. 5. Correspondingly, the (double-sided) Poincaré section of the attractor is depicted in Fig. 5d. The shape of this Poincaré section is typical of chaotic attractors.

The period-doubling scenario to chaos and the symmetry restoring crisis are observed when using $\beta$ or $\gamma$ as bifurcation control parameter (see Fig. 6a, b).

Fig. 10

Coexistence of four different attractors (a pair of period-5 limit cycles and a pair of chaotic attractors) for $\alpha =16.92$. Initial conditions (x(0), y(0), z(0)) are $\left( {\pm 1,\pm 1,\mp 0.25} \right)$ and $\left( {\pm 0.1,\pm 0.1,\pm 0.1} \right)$ respectively

Fig. 11

Cross sections of the basin of attraction for $x(0)=0, y(0)=0$ and $z(0)=0$ respectively corresponding to the asymmetric pair of period-4 cycle (blue and yellow) and the pair of chaotic attractors (green and magenta) obtained for $\alpha =16.615$. Red regions correspond to unbounded dynamics. (Color figure online)

3.3 Occurrence of multiple attractors

Despite the procedure (i.e., upward and backward continuation techniques) used to produce the bifurcation diagram of Fig. 3, no coexisting bifurcations can be captured. However, with reference to the enlargement of the same diagram shown in Fig. 7a, a window of hysteretic dynamics (and thus multiple stability) can be identified in the range $16.375\le \alpha \le 16.620$ (see Fig. 7a). In the graph in Fig. 7a, two sets of data (magenta and blue) are superimposed. The diagram in blue is obtained for increasing values of parameter $\alpha$ starting from the initial point$\left( {\alpha =16.375,x\left( 0 \right) =y\left( 0 \right) =z\left( 0 \right) =0.1} \right)$, while the one in magenta is obtained for decreasing values of $\alpha$ starting from the initial point$( \alpha =17.0,x\left( 0 \right) =y\left( 0 \right) =z\left( 0 \right) =0.1 )$. In both cases, the final state at each iteration of the bifurcation control parameter $\alpha$ serves as the initial state for the next iteration. The graphs of largest Lyapunov exponent depicted in Fig. 7b are computed using the same procedure described above. For values of $\alpha$ within the range $16.375\le \alpha \le 16.620$, the steady state dynamics of the oscillator depends on initial states, thus giving rise to the striking phenomenon of multiple attractors. Up to four different attractors (see Figs. 8, 9 and 10) can be found depending uniquely on the selection of initial conditions. For instance, the regular phase portraits (i.e., period-4 limit cycles) of Fig. (9a, b) can be obtained under the initial conditions$x\left( 0 \right) =0, y\left( 0 \right) =0, z\left( 0 \right) =\pm 0.1$; using the initial state $x\left( 0 \right) =0$, $y\left( 0 \right) =0, z\left( 0 \right) =\pm 1$, a completely different attractors (i.e., chaotic attractors) are obtained in Fig. (9c, d). Therefore, using the same parameters setting in Fig. 9 and performing a scan of initial conditions (see Fig. 11), we have defined the set of initial conditions in which each attractor can be found. The complexity of the basin boundaries is clearly highlighted in Fig. 11 where cross sections of the basins of attraction are presented, respectively, for $x\left( 0 \right) =0, y\left( 0 \right) =0$, and $z\left( 0 \right) =0$ related to the symmetric pair of limit cycles (blue and yellow) and the pair of chaotic attractors (green and magenta). Zones of unbounded motion are marked with red color. It ought to be stressed that, to the best of the author’s knowledge, the striking phenomenon of multiple stability involving four disconnected coexisting attractors, previously reported in the Leipnik–Newton system [6] and very recently in some simple models such as the linear transformation of jerk system Model MO5 [11], the memristor-based Shinriki’s oscillator [23], and the autonomous 3D Duffing Holmes type oscillator has not yet been reported in the Chua’s oscillator [22], and thus represents an enriching contribution related to the dynamics of Chua’s circuit family in general. Another situation involving the coexistence of infinitely many attractors (also called extreme multistability), arising in coupled dynamical systems was recently investigated by Hens et al. [30]. The occurrence of multiple co-existing attractors is an additional source of randomness; also some potential exploitation includes, for instance, chaos-based communication as well as random bit generation. However, this singular type of behavior is not desirable in general, and may justify the need for control. Detailed analysis on this line is out of the scope of this work; also, we refer the reader to the interesting review work on control of multistability by Pisarshik and Feudel [31].

4 Concluding remarks

This paper has considered the dynamics of Chua’s circuit with a smooth cubic nonlinearity (instead of the traditional piecewise-linear one). Using standard nonlinear analysis techniques such as bifurcation diagrams, Lyapunov exponent plots, time series, and Poincaré sections, the complex behavior of the model has been characterized in terms of its parameters. The bifurcation analysis yields the classical period-doubling, symmetry recovering crises events, and periodic windows when adjusting the bifurcation control parameter in tiny ranges. As a major result, it is found numerically that Chua’s circuit with a smooth cubic nonlinearity experiences the unusual and striking feature of multiple coexisting attractors (i.e., coexistence of four disconnected non-static periodic and chaotic attractors depending only on initial states) for a wide range of circuit parameters values. To the best of the author’s knowledge, the coexistence of four different non-static attractors has not yet been reported in Chua’s circuit despite the huge amount of related research literature. However, it should be pointed out that the occurrence of multiple attractors depends crucially on the choice of nonlinearity as well as parameters  [32]. Correspondingly, interesting phenomena such as the occurrence of multi-scroll attractors are reported in the Chua’s oscillator [32] and Jerk circuits [33] when using a sinusoidal nonlinearity.

The results obtained in this work let us conjecture that some striking behaviors of Chua’s circuit still remain unknown. Detailed exploration of the parameter space (both theoretically and experimentally) with the aim of revealing all regions in which the phenomenon of coexistence of multiple attractors occurs deserves further studies.