1 Introduction

Fractional-order calculus can date back to the emergence of integer-order calculus. For many years, it has not been used in actual project. Nevertheless, during recent decades, fractional-order calculus has attracted increasing attention in physics and engineering [1, 2]. And it was found that many systems could be better modeled and elegantly described with the help of fractional-order calculus compared with integer-order one, especially for memory and hereditary properties of various materials and processes [3, 4], for instance, wind turbine generators [5], mechanical system [6], chemical system [7], oscillation of earthquakes [8], and so on.

Nonlinearity is universal in actual project, and nonlinear dynamics and stability control for integer-order systems have been widely studied [9–14]. However, fractional-order nonlinear systems have different stability regions with integer-order ones. Could fractional-order nonlinear systems be well controlled? It is worth studying. Recently, control and synchronization of fractional-order nonlinear systems have become a hot topic [15, 16]. Many control methods have been designed for the control of fractional-order nonlinear systems such as sliding mode control [17], fuzzy control [18], pinning control [19], predictive control [20], among many others.

As we all know, Lyapunov stability theorem is often used in the analysis of integer-order system stability. However, it has not yet received satisfactory results in fractional systems, specifically in the nonlinear case. Many scholars focus on the stability study for fractional-order nonlinear systems control recently. Some researchers introduce the Mittag-Leffler stability to analysis the stability for fractional-order nonlinear systems. However, the definition of state variables and state space representation make the method could not apply widely [21]. Reference [21] proposes applying the frequency distributed model (FDM) to Lyapunov’s method for some simple linear and nonlinear fractional differential equations. In [22, 23], by using the FDM, the authors convert the FDE initial conditions problem into an equivalent ODE initialization problem. By applying FDM, stability analysis of sliding mode dynamics systems was studied in [24, 25]. Reference [26] introduces the FDM into the fractional-order complex dynamic networks, and a robust non-fragile observer-based controller is designed. The main advantage using FDM is that the approach provides a reference for generalization of integer-order system theory to fractional-order ones, which is obvious a bridge between fractional-order system and integer-order system.

Besides, most of the above-mentioned techniques are concerned about asymptotically stability for fractional-order nonlinear systems. It is also noted that the traditional controller could not guarantee the fast convergence of the system. In practical application, the finite-time controller is often designed for actual projects, which exhibits the following advantages [27], such as high-precision performance, better robustness, small overshoot and short stabilization time. From the optimization point of view, finite-time control should be studied and it has attracted increasing attention. Until now, some finite-time control techniques such as terminal sliding mode (TSM) and fast terminal sliding mode (FTSM) for integer-order and fractional-order nonlinear systems have been proposed [28–31].

That is, both FDM in analyzing the stability of fractional-order system and finite-time control in improving control quality have potential advantages. However, to the best of our knowledge, there is very little literature introducing FDM to the finite-time control of fractional-order nonlinear systems control. Can finite-time control of fractional-order nonlinear systems be implemented via FDM? If the hypothesis is true, what are the specific mathematical derivation and controller forms? There are no relevant results yet. It is still an open problem. Research in this area should be meaningful and challenging.

In light of the above analysis, there are several advantages which make our study attractive. Firstly, different with the reference [21], the FDM is proposed by an auxiliary function and the properties of fractional calculus, which is easier to implement. Secondly, a novel fractional FTSM is firstly proposed and its stability to origin is guaranteed based on the proposed FDM and Lyapunov stability theorem. Then, a robust finite-time control law to ensure the occurrence of the sliding motion in a finite time is proposed for stabilization of the fractional-order nonlinear systems regardless the model uncertainties and external disturbances. Lastly, two typical examples are implemented to demonstrate the effectiveness of the theoretic results.

The rest of this paper is organized as follows. In Sect. 2, some definitions of fractional-order calculus and relevant properties are presented. The FDM and controller design are given in Sect. 3. In Sect. 4, simulation examples are provided. Some conclusions end this paper in Sect. 5.

2 Preliminaries

In this section, some basic definitions and properties would be used related to fractional calculus are given. The two most usually used definitions of fractional derivative are Riemann–Liouville and Caputo definitions.

Definition 1

[32] The \(\alpha \hbox {th}\) fractional-order Riemann–Liouville integration of function f(t) is defined by:

$$\begin{aligned} { }_{t_0 }I_t^\alpha f(t)=_{t_0 } D_t^{-\alpha } f(t)=\frac{1}{\Gamma (\alpha )}\int _{t_0 }^t {\frac{f(\tau )}{(t-\tau )^{1-\alpha }}\hbox {d}\tau } , \end{aligned}$$
(1)

where \(\alpha \in R^{+}\) and \(\Gamma (\cdot )\) is the Gamma function.

It can be known that when \(\alpha \) approaches to zero, fractional integral (1) would change into the identity operator in the weak sense. In this paper, 0-th fractional integral is considered to be the identity operator which is defined as:

$$\begin{aligned} I^{0}f(t)=f(t). \end{aligned}$$
(2)

Remark 1

\(\Gamma (\cdot )\) is the well-known Euler’s gamma function which is defined as:

$$\begin{aligned} \Gamma (z)=\int _0^\infty {e^{-t}t^{z-1}\hbox {d}t} \;\;\;\;\;(Re(z)>0) \end{aligned}$$
(3)

and the following identity holds:

$$\begin{aligned} \Gamma (z)\Gamma (1-z)=\frac{\pi }{\sin \;\pi z}\;\;\;\;(0<Re(z)<1) \end{aligned}$$
(4)

Definition 2

[32] The Riemann–Liouville fractional derivative of order \(\alpha >0\) of a continuous function f(t) is defined as the \(n\hbox {th}\) derivative of fractional integral (1) of order \(n-\alpha \):

$$\begin{aligned} { }_{t_0 }^{RL} D_t^\alpha f(t)= & {} \left( {\frac{\hbox {d}}{\hbox {d}t}} \right) ^{n} I^{n-\alpha }f(t)\nonumber \\= & {} \frac{1}{\Gamma (n-\alpha )}\frac{\hbox {d}^{n}}{\hbox {d}t^{n}}\int _{t_0 }^t {\frac{f(\tau )}{(t-\tau )^{\alpha -n+1}}\hbox {d}\tau } ,\nonumber \\ \end{aligned}$$
(5)

where n is the smallest integer larger than or equal to \(\alpha \), and \(\Gamma (\cdot )\) denotes the Gamma function.

Definition 3

[32] The Caputo fractional derivative of order \(\alpha >0\) of a continuous function f(t) at time instant \(t\ge 0\) is defined as the fractional integral (1) of order \(n-\alpha \) of the \(n\hbox {th}\) derivative of f(t):

$$\begin{aligned} { }_{t_0 }^C D_t^\alpha f(t)= & {} I^{n-\alpha } \left( \frac{\hbox {d}}{\hbox {d}t}\right) ^{n}f(t)\nonumber \\= & {} \frac{1}{\Gamma (n-\alpha )} \int _{t_0 }^t {\frac{f^{n}(\tau )}{(t-\tau )^{\alpha -n+1}} \hbox {d}\tau } , \end{aligned}$$
(6)

where n is the smallest integer number larger than or equal to \(\alpha \), and \(\Gamma (\cdot )\) denotes the Gamma function.

The next are some useful properties of fractional differential and integral operators which will be used [33].

Property 1

The fractional integral meets the semigroup property. Let \(\alpha >0\) and \(\beta >0\), then:

$$\begin{aligned} I^{\alpha }I^{\beta }f(t)=I^{\beta }I^{\alpha }f(t)=I^{\alpha +\beta }f(t). \end{aligned}$$
(7)

Property 2

For the Caputo fractional derivative, the following equality holds:

$$\begin{aligned} I^{\alpha }{ }^CD^{\alpha }f(t)=f(t)-f(0). \end{aligned}$$
(8)

Property 3

The following equality for the Caputo derivative and the Riemann–Liouville derivative are established:

$$\begin{aligned} { }^{RL,C}D^{\alpha }({ }^{RL,C}D^{-\beta }f(t))={ }^{RL,C}D^{\alpha -\beta }f(t) \end{aligned}$$
(9)

where \(\alpha \ge \beta \ge 0\).

Remark 2

Compared with Riemann–Liouville fractional derivative, the Laplace transform of the Caputo definition allows utilization of initial conditions of classical integer-order derivatives with clear physical interpretations. And the Caputo fractional derivative has the wide spread application in the actual modeling process. Therefore in this paper, the Caputo definition of fractional derivative and integral is selected. To simplify the notation, we denote the Caputo fractional derivative of order \(\alpha \) as \(D^{\alpha }\) instead of \({ }_{t_0 }^C D_t^\alpha \).

3 Controller design based on FDM

3.1 System description

Since in the practical applications, system dynamics are often affected by model uncertainties and external disturbances. In this paper, the following n-dimensional fractional-order nonlinear system with model uncertainties and external disturbances is considered:

$$\begin{aligned} D^{\alpha }x(t)=f(x,t)+\Delta f(x,t)+d(t)+u(t), \end{aligned}$$
(10)

where \(\alpha \in (0,~1)\) is the order of the system, \(x(t)=[x_{1},x_{2},\ldots x_{n}]^{T}\in R^{n}\) denotes the state vector, and \(f(x,t)=[f(x_{1},t),f(x_{2},t),\ldots ,f(x_{n},t)]^{T}\in R^{n}\) is the given nonlinear function, \(d(t)=[d_{1}(t),d_{2}(t),\ldots d_{n}(t)]^{T}\in R^{n}\) is the external disturbance term of the system, \(\Delta f (x,t)=[\Delta f(x_{1},t),\Delta f(x_{2},t),\ldots ,\Delta f(x_{n},t)]\in R^{n}\) represents the unknown model uncertainty term of the system and \(u(t)=[u_{1}(t),u_{2}(t),\ldots u_{n}(t)]^{T}\in R^{n}\) is the control input.

Assumption 1

In practice, the exact values of the bound of the system uncertainties are difficult to know. However, in most practical examples, the upper bound of the nonlinear systems uncertainties can be estimated, and the states of the nonlinear systems are globally bounded [34]. Therefore, in this paper, the uncertainty term \(\Delta f(x,t)\) and external disturbance d(t) are considered bounded as follows:

$$\begin{aligned} \left| {\Delta f(x,t)} \right| \le \xi _1 ,\;\;\left| {d(t)} \right| \le \xi _2 \end{aligned}$$
(11)

where \(\xi _{1}\) and \(\xi _{2}\) are given positive constants.

3.2 Frequency distributed model transformation

To get the main results in this paper, the following theorem is introduced firstly. For the convenience of mathematical analysis, noting \(F(x,t)=f(x,t)+\Delta f(x,t)+d(t)+u(t)\).

The fractional-order system (10) is equally written as:

$$\begin{aligned} D^{\alpha }x(t)=F(x,t). \end{aligned}$$
(12)

Inspired by the method of the numerical approximation of fractional derivatives proposed by Yuan and Agrawal [35], an auxiliary time and frequency domain function \(\phi :(0,\infty )\times [0,X]\rightarrow R^{n}\) is defined as:

$$\begin{aligned} \phi (\omega ,t)=\mathop {\int }\limits _0^t {e^{-\omega ^{2}(t-\tau )}} F(x,\tau )\hbox {d}(\tau ) \end{aligned}$$
(13)

Theorem 1

Under the above assumptions, fractional-order system (12) can be written as:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\partial \phi (\omega ,t)}{\partial t}=-w^{2}\phi (\omega ,t)+F(x,t) \\ \displaystyle X(t)=\int _0^\infty {u(\omega )\phi (\omega ,t)\mathrm{d}\omega } \\ \end{array} \right. \end{aligned}$$
(14)

with \(u(\omega )=\frac{2\sin (\pi \alpha )}{\pi }\omega ^{1-2\alpha },\alpha \in (0,~1)\).

Proof

The proof will be divided into two steps.

Step 1: Equation (13) can be transformed into the following form:

$$\begin{aligned} \phi (\omega ,t)=e^{-\omega ^{2}t}\mathop {\int }\limits _0^t {e^{\omega ^{2}\tau }} F(x,\tau )\hbox {d}(\tau ), \end{aligned}$$
(15)

Taking its time derivative, there is:

$$\begin{aligned} \frac{\partial \phi (\omega ,t)}{\partial t}= & {} -\omega ^{2}e^{-\omega ^{2}t}\mathop {\int }\limits _{t_0 }^t {e^{\omega ^{2}\tau }F(x,\tau )\hbox {d}(\tau )} \nonumber \\&+\,\, e^{-\omega ^{2}t}e^{\omega ^{2}t}F(x,t) \nonumber \\= & {} -\omega ^{2}\mathop {\int }\limits _{t_0 }^t {e^{-\omega ^{2}(t-\tau )}F(x,\tau )\hbox {d}(\tau )} +F(x,t) \nonumber \\= & {} -\omega ^{2}\phi (\omega ,t)+F(x,t). \end{aligned}$$
(16)

Step 2: Using the definition of gamma function (3) and (1), one obtains:

$$\begin{aligned} { }_{t_0 }I_t ^{\alpha }F(x,t)= & {} \frac{1}{\Gamma (\alpha ) \Gamma (1-\alpha )}\int _{t_0 }^t {\frac{F(x,\tau )}{(t-\tau )^{1-\alpha }}} \hbox {d}\tau \nonumber \\&\int _0^\infty {e^{-z}z^{-\alpha }\hbox {d}z} \nonumber \\= & {} \frac{1}{\Gamma (\alpha )\Gamma (1-\alpha )}\nonumber \\&\int _0^\infty {\int _{t_0 }^t {\frac{F(x,\tau )}{(t-\tau )^{1-\alpha }}e^{-z}z^{-\alpha }\hbox {d}\tau \hbox {d}z} } \nonumber \\= & {} \frac{1}{\Gamma (\alpha )\Gamma (1-\alpha )}\int _0^\infty {\int _{t_0 }^t {F(x,\tau )} }\nonumber \\&\left( \frac{z}{t-\tau }\right) ^{-\alpha }\frac{1}{(t-\tau )} e^{-z}\hbox {d}\tau \hbox {d}z. \end{aligned}$$
(17)

Define the variable:

$$\begin{aligned} z=\omega ^{2}(t-\tau ), \end{aligned}$$
(18)

with \(dz=2\omega (t-\tau )d\omega \).

And then, Eq (17) can be written as:

$$\begin{aligned} { }_{t_0 }I_t ^{\alpha }F(x,t)= & {} \frac{2}{\Gamma (\alpha )\Gamma (1-\alpha )}\nonumber \\&\int _0^\infty {\int _{t_0 }^t {F(x,\tau )} } \omega ^{1-2\alpha }e^{-\omega ^{2}(t-\tau )}\hbox {d}\tau \hbox {d}\omega \nonumber \\= & {} \frac{2}{\Gamma (\alpha )\Gamma (1-\alpha )}\int _0^\infty \omega ^{1-2\alpha }\nonumber \\&\int _{t_0 }^t {F(x,\tau )} e^{-\omega ^{2}(t-\tau )}\hbox {d}\tau \hbox {d}\omega . \end{aligned}$$
(19)

According to the auxiliary function (13), one gets:

$$\begin{aligned} { }_{t_0 }I_t ^{\alpha }F(x,t)=\frac{2}{\Gamma (\alpha )\Gamma (1-\alpha )}\int _0^\infty {\omega ^{1-2\alpha }\phi (\omega ,t)} \hbox {d}\omega , \end{aligned}$$
(20)

Note \(\mu (\omega )\) as:

$$\begin{aligned} \mu (\omega )=\frac{2}{\Gamma (\alpha )\Gamma (1-\alpha )}\omega ^{1-2\alpha }. \end{aligned}$$
(21)

Based on Remark 1, Eq (21) can be written as:

$$\begin{aligned} \mu (\omega )=\frac{2\sin \alpha \pi }{\pi }\omega ^{1-2\alpha }, \end{aligned}$$
(22)

Then Eq. (20) can be written as:

$$\begin{aligned} { }_{t_0 }I_t ^{\alpha }F(x,t)=\int _0^\infty {\mu (\omega )\phi (\omega ,t)} \hbox {d}\omega \end{aligned}$$
(23)

Based on the properties 2, 3 and Eq. (23), one gets:

$$\begin{aligned} X(t)=D^{-\alpha }F(x,t)=\int _0^\infty {\mu (\omega )} \phi (\omega ,t)\hbox {d}\omega \end{aligned}$$
(24)

This completes the proof. \(\square \)

3.3 Controller design

Definition 4

[36] Consider the n-dimensional fractional-order system (12) and assume that there exists a positive constant \(T=T(X(0))\), such that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow T} \left\| {X(t)} \right\| =0, \end{aligned}$$
(25)

and \(\Vert X(t)\Vert \equiv 0\), if \(t\ge T\), then the stabilization of fractional-order nonlinear system (12) is guaranteed in the finite time T.

In general, the design process of sliding mode control can be divided into two steps. Firstly, selecting an appropriate sliding surface which represents the required system dynamic characteristics. Inspired by the integer-order FTSM presented in [37], in this paper, a novel fractional-order FTSM is defined as follows:

$$\begin{aligned} s(t)=D^{\alpha -1}x+D^{-1}\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x)\right) \end{aligned}$$
(26)

where \(s(t)=[s_{1},s_{2},\ldots s_{n}]^{T}\in R^{n}\) are the sliding surfaces, \(x=[x_{1},x_{2},\ldots x_{n}]^{T}\in R^{n}\) are the system states and \(k_{1},k_{2},\gamma \) are the given sliding surface parameters, with \(k_{1}>0,k_{2}>0, 0< \gamma <1\). Compared with reference [38], the sign function is replaced with the saturation function in the sliding mode (26) to weaken the chattering phenomenon. The saturation function sat(\(\cdot \)) is presented as:

$$\begin{aligned} \hbox {sat}(\rho )=\left\{ \begin{array}{l} \hbox {sign}(\rho /k),\;\;\left| \rho \right| >k \\ \rho /k,\;\;\;\;\;\;\left| \rho \right| \le k \\ \end{array} \right. , \end{aligned}$$
(27)

where k is a given positive constant.

When the system works on the sliding mode, the following equation satisfies [39]:

$$\begin{aligned} s(t)=0 \end{aligned}$$
(28)

As a result, considering (26) and (28), one obtains:

$$\begin{aligned} s(t)=D^{\alpha -1}x+D^{-1}\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x)\right) =0\nonumber \\ \end{aligned}$$
(29)

Then,

$$\begin{aligned} D^{\alpha -1}x=-D^{-1}\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x)\right) \end{aligned}$$
(30)

Based on Property 2 and Property 3, applying the operator \(D^{1}\) to both sides of Eq. (30), there is:

$$\begin{aligned} D^{\alpha }x=-\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x)\right) \end{aligned}$$
(31)

Theorem 2

If the terminal sliding mode is selected in the form of Eq. (26), then the sliding mode dynamics system (31) is stable and its state trajectories will converge to zero.

Proof

According to Theorem 1, the sliding mode dynamics system (31) can be expressed as:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\partial \phi (\omega ,t)}{\partial t}=-w^{2}\phi (\omega ,t)-\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x)\right) \\ \displaystyle x(t)=\int _0^\infty {u(\omega )\phi (\omega ,t)\hbox {d}\omega } \\ \end{array}\right. \end{aligned}$$
(32)

Considering the following positive definite Lyapunov function:

$$\begin{aligned} V_1 (t)=\frac{1}{2}\int _0^\infty {\mu (\omega )} \phi ^{2}(\omega ,t)\hbox {d}\omega \end{aligned}$$
(33)

Taking its time derivative, one gets:

$$\begin{aligned} \frac{\hbox {d}V_1 }{\hbox {d}t}= & {} \int _0^\infty {\mu (\omega )} \phi (\omega ,t)\frac{\partial \phi (\omega ,t)}{\partial t}\hbox {d}\omega \nonumber \\= & {} \int _0^\infty {\mu (\omega )} \phi (\omega ,t)(-w^{2}\phi (\omega ,t)\nonumber \\&-\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x))\right) \hbox {d}\omega \nonumber \\= & {} -\int _0^\infty {\mu (\omega )} \omega ^{2}\phi ^{2}(\omega ,t)\hbox {d}\omega \nonumber \\&-\int _0^\infty {\mu (\omega )\phi (\omega ,t)} (k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x))\hbox {d}\omega \nonumber \\= & {} -\int _0^\infty {\mu (\omega )} \omega ^{2}\phi ^{2}(\omega ,t)\hbox {d}\omega \nonumber \\&-\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x)\right) \int _0^\infty {\mu (\omega )\phi (\omega ,t)} \hbox {d}\omega \nonumber \\= & {} -\int _0^\infty {\mu (\omega )} \omega ^{2}\phi ^{2}(\omega ,t)\hbox {d}\omega \nonumber \\&-\,\, k_1 x^{2}-k_2 \left| x \right| ^{\gamma }x\hbox {sat}(x) \end{aligned}$$
(34)

According to the definition of saturation function \(\hbox {sat}(\cdot )\), there is:

Case 1: \(|x|>k\). In this case, one has:

$$\begin{aligned} x\hbox {sat}(x)=x\hbox {sign}(x/k) \end{aligned}$$
(35)

Based on \(x\times \hbox {sign}(x)=\left| x \right| \) and k is a given positive constant, one gets:

$$\begin{aligned} x\hbox {sat}(x)=\left| x \right| >0 \end{aligned}$$
(36)

Case 2: \(|x|\le k\). In this case, one has:

$$\begin{aligned} x\hbox {sat}(x)=x^{2}/k>0 \end{aligned}$$
(37)

Based on the above discussion, it is obvious that

$$\begin{aligned} \frac{dV_1 }{dt}<0 \end{aligned}$$
(38)

According to Lyapunov stability theory, the state trajectories of the sliding mode dynamics system (31) will converge to zero asymptotically. This completes the proof. \(\square \)

Once an appropriate sliding surface is established, then next part of the sliding mode method is to construct an input signal u(t) to guarantee the state trajectories reach to the sliding surface \(s(t)=0\) and stay on it forever. The sliding mode control law is presented as follows:

$$\begin{aligned} u(t)= & {} -(f(x)+k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x) +\eta _1 s\nonumber \\&+\left( \xi _1 +\xi _2 +L\left| s \right| ^{r}\right) \hbox {sign}(s)+k_3 \hbox {sat}(s)) \end{aligned}$$
(39)

where \(u=[u_{1},u_{2},\ldots ,u_{n}]^{T}\in R^{n}\) express the sliding mode control laws, \(s(t)=[s_{1},s_{2},\ldots s_{n}]^{T}\in R^{n}\) present the sliding surfaces, \(x=[x_{1},x_{2},\ldots x_{n}]^{T}\in R^{n}\) are the system states, \(\eta _{1},r,k_{3}\) are given positive constants with \(\eta _{1}>0,0<r<1,k_{3}>0,L>0\).

Theorem 3

Consider fractional-order system (10) with the conditions in (11) and the sliding surface in (26). If the system is controlled by the control law (39), then the states trajectories of the system will converge to the sliding surface \(s(t)=0\) in a finite time.

Proof

Selecting a Lyapunov function \(V_{2}(t)=|s|\) and taking its time derivative, one obtains:

$$\begin{aligned} \dot{V} _2 (t)=\hbox {sign}(s)\dot{s} \end{aligned}$$
(40)

Taking the time derivative of (26), one has:

$$\begin{aligned} \dot{s} =D^{\alpha }x+\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x)\right) \end{aligned}$$
(41)

Substituting (41) into (40), (40) can be written as:

$$\begin{aligned} \dot{V} _2 (t)=\hbox {sign}(s)(D^{\alpha }x+\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x))\right) \end{aligned}$$
(42)

Considering \(D^{\alpha }x=f(x)+\Delta f (x)+d(t)+u(t)\), (42) can be written as:

$$\begin{aligned} \dot{V} _2 (t)= & {} \hbox {sign}(s)(f(x)+\Delta f(x)+d(t)+u(t)\nonumber \\&+\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x))\right) \nonumber \\= & {} \hbox {sign}(s)(f(x)+u(t)+\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x))\right) \nonumber \\&+\,\, \hbox {sign}(s)(\Delta f(x)+d(t)) \end{aligned}$$
(43)

Based on Assumption 1, there is:

$$\begin{aligned} \hbox {sign}(s)(\Delta f(x)+d(t))\le & {} \left| {\hbox {sign}(s)} \right| \left| {\Delta f(x)+d(t)} \right| \nonumber \\\le & {} \left| {\hbox {sign}(s)} \right| \left( \left| {\Delta f(x)} \right| +\left| {d(\hbox {t})} \right| \right) \nonumber \\\le & {} \xi _1 +\xi _2 \end{aligned}$$
(44)

Considering (43) and (44), one has:

$$\begin{aligned} \dot{V} _2 (t)\le & {} \hbox {sign}(s)(f(x)+u(t)+(k_1 x\nonumber \\&+\,\, k_2 \left| x \right| ^{\gamma }\hbox {sat}(x)))+\xi _1 +\xi _2 \end{aligned}$$
(45)

Introducing control law (39) to (45), one gets:

$$\begin{aligned} \dot{V} _2 (t)\le & {} \hbox {sign}(s)(f(x)-(f(x)+k_1 x\nonumber \\&+\,k_2 \left| x \right| ^{\gamma }\hbox {sat}(x)+\eta _1 s \nonumber \\&+\,\left( \xi _1 +\xi _2 +L\left| s \right| ^{r}\right) \hbox {sign}(s)\nonumber \\&+\,k_3 \hbox {sat}(s))+\left( k_1 x+k_2 \left| x \right| ^{\gamma }\hbox {sat}(x))\right) \nonumber \\&+\,\xi _1 +\xi _2 \end{aligned}$$
(46)

After some manipulations, there is:

$$\begin{aligned} \dot{V} _2 (t)\le & {} \hbox {sign}(s)(-\eta _1 s-\left( \xi _1 +\xi _2 +L\left| s \right| ^{r}\right) \hbox {sign}(s)\nonumber \\&-\,k_3 \hbox {sat}(s))+\xi _1 +\xi _2 . \end{aligned}$$
(47)

Based on \(s\times \hbox {sign}(s)=\left| s \right| \) and \(\hbox {sign}(s)\times \hbox {sign}(s)=1\), one has

$$\begin{aligned} \dot{V} _2 (t)\le -\eta _1 \left| s \right| -L\left| s \right| ^{r}-k_3 \hbox {sat}(s)\hbox {sign}(s). \end{aligned}$$
(48)

Now considering the third term on the right side of Eq. (48):

According to the definition of \(\hbox {sat}(\cdot )\) function,

when \(|s|>k\),

$$\begin{aligned} \hbox {sat}(s)\hbox {sign}(s)=\hbox {sign}(s/k)\hbox {sign}(s)=1, \end{aligned}$$
(49)

when \(|s|\le k\),

$$\begin{aligned} \hbox {sat}(s)\hbox {sign}( s)=s/k\times \hbox {sign}(s)=\left| s \right| /k>0. \end{aligned}$$
(50)

Based on the above discussion, one gets

$$\begin{aligned} \dot{V} _2 (t)<0. \end{aligned}$$
(51)

According to Lyapunov stability theory, the state trajectories of the uncertain fractional-order nonlinear system (10) will converge to \(s(t)=0\) asymptotically. To show that the motion happens in a finite time, one can get the reaching time T as follows:

From inequality (48), one gets:

$$\begin{aligned} \dot{V} _2 (t)\le & {} -\eta _1 \left| s \right| -L\left| s \right| ^{r}-k_3 \hbox {sat}(s) \hbox {sign}(s) \nonumber \\\le & {} -\eta _1 \left| s \right| -L\left| s \right| ^{r} \end{aligned}$$
(52)

Then

$$\begin{aligned} \frac{\hbox {d}V_2 }{\hbox {d}t}= \frac{\hbox {d}\left| s \right| }{\hbox {d}t}\le -\eta _1 \left| s \right| -L\left| s \right| ^{r}=-\left( \eta _1 \left| s \right| + L\left| s \right| ^{r}\right) \end{aligned}$$
(53)

It is obvious that

$$\begin{aligned} dt\le & {} \frac{-d\left| s \right| }{\eta _1 \left| s \right| +L\left| s \right| ^{r}} \nonumber \\= & {} \frac{-d\left| s \right| }{\left( \eta _1 \left| s \right| ^{1-r}+L\right) \left| s \right| ^{r}} \nonumber \\= & {} \frac{1}{\left( \eta _1 \left| s \right| ^{1-r}+L\right) }\frac{-d\left| s \right| }{\left| s \right| ^{r}} \nonumber \\= & {} \frac{1}{\left( \eta _1 \left| s \right| ^{1-r}+L\right) }\frac{-d\left| s \right| ^{1-r}}{1-r} \end{aligned}$$
(54)

Taking integral of both sides of (54) from 0 to \(t_{r1}\)

$$\begin{aligned} \int _0^{t_r } {dt} \le \int _{s(0)}^{s(t_r )} {-\frac{1}{1-r}\times \frac{d\left| s \right| ^{1-r}}{\eta _1 \left| s \right| ^{1-r}+L}} \end{aligned}$$
(55)

Then

$$\begin{aligned} t\left| {_0^{t_r } } \right. \le -\frac{1}{\eta _1 (1-r)}\ln \left( \eta _1 \left| s \right| ^{1-r}+L\right) \left| {_{s(0)}^{s(t_r )} } \right. \end{aligned}$$
(56)

and let \(s(t_{r1})=0\), one gets:

$$\begin{aligned} t_r \le \frac{1}{\eta _1 (1-r)}\ln \frac{\left( \eta _1 \left| {s(0)} \right| ^{1-r}+L\right) }{L} \end{aligned}$$
(57)

Based on Definition 3, the states trajectories of the system (10) will converge to the sliding surface \(s(t)=0\) in a finite time \(T=t_r \le \frac{1}{\eta _1 (1-r)}\ln \frac{(\eta _1 \left| {s(0)} \right| ^{1-r}+L)}{L}\). This completes the proof. \(\square \)

4 Numerical simulations

In this section, the effectiveness of the proposed scheme is illustrated by applying the method to two typical fractional-order nonlinear systems.

Example 1

The fractional-order nonlinear Lorenz system are presented as follows [38]:

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha }x_1 =10(x_2 -x_1 )+\Delta f_1 (X)+\,d_1 (t)+u_1 (t) \\ D^{\alpha }x_2 =28x_1 -x_2 -x_1 x_3 +\Delta f_2 (X)+\,d_2 (t)+u_2 (t) \\ D^{\alpha }x_3 =x_1 x_2 -(8/3)x_3 +\Delta f_3 (X)+d_3 (t)+u_3 (t) \\ \end{array}\right. , \end{aligned}$$
(58)

For the convenience of comparison, the uncertainty terms and external disturbances of the system are selected the same with reference [38]:

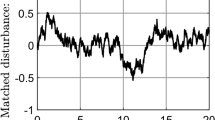
$$\begin{aligned} \Delta f_1 (X)+d_1 (t)= & {} 0.1\cos (2t)x_1 -0.1\sin (t), \nonumber \\ \Delta f_2 (X)+d_2 (t)= & {} -0.1\cos (5t)x_2 -0.1\sin (4t), \nonumber \\ \Delta f_3 (X)+d_3 (t)= & {} 0.1\sin (t)x_3 +0.1\cos (t). \end{aligned}$$
(59)

The initial conditions of fractional-order Lorenz nonlinear system are given as: \(x_{1}(0)=1, x_{2}(0)=0, x_{3}(0)=9\). The fractional-order \(\alpha = 0.98\). The time domain of the uncontrolled Lorenz system is illustrated in Fig. 1. The system is in nonlinear unstable operation, which needs to be controlled.

Regarding (26) and (39), select \(k_1 =30\), \(k_2 =1\), \(\gamma =0.2\), \(\eta _1 =1\), \(r=0.4\), \(k_3 =1\), \(L=1\), the sliding surface and control law are given as follows:

$$\begin{aligned} s_i (t)= & {} D^{-0.02}x_i +D^{-1}\left( 30x_i +\left| {x_i } \right| ^{0.2}\hbox {sat}(x_i )\right) ,\;\;i=1,2,3. \nonumber \\\end{aligned}$$
(60)
$$\begin{aligned} u_1 (t)= & {} -\left( 10(x_2 -x_1 )+30x_1 +\left| {x_1 } \right| ^{0.2}\hbox {sat}(x_1 )+s_1 \right. \nonumber \\&\left. +\left( 0.1+0.1+\left| {s_1 } \right| ^{0.4}\right) \hbox {sign}(s_1 )+\hbox {sat} (s_1 )\right) \nonumber \\ u_2 (t)= & {} -\left( 28x_1 -x_2 -x_1 x_3 +30x_2 +\left| {x_2 } \right| ^{0.2} \hbox {sat}(x_2 )+s_2 \right. \nonumber \\&\left. +\left( 0.1+0.1+\left| {s_2 } \right| ^{0.4}\right) \hbox {sign}(s_2 )+ \hbox {sat}(s_2 )\right) \nonumber \\ u_3 (t)= & {} -\left( x_1 x_2 -(8/3)x_3 +10x_1 +30x_3 +\left| {x_3 } \right| ^{0.2}\hbox {sat}(x_3 )+s_3 \right. \nonumber \\&\left. +\left( 0.1+0.1+\left| {s_3 } \right| ^{0.4}\right) \hbox {sign}(s_3 )+ \hbox {sat}(s_3 )\right) \end{aligned}$$
(61)
Fig. 1
figure 1

Time domain of nonlinear fractional-order Lorenz system (58)

Full size image
Fig. 2
figure 2

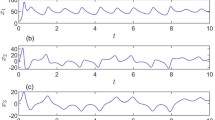
State trajectories of controlled nonlinear fractional-order Lorenz system (58)

Full size image

To compare the performance of the proposed control scheme, the states of fractional-order nonlinear Lorenz system (58) under the controller (60) and the existing controller (58) in reference [38] are shown in Fig. 2. It is clear that the sliding mode is guaranteed and the state trajectories converge to zero immediately, which implies that the nonlinear vibration of the uncertain fractional-order Lorenz system is efficiently suppressed in a finite time, and it is clear that the stabilized time is within 1.00 s. According to (57), the calculated finite time is \(t_{r}\leqslant 1.16\) s with initial value \(s(0)=[1,1,1]^{\mathrm {T}}\), which shows the validity of the proposed method. Besides, the stable time is shorter of the proposed control scheme and there is almost no chattering phenomenon, which implies the superiority and effectiveness of the designed controller in our paper.

Example 2

Consider the following fractional-order uncertain Chen system [38]:

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha }x_1 =35(x_2 -x_1 )+x_4 +\Delta f_1 (X)\\ \quad +\,\, d_1 (t)+u_1 (t) \\ D^{\alpha }x_2 =7x_1 +12x_2 -x_1 x_3 +\Delta f_2 (X)\\ \quad +\,\, d_2 (t)+u_2 (t) \\ D^{\alpha }x_3 =x_1 x_2 -8x_3 +\Delta f_3 (X)+d_3 (t)+u_3 (t) \\ D^{\alpha }x_4 =x_2 x_3 +0.3x_4 +\Delta f_4 (X)+d_4 (t)+u_4 (t) \end{array} \right. \end{aligned}$$
(62)
Fig. 3
figure 3

Time domain of nonlinear fractional-order Chen system (62)

Full size image

For the convenience of comparison, the uncertainty term and external disturbance of the system are selected the same with reference [38]:

$$\begin{aligned} \Delta f_1 (X)+d_1 (t)= & {} 0.1\cos (t)x_1 +0.1\sin (t) \nonumber \\ \Delta f_2 (X)+d_2 (t)= & {} 0.1\cos (t)x_2 -0.1\sin (2t) \nonumber \\ \Delta f_3 (X)+d_3 (t)= & {} -0.1\cos (2t)x_3 +0.1\cos (t) \nonumber \\ \Delta f_4 (X)+d_4 (t)= & {} -0.1\cos (2t)x_4 -0.1\cos (3t)\nonumber \\ \end{aligned}$$
(63)

The initial conditions of fractional-order nonlinear Chen system are given as: \(x_{1}(0)=0.2, x_{2}(0)=-0.1, x_{3}(0)=0.3, x_{4}(0)=-0.5\). The fractional-order \(\alpha = 0.98\). The time domain of the uncontrolled Chen system is shown in Fig. 3. It is clear that each state variable is in nonlinear and irregular movement. So it is necessary to design a controller to ensure the stable operation of system (62).

Regarding (26) and (39), select \(k_1 =30\), \(k_2 =1\), \(\gamma =0.2\), \(\eta _1 =1\), \(r=0.4\), \(k_3 =10\), \(L=1\), the sliding surface and control law are given as follows:

$$\begin{aligned} s_i (t)= & {} D^{-0.02}x_i +D^{-1}\left( 30x_i +\left| {x_i } \right| ^{0.2} \hbox {sat}(x_i )\right) ,\; i=1,2,3,4. \nonumber \\\end{aligned}$$
(64)
$$\begin{aligned} u_1 (t)= & {} -\left( 35(x_1 -x_2 )+x_4 +30x_1 +\left| {x_1 } \right| ^{0.2} \hbox {sat}(x_1 )+s_1 \right. \nonumber \\&\left. +\left( 0.1+0.1+\left| {s_1 } \right| ^{0.4}\right) \hbox {sign}(s_1 )+10 \hbox {sat}(s_1 )\right) \nonumber \\ u_2 (t)= & {} -\left( 7x_1 +12x_2 -x_1 x_3 +30x_2 +\left| {x_2 } \right| ^{0.2} \hbox {sat}(x_2 )+s_2 \right. \nonumber \\&\left. +\left( 0.1+0.1+\left| {s_2 } \right| ^{0.4}\right) \hbox {sign}(s_2 )+ 10\hbox {sat}(s_2 )\right) \nonumber \\ u_3 (t)= & {} -\left( x_1 x_2 -8x_3 +30x_3 +\left| {x_3 } \right| ^{0.2} \hbox {sat}(x_3 )+s_3 \right. \nonumber \\&\left. +\left( 0.1+0.1+\left| {s_3 } \right| ^{0.4}\right) \hbox {sign}(s_3 ) +10\hbox {sat}(s_3 )\right) \nonumber \\ u_4 (t)= & {} -\left( x_2 x_3 +0.3x_4 +30x_4 +\left| {x_4 } \right| ^{0.2}\hbox {sat}(x_4 )+s_4 \right. \nonumber \\&\left. +\left( 0.1+0.1+\left| {s_4 } \right| ^{0.4}\right) \hbox {sign}(s_4 )+ 10\hbox {sat}(s_4 )\right) \end{aligned}$$
(65)
Fig. 4
figure 4

State trajectories of controlled nonlinear fractional-order Chen system (62)

Full size image

To compare the performance of the designed controller, Fig. 4 shows the state trajectories of the controlled fractional-order nonlinear Chen system (62) under the controller (65) and the controller (54) in reference [38]. It is obvious that the nonlinear and irregular behavior of the system is effectively suppressed and the state trajectories of the uncertain fractional-order Chen system can reach the origin in a finite time as well as within 1.00 s. According to (57), the calculated finite time is also \(t_{r}\leqslant 1.16\) s with \(s(0)=[1,1,1,1]^{\mathrm {T}}\), which verify the effectiveness of the designed controller. By comparing the proposed scheme and the existing method in reference [38], it is clear that the control time is shorter of our method and the chattering phenomenon is well weakened, which implies the effectiveness and superiority of the proposed scheme in this paper.

5 Conclusions and discussion

In this paper, a robust FTSM control method for a class of fractional-order nonlinear systems with model uncertainties and external disturbances was studied. An auxiliary time and frequency domain function was introduced to transform the fractional-order nonlinear systems into FDM. Then, a novel FTSM is proposed and its stability to the origin was guaranteed based on the FDM and Lyapunov stability theory. Furthermore, a robust finite-time control law to ensure the occurrence of the sliding motion in a finite time was proposed for stabilization of the fractional-order nonlinear systems regardless of the model uncertainties and external disturbances. Lastly, two typical examples including three-dimensional fractional-order nonlinear Lorenz system and four-dimensional fractional-order nonlinear Chen system were implemented to demonstrate the effectiveness with the theoretic results.

The scheme designed is simple and easy to implement and could be applied to similar fractional-order nonlinear systems such as mechanical system, electrical system, chemical system, physical system, and so on. In the future work, we will consider and extend the application of FDM in the stability control for fractional-order complex networks and time delay systems.