Robust finite-time stabilization of uncertain nonlinear systems based on partial stability

Abstract

This paper presents a new approach to design a robust finite-time partial stabilization for uncertain nonlinear systems. The main contribution of this paper is to divide system state into two subsystems based on their required stability properties, and to stabilize just one of them in finite-time. First, integral sliding mode control is applied and the system is converted to a chain of integrators. Then, a finite-time state feedback controller with dynamical gains is utilized. Since guidance issue is an appropriate example in which stabilization of all of the state variables is not desirable, the proposed approach is employed to design a robust finite-time convergent guidance law. Simulation results justify that the proposed method is reliable in terms of robustness and effectiveness.

1 Introduction

The problem of partial stability concerns stabilizing a part of system states to their equilibriums  [1]. In particular, this approach has widely been utilized in the study of physical systems such as spacecraft stabilization, electromagnetics, inertial navigation systems, adaptive stabilization, etc.  [2–6]. In these works, although the plant might be unstable in the sense of Lyapunov, the plant has become partially stable using this approach, which means that the stability of a part of the system state has been guaranteed. The number of articles in the field of partial stability applications is on the rise, whereas there are a few articles which focus on proposing a control scheme which is able to partially stabilize the system. And the benefits of the partial control need to be recognized  [6]. In  [7, 8], two general approaches to design robust partial controller have been proposed. These controllers ensure that a part of system states converges to zero as time approaches infinity, whereas in many engineering problems, it is necessary that the system states converge to zero in a finite time.

Finite-time stability means leading the system states to their equilibrium point and keeping them there forever so that the convergence of state variables occurs in a finite time. The design of continuous finite-time-stabilizing feedback controllers was first introduced in  [9]. This finite-time stabilization has been expanded in  [10–12]. This concept has also been examined for uncertain nonlinear systems dominated by a lower-triangular system  [13, 14]. These papers propose controllers in order to guarantee global finite-time stability of the closed-loop system based on the finite-time Lyapunov stability theorem.

To control high-order uncertain nonlinear systems, the sliding mode control (SMC) as a robust technique is a powerful method  [15]. While this approach claims robustness property, the chattering phenomenon is the major disadvantage of this method for the implementation of it. Recently, to alleviate chattering effect, high-order SMC has been proposed which preserves the advantages of the standard SMC and provides enough precision  [16, 17]. Based on integral SMC approach, many papers exist concerning high order SMC  [18–21]. The integral SMC can be expressed by integrating an integral function into the sliding mode structure. Improving the reaching phase problem is a significant advantage of the integral SMC. In the reaching phase, state variables have not yet reached the sliding surface. So, the system is sensitive to any uncertainty or disturbance  [22]. Integral SMC can solve the reaching phase problem by omitting it. This control approach ensures that the system trajectories start from the initial time instance. As a result, the integral SMC must maintain the system trajectories on the integral sliding surface until trajectories converge to zero in spite of any disturbance and uncertainty.

Motivated by the above discussion, this paper introduces a new method for the design of a control input to partially stabilize the nonlinear system. The approach of this paper is based on integral SMC, so that a continuous feedback is produced combining the robustness of high-order sliding modes and finite-time stabilization by continuous control. The main advantage of this new design principle is its application in robust partial stabilization so that the objective of the method is to deal with unknown but bounded system uncertainties. The suggested control law is able to lead only a part of the system state to zero in a finite time in spite of any disturbances and uncertainties. In fact, for the first subsystem which its stabilization is important, by applying integral sliding mode, the subsystem is converted to a chain of integrators. Then, to control this linear system and to obtain finite-time convergence property, a finite-time state feedback with dynamical gain is employed. In many practical applications like guidance problem, the provision of partial stability is necessary; consequently, the proposed approach is employed to design a robust finite-time guidance law.

The rest of the paper is organized as follows. In the next section, some requirement definitions and theorems are presented. The main results are shown in Sect. 3, where a robust finite-time controller is developed based on partial stability. In Sect. 4, the proposed method is used to design a guidance law and simulation results are also discussed. Finally, conclusions are presented in Sect. 5.

2 Problem formulation

Before presenting main result of the control design procedure, the definitions and notations of partial stability and finite-time stability are introduced.

Definition 1

 [12] Consider the following nonlinear system:

$$\begin{aligned} \dot{x}(t)=f(x),\;\;\;f(0)=0,\;\;\;x\in R^{n} \end{aligned}$$

(1)

where $f:U_0 \rightarrow R^{n}$ is continuous on $U_0$, and $U_0$ is an open neighborhood of the origin$x=0$. The equilibrium $x=0$ of the system is finite-time convergent if, for any given initial time $t_0$ and initial state $x(t_0 )=x_0 \in U/\{0\}$, there exists a settling time $T(x_0 )>0$, such that every solution of the system (1), $x(t)=\upsilon (t,x_0 )\in U/\{0\}$ satisfies

$$\begin{aligned} \left\{ {\begin{array}{l@{\quad }l} \mathop {\lim }\limits _{t\rightarrow T(x_0 )} \;\upsilon (t,x_0 )=0, &{} t\in [0,T(x_0 )] \\ \upsilon (t,x_0 )=0, &{} t\ge T(x_0 ) \\ \end{array}} \right. \end{aligned}$$

(2)

In addition, if $U=R^{n}$, then $x=0$ is a global finite-time stable equilibrium.

Theorem 1

 [23] Consider the nonlinear system (1). Suppose that there is a $C^{1}$ (continuously differentiable) function V(x) defined in a neighborhood $\hat{{U}}\subset R^{n}$ of the origin, and that there are real numbers $\bar{{\alpha }}>0$ and $0<\bar{{\lambda }}<1$, such that V(x)is positive definite on $\hat{{U}}$ and that $\dot{V}(x)+\bar{{\alpha }}V^{\bar{{\lambda }}}(x)\le 0$ on $\hat{{U}}$. Then, the zero solution of the system (1) is finite-time stable. Furthermore, the settling time is calculated as follows:

$$\begin{aligned} T\le \frac{V^{1-\bar{{\lambda }}}(x_0 )}{\bar{{\alpha }}(1-\bar{{\lambda }})} \end{aligned}$$

(3)

Remark 1

Note that if $\hat{{U}}=R^{n}$ and V(x) is radially unbounded, then the origin is globally finite-time stable  [23].

Lemma 1

 [14] Let $D_1 =diag[1,\;2,\;\ldots ,\;(n-1),\;n]$, $D_2 =diag[n+d,\;n-1+2d,\;\ldots ,2+\;(n-1)d,\;1+nd]$ and $d\in (0,1)$ be a fraction whose numerator and denominator are odd integers, $A_0 \in R^{n\times n}$ and $B\in R^{n}$ be the matrices in the canonical controller form as:

$$\begin{aligned} A_0 =\left( {\begin{array}{l} 0\;\;\;\;1\;\;\;\;0\;\;\;\;\cdots \;\;\;\;0 \\ 0\;\;\;\;0\;\;\;\;1\;\;\;\;\cdots \;\;\;\;0 \\ \;\vdots \;\;\;\;\;\vdots \;\;\;\;\;\vdots \;\;\;\;\ddots \;\;\;\;\vdots \\ 0\;\;\;\;0\;\;\;\;0\;\;\;\;\cdots \;\;\;\;1 \\ 0\;\;\;\;0\;\;\;\;0\;\;\;\;\cdots \;\;\;\;0 \\ \end{array}} \right) , \quad B=\left( {\begin{array}{l} 0 \\ 0 \\ \;\vdots \\ 0 \\ 1 \\ \end{array}} \right) \end{aligned}$$

Then, there exist positive real numbers$\alpha _1 ,\;\alpha _2 ,\;\beta _1 , \beta _2$, a constant symmetric positive definite matrix$P\in R^{n\times n}$, and a row vector $K=\left( {a_1 ,\;a_2 , \ldots ,a_n } \right)$ satisfying:

$$\begin{aligned} \begin{array}{l} PA+A^{T}P\le -I \\ \alpha _1 I\le PD_1 +D_1 P\le \beta _1 I \\ \alpha _2 I\le PD_2 +D_2 P\le \beta _2 I \\ \end{array} \end{aligned}$$

(4)

where $A=A_0 -BK$.

Theorem 2

 [14] Consider the following chain of integrators:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{z}_1 =z_2 \\ \vdots \\ \dot{z}_{n-1} =z_n \\ \dot{z}_n =w_\mathrm{{nom}} \\ \end{array}} \right. \end{aligned}$$

(5)

A state feedback controller of the form

$$\begin{aligned} w_\mathrm{{nom}} =-L^{n+1}r^{(n+1)d}K\zeta \end{aligned}$$

(6)

can globally finite-time stabilize the system (5) where r and L are dynamically updated respectively by

$$\begin{aligned} \dot{r}= & {} -\frac{L}{4\beta _2 }r^{d}+\frac{L}{4\beta _2 }\frac{\left\| \zeta \right\| ^{2}}{r^{2-d}},\;\;\;\;\;r(0)=r_0 >0 \nonumber \\ \dot{L}= & {} \frac{\hbox {sgn}(\left\| \zeta \right\| )}{\alpha _1 }L\rho (t)\varpi (r,\zeta ),\;\;\;\;\;L(0)=M\ge 1 \end{aligned}$$

(7)

$\zeta =(\zeta _1 ,\;\zeta _2 , \ldots , \zeta _n )^{T}$ with $\zeta _i =\frac{z_i }{L^{i}r^{n-i+1+id}}$, the row vector K and constants $\alpha _1$, $\beta _2$ are given in Lemma 1, $\rho (t)$ is a nonnegative function, $\varpi (r,\zeta )$ is an appropriate continuous positive function of r and $\zeta$, and M is a large enough constant.

Definition 2

 [24] Consider the system (1). Let $f: R^{p}\times R^{n-p}\cong R^{n}\rightarrow R^{n}$, $x=(x_1 , x_2 )\in R^{p}\times R^{n-p}\mapsto f(x)\in R^{p}$ be defined and continuous on a neighborhood of $(0, 0)\in R^{p}\times R^{n-p}$. Suppose that

$$\begin{aligned} f(0, x_2 )=0. \end{aligned}$$

$(0, 0)\in R^{p}\times R^{n-p}$ will be p-partially stable in finite-time for $\dot{x}=f(x)$ if

(0, 0) is Lyapunov stable for $\dot{x}=f(x)$

there exist $r>0$ and $T>0$ such that if $\dot{x}=f(x)$ and $\left| {x(0)} \right| <r$, then $x_1 (t)=0$ for every $t\ge T$ (and therefore $t\mapsto x_2 (t)$ is constant for $t\ge T)$.

Now, consider the following nonlinear system:

$$\begin{aligned} \dot{x}_1= & {} F_1 (x_1 ,x_2 ,u(x_1 ,x_2 )), \quad x_1 (t_0 )=x_{10} \nonumber \\ \dot{x}_2= & {} F_2 (x_1 ,x_2 ,u(x_1 ,x_2 )), \quad x_2 (t_0 )=x_{20} \nonumber \\ y= & {} \sigma (x_1 ) \end{aligned}$$

(8)

where $u\in R$ and $F_1 :D\times R^{n_2 }\times R\rightarrow R^{n_1 }$ is such that for every $x_2 \in R^{n_1 }$, $F_1 (.,x_2 ,.)$ is locally Lipschitz in $x_1$ and u and $F_1 (0,x_2 ,0)=0$. Also, $F_2 :D\times R^{n_2 }\times R\rightarrow R^{n_2 }$ is such that for every$x_1 \in D$, $F_2 (x_1 ,.,.)$ is locally Lipschitz in $x_2$ and u. $\sigma (x_1 )\in R$ is the measured smooth output function (sliding variable). Now, let the $\dot{x}_1$ equation in (8) be affine with respect to the control input (the equation may have a general dynamics form). Thus

$$\begin{aligned} \dot{x}_1= & {} f_1 (x_1 ,x_2 )+g_1 (x_1 ,x_2 )u \nonumber \\ \dot{x}_2= & {} F_2 (x_1 ,x_2 ,u) \nonumber \\ y= & {} \sigma (x_1 ) \end{aligned}$$

(9)

The uncertainties $f_1 (x)$ and $g_1 (x)$ are due to unmodelled dynamics, parameter variations and external disturbances. Assume that:

Assumption 1

The relative degree $\bar{{r}}$ of the system (9) with respect to $\sigma (x_1 )$ is constant and known, and the associated zero dynamics are stable.

Definition 3

 [10] Consider the nonlinear system (9), and let the time derivative $\sigma , \dot{\sigma }, \ldots ,\sigma ^{(\bar{{r}}-1)}$ be continuous functions, and the manifold defined as $S^{\bar{{r}}}=\left\{ {x_1 \left| {\sigma =\dot{\sigma }=\cdots =\sigma ^{(\bar{{r}}-1)}=0} \right. } \right\}$ is called “$\bar{{r}}th$-order sliding set”, is non-empty and is locally an integral set in the Filippov sense  [25]. The motion on $\hbox {S}^{\bar{{r}}}$ is called “$\bar{{r}}th$-order sliding mode” with respect to the sliding variable $\sigma$.

The $\bar{{r}}th$-order SMC approach allows the finite-time stabilization to be zero of the sliding variable $\sigma$ and its $(\bar{{r}}-1)th$time derivatives by defining a suitable discontinuous control function. So, using the Lie derivative notation, the $\bar{{r}}th \sigma$ satisfies the following equation

$$\begin{aligned} \sigma ^{(\bar{{r}})}=A(x_1 ,x_2 )+B(x_1 ,x_2 )u \end{aligned}$$

(10)

where $A(x_1 ,x_2 )=L_{f_1 }^{\bar{{r}}} \sigma (x_1 )$ and $B(x_1 ,x_2 )=L_{g_1 } L_{f_1 }^{\bar{{r}}-1} \sigma (x_1 )$.

Without loss of generality, assume that

$$\begin{aligned} \left\{ {\begin{array}{l} A(x_1 ,x_2 )=\bar{{A}}(x_1 ,x_2 )+\Delta A(x_1 ,x_2 ) \\ B(x_1 ,x_2 )=\bar{{B}}(x_1 ,x_2 )+\Delta B(x_1 ,x_2 ) \\ \end{array}} \right. \end{aligned}$$

(11)

where $\bar{{A}}(x_1 ,x_2 )$ and $\bar{{B}}(x_1 ,x_2 )$ represent the nominal parts of $A(x_1 ,x_2 )$ and $B(x_1 ,x_2 )$ respectively. $\Delta A(x_1 ,x_2 )$and$\Delta B(x_1 ,x_2 )$ denote the unknown uncertain bounded functions.

Assumption 2

$\Delta A(x_1 ,x_2 )$and $\Delta B(x_1 ,x_2 )$ are bounded as follows

$$\begin{aligned}&\left\| {\Delta A(x_1 ,x_2 )} \right\| \le \rho \\&\left\| {\Delta B(x_1 ,x_2 )\bar{{B}}^{-1}(x_1 ,x_2 )} \right\| \le 1-\alpha \end{aligned}$$

where$\rho$ and $0<\alpha \le 1$ are constant.

The $\bar{{r}}th$-order sliding mode control of system (9) with respect to the $\sigma (x_1 )$ is equal to the finite-time stabilization of the uncertain system

$$\begin{aligned} \dot{z}_i= & {} z_{i+1} \nonumber \\ \dot{z}_{\bar{{r}}}= & {} A(x_1 ,x_2 )+B(x_1 ,x_2 )u \end{aligned}$$

(12)

where $1\le i\le \bar{{r}}-1$ and $z=\left[ {z_1 , z_2 , \ldots , z_{\bar{{r}}} } \right] ^{T}=\left[ {\sigma , \dot{\sigma }, \ldots ,\sigma ^{(\bar{{r}}-1)}} \right] ^{T}$.

Remark 2

Let $\bar{{\rho }}$be the relative degree of the system (9) with respect to sliding variable$\sigma$. For the sake of simplicity, this paper is only devoted to the$\bar{{r}}=\bar{{\rho }}$.

By defining a preliminary feedback as follows

$$\begin{aligned} u=\bar{{B}}^{-1}(x_1 ,x_2 )\left\{ {-\bar{{A}}(x_1 ,x_2 )+w} \right\} \end{aligned}$$

(13)

and applying it as well as (11) to the system (10) with uncertainty gives

$$\begin{aligned} y^{(\bar{{r}})}= & {} \sigma ^{(\bar{{r}})}(x_1 )=(1+\Delta B(x_1 ,x_2 )\bar{{B}}^{-1}(x_1 ,x_2 ))w \nonumber \\&-\,\Delta B(x_1 ,x_2 )\bar{{B}}^{-1}(x_1 ,x_2 )\bar{{A}}(x_1 ,x_2 )\nonumber \\&+\,\Delta A(x_1 ,x_2 ) \end{aligned}$$

(14)

Meanwhile, in Eq. (13), w is the auxiliary control input.

The $\bar{{r}}th$-order sliding mode control of the system (9) with respect to the $\sigma (x_1 )$ is equal to the finite-time stabilization of the uncertain system

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{z}_1 =z_2 \\ \vdots \\ \dot{z}_{\bar{{r}}-1} =z_{\bar{{r}}} \\ \dot{z}_{\bar{{r}}} =(1+\Delta B(x)\bar{{B}}^{-1}(x))w\nonumber \\ \qquad \,{}\,-\Delta B(x)\bar{{B}}^{-1}(x)\bar{{A}}(x)+\Delta A(x) \\ \end{array}} \right. \end{aligned}$$

3 Robust finite-time partial control design

In this section, the control objective is to employ a control scheme which is able to stabilize the first subsystem in finite time. To fulfill this task, the higher order sliding mode control is derived in two steps:

• (a) The finite-time stabilization of nominal system (5) by designing a finite-time controller $w_\mathrm{{nom}} (z)$

• (b) Rejecting the uncertainties of system (15) by designing a discontinuous control law $w_\mathrm{{disc}} (z)=-G sign(s)$

Consider the following control law to stabilize uncertain system (15) in finite time:

$$\begin{aligned} w=w_\mathrm{{nom}} -G sign(s) \end{aligned}$$

(15)

where the first term, $w_\mathrm{{nom}}$ is presented in Theorem 2, and the gain G satisfies

$$\begin{aligned} G\ge \frac{(1-\alpha )(\left\| {w_\mathrm{{nom}} } \right\| +\left\| {\bar{{A}}(x)} \right\| )+\rho +\eta }{\alpha } \end{aligned}$$

(16)

in which$\left\| {\Delta B(x)\bar{{B}}^{-1}(x)} \right\| \le 1-\alpha , \left\| {\Delta A(x)} \right\| \le \rho$ and $\eta >0$.

Let us define the integral sliding variable s(z), related to $w_\mathrm{{disc}}$, as follows:

$$\begin{aligned} s(z(t))=z_n (t)-z_n (t_0 )-\int \limits _{t_0 }^t {w_\mathrm{{nom}} } d\tau \end{aligned}$$

(17)

Note that it is $s(z(t_0 ))=0$ at $t=t_0$, so sliding mode also occurs at the beginning of the initial time instance.

Theorem 3

Consider the nonlinear system (9). If Assumption 1 and Assumption 2 are fulfilled and the control law is designed as

$$\begin{aligned} u=\bar{{B}}^{-1}(x)\left( {-\bar{{A}}(x)+w_\mathrm{{nom}} -G \hbox {sgn}(s)} \right) \end{aligned}$$

(18)

then trajectories of $\dot{x}_1$-subsystem converge to zero in finite time.

Proof

Construct a Lyapunov function

$$\begin{aligned} V=\frac{1}{2}s^{2} \end{aligned}$$

(19)

Differentiating V and using (14), (15)–(17) result in

$$\begin{aligned} \dot{V}= & {} s\dot{s}=s\left( {\dot{z}_n -w_\mathrm{{nom}} } \right) \nonumber \\= & {} s\left( (1+\Delta B(x)\bar{{B}}^{-1}(x))w\right. \nonumber \\&\left. -\Delta B(x)\bar{{B}}^{-1}(x)\bar{{A}}(x)+\Delta A(x)-w_\mathrm{{nom}} \right) \nonumber \\= & {} s\left( -(1+\Delta B(x)\bar{{B}}^{-1}(x))G \hbox {sgn}(s)\right. \nonumber \\&\left. -\Delta B(x)\bar{{B}}^{-1}(x)\bar{{A}}(x)\right. \nonumber \\&\left. +\Delta A(x)+\Delta B(x)\bar{{B}}^{-1}(x)w_\mathrm{{nom}} \right) \nonumber \\\le & {} -G\left\| s \right\| +(1-\alpha )G\left\| s \right\| +(1-\alpha )\left\| {\bar{{A}}(x)} \right\| s\nonumber \\&+\rho s+(1-\alpha )\left\| {w_\mathrm{{nom}} } \right\| s \nonumber \\\le & {} -\alpha G\left\| s \right\| +\left( {(1-\alpha )(\left\| {w_\mathrm{{nom}} } \right\| +\left\| {\bar{{A}}(x)} \right\| )+\rho } \right) \left\| s \right\| \nonumber \\\le & {} -\eta \left\| s \right\| \end{aligned}$$

(20)

Therefore, Eq. (20) implies that the system trajectories evolve on the manifold $\left\{ {x\in R^{n} : s=0} \right\}$ during a finite time interval and stays there in presence of the uncertainties. In the sliding mode, by writing $\dot{s}=0$, the equivalent control of $w_\mathrm{{disc}}$ is obtained as follows:

$$\begin{aligned} G \hbox {sgn}(s)= & {} -[1+\Delta B(x)\bar{{B}}^{-1}(x)]^{-1}[\Delta B(x)\bar{{B}}^{-1}(x)\bar{{A}}(x) \nonumber \\&-\Delta A(x)-\Delta B(x)\bar{{B}}^{-1}(x)w_\mathrm{{nom}} ] \end{aligned}$$

(21)

In the sliding mode, by substituting $w=w_{nom} -G sign(s)$ into (15), the equivalent closed-loop dynamics will be similar as the nominal system (5). The system trajectories converge to zero in finite time, because the control law $w_\mathrm{{nom}}$ is derived utilizing Theorem 2. As a result, trajectories of $\dot{x}_1$-subsystem converge to zero in finite time. $\square$

Remark 3

The proposed control scheme is a non-smooth controller which guarantees fast convergence and robustness of the system. It involves a signum function, indicating that the control variable sometimes switches. In practical application, the switching cannot be completely instantaneous. The delay of switching induces the chattering effect. To remove the chattering, the signum function can be smoothed, usually replaced with a saturation function which is expressed as

$$\begin{aligned} sat_\delta (s)= \left\{ {\begin{array}{ll} 1 ; &{} s > \delta \\ s/\delta ;&{} \left| s \right| \le \delta \\ -1 ; &{} s < -\delta \\ \end{array}} \right. \end{aligned}$$

where $\delta$ is a small positive constant.

4 Homing guidance: robust finite-time partial control

To examine the performance of the proposed scheme, it is used to design a guidance law. The reason is that the guidance problem is an appropriate example in which stabilization of all state variables is not desirable. So, partial stability can be a good idea. Since the guidance process occurs in a short time, the finite-time stabilization of state variables is required. Furthermore, the target maneuver is an external disturbance which can lead the guidance loop to instability. So, in order to hit the target, designing a robust guidance law which can reject the target maneuver is mandatory. For these reasons, the proposed law in this paper is a suitable tool to design a robust finite-time convergent guidance law based on partial stability.

4.1 Formulation of interceptor–target engagement and guidance law design

The geometry of planar interception is shown in Fig. 1. According to the principle of the kinematics, the corresponding equations of motion between the target and the interceptor can be described by  [26]:

$$\begin{aligned} \ddot{R}= & {} \dot{\lambda }^{2}R+a_{TR} -a_{MR} \end{aligned}$$

(22)

$$\begin{aligned} \ddot{\lambda }= & {} -\frac{2\dot{R}}{R}\dot{\lambda }+\frac{a_{T\lambda } }{R}-\frac{a_{M\lambda } }{R} \end{aligned}$$

(23)

where R denotes relative distance between the target and the interceptor; $\dot{\lambda }$ represents the line-of-sight (LOS) angular rate; $a_{TR}$ and $a_{MR}$ denote the target and the interceptor acceleration along the LOS, respectively; and $a_{T\lambda }$ and $a_{M\lambda }$ represent the target and the interceptor acceleration normal to the LOS, respectively.

Furthermore, the control loop dynamics can be described by a first-order differential equation as follows  [27].

$$\begin{aligned} \dot{a}_{M\lambda } =-\frac{1}{\tau }a_{M\lambda } +\frac{1}{\tau }u \end{aligned}$$

(24)

where $\tau$ represents the time constant, and u denotes the command acceleration.

Fig. 1

Planar interception geometry

According to parallel navigation concept, if LOS direction is kept unchanged with respect to inertial frame and relative range between the interceptor and the target is getting lower $(\dot{R}<0$), in that case collision will be certain. In other words, the LOS angular rate must be zero. So, in order to hit the target, the following conditions must be satisfied:

$$\begin{aligned} \dot{\lambda }= & {} 0 \end{aligned}$$

(25)

$$\begin{aligned} \dot{R}< & {} 0 \end{aligned}$$

(26)

Since in terminal guidance process, $a_{MR}$ cannot be adjustable, we aim to design u to satisfy conditions (25) and (26).

By choosing the state variables as $\left[ {\eta _1 ,\eta _2 ,\eta _3 ,\eta _4 ,\eta _5 } \right] ^{T}=\left[ {R,\dot{R},\lambda ,\dot{\lambda },a_{M\lambda } } \right]$, the nonlinear guidance system can be expressed as follows

(27)

As it can be seen, the guidance system (27) has been divided into two parts. According to condition (26), the stabilization of $\eta _2$ is not desirable and converging of this state variable can lead the guidance loop to instability. Thus, the partial stability approach is a suitable technique to fulfill this design task. We focus on stabilization of the second subsystem and the first subsystem is neglected  [8]. In the next step, we try to transform the second subsystem into normal form to use the variable structure control.

Assume that $x_1 =\dot{\lambda }$and $x_2 =\dot{x}_1 =\ddot{\lambda }$. Substituting them into Eq. (23) yields:

$$\begin{aligned} x_2 =-a_g x_1 -b_g a_{M\lambda } +b_g a_{T\lambda } \end{aligned}$$

(28)

where

$$\begin{aligned} a_g =\frac{2\dot{R}}{R},\;\;\;b_g =\frac{1}{R} \end{aligned}$$

(29)

It is clear from Eq. (28) that

$$\begin{aligned} a_{T\lambda } =a_{M\lambda } +\frac{1}{b_g }(a_g x_1 +x_2 ) \end{aligned}$$

(30)

Differentiating Eq. (28) with respect to time and using Eqs. (24) and (30) gives:

$$\begin{aligned} \dot{x}_2 =A_1 x_1 +A_2 x_2 +bu+f \end{aligned}$$

(31)

where

$$\begin{aligned} A_1= & {} -\dot{a}_g +\left( {\frac{\dot{b}_g }{b_g }-\frac{1}{\tau }} \right) a_g ,\nonumber \\ A_2= & {} -a_g +\frac{\dot{b}_g }{b_g }-\frac{1}{\tau } \nonumber \\ b= & {} -\frac{b_g }{\tau },\;\;\;\;\;\;\;f=b_g \dot{a}_{T\lambda } -ba_{T\lambda } \end{aligned}$$

(32)

Thus, the state space can be described as

$$\begin{aligned} \dot{x}_1= & {} x_2 \nonumber \\ \dot{x}_2= & {} A_1 x_1 +A_2 x_2 +bu+f \nonumber \\ y= & {} x_1 \end{aligned}$$

(33)

In Eq. (33), f denotes an external disturbance, i.e., $\left\| f \right\| \le \Delta$, where $\Delta =const.>0$. Also, the LOS angular rate is the system’s output that is measurable by the seeker.

Now, we are about to derive a robust guidance law which runs $\dot{\lambda }\rightarrow 0$ in finite time. Define an integral sliding manifold as

$$\begin{aligned} s=x_2 (t)-x_2 (t_0 )+\int \limits _{t_0 }^t {(L^{3}r^{2d}K\zeta )} d\tau \end{aligned}$$

(34)

where $L, r, \zeta$ and K have been defined in Theorem 2. So, by

Theorem 3 the robust finite-time convergent guidance law is

$$\begin{aligned} u=-\frac{1}{b}\left( {A_1 x_1 +A_2 x_2 +L^{3}r^{2d}Kz+\varepsilon \hbox {sgn}(s)} \right) \end{aligned}$$

(35)

where$\varepsilon =\Delta +\delta$ and $\delta >0$ is a constant.

4.2 Simulation results

In this section, simulation results are considered in two scenarios to illustrate the effectiveness and robustness of the robust finite-time convergent guidance law (35). The initial conditions are taken as: the interceptor and target positions in Cartesian coordinate are $R_{m_0 } =[0 0]^{T}m$ and $R_{t_0 } =[2000 \ 1000]^{T} m$, respectively. Furthermore, their initials velocities are $v_{m_0 } =[180 \ 117]^{T} m/s$and $v_{t_0 } =[50 \ 50]^{T} m/s$, respectively.

In the first scenario, we suppose that the target has no maneuvering and the goal is to investigate the effect of the coefficients of the proposed scheme on convergence rate. In the second scenario, to show the proposed finite-time control law is more effective than the robust partial control (RPC) presented in  [7] and the non-singular terminal sliding mode (NSTSM) guidance law in  [26], they are simulated under the same condition. The reason is that although in  [26] the use of partial stability approach has not been mentioned, one subsystem has been neglected and the authors of the paper have just focused on finite-time stabilization of the second subsystem. It is because the stabilization of the first subsystem is not useful even it may lead the guidance system to instability. Since the method suggested in  [26] is an application of partial stability notion in guidance system, it would be a good way to justify the performance of the approach of the present paper. In  [26], it has been shown that the NSTSM guidance law is better than the adaptive sliding mode guidance law  [28] and the finite-time convergent guidance law  [29]. So, the proposed method has been compared with four different approaches.

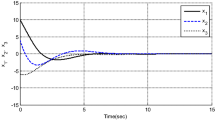
Scenario 1: We assume that the target does not maneuver. The initial conditions and the parameters of r and L in (7) which are used in the proposed guidance law (35) are chosen as $\alpha _1 =0.1, \beta _2 = 572 , r_0 =5 , M=10$. Since the initial conditions of the dynamical gain (7) have a significant contribution to convergence rate of the state variable, we will investigate the effect of them. Let $r_0 =5$ and $M=2$, 3 and 7, respectively. For different values of M, the LOS rate and the interceptor acceleration are plotted in Figs. 2 and 3. As it is seen in Fig. 2, M has a direct relationship with convergence rate so that increasing M can increase convergence rate of the LOS angular rate. Consequently, it can decrease settling time. According to Fig. 3, although increasing M makes the settling time decrease, it causes the maximum acceleration of the interceptor to increase. So, a large value of M must not be chosen to abstain from saturation of the actuator.

Fig. 2

The effect of M on LOS convergence rate

Fig. 3

The effect of M on acceleration command

To examine the impact of $r_0$, the LOS angular rate and the interceptor command with respect to $r_0$ are also plotted in Figs. 4 and  5. Suppose that $M=5$ and $r_0 =1, 10$ and 20. In contrast to M, $r_0$ has an indirect relationship with convergence rate; on the other hand, it has a direct relationship with maximum value of acceleration command. As a result, the convergence rate goes down as the value of $r_0$ increases.

Fig. 4

The effect of $r_0$ on LOS convergence rate

Fig. 5

The effect of $r_0$ on acceleration command

Scenario 2: In this case, we aim to compare the proposed law with the RPC and the NSTSM guidance laws. Assume that the target escapes with acceleration components $a_{TR} =3$ and $a_{T\lambda } =70\sin (0.25t+\pi /6)$. We suppose that the upper bound of the target acceleration is known in advance. The simulation is stopped if the interceptor hit the target (i.e. reaching zero miss distance) or the closing velocity becomes zero (i.e. missing the target).The relative distance, the variations of the closing velocity, LOS rate, the acceleration command, the trajectory of the interceptor and the target and the integral sliding mode behavior are depicted in Figs. 6,  7,  8,  9,  10 and 11.

Fig. 6

Relative distance between target and interceptor

Fig. 7

Closing velocity

Fig. 8

LOS angular rate

Fig. 9

Acceleration command

Fig. 10

Trajectory of the interceptor and the target

Fig. 11

Integral sliding surface

Figure 6 illustrates that under the proposed law the interceptor hit the target but the RPC and the NSTSM guidance laws failed to intercept the target and give rise to large miss distances. The variation of the closing velocity can be seen in Fig. 7. It is evident that under the RPC and the NSTSM guidance laws the closing velocities have been zero and the simulation has been stopped, but the closing velocity has been remained negative by using the proposed law. Figure 8 indicates the LOS rate. As it can be seen, the proposed law is able to nullify the LOS rate and preserve it at a small vicinity of origin, but the RPC and the NSTSM guidance laws cannot stabilize it due to extreme maneuver of the target. The required acceleration has been shown in Fig. 9. It is observed that under the proposed law the acceleration command converge to target acceleration. Figure 10 illustrates the trajectory of the interceptor and the target, where the red point is collision point for the proposed law. Also, it is revealed under the RPC and the NSTSM guidance laws, the interceptor missed the target and gives rise to a large miss distance. Finally, the variation of the integral sliding mode is depicted in Fig. 11. As it can been seen, under the proposed guidance law, the integral sliding variable starts from zero and it remains in a very small neighborhood of origin$(10^{-17})$ and the reaching phase has been omitted. The second scenario shows that the proposed law has gained better performance compared with that of RPC guidance law in terms of the robustness and effectiveness.

5 Conclusion

This paper proposed a general scheme to achieve a robust finite-time partial stabilization of uncertain nonlinear systems. By the procedure of the proposed approach, a criterion was proven to guarantee only a part of the states of the system converges to equilibrium in a finite time in spite of any uncertainties or disturbances. Also, the proposed control scheme benefits from robustness property of integral sliding mode. To investigate the efficiency of the proposed method, it was used in guidance law design. The performance of the robust finite-time guidance law was shown through simulation.