A Robust LMI Approach on Nonlinear Feedback Stabilization of Continuous State-Delay Systems with Lipschitzian Nonlinearities: Experimental Validation

Abstract

This paper suggests a novel nonlinear state-feedback stabilization control law using linear matrix inequalities for a class of time-delayed nonlinear dynamic systems with Lipschitz nonlinearity conditions. Based on the Lyapunov–Krasovskii stability theory, the asymptotic stabilization criterion is derived in the linear matrix inequality form and the coefficients of the nonlinear state-feedback controller are determined. Meanwhile, an appropriate criterion to find the proper feedback gain matrix F is also provided. The robustness purpose against nonlinear functions and time delays is guaranteed in this scheme. Moreover, the problem of robust H_∞ performance analysis for a class of nonlinear time-delayed systems with external disturbance is studied in this paper. Simulations are presented to demonstrate the proficiency of the offered technique. For this purpose, an unstable nonlinear numerical system and a rotary inverted pendulum system have been studied in the simulation section. Moreover, an experimental study of the practical rotary inverted pendulum system is provided. These results confirm the expected satisfactory performance of the suggested method.

1 Introduction

Time delays are often sources of instability and degradation of system efficiency in many control systems and are frequently encountered in a wide range of nonlinear dynamical systems, such as pneumatic systems (Hong et al. 2009), chemical engineering (Pellegrini et al. 2000), hydraulic systems (Chae et al. 2013), biological systems (Wan et al. 2014), nuclear reactors (Park et al. 2009) and population dynamics models (Li 2012). The problem of stabilization of the time-delayed dynamical systems and synthesis of controllers for them has received significant attention over the past few years, and different approaches have been proposed. Nevertheless, the offered methodologies remain restrictive to the specific classes of nonlinear systems, and there is not any general technique to analyze and synthesize the general class of nonlinear systems (Wu and Liu 2015; Liu et al. 2014; Gao and Wu 2015). This is the purpose of the current investigation on the analysis and control of the time-delayed nonlinear systems. For this purpose, selection of the predefined variables using a powerful computational design tool such as linear matrix inequality (LMI) technique is required.

LMIs have developed as an influential structure and design procedure for various control problems (Seuret and Gouaisbaut 2015). In the past, this method has been applied to find solutions of minimization convex problems, for instance, H₂ control (Haddad et al. 2011), H_∞ control (Hilhorst et al. 2015) and guaranteed cost control (Yang and Cai 2010). Even though LMI is a convex optimization problem, such structure offers a numerically tractable mean for hard problems in the absence of analytical solutions. Moreover, some effective interior-point algorithms are now available to solve LMI problems. In (Zong et al. 2008), an LMI-based H_∞ state-feedback stabilization problem for the uncertain switched impulsive linear systems with state-delays and nonlinear parametric uncertainties is proposed. In (Tsai et al. 2009), a robust H_∞ fuzzy control method for TS-fuzzy time-delayed discrete-time bilinear systems with disturbances is proposed where the conditions of the system stability are formulated in the form of LMIs. In (Kim et al. 2016), the problem of stabilization analysis using LMIs and robust H_∞ controller design for time-delayed systems with stochastic disturbances and parametric uncertainties is investigated. In (Leite et al. 2009), an LMI-based Robust H_∞ state-feedback controller for the uncertain discrete-time systems with state-delays is proposed. In (Li et al. 2009), using a quadratic Lyapunov functional and variation of parameters method, the problem of LMI-based delay-dependent BIBO stabilization control for the uncertain time-delayed systems is investigated. In (Dey et al. 2011), a nonlinear matrix inequality is employed as a stabilization condition for uncertain time-delayed linear systems. In (Amri et al. 2011), the robust exponential stabilization problem based on the Lyapunov parameter-dependent function and LMIs for a class of uncertain systems with time-varying delays is investigated. In (Thevenet et al. 2010), the stabilization problem of a two-dimensional Burgers equation around a stationary solution using nonlinear feedback boundary controller is investigated. In (Yan et al. 2011), the stabilization problem of uniform Euler–Bernoulli beam via nonlinear locally distributed feedback controller is studied where the energy of the beam decays exponentially. In (Zhang et al. 2012), chaotification technique based on the nonlinear time-delayed feedback control method for a two-dimensional vibration isolation floating raft structure is presented. In (Louodop et al. 2014), the synchronization problem of the uncertain time-delay chaotic systems with the unknown inputs in a drive-response framework using robust adaptive observer-based controller is investigated. In (Lei et al. 2014), the nonlinear vibration control problem of the active vehicle suspension systems with the actuator delays using feedback linearization technique is studied. In (Chatterjee 2011), the impact of delays on the self-excited oscillations of single and two degrees of freedom systems via nonlinear feedback is considered and a bounded saturated feedback control technique with controllable time delays is suggested to induce the self-excited oscillations. To the best of the author’s information, very little attention has been paid for the nonlinear state-feedback stabilization problem of time-delayed nonlinear systems with Lipschitz nonlinearities using LMIs, which is still an open problem. This stimulates the present research.

Motivated by the above discussion, the problem of robust H_∞ performance analysis for a class of nonlinear systems with state-delay and external disturbance is investigated in this paper. This work presents a state-feedback control law for the stability problem of Lipschitz nonlinear time-delayed systems. By constructing a Lyapunov–Krasovskii functional, asymptotical stabilization conditions are prepared in LMI form and the coefficients of the nonlinear state-feedback control law are determined via LMIs. The proposed controller guarantees asymptotical stability of these systems even if the nonlinear part is nonzero. Unlike the former researches, the resultant LMI conditions have fewer pre-assumed design parameters, and consequently, the planned technique can yield less conservative conditions.

The presentation of this article is listed as follows: Sect. 2 develops the problem description and some required preliminaries. Section 3 proposes the analysis of the stability and design process of nonlinear state-feedback controller based on LMIs for the nonlinear time-delayed systems. In Sect. 4, simulation results on two dynamical systems are illustrated. Moreover, experimental results on a rotary inverted pendulum (RIP) system are shown in Sect. 4. Finally, some concluding remarks are given in Sect. 5.

2 Problem Description and Required Preliminaries

The nonlinear time-delayed system is considered as:

$$\begin{aligned} \dot{x}(t) &= f(x) + Ax(t) + A_{1} x(t - \tau) + Bu(t), \hfill \\ y(t) &= Cx(t), \hfill \\ \end{aligned}$$

(1)

where $u(t) \in R^{n}$, $x(t) \in R^{n}$ and $y(t) \in R^{n}$ represent the input to system, the state variables and the output of the system, respectively. The parameter $\tau$ is the time-delay, and the nonlinear function $f(x) \in R^{n}$ is a time-varying vector. Moreover, matrices $A$, $A_{1}$, $B$ and $C$ are some constant matrices with appropriate dimensions.

Assumption 1

The nonlinear function $f(x)$ is Lipschitz for all $x \in R^{n}$ and $\bar{x} \in R^{n}$ which satisfies (Zemouche and Boutayeb 2013; Shen et al. 2011):

$$\left\| {f(x) - f(\bar{x})} \right\| \le \left\| {L(x - \bar{x})} \right\|,$$

(2)

where $L \in R^{n \times n}$ is a Lipschitz constant matrix. Equivalently, the Lipschitz inequality (2) is rewritten as follows:

$$\left({f(x) - f(0)} \right)^{T} I\left({f(x) - f(0)} \right) \le x^{T} L^{T} Lx.$$

(3)

The nonlinear state-feedback control input is specified by:

$$u(t) = Fx(t) - B^{- 1} f(0),$$

(4)

where $F$ is the state-feedback gain which will be calculated later using LMIs. The additional term $B^{- 1} f(0)$ in (4) is necessary to deal with systems possessing $f(0) \ne 0$.

Remark 1

The matrix $B$ in (4) is assumed to be square and of full row rank. When the matrix $B$ is non-square and has full rank, the nonlinear state-feedback control law can be expressed using the right inverse of $B$ as:

$$u(t) = Fx(t) - B^{T} \left({BB^{T}} \right)^{- 1} f(0).$$

(5)

Therefore, this approach can also be applied on the situations in which the matrix $B$ is non-square.

Lemma 1 (Schur complement) (Scherer and Weiland 2000)

If there exist matrices $S_{1}$, $S_{2}$ and $S_{3}$ where $S_{1} = S_{1}^{T}$ and $S_{3} = S_{3}^{T}$, then the inequality

$$S_{1} - S_{2} S_{3}^{- 1} S_{2}^{T} < 0$$

(6)

is equivalent to:

$$\left[{\begin{array}{*{20}c} {S_{1}} & {S_{2}} \\ {S_{2}^{T}} & {S_{3}} \\ \end{array}} \right] < 0$$

(7)

Lemma 2 (S-procedure) (Boyd et al. 1994)

Let $T_{0}, \ldots, T_{p}$$T_{0}, \ldots,T_{p}$ be symmetric matrices. Consider the following condition on $T_{0}, \ldots, T_{p}$:

$$\zeta^{T} T_{0} \zeta > 0\quad {\text{for}}\;{\text{all}}\quad \zeta \ne 0\;\zeta \ne 0\quad {\text{such that}}\quad \zeta^{T} T_{i} \zeta \ge 0,\quad i = 1, \ldots,p.$$

(8)

If there exist nonnegative scalars $\tau_{i}$ for $i = 1, \ldots,p$, such that $T_{0} - \sum\limits_{i = 1}^{p} {\tau_{i} T_{i} > 0} \quad T_{0} - \sum_{i = 1}^{p} \tau_{i} T_{i} > 0$ is satisfied, then (8) holds.

3 Main Results

Theorem 1

Consider the nonlinear system (1) and the control input (4) with$f(0) = 0$. Given a positive scalar$\tau_{1}$, if there exist matrices$M$, $Q = Q^{T} > 0$ and $H = H^{T} > 0$with appropriate dimensions such that the following LMI condition is satisfied:

$$\left[{\begin{array}{*{20}c} {QA^{T} + M^{T} B^{T} + AQ + BM + H} & {A_{1}} & {\beta_{1} I} & {QL^{T}} \\ * & {- \;P_{1}} & 0 & 0 \\ * & * & {- \;\beta_{1} I} & 0 \\ * & * & * & {- \;\beta_{1} I} \\ \end{array}} \right] < 0,$$

(9)

then the asymptotical stability of the state trajectories is fulfilled and one can obtain the gain matrix$F$as$F = MQ^{- 1}$.

Proof

If Eq. (4) (without $- B^{- 1} f(0)$) is substituted into (1), we obtain:

$$\dot{x}(t) = f(x) + (A + BF)x(t) + A_{1} x(t - \tau).$$

(10)

We construct the Lyapunov–Krasovsky function candidate as follows:

$$V(t) = x(t)^{T} Px(t) + \int\limits_{t - \tau}^{t} {x(s)^{T} P_{1} x(s)\text{d}s,}$$

(11)

with real symmetric matrices $P > 0$ and $P_{1} > 0$ which are determined using the LMI. The derivative of (11) with respect to time is derived as:

$$\dot{V}(t) = \dot{x}(t)^{T} Px(t) + x(t)^{T} P\dot{x}(t) + x(t)^{T} P_{1} x(t) - x(t - \tau)^{T} P_{1} x(t - \tau),$$

(12)

Substituting (10) in (12) obtains:

$$\begin{aligned} & \dot{V}(t) = f(x)^{T} Px(t) + x(t)^{T} (A^{T} + F^{T} B^{T})Px(t) + x(t - \tau)^{T} A_{1}^{T} Px(t) + x(t)^{T} Pf(x) \\ & \quad + x(t)^{T} P(A + BF)x(t) + x(t)^{T} PA_{1} x(t - \tau) + x(t)^{T} P_{1} x(t) - x(t - \tau)^{T} P_{1} x(t - \tau), \\ \end{aligned}$$

(13)

which can be rewritten by:

$$\dot{V}(t) = \left({\begin{array}{*{20}c} {x(t)} \\ {x(t - \tau)} \\ {f(x)} \\ \end{array}} \right)^{T} \left[{\begin{array}{*{20}c} {P(A + BF) + (A^{T} + F^{T} B^{T})P + P_{1}} & {PA_{1}} & P \\ * & {- P_{1}} & 0 \\ * & * & 0 \\ \end{array}} \right]\left({\begin{array}{*{20}c} {x(t)} \\ {x(t - \tau)} \\ {f(x)} \\ \end{array}} \right) < 0.$$

(14)

Note that condition (3) can be restated as:

$$\left({\begin{array}{*{20}c} {x(t)} \\ {x(t - \tau)} \\ {f(x)} \\ \end{array}} \right)^{T} \left[{\begin{array}{*{20}c} {L^{T} L} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & {- I} \\ \end{array}} \right]\left({\begin{array}{*{20}c} {x(t)} \\ {x(t - \tau)} \\ {f(x)} \\ \end{array}} \right) \ge 0.$$

(15)

By combining (14) and (15) with S-procedure (Lemma 1), the condition $\dot{V}(t) < 0$ is satisfied if there exist a scalar $\tau_{1}$ such that:

$$\left[{\begin{array}{*{20}c} {P(A + BF) + (A^{T} + F^{T} B^{T})P + P_{1} + \tau_{1} L^{T} L} & {PA_{1}} & P \\ * & {- P_{1}} & 0 \\ * & * & {- \tau_{1} I} \\ \end{array}} \right] < 0.$$

(16)

Since inequality (16) is not in the form of LMIs, assuming $Q = P^{- 1}$, $M = FQ$, $P_{1} = PHP$, and pre- and post-multiplying (16) by ${\text{diag}}(Q,I,\tau^{- 1} I)$ yields:

$$\left[{\begin{array}{*{20}c} {QA^{T} + M^{T} B^{T} + AQ + BM + H + \tau_{1} QL^{T} LQ} & {A_{1}} & {\tau_{1}^{- 1} I} \\ * & {- P_{1}} & 0 \\ * & * & {- \tau_{1}^{- 1} I} \\ \end{array}} \right] < 0.$$

(17)

Inequality (17) can be rewritten in the form of (6) as

$$\left[{\begin{array}{*{20}c} {QA^{T} + M^{T} B^{T} + AQ + BM + H} & {A_{1}} & {\tau_{1}^{- 1} I} \\ * & {- P_{1}} & 0 \\ * & * & {- \tau_{1}^{- 1} I} \\ \end{array}} \right] - \left[{\begin{array}{*{20}c} {QL^{T}} \\ 0 \\ 0 \\ \end{array}} \right]\left({- \tau_{1} I} \right)\left[{\begin{array}{*{20}c} {LQ} & 0 & 0 \\ \end{array}} \right] < 0.$$

(18)

By applying Schur complement on (18), the following inequality is obtained:

$$\left[{\begin{array}{*{20}c} {QA^{T} + M^{T} B^{T} + AQ + BM + H} & {A_{1}} & {\tau_{1}^{- 1} I} & {QL^{T}} \\ * & {- P_{1}} & 0 & 0 \\ * & * & {- \tau_{1}^{- 1} I} & 0 \\ * & * & * & {- \tau_{1}^{- 1} I} \\ \end{array}} \right] < 0,$$

(19)

where defining $\beta_{1} = \tau_{1}^{- 1}$, LMI (9) is attained. This completes the proof.□

Theorem 2

Let us consider the nonlinear time-delayed system (1) and the proposed control input (4). Assume that Assumption 1 is fulfilled. If there exist matrices $M$, $Q = Q^{T} > 0$ and $H = QP_{1} Q$ with appropriate dimensions such that:

$$\varPi = \left({\begin{array}{*{20}c} {QA^{T} + M^{T} B^{T} + AQ + BM + H} & {A_{1} Q} & I & {QL^{T}} \\ * & {- H} & 0 & 0 \\ * & * & {- I} & 0 \\ * & * & * & {- I} \\ \end{array}} \right) < 0,$$

(20)

is fulfilled, then the control signal (4) confirms the asymptotical stability of states of the considered system and we can obtain $F$ in (4) as $F = MQ^{- 1}$.

Proof

If (4) is substituted into (1), one can achieve:

$$\dot{x}(t) = f(x) - f(0) + (A + BF)x(t) + A_{1} x(t - \tau).$$

(21)

The Lyapunov–Krasovsky functional candidate is constructed as (11). The derivative of (11) with respect to time is derived as (12). Substituting (21) into (12) gives:

$$\begin{aligned} & \dot{V}(t) = (f(x) - f(0))^{T} \,P\,x(t) + x(t)^{T} (A^{T} + F^{T} B^{T})\,Px(t) \\ & \quad + \;x(t - \tau)^{T} A_{1}^{T} \,Px(t) + x(t)^{T} \,P(f(x) - f(0)) + x(t)^{T} P_{1} x(t) \\ & \quad - \;x(t - \tau)^{T} P_{1} x(t - \tau) + x(t)^{T} P(A + BF)x(t) + x(t)^{T} PA_{1} x(t - \tau), \\ \end{aligned}$$

(22)

where considering (3) and (22), one can obtain:

$$\begin{aligned} & \dot{V} \le (f(x) - f(0))^{T} Px(t) + x(t)^{T} (A^{T} + F^{T} B^{T})Px(t) + x(t - \tau)^{T} A_{1}^{T} Px(t) \\ & \quad + \;x(t)^{T} P(f(x) - f(0)) + x(t)^{T} P(A + BF)x(t) + x(t)^{T} PA_{1} x(t - \tau) \\ & \quad + \;x(t)^{T} P_{1} x(t) - x(t - \tau)^{T} P_{1} x(t - \tau)\, - (f(x) - f(0))^{T} I(f(x) - f(0)) + x(t)^{T} L^{T} Lx(t), \\ \end{aligned}$$

(23)

which, further, can be written as:

$$\dot{V} \le \varPsi^{T} \varGamma \varPsi,$$

(24)

where

$$\varPsi = \left[{x(t)^{T} \quad x(t - \tau)^{T} \quad (f(x) - f(0))^{T}} \right]^{T},$$

(25)

$$\varGamma = \left({\begin{array}{*{20}c} {(A^{T} + F^{T} B^{T})P + P(A + BF) + L^{T} L + P_{1}} & {PA_{1}} & P \\ * & {- P_{1}} & 0 \\ * & * & {- I} \\ \end{array}} \right) < 0.$$

(26)

Inequality (26) can be written in the form of (6) as

$$\left({\begin{array}{*{20}c} {(A^{T} + F^{T} B^{T})P + P(A + BF) + P_{1}} & {PA_{1}} & P \\ * & {- P_{1}} & 0 \\ * & * & {- I} \\ \end{array}} \right) - \left({\begin{array}{*{20}c} {L^{T}} \\ 0 \\ 0 \\ \end{array}} \right)\left({- I} \right)\left({\begin{array}{*{20}c} L & 0 & 0 \\ \end{array}} \right) < 0.$$

(27)

Now, applying the Schur complement on (27) yields:

$$\left({\begin{array}{*{20}c} {(A^{T} + F^{T} B^{T})P + P(A + BF) + P_{1}} & {PA_{1}} & P & {L^{T}} \\ * & {- P_{1}} & 0 & 0 \\ * & * & {- I} & 0 \\ * & * & * & {- I} \\ \end{array}} \right) < 0.$$

(28)

Since inequality (28) is non-LMI, assuming $Q = P^{- 1}$, $M = FQ$, $H = QP_{1} Q$ and pre- and post-multiplying (28) by ${\text{diag}}(Q,Q,I,I)$, LMI (20) is obtained.□

In what follows, the asymptotic stability and H_∞ performance analysis of system (1) with external disturbance are considered. Then, considering $u(t) = 0$, we have:

$$\begin{aligned} \dot{x}(t) = f(x) + Ax(t) + A_{1} x(t - \tau) + E_{\omega} \omega (t), \hfill \\ y(t) = Cx(t), \hfill \\ \end{aligned}$$

(29)

where $\omega (t)$ denotes the external disturbance and $E_{\omega}$ represents the constant matrix with suitable dimension.

Definition 1

The perturbed time-delayed system (29) is said to be robustly asymptotically stable with an H_∞ disturbance attenuation $\gamma > 0$ if system (29) with $\omega (t) = 0$ is robustly stable and under zero initial condition, there exists:

$$\int\limits_{0}^{\infty} {\left\| {y(t)} \right\|^{2} \text{d}t} \le \gamma^{2} \int\limits_{0}^{\infty} {\left\| {\omega (t)} \right\|^{2} \text{d}t}.$$

(30)

Theorem 3

Consider the nonlinear perturbed time-delayed system (29). Suppose that Assumption 1 is guaranteed. If there exist matrices $Q = Q^{T} > 0$, and $H = QP_{1} Q$ with suitable dimensions such that the LMI condition:

$$\left({\begin{array}{*{20}c} {QA^{T} + AQ + H} & {A_{1} Q} & I & {E_{\omega}} & {QL^{T}} & {QC^{T}} \\ * & {- H} & 0 & 0 & 0 & 0 \\ * & * & {- I} & 0 & 0 & 0 \\ * & * & * & {- \gamma^{2} I} & 0 & 0 \\ * & * & * & * & {- I} & 0 \\ * & * & * & * & * & {- I} \\ \end{array}} \right) < 0$$

(31)

is satisfied, then the perturbed time-delayed system (29) is asymptotically stable and fulfills the H_∞ performance condition (30).

Proof

The Lyapunov–Krasovsky candidate function is defined as (11). Substituting (29) into the time derivative of the Lyapunov–Krasovsky function gives:

$$\begin{aligned} & \dot{V}(t) = f(x)^{T} Px(t) + x(t)^{T} Pf(x) + x(t)^{T} \left[{A^{T} P + PA + P_{1}} \right]x(t) \\ & + \;x(t - \tau)^{T} A_{1}^{T} Px(t) + x(t)^{T} PA_{1} x(t - \tau) - x(t - \tau)^{T} P_{1} x(t - \tau) \\ & + \;x(t)^{T} PE_{\omega} \omega (t) + \omega (t)^{T} E_{\omega}^{T} Px(t). \\ \end{aligned}$$

(32)

Now, considering (3) and (32), we have:

$$\begin{aligned} & \dot{V} \le f(x)^{T} Px(t) + x(t)^{T} Pf(x) + x(t)^{T} \left[{A^{T} P + PA + P_{1}} \right]x(t) \\ & \quad + \;x(t - \tau)^{T} A_{1}^{T} Px(t) + x(t)^{T} PA_{1} x(t - \tau) - x(t - \tau)^{T} P_{1} x(t - \tau) \\ & \quad + \;x(t)^{T} PE_{\omega} \omega (t) + \omega (t)^{T} E_{\omega}^{T} Px(t) - f(x)^{T} \quad {\text{If}}\quad (x) + x(t)^{T} L^{T} Lx(t). \\ \end{aligned}$$

(33)

The H_∞ disturbance attenuation in (30) can be written as:

$$x(t)^{T} C^{T} Cx(t) \le \gamma^{2} \omega (t)^{T} \omega (t).$$

(34)

From (33) and (34), one can obtain:

$$\dot{V} + x(t)^{T} C^{T} Cx(t) - \gamma^{2} \omega (t)^{T} \omega (t) \le \varOmega^{T} \varTheta \varOmega$$

(35)

where using (33)–(35) gives:

$$\begin{aligned} & x(t)^{T} \left[{A^{T} P + PA + P_{1} + C^{T} C + L^{T} L} \right]x(t) + f(x)^{T} Px(t) + x(t)^{T} Pf(x) \\ & \quad + \;x(t - \tau)^{T} A_{1}^{T} Px(t) + x(t)^{T} PA_{1} x(t - \tau) - x(t - \tau)^{T} P_{1} x(t - \tau) \\ & \quad + \;x(t)^{T} PE_{\omega} \omega (t) + \omega (t)^{T} E_{\omega}^{T} Px(t) - f(x)^{T} \quad {\text{If}}\quad (x) - \gamma^{2} \omega (t)^{T} \omega (t) \le \varOmega^{T} \varTheta \varOmega. \\ \end{aligned}$$

(36)

where

$$\varOmega = \left[{\begin{array}{*{20}c} {x(t)^{T}} & {x(t - \tau)^{T}} & {f(x)^{T}} & {\omega (t)^{T}} \\ \end{array}} \right]^{T},$$

(37)

$$\varTheta = \left({\begin{array}{*{20}c} {A^{T} P + PA + C^{T} C + P_{1} + L^{T} L} & {PA_{1}} & P & {PE_{\omega}} \\ * & {- P_{1}} & 0 & 0 \\ * & * & {- I} & 0 \\ * & * & * & {- \gamma^{2} I} \\ \end{array}} \right) < 0$$

(38)

Inequality (38) can be written in the form of (6) as

$$\left({\begin{array}{*{20}c} {A^{T} P + PA + C^{T} C + P_{1} + L^{T} L} & {PA_{1}} & P & {PE_{\omega}} \\ * & {- P_{1}} & 0 & 0 \\ * & * & {- I} & 0 \\ * & * & * & {- \gamma^{2} I} \\ \end{array}} \right) - \left({\begin{array}{*{20}c} {L^{T}} \\ 0 \\ 0 \\ 0 \\ \end{array}} \right)\left({- I} \right)\left({\begin{array}{*{20}c} L & 0 & 0 & 0 \\ \end{array}} \right) < 0.$$

(39)

Applying the Schur complement on (39) gives:

$$\left({\begin{array}{*{20}c} {A^{T} P + PA + C^{T} C + P_{1}} & {PA_{1}} & P & {PE_{w}} & {L^{T}} \\ * & {- P_{1}} & 0 & 0 & 0 \\ * & * & {- I} & 0 & 0 \\ * & * & * & {- \gamma^{2} I} & 0 \\ * & * & * & * & {- I} \\ \end{array}} \right) < 0 .$$

(40)

Similarly, if the Schur complement is applied on (40), one obtains:

$$\left( {\begin{array}{*{20}c} {A^{T} P + PA + P_{1} \, } & {PA_{1} } & P & {PE_{\omega } } & {L^{T} } & {C^{T} } \\ * & { - P_{I} } & 0 & 0 & 0 & 0 \\ * & * & { - I} & 0 & 0 & 0 \\ * & * & * & { - \gamma^{2} I} & 0 & 0 \\ * & * & * & * & { - I} & 0 \\ * & * & * & * & * & { - I} \\ \end{array} } \right) < 0.$$

(41)

Since Eq. (40) is non-LMI, assuming $Q = P^{- 1}$, $H = QP_{1} Q$, and pre- and post-multiplying (40) by ${\text{diag}}(Q,Q,I,I,I,I)$, LMI (31) is achieved.□

4 Simulation Results

To illustrate the usefulness of the planned method, two simulation examples are considered. In Example A, an unstable nonlinear numerical system with state-delays is proposed. In Example B, the proposed control technique is applied on a practical RIP system with state-delays and nonlinearities.

4.1 Example A: Unstable Nonlinear Numerical System

The differential equations of this system are considered as:

$$\begin{aligned} & \dot{x} = \left({\begin{array}{*{20}c} {0.2\cos x_{1}} \\ {0.3\sqrt {x_{2}^{2} + 5}} \\ {0.4\sin x_{3}} \\ \end{array}} \right) + \left({\begin{array}{*{20}c} {0.1} & {0.2} & {0.3} \\ {0.1} & {0.1} & {- 0.5} \\ {0.3} & {- 0.4} & {- 0.3} \\ \end{array}} \right)x + \left({\begin{array}{*{20}c} 0 & {0.01} & {- 0.01} \\ {0.05} & {- 0.04} & 0 \\ {0.01} & {0.02} & {- 0.03} \\ \end{array}} \right)x(t - \tau) \\ & \quad + \left({\begin{array}{*{20}c} {0.012} & {0.013} & {0.014} & {0.016} \\ {0.01} & {0.014} & {0.01} & 0 \\ {0.013} & {0.017} & {0.018} & {0.011} \\ \end{array}} \right)u, \\ & y = \left({\begin{array}{*{20}c} {1.5} & 2 & {1.25} \\ {0.84} & {0.5} & {0.2} \\ \end{array}} \right)x. \\ \end{aligned}$$

(42)

For simulation, the initial states and time-delay value are initialized as: $x(0) = \left[{1\,0\,\,\,\,4\,\,\,\,\, - 6} \right]^{T}$, $\tau = 2$. The Lipschitzian matrix is specified by: $L = \left[{\begin{array}{*{20}c} {0.2} & 0 & 0 \\ 0 & {0.3} & 0 \\ 0 & 0 & {0.4} \\ \end{array}} \right].$ The solutions of LMI (20) are attained using LMI^® toolbox in MATLAB^® software and YALMIP^® solver as:

$$H = \left[{\begin{array}{*{20}c} {0.0141} & {0.0316} & {0.0262} \\ {0.0316} & {0.1419} & {0.0649} \\ {0.0262} & {0.0649} & {0.1196} \\ \end{array}} \right],\quad P = \left[{\begin{array}{*{20}c} {17.238} & {- 4.7564} & {- 10.5622} \\ {- 4.7564} & {27.9164} & {- 20.9467} \\ {- 10.5622} & {- 20.9467} & {39.3667} \\ \end{array}} \right].$$

$$P_{1} = \left[{\begin{array}{*{20}c} {12.5486} & {1.6137} & {- 25.1278} \\ {1.6137} & {84.36} & {- 86.4733} \\ {- 25.1278} & {- 86.4733} & {134.515} \\ \end{array}} \right],\quad F = \left[{\begin{array}{*{20}c} {- 90.2711} & {- 93.498} & {189.909} \\ {- 74.8967} & {- 56.8381} & {75.6911} \\ {100.6461} & {107.5033} & {- 216.382} \\ {- 3.705} & {46.7269} & {- 7.824} \\ \end{array}} \right]$$

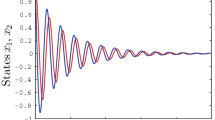
Figure 1 displays the states of the differential equations of system (42) by using the nonlinear state-feedback controller (4). All of the state trajectories are appropriately convergent to the origin. The output responses of the system are demonstrated in Fig. 2. Therefore, the simulations are robust in the presence of time delays and indicate satisfactory and reasonable performance as well.

Fig. 1

The trajectories of the system states

Fig. 2

The output responses

4.2 Example B: A Practical RIP System

RIP is a well-known test platform for evaluating control strategies. The control objective is to balance the pendulum in upright unstable equilibrium position. RIP system involves a rotational servo-motor which drives the output gear, rotational arm and an inverted pendulum. This system as an underactuated mechanical system has significant application in robotics, aerospace, marine vehicles and pointing control. In Fig. 3, the schematic diagram of the RIP system is shown. Let $\alpha_{p}$, $\theta_{a}$, $m_{p}$, $l_{p}$, $r_{a}$, $u$, $\tau_{a}$ and $J_{b}$ be the pendulum angle, drive disk angle (or arm angle), pendulum mass, pendulum length, arm length, control signal, motor torque and moment of inertia of the effective mass, correspondingly.

Fig. 3

Schematic diagram of RIP system

The dynamical equations of RIP with constant time delays, friction and backlash effects are given by:

$$\begin{aligned} & A_{p} \ddot{\theta}_{a} - (C_{p} \sin \alpha_{p})\dot{\alpha}_{p}^{2} + (B_{p} \sin 2\alpha_{p})\dot{\alpha}_{p} \dot{\theta}_{a} + F_{p} \dot{\theta}_{a} \\ & \quad + G_{p} \text{sgn} (\dot{\theta}_{a}) + H_{p} \theta_{a} = I_{p} u + \frac{{A_{p} B_{p} - C_{p}^{2}}}{{B_{p}}}\left[{\begin{array}{*{20}c} {\alpha_{p} (t - \tau)} \\ {\dot{\alpha}_{p} (t - \tau)} \\ {\theta_{a} (t - \tau)} \\ {\dot{\theta}_{a} (t - \tau)} \\ \end{array}} \right], \\ \end{aligned}$$

(43)

$$B_{p} \ddot{\alpha}_{p} - (B_{p} \sin \alpha_{p} \cos \alpha_{p})\dot{\theta}_{a}^{2} - D_{p} \sin \alpha_{p} + E_{p} \dot{\alpha}_{p} = 0$$

(44)

where $E_{p}$, $F_{p}$, $I_{p}$, $H_{p}$ and $G_{p}$ are damping constant of the pendulum, damping constant of the arm, control input coefficient, elasticity coefficients and arm Coulomb friction, respectively. The parameters $A_{p}$, $B_{p}$, $C_{p}$ and $D_{p}$ are considered as (Hassanzadeh and Mobayen 2011):

$$\begin{aligned} A_{p} = m_{p} r_{a}^{2} + J_{b}, \hfill \\ B_{p} = \frac{1}{3}m_{p} l_{p}^{2}, \hfill \\ C_{p} = \frac{1}{2}m_{p} r_{a} l_{p}, \hfill \\ D_{p} = \frac{1}{2}m_{p} gl_{p}. \hfill \\ \end{aligned}$$

(45)

The constant parameters of the nonlinear dynamical model (43), (44) are set as:

$$\begin{array}{*{20}c} {A_{p} = 3.291,} & {D_{p} = 6.052,} & {G_{p} = 1.428,} \\ {B_{p} = 0.237,} & {E_{p} = 0.0132,} & {H_{p} = 1.72,} \\ {C_{p} = 0.237,} & {F_{p} = 14.283,} & {I_{p} = 6.38.} \\ \end{array}$$

The nonlinear time-delayed model (43), (44) with some reformations can be illustrated in the form of (1) as follows:

$$\begin{aligned} \dot{x} = \left(\begin{array}{l} 0 \hfill \\ (\sin \,x_{1} \,\cos \,x_{1\,\,})x_{4\,\,}^{2} + 25.54\sin x_{1} \hfill \\ 0 \hfill \\ (0.072\sin \,x_{1} \,)x_{2\,\,}^{2} - (0.072\sin 2x_{1})x_{2} x_{4} - 0.43\text{sgn} (x_{4}) \hfill \\ \end{array} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left({\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ 0 & {- 0.056} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & {- 0.52} & {- 4.34} \\ \end{array}} \right)x + 0.93\left({\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ \end{array}} \right)x(t - \tau) + \left({\begin{array}{*{20}c} {0.2} \\ {0.1} \\ {0.1} \\ {1.94} \\ \end{array}} \right)u, \hfill \\ y = \left({\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ \end{array}} \right)x, \hfill \\ \end{aligned}$$

(46)

where $x = \left[{\begin{array}{*{20}c} {\alpha_{p}} & {\dot{\alpha}_{p}} & {\theta_{a}} & {\dot{\theta}_{a}} \\ \end{array}} \right]^{T}$. For the simulation usage, the initial states are specified as: $x(0) = \left[{\begin{array}{*{20}c} \pi & {- 1} & {- 4} & 2 \\ \end{array}} \right]^{T}$, and the time-delay is chosen as $\tau = 2$. The Lipschitzian matrix is specified by: $L = \left[{\begin{array}{*{20}c} {0.2} & 0 & 0 & 0 \\ 0 & {0.3} & 0 & 0 \\ 0 & 0 & {0.4} & 0 \\ 0 & 0 & 0 & {0.8} \\ \end{array}} \right].$ The solutions of matrices $H$, $P$, $P_{1}$, $F$ are calculated using MATLAB^® LMI^® toolbox and YALMIP^® routine as a solver as:

$$H = \left[ {\begin{array}{cccc} {0.7213} & { - \;0.1484} & {0.1765} & {1.7343} \\ { - \;0.1484} & {0.7503} & {0.1916} & {1.9435} \\ {0.1765} & {0.1916} & {0.5853} & {2.2188} \\ {1.7343} & {1.9435} & {2.2188} & {12.6601} \\ \end{array} } \right],\quad P = \left[ {\begin{array}{cccc} {1.1107} & {0.4934} & {0.4132} & {0.4817} \\ {0.4934} & {1.7864} & {0.1968} & { - \;0.1674} \\ {0.4132} & {0.1968} & {1.3576} & {0.6499} \\ {0.4817} & { - \;0.1674} & {0.6499} & {2.2046} \\ \end{array} } \right]$$

$$P_{1} = \left[ {\begin{array}{cccc} { 7. 8 5 1 2} & { 1. 6 4 6 3} & { 9. 5 2 4 5} & { 2 3. 4 5 2 6} \\ { 1. 6 4 6 3} & { 1. 2 5 9 8} & { 2. 0 7 9 0} & { 5. 7 0 1 8} \\ { 9. 5 2 4 5} & { 2. 0 7 9 0} & { 1 2. 1 9 7 3} & { 2 9. 2 4 5 7} \\ { 2 3. 4 5 2 6} & { 5. 7 0 1 8} & { 2 9. 2 4 5 7} & { 7 0. 6 6 8 2} \\ \end{array} } \right],\quad F = \left[ {\begin{array}{cccc} { - \; 3. 5 1 4 0} & { - \; 3. 2 7 0 0} & { - \; 3. 3 2 8 0} & { - \; 2. 0 2 8 0} \\ \end{array} } \right]$$

The time trajectories of states of the RIP system by using the suggested control law are presented in Fig. 4. The initial position is $x(0) = \left[{\begin{array}{*{20}c} {- 3} & 0 & 0 & 0 \\ \end{array}} \right]^{T}$, related to the experimental part. It is observed from Fig. 4 that the states of the RIP system can be regulated to the origin, irrespective of the time delays and nonlinearities. The time response of the control signal is depicted in Fig. 5, which displays the respectable efficiency of the suggested scheme. These simulations prove the robustness performance of the offered controller and show reasonable efficiency as well.

Fig. 4

The trajectories of the RIP system states

Fig. 5

The control input

In what follows, an experimental assessment of the proposed controller on the practical RIP system (from CoDAlab at Universitat Politècnica de Catalunya) is presented. The experiment is performed on an ECP Model 220 industrial emulator with inverted pendulum that includes a PC-based platform and DC brushless servo system (Model 2003). The mechatronic system includes a motor used as servo actuator, a power amplifier and two encoders which provide accurate position measurements; i.e., 4000 lines per revolution with 4X hardware interpolation giving 16,000 counts per revolution to each encoder; 1 count (equivalent to 0.000,392 radians or 0.0225 degrees) is the lowest angular measurable (Model 2003). The pendulum is fixed on the load disk (see Fig. 6). Experimental results for the pendulum angle, load disk angle and time response of the applied control signal are demonstrated in Figs. 7 and 8, revealing that the suggested control method is indeed effective in practice. The video of this experiment can be seen at https://youtu.be/CepUg2CjPu4.

Fig. 6

Practical RIP system, from CoDAlab laboratory (UPC) (see video https://youtu.be/CepUg2CjPu4)

Fig. 7

Experimental results of practical RIP system, a pendulum angle (α) and b drive disk angle (θ)

Fig. 8

Control input of practical RIP system

5 Conclusions

In this paper, the scheme of nonlinear feedback stabilization procedure is provided for the stabilization control of a class of nonlinear systems with time delays and Lipschitz nonlinearities. Based on the Lyapunov–Krasovskii stability theory, the stability performance of the system is verified in the form of LMIs and the states are convergent uniformly asymptotically to the origin. The controller gains are specified by the sufficient conditions using LMIs. Furthermore, the problem of robust H_∞ performance analysis for a class of nonlinear perturbed time-delayed systems is investigated in this paper. The obvious simulation and experimental results are displayed to confirm the effectiveness of the presented technique, and finally, some acceptable results are realized. The recommended control technique can attain favorable tracking performance for the higher-order nonlinear dynamical systems.