1 Introduction

With the rapid increase in the application of composite materials in the field of civil, aerospace, mechanical and automobile industries, etc., the quest for different methods of studying the structural responses of the composite structures has gained huge momentum. Structural analysis of advanced composite plates supported on an elastic foundation is an important area explored in the literature [1, 2] to understand the complex soil–structure interaction behavior. Analysis of structures like the raft and buttress foundations, swimming pools, storage tanks and stockpiling tanks requires the analysis of plates resting on elastic foundations. The responses of these structures under various loading conditions are dependent on the elastic medium supporting the structures [3]. Therefore, it is important to understand the interaction between the soil and structures to enhance structural safety and to provide a reliable design. Earlier studies on plates supported on an elastic foundation reveal that the one-parameter Winkler’s model is extensively used to model the deformation behavior of elastic foundations [4]. The Winkler model is a one-parameter model based on the ‘Winkler’s hypothesis,’ which states that the deflection at any point on a surface of the elastic soil is proportional to the load being applied onto the surface and is independent of the load being applied on any other points on the surface [5]. The shortcoming in this model is the discontinuity of the adjacent displacements in the mutually independent springs. Further refinement in Winkler’s model is the Pasternak’s foundation model which takes into account the proportional interaction between the pressure and deflection of any point on the surface of the elastic soil and also accommodates the continuity of the adjacent displacements by considering shear interactions among the points on the elastic soil [6].

Numerous mathematical models have been developed to date for modeling plate deformations under various external loads, and some are reviewed in [7]. The first-order shear deformation theory (FSDT) is adopted in [8] for studying the static responses of composite plates supported by elastic foundations. Mantari and Granados [9] studied the dynamic responses of advanced composite plates resting on elastic foundations with an improved FSDT model. The FSDT model is inadequate for modeling thick composites plate structures due to assumption of linear variations of in-plane displacements across the thickness of the plates. A third-order shear deformation theory (TSDT) proposed by Reddy [10] is adopted in [11, 12] for deriving the structural responses of advanced composite plates on elastic foundation with uncertain material properties. In contrary to the displacement variations in FSDT, TSDT considers nonlinear variations of in-plane displacements across the thickness of the plates. Akavci [13] presented analytically a comparison of various plate models like the classical plate theory (CPT), FSDT and TSDT for the static analysis of multilayered composite plates on elastic foundations. Shen et al. [14] extended the TSDT for investigating the thermo-mechanical effects on advanced composite plates supported on elastic foundations using a state-space approach. Additionally, the vibration and buckling responses of composite plates on the elastic foundations are also derived by Shen et al. [15, 16]. In the above-mentioned works [11,12,13,14,15,16], the higher-order terms in the kinematic expansions are introduced with polynomial terms obtained from the Taylor Series. These plate models are often referred to as the polynomial higher-order shear deformation theories (PHSDTs). Apart from the PHSDTs, there are also non-polynomial higher-order theories (NHSDTs) presented in [17, 18], where different non-polynomial functions are adopted in the kinematic expansions to model the nonlinear bending profile of the plate structures. Such models have the advantage in terms of computational costs due to less number of primary variables in the plate model. Akavci [19] adopted an NHSDT with hyperbolic function for investigating the free vibration and buckling responses of laminated composite plates on elastic foundation using Navier’s method. Exponential and trigonometric NHSDTs are employed in [20] and [21, 22] for investigating the static and vibration responses of advanced composite plates supported by elastic foundations. Sobhy [23] compared the responses of advanced composite plates with TSDT and various NHSTs with exponential, trigonometric and hyperbolic functions. The plate models in [20,21,22,23] have five numbers of primary variables like the FSDT. Additionally, four-variable plate models [24,25,26] are also developed in the literature to further reduce the computational costs while preserving a fair level of accuracy. The plate models in [24, 25] consider the in-plane displacements and transverse displacement to consist of bending and shear components. The components of in-plane displacements are further expressed in terms of linear and nonlinear functions of the derivatives of bending and shear components of transverse deformation, thereby reducing the number of field variables. In addition, the number of field variables is also reduced from five to four by writing the shear rotations in the form of integrations of a common primary variable in the expansions of in-plane displacements [26]. Such models are also known as the four-variable integral plate model [26].

The transverse shear deformation becomes very important in multilayered laminated composites as the elastic-to-shear modulus ratios are very large. Thus, significant shear deformations are noticed in thick composite plates. Additionally, the transverse normal deformation also becomes prominent in problems involving two fields like thermoelastic effects on composites. To deal with such problems, the variation of the transverse displacement across the thickness of the plates is considered to be nonlinear, thereby accommodating the transverse normal deformation along with shear deformations. These plate models are known to be the quasi-3 D plate models in the literature. The quasi-3D models are utilized in [27, 28] for the modeling the static and free vibration responses of advanced composite plates on elastic foundations. Kant and Swaminathan [29] presented a comparative study on the bending responses of laminated composite plates with various quasi-3D plate models and PHSDTs with constant transverse deformation.

Based on the aforementioned literature survey, it is observed that most of the studies dealing with the structural analysis of advanced composite plates resting on elastic foundations are carried out with plate models in the framework of the equivalent single-layer (ESL) approach [30]. The ESL approach is widely used in many problems of multilayered composite plates as the approach is easy to implement computationally. Furthermore, the global responses like displacements, fundamental frequencies and buckling loads of moderately thick and thin systems can be obtained with a fair level of accuracy. However, the responses are not efficient in thick laminated composite structures, mechanical properties are significantly different in each layer, and when materials exhibit high shear deformation [31]. The lack of accuracy in the aforesaid conditions is due to the use of global and smooth functions which have at least C1 continuity associated with the higher-order terms in the kinematic expansions. This results in a continuous transverse shear strain and discontinuous transverse shear stress field which is exactly opposite to the real phenomenon, thereby limiting the ESL models for the analysis of relatively thin systems. To overcome the drawbacks of the ESL models, layerwise (LW) [32, 33] and zigzag (ZZ) [34, 35] models are often used to derive the structural responses of laminated composite plates. In the LW approach, kinematic expansions are independently assumed for each layer, and conditions are enforced to satisfy the continuity of displacements and transverse stresses. The performance of the LW approaches is impressive in terms of the solution accuracy but requires huge computational involvement as the number of primary variables dramatically increases with the increase in the number of layers. Subsequently, the problems faced in the LW models are tackled by Di Sciuva [34, 35], Bhaskar and Varadan [36], Cho and Parmerter [37] and Chakrabarti and Sheikh [38], to name a few who have proposed efficient representations of kinematic expansion by combining the ESL field with local ZZ functions. The continuity conditions of displacements and transverse shear stresses can be satisfied a priori in the above models as the combination of the ESL field with the ZZ function results in a displacement model with slope discontinuity in the thickness direction at the interfaces between adjacent layers of different material properties. In most of the ZZ models, the displacement field is a combination of global first-order [34] and polynomial based higher-order theories (PHSDTs) [35,36,37,38] and very limited works are available on ZZ models with non-polynomial higher-order theories (NHSDTs). As mentioned earlier, the non-polynomial HSDTs adopt a single non-polynomial function to implicitly accommodate the higher-order functions present in PHSDTs, and the responses obtained with these models are also impressive at the cost of less computational efforts [20, 21]. The efficiency of the solutions can be further increased when the NHSDTs are used to model multilayered plate structures using the ZZ kinematics. Therefore, in this article, we combine the kinematics of a trigonometric NHSDT with a local ZZ function. The local ZZ function is selected in such a manner so that it is C0 continuous with discontinuous derivatives at the interfaces of the plates. Such a kinematic representation creates discontinuous transverse shear strain and continuous transverse shear stress fields. According to the best of the author’s knowledge, such a plate model has not been used in the literature to study the effect of the elastic foundations on the deformation responses of laminated composite plates.

The objective of this research is to develop analytical and finite element (FE) solutions for the static, free vibration and transient responses of multilayered composite plates supported by elastic foundations in the framework of NHSDT with ZZ kinematics. The NHSDT adopted in this research employs a secant function [39] as the shear strain function in the expansions of the in-plane displacements. The trigonometric NHSDT is further supplemented with some auxiliary variables which represents the changes in the slopes of the in-plane displacements. The auxiliary variables are defined at the interfaces with Heaviside step functions. The assumed kinematic model inherently satisfies the continuity of the displacements. The inter-laminar continuity of transverse shear stresses is enforced by which the total number of field variables reduces to the original number of field variables of the NHSDT. The elastic foundations are modeled using a two-parameter Pasternak’s foundation model. Hamilton’s principle is used to derive the governing equations, and Navier-based closed-form solutions are obtained for diaphragm-supported boundary conditions. Navier’s solutions are restricted to diaphragm-supported boundary conditions; however, the solutions are free from any numerical error. Further, to model the responses of general laminated plates with general boundary conditions, the finite element method (FEM) is also adopted in this research. An eight-noded C0 serendipity element is used to discretize the physical domain. The spatial approximation in FEM and the closed-form Navier’s solutions in the analytical approach reduce the partial differential equations (PDEs) to ordinary differential equations (ODEs) in time. The responses in the time domain are obtained using Newmark’s time integration scheme. Numerical examples are obtained using computer programs developed in MATLAB for both the analytical and FE formulation. The efficiency and the range of application of the present analytical and the FE model are established by comparing the results with standard elasticity solutions and with various plate models in the literature.

2 Mathematical formulation

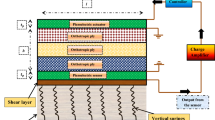
Consider a laminated composite plate supported on an elastic foundation as shown in Fig. 1. The laminated plate consists of orthotropic layers stacked in the thickness direction (z). The length, width and thickness of the plate are considered to be l, b and h, respectively. The rectangular Cartesian coordinate system (x, y, z) is chosen, such that x = 0, l, and y = 0, b define the boundaries of the plate, and z = 0 defines the mid-plane of the plate. The top surface of the plate is subjected to a transverse mechanical pressure, q = \(q_{0}\) f1 (t) f2 (x, y), where f1 (t) and f2 (x, y) are known mathematical variations of the pressure in the time and spatial domain, respectively, and \({q}_{0}\) is the magnitude of the applied mechanical pressure.

Fig. 1
figure 1

Schematic diagram of a multilayered laminated composite plate supported on elastic medium modeled with the Pasternak’s foundation with spring stiffness (\({k}_{\mathrm{w}}\)) and shear stiffness/Pasternak’s stiffness (\({k}_{\mathrm{s}}\))

Full size image

2.1 Fundamental equations

2.1.1 Stress–strain constitutive model

The state of stress at any point in the plate is defined in terms of the state of strain at that point with the stress–strain constitutive model. The material constitutive model of an orthotropic system for the kth layer along the thickness (z) is written as

$${\left\{\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\tau }_{12}\\ {\tau }_{23}\\ {\tau }_{13}\end{array}\right\}}^{(k)}={\left[\begin{array}{ccc}{Q}_{11}& {Q}_{12}& 0\\ {Q}_{12}& {Q}_{22}& 0\\ \begin{array}{c}0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\end{array}& \begin{array}{c}{Q}_{66}\\ 0\\ 0\end{array}\end{array} \begin{array}{cc}0& 0\\ 0& 0\\ \begin{array}{c}0\\ {Q}_{44}\\ 0\end{array}& \begin{array}{c}0\\ 0\\ {Q}_{55}\end{array}\end{array}\right]}^{(k)}\left\{\begin{array}{c}{\varepsilon }_{11}\\ {\varepsilon }_{22}\\ {\gamma }_{12}\\ {\gamma }_{23}\\ {\gamma }_{13}\end{array}\right\}$$
(1)

where \({\sigma }_{11}\), \({\sigma }_{22}\), \({\tau }_{12}\), \({\tau }_{23}\) and \({\tau }_{13}\) are the stresses defined at any point in the kth layer and \({\varepsilon }_{11}\), \({\varepsilon }_{22}\), \({\gamma }_{12}\), \({\gamma }_{23}\) and \({\gamma }_{13}\) are the strains defined at that point. \({Q}_{11}\), \({Q}_{12}\), \({Q}_{22}\), \({Q}_{66}\), \({Q}_{44}\) and \({Q}_{55}\) are the components of the reduced stiffness matrix for the kth layer derivable from the plane-stress condition [40].

2.1.2 Strain–displacement relations

The strains are defined in terms of the three displacements: U, V and W in the global x-, y- and z-direction, respectively, with the following linear strain displacement relations.

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{\partial U}{{\partial x}}} \\ {\frac{\partial V}{{\partial y}}} \\ {\left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}}} \right)} \\ {\left( {\frac{\partial V}{{\partial z}} + \frac{\partial W}{{\partial y}}} \right)} \\ {\left( {\frac{\partial U}{{\partial z}} + \frac{\partial W}{{\partial x}}} \right)} \\ \end{array} } \right\} $$
(2)

2.2 Plate model

This paper adopts a ZZ model, known as the trigonometric ZZ theory (TZZT) [39], which is also a refinement of the classical plate theory (CPT). The refinement is made with a trigonometric function, ‘z sec \(\left(\frac{rz}{h}\right)\)’, which implicitly takes into account the higher-order bending terms ‘\({z}^{3}\), \({z}^{5}\)…’ of the polynomial HSDTs.

$$ z\sec \left( \frac{rz}{h} \right) = \left( {{\varvec{z}} + 0.5\left( \frac{r}{h} \right)^{2} {\varvec{z}}^{3} + 0.2083\left( \frac{r}{h} \right)^{4} {\varvec{z}}^{5} + 0.0847\left( \frac{r}{h} \right)^{6} {\varvec{z}}^{7} + \cdots \infty } \right) $$
(3)

In the above equation, it is easily identified how a single non-polynomial function can accommodate the odd powered terms of z, necessary for the refinement of the bending phenomenon. In addition, some piecewise linear mathematical functions of z are also introduced in the plate model to capture the slope discontinuity of the in-plane displacements (U, V) at the interfaces of the multilayered-plate. Such discontinuities are pronounced in thick multilayered laminated composite plates confirmed by the elasticity solutions [41]. The TZZT model is defined as

(4)

where \(\overline{g }(z)\) consists of the trigonometric function, ‘z sec \(\left(\frac{rz}{h}\right)\)’. \({u}_{0}\), \({v}_{0}\), \({w}_{0}\), \({\beta }_{x}\) and \({\beta }_{y}\) are the primary variables defined at the mid-plane (z = 0), whereas \({\alpha }_{xu}^{i}\), \({\alpha }_{xl}^{j}\), \({\alpha }_{yu}^{i}\) and \({\alpha }_{yl}^{j}\) are the auxiliary variables which represent the changes in slopes of the in-plane displacements at the interfaces of the ith and jth layers of the plates. \({n}_{u}\) and \({n}_{l}\) are defined as the number of upper layers and lowers layers, respectively, with reference to the mid-plane. Implementing the inter-laminar continuity conditions of the transverse shear stresses at all the interfaces, the modified version of Eq. (4) is written as

$$\begin{aligned} \quad\quad\quad\quad\quad \left\{ {\begin{array}{*{20}c} U \\ V \\ W \\ \end{array} } \right\}\left( {x,y,z,t} \right) = & \left\{ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{0} } \\ \end{array} } \right\}\left( {x,y,t} \right) - z\left\{ {\begin{array}{*{20}c} {\frac{{\partial w_{0} }}{{\partial x}}} \\ {\frac{{\partial w_{0} }}{{\partial y}}} \\ 0 \\ \end{array} } \right\}\left( {x,y,t} \right) \\ + & f\left( z \right)\left\{ {\begin{array}{*{20}c} {\beta _{x} } \\ 0 \\ 0 \\ \end{array} } \right\}\left( {x,y,t} \right) + g\left( z \right)\left\{ {\begin{array}{*{20}c} 0 \\ {\beta _{y} } \\ 0 \\ \end{array} } \right\}\left( {x,y,t} \right) \\ \end{aligned} $$
(5a)

where \(f(z)\) = \({p}_{1}\)+ \(z{\Omega }_{x}\) and \(g(z)\) = \({p}_{2}\)+ \(z{\Omega }_{y}\)

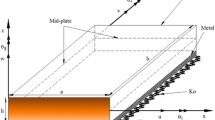
$$ \begin{gathered} p_{1} = z\sec (rz/h) + \mathop \sum \limits_{i = 1}^{{n_{u} - 1}} \left( {z - z^{iu} } \right)H\left( {z - z^{iu} } \right)\alpha_{xu}^{i} + \mathop \sum \limits_{j = 1}^{{n_{l} - 1}} \left( {z - z^{jl} } \right)H\left( { - z + z^{jl} } \right)\alpha_{xl}^{j} \hfill \\ p_{2} = z\sec (rz/h) + \mathop \sum \limits_{i = 1}^{{n_{u} - 1}} \left( {z - z^{iu} } \right)H\left( {z - z^{iu} } \right)\alpha_{yu}^{i} + \mathop \sum \limits_{j = 1}^{{n_{l} - 1}} \left( {z - z^{jl} } \right)H\left( { - z + z^{jl} } \right)\alpha_{yl}^{j} \hfill \\ q_{1} = \frac{{{\text{d}}p_{2} }}{{{\text{d}}z}};\;q_{2} = \frac{{{\text{d}}p_{1} }}{{{\text{d}}z}} \hfill \\ \end{gathered} $$
(5b)

The kinematic description of the present plate model is presented in Fig. 2.

Fig. 2
figure 2

Deformation profile of a laminated composite plate according to the kinematics of trigonometric zigzag theory (TZZT) accommodating constant, linear, nonlinear and piecewise linear deformation

Full size image

2.3 Foundation model

A two-parameter foundation model known as the Pasternak’s foundation model [21] is considered, which takes into account the proportional interaction between the pressure and deflection of any point on the surface of the elastic soil, and also maintains the continuity of the adjacent displacements by considering shear interactions among the points on the elastic soil. The reaction–deflection relationship of the Pasternak’s model is written as

$$ f_{{{\text{EF}}}} = k_{{\text{w}}} W - k_{{\text{s}}} \left( {\frac{{\partial^{2} W}}{{\partial x^{2} }} + \frac{{\partial^{2} W}}{{\partial y^{2} }}} \right) $$
(6)

where \({f}_{\mathrm{EF}}\) is the reaction, \({k}_{\mathrm{w}}\) is the modulus of the subgrade reaction or the stiffness coefficient of the springs, and \({k}_{\mathrm{s}}\) is the shear moduli of the subgrade or the shear stiffness coefficients of the foundation (shear layer).

2.4 Analytical formulation

The strain–displacement relationships for the TZZT model are written as follows with the help of Eqs. 2 and 5a.

$$ \begin{gathered} \varepsilon_{xx} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } & {z\varepsilon_{x}^{1} } & {\begin{array}{*{20}c} {p_{1} \varepsilon_{x}^{2} } & {p_{2} \varepsilon_{x}^{3} } \\ \end{array} } \\ \end{array} } \right\},\quad \varepsilon_{yy} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{y}^{0} } & {z\varepsilon_{y}^{1} } & {\begin{array}{*{20}c} {p_{1} \varepsilon_{y}^{2} } & {p_{2} \varepsilon_{y}^{3} } \\ \end{array} } \\ \end{array} } \right\}, \hfill \\ \gamma_{xy} = \left\{ {\begin{array}{*{20}c} {\gamma_{xy}^{0} } & {z\gamma_{xy}^{1} } & {\begin{array}{*{20}c} {p_{1} \gamma_{xy}^{2} } & {p_{2} \gamma_{xy}^{3} } \\ \end{array} } \\ \end{array} } \right\},\quad \gamma_{yz} = \left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } & {\begin{array}{*{20}c} {q_{1} \gamma_{yz}^{1} } & {q_{2} \gamma_{yz}^{2} } \\ \end{array} } \\ \end{array} } \right\}, \hfill \\ \gamma_{xz} = \left\{ {\begin{array}{*{20}c} {\gamma_{xz}^{0} } & {q_{1} \begin{array}{*{20}c} {\gamma_{xz}^{1} } & {q_{2} \gamma_{xz}^{2} } \\ \end{array} } \\ \end{array} } \right\} \hfill \\ \end{gathered} $$
(7a)

The strain parameters as shown in Eq. (7a) are further written in terms of the primary variables that are defined at the mid-plane.

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } & {\varepsilon_{x}^{1} } & {\begin{array}{*{20}c} {\varepsilon_{x}^{2} } & {\varepsilon_{x}^{3} } \\ \end{array} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x}} & {\left( { - \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \Omega_{x} \frac{{\partial \beta_{x} }}{\partial x}} \right)} & {\begin{array}{*{20}c} {\frac{{\partial \beta_{x} }}{\partial x}} & 0 \\ \end{array} } \\ \end{array} } \right\} \hfill \\ \left\{ {\begin{array}{*{20}c} {\varepsilon_{y}^{0} } & {\varepsilon_{y}^{1} } & {\begin{array}{*{20}c} {\varepsilon_{y}^{2} } & {\varepsilon_{y}^{3} } \\ \end{array} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial v_{0} }}{\partial y}} & {\left( { - \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + \Omega_{y} \frac{{\partial \beta_{y} }}{\partial y}} \right)} & {\begin{array}{*{20}c} 0 & {\frac{{\partial \beta_{y} }}{\partial y}} \\ \end{array} } \\ \end{array} } \right\} \hfill \\ \left\{ {\begin{array}{*{20}c} {\gamma_{xy}^{0} } & {\gamma_{xy}^{1} } & {\begin{array}{*{20}c} {\gamma_{xy}^{2} } & {\gamma_{xy}^{3} } \\ \end{array} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \right)} & {\left( { - 2\frac{{\partial^{2} w_{0} }}{\partial x\partial y} + \Omega_{x} \frac{{\partial \beta_{x} }}{\partial y} + \Omega_{y} \frac{{\partial \beta_{y} }}{\partial x}} \right)} & {\begin{array}{*{20}c} {\frac{{\partial \beta_{x} }}{\partial y}} & {\frac{{\partial \beta_{y} }}{\partial x}} \\ \end{array} } \\ \end{array} } \right\} \hfill \\ \left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } & {\begin{array}{*{20}c} {\gamma_{yz}^{1} } & {\gamma_{yz}^{2} } \\ \end{array} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\Omega_{y} \beta_{y} } & {\begin{array}{*{20}c} {\beta_{y} } & 0 \\ \end{array} } \\ \end{array} } \right\} \hfill \\ \left\{ {\begin{array}{*{20}c} {\gamma_{xz}^{0} } & {\begin{array}{*{20}c} {\gamma_{xz}^{1} } & {\gamma_{xz}^{2} } \\ \end{array} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\Omega_{x} \beta_{x} } & {\begin{array}{*{20}c} 0 & {\beta_{x} } \\ \end{array} } \\ \end{array} } \right\} \hfill \\ \end{gathered} $$
(7b)

2.4.1 Governing equations of motion

Hamilton’s principle is used to derive the governing set of equations of the TZZT model. The variation of the kinetic energy (K) and the total potential energy (\(\boldsymbol{\Pi }\)) of a plate, changing its position between two time instants (\({t}_{1}\), \({t}_{2}\)), is given by

$$ \mathop \int \nolimits_{{t_{0} }}^{{t_{1} }} \delta \left( {{\varvec{\Pi}}- {\varvec{K}}} \right){\text{d}}t = 0 $$
(8)

\(\boldsymbol{\Pi }\) is further represented as the contributions from the total strain energy of the plate ‘\({{\varvec{U}}}^{{\varvec{E}}}\)’, strain energy of the elastic foundation ‘\({{\varvec{U}}}^{\mathbf{E}\mathbf{F}}\)’ and the external work done by the applied mechanical load ‘\(\overline{{\varvec{W}} }\)’. The variation in the potential energy function for the case of transverse mechanical load is expressed as

$$ \delta{\varvec{\Pi}}= \delta {\varvec{U}}^{{\varvec{E}}} + \delta {\varvec{U}}^{{{\text{EF}}}} - \delta \overline{\user2{W}} $$
(9a)

The variations of the energies in Eq. (9a) are defined as

$$ \begin{gathered} \delta U^{E} = \mathop \int \nolimits_{0}^{l} \mathop \int \nolimits_{0}^{b} \left( {\mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left\{ {\delta \varepsilon } \right\}^{T} \left\{ \sigma \right\}{\text{d}}z} \right){\text{d}}x{\text{d}}y,\quad \delta U^{{{\text{EF}}}} = \mathop \int \nolimits_{0}^{l} \mathop \int \nolimits_{0}^{b} \left\{ {\delta W_{EF} } \right\}^{T} \left[ {K_{EF} } \right]\left\{ {W_{EF} } \right\}{\text{d}}x{\text{d}}y \hfill \\ \delta \overline{W} = \mathop \int \nolimits_{0}^{l} \mathop \int \nolimits_{0}^{b} q\delta W{\text{d}}x{\text{d}}y,\quad \delta K = \mathop \int \nolimits_{0}^{l} \mathop \int \nolimits_{0}^{b} \left( {\mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left\{ {\partial \dot{U}} \right\}^{T} \rho^{\left( k \right)} \left\{ {\dot{U}} \right\}{\text{d}}z} \right){\text{d}}x{\text{d}}y \hfill \\ \end{gathered} $$
(9b)

where \(\left\{{\varvec{\upsigma}}\right\}\) = \(\left\{\begin{array}{c}{{\sigma }_{xx}}^{(k)}\\ {{\sigma }_{yy}}^{(k)}\\ {{\tau }_{xy}}^{(k)}\\ {{\tau }_{yz}}^{(k)}\\ {{\tau }_{xz}}^{(k)}\end{array}\right\}\), \(\left\{{\varvec{\upvarepsilon}}\right\}\) = \(\left\{\begin{array}{c}{\varepsilon }_{xx}\\ {\varepsilon }_{yy}\\ {\gamma }_{xy}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\end{array}\right\}\), \(\left\{{\mathbf{W}}_{\mathbf{E}\mathbf{F}}\right\}\) = \(\left\{\begin{array}{c}W\\ \frac{\partial W}{\partial x}\\ \frac{\partial W}{\partial y}\end{array}\right\}\), \(\left[{\mathbf{K}}_{\mathbf{E}\mathbf{F}}\right]\) = \(\left[\begin{array}{ccc}{k}_{\mathrm{w}}& 0& 0\\ 0& {k}_{\mathrm{s}}& 0\\ 0& 0& {k}_{\mathrm{s}}\end{array}\right]\), \(\left\{\dot{\mathbf{U}}\right\}\) = \(\left\{\begin{array}{c}\dot{U}\\ \dot{V}\\ \dot{W}\end{array}\right\}\)

\({\rho }^{(k)}\) is the density of the kth layer. Dot mark over the displacement parameters indicates the time derivative. Substituting for the variations of the energies from Eqs. (9a, 9b) in Eq. (8), performing integration by parts in both space (x, y) and time (t) to remove any form of derivatives from the variations of the primary variables and also assuming that the variations obtained in space and at time, t = \({t}_{0}\) and \({t}_{1}\) are zero gives the following equations of motion and boundary conditions for the TZZT model.

Equations of motion

$$ \begin{gathered} \frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = \overline{I}_{0} \ddot{u}_{0} - \overline{I}_{1} \frac{{\partial \ddot{w}_{o} }}{\partial x} + \overline{I}_{3} \ddot{\beta }_{x} \hfill \\ \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{yy} }}{\partial y} = \overline{I}_{0} \ddot{v}_{0} - \overline{I}_{1} \frac{{\partial \ddot{w}_{o} }}{\partial y} + \overline{I}_{6} \ddot{\beta }_{y} \hfill \\ \frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + 2 \frac{{\partial^{2} M_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{yy} }}{{\partial y^{2} }} + q - k_{{\text{w}}} w_{0} + k_{{\text{s}}} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + k_{{\text{s}}} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} = \left( {\begin{array}{*{20}c} {\overline{I}_{1} \left( {\frac{{\partial \ddot{u}_{0} }}{\partial x} + \frac{{\partial \ddot{v}_{0} }}{\partial y}} \right) - \overline{I}_{2} \left( {\frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}_{0} }}{{\partial y^{2} }}} \right)} \\ { + \overline{I}_{4} \frac{{\partial \ddot{\beta }_{x} }}{\partial x} + \overline{I}_{7} \frac{{\partial \ddot{\beta }_{y} }}{\partial y} + \overline{I}_{0} \ddot{w}_{0} } \\ \end{array} } \right) \hfill \\ \Omega_{x} \frac{{\partial M_{xx} }}{\partial x} + \frac{{\partial N_{xx}^{*} }}{\partial x} + \Omega_{x} \frac{{\partial M_{xy} }}{\partial y} + \frac{{\partial N_{xy}^{*} }}{\partial y} - \Omega_{x} Q_{x} - T_{x}^{*} = \overline{I}_{3} \ddot{u}_{0} - \overline{I}_{4} \frac{{\partial \ddot{w}_{0} }}{\partial x} + \overline{I}_{5} \ddot{\beta }_{x} \hfill \\ \Omega_{y} \frac{{\partial M_{yy} }}{\partial y} + \frac{{\partial M_{yy}^{*} }}{\partial y} + \Omega_{y} \frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{xy}^{*} }}{\partial x} - \Omega_{y} Q_{y} - T_{y} = \overline{I}_{6} \ddot{v}_{0} - \overline{I}_{7} \frac{{\partial \ddot{w}_{0} }}{\partial y} + \overline{I}_{8} \ddot{\beta }_{y} \hfill \\ \end{gathered} $$
(10a)

Boundary conditions

Boundaries parallel to y axis, i.e, x = 0 or l

$$ \begin{gathered} N_{xx} = 0\;{\text{or}}\;u_{0} = 0,\quad N_{xy} = 0\;{\text{or}}\;v_{0} = 0,\quad M_{xx} = 0\;{\text{or}}\;\frac{{\partial w_{0} }}{\partial x} = 0, \hfill \\ \left( {\begin{array}{*{20}c} {\frac{{\partial M_{xx} }}{\partial x} + 2\frac{{\partial M_{xy} }}{\partial y} + k_{{\text{s}}} \frac{{\partial w_{0} }}{\partial x} - \overline{I}_{1} \ddot{u}_{0} + \overline{I}_{2} \frac{{\partial \ddot{w}_{0} }}{\partial x} - \overline{I}_{4} \ddot{\beta }_{x} } \\ \end{array} } \right) = 0\;{\text{or}}\;w_{0} = 0, \hfill \\ \left( {\Omega_{x} M_{xx} + N_{xx}^{*} } \right) = 0\;{\text{or}}\;\beta_{x} = 0,\quad \left( {\Omega_{y} M_{xy} + M_{xy}^{*} } \right) = 0\;{\text{or}}\;\beta_{y} = 0 \hfill \\ \end{gathered} $$

Boundaries parallel to x axis, i.e, y = 0 or b

$$ \begin{gathered} N_{xy} = 0\;{\text{or}}\;u_{0} = 0,\quad N_{yy} = 0\;{\text{or}}\;v_{0} = 0,\quad M_{yy} = 0\;{\text{or}}\;\frac{{\partial w_{0} }}{\partial y} = 0, \hfill \\ \left( {\begin{array}{*{20}c} {\frac{{\partial M_{yy} }}{\partial y} + 2\frac{{\partial M_{xy} }}{\partial x} + k_{{\text{s}}} \frac{{\partial w_{0} }}{\partial y} - \overline{I}_{1} \ddot{v}_{0} + \overline{I}_{2} \frac{{\partial \ddot{w}_{0} }}{\partial y} - \overline{I}_{7} \ddot{\beta }_{y} } \\ \end{array} } \right) = 0\;{\text{or}}\;w_{0} = 0, \hfill \\ \left( {\Omega_{x} M_{xy} + N_{xy}^{*} } \right) = 0\;{\text{or}}\;\beta_{x} = 0,\quad \left( {\Omega_{y} M_{yy} + M_{yy}^{*} } \right) = 0\;{\text{or}}\;\beta_{y} = 0 \hfill \\ \end{gathered} $$

At the corners

$$ M_{xy} = 0\;{\text{or}}\;w_{0} = 0 $$
(10b)

Stress resultants in Eqs. (10a) and (10b) are the integration of the stresses along the thickness defined over unit length of the mid-plane. These terms transform the 3 D form of the equations to 2 D. For the TZZT model, stress resultants are defined as

$$ \begin{gathered} ~~\left\langle {{\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {N_{{xx}} } \\ {N_{{yy}} } \\ {N_{{xy}} } \\ \end{array} } \right]} \\ {\left[ {\begin{array}{*{20}l} {N_{{xx}}^{*} } \\ {\begin{array}{*{20}l} 0 \\ {N_{{xy}}^{*} } \\ \end{array} } \\ \end{array} } \right]~} \\ \end{array} }} \mathrel{\left | {\vphantom {{\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {N_{{xx}} } \\ {N_{{yy}} } \\ {N_{{xy}} } \\ \end{array} } \right]} \\ {\left[ {\begin{array}{*{20}l} {N_{{xx}}^{*} } \\ {\begin{array}{*{20}l} 0 \\ {N_{{xy}}^{*} } \\ \end{array} } \\ \end{array} } \right]~} \\ \end{array} } {\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {M_{{xx}} } \\ {M_{{yy}} } \\ {M_{{xy}} } \\ \end{array} } \right]} \\ {\left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} 0 \\ {M_{{yy}}^{*} } \\ \end{array} } \\ {M_{{xy}}^{*} } \\ \end{array} } \right]} \\ \end{array} }}} \right. \kern-\nulldelimiterspace} {{\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {M_{{xx}} } \\ {M_{{yy}} } \\ {M_{{xy}} } \\ \end{array} } \right]} \\ {\left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} 0 \\ {M_{{yy}}^{*} } \\ \end{array} } \\ {M_{{xy}}^{*} } \\ \end{array} } \right]} \\ \end{array} }} \right\rangle ~~ = \mathop \sum \limits_{{k = 1}}^{{{\text{NL}}}} \left\langle {{\begin{array}{*{20}l} {\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {\left[ {\begin{array}{*{20}l} {\sigma _{{xx}} } \\ {\sigma _{{yy}} } \\ {\tau _{{xy}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)} \\ {\mathop \sum \nolimits_{{k = 1}}^{{{\text{NL}}}} \mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {p_{1} \left[ {\begin{array}{*{20}l} {\sigma _{{xx}} } \\ 0 \\ {\tau _{{xy}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)~~} \\ \end{array} }} \mathrel{\left | {\vphantom {{\begin{array}{*{20}l} {\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {\left[ {\begin{array}{*{20}l} {\sigma _{{xx}} } \\ {\sigma _{{yy}} } \\ {\tau _{{xy}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)} \\ {\mathop \sum \limits_{{k = 1}}^{{{\text{NL}}}} \mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {p_{1} \left[ {\begin{array}{*{20}l} {\sigma _{{xx}} } \\ 0 \\ {\tau _{{xy}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)~~} \\ \end{array} } {\begin{array}{*{20}l} {\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {z\left[ {\begin{array}{*{20}l} {\sigma _{{xx}} } \\ {\sigma _{{yy}} } \\ {\tau _{{xy}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)} \\ {~~\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {p_{2} \left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} 0 \\ \sigma \\ \end{array} _{{yy}} } \\ {\tau _{{xy}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)} \\ \end{array} }}} \right. \kern-\nulldelimiterspace} {{\begin{array}{*{20}l} {\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {z\left[ {\begin{array}{*{20}l} {\sigma _{{xx}} } \\ {\sigma _{{yy}} } \\ {\tau _{{xy}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)} \\ {~~\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {p_{2} \left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} 0 \\ \sigma \\ \end{array} _{{yy}} } \\ {\tau _{{xy}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)} \\ \end{array} }} \right\rangle ~ \hfill \\ \left\langle {\left[ {\begin{array}{*{20}l} {Q_{{xx}} } \\ {Q_{{yy}} } \\ \end{array} } \right]\left| {\left[ {\begin{array}{*{20}l} {T_{{xx}}^{*} } \\ 0 \\ \end{array} } \right]} \right.\left| {\left[ {\begin{array}{*{20}l} 0 \\ {T_{{yy}} } \\ \end{array} } \right]} \right.} \right\rangle = \mathop \sum \limits_{{k = 1}}^{{{\text{NL}}}} ~\left\langle {{\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {\left[ {\begin{array}{*{20}l} {\tau _{{xz}} } \\ {\tau _{{yz}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)\left| {\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {q_{2} \left[ {\begin{array}{*{20}l} {\tau _{{xz}} } \\ 0 \\ \end{array} } \right]^{k} {\text{d}}z} \right)} \right.}} \mathrel{\left | {\vphantom {{\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {\left[ {\begin{array}{*{20}l} {\tau _{{xz}} } \\ {\tau _{{yz}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)\left| {\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {q_{2} \left[ {\begin{array}{*{20}l} {\tau _{{xz}} } \\ 0 \\ \end{array} } \right]^{k} {\text{d}}z} \right)} \right.} {\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {q_{1} \left[ {\begin{array}{*{20}l} 0 \\ {\tau _{{yz}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)}}} \right. \kern-\nulldelimiterspace} {{\mathop \int \nolimits_{{z^{k} }}^{{z^{{k + 1}} }} \left( {q_{1} \left[ {\begin{array}{*{20}l} 0 \\ {\tau _{{yz}} } \\ \end{array} } \right]^{k} {\text{d}}z} \right)}} \right\rangle ~ \hfill \\ \end{gathered} $$
(11)

\(\mathrm{NL}\) is denoted as the number of layers in the thickness direction. Similarly, the density of each layer of the laminated plate is integrated along the thickness denoted as the inertia components in Eq. (10a). The inertia components are defined as

$$ \left[ {\begin{array}{*{20}l} {\overline{I}_{0} } & {\overline{I}_{1} } & {\overline{I}_{2} } \\ {\overline{I}_{3} } & {\overline{I}_{4} } & {\overline{I}_{5} } \\ {\overline{I}_{6} } & {\overline{I}_{7} } & {\overline{I}_{8} } \\ \end{array} } \right] = \left( {\mathop \sum \limits_{k = 1}^{{{\text{NL}}}} \mathop \int \nolimits_{{z^{k} }}^{{z^{k + 1} }} \left\{ {\rho^{k} \left[ {\begin{array}{*{20}l} 1 & z & {z^{2} } \\ {f\left( z \right)} & {zf\left( z \right)} & {f^{2} \left( z \right)} \\ {g\left( z \right)} & {zg\left( z \right)} & {g^{2} \left( z \right)} \\ \end{array} } \right]{\text{d}}z} \right\}} \right) $$
(12)

It is important to note that for the static and free vibration analysis, the inertia components and the loading terms must be omitted, respectively, from Eq. 10a. For the forced-vibration analysis, all the terms in Eq. 10a are required. The stress resultants can be further expressed in terms of the strain parameters. Further, the stress resultants are expressed in terms of the strains with the help of the constitutive model defined earlier in Eq. 1.

$$ \left[ {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} } \right\}} \\ {\left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} } \right\}} \\ {\left\{ {\begin{array}{*{20}c} {N_{xx}^{*} } \\ {\begin{array}{*{20}c} 0 \\ {N_{xy}^{*} } \\ \end{array} } \\ \end{array} } \right\}} \\ {\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {M_{yy}^{*} } \\ \end{array} } \\ {M_{xy}^{*} } \\ \end{array} } \right\}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left[ A \right]_{{\left( {3 \times 3} \right)}} } & {\left[ B \right]_{{\left( {3 \times 3} \right)}} } & {\left[ C \right]_{{\left( {3 \times 3} \right)}} } \\ {\left[ B \right]_{{\left( {3 \times 3} \right)}} } & {\left[ G \right]_{{\left( {3 \times 3} \right)}} } & {\left[ H \right]_{{\left( {3 \times 3} \right)}} } \\ {\begin{array}{*{20}c} {\left[ C \right]_{{\left( {3 \times 3} \right)}} } \\ {\left[ D \right]_{{\left( {3 \times 3} \right)}} } \\ \end{array} } & {\begin{array}{*{20}c} {\left[ H \right]_{{\left( {3 \times 3} \right)}} } \\ {\left[ I \right]_{{\left( {3 \times 3} \right)}} } \\ \end{array} } & {\begin{array}{*{20}c} {\left[ L \right]_{{\left( {3 \times 3} \right)}} } \\ {\left[ M \right]_{{\left( {3 \times 3} \right)}} } \\ \end{array} } \\ \end{array} \begin{array}{*{20}c} {\left[ D \right]_{{\left( {3 \times 3} \right)}} } \\ {\left[ I \right]_{{\left( {3 \times 3} \right)}} } \\ {\begin{array}{*{20}c} {\left[ M \right]_{{\left( {3 \times 3} \right)}} } \\ {\left[ P \right]_{{\left( {3 \times 3} \right)}} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\}} \hfill \\ {\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{1} } \\ {\varepsilon_{y}^{1} } \\ {\gamma_{xy}^{1} } \\ \end{array} } \right\}} \hfill \\ {\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{2} } \\ 0 \\ {\gamma_{xy}^{2} } \\ \end{array} } \right\}} \hfill \\ {\left\{ {\begin{array}{*{20}c} 0 \\ {\varepsilon_{y}^{3} } \\ {\gamma_{xy}^{3} } \\ \end{array} } \right\}} \hfill \\ \end{array} } \right] $$
(13a)
$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {Q_{yy} } \\ {Q_{xx} } \\ \end{array} } \right\}} \\ {\left\{ {\begin{array}{*{20}c} {T_{yy} } \\ 0 \\ \end{array} } \right\}} \\ {\left\{ {\begin{array}{*{20}c} 0 \\ {T_{xx}^{*} } \\ \end{array} } \right\}} \\ \end{array} = \left[ {\begin{array}{*{20}c} {\left[ {AA} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {EE} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {FF} \right]_{{\left( {2 \times 2} \right)}} } \\ {\left[ {EE} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {SS} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {TT} \right]_{{\left( {2 \times 2} \right)}} } \\ {\left[ {FF} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {TT} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {UU} \right]_{{\left( {2 \times 2} \right)}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\}} \\ {\left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{1} } \\ 0 \\ \end{array} } \right\}} \\ {\left\{ {\begin{array}{*{20}c} 0 \\ {\gamma_{xz}^{2} } \\ \end{array} } \right\}} \\ \end{array} } \right] $$
(13b)

The individual sub-matrices in Eqs. (13a, 13b) are defined in “Appendix 1.” The governing equations of motion in Eq. (10a) are further written in terms of the primary variables with the help of Eqs. (13a, 13b). The resulting partial differential equations (PDEs) are given in “Appendix 2.”

2.4.2 Analytical solution technique

To derive the exact closed-form solutions of the present model, Navier’s solution method is adopted with diaphragm-supported boundary condition on all four boundaries. Boundary condition for the diaphragm-supported conditions is obtained from Eq. (10b)

$$ \begin{gathered} {\text{At}}\;{\text{edges}}\;x = 0\;{\text{and}}\;x = l \hfill \\ v_{0}^{{}} = 0;\;w_{0} = 0;\;\beta_{y} = 0;\;N_{xx} = 0;\;M_{xx} = 0;\;\left( {\Omega_{x} M_{xx} + N_{xx}^{*} } \right) = 0 \hfill \\ {\text{At}}\;{\text{edges}}\;y = 0\;{\text{and}}\;x = b \hfill \\ u_{0} = 0;\;w_{0} = 0;\;\beta_{x} = 0;\;N_{yy} = 0;\;M_{yy} = 0;\;\left( {\Omega_{y} M_{yy} + M_{yy}^{*} } \right) = 0 \hfill \\ \end{gathered} $$
(14)

The primary variables are assumed in the form of double trigonometric series solutions by satisfying the above boundary conditions.

$$ \begin{gathered} u_{0} = \mathop \sum \limits_{m = 1, \ldots }^{\infty } \mathop \sum \limits_{n = 1, \ldots }^{\infty } \overline{u}_{{0_{mn} }} \cos \left( {\frac{m\pi x}{l}} \right)\sin \left( {\frac{n\pi y}{b}} \right) \\ v_{0} = \mathop \sum \limits_{m = 1, \ldots }^{\infty } \mathop \sum \limits_{n = 1, \ldots }^{\infty } \overline{v}_{{0_{mn} }} \sin \left( {\frac{m\pi x}{l}} \right)\cos \left( {\frac{n\pi y}{b}} \right) \\ w_{0} = \mathop \sum \limits_{m = 1, \ldots }^{\infty } \mathop \sum \limits_{n = 1, \ldots }^{\infty } \overline{w}_{{0_{mn} }} \sin \left( {\frac{m\pi x}{l}} \right)\sin \left( {\frac{n\pi y}{b}} \right) \\ \beta_{x} = \mathop \sum \limits_{m = 1, \ldots }^{\infty } \mathop \sum \limits_{n = 1, \ldots }^{\infty } \overline{\beta }_{{x_{mn} }} \cos \left( {\frac{m\pi x}{l}} \right)\sin \left( {\frac{n\pi y}{b}} \right) \\ \beta_{y} = \mathop \sum \limits_{m = 1, \ldots }^{\infty } \mathop \sum \limits_{n = 1, \ldots }^{\infty } \overline{\beta }_{{y_{mn} }} \sin \left( {\frac{m\pi x}{l}} \right)\cos \left( {\frac{n\pi y}{b}} \right) \\ \end{gathered} $$
(15a)

In the static analysis, the coefficients in Eq. (15) are constant in time and written as

$$ \overline{u}_{{0_{mn} }} = u_{{0_{mn} }} ;\;\overline{v}_{{0_{mn} }} = v_{{0_{mn} }} ;\;\overline{w}_{{0_{mn} }} = w_{{0_{mn} }} ;\;\overline{\beta }_{{x_{mn} }} = \beta_{{x_{mn} }} ;\;\overline{\beta }_{{y_{mn} }} = \beta_{{y_{mn} }} $$
(15b)

For free vibration problem, periodic solutions are assumed in time. The coefficients are modified as

$$ \overline{u}_{{0_{mn} }} = u_{{0_{mn} }} e^{i\omega t} ;\;\overline{v}_{{0_{mn} }} = v_{{0_{mn} }} e^{i\omega t} ;\;\overline{w}_{{0_{mn} }} = w_{{0_{mn} }} e^{i\omega t} ;\;\overline{\beta }_{{x_{mn} }} = \beta_{{x_{mn} }} e^{i\omega t} ;\;\overline{\beta }_{{y_{mn} }} = \beta_{{y_{mn} }} e^{i\omega t} $$
(15c)

For forced-vibration analysis, the coefficients are unknown in the time domain.

$$ \overline{u}_{{0_{mn} }} = u_{{0_{mn} }} (t);\;\overline{v}_{{0_{mn} }} = v_{{0_{mn} }} (t);\;\overline{w}_{{0_{mn} }} = w_{{0_{mn} }} (t);\;\overline{\beta }_{{x_{mn} }} = \beta_{{x_{mn} }} (t);\;\overline{\beta }_{{y_{mn} }} = \beta_{{y_{mn} }} (t) $$
(15d)

The coefficients in Eq. (15d) are obtained by solving a system of ordinary differential equations (ODEs) in time. The loading is also assumed in the form of double trigonometric series. The assumed trigonometric series along with proper Fourier coefficients can represent different variations of load in the spatial domain. The loading is represented as

$$ q = \mathop \sum \limits_{m = 1 \ldots }^{\infty } \mathop \sum \limits_{n = 1 \ldots }^{\infty } q_{mn} q\left( t \right)\sin \left( {\frac{m\pi x}{l}} \right)\sin \left( {\frac{n\pi y}{b}} \right) $$
(16)

q(t) can be any variation of the load in the time domain. \({q}_{mn}\) is equal to \({q}_{0}\) for SSL and \(\left(16{q}_{0}/{\pi }^{2}mn\right)\) for UDL, where \({q}_{0}\) is the amplitude of the applied load. The solutions assumed in Eq. (15a) along with the modified coefficients in Eqs. (15b, 15c and 15d) depending on the type of analysis are substituted in the PDEs in “Appendix 2,” to get the final governing equations. The final governing equation in the case of static analysis is a system of algebraic equations, system of homogenous algebraic equations in the free vibration problem and system of ODEs in the forced-vibration problem. The final equations are written as.

Static analysis

$$ \left[ {\overline{K}} \right]_{{\left( {5 \times 5} \right)}} \left\{ {\Delta } \right\}_{{\left( {5 \times 1} \right)}} = \left\{ {\overline{F}} \right\}_{{\left( {5 \times 1} \right)}} $$
(17a)

Free vibration analysis

$$ \left( {\left[ {\overline{K}} \right]_{{\left( {5 \times 5} \right)}} - \omega^{2} \left[ {\overline{M}} \right]_{{\left( {5 \times 5} \right)}} } \right)\left\{ {\Delta } \right\} = \left\{ 0 \right\}_{{\left( {5 \times 1} \right)}} $$
(17b)

Forced-vibration analysis

$$ \left[ {\overline{M}} \right]_{{\left( {5*5} \right)}} \left\{ {\ddot{\Delta }} \right\}_{{\left( {5 \times 1} \right)}} + \left[ {\overline{K}} \right]_{{\left( {5 \times 5} \right)}} \left\{ {\Delta } \right\}_{{\left( {5 \times 1} \right)}} = \left\{ {\overline{F}} \right\}_{{\left( {5 \times 1} \right)}} $$
(17c)

\(\left[ {\overline{M}} \right]\), \(\left[ {\overline{K}} \right]\) and \(\left\{ {\overline{F}} \right\}\) denote the mass matrix, stiffness matrix and the time-dependent external force vector. \(\left\{ {\ddot{\Delta }} \right\}\) and \(\left\{\Delta \right\}\) are the acceleration and displacement vectors containing the unknown coefficients. Equation (17a) is solved for the unknown coefficients defined in Eq. (15b). Equation (17b) is solved as an eigenvalue problem to obtain the fundamental frequency ‘\(\omega \)’ and the corresponding mode shapes given by the coefficients in Eq. (15c). Equation (17c) is further integrated in time using the Newmark’s constant average acceleration method to derive the solutions in time for the coefficients defined in Eq. (15d). A generalized analytical code is written in MATLAB software for deriving the various results reported in this work.

2.5 Finite element (FE) formulation

2.5.1 Modified displacement field and continuity requirements

The FE formulation of the TZZT model requires C1-continuity of transverse displacements due to the presence of first-order and second-order derivatives of the transverse displacement (\({w}_{0}\)) in the displacement field [Eq. (5a)] and strain–displacement relations [Eq. (7a)]. The C1-continuous FE formulations are computationally difficult; therefore, the first-order derivatives are reduced to new degrees of freedom which requires only C0 continuity.

Assuming \(\frac{\partial {w}_{0}}{\partial x}\) = \({\theta }_{x}\) and \(\frac{\partial {w}_{0}}{\partial y}\) = \({\theta }_{y}\), the modified displacement field of TZZT is written as

$$ \begin{aligned} U\left( {x,y,z,t } \right) & = u_{0} \left( {x,y,t } \right) - z\theta_{x} \left( {x,y,t} \right) + f\left( z \right)\beta_{x} \left( {x,y,t } \right) \\ V\left( {x,y,z,t } \right) & = v_{0} \left( {x,y,t } \right) - z\theta_{y} \left( {x,y,t} \right) + g\left( z \right)\beta_{y} \left( {x,y,t } \right) \\ W\left( {x,y,z,t } \right) & = w_{0} \left( {x,y,t } \right) \\ \end{aligned} $$
(18)

The new degrees of freedom ‘\({\theta }_{x}\) and \({\theta }_{y}\)’ impose artificial constraints, and in order to retain the original kinematics of the TZZT model [Eq. (5a)], we need to satisfy the following constraint equations that got generated while reducing the continuity requirements from C1 to C0.

$$ \left( {\frac{{\partial w_{0} }}{\partial x} - { }\theta_{x} } \right) = 0,\;\left( {\frac{{\partial w_{0} }}{\partial y} - { }\theta_{y} } \right) = 0 $$
(19)

The above problem is identified as a multipoint constrain problem in which there are relationships among two or more degrees of freedom, i.e., \(\frac{\partial {w}_{0}}{\partial x}\) = \({\theta }_{x}\) and \(\frac{\partial {w}_{0}}{\partial y}\) = \({\theta }_{y}\). To enforce the constraint equations in Eq. (19), penalty approach [42, 44] is used in this research.

2.5.2 Element selection

Present study adopts an eight-noded isoparametric serendipity element for the FE formulation. The field variables and the element geometry can be expressed as

$$ \left\langle {x|y} \right\rangle = \mathop \sum \limits_{i = 1}^{{{\text{NN}}}} \left\langle {N_{i} x_{i} {|} N_{i} y_{i} } \right\rangle $$
(20a)
$$ \left\langle {u_{0} |v_{0} |w_{0} |\beta_{x} |\beta_{y} |\theta_{x} |\theta_{y} } \right\rangle = \mathop \sum \limits_{i = 1}^{{{\text{NN}}}} \left\langle {N_{i} u_{0i} |N_{i} v_{0i} | \left. {N_{i} w_{0i} } \right|\left. { N_{i} \beta_{xi} } \right| \left. {N_{i} \beta_{yi} } \right|\left. { N_{i} \theta_{xi} } \right| N_{i} \theta_{yi} } \right\rangle $$
(20b)

The interpolation functions in Eqs. (20a, 20b) are given by

$$ \begin{gathered} N_{i} = \frac{1}{4}\left( {1 + \xi \xi_{i} } \right)\left( {1 + \eta \eta_{i} } \right)\left( {\xi \xi_{i} + \eta \eta_{i} - 1} \right)\quad {\text{for}}\;i = 1,3,5,7 \hfill \\ N_{i} = \frac{1}{2}\left( {1 - \xi^{2} } \right)\left( {\eta \eta_{i} + 1} \right)\quad {\text{for}}\;i = 2,6 \hfill \\ N_{i} = \frac{1}{2}\left( {1 - \eta^{2} } \right)\left( {\xi \xi_{i} + 1} \right)\quad {\text{for}}\;i = 4,8 \hfill \\ \end{gathered} $$
(21)

\(\mathrm{NN}\) is denoted as the number of nodes of an element. The local order of numbering the nodes for an eight-noded element is illustrated in Fig. 3a. Figure 3b and c shows how the physical domain is discretized using the eight-noded elements, and the global-order of element numbering followed in this work.

Fig. 3
figure 3

a Eight-noded isoparametric element used in the present FE formulation to discretize the domain of the plate (l × b). b Discretization of the plate domain in the FE formulation with eight-noded isoparametric elements. c Global number of the finite elements followed in the FE formulation

Full size image

2.5.3 Strain–displacement relations for an element

The strain vector, ‘\(\left\{\varepsilon \right\}\)’ is expressed in terms of the generalized strains given by

$$ \left\{ \varepsilon \right\}_{{\left( {5 \times 1} \right)}} = \left[ H \right]_{{\left( {5 \times 14} \right)}} \left\{ {\overline{\varepsilon }} \right\}_{{\left( {14 \times 1} \right)}} $$
(22a)

where \(\left\{\varepsilon \right\}\) = \({\left\{\begin{array}{ccc}{\varepsilon }_{xx}& {\varepsilon }_{yy}& \begin{array}{ccc}{\gamma }_{xy}& {\gamma }_{yz}& {\gamma }_{xz}\end{array}\end{array}\right\}}^{\mathrm{T}}\) and \(\left\{ {\overline{\varepsilon }} \right\} = \left\{ {\begin{array}{*{20}l} {\overline{\overline{\varepsilon }}_{1} } \hfill & {\overline{\overline{\varepsilon }}_{2} } \hfill & {\overline{\overline{\varepsilon }}_{3} } \hfill & {\overline{\overline{\varepsilon }}_{4} } \hfill & {\overline{\overline{\varepsilon }}_{5} } \hfill & {\overline{\overline{\varepsilon }}_{6} } \hfill & {\overline{\overline{\varepsilon }}_{7} } \hfill & {\overline{\overline{\varepsilon }}_{8} } \hfill & {\overline{\overline{\varepsilon }}_{9} } \hfill & {\overline{\overline{\varepsilon }}_{10} } \hfill & {\overline{\overline{\varepsilon }}_{11} } \hfill & {\overline{\overline{\varepsilon }}_{12} } \hfill & {\overline{\overline{\varepsilon }}_{13} } \hfill & {\overline{\overline{\varepsilon }}_{14} } \hfill \\ \end{array} } \right\}^{{\text{T}}}\).

The generalized strain vector is further written in terms of the nodal coordinates.

$$ \left\{ {\overline{\varepsilon }} \right\}_{{\left( {14 \times 1} \right)}} = \left[ B \right]_{{\left( {14 \times 56} \right)}} \left\{ {q^{\left( e \right)} } \right\}_{{\left( {56 \times 1} \right)}} $$
(22b)

where\(\left\{ {q^{\left( e \right)} } \right\} = \left\{ {\begin{array}{*{20}c} {\left\{ {d_{1}^{\left( e \right)} } \right\}} & {\left\{ {d_{2}^{\left( e \right)} } \right\}} & {\begin{array}{*{20}c} {\left\{ {d_{3}^{\left( e \right)} } \right\}} & {\left\{ {d_{4}^{\left( e \right)} } \right\}} & {\begin{array}{*{20}c} {\left\{ {d_{5}^{\left( e \right)} } \right\}} & {\left\{ {d_{6}^{\left( e \right)} } \right\}} & {\begin{array}{*{20}c} {\left\{ {d_{7}^{\left( e \right)} } \right\}} & {\left\{ {d_{8}^{\left( e \right)} } \right\}} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\}^{T}\)

$$\left\{ {d_{i}^{{\left( e \right)}} } \right\} = \left\{ {\begin{array}{*{20}l} {{u_{0}^{{\left( e \right)}}}_{i} } \hfill & {{v_{0}^{{\left( e \right)}}}_{i} } \hfill & {{w_{0}^{{\left( e \right)}}} _{i} } \hfill & {{\beta _{x}^{{\left( e \right)}} }_{i} } \hfill & {{\beta _{y}^{{\left( e \right)}} }_{i} } \hfill & {{\theta _{x}^{{\left( e \right)}}} _{i} } \hfill & {{\theta _{y}^{{\left( e \right)}}} _{i} } \hfill \\ \end{array} } \right\}^{{\text{T}}} $$

The details of \(\left[H\right]\), \(\left[B\right]\) and the components of \(\left\{\overline{\varepsilon }\right\}\) are given in “Appendix 3.”

2.5.4 Governing equations of motion

Governing equations of motion for an element ‘e’ are derived by substituting the variation in the potential energy and the kinetic energy in Hamilton’s principle defined in Eq. (8). The variation in the strain energy of the plate ‘\(\delta {{{\varvec{U}}}^{{\varvec{E}}}}^{({\varvec{e}})}\)’ is obtained by substituting Eqs. (22a and 22b) in the strain energy expression given in Eq. (9b), and also making use of the constitutive model in Eq. (1).

$$ \delta U^{{E}{^{\left( e \right)} }} = \left\{ {\delta q^{\left( e \right)} } \right\}^{{\text{T}}} \left( {\mathop \int \nolimits_{0}^{{l^{\left( e \right)} }} \mathop \int \nolimits_{0}^{{b^{\left( e \right)} }} \left( {\left[ B \right]^{t} \left[ {\overline{D}} \right]\left[ B \right]} \right) {\text{d}}x^{\left( e \right)} {\text{d}}y^{\left( e \right)} } \right)\left\{ {q^{\left( e \right)} } \right\} = \left\{ {\delta q^{\left( e \right)} } \right\}^{{\text{T}}} \left[ {K^{\left( e \right)} } \right]\left\{ {q^{\left( e \right)} } \right\} $$
(23)

where \(\left[\overline{D }\right]\) = \({\int }_{-\frac{h}{2}}^{\frac{h}{2}}\left({\left[H\right]}^{\mathrm{T}}{\left[\overline{Q }\right]}^{(k)}\left[H\right]\right)\mathrm{d}z\)  = \(\sum_{k=1}^{NL}\left({\int }_{{z}^{k}}^{{z}^{k+1}}\left({\left[H\right]}^{T}{\left[Q\right]}^{(k)}\left[H\right]\right)\mathrm{d}z\right)\)

\(\left[{K}^{(e)}\right]\) is the stiffness matrix of the eth element on the domain of the plate. The variation in the strain energy of the elastic foundation ‘\(\delta {{\varvec{U}}}^{\mathbf{E}\mathbf{F}}\)’ is expressed as

$$ \begin{aligned} \delta U^{{{\text{EF}}(e)}} & = \mathop \int \nolimits_{0}^{{l^{\left( e \right)} }} \mathop \int \nolimits_{0}^{{b^{\left( e \right)} }} \left( {\left\{ {\begin{array}{*{20}c} {\delta w_{0} } & {\frac{{\partial \delta w_{0} }}{\partial x}} & {\frac{{\partial \delta w_{0} }}{\partial y}} \\ \end{array} } \right\}\left[ {\begin{array}{*{20}c} {k_{{\text{w}}} } & 0 & 0 \\ 0 & {k_{{\text{s}}} } & 0 \\ 0 & 0 & {k_{{\text{s}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {w_{0} } \\ {\frac{{\partial w_{0} }}{\partial x}} \\ {\frac{{\partial w_{0} }}{\partial y}} \\ \end{array} } \right\}} \right){\text{d}}x^{\left( e \right)} {\text{d}}y^{\left( e \right)} \\ & = \mathop \int \nolimits_{0}^{{l^{\left( e \right)} }} \mathop \int \nolimits_{0}^{{b^{\left( e \right)} }} \left( {\left\{ {\delta W_{{{\text{EF}}}} } \right\}^{{\text{T}}} \left[ {K_{{{\text{EF}}}} } \right]\left\{ {W_{{{\text{EF}}}} } \right\}} \right){\text{d}}x^{\left( e \right)} {\text{d}}y^{\left( e \right)} \\ \end{aligned} $$
(24a)

The elements of the vector ‘\(\left\{{\mathbf{W}}_{\mathbf{E}\mathbf{F}}\right\}\)’ in the above equation can be expressed in the following manner

$$ \left\{ {{\mathbf{W}}_{{{\mathbf{EF}}}} } \right\} = \left[ {B_{{{\text{EF}}}} } \right]\left\{ {q^{\left( e \right)} } \right\} $$
(24b)

The elements of the matrix ‘\(\left[{B}_{\mathrm{EF}}\right]\)’ for the ith node are given by

$$ \left[ {B_{{{\text{EF}}i}} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & {N_{i} } \\ 0 & 0 & {\partial N_{i} /\partial x} \\ 0 & 0 & {\partial N_{i} /\partial y} \\ \end{array} \begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right] $$
(24c)

The variation in the strain energy of the elastic foundation can be finally obtained by substituting Eqs. (24b and 24c) in Eq. (24a).

$$ \delta U^{{{\text{EF}}}} = \left\{ {\delta q^{\left( e \right)} } \right\}^{{\text{T}}} \left( {\mathop \int \nolimits_{0}^{{l^{\left( e \right)} }} \mathop \int \nolimits_{0}^{{b^{\left( e \right)} }} \left( {\left[ {B_{{{\text{EF}}}} } \right]^{{\text{T}}} \left[ {K_{{{\text{EF}}}} } \right]\left[ {B_{{{\text{EF}}}} } \right]} \right){\text{d}}x^{\left( e \right)} {\text{d}}y^{\left( e \right)} } \right)\left\{ {q^{\left( e \right)} } \right\} = \left\{ {\delta q^{\left( e \right)} } \right\}^{{\text{T}}} \left[ {K^{{\left( F \right)^{(e)} }} } \right]\left\{ {q^{\left( e \right)} } \right\} $$
(25)

The variation in the kinetic energy for the eth element can be written as

$$ \delta K^{\left( e \right)} = \left\{ {\delta \dot{q}^{\left( e \right)} } \right\}^{{\text{T}}} \left( {\mathop \int \nolimits_{0}^{{l^{\left( e \right)} }} \mathop \int \nolimits_{0}^{{b^{\left( e \right)} }} \left( {\left[ {\overline{N}} \right]^{{\text{T}}} \left[ I \right]\left[ {\overline{N}} \right]} \right){\text{d}}x^{\left( e \right)} {\text{d}}y^{\left( e \right)} } \right)\left\{ {\dot{q}^{e} } \right\} = \left\{ {\delta \dot{q}^{\left( e \right)} } \right\}^{{\text{T}}} \left[ {M^{\left( e \right)} } \right]\left\{ {\dot{q}^{e} } \right\} $$
(26)

where

$$ \begin{aligned} [I] &= \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {\left[ Z \right]^{t} \rho^{\left( k \right)} \left[ Z \right]} \right){\text{d}}z = \mathop \sum \nolimits_{k = 1}^{{{\text{NL}}}} \mathop \int \nolimits_{{z^{k} }}^{{z^{k + } }} \left( {\left[ Z \right]^{t} \rho^{\left( k \right)} \left[ Z \right]} \right){\text{d}}z \hfill \\ [Z] &= \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \begin{array}{*{20}c} {f\left( z \right)} & 0 & { - z} \\ 0 & {g\left( z \right)} & 0 \\ 0 & 0 & 0 \\ \end{array} \begin{array}{*{20}c} 0 \\ { - z} \\ 0 \\ \end{array} } \right] \hfill \\ \end{aligned} $$

The elements of the matrix ‘\(\left[\overline{N }\right]\)’ for the ith node are given below

$$ \left[ {\overline{{N_{i} }} } \right] = \left[ {\begin{array}{*{20}l} {N_{i} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {N_{i} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {N_{i} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {N_{i} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {N_{i} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {N_{i} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {N_{i} } \hfill \\ \end{array} } \right] $$
(27)

The variation in the work potential ‘\(\delta {\mathrm{W}}^{e}\)’ is written as follows:

$$ \delta \overline{\varvec{W}}^{\left( {\varvec{e}} \right)} = \left\{ {\delta q^{\left( e \right)} } \right\}^{{\text{T}}} \mathop \int \nolimits_{0}^{{l^{\left( e \right)} }} \mathop \int \nolimits_{0}^{{b^{\left( e \right)} }} \left( {\left[ {\overline{N}} \right]^{{\text{T}}} \left\{ {f_{s} } \right\}} \right) {\text{d}}x^{\left( e \right)} {\text{d}}y^{\left( e \right)} = \left\{ {\delta q^{\left( e \right)} } \right\}^{{\text{T}}} \left\{ {F_{M}^{(e)} } \right\} $$
(28)

where \(\left\{{f}_{s}\right\}\) =\({\left\{\begin{array}{ccc}0& 0& \begin{array}{ccc}q& 0& \begin{array}{ccc}0& 0& 0\end{array}\end{array}\end{array}\right\}}^{\mathrm{T}}\)

A penalty function ‘\({U}_{\mathrm{pe}}^{(e)}\)’ is generated due to the constraint equations in Eq. (19), and it is added to the total potential energy ‘\(\delta {\boldsymbol{\Pi }}^{({\varvec{e}})}\)’ of an element in order to impose the constraint equations using penalty approach. \({U}_{\mathrm{pe}}^{(e)}\) is expressed in terms of a penalty term ‘\(\gamma \)’ and the constraint equations in the following manner

$$ U_{{{\text{pe}}}}^{\left( e \right)} = \frac{\gamma }{2}\mathop \int \nolimits_{0}^{{l^{\left( e \right)} }} \mathop \int \nolimits_{0}^{{b^{\left( e \right)} }} \left\{ {\left( {\frac{{\partial w_{0} }}{\partial x} - \theta_{x} } \right)^{{\text{T}}} \left( {\frac{{\partial w_{0} }}{\partial x} - \theta_{x} } \right) + \left( {\frac{{\partial w_{0} }}{\partial y} - \theta_{y} } \right)^{{\text{T}}} \left( {\frac{{\partial w_{0} }}{\partial y} - \theta_{y} } \right)} \right\} {\text{d}}x^{\left( e \right)} {\text{d}}y^{\left( e \right)} $$
(29)

The terms inside the above equation is further written in terms of the nodal coordinates.

$$ \left( {\frac{{\partial w_{0} }}{\partial x} - \theta_{x} } \right) = \{ P_{x} \} \left\{ {q^{\left( e \right)} } \right\};\;\left( {\frac{{\partial w_{0} }}{\partial y} - \theta_{2} } \right) = \{ P_{y} \} \left\{ {q^{\left( e \right)} } \right\} $$
(30)

The elements of the vectors ‘\(\left\{{\mathrm{P}}_{x}\right\}\)’ and ‘\(\left\{{\mathrm{P}}_{y}\right\}\)’ for the ith node are written as

$$ \begin{gathered} \left\{ {P_{xi} } \right\} = \left\{ {\begin{array}{*{20}c} 0 & 0 & {\frac{{\partial N_{i} }}{\partial x}} \\ \end{array} \begin{array}{*{20}c} 0 & 0 \\ \end{array} \begin{array}{*{20}c} { - N_{i} } & 0 \\ \end{array} } \right\}; \hfill \\ \left\{ {P_{2i} } \right\} = \left\{ {\begin{array}{*{20}c} 0 & 0 & {\frac{{\partial N_{j} }}{\partial y}} \\ \end{array} \begin{array}{*{20}c} 0 & 0 \\ \end{array} \begin{array}{*{20}c} 0 & { - N_{i} } \\ \end{array} } \right\} \hfill \\ \end{gathered} $$
(31)

Substituting Eqs. (30) in (29), the discretized equation of the penalty function is obtained as

$$ U_{{{\text{pe}}}}^{\left( e \right)} = \frac{\gamma }{2}\mathop \int \nolimits_{0}^{{l^{\left( e \right)} }} \mathop \int \nolimits_{0}^{{b^{\left( e \right)} }} \left\{ {\left\{ {q^{e} } \right\}^{{\text{T}}} \left\{ {P_{x} } \right\}^{{\text{T}}} \left\{ {P_{x} } \right\}\left\{ {q^{e} } \right\} + \left\{ {q^{e} } \right\}^{{\text{T}}} \left\{ {P_{y} } \right\}^{{\text{T}}} \left\{ {P_{y} } \right\}\left\{ {q^{e} } \right\}} \right\}{\text{ d}}x^{\left( e \right)} {\text{d}}y^{\left( e \right)} $$
(32)

The corresponding variation of the penalty function can be written as follows:

$$ \begin{aligned} \delta U_{{{\text{pe}}}}^{\left( e \right)} & = \left\{ {\delta q^{e} } \right\}^{{\text{T}}} \left( {\gamma \mathop \int \nolimits_{0}^{{l^{\left( e \right)} }} \mathop \int \nolimits_{0}^{{b^{\left( e \right)} }} \left\{ {\left\{ {P_{x} } \right\}^{{\text{T}}} \left\{ {P_{x} } \right\} + \left\{ {P_{y} } \right\}^{{\text{T}}} \left\{ {P_{y} } \right\}} \right\} {\text{d}}x^{\left( e \right)} {\text{d}}y^{\left( e \right)} } \right)\left\{ {q^{e} } \right\} \\ & = \left\{ {\delta q^{e} } \right\}^{{\text{T}}} \left[ {K_{{{\text{pe}}}}^{\left( e \right)} } \right]\left\{ {q^{e} } \right\} \\ \end{aligned} $$
(33)

It is important to note that when \(\gamma \) = 0, the constraints equations are not satisfied, i.e., \(\frac{\partial {w}_{0}}{\partial x}\) \(\ne {\theta }_{x}\) and \(\frac{\partial {w}_{0}}{\partial y}\) \(\ne {\theta }_{y}\). As the value of \(\gamma \) increases, the nodal displacement vector ‘\(\left\{{q}^{e}\right\}\)’ changes in such a way that the constraint equations are more nearly satisfied. The value of \(\gamma \) is considered to be 106 [43]. Finally, the variation in the total potential energy ‘\(\delta {\boldsymbol{\Pi }}^{({\varvec{e}})}\)’ for an element can now be written as

$$ \delta \Pi^{\left( e \right)} = \delta U^{E(e)} + \delta U^{{{\text{EF}}}} + \delta U_{{{\text{pe}}}}^{\left( e \right)} - \delta \overline{\varvec{W}}^{\left( e \right)} $$
(34)

Substituting the variations in the total potential energy and kinetic energy of an element from Eqs. (34), and (26), respectively, in Hamilton’s principle in Eq. (8), we get the following integral equation in time.

$$ \mathop \int \nolimits_{{t_{0} }}^{{t_{1} }} \left( {\begin{array}{*{20}c} {\left\{ {\delta q^{\left( e \right)} } \right\}^{{\text{T}}} \left[ {K^{{\left( F \right)^{{^{\left( e \right)} }} }} } \right] \left\{ {q^{\left( e \right)} } \right\} + \left\{ {\delta q^{\left( e \right)} } \right\}^{{\text{T}}} \left[ {K^{{\left( F \right)^{(e)} }} } \right] \left\{ {q^{\left( e \right)} } \right\}} \\ { - \left\{ {\delta q^{\left( e \right)} } \right\}^{{\text{T}}} \left\{ {F_{M}^{(e)} } \right\} + \left\{ {\delta q^{e} } \right\}^{{\text{T}}} \left[ {K_{{{\text{pe}}}}^{(e)} } \right] \left\{ {q^{e} } \right\}} \\ { - \left\{ {\delta \dot{q}^{\left( e \right)} } \right\}^{{\text{T}}} \left[ {M^{\left( e \right)} } \right]\left\{ {\dot{q}^{e} } \right\} } \\ \end{array} } \right){\text{d}}t = 0 $$
(35)

Solving the above equation and noting that the variations obtained at time, t = \({t}_{0}\) and \({t}_{1}\) is zero give the governing equation of motion for an element.

$$ \left[ {M^{\left( e \right)} } \right]\left\{ {\ddot{q}^{\left( e \right)} } \right\} + \left( {\left[ {K^{\left( e \right)} } \right] + \left[ {K^{{\left( F \right)^{(e)} }} } \right] + \left[ {K_{{{\text{pe}}}}^{(e)} } \right]} \right)\left\{ {q^{\left( e \right)} } \right\} = \left\{ {F_{M} } \right\} $$
(36)

\(\left[{K}^{(e)}\right]\) and \(\left[{{K}^{(F)}}^{(e)}\right]\) are the elemental stiffness matrices of the laminated composite plate and elastic foundation, whereas \(\left[{{K}_{\mathrm{pe}}}^{(e)}\right]\) is the elemental stiffness matrix due to the artificial constraints. \(\left[{M}^{(e)}\right]\) is defined as the elemental mass matrix. The integrations of the mass and stiffness matrices are carried out numerically using the Gauss-quadrature method. A selective integration scheme is used for a thin plate based on (3 × 3) and (2 × 2) gauss points, whereas full integration scheme is used for a thick plate based on (3 × 3) gauss points. This approach helps in eradicating any possible numerical disturbances like the shear locking phenomenon for a thin plate system. To obtain the governing equations for the entire system, the FE assembling of the matrices and the vectors are required to be carried out. The final discretized governing equations for the forced-vibration analysis of composite plates are written as follows:

Forced-vibration analysis

$$ \left[ {\overline{M}} \right]\left\{ {\ddot{q}} \right\} + \left( {\left[ {\overline{K}} \right] + \left[ {\overline{K}^{\left( F \right)} } \right] + \left[ {\overline{K}^{{\left( {pe} \right)}} } \right]} \right)\left\{ q \right\} = \left\{ {\overline{F}_{M} } \right\} $$
(37)

where \(\left[\overline{\mathbf{M} }\right]\) = \(\sum_{e=1}^{\mathrm{NE}}\left[{M}^{(e)}\right]\), \(\left[\overline{\mathbf{K} }\right]\) = \(\sum_{e=1}^{\mathrm{NE}}\left[{K}^{(e)}\right]\), \(\left[{\overline{\mathbf{K}} }^{({\varvec{F}})}\right]\) = \(\sum_{e=1}^{\mathrm{NE}}\left[{{K}^{(F)}}^{(e)}\right]\), \(\left[{\overline{\mathbf{K}} }^{(\mathbf{p}\mathbf{e})}\right]\) = \(\sum_{e=1}^{\mathrm{NE}}\left[{{K}_{\mathrm{pe}}}^{(e)}\right]\), \(\left\{{\overline{\mathbf{F}} }_{{\varvec{M}}}\right\}\) = \(\sum_{e=1}^{\mathrm{NE}}\left\{{F}_{M}\right\}\)

The governing set of equations for the static and free vibration analysis can be obtained by neglecting the inertial terms and the load vector, respectively, from Eq. (37)

Static analysis

$$ \left( {\left[ {\overline{K}} \right] + \left[ {\overline{K}^{\left( F \right)} } \right] + \left[ {\overline{K}^{{\left( {{\text{pe}}} \right)}} } \right]} \right)\left\{ q \right\} = \left\{ {\overline{F}_{M} } \right\} $$
(38)

Free vibration analysis

$$ \left[ {\overline{M}} \right]\left\{ {\ddot{q}} \right\} + \left( {\left[ {\overline{K}} \right] + \left[ {\overline{K}^{\left( F \right)} } \right] + \left[ {\overline{K}^{{\left( {{\text{pe}}} \right)}} } \right]} \right)\left\{ q \right\} = \{ 0\} $$
(39)

The following boundary conditions are used to evaluate the results from the FE formulation.

Diaphragm-support (SSSS)

\({u}_{o}\) = \({w}_{o}\) = \({\beta }_{x}\) = \({\theta }_{x}\) = 0 at y = 0, b and \({v}_{o}\) = \({w}_{o}\) = \({\beta }_{y}\) = \({\theta }_{y}\) = 0 at x = 0, l

Clamped-support (CCCC)

\({u}_{o}\) = \({w}_{o}\) = \({\beta }_{x}\) = \({\theta }_{x}\) = \({v}_{o}\)  =  \({\beta }_{y}\) = \({\theta }_{y}\)  = 0 at x = 0, l and y = 0, b

Clamped-diaphragm support (CSCS)

\({u}_{o}\) = \({w}_{o}\) = \({\beta }_{x}\) = \({\theta }_{x}\)  = 0 at y = 0, b and \({u}_{o}\) = \({w}_{o}\) = \({\beta }_{x}\) = \({\theta }_{x}\) = \({v}_{o}\)  =  \({\beta }_{y}\) = \({\theta }_{y}\)   = 0 at x = 0, l

Equation (37) is further solved using the Newmark’s constant average acceleration method. A generalized FE code is written in MATLAB software for the static, free vibration and forced-vibration analysis for producing the various results reported in this paper.

3 Results and discussion

In this section, the numerical results are obtained using the analytical and FE formulations derived in the preceding section. The non-dimensional parameters and material properties used to evaluate the numerical results are presented below.

3.1 Non-dimensional parameters

  • ND1: \(\overline{U }\) = \(\frac{{E}_{22}}{{q}_{mn}{S}^{3}h}U; \overline{W }\)  = \(\frac{{100E}_{22}}{{q}_{mn}{S}^{4}h}{w}_{o}\); \({\tilde{\sigma }}_{xx}\)=\(\frac{{\sigma }_{xx}}{{q}_{mn}{S}^{2}}\); \({\overline{K} }_{w}\) = \({\overline{K} }_{1}\)  = \(\frac{{k}_{w}{l}^{4}}{{E}_{2}{h}^{3}}\); \({\overline{K} }_{s}\) = \({\overline{K} }_{2}\)  = \(\frac{{k}_{s}{l}^{2}}{{E}_{2}{h}^{3}}\)

  • ND2: \({\overline{U} }_{3}\) =\(\frac{0.999781}{hq}{U}_{3}\left(\frac{l}{2},\frac{b}{2},0\right)\); \({\tilde{\sigma }}_{xx}^{1}\)=\(\frac{1}{q}{\sigma }_{xx}^{1}\left(\frac{l}{2},\frac{b}{2},-\frac{h}{2}\right)\); \({\overline{K} }_{w}\) = \({\overline{K} }_{1}\)  = \(\frac{{k}_{w}{l}^{4}}{{E}_{2}{h}^{3}}\); \({\overline{K} }_{s}\) = \({\overline{K} }_{2}\)  = \(\frac{{k}_{s}{l}^{2}}{{E}_{2}{h}^{3}}\)

  • ND3: \(\overline{\omega }\) = \(\frac{{l}^{2}}{h}\sqrt{\left(\frac{\rho }{{E}_{22}}\right)}\omega \); \({\overline{K} }_{w}\) = \({\overline{K} }_{1}\)  = \(\frac{{k}_{w}{l}^{4}}{{E}_{2}{h}^{3}}\); \({\overline{K} }_{s}\) = \({\overline{K} }_{2}\)  = \(\frac{{k}_{s}{l}^{2}}{{E}_{2}{h}^{3}}\)

Material properties

  • MM1 [45]

    \({E}_{11}\)/\({E}_{22}\)= 25; \({G}_{12}\)= \({G}_{13}\)= 0.5 \({E}_{22}\);\({G}_{23}\)=0.2 \({E}_{22}\); \({\vartheta }_{12}\)=0.25.

  • MM2 [39]

    Material properties of the core

    $$ \left[ Q \right]_{{{\text{core}}}} = \left[ {\begin{array}{*{20}l} {0.999781} \hfill & {0.231192} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {0.231192} \hfill & {0.524886} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {0.262931} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {0.26681} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {0.1559914} \hfill \\ \end{array} } \right]; $$
    $$ \left[ Q \right]_{{\text{face - sheets}}} = R[Q]_{{{\text{core}}}} $$

  • MM3 [19]

    \({E}_{11}\)/\({E}_{22}\)= 40; \({G}_{12}\)= \({G}_{13}\)= 0.5 \({E}_{22}\);\({G}_{23}\)=0.2 \({E}_{22}\); \({\vartheta }_{12}\)=0.25.

  • MM4 [46]

    \({E}_{11}\)/\({E}_{22}\)= variable, \({E}_{22}\) = 2.1 × 106 N/cm2, \({G}_{12}\)= \({G}_{13}\)=\({G}_{23}\)=0.5 \({E}_{22}\), \({\vartheta }_{12}\)=0.25, \(\rho \) = 8 × 10–6 Nsec2/cm4.

  • MM5 [47]

    \({E}_{11}\) = 172.369 GPa, \({G}_{12}\)=\({G}_{13}\)=3.448 GPa, \({E}_{22}\) = 6.895 GPa, \({G}_{23}\)=1.379 GPa, \({\vartheta }_{12}\)=0.25, \(\rho \)= 1603.03 kg/m3.

3.2 Static analysis of multilayered laminated composites and sandwich plates supported on elastic foundation


The first example in this section considers a four-layered (0/90/90/0) laminated composite plate with diaphragm support at all the edges. The mechanical pressure is assumed to be sinusoidal in the spatial domain (x, y). The material properties of each orthotropic layer are corresponding to the values listed in MM1. The normalized maximum transverse deflections of the plate under the given mechanical load are listed in Table 1 for various span-thickness ratios and foundation stiffness. The exact results of this problem without considering the effects of the foundation are available in [41]. The results of Setoodeh and Azizi [45] are also listed in the table for comparison. The present FE results are observed to get converged at the mesh size of 8 × 8 in the table. An excellent agreement of the present analytical and FE results with the solutions in [41] is observed in the table. The deflection of the plate decreases by 42.39% when only Winker stiffness (\({\overline{K} }_{\mathrm{w}}\)=100, \({\overline{K} }_{\mathrm{s}}\)=0) is considered, and 68.64% when both the Winkler and shear stiffness of the foundations (\({\overline{K} }_{\mathrm{w}}\)=100, \({\overline{K} }_{\mathrm{s}}\)=10) are considered. The results of Setoodeh and Azizi [45] using CPT and refined first-order shear deformation theory (RFSDT) are observed to underestimate the magnitudes of the transverse displacement for a thick plate (S = 10). As the plate becomes thin, the present results and the results of [45] do not have large differences. Figure 4a, b and c shows the convergence of the FE solutions of the maximum in-plane normal stresses \(\left({\tilde{\sigma }}_{xx},{\tilde{\sigma }}_{yy}\right)\) and in-plane shear stress \(\left({\overline{\tau }}_{xy}\right)\), respectively, for a thick plate, S = 10. An excellent convergence of the results is observed in the figures. Further, the variation of \({\tilde{\sigma }}_{xx}\left(x,\frac{b}{2},\frac{h}{2}\right)\), and \({\tilde{\sigma }}_{yy}\left(\frac{l}{2},y,\frac{h}{4}\right)\) along the length and width of the same plate is shown in Figs. 5 and 6, respectively, for various magnitudes of the foundation stiffness. The in-plane stresses, \({\tilde{\sigma }}_{xx}\) and \({\tilde{\sigma }}_{yy}\) are observed to be maximum at the center of the plate and zero at both ends. The decrement in the magnitude of the stresses is observed in the figures due to the foundation stiffness. The variation of the in-plane shear stress, \({\overline{\tau }}_{xy}\left(x,0,\frac{h}{2}\right)\) is presented in Fig. 7. The in-plane shear stress is observed to be maximum at the corner (0, 0, \(\frac{h}{2}\)) and minimum at the center (l/2, 0, \(\frac{h}{2}\)) of the boundary line. The across variations of the in-plane normal stress, \({\tilde{\sigma }}_{xx}\left(\frac{l}{2},\frac{b}{2},z\right)\) are shown in Fig. 8. The maximum value of \({\tilde{\sigma }}_{xx}\) is attained at both the extreme surfaces (z = \(\pm \) h/2) of the plate, and the values decrease when the foundation stiffness is taken into consideration. In the examples discussed above, the structural responses of the deflection and stresses are more affected due to the combined Winkler and shear stiffness (Pasternak’s stiffness) of the foundations. The inclusion of the shear stiffness (\({\overline{K} }_{s}\)= K2) creates a continuity of the transverse displacement among the points surrounded by the loaded region, resulting in more resistance against deformation compared to the Winkler’s stiffness alone. Therefore, the deflection and stresses are observed to decrease more due to the combined Winkler and shear stiffness of the foundations. The in-plane variation of the normalized transverse displacement of the same composite plate with different boundary conditions, clamped–clamped (CCCC) and clamped-diaphragm support (CSCS) is shown in Fig. 9a–f for various values of \({K}_{\mathrm{w}}\) and \({K}_{\mathrm{s}}\). The results are presented based on Winkler’s model and Pasternak’s model. The decrement in the magnitude of transverse displacement is observed to be much more in the case of fully clamped (CCCC) condition than in the clamped-diaphragm-support (CSCS) condition. In the case of the fully clamped condition, the stiffness of the plate is much more due to the complete translational and rotational restraints from the boundaries; thus, the magnitude of the deflection is lower compared to the CSCS condition. Further, the variation of the transverse displacement with the Winkler and shear stiffness of the foundation is shown in Fig. 10a–c for simply support (SSSS), CCCC and CSCS conditions. It is observed in the figures that the plate experiences minimum deflection when both the stiffness of the foundation is at its maximum value and maximum deflection when both the stiffness of the foundation is minimum. It is also observed in the figures that the plate experiences less defection due to the shear stiffness alone compared to Winkler stiffness. Next, a three-layered (0/90/0) laminated composite plate is considered with diaphragm-supported boundary condition at all the edges subjected to uniform variation of mechanical load. The elastic properties listed in MM1 are used in this problem. The results of the normalized maximum transverse deflection are presented in Table 2. Reddy [10], and Sheikh and Chakrabrati [48] have previously reported the results of this problem without considering the effects of the elastic foundations. The present results are in excellent agreement with the solutions in [10, 48] for thin and moderately thick plates. As the plate becomes thick, the slope discontinuities of the in-plane displacement components become prominent at the interfaces, and as a result, some differences in the present solutions and the solutions from the ESL-based models in [10, 48] are observed. In order to check the slope discontinuities, the through-thickness variation of the in-plane displacement ‘\(\overline{U }\)’ is shown in Fig. 11a and b. It is observed in Fig. 11a that no prominent discontinuities of \(\overline{U }\) are visible for a thin plate, S = 100. However, as the plate becomes thick, the slope discontinuities begin to develop at the interfaces of the plates. The decrement in the magnitude of \(\overline{U }\) is also visible in Fig. 11b when Winkler stiffness of the foundation is considered. Next, a three-layered soft-core sandwich plate (0/C/0) resting on elastic foundations is considered for investigating the static responses. The material properties of the core layer are listed in MM2. The material properties of the face-sheets are obtained by multiplying the properties of the core with a constant ‘R’. The results of the normalized deflection (\(\overline{W }\)) and in-plane stress (\({\tilde{\sigma }}_{xx}\)) for a thick plate (S = 10) are given in Table 3 for various values of R, and the FE convergence of the transverse deflection (\(\overline{W }\)) and in-plane stress (\({\tilde{\sigma }}_{xx}\)) are shown in Fig. 12a and b, respectively, for R = 5. An excellent convergence of the present FE results is observed in the figure. In the table, the exact solutions [49] and solutions obtained using various plate models [50, 51] in the framework of LW approach are collected in the table. The present results are in excellent agreement with the exact solutions [49] and with the results of Ferreira [50] and Roque et al. [51]. In the results of \({\tilde{\sigma }}_{xx}\), the magnitude decreases by 68.17% due to the Winkler stiffness and 86.12% when both Winkler and shear stiffness are considered for R = 5. When the difference in the material properties of the face-sheets and the core is very high (R = 100), the decrement in the magnitude of normal stress is calculated to be 29.39% and 52.56% due to Winkler and the combined Winkler-shear stiffness of the foundation, respectively.

Table 1 Convergence and validation of transverse deflection of laminated composite plate (0/90/90/0) resting on elastic foundation subjected to SSL (material properties: MM1; non-dimensional parameters: ND1)
Full size table
Fig. 4
figure 4

Finite element convergence of the results of in-plane normal stresses \(\left({\tilde{\sigma }}_{xx}, {\tilde{\sigma }}_{yy}\right)\) and in-plane shear stress \(\left({\overline{\tau }}_{xy}\right)\) of a laminated composite plate resting on elastic foundation under the action of SSL a \({\tilde{\sigma }}_{xx}\left(\frac{l}{2},\frac{b}{2},\frac{h}{2}\right)\); b \({\tilde{\sigma }}_{yy}\left(\frac{l}{2},\frac{b}{2},\frac{h}{4}\right)\); c \( \overline{\tau}_{xy}\) \(\left(\mathrm{0,0},\frac{h}{2}\right)\) (material properties: MM1, non-dimensional parameter: ND1)

Full size image
Fig. 5
figure 5

Variation of \({\tilde{\sigma }}_{xx}\left(x,\frac{b}{2},\frac{h}{2}\right)\) along the length of a thick composite plate with Winkler (Kw = K1) and shear stiffness (Ks = K2) of the foundation (material properties: MM1, non-dimensional parameter: ND1)

Full size image
Fig. 6
figure 6

Variation of \({\tilde{\sigma }}_{yy}\left(\frac{l}{2},y,\frac{h}{4}\right)\) along the width of a thick composite plate with Winkler (Kw = K1) and shear stiffness (Ks = K2) of the foundation (material properties: MM1, non-dimensional parameter: ND1)

Full size image
Fig. 7
figure 7

Variation of \({\overline{\tau }}_{xy}\left(0,x,\frac{h}{2}\right)\) along the length of a thick composite plate with Winkler (Kw = K1) and shear stiffness (Ks = K2) of the foundation (material properties: MM1, non-dimensional parameter: ND1)

Full size image
Fig. 8
figure 8

The across variation of in-plane normal stress, \({\tilde{\sigma }}_{xx}\left(\frac{l}{2},\frac{b}{2},z\right)\) for a thick composite plate with Winkler (Kw = K1) and shear stiffness (Ks = K2) of the foundation (material properties: MM1, non-dimensional parameter: ND1)

Full size image
Fig. 9
figure 9

In-plane variation of transverse displacement, \(\overline{W }\left(\frac{l}{2},\frac{b}{2},0\right)\) for a thick composite plate with various boundary conditions a CCCC, K1 = 0; K2 = 0. b CCCC, K1 = 100; K2 = 0. c CCCC, K1 = 100; K2 = 10. d CSCS, K1 = 0; K2 = 0. e CSCS, K1 = 100; K2 = 0. f CSCS, K1 = 100; K2 = 10 (material properties: MM1, non-dimensional parameter: ND1)

Full size image
Fig. 10
figure 10

Variation of the transverse displacement, \(\overline{W }\left(\frac{l}{2},\frac{b}{2},0\right)\) with Winkler kw = K1 and shear stiffness (ks = K2) of the foundation for a thick composite plate with various boundary conditions. a Diaphragm-support (SSSS). b Clamped support (CCCC). c Clamped-Diaphragm support (CSCS) (material properties: MM1, non-dimensional parameter: ND1)

Full size image
Table 2 Transverse deflection of laminated composite plate (0/90/0) resting on elastic foundation subjected to UDL (material properties: MM1; non-dimensional parameters: ND1)
Full size table
Fig. 11
figure 11

a Across variation of in-plane displacement \(\left({\overline{U} }_{x}\right)\) for a three-layered composite plate with various span–thickness ratios. b Across variation of in-plane displacement \(\left({\overline{U} }_{x}\right)\) for a three-layered composite plate by considering the effects of foundation and various span–thickness ratios (material properties: MM1, non-dimensional parameter: ND1)

Full size image
Table 3 Static response of soft-core sandwich plate (0/Core/0) subjected to uniform pressure resting on elastic foundation (material properties: MM2; non-dimensional parameters: ND2)
Full size table
Fig. 12
figure 12

Finite element convergence of transverse displacement and in-plane normal stress of a soft-core sandwich plate resting on elastic foundations: a transverse displacement (\(\overline{W }\)); b in-plane normal stress \(\left({\tilde{\sigma }}_{xx}\right)\) (material properties: MM2, non-dimensional parameter: ND2)

Full size image

3.3 Free vibration responses of laminated composites and sandwich plates supported on elastic foundation

A three-layered laminated composite (0/90/0) plate resting on elastic foundations with diaphragm support at all the edges is chosen to study the dynamic behavior. The material properties of the orthotropic layers are listed in MM3. A comparative study for determining the accuracy of the present analytical and FE model is presented in Table 4 by evaluating the fundamental natural frequencies of the plate for various span–thickness ratios and Young’s modulus ratio (MR), \({E}_{11}\)/\({E}_{22}\)= 40. The present results are compared with the solutions of different higher-order shear deformation models of Akavci [14] and Shen et al. [13]. The results show an excellent agreement for all the cases of thick, moderately thick and thin plates. Next, the fundamental frequencies of the same plate are plotted in Figs. 13 and 14 for various modulus ratios and foundation stiffness. Figure 13 illustrates the variation of the natural frequencies for different magnitudes of MR and Winkler stiffness \(\left({\overline{K} }_{\mathrm{w}}={\overline{K} }_{1}\right)\). The natural frequencies tend to increase with the increase in the magnitude of MR and Winkler stiffness. The stiffness of the plate increases with the increase in MR, and the resistance to deformation due to the stiffness of the springs (\({\overline{K} }_{\mathrm{w}}\)) increases the overall stiffness of the system, resulting in the increase in the fundamental frequencies. Figure 14 illustrates the variation of the natural frequencies of the plate with MR and the shear stiffness \(\left({\overline{K} }_{\mathrm{s}}={\overline{K} }_{2}\right)\) of the foundation. The fundamental frequencies are observed to increase more with the shear stiffness. The shear layer in the foundation model maintains continuity of the displacements among the points in the vicinity of the loaded surface resulting in the increase in the overall stiffness of the system. Therefore, the fundamental frequencies are observed to increase more with the shear stiffness. Figure 15 shows the variation of the normalized natural frequencies of the same plate with MR and span–thickness ratio by considering the combined Winkler stiffness (\({\overline{K} }_{\mathrm{w}}=100\)) and shear stiffness (\({\overline{K} }_{\mathrm{s}}=10\)) of the foundation. The natural frequencies are observed to increase with the increase in the span–thickness ratios. In Fig. 16, the effect of the plate boundary condition on the natural frequencies is shown by considering the same plate with clamped–clamped (CCCC) boundary conditions resting on Pasternak’s foundation. The fundamental frequencies are observed to be higher in the CCCC boundary condition compared to the diaphragm-supported (SSSS) condition. The CCCC boundary condition provides greater stiffness in comparison with the SSSS condition due to complete translational and rotational restraints at the boundaries, resulting in the increase in the fundamental frequencies.

Table 4 Natural frequencies of a three-layered (0/90/0) laminated composite plate resting on elastic foundation (material properties: MM3; non-dimensional parameters: ND3)
Full size table
Fig. 13
figure 13

Variation of the normalized natural frequency of the laminated composite plate on elastic foundation with modulus ratio (MR) and Winkler stiffness (\({\overline{K} }_{\mathrm{w}}={\overline{K} }_{1}\)) of the foundation (material properties: MM3, non-dimensional parameter: ND3)

Full size image
Fig. 14
figure 14

Variation of the normalized natural frequency of the laminated composite plate on elastic foundation with modulus ratio (MR) and shear stiffness (\({\overline{K} }_{\mathrm{s}}={\overline{K} }_{2}\)) of the foundation (material properties: MM3, non-dimensional parameter: ND3)

Full size image
Fig. 15
figure 15

Variation of the normalized natural frequency of the laminated composite plate on elastic foundation with modulus ratio (MR) and span–thickness ratio (material properties: MM3, non-dimensional parameter: ND3)

Full size image
Fig. 16
figure 16

Variation of the natural frequencies of the laminated composite plate supported on an elastic foundation with CCCC boundary condition (\({\overline{K} }_{\mathrm{w}}\)= K1; \({\overline{K} }_{\mathrm{s}}\)= K2) (material properties: MM3, non-dimensional parameter: ND3)

Full size image

3.4 Forced-vibration analysis of laminated composite plates on elastic foundation

At first, the validation of the forced-vibration responses is presented by considering three-layered (0/90/0) and five-layered (0/90/0/90/0) laminated composite plates with diaphragm-support at all the edges. The material properties used in this problem are listed in MM4. The laminated plate is subjected to a suddenly applied constant pulse load in time. The maximum transient deflection of the plate under the loading is presented in Table 5 for various magnitudes of modulus ratio (MR). The solutions obtained by Reddy [46] and Kant et al. [52] using FSDT and HSDT, respectively, are collected in the table for comparison of the present analytical and FE solutions. The present analytical and FE solutions are in close agreement with the references [46, 52].

Table 5 Convergence and validation of the transient deflection of composite plates (material properties: MM4)
Full size table

The effects of the elastic foundation on the forced-vibration responses of laminated composite plates are now investigated. A three-layered diaphragm-supported laminated composite plate is chosen with material properties corresponding to MM5. The plate structure is first loaded with a pulse load acting for 0.006 s and then removed from the plate as shown in Fig. 17a. The applied load is sinusoidal in spatial domain (x, y). The displacement–time response of the plate is shown in Fig. 17b for three different conditions, namely, without considering any foundation, considering only the Winkler foundation, and considering Pasternak’s foundation. The FE results of the vibration have converged at a mesh size of 8 × 8; therefore, the results presented in the forced-vibration analysis are corresponding to this mesh size unless specified. A good agreement of the present analytical and FE results is observed in the figure. The amplitude of the vibration decreases, while the frequency increases due to the elastic foundation. The behavior of the plot can be explained as the Winkler and Pasternak’s foundations provide additional resistance to deformation via Winkler and shear stiffness of the springs and the shear layer. The coefficients of the mass matrix do not change, while the coefficients of the stiffness matrix corresponding to \(\overline{w }\) increase, resulting in the increase in the frequency of the vibration. The decrement in the amplitude and increment in the frequency of the vibration are much more when both the Winkler stiffness and shear stiffness of the foundation are considered. Next, a time-dependent triangular load acts on the plate for 0.006 s as shown in Fig. 18a, and the corresponding vibration responses are shown in Fig. 18b. The amplitude of the vibration decreases with time up to t = 0.006 s, and then the amplitude becomes constant in time. Also, an excellent correlation of the analytical and FE responses can be observed in the figure. Next, a sinusoidal excitation is allowed to act on the plate for 0.006 s and then removed as shown in Fig. 19a. The corresponding vibration response under the load is shown in Fig. 19b. The pattern of the response is similar to the variation of the load in the time domain; the amplitude of the vibration increases like the sinusoidal pulse under the action of the load in the forced-vibration regime. Also, the amplitude under the forced vibration (t \(\le \) 0.006 s) is higher in comparison to the amplitude under the free vibration regime (t > 0.006 s). However, the amplitude of the free vibration response is smaller compared to the previous cases of constant pulse and triangular load. Next, we apply a sinusoidal excitation at a frequency equal to the natural frequency of the laminated composite plate. The natural frequency of the plate without considering the stiffness of the foundation is first evaluated by solving an eigenvalue problem and found out to be 4373 rad/sec. The variation of the sinusoidal excitation with time at the same frequency is shown in Fig. 20a. Figure 20b shows the forced-vibration response under the sinusoidal excitation without considering the foundation stiffness. As expected, the plate vibrates under the resonance condition as the frequency of the excitation is equal to the fundamental frequency of the plate. Figure 20c shows the forced-vibration response under the same sinusoidal excitation by considering the Winkler and shear stiffness of the foundation. The plate does not vibrate under the resonance condition anymore as the foundation stiffness has altered the fundamental frequency of the plate. Next, the vibration responses of the laminated composite plates are shown in Figs. 21, 22, 23, 24, 25 and 26 under various time-dependent loads like pulse, ramp, ramp-constant and exponential blast load. In all the figures, the individual effect of the Winkler stiffness (\({\overline{K} }_{\mathrm{w}}\)) and shear stiffness (\({\overline{K} }_{\mathrm{s}}\)) of the foundations is investigated. Figure 21a and b shows the vibration response of the laminated plate under constant-pulse acting for the entire duration of the plate vibration by considering Winkler and shear stiffness, respectively. The vibration response is exactly similar in both the figures when \({\overline{K} }_{\mathrm{w}}\) and \({\overline{K} }_{\mathrm{s}}\) = 0. As the value of the stiffness increases, the amplitude of the vibration decreases and the frequency increases with greater effect noticed in Fig. 21b due to shear stiffness compared to Winkler stiffness. Figure 22a shows the time-dependent variation of another mechanical load known as the ramp variation, and the resulting vibration responses under the load are presented in Fig. 22b and c by considering the Winkler and shear stiffness of the foundation, respectively. The amplitude of the vibration in both the figures is linearly increasing like the load profile. As the value of the stiffness increases, the effect of the foundation gets evident in the figures. Figure 23b and c shows the vibration response of the plate under the action of the ramp load acting for t = 0.006 s, and then it is removed from the plate. It is observed in the figures that the amplitude of the vibration is increasing as long as the load acts, and then, the plate vibrates with constant free vibration amplitude at t > 0.006 s. Figure 24a shows the ramp-constant variation of the mechanical load in time, in which the portion of the ramp variation is up to 0.004 s and then constant in time after t > 0.004 s. The vibration of the plate under the action of the load is shown in Fig. 24b and c. It is observed in the figures that the entire vibration response is under the forced-vibration just like the load profile. The vibration of the plate when t < 0.004 s is exactly similar to the responses presented earlier under the action of ramp load; however, when the plate is under the action of the constant pulse (t > 0.004 s), the plate oscillates around the transverse displacement at t = 0.004 s. Figure 25a shows the variation of an exponential blast load (q (t) = \({e}^{\overline{\gamma }t}\)) in time with decay parameter, \(\overline{\gamma }\) =  − 1320 s−1. The vibration response of the plate under the action of the load is presented in Fig. 25b and c for duration of 0.0025 s. The vibration response has decreasing amplitude due to the presence of the decay constant (\(\overline{\gamma }\)) in the blast load. Initially, the plate vibrates with high amplitude under the action of the strong blast; thereafter, the plate vibrates with decreasing amplitude of vibration similar to the load profile in Fig. 25a. The effect of the decay constant in the blast load is further investigated by considering several values of the decay constant in the blast load profile. Figure 26a shows the variation of the blast load in time for several values of the decay constant. Figure 26b shows the 3 D graphical representation of the displacement–time response of the laminated plate supported on an elastic foundation with foundation stiffness, \({\overline{K} }_{\mathrm{w}}=100;{\overline{K} }_{\mathrm{s}}=10\) under the action of the load. It is observed in the figure that as the magnitude of the decay constant increases, the faster the plate enters the steady-state condition.

Fig. 17
figure 17

a Variation of the pulse mechanical loading in time acting for t = 0.006 s. b Vibration response of the laminated composite plate resting on an elastic foundation under pulse loading acting for 0.006 s (material properties: MM5)

Full size image
Fig. 18
figure 18

a Triangular variation of the mechanical load in time acting for t = 0.006 s on the plate. b Forced and free vibration response of a laminated composite plate resting on elastic foundation under triangular loading acting for 0.006 s (material properties: MM5)

Full size image
Fig. 19
figure 19

a Sinusoidal variation of the mechanical load in time acting for t = 0.006 s on the plate. b Variation of the sinusoidal excitation with time. b Forced and free vibration response of a laminated composite plate resting on elastic foundation under sinusoidal loading acting for 0.006 s (material properties: MM5)

Full size image
Fig. 20
figure 20

a Sinusoidal mechanical excitation acting at a frequency equal to the natural frequency of the plate. b Vibration response under the sinusoidal excitation without considering the foundation stiffness. c Vibration response of the plate under the sinusoidal excitation by considering the foundation stiffness (material properties: MM5)

Full size image
Fig. 21
figure 21

a 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering Winkler stiffness under pulse loading. b 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering shear stiffness under pulse loading (material properties: MM5)

Full size image
Fig. 22
figure 22

a Ramp variation of the mechanical load in time. b 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering Winkler stiffness under ramp loading. c 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering shear stiffness under ramp loading (material properties: MM5)

Full size image
Fig. 23
figure 23

a 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering Winkler stiffness under ramp loading acting for 0.006 s. b 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering shear stiffness under ramp loading acting for 0.006 s (material properties: MM5)

Full size image
Fig. 24
figure 24

a Ramp-constant variation of the mechanical load in time. b 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering Winkler stiffness under ramp-constant load. c 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering shear stiffness under ramp-constant load (material properties: MM5)

Full size image
Fig. 25
figure 25

a Variation of the exponential blast load in time with decay parameter, \(\gamma \) = -1320 s−1. b 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering Winkler stiffness under exponential blast load. c 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation by considering shear stiffness under exponential blast load (material properties: MM5)

Full size image
Fig. 26
figure 26

a Variation of the exponential blast load in time with various decay parameters, \(\gamma \). b 3D graphical representation of forced-vibration response of laminated composite plate on elastic foundation subjected to exponential blast load with various decay constants (material properties: MM5)

Full size image

4 Conclusions

This article studies the influence of the elastic foundations on the static, free vibration and transient behavior of advanced composite plates using a non-polynomial shear deformation theory (NSDT) with zigzag kinematics. The plate model consists of an ESL-based non-polynomial higher-order theory to accurately model the nonlinearity of the transverse shear strains across the thickness of the plates, and a ZZ field for satisfying the piecewise continuous displacement requirements that are essential for accurately representing the transverse shear strain/stress fields. The interaction between the foundation and the plate is modeled using Pasternak’s foundation model. Analytical solutions for diaphragm-supported boundary conditions of the plate are proposed using Navier’s solution, and the numerical solutions for different boundary conditions are obtained using the finite element method. The structural responses are obtained by considering various parameters like the span–thickness ratio, modulus ratio, different types of static and dynamic loadings and foundation stiffness. The results reflect that the foundation stiffness has a significant effect on the structural responses of deflection, stresses, natural frequencies, amplitude and frequency of the vibration. The deflection and stresses are observed to decrease due to the elastic foundations. The fundamental frequencies tend to increase with the increase in the stiffness of the foundations. The amplitude and frequency of the vibration response tend to decrease and increase, respectively, with the increase in the foundation stiffness. The effect of the Pasternak’s foundation on the structural response is more than the Winkler’s foundation. An excellent agreement of the results obtained by the proposed analytical and FE model is observed in all the problems. Based on the results, it can be concluded that the present analytical and the FE formulations are capable of modeling the deformation responses of advanced composite plates supported on an elastic foundation.