Stability analysis of reduced rotor pedestal looseness fault model

Abstract

In this paper, the nonlinear dynamic characteristics of a rotor system supported by ball bearings with pedestal looseness are analyzed. The model of seven-degrees of freedom (DOFs) rotor system is established by the Newton’s second law, which comprises a pair of ball bearings with pedestal looseness at one end. Energy analysis of the original model states that the first two-order proper orthogonal modes occupy almost all the energy of the system, and it demonstrates that the reduced model reserves main dynamical topological characteristics of the original one. A modified proper orthogonal decomposition method is applied in order to reduce the DOFs from seven to two, and the reduced system preserves the bifurcation and amplitude–frequency characteristics of the original one. The harmonic balance method with the alternating frequency–time domain technique is used to calculate the periodic response of the reduced system. Moreover, stability of the two-DOFs model is analyzed based on the known harmonic solution by the Floquet theory.

1 Introduction

The pedestal looseness fault of rotor system has become one of the special faults in rotor dynamics, attracting the attention of researchers in many areas. Ji et al. [1] utilized multi-scale method to analyze the vibration characteristics of autonomous rotor-bearing system with supporting looseness. An et al. [2] studied the fault features of front and rear bearing pedestal looseness of wind turbine, and the relevant experiments. Chu [3] analyzed the periodic, chaos, quasiperiodic characteristics of a rotor-bearing system with pedestal looseness. Agnes and Paul [4] studied the chaotic responses of the unbalanced rotor–stator system with both looseness and rubs faults. The nonlinear finite element method was applied to study the nonlinear characters of overhanging dual-disk rotor bearing for pedestal looseness fault in ref. [5]. Goldman and Muszynska [6] performed experiments and analytical and numerical investigations on the unbalanced response of a rotating machine with looseness pedestal at one end, and that model was simplified as a bilinear form vibrating system. In ref. [7], it presented a finite element model of a rotor system with pedestal looseness stems from a loosened bolt, analyzing the effects of the looseness parameters on its dynamic characteristics.

The qualitative characters of the nonlinear fault model were studied by a number of researchers in many areas, for example, the stability of the unbalanced rigid rotor on lubricated journal bearings model [8], the bifurcation, chaos, reliability sensitivity of rub–impact fault [9–11], the unsteady motion and nonlinear instability analysis of the nonlinear oil-film model [12] and so on. While the qualitative analysis of the pedestal looseness system (piecewise linear system) was studied by few researchers, such as the stability and response of piecewise linear oscillators under multi-forcing frequencies were analyzed in ref. [13], and Kim [14] did the stability and bifurcation analysis of oscillators with piecewise linear characters. But almost no one did the work about combining the stability analysis of the pedestal looseness system with the order reduction method. As an effective order reduction method, the modified POD method can ensure that the reduced system reserves the dynamical characteristics of the original one [15–17]. So it is essential to study the stability of the reduced system based on the modified POD method.

The motivation of this paper is to analyze the stability of two-DOFs model reduced from the seven-DOFs pedestal looseness rotor-bearing model based on the modified POD method. The number of DOF of the reduced model is determined by the first few-order POMs which occupy almost all the energy of the system, and this energy judgment method is to guarantee reliability of the reduced model. The efficiency of the modified POD method is presented by comparing the reduced system with the original one. The stability of the reduced system is analyzed which stands for the qualitative characteristics of the original system.

2 Model of rotor pedestal looseness

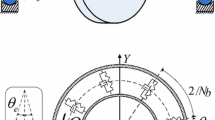
For the rotor model with pedestal looseness at one end shown in Fig. 1, the dynamical equation of seven-DOFs model with ball bearings at both ends is established by Newton’s second law, and the equation is expressed as:

$$\begin{aligned}&{m_1 \ddot{X}_1 +c_1 \dot{X}_1 +k\left( {X_1 -X_2} \right) =F_{xL} \left( {X_1 ,Y_1 -Y_4} \right) } \nonumber \\&\quad {m_1 \ddot{Y}_1 +c_1 \dot{Y}_1 +k\left( {Y_1 -Y_2} \right) }\nonumber \\&\qquad {=F_{yL} \left( {X_1 ,Y_1 -Y_4} \right) -m_1 g} \nonumber \\&\quad {m_2 \ddot{X}_2 +c_2 \dot{X}_2 +k\left( {X_2 -X_3} \right) +k\left( {X_2 -X_1} \right) }\nonumber \\&\qquad {=m_2 e\omega ^{2}\cos \left( {\omega t} \right) } \nonumber \\&\quad {m_2 \ddot{Y}_2 +c_2 \dot{Y}_2 +k\left( {Y_2 -Y_3} \right) +k\left( {Y_2 -Y_1} \right) }\nonumber \\&\qquad {=m_2 e\omega ^{2}\sin \left( {\omega t} \right) -m_2 g} \nonumber \\&\quad {m_3 \ddot{X}_3 +c_3 \dot{X}_3 +k\left( {X_3 -X_2} \right) =F_{xR} \left( {X_3 ,Y_3} \right) } \nonumber \\&\quad {m_3 \ddot{Y}_3 +c_3 \dot{Y}_3 +k\left( {Y_3 -Y_2} \right) =F_{yR} \left( {X_3 ,Y_3} \right) -m_3 g} \nonumber \\&\quad {m_4 \ddot{Y}_4 +c_s \dot{Y}_4 +k_s Y_4} \nonumber \\&\qquad {=-F_{yL} \left( {X_1 ,Y_1 -Y_4} \right) -m_4 g} \end{aligned}$$

(1)

$$\begin{aligned} k_s= & {} \left\{ {{ \begin{array}{l} {k_{s1} \left( {Y_4 >\delta _1} \right) } \\ {0 \;\left( {0\le Y_4 \le \delta _1} \right) } \\ {k_{s2} \left( {Y_4 <0} \right) } \\ \end{array}}} \right. \quad c_s =\left\{ {{ \begin{array}{l} {c_{s1} \left( {Y_4 >\delta _1} \right) } \\ {0 \;\left( {0\le Y_4 \le \delta _1} \right) } \\ {c_{s2} \left( {Y_4 <0} \right) } \\ \end{array}}} \right. \end{aligned}$$

(2)

$$\begin{aligned} F_x= & {} \sum _{i=1}^{N_b} {C_b \left( {x\sin \theta _i +y\sin \theta _i -r_0} \right) } ^{3/2}\cdot H\left( x\sin \theta _i \right. \nonumber \\&\left. {}+y\sin \theta _i -r_0 \right) \cos \theta _i \nonumber \\ F_y= & {} \sum _{i=1}^{N_b} {C_b \left( {x\sin \theta _i +y\sin \theta _i -r_0} \right) } ^{3/2}\cdot H\left( x\sin \theta _i \right. \nonumber \\&\left. {}+y\sin \theta _i -r_0 \right) \sin \theta _i \end{aligned}$$

(3)

$$\begin{aligned} \theta _i= & {} \omega _1 \times t+\frac{2\pi }{N_b}\left( {i-1} \right) , i=1,2,\ldots ,N_b .\nonumber \\ \omega _1= & {} \omega \times \frac{r}{R+r}. \quad \omega _2 =\omega _1 \times N_b \end{aligned}$$

(4)

In the above equations, each parameter represents as follows:

Fig. 1

Rotor model with pedestal looseness at one end

$m_1 , m_3$: lumped mass of rotor in the left and right bearing. $m_2$: equivalent mass of rotor in the disk.

$m_4$: mass of pedestal looseness. $H\left( \cdot \right)$: Heaviside function. $C_b$: Hertz contact stiffness.

$c_1 , c_2 , c_3$: damping coefficient of rotor in the left bearing, disk and right bearing. k: stiffness of elastic shaft.

R: outer raceway radius. r: inner raceway radius. $\theta _i$: angle position of the ith ball. $\omega$: rotation speed.

$\omega _1$: cage speed. $\omega _2$: frequency of ball passes. $k_s , c_s$: support stiffness and damp. e: eccentricity.

$\delta _1$: maximum of loosing clearance. c: bearing clearance. $o_1 , o_4$: geometric centers of the left and right bearings. $o_2$: geometric center of the disk. $o_3$: center of gravity.

The values of detailed parameters are expressed as:

$$\begin{aligned}&k=2\times 10^{7}\,\hbox {N/m}, m_1 =m_3 =4\,\hbox {kg}, m_2 =30\,\hbox {kg},\\&m_4 =50\,\hbox {kg}, \delta =0.55\,\hbox {mm}, e=0.01\,\hbox {mm}, c=0.005\,\hbox {mm} \\&k_{s1} =7\times 10^{7}\,\hbox {N/m}, k_{s2} =2\times 10^{9}\,\hbox {N/m},\\&\hbox {c}_{s1} =350\,\hbox {N} \,\hbox {s/m},\hbox {c}_{s2} =350\,\hbox {N} \,\hbox {s/m}, \\&c_1 =c_3 =1050\,\hbox {N} \,\hbox {s/m}\; c_2 =2100\,\hbox {N} \,\hbox {s/m},\\&R=40\,\hbox {mm}, r=64\,\hbox {mm}, \\&N_b =8, C_b =13.3\times 10^{9}\,\hbox {N/m} \end{aligned}$$

By nondimensionalizing Eq. (1), the dimensionless form can be obtained, and the dimensionless transformation and the equation are expressed as:

$$\begin{aligned}&\tau =\omega t, x_i =\frac{X_i}{c}, y_i =\frac{Y_i}{c}, \dot{x}_i =\frac{\hbox {d}x_i}{\hbox {d}\tau }, \dot{y}_i =\frac{\hbox {d}y_i}{\hbox {d}\tau },\nonumber \\&\ddot{x}_i =\frac{\hbox {d}\dot{x}_i}{\hbox {d}\tau }, \ddot{y}_i =\frac{\hbox {d}\dot{y}_i}{\hbox {d}\tau } \nonumber \\&f_{x_1} =\frac{F_{xL}}{m_1 c\omega ^{2}}, f_{y_1} =\frac{F_{yL}}{m_1 c\omega ^{2}}, f_{x_2} =\frac{F_{xR}}{m_3 c\omega ^{2}},\nonumber \\&f_{y_2} =\frac{F_{yR}}{m_3 c\omega ^{2}}, f_{y_s} =\frac{F_{yL}}{m_4 c\omega ^{2}} \nonumber \\&\ddot{x}_1 +\frac{c_1}{m_1 \omega }\dot{x}_1 +\frac{k}{m_1 \omega ^{2}}\left( {x_1 -x_2} \right) =f_{x_1} \left( {x_1 ,y_1 -y_4} \right) \nonumber \\&\ddot{y}_1 +\frac{c_1}{m_1 \omega }\dot{y}_1 +\frac{k}{m_1 \omega ^{2}}\left( {y_1 -y_2} \right) \nonumber \\&\quad =\,f_{y_1} \left( {x_1 ,y_1 -y_4} \right) -\frac{g}{\omega ^{2}c}\nonumber \\&\ddot{x}_2 +\frac{c_2}{m_2 \omega }\dot{x}_2 +\frac{k}{m_2 \omega ^{2}}\left( {x_2 -x_3} \right) \nonumber \\&\quad \, +\,\frac{k}{m_2 \omega ^{2}}\left( {x_2 -x_1} \right) =\frac{e}{c}\cos \tau \nonumber \\&\ddot{y}_2 +\frac{c_2}{m_2 \omega }\dot{y}_2 +\frac{k}{m_2 \omega ^{2}}\left( {y_2 -y_3} \right) \nonumber \\&\quad \, +\,\frac{k}{m_2 \omega ^{2}}\left( {y_2 -y_1} \right) =\frac{e}{c}\sin \tau -\frac{g}{\omega ^{2}c}\nonumber \\&\ddot{x}_3 +\frac{c_3}{m_3 \omega }\dot{x}_3 +\frac{k}{m_3 \omega ^{2}}\left( {x_3 -x_2} \right) =f_{x_2} \left( {x_3 ,y_3} \right) \nonumber \\&\ddot{y}_3 +\frac{c_3}{m_3 \omega }\dot{y}_3 +\frac{k}{m_3 \omega ^{2}}\left( {y_3 -y_2} \right) =f_{y_2} \left( {x_3 ,y_3} \right) -\frac{g}{\omega ^{2}c}\nonumber \\&\ddot{y}_4 +\frac{c_s}{m_4 \omega }\dot{y}_4 +\frac{k_s}{m_4 \omega ^{2}}y_4 =-f_{y_s} \left( {x_1 ,y_1 -y_4} \right) -\frac{g}{\omega ^{2}c}\nonumber \\ \end{aligned}$$

(5)

3 Mode energy analysis based on modified POD method

In this section, the mode energy analysis method is applied to estimate the number of DOFs of the reduced system. Compared with the traditional POD method [18–20], the modified one is more efficient for the multi-DOFs rotor-bearing system. The basic construction process of the modified POD method can be expressed as follows: obtaining a set of POMs by utilizing POD from the transient process of the system, taking the first two orders of the POMs to form the projection space and projecting original system onto this space. Nevertheless, the traditional POD method considers to be the steady process of the system. The transient time series contain the forced and free vibration information, involving more dynamical characteristics than the steady time series with only forced vibration information. Based on the modified POD method, the reduced system reserves the bifurcation and the amplitude–frequency characters of the original one, and the relative error of this method is less than 5%. However, the reduced system loses most of the dynamical characteristics of the original one based on the traditional POD method [16, 17].

We apply the modified POD method to reduce the original system, and then we calculate the eigenvalues of the covariance matrix and confirm the first few POMs associated with the first few largest POVs to occupy the energy percentage of all nonnegative POVs, i.e., the physical interpretation of POM energy in the vibration is applied [21–26]. The mathematical construction process of the modified POD method is introduced particularly in ref. [16].

For the time history of $x_3$ shown in Fig. 2, the modified POD method is applied to truncate the transient process of the system. Lu et al. applied this method in 23-DOFs rotor system with pedestal looseness successfully and verified the efficiency of the method in ref. [16]. What is more, he explained the physical interpretation of the truncation of the transient process [17].

Fig. 2

Time history of $x_3$ under initial conditions when $\omega =1250\left( {\hbox {rad}/\hbox {s}} \right)$

Given the initial conditions that the integral step is $\pi /256$, the displacement and the velocity are $x_3 =y_3 =0.5, x_i =y_i =y_4 =0 \;(i=1,\hbox {2}), \dot{x}_i =\dot{y}_i =\dot{y}_4 =0.001\left( {i=1,\hbox {2}} \right)$ and $\omega =1250\left( {\hbox {rad}/\hbox {s}} \right)$. As is shown in Fig. 2, the horizontal ordinate time history of the right bearing is provided. If $\tau$ in formula (5) is selected between 0 and 30$\pi$, the system is the transient process, and the system is in the periodic motion state after $30\pi$. According to the POM algorithm of section 2.2 in ref. [16], the coordinate transformation matrix utilized the signal of the transient process to gain is:

$$\begin{aligned} V=10^{-2}\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {-0.001}&{} {65.03}&{} {-5.820}&{} {39.01}&{} {-0.002}&{} {-0.090}&{} {64.93} \\ {-0.002}&{} {26.78}&{} {43.50}&{} {-81.86}&{} {-0.003}&{} {-0.520}&{} {26.25} \\ \end{array}}} \right) ^{T} \end{aligned}$$

The POM associated with the largest POV is the optimal vector to characterize the ensemble of snapshots. The POM with the second largest POV restricted to the space orthogonal to the first POM is also the optimal vector to characterize the ensemble of snapshots, and so as follows. The energy contained in the data can be expressed by the POVs of the covariance matrix, i.e., the sum of the POVs, and the energy percentage captured by the kth POM is expressed as $\lambda _k /\sum _i {\lambda _i} \left( {\lambda _\mathrm{i} \ge 0} \right)$ [27].

For the model in Sect. 2, we choose the first and second POM associated with the largest POVs to observe the energy percentage captured by the POMs. Through numerical simulation, the transient time series displacement information of all DOFs was obtained in equal time interval, denoted by $x_1 (t),x_2 \left( t \right) ,\ldots ,x_m \left( t \right)$, where m is the number of DOF. We gain n equal time interval displacement series for each DOF, written as $x_i =\left( {x_i \left( {t_1} \right) ,x_i \left( {t_2} \right) ,\ldots ,x_i \left( {t_n} \right) } \right) ^{T}, i=1,\ldots ,m$, the time series form the matrix $X=\left[ {x_1 ,x_2 ,\ldots ,x_m} \right]$, and the order of X is $n\times m$. Thus, we get the correlation matrix $T=\frac{1}{n}X^{T}X$ with order of $m\times m$. The eigenvectors of the correlation matrix are $\varphi _1 ,\varphi _2,\ldots ,\varphi _m$, which are called POMs, and the corresponding eigenvalues are denoted by $\lambda _1 \ge \lambda _2 \ge \cdots \ge \lambda _m \ge 0$, referred as POVs. We calculate the sum of eigenvalues $\lambda _1 ,\lambda _2$ to get the energy of the first two POMs, and the energy is denoted by s as follows.

$$\begin{aligned} s=(\lambda _1 +\lambda _2 )\Big /\sum _{i=1}^m {\lambda _i} \end{aligned}$$

(6)

For the convenience of calculation, formula (5) is written as (7) briefly:

$$\begin{aligned} \ddot{Z}=-C\dot{Z}-KZ+F \end{aligned}$$

(7)

In formula (7), C is damping matrix, K is stiffness matrix and F is force vector, which includes Hertz contact force and external excitation force. Here, $Z=\left[ {z_1 z_2 \ldots z_7} \right] ^{T}$ corresponds to $[x_1 y_1 \ldots x_3 y_3 y_4 ]^{T}$ in the Eq. (5).

After utilizing nonlinear transient POD method to deal with the seven-DOFs rotor system with bearing loose, the transient process displacement information for each DOF is derived at the speed of $\omega =1250\left( {\hbox {rad}/\hbox {s}} \right)$, denoted by $z_1 \left( t \right) ,z_2 \left( t \right) ,\ldots ,z_7 \left( t \right)$; each DOF produces equal time interval displacement series with 7680 points, which can be written as the format $z_i =\left( {z_i \left( {t_1} \right) ,z_i \left( {t_2} \right) ,\ldots ,z_i \left( {t_{7680}} \right) } \right) ^{T}, i=1,\ldots ,7$, and these time series form the matrix $\Upsilon =\left[ {z_1 ,z_2 ,\ldots ,z_7} \right]$, and the order of $\Upsilon$ is $7680\times 7$. The correlation matrix is $T=\frac{1}{7}\Upsilon ^{T}\Upsilon$. The first two orders of the correlation matrix is V, the original model is reduced to two-DOFs model, and the energy $s=(\lambda _1 +\lambda _2 )/\sum _{i=1}^7 {\lambda _i} \approx 99.99\,\%$.

As is analyzed above, the first two POMs of the seven-DOFs rotor model occupy almost all the energy of the original system, and we reduce the original system to the two-DOFs one based on the modified POD method. The equation of the reduced model is expressed as formula (8).

$$\begin{aligned} \ddot{P}=-C_2 \dot{P}-K_2 P+F_2 \end{aligned}$$

(8)

When the damping matrix, stiffness matrix and the external excitation matrix are $C_2, K_2$ and $F_2$, respectively, the followings are the coefficients of the matrixes:

$$\begin{aligned} C_2= & {} \left( {{\begin{array}{l@{\quad }l} {c_{11}}&{} {c_{12}} \\ {c_{21}}&{} {c_{22}} \\ \end{array}}} \right) , K_2 =\left( {{\begin{array}{l@{\quad }l} {k_{11}}&{} {k_{12}} \\ {k_{21}}&{} {k_{22}} \\ \end{array}}} \right) ,\\ F_2= & {} \left( {{\begin{array}{lll} {f_1 +f_{\omega 1} +g_1} \\ {f_2 +f_{\omega 2} +g_2} \\ \end{array}}} \right) . \end{aligned}$$

These parameters are given in Appendix 1.

4 Efficiency of order reduction method

In order to show the efficiency of the modified order reduction method, this section highlights the dynamical behaviors of the original system and the reduced system. We therefore analyze the phase portraits, trajectories of orbit of shaft center, bifurcations diagrams and amplitude–frequency curves. Comparison of the original system with the reduced system shows that the reduced system preserves the dynamical topological structures of the original system by applying the modified POD method.

As is shown in Figs. 3 and 4, they reflect the comparison of the phase portraits and trajectories of orbit of shaft center between the original system and the reduced one. On the one hand, the comparison shows that the reduced system reserves the dynamical characteristics of the original system. On the other hand, it verifies the efficiency of order reduction method.

Fig. 3

Phase portraits of shaft center $o_2 (\bar{{o}}_2)$ for the original and reduced system when $\omega =1250\left( {\hbox {rad}/\hbox {s}}\right)$. a Phase portrait of shaft center $o_2$ for the original system. b Phase portrait of shaft center $\bar{{o}}_2$ for the reduced system

Fig. 4

Trajectories of orbit of shaft center of $o_2(\bar{{o}}_2 )$ for the original and reduced system when $\omega =1250\left( {\hbox {rad}/\hbox {s}} \right)$. a Trajectory of orbit of shaft center of $o_2$ for the original system. b Trajectory of orbit of shaft center of $\bar{{o}}_2$ for the reduced system

Figure 5a shows when $\omega \in \left( {0,876} \right)$, the system is in the state of periodic motion. The bifurcation occurs when $\omega =876$, and the system is in the region of complex motion when $\omega \in \left( {876,1032} \right)$. The jumping phenomenon arises when $\omega =1032$ and $\omega \in \left( {1068,1200} \right)$, complex motion occurs in the system. $\omega \in \left( {1200,1260} \right)$, inverse period-doubling bifurcation occurs. When $\omega \in \left( {1260,1392} \right)$, the system is in the state of periodic motion again. After $\omega =1392$, the system is in the complex motion once more. Figure 5b demonstrates that the bifurcation points and properties of the reduced system keep almost the same as the original system. The reduced system maintains primary bifurcation characteristics and topological structures of the original system. As a result, the bifurcation point can be found accurately by the modified POD method.

Similarly, as is shown in Fig. 6, by using the modified POD method, the reduced system reserves the amplitude–frequency character of the original system. Moreover, the reduced model basically retains the dynamical topological structures of the original model.

Fig. 5

Bifurcation diagrams. a Bifurcation diagram for the original system. b Bifurcation diagram for the reduced system

Fig. 6

Amplitude–frequency curves. a Amplitude–frequency curve for the original system. b Amplitude–frequency curve for the reduced system

From what has been discussed above, the reduced system maintains most of dynamical characteristics of the original system by applying the modified POD method, such as the phase portrait, trajectory of orbit of shaft center, bifurcation and amplitude–frequency characters.

5 Stability analysis

Based on the analysis above, the reduced system basically keeps the dynamical characteristics of the original system, so the reduced model is able to replace the original one to research the qualitative characters. In this section, we will study the stability of the two-DOFs reduced system to replace the seven-DOFs original system. We will introduce the HB-AFT method to dispose the equation of motion (8) and discuss the results of stability analysis.

5.1 Harmonic balance method

First, we change the form of formula (8) as (9), so as to apply the HB-AFT method. Equation (9) is expressed as:

$$\begin{aligned} \ddot{P}+C\dot{P}+KP=F\left( {\dot{P},P,\omega ,\tau } \right) \end{aligned}$$

(9)

where C is the damping matrix, K is the stiffness matrix, P is the displacement vector, $\omega$ is the rotating frequency, t is the time and $F\left( {\dot{P},P,\omega ,\tau } \right)$ is the vector containing all the efforts acting on the system. For simplicity, $F\left( {\dot{P},P,\omega ,\tau } \right)$ will be written as F.

We assume that the harmonic excitation causes a harmonic response [28], and $P\left( \tau \right)$ can be written as a Fourier series up to the uth term:

$$\begin{aligned} P\left( \tau \right) =B_0 +\sum _{k=1}^u {\left[ {B_k \cos (k\omega \tau )+A_k \sin (k\omega \tau )} \right] } \end{aligned}$$

(10)

Similarly, the forcing term F can also be expanded as a Fourier series:

$$\begin{aligned} F=C_0 +\sum _{k=1}^u {\left[ {C_k \cos (k\omega \tau )+D_k \sin (k\omega \tau )} \right] } \end{aligned}$$

(11)

The Fourier series representation of Eqs. (10) and (11) is put into Eq. (9), and the terms of same frequency are balanced. For the constant terms, the balance leads to

$$\begin{aligned} KB_0 =C_0 \end{aligned}$$

(12)

For the ith sine term, the result of the balance is

$$\begin{aligned} \left( {K+\omega ^{2}} \right) A_i -\left( {i\omega } \right) CB_i =D_i \end{aligned}$$

(13)

For the ith cosine term, the result of the balance is

$$\begin{aligned} -\left( {i\omega } \right) CA_i +\left( {K+\omega ^{2}} \right) B_i =C_i \end{aligned}$$

(14)

The following system of equations of order $\left( {4u+2} \right)$ is obtained by gathering all the harmonics together, which is expressed as:

$$\begin{aligned} \left[ {{\begin{array}{lllllll} K&{} &{} &{} &{} &{} \\ &{} {\Delta _1}&{} &{} &{} &{} \\ &{} &{} \ddots &{} &{} &{} \\ &{} &{} &{} {\Delta _i}&{} &{} \\ &{} &{} &{} &{} \ddots &{} \\ &{} &{} &{} &{} &{} {\Delta _u} \\ \end{array}}} \right] \left[ {{\begin{array}{l} {B_0} \\ {\Psi _1} \\ \vdots \\ {\Psi _i} \\ \vdots \\ {\Psi _u} \\ \end{array}}} \right] -\left[ {{\begin{array}{l} {C_0} \\ {\Lambda _1} \\ \vdots \\ {\Lambda _i} \\ \vdots \\ {\Lambda _u} \\ \end{array}}} \right] =0 \end{aligned}$$

(15)

where

$$\begin{aligned}&\Delta _i =\left( {{\begin{array}{l@{\quad }l} {K+\omega ^{2}}&{} {-\left( {i\omega } \right) C} \\ {\left( {i\omega } \right) C}&{} {K+\omega ^{2}} \\ \end{array}}} \right) \quad \Psi _i =\left( {{\begin{array}{l} {A_i} \\ {B_i} \\ \end{array}}} \right) \nonumber \\&\qquad \ \ \Lambda _i =\left( {{\begin{array}{l} {D_i} \\ {C_i} \\ \end{array}}} \right) \end{aligned}$$

(16)

$$\begin{aligned}&\left( {{\begin{array}{l} M \\ O \\ \end{array}}} \right) ^{T}=\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {B_0}&{} {B_1}&{} {A_1}&{} \cdots &{} {B_u}&{} {A_u} \\ {C_0}&{} {C_1}&{} {D_1}&{} \cdots &{} {C_u}&{} {D_u} \\ \end{array}}} \right) ^{T} \end{aligned}$$

(17)

where M and O represent the coefficients of harmonics of displacements and nonlinear restore forces, respectively.

Taking M as an unknown variable, using Eqs. (10–14), the fixed point M can be found by the iteration method. The Newton–Raphson method is applied for the iteration, which is

$$\begin{aligned} J^{(i)}\left( {M^{(i+1)}-M^{(i)}} \right) +h^{(i)} \end{aligned}$$

(18)

where J is the Jacobian matrix, $J=\partial h/\partial M$.

The values of O, J in each step of iteration could be obtained by the AFT technique after the process of harmonic balance. We apply inverse discrete Fourier transform method to obtain the discrete values of $P_x \left( \tau \right)$ and $P_y \left( \tau \right)$ based on a supposed M, which can be expressed as:

$$\begin{aligned} P\left( n \right)= & {} B_0 +\sum _{k=1}^u \left[ B_k \cos \left( {\frac{2\pi kn}{N}} \right) \right. \nonumber \\&\left. {}-A_k \sin \left( {\frac{2\pi kn}{N}} \right) \right] \end{aligned}$$

(19)

where $n=0, \ldots , N$. Here, $x\left( n \right) , y\left( n\right)$ denote the sampled points at the nth discrete time, that is to say, $x\left( {n\Delta T} \right) , y\left( {n\Delta T} \right)$ and $\Delta T=2\pi /N, where N$ is the number of samples in the time domain.

Based on the Eqs. (9) and (19), we discrete the nonlinear restoring force $F_x \left( {x,y,\tau } \right) ,F_y \left( {x,y,\tau } \right)$ into:

$$\begin{aligned} \left[ {\begin{array}{l} F_x (n) \\ F_y (n) \\ \end{array}} \right] =\left[ {\begin{array}{l} F_x (x\left( n \right) ,y(n),2\pi n/N) \\ F_y (x\left( n \right) ,y(n),2\pi n/N) \\ \end{array}} \right] \end{aligned}$$

(20)

The discrete values of $F_x \left( {x,y,\tau } \right) ,F_y \left( {x,y,\tau } \right)$ in frequency can be obtained to use the DFT as O, which is

$$\begin{aligned} C_0= & {} \frac{1}{N}\sum _{n=0}^{N-1} {\left[ {{\begin{array}{l} {F_x \left( n \right) } \\ {F_y \left( n \right) } \\ \end{array}}} \right] } \end{aligned}$$

(21)

$$\begin{aligned} C_k= & {} \frac{2}{N}\sum _{n=0}^{N-1} {\left[ {{\begin{array}{l} {F_x \left( n \right) } \\ {F_y \left( n \right) } \\ \end{array}}} \right] } \cos \left( {\frac{2\pi kn}{N}} \right) \end{aligned}$$

(22)

$$\begin{aligned} D_k= & {} \frac{2}{N}\sum _{n=0}^{N-1} {\left[ {{\begin{array}{l} {F_x \left( n \right) } \\ {F_y \left( n \right) } \\ \end{array}}} \right] } \sin \left( {\frac{2\pi kn}{N}} \right) \end{aligned}$$

(23)

where $k=1,\ldots u$.

By means of Eqs. (10–12), (19–23), the elements of Jacobian J in Eq. (18) can be deduced into:

$$\begin{aligned}&\frac{\partial C_{x0}}{\partial B_{x0}}=\frac{3}{2N}\bar{{C}}_b \sum _{n=0}^{N-1} {\sum _{i=1}^{N_b} {G\left( {\delta _i \left( n \right) } \right) ^{0.5}\cos ^{2}\bar{{\theta }}_{i,n}}} \nonumber \\&\frac{\partial C_{x0}}{\partial B_{y0}}=\frac{3}{2N}\bar{{C}}_b \sum _{n=0}^{N-1} {\sum _{i=1}^{N_b} {G\left( {\delta _i \left( n \right) } \right) ^{0.5}\sin \bar{{\theta }}_{i,n} \cos \bar{{\theta }}_{i,n}}} \nonumber \\&\qquad \qquad \qquad \qquad \vdots \nonumber \\&\frac{\partial D_{yk}}{\partial A_{xj}}=\frac{3}{N}\bar{{C}}_b \sum _{n=0}^{N-1} \sum _{i=1}^{N_b}\nonumber \\&\quad \times \,{\left[ {G\left( {\delta _i \left( n \right) } \right) ^{0.5}\sin \bar{{\theta }}_{i,n} \cos \bar{{\theta }}_{i,n}} \right] \sin \frac{2\pi jn}{N}\sin \frac{2\pi kn}{N}} \nonumber \\&\frac{\partial D_{yk}}{\partial A_{yj}}=\frac{3}{N}\bar{{C}}_b \sum _{n=0}^{N-1} \sum _{i=1}^{N_b}\nonumber \\&\quad \times \,\left[ {G\left( {\delta _i \left( n \right) } \right) ^{0.5}\cos ^{2}\bar{{\theta }}_{i,n}} \right] \sin \frac{2\pi jn}{N}\sin \frac{2\pi kn}{N} \end{aligned}$$

(24)

where $k,j=1,\ldots ,u, \bar{{\delta }}_i \left( n \right) =x\left( n \right) \cos \bar{{\theta }}_{i,n} +y\left( n \right) \sin \bar{{\theta }}_{i,n} -r_0 ,\bar{{\theta }}_{i,n} =2\pi \left( {i-1} \right) /N_b +2\pi n/N$.

M can be obtained by iterations of Eq. (18) in proper accuracy by combining the process of harmonic balance with AFT. For a supposed $M^{0}, O^{0}$ and $J^{0}$ are obtained from Eqs. (19), (21–23), (24); and iterating Eq. (18), we can get $M^{1}$; continue the two steps, until the norm of $M^{\left( m \right) }-M^{\left( {m-1} \right) }$ is less than an allowed $\varepsilon$.

5.2 Brief introduction to Floquet theory

For the stability analysis of the reduced piecewise linear system, we need to analyze the stability of periodic solutions obtained by HB-AFT so that to make a systematic study on the bifurcation characteristics of the system. In this research, the Floquet theory is employed [29], and the method proposed by Hsu is applied to approximate the monodromy matrix. Based on the characteristics of HB-AFT, the specific process to analyze the stability is studied in ref. [30], and a brief introduction is listed here.

Let $U=\left[ {x, x^{{\prime }}, y, y^{{\prime }}} \right] ^{T}=\left[ {p_1 , p_2 , p_3 , p_4} \right] ^{T}$, Eq. (9) can be transformed into

$$\begin{aligned} F\left( {\tau ,U\left( \tau \right) } \right) =U^{{\prime }}\left( \tau \right) \end{aligned}$$

(25)

And define $A\left( {\tau ,U\left( \tau \right) } \right)$as

$$\begin{aligned} A\left( {\tau ,U\left( \tau \right) } \right) =\frac{\partial F}{\partial U}=\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 0&{} 1&{} 0&{} 0 \\ {A_{21}}&{} {A_{22}}&{} {A_{23}}&{} 0 \\ 0&{} 0&{} 0&{} 1 \\ {A_{41}}&{} 0&{} {A_{43}}&{} {A_{44}} \\ \end{array}}} \right) \end{aligned}$$

(26)

where the parameters in Eq. (26) are expressed in Appendix 2.

Based on the Eq. (25), $\Delta U$ is given to perturb the assumed equilibrium $U^{*}$ and then get

$$\begin{aligned} \Delta U^{{\prime }}=F\left( {\tau ,U^{*}+\Delta U} \right) \end{aligned}$$

(27)

The stability of $U^{*}$ can be obtained by the linear stability of $\Delta U$ in the following system

$$\begin{aligned} \Delta U^{{\prime }}=\partial F\left( {\tau ,U^{*}} \right) {/}\partial U^{*}\cdot \Delta U=A\left( {\tau ,U^{*}\left( \tau \right) } \right) \Delta U \end{aligned}$$

(28)

In ref. [31], the approximating monodromy matrix is expressed as formula (29) according to Hsu’s method

$$\begin{aligned} \bar{{M}}= & {} \psi \left( T \right) =\prod _{n=N}^1 {\exp \left( {A_n \Delta T} \right) }\nonumber \\= & {} \prod _{n=N}^1 {\left( {I+\sum _{j=1}^{n_j} {\frac{\left( {A_n \Delta T} \right) ^{j}}{j!}}} \right) } \end{aligned}$$

(29)

In the nth time interval, substituting the time-varying matrix $A\left( {\tau ,U\left( \tau \right) } \right)$ with $A_n$, we can get the equation

$$\begin{aligned} A_n =\frac{1}{\Delta T}\int _{\tau _{n-1}}^{\tau _n} {A\left( {\tau ,U^{*}\left( \tau \right) } \right) } d\tau \end{aligned}$$

(30)

5.3 Results and discussion

The two-DOFs rotor-bearing system is shown in Eq. (9), and the parameters are presented in Sect. 2 and Appendix. Both the damping term C and the stiffness term K are piecewise linear. Similarly, the studied reduced system is a parametrical excited system, $T=2\pi /\omega$ is the excited period, and $\omega$ is the rotating angular velocity of balls. The harmonic terms, whose coefficients less than $\varepsilon$, are ignored and not presented as following. We assign $u=36$ [in Eq. (10)], $\omega =1250\left( {\hbox {rad}/\hbox {s}} \right) \varepsilon =10^{-18},N=144$ [in Eq. (19)]. The reduced model is a piecewise linear system, and the parameters of stiffness and damping are given in Appendix. The analytical approximation of the period-1 solution obtained by the HB-AFT method is:

$$\begin{aligned} x\left( t \right)= & {} 2.230126813\times 10^{-5} \\&+\,7.134694212\times 10^{-7}\cos \left( {\omega _2 t} \right) \nonumber \\&-\,6.213875901\times 10^{-8}\sin \left( {\omega _2 t} \right) \\&+\,4.315942659\times 10^{-8}\cos \left( {2\omega _2 t} \right) \\&-\,4.951881057\times 10^{-9}\sin \left( {2\omega _2 t} \right) \\&-\,2.474912408\times 10^{-9}\cos \left( {3\omega _2 t} \right) \\&-\,6.286192369\times 10^{-10}\sin \left( {3\omega _2 t} \right) \\&-\,8.922238611\times 10^{-11}\cos \left( {4\omega _2 t} \right) \\&+\,1.770234142\times 10^{-10}\sin \left( {4\omega _2 t} \right) \end{aligned}$$

where $\omega _2 =\frac{\omega r}{R+r}\cdot N_b$.

Figure 7 represents the phase portrait of the periodic-1 solution, and the four-order Runge–Kutta (R–K) method has a good agreement with the HB-AFT results. As is shown in Fig. 8, the horizontal and vertical ordinate is time and displacement, respectively, and the calculation based on the HB-AFT has a fast convergence rate and a large convergent region [in Eq. (29)]. In this figure, giving the initial iterative values $M^{\left( 0 \right) }=\left[ 0 \right]$ except $M^{\left( 0 \right) }\left( 1 \right) =1$, the HB-AFT goes through 5th iterative and arrives at a solution close to R–K integration corresponding to the fine line markers.

Fig. 7

Phase portrait of the periodic-1 solution when $\omega = 500\,\hbox {rad}/\hbox {s}$

Fig. 8

Convergence of HB-AFT results and R–K results

The HB-AFT method is used to analyze the global periodic characteristics of the system, taking $\omega$ as a control parameter and searching the periodic-1 solutions between 800 to $1280\,\hbox {rad}/\hbox {s}$ with a step size of $6\,\hbox {rad}/\hbox {s}$. The methods in Sects. 5.1 and 5.2 are applied to analyze the stability of the obtained period-1 solutions. The results in Sect. 4 have indicated that the reduced system reserves the dynamical characters of the original one. So we study the vibration properties of the looseness direction owns more complex movement form, which contains more bifurcation behaviors that can reflect the stability characteristics of the original system. Figure 9 shows that the leading multipliers are inside the unit circle at $\omega$  = 800–872 $\hbox {rad}/\hbox {s}$, and the periodic-1 solutions are stable. The corresponding periodic-1 solutions are unstable when $\omega$ changes from 880 to $1254\hbox {rad}/\hbox {s}$ and for the leading multipliers are less than $-1$. Until $\omega =1260\,\hbox {rad}/\hbox {s}$, the solutions change from unstable to stable, and the leading multipliers come back to unit circle from negative real axis. Table 1 further indicates that the bifurcation occurs when $\omega$ varies from 878 to $879\hbox {rad}/\hbox {s}$ and 1256 to $1257\hbox {rad}/\hbox {s}$, which is basically consistent with the numerical results in Fig. 9.

Fig. 9

Bifurcation diagrams versus parameter $\omega$ and the bifurcation locations of period-1 motion obtained by HB-AFT with Floquet theory

6 Conclusions

In this paper, the stability of the two-DOFs system reduced from the seven-DOFs pedestal looseness system has been analyzed. The method of POM energy analysis has been applied to confirm the number of DOF of the reduced system, and the modified POD method has been applied to reduce the original system to a two-DOFs one. It is shown that the reduced system reserves most dynamical characters of the original one. Finally, by combining the treatment of the HB-AFT method with the Floquet theory, the movement characteristics stability of the two-DOFs system is studied. Further studies on this subject are being carried out by the present authors in two aspects: One is to study the dynamical characters of the ball bearings deeply and the other is to lucubrate the singular bifurcation analysis of the reduced system.

Table 1 Leading multipliers of period-1 solutions in the velocity range of period-doubling bifurcation developing

Appendices

Appendix 1

$$\begin{aligned} G=\frac{g}{\omega ^{2}c}, M_1 =m_1 c\omega ^{2}, M_3 =m_3 c\omega ^{2}, M_4 =m_4 c\omega ^{2} \end{aligned}$$

$$\begin{aligned} k_{11}= & {} 10^{-7}\left( 1.5348\frac{k_1}{m_1}-0.88997\frac{k_1}{m_2 }+1.4140\frac{k_2}{m_2} \right. \\&-\,2.6370\times 10^{-6}\frac{k_2}{m_3}\hbox {+2.9447} \times \hbox {10}^{-5}\frac{k_3}{m_3} \\&\left. +\,3.8241\frac{k_s}{m_4}\right) \\ k_{12}= & {} 10^{-7}\left( 6.4076\frac{k_1}{m_1}-4.0730\frac{k_1}{m_2 }-3.1074\frac{k_2}{m_2} \right. \\&+\,1.9730\times 10^{-5}\frac{k_2}{m_3}+1.1909\times 10^{-5}\frac{k_3}{m_3}\\&\left. +\,1.5463\frac{k_s}{m_4}\right) \\ k_{21}= & {} 10^{-7}\left( 0.63198\frac{k_1}{m_1}+1.7027\frac{k_1}{m_2 }-3.1327\frac{k_2}{m_2} \right. \\&-\,2.2678\times 10^{-5}\frac{k_2}{m_3}\\&\left. +\,2.5325\times 10^{-4}\frac{k_3}{m_3}+1.5463\frac{k_s }{m_4}\right) \\ k_{22}= & {} 10^{-7}\left( 2.6385\frac{k_1}{m_1}+9.7827\frac{k_1 }{m_2} \right. \\&+\,7.7564\frac{k_2}{m_2}+1.6968\times 10^{-4}\frac{k_2}{m_3} \\&\left. +\,1.0242\times 10^{-4}\frac{k_3}{m_3}+0.62523\frac{k_s }{m_4}\right) \\ c_{11}= & {} \left( 0.42286\frac{c_1}{m_1}+0.15553\frac{c_2}{m_2 }+8.9684\times 10^{-7}\frac{c_3}{m_3} \right. \\&\left. +\,0.42160\frac{c_s}{m_4} \right) \\ c_{12}= & {} \left( 0.17412\frac{c_1}{m_1}-0.34460\frac{c_2}{m_2 }\right. \\&\left. +\,4.8792\times 10^{-6}\frac{c_3}{m_3}+0.17048\frac{c_s }{m_4} \right) \\ c_{21}= & {} \left( 0.17412\frac{c_1}{m_1}-0.34460\frac{c_2}{m_2}\right. \\&\left. +\,4.8792\times 10^{-6}\frac{c_3}{m_3}+0.17048\frac{c_s}{m_4} \right) \\ c_{22}= & {} \left( 0.71697\frac{c_1}{m_1}+0.85934\frac{c_2}{m_2} \right. \nonumber \\&\left. +\,2.6545\times 10^{-5}\frac{c_3}{m_3}+6.8932\times 10^{-2}\frac{c_s }{m_4} \right) \\ \end{aligned}$$

$$\begin{aligned} f_1= & {} -\frac{1.0045\times 10^{-6}}{M_1}f_{1x} +\frac{0.65028}{M_1 }f_{1y} \\&-\,\frac{5.0023\times 10^{-6}}{M_3}f_{2x} -\frac{9.4701\times 10^{-4}}{M_3}f_{2y} \\&-\,\frac{0.64931}{M_4}f_{sy} \\ f_2= & {} -\frac{2.5013\times 10^{-5}}{M_1}f_{1x} +\frac{0.26776}{M_1 }f_{1y} \\&-\,\frac{4.3012\times 10^{-5}}{M_3}f_{2x} -\frac{5.120\times 10^{-3}}{M_3}f_{2y} \\&-\,\frac{0.26255}{M_4}f_{sy} \\ f_{1x}= & {} f_x (-1.0013\times 10^{-6}p_1 \\&-\,2.5022\times 10^{-5}p_2 ,0.65028p_1 +0.26776p_2 \\&-\,1.0013\times 10^{-6}\dot{p}_1 \\&-\,2.5022\times 10^{-5}\dot{p}_2 ,0.65028\dot{p}_1 +0.26776\dot{p}_2 ) \\ f_{1y}= & {} f_y (-1.0013\times 10^{-6}p_1 \\&-\,2.5022\times 10^{-5}p_2 ,0.65028p_1 +0.26776p_2 \\&-\,1.0013\times 10^{-6}\dot{p}_1 \\&-\,2.5022\times 10^{-5}\dot{p}_2 ,0.65028\dot{p}_1 +0.26776\dot{p}_2 ) \\ f_{2x}= & {} f_x (-5.8151\times 10^{-2}p_1 \\&+\,0.43501p_2 ,0.39006p_1 -0.81860p_2 \\&-\,5.8151\times 10^{-2}\dot{p}_1 \\&+\,0.43501\dot{p}_2 ,0.39006\dot{p}_1 -0.81860\dot{p}_2 ) \\ f_{2y}= & {} f_y (-5.8151\times 10^{-2}p_1 \\&+\,0.43501p_2 ,0.39006p_1 -0.81860p_2 \\&-\,5.8151\times 10^{-2}\dot{p}_1 \\&+\,0.43501\dot{p}_2 ,0.39006\dot{p}_1 -0.81860\dot{p}_2 ) \\ f_{sy}= & {} f_y (-5.0012\times 10^{-6}p_1 -4.3024\times 10^{-5}p_2, \\&-\,9.4733\times 10^{-4}p_1 -5.1520\times 10^{-3}p_2 \\&-\,5.0012\times 10^{-6}\dot{p}_1 -4.3024\times 10^{-5}\dot{p}_2, \\&-\,9.4733\times 10^{-4}\dot{p}_1 -5.1520\times 10^{-3}\dot{p}_2 ) \\ g_1= & {} -1.68866G,\hbox {g}_2 =0.29344G \\ f_{\omega 1}= & {} -0.0581516b\cos \tau +0.39006b\sin \tau , \\&f_{\omega 2} =0.43501b\cos \tau -0.81860\sin \tau \end{aligned}$$

Appendix 2

$$\begin{aligned} A_{21}= & {} -\frac{3C}{2}\sum _{i=1}^{N_b} {G\left( {\delta _i \left( n \right) } \right) ^{0.5}\cos ^{2}\bar{{\theta }}_{i,n}} , \\ A_{22}= & {} A_{44} =-C, \\ A_{23}= & {} A_{41} =-\frac{3C}{2}\sum _{i=1}^{N_b} {G\left( {\delta _i \left( n \right) } \right) ^{0.5}\sin \bar{{\theta }}_{i,n} \cos \bar{{\theta }}_{i,n}} \\ A_{43}= & {} -\frac{3C}{2}\sum _{i=1}^{N_b} {G\left( {\delta _i \left( n \right) } \right) ^{0.5}\sin ^{2}\bar{{\theta }}_{i,n}} . \end{aligned}$$