1 Introduction

Improving high speed and high efficiency of turbo-machines may be achieved by reducing the rotor-stator clearance. As a result, rub-impact between rotatory and stationary components becomes one of the main serious malfunctions that often occur in rotating machinery. Therefore, the need for understanding the rub-impact phenomenon is important to engineers for the purpose of fault diagnosis.

Usually, rub-impact faults belong to secondary faults with apparent coupling faults’ characteristics, which may result from the unbalance, misalignment, pedestal looseness, thermal failure and oil whirl [1, 2]. When rub-impact happens, highly complex nonlinear dynamic behaviours possibly appear, including not only periodic (synchronous and non-synchronous) components but also quasi-periodic and chaotic motions, even in the case of very simple rotor [3].

Rub-impact shows a very complicated vibration phenomenon. According to the rubbing components, it can be divided into two classes: blades to casing [4, 5] and rotor to stator [6–9]. Due to the contact area in the rub-impact fault of rotor-stator, it can also be classified as fixed-point rubbing, partial rubbing, full annular rubbing [10, 11]. Rub-impact in a rotating assembly has attracted great concerns from researchers, and numerous articles on the topic of unfixed-point rubbing have been published. Based on the chaos and bifurcation theory, Chu et al. [12] investigated periodic, quasi-periodic and chaotic motion of a Jeffcott rotor system with rub-impact fault. Zhang et al. [13] set up a general model for a Jeffcott microrotor system with rub-impact based on the classic impact theory. Meanwhile, an investigation was carried out on the stability of the rub solutions and the transition among periodic, quasi-periodic and chaotic responses [13]. Yuan et al. [14] developed a full-degree-of-freedom dynamic model for a Jeffcott rotor with unbalances and axial rub-impact. In addition, the effect of the radial rub-impact on the responses of mass unbalance was investigated comprehensively [14]. The above works all adopt the simple Jeffcott rotor model, which is obviously different from the actual rotor system. In the research on the actual rotor system, the finite element (FE) method [15] and the transfer matrix method [9] are the main methods. Nelson et al. [16] established a dynamic model of rotor-bearing system, which consisted of rigid discs, distributed finite rotor elements and discrete bearings, by using the FE method. Based on the model, the natural whirl speeds and unbalance response of a typical overhung system were analysed [16]. Due to rotor-stator contact, Chen et al. [17] investigated the nonlinear transient response of a finite element model for a rotor system. Behzad et al. [18] developed an algorithm for more realistic investigation of rotor-stator rubbing vibration based on the finite element theory with unilateral contact and frictional conditions, and then the synchronous and subsynchronous responses of the partial rubbing were obtained.

Convex point may exist in aero-engine casing because of thermal deformation, external suspension and so on. Under this circumstance, the fixed-point rub-impact fault between rotor and convex point may occur. However, as another rubbing form, fixed-point rubbing has not been deeply investigated compared with unfixed-point rubbing. Aiming at a test rig with dual discs, Han et al. [19] presented a rotor system by using the FE method, in which two rub-impacts might happen at two fixed limiters, respectively. The typical multi-periodic characteristics of fixed rubbing were obtained by numerical simulation and experiment [19]. Ma et al. [20] investigated the vibration features of a single span rotor system with two discs, when the rub-impact between a disc and an elastic rod occurred. In [20], the augmented Lagrange method was employed to deal with contact constraint conditions and the Coulomb frictional model was used to simulate rotor-stator frictional characteristics. Lahriri et al. [21] designed a new unconventional backup bearing to study the fixed-point rub-impact fault. Tai et al. [22] investigated the stability and steady-state response of a rotor system with fixed-point rubbing using lumped mass method.

Fig. 1
figure 1

Schematic diagram of a dual-disc cantilever rotor system

Full size image

In the above literatures, the mechanical mechanism of the rotor-stator rub-impact, including unfixed-point rub-impact and fixed-point rub-impact, is mostly described by the piecewise linear force model [23] and the Coulomb frictional model [24]. However, as a key parameter, the impact stiffness in the piecewise linear force model is given only by engineering experience. In most of work, it is treated as the structural stiffness of casing [25]. For actual aero-engine, coating is applied to increase the component service life, which is to coat the component with a layer of special material [26]. When rub-impact with coating happens, the local contact stiffness of coating may be far less than the structural stiffness of casing. In this condition, the piecewise linear force model may not be suitable. Many researchers have studied the influences of sensitive parameters on the nonlinear dynamic characteristics of the rotor system, such as rotating speed [27, 28], unbalance [29], support stiffness [30]. However, to our knowledge, very few papers focus on the characteristics of the casing convex point. Actually, for the various characteristics of the casing convex point, the impact stiffness between rotor and convex point is changed rather than constant. In other words, the impact stiffness is determined by the physical parameters of the convex point, including convexity, sharpness and material property. Hence, the effect of the casing convex point on the dynamic responses of the rotor system should be taken into account in the design of aero-engine. The investigation of the rotor system with casing convex point is of practical significance to the understanding of the dynamic characteristics of turbo-machines.

In this paper, a dual-disc rotor model, which consists of a cantilever rotor, two discs and two supports, is taken into consideration. The finite element (FE) method is employed to establish the corresponding dynamic equations. The rub-impact forces between two discs and two casing convex points are yielded by the Lankarani–Nikravesh model [31] and the Coulomb frictional model [24]. To determine the initial impact velocity, the linear interpolation method is put forward in the numerical simulation. Subsequently, the Runge–Kutta method and the linear interpolation method are utilized to calculate the dynamic responses of the rotor system, which are represented in bifurcation diagrams, waveforms, whirl orbits, Poincaré maps and frequency spectrums. Finally, the influences of the model parameters on the dynamic responses of the rotor system are investigated, such as rotating speed, phase difference of unbalances, casing convex point and initial clearance.

2 Dynamic model of a rotor system with rub-impact

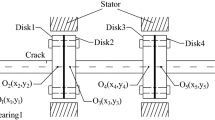
Consider a rotor model which consists of two discs, rotor segments with distributed masses and elastic characteristics, and two supports, as shown in Fig.1. Due to the complicated external suspension, such as fuel tank, cooler bin, pipeline, the convex point is more likely to appear in the vertical direction of casing. Under this engineering circumstance, two convex points are set in the vertical direction of casing in this paper. Meanwhile, in order to study conveniently, the following simplifications are made as follows

  1. (1)

    The compressor disc and turbine disc are rigid and mounted in the both ends of the flexible shaft.

  2. (2)

    The shaft is modelled by an Euler beam, and the two discs are assumed to be two lumped masses.

  3. (3)

    The supports are ideally modelled by linear springs and viscous dampers.

  4. (4)

    All the softer coatings painted on the surfaces of the rotor system are same.

  5. (5)

    The structural deformation of casing is negligible, and only the local deformation of surface coatings is taken into account.

  6. (6)

    The mass eccentricity of the compressor disc is equal to that of the turbine disc, and the phase angles between two unbalance forces may be the same or not.

  7. (7)

    The initial clearances between discs (compressor disc and turbine disc) and convex points (convex point 1 and convex point 2) are the same.

  8. (8)

    The thermal effects and frictional torque in rub-impact are not considered.

  9. (9)

    The origin of the coordinate system (\(o-xyz\)) locates at the centre of the compressor disc.

2.1 Rub-impact force models

In this research, two fixed elastic limiters are used to describe the convex point 1 and convex point 2 shown in Fig. 1. Due to the whirling of the rotor system caused by the eccentric excitation, rub-impact may happen at a single convex point or two convex points. The impact form is treated as a point-point contact, as shown in Fig. 2, where t and \(t^{*}\) are the initial moment and the rubbing moment, respectively.

Fig. 2
figure 2

Rub-impact force model for the disc-fixed limiter

Full size image

For the low pressure rotor system of aero-engine, the softer coating is painted on the surfaces of discs and casing. Generally, the local stiffness of soft coating is far less than the structural stiffness of casing. According to the reference [32], for the rub-impact with softer coating, the impact stiffness is dominated by the local contact stiffness of coating rather than the structural stiffness of casing. In this condition, the mechanical mechanism of rub-impact with softer coating is hardly characterized by the piecewise linear force model. On the basis of the work mentioned in [32], the Lankarani–Nikravesh force model, which is an improved model of the Hertz model, is proved to be suitable to solve this kind of rub-impact. Meanwhile, the Coulomb model is applied to simulate the frictional characteristics. Therefore, when rub-impact happens, the radial impact force \(F_\mathrm{N}\) and the tangential frictional force \(F_\mathrm{T}\) can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{l} F_\mathrm{N} =-H\left( {y-\delta _0 } \right) k_\mathrm{h} y^{\frac{3}{2}}\left[ {1+\frac{3\left( {1-c_\mathrm{e}^{2} } \right) \dot{y}}{4\dot{y}^{-}}} \right] , \\ F_\mathrm{T} =F_\mathrm{N} \mu , \\ \end{array}} \right. \end{aligned}$$
(1)

where y and \(\dot{y}\) are the vertical displacement and velocity of disc, \(\delta _0 \) is the initial clearance between disc and fixed limiter, \(c_\mathrm{e} \) is the coefficient of restitution, \(\dot{y}^{-}\) is the initial impact velocity, \(\mu \) is the frictional coefficient.

The Hertz contact stiffness \(k_\mathrm{h} \) is

$$\begin{aligned} k_\mathrm{h} =\frac{4}{3\left( {\frac{1-\nu _1^2 }{E_1 }+\frac{1-\nu _2^2 }{E_2 }} \right) }\left( {\frac{R_1 R_2 }{R_1 +R_2 }} \right) ^{\frac{1}{2}}, \end{aligned}$$
(2)

where \(\nu _1 \) and \(\nu _2 \) are the Poisson ratio of coatings painted on disc and casing, \(E_1 \) and \(E_2 \) are the elastic modulus of coatings painted on disc and casing, \(R_1 \) and \(R_2 \) are the curvature radii of disc and convex point.

The Heaviside function in Eq. (1) is written as

$$\begin{aligned} H\left( {y-\delta _0 } \right) =\left\{ {\begin{array}{l} 0 \qquad y<\delta _0 , \\ 1 \qquad y \ge \delta _0 . \\ \end{array}} \right. \end{aligned}$$
(3)

2.2 Finite element (FE) formulation

The dual-disc rotor system can be divided into rigid discs, rotor segments and linear supports, as shown in Fig. 3. Segments 1 and 5 are discs, the nodes between segments 2 and 3, segments 3 and 4, are the support locations, and two eccentricities exist in segments 1 and 5, respectively.

Fig. 3
figure 3

Rotor-support system elements

Full size image

Figure 4a shows a two-node Euler shaft element with eight degrees of freedom, in which the local coordinate system is regarded as the same as the original coordinate system in a simple way. Therefore, the generalized displacement vector of the shaft element can be expressed as

$$\begin{aligned} u_\mathrm{b}^\mathrm{e} =\left\{ {x_\mathrm{A} \,\,\theta _{y\mathrm{A}} \,\,x_\mathrm{B} \,\,\theta _{y\mathrm{B}} \,\,y_\mathrm{A} \,\,\theta _{x\mathrm{A}} \,\,y_\mathrm{B} \,\,\theta _{x\mathrm{B}} } \right\} ^{\mathrm{T}}, \end{aligned}$$
(4)

where \(x_\mathrm{A} \) and \(y_\mathrm{A} \) denote two translations at node A, \(\theta _{x\mathrm{A}} \) and \(\theta _{y\mathrm{A}} \) denote two rotations at node A, \(x_\mathrm{B} \) and \(y_\mathrm{B} \) denote two translations at node B, \(\theta _{x\mathrm{B}} \) and \(\theta _{y\mathrm{B}} \) denote two rotations at node B, respectively.

Fig. 4
figure 4

Schematic diagram of discrete elements. a Euler beam element. b Disc element

Full size image

According to the finite element theory, the displacements (translation and rotation) of an arbitrary cross section in the shaft element can be described by the product of its nodal displacements and shape functions. The mass, gyroscopic and stiffness matrices of the shaft element can be expressed as

$$\begin{aligned} {{\varvec{M}}}_\mathrm{b}^\mathrm{e}= & {} \frac{m_\mathrm{b} l_\mathrm{b} }{420}\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {156}&{} {22l_\mathrm{b} }&{} {54}&{} {-13l_\mathrm{b} } \\ {22l_\mathrm{b} }&{} {4l_\mathrm{b} ^{2}}&{} {13l_\mathrm{b} }&{} {-3l_\mathrm{b} ^{2}} \\ {54}&{} {13l_\mathrm{b} }&{} {156}&{} {-22l_\mathrm{b} } \\ {-13l_\mathrm{b} }&{} {-3l_\mathrm{b} ^{2}}&{} {-22l_\mathrm{b} }&{} {4l_\mathrm{b} ^{2}} \\ \end{array} }} \right] \nonumber \\&+\,\frac{m_\mathrm{b} (R^{2}+r^{2})}{120l_\mathrm{b} }\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {36}&{} {3l_\mathrm{b} }&{} {-36}&{} {3l_\mathrm{b} } \\ {3l_\mathrm{b} }&{} {4l_\mathrm{b} ^{2}}&{} {-3l_\mathrm{b} }&{} {-l_\mathrm{b} ^{2}} \\ {-36}&{} {-3l_\mathrm{b} }&{} {36}&{} {-3l_\mathrm{b} } \\ {3l_\mathrm{b} }&{} {-l_\mathrm{b} ^{2}}&{} {-3l_\mathrm{b} }&{} {4l_\mathrm{b} ^{2}} \\ \end{array} }} \right] , \nonumber \\ \end{aligned}$$
(5)
$$\begin{aligned} {{\varvec{J}}}_\mathrm{b}^\mathrm{e}= & {} \frac{m_\mathrm{b} (R^{2}+r^{2})}{60l_\mathrm{b} }\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {36}&{} {3l_\mathrm{b} }&{} {-36}&{} {3l_\mathrm{b} } \\ {3l_\mathrm{b} }&{} {4l_\mathrm{b} ^{2}}&{} {-3l_\mathrm{b} }&{} {-l_\mathrm{b} ^{2}} \\ {-36}&{} {-3l_\mathrm{b} }&{} {36}&{} {-3l_\mathrm{b} } \\ {3l_\mathrm{b} }&{} {-l_\mathrm{b} ^{2}}&{} {-3l_\mathrm{b} }&{} {4l_\mathrm{b} ^{2}} \\ \end{array} }} \right] , \nonumber \\\end{aligned}$$
(6)
$$\begin{aligned} {{\varvec{K}}}_\mathrm{b}^\mathrm{e}= & {} \frac{EI}{l_\mathrm{b}^\mathrm{3} }\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {12}&{} {6l_\mathrm{b} }&{} {-12}&{} {6l_\mathrm{b} } \\ {6l_\mathrm{b} }&{} {4l_\mathrm{b}^2 }&{} {-6l_\mathrm{b} }&{} {2l_\mathrm{b}^\mathrm{2} } \\ {-12}&{} {-6l_\mathrm{b} }&{} {12}&{} {-6l_\mathrm{b} } \\ {6l_\mathrm{b} }&{} {2l_\mathrm{b}^\mathrm{2} }&{} {-6l_\mathrm{b} }&{} {4l_\mathrm{b}^\mathrm{2} } \\ \end{array} }} \right] , \end{aligned}$$
(7)

where \({{\varvec{M}}}_\mathrm{b}^\mathrm{e} \) includes the translational inertial matrix and rotational inertial matrix, \(l_\mathrm{b} , E\) and I are the length of shaft element, elastic modulus, and the cross initial moment of shaft element, respectively.

The shaft mass per unit length obeys

$$\begin{aligned} m_\mathrm{b} =\rho _\mathrm{b} \pi \left( {R^{2}-r^{2}} \right) , \end{aligned}$$
(8)

where R and r are the outer and inner radii of the cross section of the shaft, respectively.

For a typical rotor disc shown in Fig. 4b, the strain energy is neglected in view of the rigid body assumption, and it can be modelled as a four-degree-of-freedom element. The generalized displacement vector of the disc is written as

$$\begin{aligned} u_\mathrm{d}^\mathrm{e} =\left\{ {x_\mathrm{d} \,\,\theta _{y\mathrm{d}} \,\,y_\mathrm{d} \,\,\theta _{x\mathrm{d}} } \right\} ^{\mathrm{T}}, \end{aligned}$$
(9)

where \(x_\mathrm{d} \) and \(y_\mathrm{d} \) denote two translations of disc element, \(\theta _{x\mathrm{d}} \) and \(\theta _{y\mathrm{d}} \) denote two rotations of disc element.

For the disc element, the mass and gyroscopic matrices are derived by using Lagrange equation, namely

$$\begin{aligned} M_\mathrm{d}^\mathrm{e}= & {} \left[ {{\begin{array}{l@{\quad }l} {m_\mathrm{d} }&{} 0 \\ 0&{} {J_{\mathrm{dd}} } \\ \end{array} }} \right] , \end{aligned}$$
(10)
$$\begin{aligned} J_\mathrm{d}^\mathrm{e}= & {} \left[ {{\begin{array}{l@{\quad }l} 0&{} \quad 0 \\ 0&{} \quad {J_{\mathrm{dp}} } \\ \end{array} }} \right] , \end{aligned}$$
(11)

where \(m_\mathrm{d} , J_{\mathrm{dd}} \) and \(J_{\mathrm{dp}} \) are the mass, diametric inertial moment and polar inertial moment of the disc.

2.3 Global equation of motion

The global equation of motion of the dual-disc rotor system is obtained after assembling all the elements shown in Fig. 3. For the state variable \(u=\left\{ x_1 ,\theta _{y1} ,y_1 ,\theta _{x1} \ldots x_\mathrm{n} ,\theta _{y\mathrm{n}} ,y_\mathrm{n} ,\theta _{x\mathrm{n}} \right\} ^{\mathrm{T}}\) of size \(4\hbox {n}, \hbox {n}=4\), which is the total number of degrees of freedom of the system, the equation of motion is

$$\begin{aligned} {{\varvec{M}}}\ddot{{\varvec{u}}}+{{\varvec{C}}}\dot{{\varvec{u}}}+{{\varvec{Ku}}}={{\varvec{Q}}}, \end{aligned}$$
(12)

where \({{\varvec{M}}}\), \({{\varvec{C}}}\) and \({{\varvec{K}}}\) denote mass, damping (including gyroscopic term and support damping) and stiffness (including rotor and support stiffness) matrices, respectively. The dynamics model developed here has two to four sources of excitation \({{\varvec{Q}}}\), including

  1. (1)

    Unbalance excitation of the compressor disc;

  2. (2)

    Unbalance excitation of the turbine disc;

  3. (3)

    Probable rub-impact force at the casing convex point 1;

  4. (4)

    Probable rub-impact force at the casing convex point 2.

3 Numerical results and discussions

Because the initial impact velocity is a key factor for the impact force \(F_\mathrm{N} \), a linear interpolation method is adopted to modify the time step in the simulation. A case of ‘no rubbing to rubbing’ is illustrated in Fig. 5, where \(\delta _0 \), \(\gamma \) and \(\Delta t\) represent the initial clearance, calculation tolerance and time step, respectively.

Furthermore, \(y_\mathrm{k} \) and \(y_{\mathrm{k}+1} \) denote the vertical displacement of the disc at the previous and following moment, respectively, and obey

$$\begin{aligned} \left\{ {\begin{array}{l} y_\mathrm{k} -\delta _0 <0, \\ y_{\mathrm{k+1}} -\delta _0 >0. \\ \end{array}} \right. \end{aligned}$$
(13)
Fig. 5
figure 5

Schematic diagram of a linear interpolation method

Full size image

If \(\left| {y_{\mathrm{k}+1} -\delta _0 } \right| \le \gamma \) is satisfied, the time step remains the same. Otherwise, the new time step modified by the linear interpolation can be expressed as

$$\begin{aligned} \Delta t_1 =\frac{\delta _0 -y_\mathrm{k} }{y_{\mathrm{k}+1} -y_\mathrm{k} }\Delta t. \end{aligned}$$
(14)

Taking \(y_\mathrm{k} \) as the initial value, the Runge–Kutta method is applied to carry out the numerical calculation in the condition of the new time step \(\Delta t_1 \). If \(\left| {y_{\mathrm{k}+1}^*-\delta _0 } \right| \le \gamma \) is satisfied, the interpolation is finished, and the impact velocity at this time is treated as the initial impact velocity. Otherwise, the next iteration will continue based on the linear interpolation method.

For the rotor system shown in Fig. 1, rub-impact fault in this paper can be concluded as follows

  1. (1)

    Rub-impact of single point (point 1 or point 2): When rub-impact happens at one point, according to Eq. (14), the modified time step of compressor disc (or turbine disc) can be expressed as \(\Delta t_\mathrm{c} \) (or \(\Delta t_\mathrm{d}\) ) during the process of no rubbing to rubbing.

  2. (2)

    Rub-impact of two points (point 1 and point 2): When rub-impact happens at two points, the modified time step of the rotor system can be written as

    $$\begin{aligned} \quad \Delta t^{*}=\min \left( {\Delta t_\mathrm{c} ,\quad \Delta t_\mathrm{d} } \right) , \end{aligned}$$
    (15)

    where \(\Delta t_\mathrm{c}\) and \(\Delta t_\mathrm{d} \) denote the modified time steps of point 1 and point 2, respectively.

After rub-impact happening at two points, there are four motion states of the rotor system, as shown in Fig. 6, where \(y_\mathrm{c} \) and \(y_\mathrm{d} \) denote the vertical displacements of compressor and turbine discs, \(\delta _{\mathrm{t1}} \) and \(\delta _{\mathrm{t2}} \) denote the initial clearances of compressor and turbine discs, respectively. (i) Rub-impact continues to happen at two points in the next time step, and the initial impact velocity remains the same as that at the black triangle point, as shown in Fig. 6a, b. (ii) Figure 6 c, d shows that the rub-impact at point 1 continues to happen, while that at point 2 stops in the next time step. (iii) The rub-impact at point 2 continues to happen, while that at point 1 stops, as shown in Fig. 6e, f. (iv) Figure 6g, h illustrates that both points lose contact within the interval. Referring to the parameter design of the experimental set-up, the detailed model parameters are shown in Table 1.

Fig. 6
figure 6

Four motion states of compressor disc and turbine disc

Full size image

With parameters given in Table 1, the bifurcation diagrams of the compressor disc and turbine disc are shown in Fig. 7a, b, respectively, where \(\omega \) is the rotating speed, y is the vertical displacement. In Fig. 7, it can be observed that there are rich nonlinear dynamic phenomena in the response of the rotor system within the speed range 200–800 \(\hbox {rad/s}\).

Table 1 Model parameters of the dual-disc rotor system
Full size table
Fig. 7
figure 7

Bifurcation diagrams for vertical response of two discs. a Compressor disc. b Turbine disc

Full size image

It can be seen from Fig. 7a, b that the 1T-periodic motion is found, when the rotating speed \(\omega \) is less than \(450\,\hbox {rad/s}\). At \(\omega =440\,\hbox {rad/s}\), a jump phenomenon occurs in the response of compressor and turbine discs, and then the motions of two discs enter into 2T-period.

Fig. 8
figure 8

Response of the compressor disc at different rotating speeds (rad/s). a \(\omega =250\). b \(\omega =470\). c \(\omega =550\). d \(\omega =650\). e \(\omega =730\). f \(\omega =800\)

Full size image
Fig. 9
figure 9

Response of the turbine disc at different rotating speeds (rad/s). a \(\omega =250\). b \(\omega =470\). c \(\omega =550\). d \(\omega =650\). e \(\omega =730\). f \(\omega =800\)

Full size image

At the rotating speed \(\omega =250\,\hbox {rad/s}\), Figs. 8a and 9a show the vertical response of compressor disc and turbine disc, including waveform, whirl orbit, Poincaré map and spectrum plot. The waveform and whirl orbit is regular, and the Poincaré map consists of only one point. These phenomena suggest that the response of the rotor system is 1T-periodic motion.

At the interval of \(\omega =450{-}480\,\hbox {rad/s}\), the response of the system exhibits 2T-periodic or quasi-periodic motion. Figures 8b and 9b show the response of compressor disc and turbine disc at the rotating speed \(\omega =470\,\hbox {rad/s}\). Only two points are observed in the Poincaré map, which confirms that the response is indeed 2T-periodic motion.

With the rotating speed increasing, the 2T-periodic motion loses its stability and the 1T-periodic motion appears again. Within the speed range 550–610 \(\hbox {rad/s}\), the quasi-periodic motion occurs. At \(\omega =550\,\hbox {rad/s}\) the rotor response enters the window of quasi-periodic motion, as shown in Figs. 8c and 9c. The Poincaré map consists of a large number of points lying on a closed curve.

Figures 8d and 9d show that the 2T-periodic motion appears at \(\omega =650\,\hbox {rad/s}\) after the quasi-periodic motion and 1T-periodic motion. It can be observed that there are two attractors in the Poincaré map.

From about \(\omega =730\,\hbox {rad/s}\), there exists a region of 4T-periodic motion. The waveform, whirl orbit, Poincaré map and spectrum plot are shown in Figs. 8e, f and 9e, f at the rotating speed \(\omega =730\,\hbox {rad/s}\) and \(\omega =800\,\hbox {rad/s}\), respectively.

Fig. 10
figure 10

Impact forces of the compressor disc at different rotating speeds (rad/s). a \(\omega =250\). B \(\omega =470\). c \(\omega =550\). d \(\omega =650\). e \(\omega =730\). f \(\omega =800\)

Full size image

Figures 10 and 11 show the impact forces of compressor disc and turbine disc at different rotating speeds. At \(\omega =250\,\hbox {rad/s}\), the impact force of the compressor disc is about \(28\hbox {N}\), while that of the turbine disc is zero, which confirms that the rub-impact of the compressor disc first occurs. At \(\omega =470\), 550 and \(650\,\hbox {rad/s}\), the rub-impact of both discs happens and the rubbing intensity of the turbine disc is greater than that of the compressor disc. However, the rub-impact force of the compressor disc is greater than that of the turbine disc at \(\omega =730\) and \(800\,\hbox {rad/s}\). These phenomena indicate that the energy transfer between compressor and turbine disc indeed exists, and the impact forces are correlated with the motion states of the rotor system.

Fig. 11
figure 11

Impact forces of the turbine disc at different rotating speeds (rad/s). a \(\omega =250\). b \(\omega =470\). c \(\omega =550\). d \(\omega =650\). e \(\omega =730\). f \(\omega =800\)

Full size image
Fig. 12
figure 12

Bifurcation diagrams for vertical response of two discs in the condition of \(\xi =90^{\circ }\). a Compressor disc. b Turbine disc

Full size image
Fig. 13
figure 13

Bifurcation diagrams for vertical response of two discs in the condition of \(\xi =180^{\circ }\). a Compressor disc. b Turbine disc

Full size image

3.1 Effects of the eccentric phase difference

In this subsection, a variable \(\xi \) is defined to describe the phase difference between two unbalance forces shown in Fig. 1. With parameters given in Table 1, the effects of the phase difference \(\xi \) on the dynamic characteristics of the dual-disc rotor system are discussed.

Figure 12 is the bifurcation diagrams of the compressor disc and turbine disc in the condition of \(\xi =90^{\circ }\), where the rotating speed \(\omega \) is the control parameter. By comparing Fig. 7a with Fig. 12a, it can be observed that the rotating speed corresponding to the jump phenomenon changes slightly, while the vibration amplitude decreases obviously. In the condition of \(\xi =90^{\circ }\), the jump phenomenon no longer occurs in the response of the turbine disc, and there is no significant change about the vibration amplitude of the turbine disc. At the interval of \(\omega =200{-}800\,\hbox {rad/s}\), the response of the rotor system is mainly exhibited as periodic or quasi-periodic motion.

Figure 13 shows the bifurcation diagrams of the compressor disc and turbine disc in the condition of \(\xi =180^{\circ }\). It can be seen that the vibration amplitude of the compressor disc at \(\xi =180^{\circ }\) is less than those at \(\xi =0^{\circ }\) and \(\xi =90^{\circ }\). The motions of the compressor disc and turbine disc are stable period-one within the speed range 670–800 \(\hbox {rad/s}\).

3.2 Effects of the convexity of the casing convex point

Casing convex point is a crucial part for fixed-point rubbing, which has an obvious effect on the dynamic characteristics of the rotor system. Therefore, in this section, three cases of casing convex point are analysed: (a) \(R_{\mathrm{t1}} =R_{\mathrm{t2}} =1.27\times 10^{-4}\,\hbox {m}\) (original condition), (b) \(R_{\mathrm{t1}} =1.27\times 10^{-5}\,\hbox {m}\), (c) \(R_{\mathrm{t2}} =1.27\times 10^{-5}\,\hbox {m}\), as shown in Fig. 14.

In the condition of \(R_{\mathrm{t1}} =1.27\times 10^{-5}\,\hbox {m}\), the bifurcation diagrams of the compressor disc and turbine disc are obtained by using the rotating speed \(\omega \) as control parameter, as shown in Fig. 15. By comparing Fig. 7 with Fig. 15, it can be seen that the jump phenomenon appears at different rotating speed, i.e. \(\omega =420\,\hbox {rad/s}\). The speed range of quasi-periodic motion decreases obviously, i.e. \(\left[ {545,\hbox { 575}} \right] \hbox {rad/s}\). At higher rotating speed, the response of the rotor system is exhibited as simple 1T-periodic motion, rather than periodic change among 1T-periodic, 2T-periodic, 3T-periodic and 4T-periodic motion. By changing the curvature radius of the convex point 1 shown in Fig. 1, some interesting results can be concluded that the vibration complexity of the rotor system is affected obviously, while the change of the vibration amplitude of the rotor system is slight.

Vibration responses for \(R_{\mathrm{t2}} =1.27\times 10^{-5}\,\hbox {m}\) are shown in Fig. 16. When the convex point 2 becomes sharp, there is a jump phenomenon at \(\omega =440\,\hbox {rad/s}\). The change of the response between Figs. 7 and 16 is not obvious. The phenomenon suggests that the dynamic characteristics of the rotor system are not sensitive to the convex point 2 in this study.

Fig. 14
figure 14

Schematic diagrams of different casing convex point. a Original condition. b \(R_{\mathrm{t1}} =1.27\times 10^{-5}\,\hbox {m}\).c \(R_{\mathrm{t2}} =1.27\times 10^{-5}\,\hbox {m}\)

Full size image
Fig. 15
figure 15

Bifurcation diagrams for vertical response of two discs in the condition of \(R_{\mathrm{t1}} =1.27\times 10^{-5}\hbox {m}\). a Compressor disc. b Turbine disc

Full size image
Fig. 16
figure 16

Bifurcation diagrams for vertical response of two discs in the condition of \(R_{\mathrm{t2}} =1.27\times 10^{-5}\hbox {m}\). a Compressor disc. b Turbine disc

Full size image

3.3 Effects of the initial clearance between the rotor and the convex point

The effect of initial clearance on the dynamic characteristics of the rotor system is evaluated here. Three cases of initial clearance are analysed: (a) \(\delta _{\mathrm{t1}} =\delta _{\mathrm{t2}} =0.02\,\hbox {mm}\) (original condition), (b) \(\delta _{\mathrm{t1}} =0.03\,\hbox {mm}\), (c) \(\delta _{\mathrm{t2}} =0.03\,\hbox {mm}\), as shown in Fig. 17.

Fig. 17
figure 17

Schematic diagrams of different initial clearance. a original condition. b \(\delta _{\mathrm{t1}} =0.03\,\hbox {mm}\). c \(\delta _{\mathrm{t2}} =0.03\,\hbox {mm}\)

Full size image
Fig. 18
figure 18

Bifurcation diagrams for vertical response of two discs in the condition of \(\delta _{\mathrm{t1}} =0.03\,\hbox {mm}\). a Compressor disc. b Turbine disc

Full size image
Fig. 19
figure 19

Bifurcation diagrams for vertical response of two discs in the condition of \(\delta _{\mathrm{t2}} =0.03\,\hbox {mm}\). a Compressor disc. b Turbine disc

Full size image

Figure 18 is the bifurcation diagrams of the compressor disc and turbine disc in the condition of \(\delta _{\mathrm{t1}} =0.03\,\hbox {mm}\), where \(\omega \) is the rotating speed, y is the vertical displacement. Compared with the dynamic phenomena exhibited in Fig. 7, the responses shown in Fig. 18 are more rich within the speed range 280–330 \(\hbox {rad/s}\). The vibration amplitude of the jump phenomenon at \(\omega =420\,\hbox {rad/s}\) shown in Fig. 18a is less than that at \(\omega =440\,\hbox {rad/s}\) shown in Fig. 7a. In the condition of \(\delta _{\mathrm{t1}} =0.03\,\hbox {mm}\), the motions of the rotor system keep regular period 1 and period 2 in the wide range of rotating speed. With the increase of \(\delta _{\mathrm{t1}} \), the quasi-periodic process shortens obviously.

To gain more insight into the performance of the dual-disc rotor system, the effect of the initial clearance between turbine disc and convex point 2 is studied. In the condition of \(\delta _{\mathrm{t2}} =0.03\,\hbox {mm}\), the response of the rotor system is shown in Fig. 19. It can be seen that the vibration complexity and amplitude change slightly as \(\delta _{\mathrm{t2}} \) increases. According to Figs. 7, 18 and 19, we can conclude that the response of the rotor system is more sensitive to the initial clearance of the compressor disc \(\delta _{\mathrm{t1}} \) rather than that of the turbine disc \(\delta _{\mathrm{t2}} \).

4 Conclusion

In this study, taking into account the coupling fault of multi-unbalances and multi-fixed-point rub-impacts, the dynamics model of a dual-disc rotor system has been established by using the finite element theory. For contact analysis, the Lankarani–Nikravesh model has been employed to describe the impact force of rotor-stator with surface coatings. Meanwhile, the Coulomb model has been used to simulate the frictional force. The dynamic equation of the rotor system has been numerically solved using the Runge–Kutta method. During the process of the numerical simulation, the linear interpolation method has been adopted to modify the time step at the moment of rub-impact happening. Then, the bifurcation diagram, whirl orbit, Poincaré map, spectrum plot, etc., have been employed to analyse the nonlinear dynamic behaviour of the rotor system. The typical conclusions are summarized as follows:

  1. (1)

    The typical nonlinear dynamic behaviours, such as the periodic, multi-periodic and quasi-periodic motions are revealed. As the rotating speed gradually increases, the energy transfer between compressor disc and turbine disc appears. Meanwhile, the magnitudes, intervals and complexities of impact forces change obviously.

  2. (2)

    When the direction of the first unbalance force is the same as that of the second unbalance force, the response of the rotor system is very complicated. When the directions of two unbalance forces are exactly opposite, the response of the rotor system is relatively simple and the vibration amplitude decreases obviously.

  3. (3)

    The motions of the rotor system are more sensitive to the parameters of the compressor disc, while those of the turbine disc can only affect the motions of the rotor system slightly.

  4. (4)

    The simulation results can enrich our understanding to fixed-point rub-impact fault of aero-engine and may promote the investigation into fault diagnosis.