A modified nonlinear POD method for order reduction based on transient time series

Abstract

In this paper, a modified nonlinear proper orthogonal decomposition (POD) method based on transient time series on account of approximate inertial manifold method is proposed to reduce the order of the multiple degrees of freedom (DOFs) of a rotor system. A model of 23 DOFs rotor system comprising a pair of liquid-film bearing with pedestal looseness at one end is established by using the Newton’s second law. The multi-DOFs system is reduced to a two-DOFs model by using the modified POD method, which preserves the original dynamics behaviors. The comparison between the modified and the traditional POD method shows that the modified POD method is more effective especially in finding the bifurcation point and detecting the bifurcation diagrams and the mean square error of amplitudes curves. Finally, a relative error analysis is also carried out to evaluate the accuracy of the proposed order reduction method, indicating that the relative error is below 5 % excluding the interval between original bifurcation point and the shift of the reduced system.

1 Introduction

The order reduction of multi-degrees of freedom (DOFs) rotor system has become central issue of concerns in nonlinear dynamics, attracting the attention of researchers in many areas. Order reduction methods, including the center manifold method, the Lyapunov–Schmidt (LS) method, the Galerkin method, and the proper orthogonal decomposition (POD) method, were summarized by Rega and Steindl in their applied studies of nonlinear dynamics [1, 2]. The center manifold approach reduces the original system to a center manifold associated with the part of the original system characterized by the eigenvalues with zero real parts at the bifurcation point, which may have smaller dimensions than that of the original system [3]. Anael [4] used center manifold theory to analyze a model of gene transcription and protein synthesis which consists of an ordinary differential equation coupled to a delay differential equation. The center manifold theory and the stability analysis were applied to reduce and simplify the nonlinear system, obtaining a number of bifurcation results and providing the rigorous theoretical proof [5–7]. The LS method was introduced to process the inhomogeneous term and the higher derivative of the boundary [8, 9]. Gentile et al. [10] used the LS method to research the periodic solutions of the resonant nonlinear wave equations, and Sandfry and Hall [11] studied the bifurcation characters of the dynamical equations.

A nonlinear finite dimensional analytic manifold, which approximates closely the global attractor in the two-dimensional case and certain bounded invariant sets in the three-dimensional case were presented in Ref. [12]. The two-dimensional Navier–Stokes (N–S) equations with finite dimensional global attractor and the geometric properties of the solutions of the N–S equations were discussed by Constantin and Foias [13–15]. Inertial manifold (IM) of the nonlinear evolutionary equations was proposed in the order reduction for the infinite system [16], approximate inertial manifold (AIM) was applied in the reaction–diffusion equations and Cahn–Hilliard equations in the high space dimension by Marion [17, 18]. The Lyapunov projection method was presented to determine the dimension and state space geometry of IM of dissipative extended dynamical systems and provide a possible way to determine the geometric characteristics of IM [19]. The nonlinear Galerkin method was proposed to integrate evolution differential equations that were well adapted to the long-term integration of such questions, which were related to the projection of equation on a nonlinear manifold [20]. The POD method was proposed by Loeve and Karhunen, being widely applied to dynamic diagnosis of the railway tracks [21–23]. Kerschen [24] reviewed the POD method which has been used in the dynamical characterization and order reduction of nonlinear dynamical systems of beam and shell [25–27]. Liang verified all kinds of POD methods from the theoretical perspective and provided the applications to the practical applications of nonlinear dynamics [28, 29]. The same method to analyze bifurcation properties in the dissipative systems was used and the Galerkin method was combined together for more researches on the order reduction of the high-dimensional systems [30–34].

Center manifold is a mapping, which maps the stable subspace to the center subspace. The L–S reduction method is similar as the center manifold method, which projects the original space to the null space [35, 36]. The two order reduction methods are discussed in the state space. In the actual multi-DOFs rotor system, the reduced model considers the main vibration directions of the original system, that is to say, the impact of the first n modes in the modal space. Even though the center manifold and L–S methods have thorough theory in the state space, they are not suitable in the modal space. The POD is a powerful and effective method for data analysis aimed at obtaining low-order modes of the original system [28]. The traditional POD method relies on the steady process of the system, which neglects the free vibration information and gives large relative error for the traditional POD method. For the modified POD method, which can be seen as a kind of construction of AIM, the transient time series contain the forced and free vibration information, involving more dynamical characteristics than the steady time series with only forced vibration information. Therefore, the reduced system maintains the main dynamical characteristics of the original system [37].

The motivation of this paper is to modify the traditional POD method based on the AIM method to reduce the order of a high-dimensional dynamical system. The modified POD method is applied to reduce a 23-DOFs rotor model with bearing loose to a two-DOFs system, which preserves the main dynamical topological structures of the original system. The efficiency of the modified method is presented by comparing with the traditional one and analyzing the relative error.

2 Preliminaries

In this section, we focus on the IM and AIM method to propose the modified nonlinear POD method which can be used in the order reduction of the multi-DOFs systems.

2.1 Inertial manifold and approximate inertial manifold

In the Hilbert space $H$, we give the inner product ($\cdot$,$\cdot$), the nonlinear evolution equation can be expressed as:

$$\begin{aligned}&\frac{\hbox {d}u}{\hbox {d}t}+vAu+B\left( {u,u} \right) +Cu=f\nonumber \\&u(0)=u_0\nonumber \\&R(u)=B(u,u)+Cu-f \end{aligned}$$

(1)

where $A$ is the unbounded linear self-conjugate operator in $H$ with domain $D(A)$ dense in $A$. Since $A^{-1}$ is a compact operator, there exists an orthogonal basis $\{\omega _j\}_{j=1}^\infty$ of $H$ consisting of eigenvectors of $A$. The corresponding eigenvalues are denoted by $\lambda _1,\lambda _2 ,\ldots \lambda _i \ldots \lambda _j \ldots ,$ which satisfy $0<\lambda _1 \le \lambda _2 \le \cdots \le \lambda _j \le \cdots , \lambda _j \rightarrow +\infty$, as $j\rightarrow \infty$. We assume that $A$ is positive, thus $(Av,v)>0,\forall v\in D(A), v\ne 0$. $R(u)$ is the nonlinear term and $B(u,u)$ is bilinear operator $D(A)\times D(A)\rightarrow H, C$ is the linear operator $D(A)\rightarrow H, f\in D(A^{1/2})$.

We denote that $P_m$ is the orthogonal projection of $H$ onto $H_m =\hbox {span}(\omega _1,\ldots \omega _m ), Q_m =I-P_m$, the set $p=P_m(u)$ and $q=Q_m (u)$, then the Eq. (1) is equivalent to the equations as follows:

$$\begin{aligned}&\frac{\hbox {d}p}{\hbox {d}t}+vAp+P_m B\left( {p+q,p+q} \right) +P_m C(p+q)\nonumber \\&\quad =P_m f\end{aligned}$$

(2)

$$\begin{aligned}&\frac{\hbox {d}q}{\hbox {d}t}+vAq+Q_m B\left( {p+q,p+q} \right) +Q_m C(p+q)\nonumber \\&\quad =Q_m f \end{aligned}$$

(3)

Under the condition of spectrum gap [16], an inertial manifold for Eq. (1) is a subset $\mu \subseteq H$, which has the following three properties:

• (i) $\mu$ is positively invariant under the flow [i.e., for all $t>0$, if $u_0 \in \mu$ then the solution of (1) $u(t)\in \mu$];

• (ii) $\mu$ is finite dimensional Lipschitz manifold;

• (iii) $\mu$ attracts every trajectory exponentially [that is to say, for every solution $u(t)$ of (1) $\hbox {dist}(u(t),\mu )\rightarrow 0$ exponentially];

We require $\mu$ to be a graph of Lipschitz function $\varPsi :H_m \rightarrow Q_m H$, that is to say $\mu =\{p,\varPsi (p)\}$, then the condition (i) is equivalent to recite that for the solution $p(t)$ and $q(t)$ of (2), (3) with $q(0)=\varPsi (p(0))$, one has $q(t)=\varPsi (p(t))$ for all $t>0$. Therefore, if the function $\varPsi$ exists, the reduction of system (2), (3) to $\mu$ is equivalent to the ordinary differential system called an inertial form, as follows:

$$\begin{aligned}&\frac{\hbox {d}p}{\hbox {d}t}+vAp+P_m B\left( p+\varPsi (p),p+\varPsi (p)\right) \nonumber \\&\quad +\,P_m C\left( p+\varPsi (p)\right) =P_m f \end{aligned}$$

(4)

The spectrum gap is not taken into account in the AIM theory. In general, the spectrum gap condition is difficult to be satisfied, so the AIM theory is proposed. AIM is defined as a class of manifold is nonlinear finite dimensional with a certain smoothness which is approximate to the global attractor. As usual, the Galerkin approximation method associated with the eigenvectors of the Stokes operator $A$ obtains the linear manifold $H_m$ as an AIM. However, replacing the mapping $\varPsi$ in (4) by zero, we can obtain the usual Galerkin approximation [38]:

$$\begin{aligned}&\frac{\hbox {d}u_m }{\hbox {d}t}+vAu_m +P_m B(u_m ,u_m)+P_m Cu_m =P_m f,\nonumber \\&\quad u_m \in H_m \end{aligned}$$

(5)

The theory of AIM has shown that long time behavior of partial differential equation can be fully described by that of a finite ordinary differential system [12]. AIM method can be regarded as the nonlinear Galerkin approximation [39]. Steindl and Troger [2] states that: “The qualitative idea is that if a system possesses a complicated attractor $A$, then it can often be better approximated by a nonlinear manifold as given by the inertial manifold than by the linear space used in the standard Galerkin method.”

As mentioned above, there is a certain relationship between the Galerkin method and the AIM method, which can be viewed as a kind of special nonlinear Galerkin approximation applied in the ordinary differential systems. This modified POD method can be considered as a kind of construction method of AIM in the high-dimensional nonlinear system.

2.2 Modified POD method based on transient time series

On account of the AIM method, a modified order reduction method is proposed, which is called modified nonlinear POD method based on transient time series. This new method will be applied to the order reduction of the high-dimensional dynamical systems.

Under the given initial conditions, the transient process of the system is a complex process containing not only free vibration information but also forced vibration information. Therefore, we put forward a modified nonlinear POD method based on transient time series: obtaining a set of POMs by utilizing POD from the transient process of the system, taking the first two orders of the POMs to form the projection space, and projecting original system onto this space. Thus, we gain the approximate equivalent model of two-DOFs. This method can be viewed as a structured approach of AIM in the high-dimensional nonlinear systems.

In general, through the equivalent transformation, the multiple-DOFs system can be written as:

$$\begin{aligned} \ddot{Z}=-C\dot{Z}-KZ+F \end{aligned}$$

(6)

where $C$ is the equivalent damping matrix. $K$ is the equivalent stiffness matrix. $F$ is the equivalent force vector.

The construction process are as follows:

• (1) Provide the initial conditions, proceed numerical simulation and obtain displacement information from transient process of various DOFs, which is denoted by $z_1 (t),z_2 (t),\ldots z_M (t)$. $M$ is the number of DOFs in the system, recording transient time interval displacement sequence of all DOFs $z_i =(z_i (t_1 ),z_i (t_2),\ldots z_i (t_N))^{T},i=1,\ldots ,M$. The number of time interval is $N$ and the interval is equal to each other, the time series form the matrix $X=[z_1 ,z_2 ,\ldots ,z_M]$, the order of $X$ is $N\times M$.

When calculating the self-correlation matrix $T=X^{T}X$, the order of matrix is $M\times M$. The eigenvector of the matrix can therefore be denoted by $\varphi _1 ,\varphi _2 ,\ldots ,\varphi _M$, and the corresponding eigenvalues are $\lambda _1 >\lambda _2 >\cdots >\lambda _M$.

• (2) $U$ is the matrix formed by the first $n$ orders of $T=X^{T}X$, and it can also indicate that the matrix $U$ contains the first $n$ largest eigenvalues of $T$. The order of $U$ is $M\times n$, so we know that the order of $U^{T}U$ is $n\times n$. Taking the coordinates transformation on system coordinates $Z$, acquiring the new coordinates $P, Z=UP$, substituting $Z$ into Eq. (6), gaining the Eq. (7):

  $$\begin{aligned} U\ddot{P}=-CU\dot{P}-KUP+F \end{aligned}$$

  (7)

Due to the column vector of $U$ is orthogonal and nonzero, and the matrix $U^{T}U$ is $n$ order diagonal and full rank, hence there exits inverse matrix of $U^{T}U$. For the Eq. (7), taking $(U^{T}U)^{-1}U^{T}$ left multiplication on both sides, we can obtain (8):

$$\begin{aligned} \ddot{P}&= -(U^{T}U)^{-1}U^{T}CU\dot{P}-(U^{T}U)^{-1}U^{T}KUP\nonumber \\&\quad +\,(U^{T}U)^{-1}U^{T}F \end{aligned}$$

(8)

Setting

$$\begin{aligned} C_R&= -(U^{T}U)^{-1}U^{T}CU,K_R \!=\!(U^{T}U)^{-1}U^{T}KU,F_R\\&= (U^{T}U)^{-1}U^{T}F, \end{aligned}$$

then we receive the formula (9):

$$\begin{aligned} \ddot{P}=-C_R \dot{P}-K_R P+F_R \end{aligned}$$

(9)

In this way, the original system is transformed into the $n$-DOFs reduced system by the new order reduction method.

3 Twenty-three-DOFs rotor system with bearing loose

In this section, a rotor model with bearing loose is established according to the Newton’s second law and the reduced system is introduced in detail. The efficiency of the order reduction is evaluated through the comparison of the bifurcation diagrams and mean square error of amplitudes curves. The relative error of the modified order reduction method is analyzed at last.

3.1 Original model

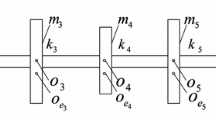
The 23-DOFs model is shown in Fig. 1, suggesting that the axial, torsional vibrations of the system and the gyroscopic moment are neglectful. $o_i (i=2\ldots 9)$ are the geometric centers of the discs, $o_1, o_{10}$ are the geometric centers of the left and right bearing. Here, $o_{e_i} (i=1\ldots 11)$ are the centers of gravity; $m_i (i=1\ldots 11)$ are the equivalent lumped mass; $k_i(i=1\ldots 10)$ are the equivalent stiffness of the corresponding discs; $c_i (i=1\ldots 11)$ are the equivalent damping coefficients at the position of the lumped mass. Assuming that the left bearing is loose, the maximum clearance between the loose side bearing and the foundation is $\delta _1$. The shaft between rotor discs and the bearing is massless elastic. Also $c_s$ is the damping coefficient of pedestal loose, and $k_s$ is the supporting stiffness. When loosing occurs, $c_s$ and $k_s$ are piecewise linear, $Y_{12}$ is the pedestal displacement, the expression is:

$$\begin{aligned} k_s =\left\{ {{\begin{array}{lll} k_{s1} &{}\quad \left( {Y_{12} >\delta _1 } \right) \\ 0&{}\quad \left( {0\le Y_{12} \le \delta _1 } \right) \\ k_{s2}&{} \quad \left( {Y_{12} <0} \right) \\ \end{array} }} \right. \quad c_s =\left\{ {{\begin{array}{lll} c_{s1}&{} \quad \left( {Y_{12} >\delta _1 } \right) \\ 0&{}\quad \left( {0\le Y_{12} \le \delta _1 } \right) \\ c_{s2}&{} \quad \left( {Y_{12} <0} \right) \\ \end{array} }} \right. \end{aligned}$$

Fig. 1

Rotor models with pedestal looseness at one end

By using the Newton’s second law, we can receive the differential equations of motion and the dimensionless form can be obtained as well, which are shown as formulas (10) and (11).

$$\begin{aligned}&M\ddot{Z}+C\dot{Z}+KZ=F\nonumber \\&Z=\left( {X_1 ,Y_1 ,\ldots Y_{11} ,Y_{11} ,Y_{12} } \right) ^{T}\nonumber \\&M=\left( {{\begin{array}{cccccc} {m_1 }&{} &{} &{} &{} &{} \\ &{} {m_1 }&{} &{} &{} &{} \\ &{} &{} \ddots &{} &{} &{} \\ &{} &{} &{} {m_{11} }&{} &{} \\ &{} &{} &{} &{} {m_{11} }&{} \\ &{} &{} &{} &{} &{} {m_{12} } \\ \end{array} }} \right) _{23\times 23} \end{aligned}$$

(10)

We nondimensionalize the Eq. (10) and the dimensionless transformation is defined as:

$$\begin{aligned}&\tau =\omega t, x_i =\frac{X_i }{c}, y_i =\frac{Y_i }{c}, \dot{x}_i =\frac{\hbox {d}x_i }{\hbox {d}\tau }, \dot{y}_i =\frac{\hbox {d}y_i }{\hbox {d}\tau },\\&\ddot{x}_i =\frac{\hbox {d}\dot{x}_i }{\hbox {d}\tau }, \ddot{y}_i =\frac{\hbox {d}\dot{y}_i }{\hbox {d}\tau },M_1 =\frac{m_1 c\omega ^{2}}{sP}, M_{11} =\frac{m_{11} c\omega ^{2}}{sP}, \\&M_{12}=\frac{m_{12} c\omega ^{2}}{sP}, b_i =\frac{B_i }{c}(i=2,\ldots 10), f_x =\frac{F_x }{sP},\\&f_y =\frac{F_y }{sP} \end{aligned}$$

$$\begin{aligned}&C=\left( {{\begin{array}{cccccc} {c_1 }&{} &{} &{} &{} &{} \\ &{} {c_1 }&{} &{} &{} &{} \\ &{} &{} \ddots &{} &{} &{} \\ &{} &{} &{} {c_{11} }&{} &{} \\ &{} &{} &{} &{} {c_{11} }&{} \\ &{} &{} &{} &{} &{} {c_s } \\ \end{array} }} \right) _{23\times 23} \end{aligned}$$

$$\begin{aligned}&K=\left( {{\begin{array}{cccccccccccccc} {k_1 }&{} &{} {-k_1 }&{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} {k_1 }&{} &{} {-k_1 }&{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ {-k_1 }&{} &{} {k_1 +k_2 }&{} &{} {-k_2 }&{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} {-k_1 }&{} &{} {k_1 +k_2 }&{} &{} {-k_2 }&{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} \ddots &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} {-k_9 }&{} &{} {k_9 +k_{10} }&{} &{} {-k_{10} }&{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} {-k_9 }&{} &{} {k_9 +k_{10} }&{} &{} {-k_{10} }&{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} {-k_{10} }&{} &{} {k_{10} }&{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} {-k_{10} }&{} &{} {k_{10} }&{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} {k_s } \\ \end{array} }} \right) _{23\times 23} \end{aligned}$$

$$\begin{aligned}&F=\left( {{\begin{array}{c} {F_x \left( {X_1 ,Y_1 -Y_{12} ,\dot{X}_1 ,\dot{Y}_1 -\dot{Y}_{12} } \right) } \\ {F_y \left( {X_1 ,Y_1 -Y_{12} ,\dot{X}_1 ,\dot{Y}_1 -\dot{Y}_{12} } \right) -m_1 g} \\ {m_2 B_2 \omega ^{2}\cos (\omega t)} \\ {m_2 B_2 \omega ^{2}\sin (\omega t)-m_2 g} \\ \vdots \\ {m_{10} B_{10} \omega ^{2}\cos (\omega t)} \\ {m_{10} B_{10} \omega ^{2}\sin (\omega t)-m_{10} g} \\ {F_x \left( {X_{11} ,Y_{11} ,\dot{X}_{11} ,\dot{Y}_{11} } \right) } \\ {F_y \left( {X_{11} ,Y_{11} ,\dot{X}_{11} ,\dot{Y}_{11} } \right) -m_{11} g} \\ {-F_y \left( {X_1 ,Y_1 -Y_{12} ,\dot{X}_1 ,\dot{Y}_1 -\dot{Y}_{12} } \right) -m_{12} g} \\ \end{array} }} \right) _{23\times 1} \end{aligned}$$

where $f_x$ and $f_y$ are the model of dimensionless nonlinear oil-film force, $f_x =\frac{F_x }{sP}, f_y =\frac{F_y }{sP}$. $F_x$ and $F_y$ are the $x, y$ directional components of bearing nonlinear oil-film force. $c$ is the bearing clearance,

$$\begin{aligned} \bar{{c}}=\left( {{\begin{array}{cccccc} \frac{c_1 }{m_1 \omega }&{} &{} &{} &{} &{} \\ &{} {\frac{c_1 }{m_1 \omega }}&{} &{} &{} &{} \\ &{} &{} \ddots &{} &{} &{} \\ &{} &{} &{} {\frac{c_{11} }{m_{11} \omega }}&{} &{} \\ &{} &{} &{} &{} {\frac{c_{11} }{m_{11} \omega }}&{} \\ &{} &{} &{} &{} &{} {\frac{c_s }{m_{12} \omega }} \\ \end{array} }} \right) _{23\times 23} \end{aligned}$$

$s=\frac{\mu \omega RL}{P}\left( {\frac{R}{c}} \right) ^{2}\left( {\frac{L}{2R}} \right) ^{2}$ is the Sommerfeld number. $\mu$ is the lubricating oil viscosity, $L$ is the bearing length, $R$ is the radius of the bearing, $\omega$ is the external excitation, $P$ is the loading, and $\tau$ is the dimensionless time.

$$\begin{aligned} \bar{{f}}=\left( {{\begin{array}{c} {\frac{1}{M_1 }f_x \left( {x_1 ,y_1 -y_{12} ,\dot{x}_1 ,\dot{y}_1 -\dot{y}_{12} } \right) } \\ {\frac{1}{M_1 }f_y \left( {x_1 ,y_1 -y_{12} ,\dot{x}_1 ,\dot{y}_1 -\dot{y}_{12} } \right) -\frac{g}{\omega ^{2}c}} \\ {b_2 \cos \tau } \\ {b_2 \sin \tau -\frac{g}{\omega ^{2}c}} \\ \vdots \\ {b_{10} \cos \tau } \\ {b_{10} \sin \tau -\frac{g}{\omega ^{2}c}} \\ {\frac{1}{M_{11} }f_x \left( {x_{11} ,y_{11} ,\dot{x}_{11} ,\dot{y}_{11} } \right) } \\ {\frac{1}{M_{11} }f_y \left( {x_{11} ,y_{11} ,\dot{x}_{11} ,\dot{y}_{11} } \right) -\frac{g}{\omega ^{2}c}} \\ {-\frac{1}{M_{12} }f_y \left( {x_1 ,y_1 -y_{12} ,\dot{x}_1 ,\dot{y}_1 -\dot{y}_{12} } \right) -\frac{g}{\omega ^{2}c}} \\ \end{array} }} \right) _{23\times 1} \end{aligned}$$

The dimensionless equation of (10) is expressed as:

$$\begin{aligned} \ddot{z}=-\bar{{c}}\dot{z}-\bar{{k}}z+\bar{{f}} \end{aligned}$$

(11)

The expression of $\bar{{c}}, \bar{{k}}, \bar{{f}}$ are shown as above,

$$\begin{aligned} z=(x_1 ,y_1 ,\ldots ,x_{11} ,y_{11} ,y_{12})^{T}. \end{aligned}$$

The parameters in the system are shown as follows:

$$\begin{aligned}&m_1 =4\,\hbox {kg}, m_2 =21.9339\,\hbox {kg}, m_3 =7.7990\,\hbox {kg}, \\&m_4=6.3545\,\hbox {kg} \\&m_5 =9.0666\,\mathrm{kg}, m_6 =5.9773\,\mathrm{kg},m_7 =5.9773\,\hbox {kg}, \\&m_8=6.9809\,\hbox {kg} \\&m_9 =7.2284\,\hbox {kg}, m_{10} =3.90146\,\hbox {kg}, m_{11} =4\,\hbox {kg},\\&m_{12}=75\,\hbox {kg} \\&R=L=30\,\hbox {mm}, c=0.11\,\hbox {mm},\mu =0.018\,\mathrm{pa\,s},\\&c_1 =c_{11}=800\,\mathrm{N\,s/m}\\&c_2 =c_{10} =1{,}250\,\mathrm{N\,s/m},c_3 =c_9 =1{,}050\,\mathrm{N\,s/m},\\&c_4=c_8 =850\,\mathrm{N\,s/m} \\&c_5 =c_7 =1{,}050\,\mathrm{N\,s/m}, c_6 =1{,}250\,\mathrm{N\,s/m}, \\&k_i=2\times 10^{7}\,\mathrm{N/m}(i=1,\ldots ,10, i\ne 5) \\&k_{s1} =7.5\times 10^{7}\,\mathrm{N/m}, k_{s2} =2.5\times 10^{8}\,\mathrm{N/m}, \\&c_{s1}=350\,\mathrm{N\,s/m}, \delta _1 =0.22\,\hbox {mm} \\&c_{s2} =500\,\mathrm{N\,s/m}, B_5 =0.01\,\hbox {mm}, \\&\hbox {B}_i=0\left( {i=2,\ldots 10,i\ne 5} \right) \end{aligned}$$

$$\begin{aligned}&\bar{{k}}=\left( {{\begin{array}{cccccccccccccc} {\frac{k_1 }{m_1 \omega ^{2}}}&{} &{} {-\frac{k_1 }{m_1 \omega ^{2}}}&{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} {\frac{k_1 }{m_1 \omega ^{2}}}&{} &{} {-\frac{k_1 }{m_1 \omega ^{2}}}&{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ {-\frac{k_1 }{m_2 \omega ^{2}}}&{} &{} {\frac{k_1 +k_2 }{m_2 \omega ^{2}}}&{} &{} {\frac{-k_2 }{m_2 \omega ^{2}}}&{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} {-\frac{k_1 }{m_2 \omega ^{2}}}&{} &{} {\frac{k_1 +k_2 }{m_2 \omega ^{2}}}&{} &{} {\frac{-k_2 }{m_2 \omega ^{2}}}&{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} \ddots &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} {\frac{-k_9 }{m_{10} \omega ^{2}}}&{} &{} {\frac{k_9 +k_{10} }{m_{10} \omega ^{2}}}&{} &{} {\frac{-k_{10} }{m_{10} \omega ^{2}}}&{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} {\frac{-k_9 }{m_{10} \omega ^{2}}}&{} &{} {\frac{k_9 +k_{10} }{m_{10} \omega ^{2}}}&{} &{} {\frac{-k_{10} }{m_{10} \omega ^{2}}}&{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} {\frac{-k_{10} }{m_{11} \omega ^{2}}}&{} &{} {\frac{k_{10} }{m_{11} \omega ^{2}}}&{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} {\frac{-k_{10} }{m_{11} \omega ^{2}}}&{} &{} {\frac{k_{10} }{m_{11} \omega ^{2}}}&{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} {\frac{k_s }{m_{12} \omega ^{2}}} \\ \end{array} }} \right) _{23\times 23} \end{aligned}$$

The nonlinear oil-film force [40] of $x$ and $y$ directions can be found in formula (12):

$$\begin{aligned}&\left\{ {{\begin{array}{l} {f_x } \\ {f_y } \\ \end{array} }} \right\} =-\frac{[(x-2\dot{y})^{2}+(y+2\dot{x})^{2}]^{1/2}}{1-x^{2}-y^{2}}\nonumber \\&\quad \times \left\{ {{\begin{array}{l} {3xV(x,y,\alpha )-\sin \alpha G\left( {x,y,\alpha } \right) -2\cos \alpha S\left( {x,y,\alpha } \right) } \\ {3yV(x,y,\alpha )+\cos \alpha G\left( {x,y,\alpha } \right) -2\sin \alpha S\left( {x,y,\alpha } \right) } \\ \end{array} }} \right\} \nonumber \\ \end{aligned}$$

(12)

The parameters in (12) can be identified as:

$$\begin{aligned} \alpha&= \arctan \left( {\frac{y+2\dot{x}}{x-2\dot{y}}} \right) -\frac{\pi }{2}\hbox {sign}\left( {\frac{y+2\dot{x}}{x-2\dot{y}}} \right) \nonumber \\&\quad \quad -\,\frac{\pi }{2}\hbox {sign}(y+2\dot{x}) \end{aligned}$$

(13)

$$\begin{aligned} G(x,y,\alpha )&= \frac{2}{\left( {1-x^{2}-y^{2}} \right) ^{1/2}}\Bigg [\frac{\pi }{2}\nonumber \\&\quad +\,\arctan \frac{y\cos \alpha -x\sin \alpha }{\left( {1-x^{2}-y^{2}} \right) ^{1/2}}\Bigg ]\end{aligned}$$

(14)

$$\begin{aligned} V\left( {x,y,\alpha } \right)&= \frac{2+(y\cos \alpha -x\sin \alpha )G\left( {x,y,\alpha } \right) }{1-x^{2}-y^{2}} \end{aligned}$$

(15)

$$\begin{aligned} S\left( {x,y,\alpha } \right)&= \frac{x\cos \alpha +y\sin \alpha }{1-(x\cos \alpha +y\sin \alpha )^{2}} \end{aligned}$$

(16)

In order to facilitate the theory analysis, providing the Taylor series expansion on the oil-film force, $\alpha$ can be rewritten as:

$$\begin{aligned} \alpha&= \arctan \frac{y+2\dot{x}}{x-2\dot{y}}-\frac{\pi }{2}\left( {\frac{\left( {y+2\dot{x}} \right) \left( {x-2\dot{y}} \right) }{\left| {y+2\dot{x}} \right| \left| {x-2\dot{y}} \right| }} \right) \nonumber \\&\quad -\,\frac{\pi }{2}\left( {\frac{y+2\dot{x}}{\left| {y+2\dot{x}} \right| }} \right) \end{aligned}$$

(17)

For convenience of the calculation, formula (11) is written as (18):

$$\begin{aligned} \ddot{Z}=-C\dot{Z}-KZ+F \end{aligned}$$

(18)

As above, $C$ is the damping matrix, $K$ is the stiffness matrix, and $F$ is the force vector, which includes oil-film force and external excitation. $Z=\left[ {z_1 \,z_2 \ldots z_{23} } \right] ^{T}$ corresponds to $[x_1 \,y_1 \ldots x_{11} \,y_{11} \,y_{12} ]^{T}$ in the Eq. (11).

3.2 Reduced model

Given the initial conditions that the integral step is $\pi /256,$ the displacement and the velocity are $x_4 =y_4 =0.5, x_i =y_i =y_{12} =0\,(i=1\ldots 11,i\ne 4), \dot{x}_i =\dot{y}_i =\dot{y}_{12} =0.001\left( {i=1,\ldots ,11} \right)$, and $\omega =750\left( \mathrm{rad/s} \right)$. As is shown in Fig. 2, the horizontal ordinate time history of the right bearing is provided. If $\tau$ in formula (11) is selected between 0 and 50 $\pi$, the system is the transient process, and the system is in the periodic motion state after $50\pi$. According to Sect. 2.2, the coordinate transformation matrix utilizes the signal of the transient process to gain is:

$$\begin{aligned}&U^{T}=10^{-2}\left( {{\begin{array}{l} {U_1 } \\ {U_2 } \\ \end{array} }} \right) \\ \end{aligned}$$

$$\begin{aligned}&U_1 =\left( {\begin{array}{l} 13.14, 4.46, 25.06, 1.93, 31.55, 0.15, 35.96, 1.63, \\ 38.56, 2.51, 38.51, 2.52, 36.77, 1.68, 33.22, 0.16, \\ 27.79, 1.85, 20.59, 4.27, 12.50, 6.98, 3.74 \\ \end{array}} \right) \\&U_2 =\left( {\begin{array}{l} 7.44, 18.47, 4.14, 27.50, 1.23, 32.50, 1.03, 35.80, \\ 2.59, 37.56, 3.12, 37.11, 2.57, 35.21, 1.12, 31.82, \\ 1.01, 26.96, 3.76, 20.79, 7.00, 14.02, 2.59 \\ \end{array}} \right) \end{aligned}$$

Thus, in formula (9), $n=2$, the equation of the two-DOFs reduced system is (19):

$$\begin{aligned} \ddot{P}=-C_2 \dot{P}-K_2 P+F_2 \end{aligned}$$

(19)

When the damping matrix, stiffness matrix, the external excitation matrix are $C_2, K_2, F_2$, the followings are the coefficients of the matrixes:

$$\begin{aligned}&C_2 =\left( {{\begin{array}{cc} {c_{11} }&{} {c_{12} } \\ {c_{21} }&{} {c_{22} } \\ \end{array} }} \right) ,\,K_2 =\left( {{\begin{array}{cc} {k_{11} }&{} {k_{12} } \\ {k_{21} }&{} {k_{22} } \\ \end{array} }} \right) , \\&F_2=\left( {{\begin{array}{c} {f_1 +f_{\omega 1} +g_1 } \\ {f_2 +f_{\omega 2} +g_2 } \\ \end{array} }} \right) \end{aligned}$$

The parameters in the above matrixes are shown in the “Appendix”.

Fig. 2

The time history of $x_{11}$ under the initial conditions when $\omega =750(\mathrm{rad/s})$

3.3 Results of order reduction

In order to show the efficiency of the modified order reduction method, this section highlights the dynamical behaviors of the original system and the reduced system. We therefore analyze the bifurcation diagrams, the mean square error of amplitudes curves and the relative error. Comparison of the original system with the reduced system shows that the reduced system preserves the dynamical topological structures of the original system by applying the modified POD method and reserves none by the traditional one.

Figure 3a shows the bifurcation diagram of the original system, Fig. 3b, c shows the bifurcation diagrams of the reduced systems by applying the modified and traditional POD method, horizontal axis is the rotate speed of the rotor system, and vertical axis is the amplitude of $x_{11}$. Figure 3b suggests that the reduced system maintains main bifurcation character of the original system, and the topological structure of the reduced system is basically the same as the original system. Figure 3c indicates that the reduced system loses most dynamics behaviors and preserves no topological structures of the original system.

Fig. 3

Bifurcation diagrams. a Bifurcation diagram for original system, b bifurcation diagram for reduced system, c bifurcation diagram for traditional POD method

Figure 4 gives the mean square error of amplitudes curves of the original system and the reduced system. As can be seen, a new pattern of manifestation is found. Figure 4 reflects the relation between the rotate speed and the mean square error of amplitudes, which stands for the mean square error of the point displacements, and the algorithm is indicated in formula (20). Again, in Fig. 4a, the bifurcation occurs when $\omega =1{,}340\,\mathrm{rad/s}$ in the original system and when $\omega =1{,}410\,\hbox {rad/s}$ in the reduced system as shown in Fig. 4b. The difference of the interval $\omega \in \left[ {1{,}340,1{,}410} \right]$ is clearly shown. However, the curve keeps basically the same in other intervals, and which demonstrates the reduced system preserves the dynamics behaviors of the original system.

Fig. 4

Mean square error of amplitudes curve. a The original system, b the reduced system

Also, here $x_i \left( {i=1,\ldots N} \right)$ stands for the displacements of the points, $N$ is the number of the point, $\mu$ is the mean value and $\sigma$ is the mean square error.

$$\begin{aligned} \mu =\frac{\sum \nolimits _{i=1}^N {x_i } }{N}, \quad \sigma =\sqrt{\sum _{i=1}^N {\frac{\left( {x_i -\mu } \right) ^{2}}{N}} } \end{aligned}$$

(20)

In Fig. 5, the relative error of the modified POD method is found, the horizontal coordinate represents the rotate speed of the rotor system, the vertical coordinate stands for the mean square error difference between original system and reduced system. The equation $e=\left| {r_m -r_n } \right| /r_m$ suggests that $e$ is the relative error and that $r_m, r_n$ is the original and reduced system mean square error of amplitude, respectively. We can see that the relative error of the modified POD method is $<$5 % excluding the interval between original bifurcation point and the shift of the reduced system, merely rising up obviously when $\omega \in \left[ {1{,}340,1{,}410} \right]$, which is not in the range of the normal value. Although there is a certain relative error of the order reduction method, the reduced system maintains the main dynamical characteristics of the original system as a whole. With the relative error analysis, we obtain the efficiency of the modified POD method based on transient time series. This new method can be used as an effective order reduction method of the multiple-DOFs systems.

Fig. 5

The order reduction relative error

4 Conclusions

In this paper, a modified nonlinear POD method has been proposed based on the AIM method to reduce a 23-DOFs rotor model with bearing loose to a two-DOFs model. It is shown that the dynamical characteristics of the original model has been preserved in the reduced model by the comparison between the bifurcation diagram and the mean square error of amplitudes. Finally, the efficiency of the modified POD method has also been demonstrated that the relative error of the rotor system is $<$5 % excluding the interval between bifurcation points of the original system and the shift in the reduced system. Further studies on this subject are being carried out by the present authors in two aspects: One is the reason of extracting transient time series and the other is to elaborate the missed information of the reduced system.

Appendix

$$\begin{aligned} c_{11}&= 10^{-2}\left( 1.9979\frac{c_1 }{m_1 }+6.3193\frac{c_2 }{m_2 }+9.9517\frac{c_3 }{m_3 }\right. \\&\quad +\,12.954\frac{c_4 }{m_4 }+14.934\frac{c_5 }{m_5 }+14.896\frac{c_6 }{m_6 } \\&\quad +\,13.546\frac{c_7 }{m_7 }+11.033\frac{c_8 }{m_8 }+7.7582\frac{c_9 }{m_9 }\\&\quad \left. +\,4.4199\frac{c_{10} }{m_{10} }+2.0503\frac{c_{11} }{m_{11} }+0.14015\frac{c_s }{m_{12} }\right) \\ c_{12}&= 10^{-2}\left( 0.1747\frac{c_1 }{m_1 }+0.50805\frac{c_2 }{m_2 }+0.43517\frac{c_3 }{m_3 }\right. \\&\quad +\,0.21398\frac{c_4 }{m_4 }-0.05375\frac{c_5 }{m_5 }-0.26634\frac{c_6 }{m_6 } \\&\quad -\,0.35194\frac{c_7 }{m_7 }-0.31994\frac{c_8 }{m_8 }-0.21875\frac{c_9 }{m_9 }\\&\quad \left. -\,0.11377\frac{c_{10} }{m_{10} }\!-\!0.1043\frac{c_{11} }{m_{11} }\!+\!0.096872\frac{c_s }{m_{12} }\right) \\ c_{21}&= 10^{-2}(0.1747\frac{c_1 }{m_1 }+0.50805\frac{c_2 }{m_2 }+0.43517\frac{c_3 }{m_3 }\\&\quad +\,0.21398\frac{c_4 }{m_4 }-0.05375\frac{c_5 }{m_5 }-0.26634\frac{c_6 }{m_6 } \\&\quad -\,0.35194\frac{c_7 }{m_7 }-0.31994\frac{c_8 }{m_8 }-0.21875\frac{c_9 }{m_9 }\\&\quad -\,0.11377\frac{c_{10} }{m_{10} }-0.1043\frac{c_{11} }{m_{11} }+0.096872\frac{c_s }{m_{12} }) \\ c_{22}&= 10^{-2}\left( 3.9645\frac{c_1 }{m_1 }+7.7322\frac{c_2 }{m_2 }+10.581\frac{c_3 }{m_3 }\right. \\&\quad +\,12.825\frac{c_4 }{m_4 }+14.171\frac{c_5 }{m_5 }+13.867\frac{c_6 }{m_6 } \\&\quad +\,12.461\frac{c_7 }{m_7 }+10.136\frac{c_8 }{m_8 }+7.2763\frac{c_9 }{m_9 }\\&\quad \left. +\,4.4643\frac{c_{10} }{m_{10} }+2.455\frac{c_{11} }{m_{11} }+0.0066975\frac{c_s }{m_{12} }\right) \end{aligned}$$

$$\begin{aligned} k_{11}&= 10^{-8}\left( -0.03547\frac{k_5 }{m_6 }+1.3019\frac{k_6 }{m_6 }+0.263\frac{k_s }{m_{12} }\right. \\&\quad -\,2.7589\frac{k_8 }{m_9 }+3.6742\frac{k_9 }{m_9 }+5.3886\frac{k_1 }{m_2 }\\&\quad -\,2.9737\frac{k_2 }{m_2 }+3.0203\frac{k_3 }{m_4 } \\&\quad -\,1.7859\frac{k_4 }{m_4 }+1.928\frac{k_4 }{m_5 }+0.035518\frac{k_5 }{m_5 }\\&\quad -\,1.5408\frac{k_{10} }{m_{11} }-1.2315\frac{k_6 }{m_7 }+2.4972\frac{k_7 }{m_7 }\\&\quad +\,3.8427\frac{k_2 }{m_3 }-2.6143\frac{k_3 }{m_3 } \\&\quad +\,2.5903\frac{k_9 }{m_{10} }+2.9058\frac{k_{10} }{m_{10} }-2.2172\frac{k_7 }{m_8 }\\&\quad \left. -\,2.7206\frac{k_1 }{m_1 }+3.3869\frac{k_8 }{m_8 }\right) \\ k_{12}&= 10^{-8}\left( -0.40584\frac{k_5 }{m_6 }-0.30843\frac{k_6 }{m_6 }\right. \\&\quad +\,0.18178\frac{k_s }{m_{12} }\\&\quad +\,1.277\frac{k_8 }{m_9 }-1.6474\frac{k_9 }{m_9 }-1.8797\frac{k_1 }{m_2 }\\&\quad +\,1.5507\frac{k_2 }{m_2 }-1.4206\frac{k_3 }{m_4 } \\&\quad +\,0.99842\frac{k_4 }{m_4 }-1.0456\frac{k_4 }{m_5 }+0.40628\frac{k_5 }{m_5 }\\&\quad +\,1.6473\frac{k_{10} }{m_{11} }+0.32023\frac{k_6 }{m_7 }-0.89506\frac{k_7 }{m_7 }\\&\quad -\,1.7101\frac{k_2 }{m_3 }+1.3256\frac{k_3 }{m_3 } \\&\quad +\,1.5552\frac{k_9 }{m_{10} }-1.7937\frac{k_{10} }{m_{10} }+0.89517\frac{k_7 }{m_8 }\\&\quad \left. +\,1.5869\frac{k_1 }{m_1 }-1.3098\frac{k_8 }{m_8 }\right) \end{aligned}$$

$$\begin{aligned} k_{21}&= 10^{-8}\left( -0.0073538\frac{k_5 }{m_6 }+0.48086\frac{k_6 }{m_6 }\right. \\&\quad +\,0.18178\frac{k_s }{m_{12} }-\,1.1199\frac{k_8 }{m_9 }+1.3582\frac{k_9 }{m_9 }\\&\quad +2.2124\frac{k_1 }{m_2 }-\,1.5733\frac{k_2 }{m_2 }+0.91057\frac{k_3 }{m_4 } \\&\quad -\,0.54315\frac{k_4 }{m_4 }+0.49602\frac{k_4 }{m_5 }-0.0069134\frac{k_5 }{m_5 }\\&\quad -\,1.7759\frac{k_{10} }{m_{11} }-0.46906\frac{k_6 }{m_7 }+0.83512\frac{k_7 }{m_7 }\\&\quad +\,1.4139\frac{k_2 }{m_3 }+1.0056\frac{k_3 }{m_3 } \\&\quad -\,1.4504\frac{k_9 }{m_{10} }+1.6295\frac{k_{10} }{m_{10} }-0.83501\frac{k_7 }{m_8 }\\&\quad \left. -\,2.5053\frac{k_1 }{m_1 }+1.0871\frac{k_8 }{m_8 }\right) \\ k_{22}&= 10^{-8}\left( -2.8136\frac{k_5 }{m_6 }\!+\!1.3556\frac{k_6 }{m_6 }\!+\!0.12565\frac{k_s }{m_{12} }\right. \\&\quad -\,2.4191\frac{k_8 }{m_9 }+3.0657\frac{k_9 }{m_9 }+4.4024\frac{k_1 }{m_2 }\\&\quad -\,2.3578\frac{k_2 }{m_2 }+2.255\frac{k_3 }{m_4 } \\&\quad -\,1.2115\frac{k_4 }{m_4 }+0.29045\frac{k_4 }{m_5 }-1.3564\frac{k_5 }{m_5 }\\&\quad -\,1.2821\frac{k_{10} }{m_{11} }\\&\quad +\,2.309\frac{k_6 }{m_7 }+2.9876\frac{k_7 }{m_7 }-1.9562\frac{k_2 }{m_3 }\\&\quad -\,2.2111\frac{k_3 }{m_3 } \\&\quad +\,2.414\frac{k_9 }{m_{10} }-2.0539\frac{k_{10} }{m_{10} }-2.0539\frac{k_7 }{m_8 }\\&\quad \left. -\,2.6678\frac{k_1 }{m_1 }+2.9474\frac{k_8 }{m_8 }\right) \end{aligned}$$

$$\begin{aligned} f_1&= -\frac{0.13413}{M_1 }f_{1x} -\frac{0.044593}{M_1 }f_{1y} -\frac{0.12501}{M_{11} }f_{2x} \\&\quad -\,\frac{0.069826}{M_{11} }f_{2y} -\frac{0.037437}{M_{12} }f_{1y}\\ f_{1x}&= f_x (-0.31552p_1 -0.012433p_2 , 0.001973p_1\\&\quad +\,0.34105p_2 \\&\quad -\,0.34855\dot{p}_1 +0.011375\dot{p}_2 , 0.014298\dot{p}_1\\&\quad +\,0.35867\dot{p}_2 ) \\ f_{1y}&= f_y (-0.31546p_1 -0.012273p_2 , 0.001477p_1\\&\quad +\,0.32505p_2 \\&\quad -\,0.35955\dot{p}_1 +0.010275\dot{p}_2 , 0.016298\dot{p}_1\\&\quad +\,0.35797\dot{p}_2 ) \\ f_{\omega 1}&= -0.25064b_2 \cos t-0.31546b_3 \cos t\\&\quad -\,0.35955b_4 \cos t-0.38562b_5 \cos t\\&\quad -\,0.38513b_6 \cos t-0.36766b_7 \cos t \\&\quad -\,0.33216b_8 \cos t-0.27792b_9 \cos t\\&\quad -\,0.20586b_{10} \cos t+0.001592b_8 \sin t\\&\quad +\,0.016822b_7 \sin t+0.016298b_4 \sin t \\&\quad -\,0.018518b_9 \sin t+0.025132b_5 \sin t\\&\quad +\,0.025196b_6 \sin t-0.019256b_2 \sin t\\&\quad +\,0.001477b_3 \sin t-0.042671b_{10} \sin t \end{aligned}$$

$$\begin{aligned} f_2&= -\frac{0.074424}{M_1 }f_{1x} +\frac{0.18468}{M_1 }f_{1y} -\frac{0.069966}{M_{11} }f_{2x} \\&\quad +\,\frac{0.1402}{M_{11} }f_{2y} -\frac{0.025876}{M_{12} }f_{1y}\\ \end{aligned}$$

$$\begin{aligned} f_{2x}&= f_x (-0.38562p_1 +0.02587p_2 , 0.025132p_1\\&\quad +\,0.37556p_2 \\&\quad -\,0.38513\dot{p}_1 +0.031192\dot{p}_2 , 0.025196\dot{p}_1\\&\quad +\,0.37107\dot{p}_2 ) \\ f_{2y}&= f_y (-0.36766p_1 +0.02568p_2 , 0.016822p_1\\&\quad +\,0.35207p_2 \\&\quad -\,0.33216\dot{p}_1 +0.011157\dot{p}_2 , 0.001592\dot{p}_1\\&\quad +\,0.31818\dot{p}_2 ) \end{aligned}$$

$$\begin{aligned} f_{\omega 2}&= -0.041395b_2 \cos t-0.012273b_3 \cos t\\&\quad +\,0.010275b_4 \cos t+0.02587b_5 \cos t\\&\quad +\,0.031192b_6 \cos t+0.025681b_7 \cos t \\&\quad +\,0.01157b_8 \cos t-0.01009b_9 \cos t\\&\quad -\,0.037572b_{10} \cos t+0.31818b_8 \sin t\\&\quad +\,0.35207b_7 \sin t+0.35797b_4 \sin t \\&\quad +\,0.26956b_9 \sin t+0.37556b_5 \sin t\\&\quad +\,0.27497b_6 \sin t+0.32505b_2 \sin t\\&\quad +\,0.001477b_3 \sin t+0.20792b_{10} \sin t \\ g_1&= 0.07091G, g_2 =3.2031G \end{aligned}$$