Non-smooth bifurcation control of non-smooth systems with a canonical form

Abstract

In this paper, we investigated non-smooth bifurcation control of a piecewise-linear continuous system with a canonical form for the first time. We presented the conditions under which the system has only one stable or unstable equilibrium point. Furthermore, we eliminated some non-smooth bifurcations of the system, by designing two controllers, such as simultaneous feedback controller and switched feedback controller. Simultaneous feedback controller is linear, and switched feedback controller is piecewise-linear, which have all a simple structure and available control properties. Numerical simulations showed that these methods were effective.

1 Introduction

Piecewise-linear continuous systems are the natural extension to linear systems in order to capture nonlinear systems. They have rich dynamical behaviors such as limit cycles, homoclinic and heteroclinic orbits, and stranger attractor, which is almost same to that of general nonlinear systems. Generally, we study the bifurcation of piecewise smooth continuous systems by using the piecewise-linearized representation. We consider a planar piecewise-linear continuous system with the special form:

$$\begin{aligned} \dot{X}=f(X)=\left\{ { \begin{array}{ll} J_{L}X+C1&{}\quad \hbox {for}\;x\le 0 \\ J_{R}X+C1&{}\quad \hbox {for}\;x>0 \\ \end{array}}\right. , \end{aligned}$$

(1)

where $X\!=\!\left[ {{\begin{array}{l} x \\ y \\ \end{array}}}\right] ,\,J_{L}=\left[ {{\begin{array}{ll} {l_{11}}&{} {a_{12}} \\ {l_{21}}&{} {a_{22}} \\ \end{array}}}\right] ,J_{R}=\left[ {{\begin{array}{ll} {r_{11}}&{} {a_{12}} \\ {r_{21}}&{} {a_{22}} \\ \end{array}}}\right] ,C1=\left[ {{\begin{array}{l} {c_{1}} \\ {c_{2}} \\ \end{array}}}\right]$. It is noted that switching boundary function $h(x)\!=\!x\!=\!0$ separates the space $R^{2}$ into three domains: $v_{-} =\left\{ {(x,y)\left| {h(x)\!<\!0} \right. } \right\}$, $\Sigma =\left\{ {(x,y)\left| {h(x)\!=0} \right. } \right\}$ and $v_{+} =\left\{ {(x,y)\left| {h(x)>0} \right. } \right\}$, where $\Sigma$ is a switching boundary. System (1) has eight parameters, which leads to the complexity in analyzing it.

The existence of a canonical form with fewer parameters helps us to descript the dynamical behavior of this system. For example, canonical forms of a system can be useful to analyze its properties and sometimes to derive theoretical proofs of asymptotic stability [1]. For piecewise-linear continuous systems, some authors initially derived piecewise-linear canonical representations to facilitate the design of nonlinear electrical circuits and their analysis [2]. Recently, various equivalent state space representations and transformations have been proposed to fulfill different theoretical aims. Canonical forms have been used as a tool for the analysis and classification of so called discontinuity-induced bifurcation phenomena [3], which is also called non-smooth bifurcation. Moreover, canonical forms of piecewise-linear systems have been talked in [4–6]. By using a linear change of variables, system (1) can be transformed into the canonical form (Liénard’s form) [7]:

$$\begin{aligned} \dot{X}=f(X)=\left\{ { \begin{array}{ll} A_{L}X+C&{}\quad \hbox {for}\;x\le 0 \\ A_{R}X+C&{}\quad \hbox {for}\;x>0 \\ \end{array}}\right. , \end{aligned}$$

(2)

where $X\!=\!\left[ {{\begin{array}{l} x \\ y \\ \end{array}}}\right] ,A_{L}=\left[ {{ \begin{array}{l@{\quad }l} t&{} 1 \\ {-d}&{} 0 \\ \end{array}}}\right] ,A_{R}=\left[ {{ \begin{array}{l@{\quad }l} T&{} 1 \\ {-D}&{} 0 \\ \end{array}}}\right] ,C=\left[ {{ \begin{array}{l} 0 \\ a \\ \end{array}}}\right]$. Similarly, $h(x)=0$ still separates the space $R^{2}$ into three domains: $v_{-}$, $\Sigma$ and $v_{+}$, and system (2) has only five parameters. Suppose that $t,T,d$ and $D$ are unequal to zero.

It has been noted that piecewise smooth continuous (PWSC) systems can exhibit a unique class of bifurcation phenomena, called non-smooth bifurcations expect for classical bifurcations such as folds and Hopf bifurcations. Leine gave a definition of non-smooth bifurcation and presented that multiple crossing bifurcations can occur in PWSC systems [8–10]. Especially for piecewise-linear continuous system (1), it can be transformed into a canonical form with four parameters when it has a limit cycle, and its Hopf bifurcations have been investigated [11, 12]. Xu studied homoclinic orbits and homoclinic bifurcations of system (2) [13].

As the development of the bifurcation, bifurcation control as an emerging research filed has become challenging and stimulating. It involves designing a control input for a system to result in desired modification to the system’s bifurcation behavior. Typical bifurcation control objectives include delaying the onset of an inherent bifurcation [14], introducing a new bifurcation at a preferable parameter value [15], changing the parameter value of an existing bifurcation point [16], modifying the shape or type of a bifurcation chain [17], etc. Bifurcation is often considered as undesirable and should be eliminated. Although some authors investigated the bifurcation control, their object is mainly classical bifurcation. At the same time, non-smooth bifurcation is theoretically not well developed, and few authors took care of non-smooth bifurcation control for non-smooth systems. Especially no author investigated the non-smooth bifurcation control of system (2). On the other hand, bifurcation and chaos usually occur as “twins,” and chaos control of non-smooth systems has been investigated by many authors [17–20], which also encourages us to study non-smooth bifurcation control of non-smooth systems. Hassouneh derived a sufficient condition for non-bifurcation with persistent stability for piecewise smooth discrete-time systems by Lyapunov and linear matrix inequality (LMI) techniques [21]. In this paper, we will furthermore expand the way to study the bifurcation control of system (2). The organization of this paper is as follows:

In Sect. 2, we will design two controllers: simultaneous feedback controller and switched feedback controller, which eliminate non-smooth bifurcations of system (2). In Sect. 3, numerical simulations show that these methods are effective. Finally, the conclusion is drawn.

2 Non-smooth bifurcation control of system (2)

In this section, in order to eliminate non-smooth bifurcations of system (2), we will firstly give the conditions under which system (2) has non-smooth bifurcation with persistent stability or instability for any $a\in R$. Let $E_{-} =\left( {{ \begin{array}{ll} {\frac{a}{d}}&{} {-\frac{ta}{d}} \\ \end{array}}}\right)$ and $E_{+} =\left( {{ \begin{array}{ll} {\frac{a}{D}}&{} {-\frac{Ta}{D}} \\ \end{array}}}\right)$. It is noted that system (2) has one equilibrium point $E_{-}$ or $E_{+}$ for $dD>0$, while it either has two equilibria $E_{-}$ and $E_{+}$ or has no equilibrium point for $dD<0$.

Theorem 1

System (2) has an asymptotically stable equilibrium point for any $a\in R$ if

• (1) $d>0,t<0$;

• (2) $D>0,T<0$;

• (3) there exist $a_{1}>0,a_{2}<0,a_{3}>0$ satisfied with $4a_{2}(a_{1}t-a_{2}d)-(a_{1}+a_{2}t-a_{3}d)^{2}>0$, $4a_{2}(a_{1}T-a_{2}D)-(a_{1}+a_{2}T-a_{3}D)^{2}>0$, $a_{2}>\frac{t}{d}a_{1}$, $a_{2}>\frac{T}{D}a_{1}$ and $a_{1}a_{3}-a_{2}^{2}>0$.

Proof

If $d>0$ and $D>0$, i.e., $dD>0$, system (2) has only one equilibrium point for $a\in R$. In the following, we study the stability of this equilibrium point by two cases.

(i) $a\le 0$

System (2) has an equilibrium point $E_{-} \!=\!\left( {{\begin{array}{ll} {\frac{a}{d}}&{} {-\frac{ta}{d}} \\ \end{array}}}\right)$. Let $z_{1}=x-\frac{a}{d}$ and $z_{2}=y+\frac{ta}{d}$, system (2) is rewritten to

$$\begin{aligned} \dot{Z}=f(Z)=\left\{ { \begin{array}{ll} A_{L}Z&{}\quad \hbox {for}\;z_{1}\le -\frac{a}{d} \\ A_{R}Z+C_{1}a&{}\quad \hbox {for}\;z_{1}>-\frac{a}{d} \\ \end{array}} \right. , \end{aligned}$$

(3)

where $Z=\left[ {{\begin{array}{l} {z_{1}} \\ {z_{2}} \\ \end{array}}}\right] ,C_{1}=\left[ {{\begin{array}{l} {\frac{T-t}{d}} \\ {\frac{d-D}{d}} \\ \end{array}}}\right]$. Let the Lyapunov function:

$$\begin{aligned} v(Z)=Z^{T}PZ, \end{aligned}$$

where $P=\left[ {{\begin{array}{ll} {a_{1}}&{} {a_{2}} \\ {a_{2}}&{} {a_{3}} \\ \end{array}}}\right] >0$ for $a_{1}>0,a_{3}>0,a_{1}a_{3}-a_{2}^{2}>0$. For $z_{1}\le -\frac{a}{d}$, we have

$$\begin{aligned} \dot{v}(t)= & {} \dot{v}_{L}(t)=\dot{Z}^{T}PZ+Z^{T}P\dot{Z} \nonumber \\= & {} Z^{T}\left( A_{L}^{T}P+PA_{L}\right) Z, \end{aligned}$$

(4)

For $z_{1}>-\frac{a}{d}$, we have

$$\begin{aligned} \dot{v}(t)= & {} \dot{v}_{R}(t)=\dot{Z}^{T}PZ+Z^{T}P\dot{Z}\nonumber \\= & {} Z^{T}\left( A_{R}^{T}P+PA_{R}\right) Z+aC_{1}^{T}PZ+aZ^{T}PC_{1}\nonumber \\= & {} (Z-\alpha )^{T}\left( A_{R}^{T}P+PA_{R}\right) (Z-\alpha )\nonumber \\&+ \,\,\alpha ^{T}\left( A_{R}^{T}P+PA_{R}\right) \alpha , \end{aligned}$$

(5)

where $\alpha =-a(A_{R}^{T}P+PA_{R})^{-1}PC_{1}$. The conditions of Theorem 1 show that $a_{1}t-a_{2}d<0, \, 4a_{2}(a_{1}t-a_{2}d)-(a_{1}+a_{2}t-a_{3}d)^{2}>0$, $4a_{2}(a_{1}T-a_{2}D)-(a_{1}+a_{2}T-a_{3}D)^{2}>0$, $a_{1}T-a_{2}D<0$, i.e., $A_{L}^{T}P+PA_{L}<0$ and $A_{R}^{T}P+PA_{R}<0$. In what follows, we will prove that $\dot{v}(t)$ is negative definite if $A_{L}^{T}P+PA_{L}<0$ and $A_{R}^{T}P+PA_{R}<0$.

If $A_{L}^{T}P+PA_{L}<0$, $\dot{v}=\dot{v}_{L}<0$ for $\forall Z\ne \left( {{\begin{array}{ll} 0&{} 0 \\ \end{array}}}\right) ^{T}$ from (4). It remains to show that $\dot{v}=\dot{v}_{R}<0$. Due to the continuity of $v$ and system (2), $\dot{v}$ is continuous for all $Z$, which induces to $\dot{v}_{R}<0$ at the border $\left\{ {z_{1}=-\frac{a}{d}} \right\}$. If $\frac{d^{2}\dot{v}_{R}}{dZ^{2}}=A_{R}^{T}P+PA_{R}<0$ from (5), $\dot{v}_{R}$ is strictly convex. For any $Z$, $Y$, and $\theta \in \left( {0,1}\right)$, $\dot{v}_{R}(\theta Z+(1-\theta )Y)>\theta \dot{v}_{R}(Z)+(1-\theta )\dot{v}_{R}(Y)$. Next, we will show that $\dot{v}_{R}<0$ for any$\;z_{1}>-\frac{a}{d}$ by contradiction. Suppose there is a $Y>-\frac{a}{d}$ such that $\dot{v}_{R}(Y)\ge 0$, then $\dot{v}_{R}$ is positive along the line segment connecting 0 and $Y$: $\dot{v}_{R}(\theta 0+(1-\theta )Y)>\theta \dot{v}_{R}(0)+(1-\theta )\dot{v}_{R}(Y)\ge 0$. But there is a $Z^{*}$ with $z_{1}^{*}=-\frac{a}{d}$ along the line, where $\dot{v}_{R}(Z^{*})<0$, which is a contradiction. Then $\dot{v}(t)=\dot{v}_{R}<0$ for $z_{1}>-\frac{a}{d}$. And $\dot{v}=\dot{v}_{L}<0$ for $z_{1}\le -\frac{a}{d}$. Hence $\dot{v}(t)<0$, i.e., $E_{-}$ is asymptotically stable for $a\le 0$.

(ii) $a>0$

System (2) has an equilibrium point $E_{+} \!=\!\left( \!{{ \begin{array}{ll} {\frac{a}{D}}&{} {-\frac{Ta}{D}} \\ \end{array}}}\!\right)$. Similarly we can prove that $E_{+}$ is asymptotically stable for $a>0$ if the conditions of Theorem 1 hold. The proof is finished. $\square$

Theorem 2

System (2) has an unstable equilibrium point for any $a\in R$ if

• (1) $d>0$, $t>0;$

• (2) $D>0$, $T>0;$

• (3) there exist $a_{1}>0,a_{2}>0,a_{3}>0$ satisfied with $4a_{2}(a_{1}t-a_{2}d)-(a_{1}+a_{2}t-a_{3}d)^{2}>0$, $4a_{2}(a_{1}T-a_{2}D)-(a_{1}+a_{2}T-a_{3}D)^{2}>0$, $a_{2}<\frac{t}{d}a_{1}$, $a_{2}<\frac{T}{D}a_{1}$ and $a_{1}a_{3}-a_{2}^{2}>0$.

We only give the proof for $a>0$. The same way can be the case for $a\le 0$. For $a>0$, system (2) has an equilibrium point $E_{+} =\left( {{\begin{array}{ll} {\frac{a}{D}}&{} {-\frac{Ta}{D}} \\ \end{array}}}\right)$.

Let $z_{1}=x-\frac{a}{D}$ and $z_{2}=y+\frac{Ta}{D}$, system (2) is rewritten to

$$\begin{aligned} \dot{Z}=f(Z)=\left\{ { \begin{array}{ll} A_{L}Z+C_{2}a&{}\quad \hbox {for}\;z_{1}\le -\frac{a}{D} \\ A_{R}Z&{}\quad \hbox {for}\;z_{1}>-\frac{a}{D} \\ \end{array}} \right. , \end{aligned}$$

where $Z=\left[ {{\begin{array}{l} {z_{1}} \\ {z_{2}} \\ \end{array}}}\right] ,C_{2}=\left[ {{\begin{array}{l} {\frac{t-T}{D}} \\ {\frac{D-d}{D}} \\ \end{array}}}\right]$. Let the Lyapunov function:

$$\begin{aligned} v(Z)=Z^{T}PZ, \end{aligned}$$

where $P=\left[ {{\begin{array}{ll} {a_{1}}&{} {a_{2}} \\ {a_{2}}&{} {a_{3}} \\ \end{array}}}\right] >0$. For $z_{1}>-\frac{a}{D}$, we have

$$\begin{aligned} \dot{v}(t)= & {} \dot{v}_{R}(t)=\dot{Z}^{T}PZ+Z^{T}P\dot{Z} \\= & {} Z^{T}\left( A_{R}^{T}P+PA_{R}\right) Z. \end{aligned}$$

For $z_{1}\le -\frac{a}{D}$, we also have

$$\begin{aligned} \dot{v}(t)= & {} \dot{v}_{L}(t)=\dot{Z}^{T}PZ+Z^{T}P\dot{Z} \\= & {} Z^{T}\left( A_{L}^{T}P+PA_{L}\right) Z+aC_{2}^{T}PZ+aZ^{T}PC_{2}\\= & {} (Z-\alpha )^{T}\left( A_{L}^{T}P+PA_{L}\right) (Z-\alpha )\\&+ \,\,\alpha ^{T}\left( A_{L}^{T}P+PA_{L}\right) \alpha , \end{aligned}$$

where $\alpha =-a\left( A_{L}^{T}P+PA_{L}\right) ^{-1}PC_{2}$. Similarly the conditions of Theorem 2 present that that $A_{L}^{T}P+PA_{L}>0$ and $A_{R}^{T}P+PA_{R}>0$. In what follows, we will show that $\dot{v}(t)$ is positive definite if $A_{L}^{T}P+PA_{L}>0$ and $A_{R}^{T}P+PA_{R}>0$.

If $A_{R}^{T}P+PA_{R}>0$, $\dot{v}=\dot{v}_{R}>0$ for $\forall Z\ne \left( {{\begin{array}{ll} 0&{} 0 \\ \end{array}}}\right) ^{T}$. Due to the continuity of $v$ and system (2), $\dot{v}$ is continuous for all $Z$, which induces to $\dot{v}_{L}>0$ at the border $\left\{ {z_{1}=-\frac{a}{D}} \right\}$. Similarly $\frac{d^{2}\dot{v}_{L}}{dZ^{2}}=A_{L}^{T}P+PA_{L}>0$ implies that $\dot{v}_{L}$ is strictly concave, i.e., $\dot{v}_{L}(\theta Z+(1-\theta )Y)<\theta \dot{v}_{L}(Z)+(1-\theta )\dot{v}_{L}(Y)$ for any $Z,Y$ and $\theta \in \left( {0,1}\right)$. Suppose there is a $Y<-\frac{a}{D}$ such that $\dot{v}_{L}(Y)\le 0$, then $\dot{v}_{L}(\theta 0+(1-\theta )Y)<\theta \dot{v}_{L}(0)+(1-\theta )\dot{v}_{L}(Y)\le 0$ for the line segment connecting 0 and $Y$. But there is a $Z^{*}$ with $z_{1}^{*}=-\frac{a}{D}$ such that $\dot{v}_{L}(Z^{*})>0$, which is a contradiction. Then $\dot{v}(t)=\dot{v}_{L}>0$ for $z_{1}<-\frac{a}{D}$. Hence $\dot{v}(t)>0$, i.e., $E_{+}$ is unstable for $a>0$.

It is noted that when the conditions of Theorem 1 and Theorem 2 hold, system (2) has no bifurcation for parameter $a$. For this, we will design the controllers by two ways in what follows:

(1) Simultaneous feedback control design

We add a static linear state feedback to system (2), where the controller is same both sides of the switching boundary:

$$\begin{aligned} \dot{X}\!=\!f(X)+g(X)\!=\!\left\{ { \begin{array}{ll} A_{L}X+C+UX&{}\quad \hbox {for}\;x\le 0 \\ A_{R}X+C+UX&{}\quad \hbox {for}\;x>0 \\ \end{array}} \right. \!, \end{aligned}$$

(6)

where $U=\left[ {{\begin{array}{l@{\quad }l} {t^{1}}&{} 1 \\ {-d^{1}}&{} 0 \\ \end{array}}}\right]$ and the controller

$$\begin{aligned} g(X)=UX. \end{aligned}$$

(7)

Theorem 3

We design $t^{1},d^{1}$ such that

• (1) $d+d^{1}>0$, $t+t^{1}<0;$

• (2) $D+d^{1}>0$, $T+t^{1}<0;$

• (3) there exist $a_{1}>0,\,a_{2}<0,\,a_{3}>0$ satisfied with $4a_{2}(a_{1}(t+t^{1})-a_{2}(d+d^{1}))-(a_{1}+a_{2}(t+t^{1}) -a_{3}(d+d^{1}))^{2}>0$, $a_{2}>\frac{t+t^{1}}{d+d^{1}}a_{1}$, $a_{2}>\frac{T+t^{1}}{D+d^{1}}a_{1}, 4a_{2}(a_{1}(T+t^{1})-a_{2}(D+d^{1}))-(a_{1} +a_{2}(T+t^{1})-a_{3}(D+d^{1}))^{2}>0$, and $a_{1}a_{3}-a_{2}^{2}>0$, then the controlled system (6) has non-bifurcation with persistent stability for any $a\in R$.

Proof

System (6) is rewritten as

$$\begin{aligned} \dot{X}\!=\!f(X)+g(X)\!=\!\left\{ { \begin{array}{ll} (A_{L}+U)X+C&{}\quad \hbox {for}\;x\le 0 \\ (A_{R}+U)X+C&{}\quad \hbox {for}\;x>0 \\ \end{array}} \right. , \end{aligned}$$

where $A_{L}+U=\left[ {{\begin{array}{l@{\quad }l} {t+t^{1}}&{} 1 \\ {-(d+d^{1})}&{} 0 \\ \end{array}}}\right]$ and $A_{R}+U=\left[ {{\begin{array}{l@{\quad }l} {T+t^{1}}&{} 1 \\ {-(D+d^{1})}&{} 0 \\ \end{array}}}\right]$. According to Theorem 1, the conclusion can be obtained. $\square$

Theorem 4

We design $t^{1},d^{1}$ such that

• (1) $d+d^{1}>0$, $t+t^{1}>0;$

• (2) $D+d^{1}>0$, $T+t^{1}>0;$

• (3) there exist $a_{1}>0,\,a_{2}>0,\,a_{3}>0$ satisfied with $a_{2}<\frac{t+t^{1}}{d+d^{1}}a_{1}$, $a_{2}<\frac{T+t^{1}}{D+d^{1}}a_{1}$, $4a_{2}(a_{1}(t+t^{1})-a_{2}(d+d^{1}))-(a_{1}+a_{2}(t+t^{1}) -a_{3}(d+d^{1}))^{2}>0$, $4a_{2}(a_{1}(T+t^{1})-a_{2}(D+d^{1})) -(a_{1}+a_{2}(T+t^{1})-a_{3}(D+d^{1}))^{2}>0$, and $a_{1}a_{3}-a_{2}^{2}>0$, then the controlled system (6) has non-bifurcation with persistent instability for any $a\in R$.

The proof is referred to Theorem 2.

(2) Switched feedback control design

Now we consider the closed-loop system by static piecewise-linear state feedback, where the controller is not same both sides of the switching boundary:

$$\begin{aligned} \dot{X}\!=\!f(X)+g(X)\!=\!\left\{ { \begin{array}{ll} A_{L}X+C+U_{1}X&{}\quad \hbox {for}\;x\le 0 \\ A_{R}X+C+U_{2}X&{}\quad \hbox {for}\;x>0 \\ \end{array}} \right. , \end{aligned}$$

(8)

where $U_{1}=\left[ {{\begin{array}{ll} {t_{1}}&{} 1 \\ {-d_{1}}&{} 0 \\ \end{array}}}\right]$, $U_{2}=\left[ {{ \begin{array}{ll} {T_{1}}&{} 1 \\ {-D_{1}}&{} 0 \\ \end{array}}}\right]$ and the controller

$$\begin{aligned} g(X)=\left\{ { \begin{array}{ll} U_{1}X&{}\quad \hbox {for}\;x\le 0 \\ U_{2}X&{}\quad \hbox {for}\;x>0 \\ \end{array}} \right. . \end{aligned}$$

(9)

Theorem 5

We design $t_{1},d_{1},T_{1},D_{1}$ such that

• (1) $d+d_{1}>0$, $t+t_{1}<0;$

• (2) $D+D_{1}>0$, $T+T_{1}<0;$

• (3) there exist $a_{1}>0,\,a_{2}<0,\,a_{3}>0$ satisfied with $a_{2}>\frac{t+t_{1}}{d+d_{1}}a_{1}$, $a_{2}>\frac{T+T_{1}}{D+D_{1}}a_{1}$, $4a_{2}(a_{1}(t+t_{1})-a_{2}(d+d_{1}))-(a_{1}+a_{2}(t+t_{1}) -a_{3}(d+d_{1}))^{2}>0$, $4a_{2}(a_{1}(T+T_{1})-a_{2}(D+D_{1}))-(a_{1}+a_{2}(T+T_{1}) -a_{3}(D+D_{1}))^{2}>0$, and $a_{1}a_{3}-a_{2}^{2}>0$, then the controlled system (8) has non-bifurcation with persistent stability for any $a\in R$.

The proof is referred to Theorem 1.

Theorem 6

We design $t_{1},d_{1},T_{1},D_{1}$ such that

• (1) $d+d_{1}>0$, $t+t_{1}>0;$

• (2) $D+D_{1}>0$, $T+T_{1}>0;$

• (3) there exist $a_{1}>0,\,a_{2}>0,\,a_{3}>0$ satisfied with $a_{2}<\frac{t+t_{1}}{d+d_{1}}a_{1}$, $a_{2}>\frac{T+T_{1}}{D+D_{1}}a_{1}$, $4a_{2}(a_{1}(t+t_{1})-a_{2}(d+d_{1}))-(a_{1}+a_{2}(t+t_{1}) -a_{3}(d+d_{1}))^{2}>0$, $4a_{2}(a_{1}(T+T_{1})-a_{2}(D+D_{1}))-(a_{1}+a_{2}(T+T_{1}) -a_{3}(D+D_{1}))^{2}>0$, and $a_{1}a_{3}-a_{2}^{2}>0$, then the controlled system (8) has non-bifurcation with persistent instability for any $a\in R$.

The proof is referred to Theorem 2.

In order to verify the correctness of these methods, we will present some numerical simulations.

3 Numerical simulations

In this section, we firstly present the definition about non-smooth bifurcation.

Definition 1

(Non-smooth Bifurcation) [10]. Let $x_{\mu }$ be an equilibrium point, depending on $\mu \in R$, of a non-smooth continuous system $\dot{x}=f(x,\mu )$ which has a finite number of switching boundaries $\Sigma _{j},j=1,\ldots ,k$. Let $x_\mu =x_{\Sigma }$ for $\mu =\mu _{\Sigma }$ be an equilibrium point located on one or more switching boundaries, i.e., $x_{\Sigma } \in \Sigma _{1}\cap \Sigma _{2}\cdots \cap \Sigma _{l},1\le l\le k$. Let $(x_{\Sigma }, \mu _{\Sigma })$ be a bifurcation point. A bifurcation point $(x_{\Sigma },\mu _{\Sigma })$ is a non-smooth bifurcation point if the generalized Jacobian $J(x_{\Sigma }, \mu _{\Sigma })$ is set-valued and if there exists an $i$ such that $0\in \hbox {Re}(\lambda _{i}),\,\lambda =\hbox {eig}(J(x_{\Sigma }, \mu _{\Sigma }))$.

Note that $J(x_{\Sigma }, \mu _{\Sigma })$ is a generalized Jacobian matrix. According to Definition 1, we will give some non-smooth bifurcations of system (2) when the parameter $a$ varies. At $a=0$, the system has one equilibrium point $E_{0}=({\begin{array}{ll} 0&{} 0 \\ \end{array}})$. For it lies in the switching boundary $\Sigma$, $E_{0}$ is a boundary equilibrium point, whose generalized Jacobian matrix is

$$\begin{aligned} J(E_{0})=qA_{L}+(1-q)A_{R} \quad \left( q\in \left[ {0,1}\right] \right) . \end{aligned}$$

(10)

The generalized characteristic polynomial is

$$\begin{aligned} P_{q}(\lambda )=\lambda ^{2}-\left[ {qt+(1-q)T}\right] \lambda +qd+(1-q)D=0. \end{aligned}$$

(11)

Lemma 1

A non-smooth bifurcation of $E_{0}$ occurs at $a=0$ if at least one of the following conditions holds:

• (1) $dD<0$;

• (2) $tT<0,d>\frac{t}{T}D$;

Proof

According to definition 1, a non-smooth bifurcation occurs if the generalized characteristic polynomial (11) at least has zero root or a pair of pure imaginary for certain $q\in [0,1]$. when $dD<0$, there must exist $q=\frac{D}{D-d}\in [0,1]$ ensuring that (11) has zero root. If $tT<0$, there must exist $q=\frac{T}{T-t}\in [0,1]$ such that $qt+(1-q)T=0$. Furthermore, if $d>\frac{t}{T}D$, i.e., $\frac{\mathrm{d}T-tD}{T}>0$, then $\frac{\mathrm{d}T-tD}{T}\frac{T}{T-t}>0$, i.e., $qd+(1-q)D>0$, which implies that (11) has a pair of pure imaginary. The proof is finished. $\square$

Proposition 1

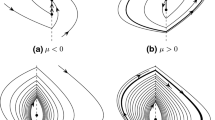
A non-smooth turning point bifurcation of $E_{0}$ occurs at $a=0$ for $dD<0$ and $tT>0$.

Proof

By Lemma 1, a non-smooth bifurcation of $E_{0}$ occurs at $a=0$ for $dD<0$. That $dD<0$ and $tT>0$ means that $d<0,D>0,T>0,t>0$, $d<0,D>0,T<0,t<0$, $d>0,D<0,T>0,t>0$ and $d>0,D<0,T<0,t<0$. We only give the proof for $d<0,D>0,T>0,t>0$. Similar conclusions can also be drawn for other cases. For $d<0,D>0$, system (2) has no equilibrium point for $a<0$, one boundary equilibrium point $E_{0}$ at $a=0$, and two equilibria $E_{-}$ and $E_{+}$ for $a>0$. Furthermore, $E_{-}$ is a saddle point and $E_{+}$ is an unstable focus or node for $d<0,D>0,T>0,t>0$. Then it is a non-smooth turning point bifurcation. The proof is finished. $\square$

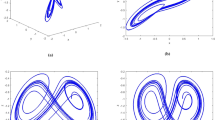
For example, we take $d=-1<0,D=3>0,T=5>0,t=4>0$ and $a\in [-1,1]$. Figure 1a indicates the non-smooth bifurcation structure, where unstable equilibrium points are described by dotted lines. We will describe stable equilibrium points by solid lines later. The path of the set-valued eigenvalues crosses the imaginary axis through the origin indicated in Fig. 1b.

Fig. 1

Take $d=-1<0,D=3>0,T=5>0,t=4>0$ and $a\in [-1,1]$, a bifurcation diagram of system (2), b path of set-valued eigenvalues of $J(E_{0})$

Firstly we will eliminate the non-smooth turning point bifurcation of system (2), where the controlled system is persistently stable. We add the controller (7) to system (2) and obtain a controlled system (6). We take $t^{1}=-6,d^{1}=4$. At this time, $d+d^{1}=3>0$, $t+t^{1}=-2<0$, $D+d^{1}=7>0$, $T+t^{1}=-1<0$ are satisfied with the first and second conditions of Theorem 3. There are $a_{1}=8,a_{2}=-1,a_{3}=1.5$ such that the third condition of Theorem 3 holds. For any $a\in R$, the controlled system (6) is asymptotically stable and system (6) has no bifurcation, which is depicted in Fig. 2a. Numerical conclusion shows that we can eliminate the turning point bifurcation of system (2) by the controller (7), where the equilibrium point is stable for any $a$. We add the controller (9) to system (2) and take $t_{1}=-5,d_{1}=7,T_{1}=-6,D_{1}=0$, i.e., $d+d_{1}=6>0$, $t+t_{1}=-1<0$, $D+D_{1}=3>0$, $T+T_{1}=-1<0$, which is satisfied with the first and second conditions of Theorem 5. There exist $a_{1}=8,a_{2}=-1,a_{3}=1.8$ satisfied with the third condition of Theorem 5. Thus no bifurcation exists, and the equilibrium point is asymptotically stable for any $a\in R$ in the controlled system (8). Figure 2b shows the corresponsive bifurcation diagram. Numerical conclusion also shows that we can eliminate the bifurcation of system (2) by the controller (9), where the equilibrium point is also stable for any $a$.

Fig. 2

Bifurcation diagram for $d=-1,D=3,T=5,t=4$, $a\in [-1,1]$, a controlled system (6) at $t^{1}=-6,d^{1}=4$, b controlled system (8) at $t_{1}=-5,d_{1}=7,T_{1}=-6,D_{1}=0$.

Secondly we will eliminate the non-smooth turning point bifurcation of system (2), where the controlled system is persistently unstable. For the controlled system (6), we take $t^{1}=-3,d^{1}=4$. At this time, $d+d^{1}=3\,{>}\,0$, $t+t^{1}=1\,{>}\,0$, $D+d^{1}=7\,{>}\,0$, $T+t^{1}=2\,{>}\,0$. There are $a_{1}=4,a_{2}=1,a_{3}=1.1$ such that the conditions of Theorem 4 hold. Hence no bifurcation exists in system (6) with unstable equilibrium point for any $a\in R$. The bifurcation diagram is depicted in Fig. 3a, which shows that we can eliminate the turning point bifurcation of system (2) by the controller (7), and the equilibrium point is unstable for any $a$. For the controlled system (8), we take $t_{1}=-3,d_{1}=7,T_{1}=-4,D_{1}=0$, and $a_{1}=8,a_{2}=1,a_{3}=1.8$, which are satisfied with the conditions of Theorem 6. The controlled system (8) has no bifurcation and has unstable equilibrium point for any $a\in R$. Numerical conclusion also shows that the controller (9) is effective depicted in Fig. 3b.

Fig. 3

Bifurcation diagram for $d=-1,D=3,T=5,t=4$, $a\in [-1,1]$, a controlled system (6) at $t^{1}=-3,d^{1}=4$, b controlled system (8) at $t_{1}=-3,d_{1}=7,T_{1}=-4,D_{1}=0$.

Proposition 2

A non-smooth transcritical bifurcation of $E_{0}$ occurs at $a=0$ for $tT<0$, $0<D<\frac{T^{2}}{4}$, $0<d<\frac{t^{2}}{4}$, while a non-smooth Hopf bifurcation appears for $tT<0$, $D>0$, $d>0$ except $tT<0$, $0<D<\frac{T^{2}}{4}$, $0<d<\frac{t^{2}}{4}$.

Proof

For $d>0,D>0$ and $tT<0$, we have $d>\frac{t}{T}D$. By Lemma1, a non-smooth bifurcation of $E_{0}$ may occur at $a=0$. If $t<0,T>0$, $0<d<\frac{t^{2}}{4}$, $0<D<\frac{T^{2}}{4}$, system (2) has a stable node $E_{-}$ for $a<0$, one boundary equilibrium point $E_{0}$ at $a=0$, and an unstable node $E_{+}$ for $a>0$. There does not exist the periodic motion for only one equilibrium point in the interior of every periodic motion is a topological center or a focus [11]. The bifurcation at $a=0$ is a non-smooth transcritical bifurcation. The similar conclusion can be obtained for $t>0,T<0$, $0<D<\frac{T^{2}}{4}$, $0<d<\frac{t^{2}}{4}$. Hence a non-smooth transcritical bifurcation of $E_{0}$ occurs at $a=0$ for $tT<0$, $0<D<\frac{T^{2}}{4}$, $0<d<\frac{t^{2}}{4}$. If $t<0,T>0$, $D>\frac{T^{2}}{4}$, $d>\frac{t^{2}}{4}$, system (2) has a stable focus $E_{-}$ for $a<0$, one boundary equilibrium point $E_{0}$ at $a=0$, and an unstable focus $E_{+}$ for $a>0$. There exists a periodic motion which is stable for $\frac{t}{\sqrt{4d-t^{2}}}+\frac{T}{\sqrt{4D-T^{2}}}<0$ and unstable for $\frac{t}{\sqrt{4d-t^{2}}}+\frac{T}{\sqrt{4D-T^{2}}}>0$ [11], and the bifurcation is a non-smooth Hopf bifurcation. Similarly non-smooth Hopf bifurcations can also be found at $a=0$ for other cases: (1) $t>0,T<0$, $D>\frac{T^{2}}{4}$, $d>\frac{t^{2}}{4}$, (2) $tT<0$, $D<\frac{T^{2}}{4}$, $d>\frac{t^{2}}{4}$, (3) $tT<0$, $D>\frac{T^{2}}{4}$, $d<\frac{t^{2}}{4}$. Thus one non-smooth Hopf bifurcation maybe occur for $tT<0$, $D>0$, $d>0$ except $tT<0$, $0<D<\frac{T^{2}}{4}$, $0<d<\frac{t^{2}}{4}$. $\square$

We take $T=5,t=-4$, $D=3$, $d=1$ and $a\in [-1,1]$, system (2) has a non-smooth transcritical bifurcation shown in Fig. 4a, whose path of the set-valued eigenvalues is presented in Fig. 4b. We can eliminate the non-smooth transcritical bifurcation, where the controlled system is persistently stable. For the controlled system (6), we design $t^{1}=-6,d^{1}=0$, $a_{1}=4,a_{2}=-1,a_{3}=2$. By Theorem 3, the controlled system (6) has one asymptotically stable equilibrium point and has no bifurcation for any $a\in R$ presented in Fig. 5a. Then we investigate the bifurcation control of system (2) by the controller (9). At the same time, we take $t_{1}=0,d_{1}=0,T_{1}=-13,D_{1}=-1$, $a_{1}=2,a_{2}=-1,a_{3}=2$, which is satisfied with all conditions of Theorem 5. Hence no bifurcation exists and the equilibrium point is asymptotically stable in the controlled system (8) for any $a\in R$. The bifurcation diagram is depicted in Fig. 5b. Numerical simulation presents that the controllers (7) and (9) are effective. Similarly we also can eliminate the non-smooth transcritical bifurcation, where the controlled system has only persistently unstable equilibrium point. We take $t^{1}=5,d^{1}=0$, $a_{1}=2,a_{2}=1,a_{3}=1.5$ satisfied with Theorem 4. The controlled system (6) has one unstable equilibrium point and has no bifurcation for any $a\in R$ in Fig. 6a. We take $t_{1}=8,d_{1}=0,T_{1}=3,D_{1}=-1$, $a_{1}=2,a_{2}=1,a_{3}=2$ satisfied with Theorem 6. The controlled system (8) has also one unstable equilibrium point and has no bifurcation for any $a\in R$ in Fig. 6b.

Fig. 4

Take $T=5>0,t=-4<0$, $0<D=3<\frac{T^{2}}{4}$, $0<d=1<\frac{t^{2}}{4}$ and $a\in [-1,1]$, a bifurcation diagram of system (2), b path of set-valued eigenvalues of $J(E_{0})$

Fig. 5

Bifurcation diagram for $T=5,t=-4$, $D=3$, $d=1$, $a\in [-1,1]$, a controlled system (6) at $t^{1}=-6,d^{1}=0$, b controlled system (8) at $t_{1}=0,d_{1}=0,T_{1}=-13,D_{1}=-1$

Fig. 6

Bifurcation diagram for $T=5,t=-4$, $D=3$, $d=1$, $a\in [-1,1]$, a controlled system (6) at $t^{1}=5,d^{1}=0$, b controlled system (8) at $t_{1}=8,d_{1}=0,T_{1}=3,D_{1}=-1$

We take $t=-4,T=2$, $D=2$, $d=5$ and $a\in [-1,1]$, and system (2) has a limit cycle depicted in Fig. 7a. We can eliminate the non-smooth Hopf bifurcation by two different controllers (7) and (9), and the controlled system has stable equilibrium point. For example, we design $t^{1}=-3,d^{1}=0$ and there are $a_{1}=3,a_{2}=-1,a_{3}=2$ such that all conditions of Theorem 3 hold. System (6) has only one asymptotically stable equilibrium point and has no bifurcation, where the limit cycle disappears shown in Fig. 8a. We can also take $t_{1}=0,d_{1}=-4,T_{1}=-10,D_{1}=0$, and there occur $a_{1}=2,a_{2}=-1,a_{3}=2$ satisfied with the conditions of Theorem 5. At the same time, the limit cycle disappears, one equilibrium point is asymptotically stable for any $a\in R$, and no bifurcation exists in the controlled system (8), whose bifurcation diagram is given in Fig. 8b. We can also eliminate the bifurcation by controllers (7) and (9), and the controlled system has unstable equilibrium point. For example, we take $t^{1}=5,d^{1}=0$, $a_{1}=7,a_{2}=1,a_{3}=1.5$. System (6) has one unstable equilibrium point and has no bifurcation by Theorem 4, where the limit cycle disappears shown in Fig. 9a. When we take $t_{1}=8,d_{1}=-4,T_{1}=6,D_{1}=0$, $a_{1}=2,a_{2}=1,a_{3}=2$, the limit cycle and non-smooth Hopf bifurcation disappear and there only exists one unstable equilibrium point in the controlled system (8) by Theorem 6, whose bifurcation diagram is given in Fig. 9b. These numerical simulations show that controllers (7) and (9) are effective on the study of the bifurcation, control.

Fig. 7

Take $t=-4,T=2$, $D=2$, $d=5$, a a limit cycle of system (2) at $a=0.1$, b path of set-valued eigenvalues of $J(E_{0})$ for $a\in [-1,1]$

Fig. 8

Bifurcation diagram for $t=-4,T=2$, $D=2$, $d=5$, $a\in [-1,1]$, a controlled system (6) at $t^{1}=-3,d^{1}=0$, b controlled system (8) at $t_{1}=8,d_{1}=-4,T_{1}=6,D_{1}=0$

Fig. 9

Bifurcation diagram for $t=-4,T=2$, $D=2$, $d=5$, $a\in [-1,1]$, a controlled system (6) at $t^{1}=5,d^{1}=0$, b controlled system (8) at $t_{1}=0,d_{1}=-4,T_{1}=-10,D_{1}=0$

4 Conclusion

Generally we investigate bifurcations of the piecewise smooth continuous system by its linearized system. A canonical form with fewer parameters helps us to analyze the dynamics of the system. Hence in this paper, we mainly studied nonlinear dynamics for a piecewise-linear continuous system (2) with a canonical form. For bifurcation is often considered as undesirable and few authors take care of non-smooth bifurcation control, we design two controllers to eliminate non-smooth bifurcations of system (2). Main conclusions are:

• (1) In order to eliminate non-smooth bifurcations of system (2), we firstly give two conditions under which it has only one stable or unstable equilibrium point for any $a$, which is not investigated by other authors.

• (2) We design simultaneous feedback control and switched feedback control and eliminate non-smooth bifurcations of system (2). At this time, the controlled system has one stable or unstable equilibrium point for any $a\in R$. Moreover they are either liner or piecewise-linear, whose topological structures are simple and easy to be realized in some applications. Numerical examples demonstrate that proposed control techniques are effective. In this paper, we only investigate non-smooth bifurcation control of two-dimension piecewise-linear continuous system. Actually, we also can apply similar controllers to $n$-dimension piecewise—smooth continuous systems and eliminate their non-smooth bifurcations.