1 Introduction

Blind source separation (BSS) techniques aim at recovering the original source signals from observed mixtures based on a few general assumptions about the data. The BSS has much evolved during the last two decades and found a wide range of applications which are currently used in major areas of research such as multichannel telecommunications [61], biomedical signal analysis [18, 42, 51], multispectral astronomical imaging [48], geophysical data processing [57], detection and radar localization [6] and many other applications [27, 32,33,34]. In some simple situations such as in biomedical signal processing [22], each recording of the mixture can be modeled as a weighted sum of the source signals. This model is known as instantaneous mixture. In many real-world applications such as in radio communications [16] and multipath propagation of acoustic signals [35], each recording of the mixture is modeled as a weighted sum of delayed versions of the source signals. This model is called convolutive mixture.

The problem of BSS can be formulated either in the time domain or in the frequency domain. Time-domain BSS methods are computationally cumbersome. Frequency domain BSS techniques are computationally more efficient; moreover, the convolutive mixture is turned into an instantaneous mixture in the frequency domain. The most important hypothesis in BSS is that the sources are mutually independent or, mutually uncorrelated over time. This assumption is exploited by BSS methods to extract the sources. Most techniques of BSS use a cost function as a measure of the statistical independence of sources.

A large number of BSS algorithms have been proposed in the literature. Independent component analysis (ICA) is the conventional statistical method commonly used in BSS. The ICA technique transforms the data vector into a vector whose components are statistically independent. The ICA techniques for BSS are based on high-order statistics to optimize the cost function using maximum likelihood, mutual information, entropy and negentropy and non-Gaussianity measures [2, 9, 10, 15, 43, 44, 52].

Recently, a new ICA algorithm called independent component analysis by entropy bound minimization (ICA-EBM) has been introduced. The technique uses the projected conjugate gradient and accurate estimates of the entropy and can efficiently exploit both the non-circularity and non-Gaussianity to solve the problem of BSS by minimizing mutual information [37]. The major advantage of ICA-EBM is that it does not require any prior knowledge about source distribution. In [25], an extension of the ICA-EBM algorithm called independent component analysis by entropy rate bound minimization (ICA-ERBM) has been proposed. The method is based on ICA-EBM and a flexible correlation model. The ICA-ERBM has been used in [12] to separate and classify the EEG fatigue data.

A drawback of the ICA-based techniques for BSS is their restricted application to real-valued signals. Furthermore, they cannot be directly used to solve the problem of BSS of complex-valued signals. The problem of separating complex-valued signals arises in many situations. Indeed, the separation of convolutive mixtures of real-valued signals is turned into the separation of instantaneous mixtures of complex-valued signals via the Fourier transform. Several algorithms have been proposed to solve the problem of BSS in the case of complex-valued signals [1, 19, 26]. In general, complex ICA algorithms exploit two signal characteristics which are the non-Gaussianity and the non-circularity. In the literature, some algorithms ignore the non-Gaussianity and exploit only the non-circularity by using the joint diagonalization of the covariance and complementary covariance matrices [17, 49], while other algorithms exploit only the non-Gaussianity as in [55] where the estimation of the unmixing matrix for each frequency is performed using the maximum likelihood with an adaptive arrangement to apply some frequency coupling for neighboring frames, and in [5] where the electroencephalographic signals have been decomposed using complex infomax ICA algorithm in order to capture and understand their dynamics.

Several methods that exploit both the non-Gaussianity and non-circularity of the sources have been developed. In [47], the correlation magnitude has been used as a nonlinear constraint function for negentropy maximization in order to perform a permutation correction. In [20], an extension of the algorithm proposed in [17] has been presented. The technique uses the normalized kurtosis adapted to non-circular sources as a cost function. These algorithms cannot solve the problem of BSS for non-circular Gaussian sources. Moreover, the presence of outliers results in a degraded separation performance. In [38], the ICA-EBM algorithm developed in [37] has been extended to complex-valued signals. The technique is based on the projected conjugate gradient and provides accurate estimates of the entropy by bounding the entropy estimates; moreover, it approximates a wide range of probability density functions.

The empirical mode decomposition (EMD) [29] is a local self-adaptive decomposition method that allows analyzing data from non-stationary and/or nonlinear processes. Its principle is based on the sequential extraction of different amplitude and frequency modulation (AM–FM) single-component contributions called intrinsic mode functions (IMFs). The EMD has given rise to many research works on both theory and applications [8, 11, 13, 21, 24]. Several improved versions of the EMD algorithm have been proposed in the literature. The ensemble empirical mode decomposition (EEMD) [60] and the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) [14, 40] have been used for noisy data processing. The EMD algorithm has been combined with ICA in several studies to separate the source signals from observed mixture recordings. In [62], an EMD-ICA-based method has been used to separate the source signals from single-channel and two-channel recordings. In [45], the EEMD combined with the ICA algorithm has been used to classify neuromuscular disorders based on the data recorded from a single-channel EMG sensor. An adaptive algorithm called local mean decomposition which resembles in its principle to the EMD has been proposed in [56] to demodulate amplitude and frequency modulated signals; also it has been used in [28, 39] to solve the problem of BSS.

Relying essentially on local extrema, the conventional EMD is confined to the analysis of scalar signals because the notion of extrema does not exist for vector-valued signals. Thus, this decomposition is not directly applicable to complex-valued signals. The rotation invariant empirical mode decomposition (RIEMD) [3] and bivariate empirical mode decomposition (BEMD) [54] are two variants of complex EMD that have been proposed to decompose complex-valued signals. They have the advantage to yield the same number of the IMFs for the real part as for the imaginary part of the complex-valued signals. The complex empirical mode decomposition (CEMD) [58] uses the intrinsic relationship between the positive and negative frequency components of a complex signal spectrum and the Hilbert transform (HT) to estimate the IMFs. However, this method does not guarantee the same number of IMFs for real and imaginary parts. Extensions of the EMD to the more general case of multivariate signals have also been proposed [53, 65].

In this paper, the BEMD algorithm combined with complex ICA-EBM technique is proposed as an alternative to separate convolutive mixtures of speech signals. The performance of the proposed approach is tested on real speech chosen from available databases, and compared to the results obtained via conventional ICA and BEMD-ICA-based separation [41] for convolutive mixtures in terms of source-to-distortion ratio (SDR), source-to-artifact ratio (SAR), source-to-interference ratio (SIR) using BSS EVAL toolbox [23]. In order to measure the distortion between the original source and the estimated source, the improvement in signal-to-noise ratio (ISNR) is also computed.

The remainder of the paper is organized as follows. Complex independent component analysis by entropy bound minimization algorithm is presented in Sect. 2. Bivariate empirical mode decomposition is presented in Sect. 3. Blind source separation combining BEMD and complex ICA-EBM is developed in Sect. 4. Simulation results are presented in Sect. 5. Finally, conclusions are given in Sect. 6.

2 Complex Independent Component Analysis by Entropy Bound Minimization Algorithm

Let \(\mathbf{s}\left( t \right) =\left[ {s_1 \left( t \right) ,\ldots ,s_N \left( t \right) } \right] ^{T}\) be a vector of N independent sources at the discrete time instant t. The vector \(\mathbf{x}\left( t \right) =\left[ {x_1 \left( t \right) ,\ldots ,x_M \left( t \right) } \right] ^{T}\) of the M observed instantaneous mixtures is modeled as \(\mathbf{x}\left( t \right) =\mathbf{As}\left( t \right) \), where \(\mathbf{A}\) is the \(\left( {M\times N} \right) \) mixing matrix. The goal is to recover the N source signals from the M observed mixtures by computing the unmixing matrix W whose output z(t) is an estimate of the vector s(t) of the source signals \(\mathbf{z}\left( t \right) =\mathbf{Wx}\left( t \right) \), where \(\mathbf{z}\left( t \right) =\left[ {z_1 \left( t \right) ,\ldots ,z_N \left( t \right) } \right] ^{T}\) and \(\mathbf{W}=\left[ {\mathbf{w}_1 \left( t \right) ,\ldots ,\mathbf{w}_N \left( t \right) } \right] ^{T}\). To perform the separation of the N independent sources, the ICA-EBM method minimizes the mutual information \(I\left( {z_1 ;\ldots ;z_N } \right) \) defined as

$$\begin{aligned} I\left( {z_1 ;\ldots ;z_N } \right) =\mathop \sum \limits _{n=1}^N H\left( {z_n } \right) -\hbox {log}|\det \left( \mathbf{W} \right) |-H\left( \mathbf{x} \right) \end{aligned}$$
(1)

where \(H\left( {z_n } \right) \) is the entropy of the nth separated source, and \(H\left( \mathbf{x} \right) \) is the entropy of the observed mixture signals.

In unitary ICA approaches, prewhitening the mixtures allows having \(\left| {\hbox {det}\left( \mathbf{W} \right) } \right| =1\), under the constraint of an orthogonal unmixing matrix. The orthogonality constraint guarantees the properties of stability and convergence of the ICA algorithms. The cost function to be minimized becomes as follows:

$$\begin{aligned} {\varvec{I}}\left( {z_1 ,\ldots ,z_N } \right) =\mathop \sum \limits _{n=1}^N {\varvec{H}}\left( {z_n } \right) -{\varvec{H}}\left( \mathbf{x} \right) \end{aligned}$$
(2)

To simplify the algorithm, the authors in [38] propose to divide \({\varvec{I}}\left( {z_1 ,\ldots ,z_N } \right) \) into a series of sub problems.

The ICA-EBM algorithm is summarized as follows:

For \(n=1,\ldots ,N\)

  1. 1.

    Calculate the vector \(\mathbf{h}_n \) which is a unit-length vector obtained via the Gram–Schmidt orthogonalization procedure and satisfies \(\mathbf{W}_n \mathbf{h}_n =0\) where \(\mathbf{W}_n =\left[ {\mathbf{w}_1 ,\ldots \mathbf{w}_{n-1} ,\mathbf{w}_{n+1} ,\ldots ,\mathbf{w}_N } \right] ^{H}\).

  2. 2.

    Set \(z_n =\mathbf{w}_n^H \mathbf{x}\) and estimate the entropy of \(z_n \). The complex random variable entropy estimation is based on the principle of maximum entropy introduced in [31]. Several entropy maxima are calculated and then bounded using numerical computations. The final entropy estimate is the tightest one, which is achieved when the estimated negentropy is always nonnegative. For the estimation procedure, the quit flexible entropy estimator is based on QR decomposition.

  3. 3.

    Calculate the conjugate gradient defined as

    $$\begin{aligned} \frac{\partial \mathbf{J}_{n} \left( {\mathbf{w}_{n} } \right) }{\partial \mathbf{w}_{n}^{*}}=\frac{\partial {\hat{\mathbf{H}}}\left( {{z}_{n} } \right) }{\partial \mathbf{w}_{n}^{*} }-\frac{\mathbf{h}_{n} }{\mathbf{w}_{n}^{H} \mathbf{h}_{n} } \end{aligned}$$
    (3)

    and

    $$\begin{aligned} \frac{\partial \mathbf{L}_{n} \left( {\mathbf{w}_{n} ,\uplambda } \right) }{\partial \mathbf{w}_{n}^{*}}=\frac{\partial \mathbf{J}_{n} \left( {\mathbf{w}_{n} } \right) }{\partial \mathbf{w}_{n}^{*} }+{\uplambda }\mathbf{w}_{n} \end{aligned}$$
    (4)

    where \({L}_{n} \left( {{w}_{n} ,\uplambda } \right) \) denotes the Lagrangian defined as

    $$\begin{aligned} \mathbf{L}_{n} \left( {\mathbf{w}_{n} ,\uplambda } \right) =\mathbf{J}_{n} \left( {\mathbf{w}_{n} } \right) +\uplambda \left( {\mathbf{w}_{n}^{H} \mathbf{w}_{n} -1} \right) \end{aligned}$$
    (5)

    where \(\hat{{H}}\) denotes the estimated entropy, and \(\mathbf{J}_{{n}}\) is the cost function expressed as

    $$\begin{aligned} \hbox {min}\,\mathbf{J}_{n} \left( {{w}_{n} } \right) ={\hat{\mathbf{H}}} \left( {{z}_{n} } \right) -2\log \left| {{h}_{n}^{H} \mathbf{w}_{n} } \right| +{C} \end{aligned}$$
    (6)

    where C is a constant term.

  4. 4.

    Calculate the projected conjugate gradient on the constraint surface \(\Vert {w}_{n}\Vert =1\) as

    $$\begin{aligned} \mathbf{u}_{n} =\frac{\mathbf{u}_{n}^+ }{\Vert \mathbf{u}_{n}^+ \Vert } \end{aligned}$$
    (7)

    where \(\Vert .\Vert \) denotes the \(l^{2}\)-norm, and

    $$\begin{aligned} \mathbf{u}_{n}^+ =\frac{\partial \mathbf{J}_{n} \left( {\mathbf{w}_{n} } \right) }{\partial \mathbf{w}_{n}^{*} }-\hbox {Re}\left\{ {\mathbf{w}_{n}^{H} \frac{\partial \mathbf{J}_{n} \left( {\mathbf{w}_{n} } \right) }{\partial \mathbf{w}_{n}^{*} }} \right\} \mathbf{w}_{n} \end{aligned}$$
    (8)
  5. 5.

    update \(\mathbf{w}_\mathbf{n} \) as follows

    $$\begin{aligned} \mathbf{w}_{n}^{\left[ {\mathrm{new}} \right] } =\frac{\mathbf{w}_{n} -\upmu \mathbf{u}_{n} }{\mathbf{w}_{n}-\upmu \mathbf{u}_{n} } \end{aligned}$$
    (9)

    where \(\mu >0\) is a real-valued step size.

The complex ICA-EBM algorithm repeats the procedure over different row vectors of \(\mathbf{W}\) until convergence.

3 Bivariate Empirical Mode Decomposition

The empirical mode decomposition (EMD) algorithm proposed in [29] is a method that decomposes adaptively a real-valued signal into a sum of amplitude and frequency modulated signals called intrinsic mode functions (IMFs), and a residue which represent fast to slow oscillations in the signal.

The bivariate EMD (BEMD) is an extension of the EMD to bivariate or complex-valued signals. Let x(t) be a complex-valued signal. The BEMD algorithm can be summarized as follows [3].

  1. 1.

    Initialize the residue \(k\leftarrow 1\left( {k\hbox {th}~\hbox {IMF}} \right) ;r_k \left( t \right) \leftarrow x\left( t \right) \)

  2. 2.

    Extract the kth IMF:

    1. 2.1

      Estimate the envelope curves

      1. 2.1.1.

        Project the bivariate-value signal \(r_k \left( t \right) \) on the direction \(\varphi _k \) where \(\varphi _k =2k\pi /K\) for \(k=1\ldots K\)

        $$\begin{aligned} p_{\varphi _k } \left( t \right) =Re\left( {e^{-i\varphi _k }r_k \left( t \right) } \right) \end{aligned}$$
      2. 2.1.2.

        Extract the location \(\left\{ {t_j^k } \right\} \) of the maxima of \(p_{\varphi _k } \left( t \right) \)

      3. 2.1.3.

        Interpolate the set \(\left\{ {\left( {t_j^k ,r_k \left( {t_j^k } \right) } \right) } \right\} \) to obtain the envelope curve in the direction \(\varphi _k \)

    2. 2.2

      Compute the mean of all envelope curves \(\mu \left( t \right) =\frac{1}{K}\mathop \sum \limits _k e_{\varphi _k } \left( t \right) \)

    3. 2.3

      Substract the mean to obtain \(d\left( t \right) =r_k \left( t \right) -\mu \left( t \right) \)

    4. 2.4

      Iterate on the detail \(d\left( t \right) \) by repeating steps 2.1 to 2.3 until the stopping criterion based on the standard deviation between two consecutive details is below a predefined threshold leading to the \(\hbox {IMF}_k \) signal

  3. 3.

    Update the residue \(k\leftarrow k+1;r_k \left( t \right) \leftarrow r_{k-1} \left( t \right) -\hbox {IMF}_k \left( t \right) \)

  4. 4.

    Iterate on the residue by repeating steps 2 and 3 until the number of extrema of \(r_k \left( t \right) \) is less than 2.

The signal is reconstructed by summing the IMFs computed via the BEMD and the residue

$$\begin{aligned} x\left( t \right) =\mathop \sum \limits _{k=1}^K \hbox {IMF}_k \left( t \right) +r_K \left( t \right) \end{aligned}$$
(10)

The major advantage of the BEMD is that it guarantees accurate values of the local mean and results in an equal number of IMFs of the real and imaginary parts of the signal.

4 Blind Source Separation Combining BEMD and Complex ICA-EBM

In this paper, we will be interested in convolutive mixtures. The N source signals \(\mathbf{s}(t)=[s_{1}(t)\, s_{2}(t)\, {\ldots }\, s_{N}(t)]^{{T}}\) are convolutively mixed. Each observed mixture \(x_{{j}}(t)\) is a weighted sum of K delayed versions of the N source signals:

$$\begin{aligned} x_j (t)=\sum _{i=1}^N {\sum _{k=0}^{K-1} {a_{ji} (k)s_i } (t-k)} \end{aligned}$$
(11)

where \(a_{ji}\) denotes the impulse response from source i to sensor j.

In matrix form, the vector \(\mathbf{x}\left( t \right) =\left[ {x_1 \left( t \right) ,\ldots ,x_M \left( t \right) } \right] ^{T}\) of the M observed convolutive mixtures is modeled as

$$\begin{aligned} \mathbf{x}(t)=\sum _{k=0}^{K-1} {\mathbf{A}_k \mathbf{s}(t-k)} \end{aligned}$$
(12)

where \(\mathbf{A}_{{k}}\) is an \(M\times N\) matrix which contains the kth filter coefficients.

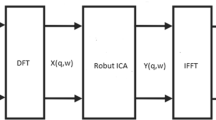
Taking the Fourier transform of both sides of (12), each convolutive mixture in the time domain is transformed into instantaneous mixtures in the frequency domain:

$$\begin{aligned} \mathbf{X}(f)=\mathbf{A}(f)\mathbf{S}(f) \end{aligned}$$
(13)

where f denotes frequency, \(\mathbf{A}(f)\) is an \(M\times N\) complex matrix whose elements \(A_{ji}(f)\) are the frequency responses from source i to sensor j, \(\mathbf{X}(f)\) is an \(M\times 1\) complex vector whose elements \(X_{j}(f)\) are the Fourier transforms of the mixture signals \(x_{j}(t)\) and \(\mathbf{S}(f)\) is an \(N\times 1\) complex vector whose elements \(S_{i}(f)\) are the Fourier transforms of the source signals \(s_{i}(t)\).

Since the separation of the signal is performed frame by frame, short-time Fourier transform (STFT) is used. The mixing model of each frame can be written as:

$$\begin{aligned} \mathbf{X}(f,m)=\mathbf{A}(f)\mathbf{S}(f,m) \end{aligned}$$
(14)

where m denotes the frame index, \(\mathbf{X}(f,m)\) and \(\mathbf{S}(f,m)\) are complex vectors corresponding to the frame \(m{:}\mathbf{S}(f,m)=\left[ {S_1 (f,m)}\, \ldots \, {S_N (f,m)}\right] ^{T}\mathbf{X}(f,m)=\left[ {X_1 (f,m)}\, \ldots \, {X_M (f,m)} \right] ^{T}\).

The solution of the problem of BSS in the case of convolutive mixtures, consists in finding for each frequency bin the separation matrix \(\mathbf{W}(f)\) which outputs an estimate of the source signals: \(\mathbf{Z}(f,m)=\mathbf{W}(f)\mathbf{X}(f,m),\) where \(\mathbf{Z}(f,m)\) denotes the estimate of the vector \(\mathbf{S}(f,m)\) of the source signals \(\mathbf{Z}\left( {f,m} \right) =\left[ {Z_1 \left( {f,m} \right) ,\ldots ,Z_N \left( {f,m} \right) } \right] ^{T}\).

The problem of BSS for convolutive mixtures can be solved in the frequency domain by using the complex-valued version of ICA methods [5, 7, 30] combined with the BEMD algorithm. First, the convolutive mixtures in the frequency domain are decomposed into a set of IMFs using the BEMD algorithm and then, the complex ICA is applied to extract the independent sources.

The BEMD enables to decompose a complex-valued signal into a set of IMFs. The main characteristic of the BEMD is that it results in an equal number of IMFs of the real and imaginary parts of the signal. In this paper, the BEMD is applied in the frequency domain, to decompose the real and imaginary parts of the Fourier transform of each frame of the observed mixtures into a set of IMFs.

The proposed method is summarized by the flowchart shown in Fig. 1. The different steps of the method combining BEMD and complex ICA-EBM are the following:

  1. 1.

    Compute the Fourier transform of each frame of the observed mixture signals. The frame length is set to 1024 samples.

  2. 2.

    Apply the BEMD to the Fourier transform of each frame of the observed mixtures. So for each frame, we obtain two sets of IMFs corresponding to the real and imaginary parts of the Fourier transform.

  3. 3.

    Extract independent components in the frequency domain by using ICA-EBM algorithm.

  4. 4.

    Solve the permutation and scaling ambiguity.

  5. 5.

    Compute the inverse Fourier transform to obtain the independent components in the time domain.

Several algorithms have been proposed to solve the permutation and scaling ambiguity [4, 50, 63], and in this paper, we use the method proposed in [64].

As an illustration example, the proposed method is applied to separate a convolutive mixture of two speech signals. Figure 2a, b shows the source signals, and Fig. 2c, d shows their respective spectrograms. The sources are convolutively mixed using the following mixture matrix in the z-transform domain.

$$\begin{aligned} {\varvec{A}}\left( z \right) =\left[ {{\begin{array}{ll} {1+.08z^{-1}+0.5z^{-2}}&{} {0.8+0.7z^{-1}+0.4z^{-2}} \\ {0.7+z^{-1}+0.6z^{-2}}&{} {1+0.9z^{-1}+0.3z^{-2}} \\ \end{array} }} \right] \end{aligned}$$
(15)

The observed mixture signals are shown in Fig. 2e, f. The real and imaginary parts of the Fourier transform of the frames are extracted from both mixture signals, and their corresponding IMFs are shown in Fig. 3. The real and imaginary parts of the estimated sources corresponding to both frames of mixture signals in the frequency domain are shown in Fig. 4, and the estimated sources are shown in Fig. 5.

Fig. 1
figure 1

Blind source separation combining bivariate empirical mode decomposition (BEMD) and complex independent component analysis by entropy bound minimization (ICA-EBM)

Full size image
Fig. 2
figure 2

Illustration example of the separation of a convolutive mixture of two speech signals. a Source signal 1, b source signal 2, c spectrogram of source 1, d spectrogram of source 2, e observed signal 1, f observed signal 2

Full size image
Fig. 3
figure 3

Real and imaginary parts of the Fourier transform of the frames of 1024 samples length extracted from mixture signals and their corresponding IMFs. a Fourier transform of the frame from mixture 1, b IMFs and residue of the Fourier transform of the frame from mixture 1, c Fourier transform of the frame from mixture 2, d IMFs and residue of the Fourier transform of the frame from mixture 2

Full size image
Fig. 4
figure 4

Estimated frames of sources 1 and 2 in the frequency domain. a Estimated frame of source 1, b estimated frame of source 2

Full size image
Fig. 5
figure 5

Estimated sources and their spectrograms. a Estimated source 1, b estimated source 2, c spectrogram of the estimated source 1, d spectrogram of the estimated source 2

Full size image

As can be seen, the estimated signals are highly similar to the sources signals. The BEMD combined with complex ICA-EBM provides an accurate estimate of the source signals and results in a spectral content located with high accuracy.

5 Simulation Results

The performance of the proposed approach is evaluated and compared to the performance of the conventional frequency ICA (FICA) method and to the combined BEMD-ICA algorithm proposed in [41] that we have adapted to convolutive mixtures. For this goal, two speech datasets comprising convolutive mixtures are constructed. The first speech dataset is constructed from TIMIT database available online [59] by simulating convolutive mixtures using the recordings of two sentences of 3 s sampled at 16 kHz pronounced by male and female speakers. A set of 4 noisy mixtures are simulated by corrupting clean mixtures at a signal-to-noise ratio (SNR) ranging from 5 to 20 dB with a step of 5 dB. The second speech dataset is constructed by simulating convolutive mixtures using 20 pairwise sentences randomly chosen from the NOIZEUS database [46]. The speech mixtures are corrupted by additive white Gaussian noise with the SNR fixed at 10 dB.

The performance of the proposed technique is analyzed by using the bsseval toolbox [23]. For the objective performance criteria measurement, the estimated sources are expressed as \(\hat{s}=s_\mathrm{target} +e_\mathrm{interf} +e_\mathrm{noise} +e_\mathrm{artif} \), where \(s_\mathrm{target} \) is the source signals, and \(e_\mathrm{interf} \) denotes the interferences from other sources, \(e_\mathrm{noise} \) is the distortion caused by the noise and \(e_\mathrm{artif} \) includes all other artifacts introduced by the separation algorithm. The performance criteria are as follows:

$$\begin{aligned} \hbox {SDR}= & {} 10\log _{10} \frac{\Vert s_\mathrm{target}\Vert ^{2}}{\Vert e_\mathrm{interf} +e_\mathrm{noise} +e_\mathrm{artif}\Vert ^{2}} \end{aligned}$$
(16)
$$\begin{aligned} \hbox {SAR}= & {} 10\log _{10} \frac{\Vert s_\mathrm{target} +e_\mathrm{interf} +e_\mathrm{noise}\Vert ^{2}}{\Vert e_\mathrm{artif}\Vert ^{2}} \end{aligned}$$
(17)
$$\begin{aligned} \hbox {SIR}= & {} 10\log _{10} \frac{\Vert s_\mathrm{target}\Vert ^{2}}{\Vert e_\mathrm{interf}\Vert ^{2}} \end{aligned}$$
(18)

In order to measure the distortion between the original sources and the estimated sources, the improvement signal-to-noise ratio (ISNR) is computed. The ISNR is defined as

$$\begin{aligned} \hbox {ISNR}=\hbox {SNR}_\mathrm{output} -\hbox {SNR}_\mathrm{input} \end{aligned}$$
(19)

The input and output SNR are defined as

$$\begin{aligned} \hbox {SNR}_\mathrm{input}= & {} 10\log \frac{\sum \nolimits _t \left| {s\left( t \right) } \right| ^{2}}{\sum \nolimits _t \left| {x\left( t \right) -\hat{s}\left( t \right) } \right| ^{2}} \end{aligned}$$
(20)
$$\begin{aligned} \hbox {SNR}_\mathrm{output}= & {} 10\log \frac{\sum \nolimits _t \left| {s\left( t \right) } \right| ^{2}}{\sum \nolimits _t \left| {s\left( t \right) -{\hat{s}}\left( t \right) } \right| ^{2}} \end{aligned}$$
(21)

where \(x\left( t \right) \) is the observed mixture, \(s\left( t \right) \) is the original sources, and \(\hat{s}\left( t \right) \) is the estimated source.

The performance criteria of the three BSS methods corresponding to the first dataset are shown in Fig. 6 for different SNR values. The proposed method results in a better performance in terms of the four performance criteria compared to both FICA and BEMD-ICA methods for convolutive mixtures. For all SNR values, the BEMD combined with the ICA-EBM method results in higher performance criteria.

Fig. 6
figure 6

Comparison between proposed method and independent component analysis combined with bivariate empirical mode decomposition (ICA-BEMD) separation method and conventional frequency ICA (FICA) in terms of SIR, SAR, SDR and ISNR

Full size image

To test whether the difference between the performance criteria of the proposed method and those of FICA and BEMD-ICA methods is statistically significant, Kruskal–Wallis statistical test [36] has been performed on the second speech dataset. Kruskal–Wallis statistical test is a nonparametric statistical test that does not require assumptions on data distribution. The advantage of this test is to remain as powerful as ANOVA statistical test. Kruskal–Wallis statistical test shows that the averages of the performance criteria values of the proposed method differ statistically significantly from those of FICA and BEMD-ICA methods for convolutive mixtures. The p values of the test are given in Table 1.

Table 1 p values of Kruskal–Wallis statistical test for SIR, SAR, SDR and ISNR of 20 speech mixtures
Full size table

6 Conclusion

A new method combining bivariate empirical mode decomposition and EBM-ICA for blind separation of convolutive mixtures has been presented. The method operates in the frequency domain. The observed convolutive mixtures in the time domain are transformed into instantaneous mixtures in the frequency domain, and hence, the bivariate empirical mode decomposition is used to decompose the complex mixtures into a set of IMFs from which the independent components are extracted using the ICA-EBM algorithm. The proposed method has been tested on speech datasets constructed from TIMIT and NOIZEUS databases; the results are very satisfactory compared to BEMD-ICA separation for convolutive mixtures and conventional FICA, indicating the high values of SIR, SAR, SDR and ISNR, and confirmed by Kruskal–Wallis statistical test.