Several Novel Dynamic Ensemble Selection Algorithms for Time Series Prediction

Abstract

The goal to improve prediction accuracy and robustness of predictive models is quite important for time series prediction (TSP). Multi-model predictions ensemble exhibits favorable capability to enhance forecasting precision. Nevertheless, a static ensemble system does not always function well for all the circumstances. This work proposes six novel dynamic ensemble selection (DES) algorithms for TSP, including one DES algorithm based on Predictor Accuracy over Local Region (DES-PALR), two DES algorithms based on the Consensus of Predictors (DES-CP) and three Dynamic Validation Set determination algorithms. The first dynamic validation set determination algorithm is designed based on the similarity between the Predictive value of the test sample and the Objective values of the training samples. The second one is constructed based on the similarity between the Newly constituted sample for the test sample and All the training samples. Finally, the third one is developed based on the similarity between the Output profile of the test sample and the Output profile of each training sample. These proposed algorithms successfully realize dynamic ensemble selection for TSP. Experimental results on twelve benchmark time series datasets have demonstrated that the proposed DES algorithms greatly improve predictive performance when compared against current state-of-the-art prediction algorithms and the static ensemble selection techniques.

1 Introduction

Time series can be defined as a set of sequential observations, of a variable of interest, recorded over a predefined period of time [1]. Time series are widely used today because we need to know the future behavior of certain relevant phenomena in order to plan, prevent, and so on. That is, to predict what will happen with a variable in the future from the behavior of that variable in the past [2]. The word “prediction” comes from the Latin “prognosticum”, which means “I know in advance” [3]. Time series forecasting techniques could be conditionally classified into long-term time series forecasting techniques and short-term time series forecasting ones [4].

Time series prediction (TSP) is an important and active research topic in machine learning, and it has indispensable importance in many practical data mining applications. In general, time series involves a subject of research interest in various areas of knowledge engineering, such as: agriculture (the number of pigs slaughtered, sheep population, and milk production), health (suicide rates, fertility rates and number of cases of measles), finance (stocks, loans and exchange rates), and production (beer shipments, motor vehicle production and electricity production), etc.

Financial time series forecasting (such as stock forecasting and crude oil price forecasting) is one of the most popular research directions in the field of time series prediction. However, there exist many factors that will influence a stock market, including the basic situation of listed companies, national macroeconomic policies, market supply and the technical indicators of shares [5]. Investors are facing with a great challenge that they do not know how to precisely forecast price fluctuation in financial markets. It is a hard task to predict the trend of stock market because of its high volatility and the noisy environment.

There has been an increasing interest in using Neural Networks (NNs) to model and forecast time series over the last decades. NNs have been found to be a viable contender to various traditional time series models [6,7,8]. Lapedes and Farber [9] reported the first attempt to model nonlinear time series with NNs. Chakraborty et al. [10] conducted an empirical study on multivariate time series forecasting with NNs. What’s more, several forecasting competitions [6, 11] show that NNs could be a very useful addition to the time series forecasting toolbox.

One of the major developments in NNs over the last decade is models combining or ensemble learning. An ensemble can be formed by multiple network architectures, different initial random weights, different number of hidden nodes, or even different activation functions. Multi-model ensemble prediction systems show convincing ability to improve the forecast performance in different areas of computational science [12, 13]. In short, two heads are better than one.

Multiple Predictor Systems (MPSs) are typically composed of three stages [14]: (1) Generation; (2) Selection; and (3) Integration. In the first stage, a pool of predictors is generated. In the second stage, a single predictor (or several predictors) having better predictive prediction on the validation set than the others is (are) selected into the ensemble. We refer to the subset of predictors as Ensemble of Predictors (EoP). In the last stage, the predictions of the selected predictors are combined by some ways for the final results [15, 16].

For the second stage, there exist two types of selective ensemble paradigms, i.e., static and dynamic ensemble selection [17]. Within the static ensemble selection paradigm, the selected predictors of the ensemble will remain unchanged for the prediction of all the test samples [18,19,20]. While the assumption of dynamic ensemble selection (DES) paradigm is that every predictor is an expert in some specific local regions. Just the opposite to static ensemble selection, a predictor or several predictors which specializes (specialize) in conducting prediction for the new test sample will be selected into the final ensemble dynamically within the DES paradigm. Recently, several literatures show that DES is a very effective tool for TSP problems [21,22,23].

The important basis of DES is how to determine, with regard to the current test sample, the appropriate validation samples from the training set. This topic has received considerably limited research attention so far in TSP problems. However, for classification problems, Woods et al. [24] proposed an approach that is Dynamic Classifier Selection by Local Accuracy (DCS-LA), and the validation samples are chosen as the K-nearest neighbors (KNNs) training samples to the new test one. Smits [25] proposed the measure of Modified Local Accuracy (MLA), which is similar to DCS-LA, with the only difference being that each sample belonging to the validation set is weighted by its Euclidean distance to the test sample. And the MLA outperforms DCS-LA with respect to minimum accuracy, maximum accuracy and kappa value. Kuncheva [26] conducted a study that the validation set is determined by using the clustering techniques.

Due to the fact that the above methods, which are used to select the validation data, is prone to be limited by the quality of the region of competence defined in the training data. Hence, the decision templates (DT) [27] technique is considered to select validation set. The goal of DT is also to select samples that are close to the test instance. However, the similarity is computed over decision space rather than feature space. This is performed by transforming both the test instance and the training data into the corresponding output profiles. The output profile of one sample is a vector that consists of the predicted values obtained by the base predictors for that sample.

As mentioned above, determining a proper validation set is a critical issue for the successful implementation of DES algorithms, which has received very limited attention for the research of TSP. Therefore, we decide to carry out some innovative research work in this area, so as to further promote the research progress in the respect of TSP. We find through analysis that, there are mainly three schemes to address this issue, i.e., the dynamic determination of the validation set based upon feature space solely, decision space solely, or based on the integration of feature and decision space. The DES algorithm based on Predictor Accuracy over Local Region (DES-PALR) proposed in this work belongs to the first scheme. It performs k-means clustering algorithm on the feature space of the training set, which generates several clusters of the training samples. The cluster whose center is the nearest to the feature vector of the current test sample will be selected as the validation set dynamically.

The proposed Dynamic Validation Set determination algorithm based on the similarity between the Predictive value of the test sample and the Objective values of the training samples (DVS-PvOv) belongs to the second scheme. While the proposed Dynamic Validation Set determination algorithm based on the similarity between the Newly constituted sample for the test sample and All the training samples (DVS-NsAs) is part of the third scheme, determining the validation set based on the integration of feature and decision space. The finally proposed Dynamic Validation Set determination algorithm based on the similarity between the Output profile of the test sample and the Output profile of each training sample (DVS-OpOp) belongs to the second scheme.

Another important point of DES is how to dynamically choose an appropriate ensemble constituted with some selected models. Adhikari et al. [16] proposed an ensemble selection method that selectively combines some of the constituent forecasting models, instead of combining all of them. And on each time series, the constituent models are successively ranked as per their past forecasting accuracies. Then the forecasts of a group of high ranked models are combined to produce the final predictive results. In the respects of selective ensemble, Zhou et al. [28] proposed an approach which trains several individual NNs and then employs genetic algorithm to select an optimum subset of individual networks to constitute the final ensemble.

On the other hand, there exist some DES techniques which are based upon other criteria, such as the degree of consensus or confidence of the ensemble decision. Dos Santos et al. [29] proposed the Margin-based Dynamic Selection (MDS) and Ambiguity-guided Dynamic Selection (ADS). The criterion of MDS is the margin between the most voted class and the second most voted class. ADS uses the ambiguity among the base classifiers of a pool of ensembles of classifiers as the criterion for measuring its competence level. The ambiguity is determined as the number of base classifiers of an ensemble that disagree with the ensemble decision.

Inspired by the existing research work, we propose a Dynamic Ensemble Selection algorithm based on the Consensus of Predictors (DES-CP) for TSP in this paper. DES-CP is developed based on the extent of the ensemble consensus, similarly. And it works by considering a pool of ensembles of predictors (EoPs) rather than a pool of predictors. Several EoPs are generated by the Genetic Algorithm based Selective ENsemble (GASEN) [28]. And according to the different approaches employed to evaluate the extent of consensus, the proposed DES-CP algorithm is further subdivided into two algorithms: (1) for each test sample, the consensus of each EoP is evaluated by calculating its Variance (namely, DES-CP-Var); (2) conducting Clustering algorithm for evaluating the consensus of each EoP (namely, DES-CP-Clustering). The ensemble, which has the highest consensus, is chosen as the final EoP.

Our motivations behind the developments of these novel dynamic ensemble selection algorithms for the research of TSP mainly lie in that, in the domain of TSP, instead of splitting the original dataset into three disjunctive parts, i.e., training set, validation set and test set, like most of the static ensemble pruning methods, dynamically determining the validation dataset for each distinctive test sample is more reasonable. The superiority of DES over static ensemble selection on prediction performance has been verified in the literatures.

Specifically, the motivation for the proposal of DES-PALR is that, predictive accuracy is the most essential criterion for the implementation of DES for TSP. With the design of DES-PALR, the local region has more similar distribution with the test sample than other training samples. The predictors which perform better on the local region could also perform better on the test sample, while different test sample locates different region of competence, effectively achieving dynamic ensemble selection.

The proposal of the three novel algorithms, i.e., DVS-PvOv, DVS-NsAs and DVS-OpOp, further facilitates the effective implementation of DES for TSP. Their common characteristic is that, they are not limited by the quality of the local region of competence solely defined in the feature space, which is beneficial to their predictive performances.

With the proposed DES-CP algorithm, the higher the consensus among the member predictors is, the higher the level of prediction confidence will be. By maximizing the extent of ensemble consensus, the certainty that the ensemble will make a more accurate prediction is improved. Its major merit is that, it does not need any information from the region of competence, and therefore, it is not restricted by the algorithms which define the region of competence.

In Table 1, the advantages and disadvantages of the proposed five DES algorithms are listed, so as to provide a brief and clear comparison among these algorithms.

Table 1 The advantages and disadvantages of the proposed DES algorithms

To our best knowledge, it is the first time that all these new dynamic ensemble selection algorithms are proposed for the research of TSP.

There exist two other advantages of this work. Firstly, ELM is used to be the base model; therefore our algorithms naturally inherit those salient advantages of ELM, including better generalization capability, fast learning speed and the avoidance of local minima problem. Secondly, the GASEN algorithm is employed to generate some EoPs for the proposed DES-CP algorithm. Comparing with the popular ensemble approach, i.e., averaging all, and the theoretically optimum selective ensemble approach, i.e., enumerating, GASEN has preferable performance in generating EoPs with both strong generalization ability and small computational cost.

To verify the efficacy of the proposed six DES algorithms, we conducted experiments to compare the predictive performance of the proposed algorithms with three static ensemble selection algorithms and three other state-of-the-art models on twelve benchmark time series prediction datasets. The experimental results indicate that, in most cases, our proposed DES algorithms significantly outperform their competitors on the twelve datasets.

The remainder of the paper is organized as follows. Section 2 introduces some important concepts of ELM, and presents some theoretical analysis on ensemble pruning for time series forecasting tasks. Section 3 gives the novel ideas and details of the proposed DES algorithms for TSP. Section 4 reports and discusses the experimental results. Finally, Sect. 5 concludes this paper and suggests directions for future work.

2 Background Knowledge of ELM and Theoretical Analysis on Ensemble Pruning for TSP

2.1 Preview with ELM

Recently, extreme learning machine (ELM) has become an increasingly significant research topic for machine learning and artificial intelligence, due to its unique advantages, i.e., good generalization performance, extremely fast training speed and universal approximation ability. ELM is a valid solution for single-hidden layer feedforward neural networks (SLFNs). SLFNs have relatively strong ability of nonlinear approximation for regression problems, and can form separable decision regions for classifying arbitrary dimensional data.

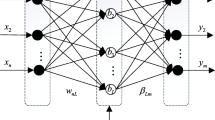
It was Huang et al. [30] who originally developed the ELM algorithm. It possesses the same architecture as the SLFN, as illustrated in Fig. 1. The most outstanding feature of ELM lies in the random initialization of its input weights and hidden layer biases, while its output weights are calculated simply by performing a matrix inversion on the hidden layer output matrix. ELM gets its name from its extremely fast learning speed, while it is also extremely easy to implement [31].

Fig. 1

ELM network topology

Suppose there are N arbitrarily different samples $({\mathbf{x}}_{i} ,{\mathbf{t}}_{i} )$, where ${\mathbf{x}}_{i} = [x_{i1} ,x_{i2} , \ldots ,x_{in} ]^{T} \in {\mathbf{R}}^{n}$ and ${\mathbf{t}}_{i} = [t_{i1} ,t_{i2} , \ldots ,t_{im} ]^{T} \in {\mathbf{R}}^{m}$, a normal SLFNs with $\tilde{N}$ hidden nodes and activation function g(x) is analytically modeled by:

$$ \sum\limits_{i = 1}^{{\tilde{N}}} {\beta_{i} g({\mathbf{w}}_{i} \cdot {\mathbf{x}}_{j} + b_{j} )} = {\mathbf{t}}_{j} ,\quad j = 1, \ldots ,N $$

(1)

where ${\mathbf{w}}_{i} = [w_{i1} ,w_{i2} , \ldots ,w_{in} ]^{T}$ denotes the connection weight vector between the ith hidden node and the input nodes, $[\beta_{i1} ,\beta_{i2} , \ldots ,\beta_{in} ]^{T}$ denotes the connection weight vector between the ith hidden node and the output nodes, and b_i represents the bias of the ith hidden neuron.

Equation (1) can also be written compactly as:

$$ {\mathbf{H}} {\varvec{\upbeta}} = {\mathbf{T}} $$

(2)

where ${\mathbf{H}}({\mathbf{w}}_{1} , \ldots ,{\mathbf{w}}_{{\tilde{N}}} ,b_{1} , \ldots ,b_{{\tilde{N}}} ,{\mathbf{x}}_{1} , \ldots ,{\mathbf{x}}_{N} ) = \left[ {\begin{array}{*{20}c} {\text{g(}{\mathbf{w}}_{\text{1}} \cdot {\mathbf{x}}_{\text{1}} + \text{b}_{\text{1}} \text{)}} & \ldots & {\text{g(}{\mathbf{w}}_{{\tilde{N}}} \cdot {\mathbf{x}}_{\text{1}} + \text{b}_{{\tilde{N}}} \text{)}} \\ \vdots & \vdots & {} \\ {\text{g(}{\mathbf{w}}_{\text{1}} \cdot {\mathbf{x}}_{N} + \text{b}_{\text{1}} \text{)}} & \cdots & {\text{g(}{\mathbf{w}}_{{\tilde{N}}} \cdot {\mathbf{x}}_{N} + \text{b}_{{\tilde{N}}} \text{)}} \\ \end{array} } \right]_{{N \times \tilde{N}}}$, ${\varvec{\upbeta}} = \left[ {\begin{array}{*{20}c} {\beta_{1}^{T} } \\ \vdots \\ {\beta_{{\tilde{N}}}^{T} } \\ \end{array} } \right]_{{\tilde{N} \times m}}$ and ${\mathbf{T}} = \left[ {\begin{array}{*{20}c} {t_{1}^{T} } \\ \vdots \\ {t_{N}^{T} } \\ \end{array} } \right]_{N \times m}$.

Here, ${\mathbf{w}}_{i} \cdot {\mathbf{x}}_{j}$ denotes the inner product of w_i and x_j. As named by Huang et al. [32], H is termed the hidden layer output matrix of the neural network; the ith column of H is the ith hidden node output in relation to inputs ${\mathbf{x}}_{1} ,{\mathbf{x}}_{2} , \ldots ,{\mathbf{x}}_{N}$.

Traditionally, to train a SLFN, we might expect to acquire specific ${\hat{\mathbf{w}}}_{i} ,b_{i} ,{\hat{\varvec{\upbeta }}}$$(i = 1, \ldots ,\tilde{N})$ to minimize $\left\| {\mathbf{H}}{\varvec{\upbeta}} - {\mathbf{T}} \right\|$. Specifically,

$$ \left\| {H({\hat{\mathbf{w}}}_{1} , \ldots ,{\hat{\mathbf{w}}}_{{\tilde{N}}} ,\hat{b}_{1} , \ldots ,\hat{b}_{{\tilde{N}}} )\hat{\beta } - {\mathbf{T}}} \right\| = \mathop {\hbox{min} }\limits_{{{\mathbf{w}}_{i} ,b_{i} ,\beta }} \left\| {H({\mathbf{w}}_{1} , \ldots ,{\mathbf{w}}_{{\tilde{N}}} ,b_{1} , \ldots ,b_{{\tilde{N}}} )\beta - {\mathbf{T}}} \right\| $$

(3)

which amounts to minimizing the cost function

$$ E = \sum\limits_{j = 1}^{N} {\left( {\sum\limits_{i = 1}^{{\tilde{N}}} {{\varvec{\upbeta}}_{i} g({\mathbf{w}}_{i} \cdot {\mathbf{x}}_{j} + b_{i} ) - {\mathbf{t}}_{j} } } \right)^{2} } . $$

(4)

The gradient-decent learning algorithms are typically implemented to optimize these parameters, which update parameter vector w iteratively according to:

$$ {\mathbf{w}}_{k} = {\mathbf{w}}_{k - 1} - \eta \frac{{\partial E({\mathbf{w}})}}{{\partial {\mathbf{w}}}} $$

(5)

Here η is learning rate. The most popular algorithm utilized is the BP learning algorithm. However, BP algorithm faces a series of problems, such as the difficulty to find an appropriate learning rate η; easy to fall into local minima; easy to overfitting; and rather time-consuming.

However, ELM resolves the above issues. It sets input weights w_i and hidden neuron bias b_i at random, after which matrix H is calculated directly. Then the problem of minimizing cost function in Eq. (3) equates acquiring a least-squares solution ${\hat{\varvec{\upbeta }}}$ of the linear system $\left\| {\mathbf{H}}{\varvec{\upbeta}} - {\mathbf{T}} \right\|$:

$$ \left\| {H({\mathbf{w}}_{1} , \ldots ,{\mathbf{w}}_{{\tilde{N}}} ,b_{1} , \ldots ,b_{{\tilde{N}}} ){\hat{\varvec{\upbeta }}} - {\mathbf{T}}} \right\| = \mathop {\hbox{min} }\limits_{{{\mathbf{w}}_{i} ,b_{i} ,\beta }} \left\| {H({\mathbf{w}}_{1} , \ldots ,{\mathbf{w}}_{{\tilde{N}}} ,b_{1} , \ldots ,b_{{\tilde{N}}} ){\varvec{\upbeta}} - {\mathbf{T}}} \right\| $$

(6)

If the number $\tilde{N}$ of hidden nodes is equal to the number N of distinct training samples, $\tilde{N} = N$, matrix H is square and invertible when the input weight vectors w_i and the hidden biases b_i are randomly chosen, and these training samples can be approximated with zero error. However, in most cases, the number of hidden nodes is much less than the number of distinct training samples, $\tilde{N}$, H is nonsquare matrix and there may not exist ${\mathbf{w}}_{i} ,b_{i} ,\beta_{i} (i = 1, \ldots ,\tilde{N})$ such that ${\mathbf{H}} {\varvec{\upbeta}} = {\mathbf{T}}$. ELM learns the output weights ${\varvec{\upbeta}}$ with the use of a Moore–Penrose generalized inverse of the matrix H, denoted as ${\mathbf{H}}^{\dag }$ [32]. The smallest norm least squares solution of the above linear system is

$$ {\hat{\varvec{\upbeta }}} = {\mathbf{H}}^{\dag } {\mathbf{T}} $$

(7)

The solution ${\hat{\varvec{\upbeta }}}$ defined in Eq. (7) has the norm minimum over all the solutions of the least squares solutions of linear system in Eq. (2). Thus, ${\hat{\varvec{\upbeta }}}$ deserves the best generalization performance across all the other least squares solutions [33].

A few apparent advantages exist in ELM: (1) the extremely fast learning speed; (2) the obviously better generalization performance; (3) without problems like local minima and slow rate of convergence, etc. [30].

2.2 Theoretical Analysis on Ensemble Pruning for TSP

Provided an equidistant sampled time series $\{ \alpha_{v} \}_{v = 1, \ldots ,N}$, one m-dimensional state space vector x_t is constructed as the form:

$$ \varvec{x}_{t} = \left( {\alpha_{{t + \text{1}}} , \alpha_{{t + \text{2}}} , \ldots ,\alpha_{t + m} } \right) $$

(8)

$$ \alpha_{t + m + s}^{{\prime }} = f\left( {\varvec{x}_{t} } \right) $$

(9)

where s denotes the scope of prediction, m represents the time window size (TWS), and the function $f:R^{m} \to R$ is called the approach function.

As only one-step-ahead prediction is focused on in this paper, s is set as one. And the TSP problem here is considered as a special case of the function approximation problem. Suppose an ensemble comprising M base models is used to approximate the function $f:R^{m} \to R$, and the predictions of M base models are combined through weighted averaging for developing the final result. The weight $w_{i} (i = 1,2, \ldots ,M)$ that satisfies both Eqs. (10) and (11) is assigned to the i-th base model f_i.

$$ 0 \le w_{i} \le 1 $$

(10)

$$ \sum\limits_{{i = \text{1}}}^{M} {w_{i} = \text{1}} $$

(11)

The outcome of the ensemble is computed according to Eq. (12):

$$ \tilde{f} = \sum\limits_{{i = \text{1}}}^{M} {w_{i} f_{i} } $$

(12)

For convenience of discussion, here it is supposed that all the base models possess identical weights, just as in Eq. (13):

$$ w_{i} = 1/M\quad (i = 1,2, \ldots ,M) $$

(13)

Then Eq. (12) becomes Eq. (14):

$$ \tilde{f} = \frac{\text{1}}{M}\sum\limits_{{i = \text{1}}}^{M} {f_{i} } $$

(14)

According to Zhou et al.’s analyses [28, 34], the reason why combining a proper subset of the original ensemble might outperform combining the entire one is explained as follows:

Suppose $\varvec{x}_{\text{t}} \in \text{R}^{\text{m}}$ is randomly sampled on the basis of a distribution p(x_t). The generalization error of the i-th individual model and that of the entire ensemble on x_t are respectively:

$$ E_{i} = \left( {f_{i} \left( {\varvec{x}_{t} } \right) - \alpha_{{t + m + \text{1}}} } \right)^{\text{2}} $$

(15)

$$ \tilde{E} = \left( {\tilde{f}\left( {\varvec{x}_{t} } \right) - \alpha_{{t + m + \text{1}}} } \right)^{\text{2}} $$

(16)

The correlation between the i-th and the j-th base models is calculated as below:

$$ C_{ij} = \int {d\varvec{x}_{t} p\left( {\varvec{x}_{t} } \right)\left( {f_{i} \left( {\varvec{x}_{t} } \right) - \alpha_{{t + m + \text{1}}} } \right)} \left( {f_{j} \left( {\varvec{x}_{t} } \right) - \alpha_{{t + m + \text{1}}} } \right) $$

(17)

Then, it can be obtained that:

$$ \tilde{E} = \sum\limits_{{i = \text{1}}}^{M} {\sum\limits_{{j = \text{1}}}^{M} {{{C_{ij} } \mathord{\left/ {\vphantom {{C_{ij} } {M^{\text{2}} }}} \right. \kern-0pt} {M^{\text{2}} }}} } $$

(18)

If the k-th base model is removed from the pool of base models, the generalization error of current ensemble will be:

$$ \tilde{E}^{\prime } = \sum\limits_{\begin{subarray}{l} i = \text{1} \\ i \ne k \end{subarray} }^{M} {\sum\limits_{\begin{subarray}{l} j = \text{1} \\ j \ne k \end{subarray} }^{M} {{{C_{ij} } \mathord{\left/ {\vphantom {{C_{ij} } {(M - 1)^{2} }}} \right. \kern-0pt} {(M - 1)^{2} }}} } $$

(19)

Considering Eqs. (18) and (19), it can be gotten that:

$$ \tilde{E} - \tilde{E}^{'} = \frac{{\text{2}\sum\nolimits_{\begin{subarray}{l} i = \text{1} \\ i \ne k \end{subarray} }^{M} {C_{ik} + E_{k} - \left( {\text{2}M - \text{1}} \right)\tilde{E}} }}{{\left( {M - \text{1}} \right)^{\text{2}} }} $$

(20)

In this circumstance, the generalization error of the pruned ensemble is clearly smaller than that of the original entire ensemble, i.e., $\tilde{E}^{\prime } < \tilde{E}$. Consequently, the conclusion could be reached that, aggregating an appropriate subensemble of the original ensemble might achieve preferable generalization performance, compared with aggregating the entire one.

3 The Proposed Several Novel Dynamic Ensemble Selection Algorithms for TSP

According to the literature, it can be found that the predictive precision of ELM is usually better than BP and SVM in many fields. However, the input weights and biases of ELM are randomly assigned, which will produce much uncertainty, especially when every new sample owns its particular property. Therefore, they should not be treated equally without discrimination [30]. Hence, an ensemble of ELMs rather than a single ELM is used in this work for the research of TSP, as an ensemble has better adaptability and stronger robustness compared to a single ELM.

In this work, several novel dynamic ensemble selection algorithms are proposed specifically for the research of TSP. Let $P = \left\{ {p_{1} ,p_{2} , \ldots ,p_{M} } \right\}$ be the initial pool of predictors, where p_i, $i = 1,2, \ldots ,M$ denote the base predictors belonging to the initial pool P, and M is the size of P. The aim of dynamic ensemble selection is to find a subensemble $P^{\prime } \subseteq P$ that is composed of the proper set of predictors to predict a specific test sample. Figure 2 shows an overview of a dynamic predictors selection system. The details about the proposed algorithms are presented in the following subsections.

Fig. 2

Overview of a dynamic predictors selection system

The research of this paper is mainly focused on the DES paradigm that allows for dynamically selecting ensemble members for each forecast rather than the training of each predictor. However, for completeness and continuity, the generation of an ELMs ensemble is introduced briefly as follows.

Let $\varvec{x}_{t} = \left\{ {\alpha_{t + 1} ,\alpha_{t + 2} , \ldots ,\alpha_{t + m} } \right\}$ be the input values of the time series, and $y_{t} = \alpha_{t + m + 1}$ be the target value of the time series, where m denotes the size of time window. Let g(x) denote the activation function, such as sigmoid function in Eq. (21), sine function in Eq. (22), hard limit transfer function in Eq. (23), triangular basis transfer function in Eq. (24), and radial basis transfer function in Eq. (25). Let $\tilde{N} \in \left[ {1,20} \right]$ be the range of the number of hidden nodes. Although when the number of hidden nodes increases, the predictive accuracy on the training set will be improved, however, this is prone to the over-fitting problem. We found by trial-and-error that it is appropriate to set the range of the numbers of hidden nodes as $\left[ {1,20} \right]$.

$$ g\left( x \right) = \frac{1}{{1 + e^{ - x} }} $$

(21)

$$ g\left( x \right) = sin\left( x \right) $$

(22)

$$ g\left( x \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {if\;\;x > 0;} \hfill \\ {0,} \hfill & {otherwise.} \hfill \\ \end{array} } \right. $$

(23)

$$ g\left( x \right) = \left\{ {\begin{array}{*{20}l} {1 - \left| x \right|,} \hfill & {if\;\; - 1 \le x \le 1;} \hfill \\ {0,} \hfill & {otherwise.} \hfill \\ \end{array} } \right. $$

(24)

$$ g\left( x \right) = e^{{ - x^{2} }} $$

(25)

One hundred ELMs are generated based on the above five kinds of activation functions, with the number of hidden nodes varying from one to twenty. Let $P = \left\{ {p_{1} ,p_{2} , \ldots ,p_{M} } \right\}$ denote the pool of generated ELM predictors, the proposed algorithms are introduced in detail in the following.

3.1 DES Algorithm Based on Predictor Accuracy over the Local Region (DES-PALR)

The first algorithm proposed in this work is the DES algorithm based on Predictor Accuracy over the Local Region (DES-PALR). Predictor accuracy is the most common criterion for the implementation of DES [24, 35, 36]. For this criterion, a small region in the training data surrounding the given testing instance $\left( {\varvec{x}_{j} , y_{j} } \right)$ is defined. The region can be computed using the K-NN algorithm [24, 35], or can be computed by using other clustering algorithms [26, 36]. The samples in this region constitute the validation dataset for DES. Figure 3 shows an overview of this algorithm.

Fig. 3

Overview of the DES-PALR algorithm

The proposed DES-PALR algorithm is shown as follows:

The time complexities of DES-PALR algorithm in training and testing phase are $O\text{(}M + tkNn\text{)}$ and $O\text{(}k + MlogZ\text{)}$, respectively, where M represents the size of initial pool of predictors, t represents the number of iterations of k-means algorithm, k denotes the number of clusters of k-means algorithm, N represents the size of training set, n denotes the dimension of training samples, and Z represents the number of selected predictors.

Before the explanation of the proposed DES-PALR algorithm, we would like to introduce the k-means clustering algorithm briefly [37, 38]. The k-means clustering algorithm is one of the most widely used clustering algorithms. In k-means algorithm, the center of each class is computed as the average of samples belonging to that cluster, which well reflects the geometric and statistical significance of the clustering, with the computational complexity being O(n) [37, 38]. A key problem of k-means algorithm lies in that, the number of clusters is required to be set in advance. However, for the time series problems of great majority, it is difficult to determine the number of clusters.

In [39], the clusters number is determined by optimizing a clustering validity function, which is defined by the ratio of scatter between-class to scatter within-class. This method is called the rule of variance ratio criterion (VRC):

$$ max\frac{tr\left[ S_{B} \right] /( K - 1)}{tr\left[ S_{W} \right] /(l - K)}, $$

(26)

where l is the samples number, $tr\left[ {S_{B} } \right]$ denotes the trace of scatter between-class matrix and $tr\left[ {S_{W} } \right]$ denotes the trace of scatter within-class matrix. VRC well embodies the compactness and separability of clustering results, and is closely related to the number of clusters. Therefore, VRC is widely used to measure the appropriateness of the number of clusters. Here, we take this criterion to determine K_opt ($K_{opt} \le \sqrt l$), similar as in [40]. When the rule of VRC is utilized to determine the number of clusters, it is required to check all of the possible numbers of clusters. Therefore, a reasonable search scope to the clusters numbers is required to be set, so as to reduce the amount of calculation. The greater l is, the greater the search scope becomes. Moreover, when K_opt is too large, the samples number in each class becomes very small, which will cause the decline of the model generalization ability. Therefore, in this work by trial-and-error, K_opt is set to values between 2 and 4, i.e., $\text{2} \le K_{opt} \le \text{4}$.

When K_opt is determined, and the training set has been clustered into K_opt clusters, $c_{{i^{*} }}$, whose center is the nearest to the current test sample $\left( {\varvec{x}_{j} , y_{j} } \right)$, will be determined. The constituent samples in $c_{{i^{*} }}$ are defined as the region of competence for this specific test sample. Based on the region of competence, the local predictor accuracy of a base predictor is evaluated. The predictor possessing the highest predictive accuracy is considered the most competent one. Because the local region has more similar distribution with the testing sample than other samples in the training datasets, therefore, the predictors which have better performance on the local region could perform better on the testing sample than other predictors, and will be selected into the final ensemble. What’s more, different testing sample locates different region of competence, yielding effective realization of dynamic ensemble selection.

The main issue with DES-PALR arises from the fact that it depends on the performance of the technique that defines the region of competence, such as K-NN algorithm or other clustering techniques. The algorithm is inclined to commit errors when outlier instances exist around the testing sample. Only using the local accuracy information alone is not sufficient to achieve results close to the Oracle. Moreover, any difference between the distribution of validation and test datasets may negatively affect the DES-PALR algorithm performance. Consequently, more information should be considered during dynamic ensemble selection for its successful application on time series prediction.

3.2 A Group of Three Novel Algorithms for Dynamic Validation Set Determination for TSP

The determination of an appropriate validation set is crucial for the performance of DES algorithms. In this section, a group of three novel algorithms for selecting validation set dynamically and effectively is proposed.

First of all, the training set is denoted as $Tr = \left\{ {\left( {\varvec{x}_{t} , y_{t} } \right)|\varvec{x}_{t} = \left\{ {\alpha_{t + 1} , \ldots ,\alpha_{t + m} } \right\},y_{t} = \alpha_{t + m + 1} } \right\}$. And the output profile of the test instance $\left( {\varvec{x}_{j} , y_{j} } \right)$ is denoted as $\tilde{\varvec{y}}_{j} = \left( {\tilde{y}_{j,1} ,\tilde{y}_{j,2} , \ldots ,\tilde{y}_{j,M} } \right)$, where $\tilde{y}_{{j, i}}$ is the predictive decision yielded by the base predictor p_i for the sample $\left( {\varvec{x}_{j} ,y_{j} } \right)$.

3.2.1 The Dynamic Validation Set Determination Algorithm Based on the Similarity Between the Predictive Value of the Test Sample and the Objective Values of the Training Samples (DVS-PvOv)

In this algorithm, specifically, the dynamic validation set is determined based on the similarity between the predictive value of the test sample and the objective values of the training samples. We term this algorithm as DVS-PvOv, for short. All the training samples $\left( {\varvec{x}_{{t^{*} .i}} ,y_{{t^{*} .i}} } \right)$$\left( {\text{1} \le i \le M} \right)$ satisfying Eq. (27) are selected into the validation set.

$$ t^{*} = \mathop {argmin}\limits_{{\text{1} \le t \le N}} \left| {y_{t.i} - \tilde{y}_{{j,i}} } \right|,\;\;\text{1} \le i \le M $$

(27)

The algorithm can be described as follows:

The time complexities of DVS-PvOv algorithm in its training and testing phase are O(M) and $O\text{(}M + MN + MlogZ\text{)}$, respectively, where M represents the size of initial pool of predictors, N represents the size of training set, and Z represents the number of selected predictors.

3.2.2 The Dynamic Validation Set Determination Algorithm Based on the Similarity Between the Newly Constituted Sample for the Test Sample and All the Training Samples (DVS-NsAs)

This algorithm determines the validation set not only based on the predictive value, but also based on the input values of the testing sample. A completely new sample $\left( {\varvec{x}_{j} ,\tilde{y}_{{j,i}} } \right)$ is constituted by $\tilde{y}_{{j,i}}$ and the input vector x_j of the testing sample $\left( {\varvec{x}_{j} ,y_{j} } \right)$. In this algorithm, in particular, the dynamic validation set is determined based on the similarity between the newly constituted sample $\left( {\varvec{x}_{j} ,\tilde{y}_{{j,i}} } \right)$ for the test sample and all the training samples. Therefore, we term this algorithm as DVS-NsAs, for short. All the training samples $\left( {\varvec{x}_{{t^{*} .i}} ,y_{{t^{*} .i}} } \right)$$\left( {\text{1} \le i \le M} \right)$ satisfying Eq. (28) are selected into the validation set.

$$ t^{*} = \mathop {argmin}\limits_{{\text{1} \le t \le N}} \sqrt {\left( {\varvec{x}_{t.i} - \varvec{x}_{j} ,y_{t.i} - \tilde{y}_{{j,i}} } \right)\left( {\varvec{x}_{t.i} - \varvec{x}_{j} ,y_{t.i} - \tilde{y}_{{j,i}} } \right)^{T} } ,\quad \text{1} \le i \le M $$

(28)

The DVS-NsAs algorithm is showed as follows:

The time complexity of DVS-NsAs algorithm is O(M) in its training phase and $O\text{(}M + MN + MlogZ\text{)}$ in its testing phase, where M represents the size of initial pool of predictors, N represents the size of training set, and Z represents the number of selected predictors.

The peculiarity of the DVS-NsAs algorithm lies in: it establishes a relationship between the predictive value of every predictor and the input vector of the testing sample. The DVS-NsAs algorithm selects validation samples, not only depend on the characteristic of current test sample but also take the special field in which each predictor is proficient into consideration. Hence, the predictors that possess the better performance than others on the selected validation samples could have higher predictive accuracy.

3.2.3 The Dynamic Validation Set Determination Algorithm Based on the Similarity Between the Output Profile of the Test Sample and the Output Profile of Each Training Sample (DVS-OpOp)

This algorithm dynamically determines the validation set based on the similarity between the output profile of the specific test sample and the output profile of each training sample, which is abbreviated as DVS-OpOp. In this algorithm, the set of output profiles of all the training samples are computed, which is denoted as $Y = \left\{ {\tilde{\varvec{y}}_{t} } \right\}_{{t = \text{1}}}^{N}$, where $\tilde{\varvec{y}}_{t} = \left( {\tilde{y}_{t,1} ,\tilde{y}_{t,2} , \ldots ,\tilde{y}_{t,M} } \right)$. The similarity is evaluated based on the Euclidean distance between the two corresponding output profiles, computed as below:

$$ dist\text{(}t,j\text{)} = \sqrt {\left( {\tilde{\varvec{y}}_{t} - \tilde{\varvec{y}}_{j} } \right)\left( {\tilde{\varvec{y}}_{t} - \tilde{\varvec{y}}_{j} } \right)^{T} } ,\quad \text{1} \le t \le N $$

(29)

All the training samples are ranked according to the Euclidean distances between their output profiles with the output profile of the specific test sample, and an appropriate number of top-ranking training samples are selected into the validation set.

The algorithm is showed in detail as follows:

The time complexities of DVS-OpOp algorithm in the training and testing phase are O(M) and $O\text{(}M + MN + NlogM + MlogZ\text{)}$, respectively, where M represents the size of initial pool of predictors, N represents the size of training set, and Z represents the number of selected predictors.

The aim of the proposed DVS-OpOp is also to select samples that are close to the test sample. However, the similarity is computed over the decision space through the concept of decision templates rather than feature space.

The proposed three new algorithms, i.e., DVS-PvOv, DVS-NsAs and DVS-OpOp, give impetus to the effective realization of DES for TSP further. Their common advantage lies in that, they are not limited by the quality of the local region of competence defined solely in the feature space.

3.3 Dynamic Ensemble Selection Based on Consensus of Predictors (DES-CP)

The fifth DES algorithm put forward by us is the DES-CP algorithm. It is designed based on the extent of consensus of the predictors, and it works by considering a pool of ensembles of predictors (EoPs) rather than a pool of predictors.

Firstly, a population of ensembles of predictors should be generated, i.e., $P^{*} = \left\{ {P_{1}^{\prime } ,P_{2}^{\prime } , \ldots ,P_{n}^{\prime } } \right\}$, where n is the number of the ensembles of predictors, and $P_{m}^{\prime } \subseteq P,m = 1, \ldots ,n$. The method employed to generate $P^{*}$ can be an optimization algorithm, such as genetic algorithm or greedy search methods [41, 42]. Then, for each test sample $\left( {\varvec{x}_{j} ,y_{j} } \right)$, $P_{con}^{\prime }$, which has the highest consensus, is chosen as the final ensemble of predictors. In DES-CP, the extent of consensus among the base predictors of an ensemble is regarded as its level of competence. Figure 4 shows an overview of the DES-CP algorithm.

Fig. 4

Overview of the DES-CP algorithm

The difficulty of the DES-CP algorithm lies in how to generate the appropriate $P^{*} = \left\{ {P_{1}^{\prime } ,P_{2}^{\prime } , \ldots ,P_{n}^{\prime } } \right\}$ and make sure the quality of each $P_{m}^{'}$. In the following, Zhou et al.’s analyses are presented [28].

Assume that each individual predictor has been assigned an optimum weight that exhibits its importance in the ensemble. Then the predictors whose weights are bigger than a pre-set threshold $\lambda$ are selected to constitute the final ensemble. And $\lambda$ is set to 1/M. The weight of the i-th predictor is denoted as w_i, which should satisfy both Eqs. (10) and (11). A weights vector is built as $\varvec{w} = \left( {w_{1} ,w_{2} , \ldots ,w_{M} } \right)$. Since the best weights should minimize the generalization error of the new ensemble, considering Eq. (18), the best weights vector w_opt is expressed as:

$$ \varvec{w}_{opt} = argmin\left( {\sum\limits_{{i = \text{1}}}^{M} {\sum\limits_{{j = \text{1}}}^{M} {\varvec{w}_{i} \varvec{w}_{j} C_{ij} } } } \right) $$

(30)

$w_{{opt,k}}$, i.e. the k-th (k = 1, 2, … , M) component of w_opt, can be solved by lagrange multiplier. $w_{{opt,k}}$ satisfies:

$$ \frac{{\partial \left( {\sum\nolimits_{i = 1}^{M} {\sum\nolimits_{j = 1}^{M} {w_{i} w_{j} C_{ij} - 2\lambda \left( {\sum\nolimits_{i = 1}^{M} {w_{i} - 1} } \right)} } } \right)}}{{\partial w_{opt,k} }} = 0 $$

(31)

Equation (31) can be simplified as:

$$ \sum\limits_{\begin{subarray}{l} j = \text{1} \\ j \ne k \end{subarray} }^{M} {w_{{opt,k}} C_{kj} = \lambda } $$

(32)

Considering that $w_{{opt,k}}$ satisfies Eq. (11), we get:

$$ w_{opt,k} = \frac{{\sum\nolimits_{j = 1}^{M} {C_{kj}^{ - 1} } }}{{\sum\nolimits_{i = 1}^{M} {\sum\nolimits_{j = 1}^{M} {C_{ij}^{ - 1} } } }} $$

(33)

Though Eq. (33) is enough to solve w_opt in theory, it rarely works well in real-world applications. Neither does it work well in this work, because many ELM models have homogeneous performance in most tasks, which makes the correlation matrix $\left( {C_{ij} } \right)_{M \times M}$ of the ensemble become irreversible or ill-conditioned. In such circumstances, Eq. (33) cannot be solved directly.

Since Eq. (30) can be viewed as an optimization problem, considering the success that has been obtained by genetic algorithms in optimization area [43], the Genetic Algorithm based Selective ENsemble (GASEN) algorithm proposed by Zhou et al. [28] is utilized in this work. GASEN is used for finding out the subsets of P, which employs the standard genetic algorithm (GA) to evolve the optimum weight vector w_opt [43]. Next, the base ELMs, whose corresponding optimum weights are bigger than $\lambda$, are chosen to constitute $P_{m}^{'}$. We denote the validation set as V, the estimated value of the correlation between the i-th ELM and j-th ELM is computed as:

$$ C_{ij}^{V} = \frac{{\sum\nolimits_{{\varvec{x}_{t} \in V}} {\left( {f_{i} \left( {\varvec{x}_{t} } \right) - y_{t} } \right)\left( {f_{j} \left( {\varvec{x}_{t} } \right) - y_{t} } \right)} }}{\left| V \right|} $$

(34)

The estimated generalization error of the ELMs ensemble corresponding to the base weights vector w in the evolving population is:

$$ E_{w}^{V} = \sum\limits_{{i = \text{1}}}^{M} {\sum\limits_{{j = \text{1}}}^{M} {w_{i} w_{j} C_{ij}^{V} } } = \varvec{w}^{T} C^{V} \varvec{w} $$

(35)

Equation (35) shows the goodness of w. The smaller the $E_{\varvec{w}}^{V}$ is, the better quality the w possesses. So the standard GA uses $f\left( \varvec{w} \right) = 1/E_{\varvec{w}}^{V}$ as the fitness function. And the evolved optimum w is required to be normalized, so that its components can be compared with $\lambda$. A simple normalization scheme is used here:

$$ w_{opt.i} = {{w_{i} } \mathord{\left/ {\vphantom {{w_{i} } {\sum\limits_{{i = \text{1}}}^{M} {w_{i} } }}} \right. \kern-0pt} {\sum\limits_{{i = \text{1}}}^{M} {w_{i} } }} $$

(36)

What’s more, GASEN has randomness of itself and initializes w randomly for every run, so it will generate a different pruning ensemble $P_{m}^{'}$ for each time. The difference mainly lies in that the number of the selected base models is different. And even though the numbers are the same, it cannot be guaranteed that the selected base models remain completely same.

The GASEN algorithm is performed n times to generate $P^{*} = \left\{ {P_{1}^{\prime } ,P_{2}^{\prime } , \ldots ,P_{n}^{\prime } } \right\}$. When a new test sample is to be predicted, the consensus of each ensemble of predictors is calculated, and then the ensemble of predictors which possesses the highest consensus is chosen as the final ensemble.

In regard to the problem of how to evaluate the consensus of an ensemble, two methods are designed. Let $P_{m}^{\prime } = \left( {p_{m.1}^{\prime } ,p_{m.2}^{\prime } , \ldots ,p_{m.s}^{\prime } } \right)$ denote the m-th ensemble of selected predictors, and s denotes the size of the m-th ensemble $P_{m}^{'}$. $P_{m}^{{\prime }} \left( {\varvec{x}_{j} } \right) = \left( {p_{m.1}^{\prime } \left( {\varvec{x}_{j} } \right),p_{m.2}^{\prime } \left( {x_{j} } \right), \ldots ,p_{m.s}^{\prime } \left( {\varvec{x}_{j} } \right)} \right)$ denote the predicted values of all the predictor in the m-th ensemble. One method of evaluating the consensus of the m-th ensemble is to calculate the variance of the predicted values made by its constituent predictors. The algorithm developed in this way is termed Dynamic Ensemble Selection based on Consensus of Predictors evaluated with predictions Variance (DES-CP-Var), which is calculated as below:

$$ var\left( {P_{m}^{'} \left( {\varvec{x}_{j} } \right)} \right) = \frac{{\sum\nolimits_{{i = \text{1}}}^{s} {\left( {p_{m.i}^{'} \left( {\varvec{x}_{j} } \right) - \frac{{\sum\nolimits_{{a = \text{1}}}^{s} {p_{m.a}^{'} \left( {\varvec{x}_{j} } \right)} }}{s}} \right)} }}{s} $$

(37)

The smaller the variance is, the higher the consensus will be.

Another method which called Dynamic Ensemble Selection based on Consensus of Predictors evaluated with Clustering (DES-CP-Clustering) is also proposed as another specific implementation for the DES-CP algorithm. In this method, k-means clustering is performed on $P_{m}^{'} \left( {\varvec{x}_{j} } \right)$, and all the predicted values are divided into k clusters. And the criterion is originally designed as the margin between the size of the cluster (s₁) containing the most predicted values and the size of cluster (s₂) containing the second most predicted values, i.e., the margin is calculated as $\varGamma = \left| { s_{\text{1}} - s_{\text{2}} } \right|$, originally. However, GASEN is used here for the generation of $P^{*}$. The size of each generated ensemble is uncertain, which should also be taken into account. Therefore, the margin is calculated as $\varGamma = \frac{{\left| { s_{\text{1}} - s_{\text{2}} } \right|}}{s}$. And under this definition, the bigger the value of $\varGamma$ becomes, the higher the consensus is.

The entire algorithm is displayed as follows:

$O(ngM^{2} (r + \frac{1}{2}r + rf)$ and $\text{O(}\sum\nolimits_{{i = \text{1}}}^{n} {\left| {P^{\prime}_{i} } \right|} \text{)}$ are the time complexities of DES-CP algorithm in its training and testing phase, respectively, where n denotes the size of $P^{*}$, M represents the size of initial pool of predictors, N represents the size of training set, Z denotes the number of selected predictors, g is the number of generations, r represents the size of population, and f denotes the length of chromosome.

The standpoint is that the higher the consensus among the constituent predictors is, the higher the level of confidence in the decision will be. Consequently, by maximizing the extent of consensus of an ensemble, the degree of certainty that it will make a better prediction is increased.

The main advantage of this technique stems from the fact that it does not require information from the region of competence. Therefore, it does not suffer from the limitation of the algorithm which defines the region of competence.

4 Empirical Analysis and Evaluation

4.1 Experimental Data and Data Pre-processing

A total of twelve benchmark datasets from Time Series Data Library [44] are conducted in comparative experiments. DES-PALR, DVS-PvOv, DVS-NsAs, DVS-OpOp, DES-CP-Var and DES-CP-Clustering models are implemented on Dow-Jones Industrial Average (DJI), St. Louis Fed Financial Stress index (STLFSI), Odonovan, Montgome, M3-U.S (MUS), Wolf River at New London (WRNL), Clearwater River at Kamiah (CRK), Mean monthly Flow in piper’s hole River (MFR), Exchange rate of Australian dollar: $A for 1US dollar (EAFUS), Annual Copper Prices (ACP), Mean Annual Nile Flow (MANF), U.K. Deaths from Bronchitis, Emphysema and Asthma (UKDBEA). The concrete scale of each dataset is shown respective in Table 2.

Table 2 Key features of the datasets conducted in our experiments

Since the attributes of sample sets have different ranges, it is necessary to adjust the value domain of each attribute into the range between 0 and 1. This ensures that the input attributes with larger value do not overwhelm the smaller value inputs, and then helps to reduce prediction errors. The normalization method is presented as follows:

Each of the series value x_t is normalized by the linear interpolation as in Eq. (38):

$$ x_{t}^{new} = \frac{{x_{t} - x^{min} }}{{x^{max} - x^{min} }} $$

(38)

where $x_{t}^{new}$ = normalized value; x_t= value to be normalized; x^min = minimum value of the series to be normalized; x^max = maximum value of the series to be normalized.

4.2 Experimental Methodology

4.2.1 Performance Measurements

A performance measurement is necessary to appropriately evaluate the predictive performance of the pruned ensemble obtained by using different ensemble pruning techniques. The performance measurements are defined on the basis of prediction errors, which are computed as the difference between the real value of the series and the predicted value, just as below:

$$ e_{t} = \left( {target_{t} - output{}_{t}} \right) $$

(39)

where target_t denotes the desired output of the prediction model at time t, and output_t denotes the output of the ensemble at time t. Based on the prediction errors, two performance measurements employed to evaluate the predictive performance of the pruned ensembles are described below.

4.2.1.1 Root Mean Square Error (RMSE)

Root mean square error (RMSE) [45] is the most common metric used to analyze ensembles performance, and it is defined by the equation:

$$ \text{RMSE} = \frac{\text{1}}{N}\sqrt {\sum\limits_{{t = \text{1}}}^{N} {\left( {e_{t} } \right)^{\text{2}} } } $$

(40)

where N denotes the number of data values of the testing time series. Obviously, the lower the value of RMSE, the better the prediction result will be. Although RMSE is quite common as a performance measurement, it does not provide complete and convincing evidence about the accuracy obtained by the predictive model. Therefore, another metric of Mean Absolute Error is also used to evaluate the performance of the proposed algorithms.

4.2.1.2 Mean Absolute Error (MAE)

In statistics, mean absolute error (MAE) [46] is a quantity used to measure how close forecasts or predictions are to the eventual outcomes. MAE is defined as:

$$ \text{MAE} = \frac{\text{1}}{N}\sum\limits_{{t = \text{1}}}^{N} {\left| {e_{t} } \right|} $$

(41)

Clearly, the lower the value of MAE, the closer is the desired result from the predicted one.

4.2.2 Experimental Setup

First of all, 100 well-trained ELMs are constructed by changing the type of activation function and the number of hidden neurons, where the former is represented by Eqs. (21–25), and the latter is in the range of $\left[ {1,20} \right]$. These well-trained ELMs are utilized to form the initial pool of basic models.

Every dataset is spilt into two distinctive parts, i.e., a training set and a testing set, with 70% and 30% of the initial dataset, respectively. With respect to the time window size (TWS), considering the size of the datasets and by trial-and-error, the feasible value is set to 5. Considering the randomness of the input weights and biases, which will lead to instability of ELM, the proposed algorithms are run repeatedly for 20 times. The final performance measurements are obtained by averaging the performances of these 20 rounds.

In our experiments, the proposed algorithms are compared with Static Averaging All (AA), Static Ensemble Selective (SES), GASEN, ELM, Hierarchical Extreme Learning Machine (H-ELM), BP, Deep representations via Extreme Learning Machine (DrELM), Algebraic Prediction External Smoothing (APES) [4], Algebraic Prediction Internal Smoothing (APIS) [4], and Algebraic Prediction Mixed Smoothing (APMS) [4].

4.3 Experimental Results

In this section, the experimental results of RMSE and MAE obtained by the proposed six algorithms, static ensemble selection methods and some other state-of-the-art methods on the twelve benchmark time series datasets are listed out in Tables 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13.

Table 3 RMSE and rankings based on RMSE on DJI, STLFSI and Odonovan time series

Table 4 RMSE and rankings based on RMSE on Montgome, MUS and WRNL time series

Table 5 RMSE and rankings based on RMSE on CRK, MFR and EAFUS time series

Table 6 RMSE and rankings based on RMSE on ACP, MANF and UKDBEA time series

Table 7 MAE and rankings based on MAE on DJI, STLFSI and Odonovan time series

Table 8 MAE and rankings based on MAE on Montgome, MUS and WRNL time series

Table 9 MAE and rankings based on MAE on CRK, MFR and EAFUS time series

Table 10 MAE and rankings based on MAE on ACP, MANF and UKDBEA time series

Table 11 The average ranking of the proposed DES algorithms and the comparative methods on the twelve time series based on RMSE, MAE, and overall

Table 12 The detailed RMSE performance of APES, APIS and APMS on the first four time series

Table 13 The detailed MAE performance of APES, APIS and APMS on the first four time series

Tables 3, 4, 5 and 6 give the detailed RMSE performance and the ranking results based on RMSE on the twelve time series. From the results, it is obviously shown that, the proposed DES algorithms achieve higher ranks than other state-of-the-art algorithms, i.e., GASEN, AA, SES, ELM, H-ELM, BP and DrELM. At the same time, the algorithms that obtain the best performance on each time series are all the proposed DES algorithms. According to the average ranking results shown in column 3 of Table 11 that, DES-CP-Clustering achieves the best average ranking on the twelve time series based on RMSE, while ELM and BP get the worst ones.

Tables 7, 8, 9 and 10 show the detailed MAE performance and the ranking results based on MAE on the twelve time series. It can be observed from Tables 7, 8, 9 and 10 that, only on EAFUS time series, SES achieves the best MAE performance. Except for that, on other eleven time series datasets, the algorithms which achieve the best MAE performance are all the proposed DES methods. Table 11 lists out the average ranking of the proposed DES algorithms and the comparative methods on the twelve time series based on MAE. It is clearly shown in column 4 of Table 11 that, the top six are all the proposed six DES algorithms, while BP is the last one.

Column 5 of Table 11 also gives the average comprehensive ranking of the proposed DES algorithms and the comparative methods on the twelve time series based on both RMSE and MAE. The results demonstrate that: (1) the performances of the proposed DES algorithms are obviously better than that of the static ensemble selection methods, especially for DES-CP-Clustering and DES-CP-Var algorithms; (2) ensembles of predictors outperform single models; (3) the two deep neural networks, i.e., H-ELM and DrELM, achieve better performance than the single hidden layer neural networks; (4) ELM is slightly better than BP on the twelve time series datasets.

It can be concluded from Tables 3, 4, 5, 6, 7, 8, 9, 10 and 11 that DES-CP-Var and DES-CP-Clustering achieve more excellent performance than other proposed algorithms on most of the twelve time series datasets, and they obtain the highest overall rankings (3.75 and 4.21) within the six DES algorithms. The reason might be that, DES-CP-Clustering and DES-CP-Var algorithms are designed based on the extent of consensus of the predictors, and they work by considering a pool of EoPs generated by GASEN, rather than a pool of predictors. However, the disadvantage of these two proposed algorithms is time-consuming. Therefore, whether to choose DES-CP-Clustering or DES-CP-Var depends on the training time demanded by the specific systems. If real time response is required, DES-PALR algorithm is recommended, owing to its low time-complexity and good performance.

It can also be concluded from Table 11 that, if the criterion of performance measurement is RMSE, DVS-OpOp algorithm is a good choice (the second best). The reason is that, it costs less time than DES-CP-Clustering and DES-CP-Var algorithms. Meanwhile it is not trapped by the techniques which define the local region. Although the proposed DVS-PvOv and DVS-NsAs algorithms do not achieve better performance than the other DES algorithms proposed by us on the twelve time series datasets, they still obtain higher accuracy than the compared methods. As stated by the principle of “No Free Lunch”, no algorithm performs better than any other ones on all the problems. For example, DVS-PvOv algorithm achieves the best RMSE performance on EAFUS time series dataset, while DVS-NsAs algorithm achieves the most superior MAE performance on UKDBEA, STLFSI and Odonovan time series datasets.

Tables 12 and 13 give the detailed RMSE and MAE performance of APES, APIS and APMS on the first four time series datasets, respectively. It can be concluded that, APIS achieves the best RMSE and MAE performance on the Odonovan time series only, outperforming the proposed six DES algorithms. At the same time, APES and APMS do not obtain good performance compared with the proposed DES algorithms.

Next, to ascertain whether the proposed DES algorithms are significantly better than GASEN, SES, AA, ELM, H-ELM, BP and DrELM in a statistic sense, t-tests are implemented to the rankings of all the algorithms obtained on the twelve time series datasets. However, if the rankings of algorithms are not normally distributed, t test may lead to error conclusions. Therefore, we conduct normality tests firstly, with the results shown in Table 14. The built-in function JBTEST of MATLAB is employed to implement normality tests, where the significance level ALPHA was set to 0.01. The values reported in Table 14 are the test statistic JBTEST returned by function JBTEST, where H = 0 indicates that the null hypothesus cannot be rejected at the 1% significance level, and H = 1 indicates that the null hypothesis can be rejected at the 1% level. Null hypothesis is that ranking is normally distributed.

Table 14 The results of normality tests

It is clearly shown in Table 14 that, the rankings of almost all algorithms obey normal distribution, with only one exception, i.e., H-ELM.

Then, t-tests are conducted to compare the rankings of the proposed DES algorithms with those of the GASEN, SES, AA, and other state-of-the-art algorithms, with the significance level ALPHA set to 0.05 and TAIL set to left. The results are listed in Table 15. The null hypothesis H = 0 indicates that there is no significant difference between Model A and Model B. The null hypothesis H = 1 indicates that Model A is significantly better than Model B at the 5% significance level (t value ≤ − 1.7139).

Table 15 Results of t-tests applied to the rankings of the proposed DES algorithms with others on the twelve datasets

As shown in Table 15, for 36 of the 42 t tests (85.7%), the proposed DES algorithms achieve significant improvements on the rankings of the comparative approaches at 5% significance level. These results clearly show that DES-CP-Clustering, and DES-CP-Var are significantly better than the state-of-the-art algorithms. At the same time, the proposed DES algorithms are all significantly better than ELM, H-ELM, BP and DrELM at the 5% significance level. Although it can be obviously concluded from Table 11 that, the average comprehensive of rankings of DES-PLAR, DVS-OpOp, DVS-NsAs and DVS-PvOv are superior to all the comparative algorithms, the performances of the four are not siginificantly better than the comparative algorithms at the 5% significance level, except for ELM, H-ELM, BP and DrELM in Table 15. This phenomenon is easy to understand. Since the seven comparative algorithms are all state-of-the-art algorithms in the literature, the phenomenon that the difference between DES-PLAR, DVS-OpOp, DVS-NaAs, DVS-PvOv and the comparative algorithms especially GASEN and SES are not significant is natural.

Finally, Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16 display the prediction values of one of the proposed DES algorithms which performs the best, i.e., DES-CP-Clustering, and GASEN on the twelve benchmark time series datasets, respectively. The prediction errors obtained by DES-CP-Clustering and GASEN are displayed in Figs. 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 and 28.

Fig. 5

Dow Jones Industrial Average (prediction values)

Fig. 6

St. Louis Fed Financial Stress Index (prediction values)

Fig. 7

Odonovan (prediction values)

Fig. 8

Montgome (prediction values)

Fig. 9

M3-U.S (prediction values)

Fig. 10

Wolf River at New London (prediction values)

Fig. 11

Clearwater River at Kamiah (prediction values)

Fig. 12

Mean monthly Flow in piper’s hole River (prediction values)

Fig. 13

Exchange rate of Australian dollar: $A for 1 US dollar (prediction values)

Fig. 14

Annual Copper Prices (prediction values)

Fig. 15

Mean Annual Nile Flow (prediction values)

Fig. 16

U.K. Deaths from Bronchitis, Emphysem and Asthma (prediction values)

Fig. 17

Dow Jones Industrial Average (prediction errors)

Fig. 18

St. Louis Fed Financial Stress Index (prediction errors)

Fig. 19

Odonovan (prediction errors)

Fig. 20

Montgome (prediction errors)

Fig. 21

M3-U.S (prediction errors)

Fig. 22

Wolf River at New London (prediction errors)

Fig. 23

Clearwater River at Kamiah (prediction errors)

Fig. 24

Mean monthly Flow in piper’s hole River (prediction errors)

Fig. 25

Exchange rate of Australian dollar: $A for 1 US dollar (prediction errors)

Fig. 26

Annual Copper Prices (prediction errors)

Fig. 27

Mean Annual Nile Flow (prediction errors)

Fig. 28

U.K. Deaths from Bronchitis, Emphysem and Asthma (prediction errors)

From the above comparisons, it can be concluded that DES-CP-Clustering, one representative of the proposed DES algorithms, has better generalization performance than GASEN on the twelve benchmark time series prediction problems. In addition, a conclusion can be reached that the more training samples provided to the proposed models, the better performance can the models obtain. Therefore, in order to achieve better performance, adequate training samples are indispensable.

5 Conclusions and Future Works

Among the two types of selective ensemble paradigms, i.e., static and dynamic ensemble selection, the latter one has shown to be a very effective scheme for TSP problems. In this paper, several new DES algorithms are designed for enhancing the ensemble generalization performance.

With the proposed DES-PALR algorithm, the predictors performing better on the local region could also perform better on the test sample, while different test sample locates different region of competence, thereby successfully realizing dynamic ensemble selection.

The strength of the proposed group of DVS-PvOv, DVS-NsAs and DVS-OpOp algorithms mainly lies in that, they are not limited by the quality of the local region of competence solely defined in the feature space, which greatly boost their predictive performances.

The major advantage of DES-CP is that, it does not need any information from the region of competence, and therefore, it is not restricted by the algorithms which define the region of competence.

The innovation of this work manifests in that, to our best knowledge, it is the first time that all these new DES algorithms are developed for the research of TSP.

Experimental results on twelve benchmark time series datasets verify that the proposed six DES algorithms achieve significantly higher predictive performance than the comparative state-of-the-art methods, including GASEN, ELM, H-ELM, BP and DrELM.

Future works on this topic will involve: (a) finding the ensemble of predictors that are complementary and diverse for solving TSP problems; (b) trying some different performance measurements so as to better assess prediction performance of models.