DWE-IL: a new incremental learning algorithm for non-stationary time series prediction via dynamically weighting ensemble learning

Abstract

In this work, an Incremental Learning Algorithm via Dynamically Weighting Ensemble Learning (DWE-IL) is proposed to solve the problem of Non-Stationary Time Series Prediction (NS-TSP). The basic principle of DWE-IL is to track real-time data changes by dynamically establishing and maintaining a knowledge base composed of multiple basic models. It trains the base model for each non-stationary time series subset, and finally combine each base model with dynamically weighting rules. The emphasis of the DWE-IL algorithm lies in the update of data weights and base model weights and the training of the base model. Finally, the experimental results of the DWE-IL algorithm on six non-stationary time series datasets are presented and compared with those of several other excellent algorithms. It can be concluded from the experimental results that the DWE-IL algorithm provides a good solution to the challenges of the NS-TSP tasks and has significantly superior performance over other comparative algorithms.

1 Introduction

A time series is a series of observations collected in a fixed sampling interval. Many dynamic processes in the real world can be modeled as time series, such as stock price changes, weather prediction, number of sunspots, and disease incidence, etc. If we want to predict these processes to help production and life, we need to understand the knowledge of time series prediction (TSP). TSP refers to the process of predicting future trends based on historical time series generation models. Time series can be divided into stationary time series and non-stationary time series (NS-TS). In the narrow sense, stationary means that the probability distribution of a sequence does not change with time, while in the broad sense, stationary means that there are primary and secondary moments in a sequence, the mean value is constant, and the covariance is a function related to the sampling interval. On the contrary, non-stationary means that the mean and covariance of a sequence change over time. The change is affected by many factors, some of which play a long-term and decisive role, making the change of a sequence shows a certain trend and regularity. Others play a short-term and inconclusive role.

Many traditional machine learning methods usually use batch learning or off-line learning paradigms to solve problems. With the explosion of real-time data, it has become increasingly difficult for off-line machine learning algorithms to play a role. In order to deal with the situation that data arrive continuously rather than once, on-line learning paradigm has been proposed. Generally speaking, there are two main application scenarios of on-line learning. One is to improve the existing off-line learning methods to enhance their efficiency and scalability. The second is using on-line learning directly to deal with the arrival of new samples. As a classic on-line forecasting process, the non-stationary time series prediction (NS-TSP) inevitably needs that the algorithm proposed for it has the on-line forecasting ability, which is a basic premise.

Regarding NS-TSP, there are the following challenges: 1) NS-TS is considered a deterministic chaotic time series. It is sensitive to initial conditions, so it is unrealistic to use historical data to make long-term predictions; 2) NS-TS has non-linear and non-stationary characteristics, which leads to the “stability -plasticity” dilemma. How to balance the two is a difficult problem.; 3) NS-TS has high-noise characteristics, which means that no matter what model is built, the complete information of the sequence cannot be obtained, so we need to eliminate the influence of noise; 4) Some NS-TS have periodic characteristics. How to respond accurately and quickly when the historical environment reappears is a question worthy of our consideration.

The early researchers mainly focus on the investigation of linear and stationary TSP problems. However, with the development of theory and technology, more and more evidences show that the time series in real life are mostly NS-TS. Therefore, some prediction methods for NS-TS are proposed. The existing NS-TSP methods can be roughly divided into three categories:

• 1) Traditional statistical methods. The traditional statistical methods are the earliest methods applied to NS-TSP, among which the representative methods are Auto-Regressive Integrated Moving Average (ARIMA) model [1] and Generalized Auto-Regressive Conditional Heteroscedasticity (GARCH) model [2]. The ARIMA model has been widely used in the NS-TSP task. However, it needs to smooth the NS-TS through a difference process, which inevitably affects its prediction accuracy and efficiency. The GARCH model is a method that uses past changes and variance to predict future changes. It can fit sequences with fluctuation characteristics well. But like ARIMA, it also needs to smooth NS-TS.

• 2) Computational intelligence methods. The representative methods of computational intelligence methods include Artificial Neural Networks (ANNs) [3], Fuzzy Logic (FL) [4], and Support Vector Machine (SVM) [5], etc. As a nonlinear prediction model, ANNs have good self-learning and function approximation abilities, being widely used in the field of NS-TSP. However, ANNs often require a lot of training data, their structures and parameters are difficult to determine, their convergence speed is slow, and they are easy to fall into the local optima. FL generates uncertain knowledge by generating fuzzy NS-TS, simulating human thinking, and then transforming it into accurate prediction values ​​to complete the prediction task. But how to generate suitable fuzzy rules is a challenging issue to be addressed. SVM has a simple structure and strong generalization ability. It has been well applied in the field of NS-TSP, but it is only suitable for small sample learning.

• 3) Combination prediction methods. Experiments show that it is difficult for a single model and method to fully reflect the overall change law of the prediction object, especially for tasks with highly uncertain features such as NS-TSP, and therefore, combination prediction methods have emerged and become the most popular methods at the moment. The combination prediction methods obtain comprehensive information by combining multiple methods, including the traditional statistical methods and computational intelligence methods mentioned above, to improve their prediction performance and stability. There are three ways to implement combination forecasting methods: 1) through incremental learning (IL) [6] and ensemble learning (EL) [7], such as the research work carried out in [8, 9]; 2) through the staged idea, such as the research work carried out in [10]. The basic idea is to decompose NS-TS, using several models to predict them separately, and then combining their prediction results; 3) through the monitoring mechanism, such as the research work carried out in [11]. The basic idea is to track changes by monitoring the performance of models and trigger different model update mechanisms based on the degree of changes.

  The mainstream IL and EL methods in non-stationary environment include sliding window technique, concept drift detection technique and data block one. Sliding window technology is a widely used method to deal with non-stationary forecasting tasks. It uses a simple forgetting mechanism to maintain a series of newest data to capture data changes in the current environment. The determination of an appropriate window size is a very important problem in sliding window technology. Large windows contain enough information to make the model maintain good generalization performance under the condition of stable data distribution. However, with large windows, the model cannot be updated timely to adapt to data changes. Conversely, a small window can respond to changes in a non-stationary environment in a timely manner, but it may also result in poor performance due to less available information available. Therefore, the adaptive sliding window technology, whose window size can be adapted autonomously according to relevant rules, can better adapt to non-stationary environment. Different from sliding window technique, concept drift detection technique is an explicit method to deal with non-stationary environment. It can select the appropriate model update method by measuring the change degree of data in non-stationary environment. While in the data block technology, each base model is trained based upon a data block, so each base model contains the historical data distribution information of its training data block, which increases the diversity and stability of the ensemble model.

IL refers to the process in which the model continuously learns new knowledge from new data and saves most of the previously learned knowledge, which is very similar to the human learning model. The idea of IL is when the new data arrives, it is not necessary to re-learn all the data, but to update the original knowledge with the new data. IL paradigm has been extensively employed in various research areas, such as image recognition [12], document classification [13] and intrusion detection [14, 15], etc. The IL algorithms used in NS-TSP need to meet the following conditions [16, 17]:

• a) Any training dataset is only learned once and will not be used for subsequent training. The knowledge learned are stored incrementally in the model parameters.

• b) Because the latest dataset can best represent the current environment, knowledge should be classified according to the relationship between knowledge and the current environment, and knowledge should be dynamically updated.

• c) The model should have a strategy to coordinate the conflict between old knowledge and new knowledge, that is, there should be a mechanism to monitor the performance of the model on new data and old data.

• d) The model should forget or discard knowledge that is no longer relevant but can recall it when the environment reappears.

The EL paradigm is a process of generating and merging multiple models according to a certain strategy to solve a specific computational intelligence problem [18]. It has three elements: data sampling, training base models, and combining base models. EL algorithms have been widely utilized in a variety of research areas, such as face recognition [19, 20], text classification [21] basic expression analysis [22], and several other important investigation fields. The EL methods used in NS-TSP can be divided into three categories:

• a) Changing the combination rule to adapt the non-stationary environment for the previously trained base models, such as weighted majority voting and Winnow based algorithms [23].

• b) Updating the online model and all ensemble members with the new dataset, such as the online promotion algorithm [24].

• c) Adding new ensemble members [25] or replacing the minimum contributor or youngest member in the ensemble with the base model generated by utilizing the new dataset [26].

In EL paradigm, many mature machine learning algorithms can be used as the basic learning algorithm, such as SVM and ANNs. Compared with SVM and traditional ANNs, Extreme Learning Machine (ELM) [27] has high scalability and low computational complexity, which can greatly accelerate the generalization speed while ensuring the generalization performance. Extreme Learning Machine with Kernels (ELMK) [28] is a further improvement of ELM, which overcomes the randomness of ELM and is a good choice for the basic learning algorithm.

Based on the above, we can know that the traditional statistical methods assume that there is a linear structure among data variables, but ignore the correlation and multi-level of information, which makes them difficult to obtain excellent prediction results in practical applications. Computational intelligence methods are a type of nonlinear prediction methods, including some classical machine learning models. However, it is difficult for a single model and method to fully reflect the overall change rule of the predicted objects, especially for tasks with high uncertainty. Combination prediction methods combine multiple methods, including traditional statistical methods and computational intelligence ones, to obtain comprehensive information, so as to improve their prediction performance and stability. However, many combination prediction methods propose solutions based on specific NS-TSP tasks, or on specific influencing factors in NS-TS.

Aiming at the challenges of NS-TSP and the disadvantages of the above methods, we hope to develop a unified on-line forecasting framework, which does not need to specify the internal changes of NS-TS. This will greatly reduce the computational complexity and, simultaneously, increase the practicability of the proposed algorithm. Besides, for the base algorithms without on-line forecasting ability, IL and EL are important technologies for them to realize on-line forecasting. Therefore, this paper proposes an Incremental Learning Algorithm via Dynamically Weighting Ensemble Learning, abbreviated as the DWE-IL algorithm.

The basic principle of DWE-IL is to track real-time data changes by building and maintaining a knowledge base composed of multiple base learners, dynamically. DWE-IL believes that, because the distribution of data will change over time, the latest data commonly best reflects the latest state of the current environment. In response to new data, DWE-IL reorganizes and integrates the existing knowledge, while updating the existing knowledge base, so as to accurately reflect the current environment and predict the next environment. The reason why the proposed method can solve the non-stationary prediction better than the other ones is that DWE-IL provides a unified and efficient on-line forecasting framework for NS-TSP through a double IL mechanism and a double dynamically weighting mechanism according to the characteristics of NS-TS. In the learning process, there is no need to consider specific influencing factors in NS-TS. In addition, DWE-IL not only has higher prediction accuracy, but also has lower computational complexity and time cost. Therefore, compared with many traditional statistical methods, computational intelligence methods and combination prediction ones, DWE-IL possesses excellent generalization performance and wide applicability.

The performance of “dynamical” of DWE-IL is mainly reflected in the weight update, which is divided into the following two points: 1) The update of data weights. We initialize the data weights of each newly arrived dataset to be uniform distribution, and then dynamically update the weights according to the performance of the current ensemble model on this dataset. This reflects the adaptability of the old knowledge to the new data, and also makes the samples with higher prediction difficulty in the new data get more attention; 2) The update of the weights of the base models. We use a double dynamically weighting mechanism to obtain the final weights of the base models. From the point of view of a single base model, the performance of each base model in each environment since its generation is dynamically time-weighted, because the performance of each base model in the newer environment should get higher weight. From the perspective of the ensemble model, we dynamically update the weights of the base models mainly based on their performance. In particular, some basic models are temporarily forgotten when they no longer fit into the current environment, but they can be remembered again when the historical training environment returns. Intuitively, the DWE-IL algorithm retains all the acquired knowledge, but only selectively activates and uses the part that is effective at the moment, according to the real-time state of the environment.

It can be seen from the above descriptions that the advantages of “dynamical” of DWE-IL are as follows: 1) The update of data weights and the weights of the base models is conducive to coordinating the old and new knowledge and coping with the “stability -plasticity” problem in NS-TSP, which improves the generalization performance and efficiency of DWE-IL, while ensuring its robustness; 2) The update of the weights of the base models is conducive to dealing with the high noise and periodicity problems in NS-TSP.

Overall, the DWE-IL algorithm can be divided into three parts:

• 1) Data pretreatment. In this part, we first need to normalize the original NS-TS, and then convert it into the dataset required for the prediction task according to the time window.

• 2) Models training. This part is the most important one, mainly related to the update of data weights and base model weights and the training of the base models. The update of data weights depends on the performance of the current ensemble model on the latest dataset. The update of the weight of a specific base model depends on its comprehensive performance over a period of time in the past, while the performance at a newer moment contributes more to its weight. In addition, unlike other ensemble learning algorithms, DWE-IL can temporarily forget irrelevant knowledge, but when the historical environment reappears, it can recall this knowledge again. The whole training process is similar to the process of human gradual learning and fully reflects the idea of ​​IL.

• 3) Models combination. In this part, DWE-IL uses the Weighted Median [17] method for the combination of models. The basic idea is to sort the outputs of all basic models and select the predictive value with a cumulative weight of 50% as the ensemble result, according to their respective ensemble weights.

In view of the challenges of NS-TSP, we put forward several novel strategies in the models training part of the DWE-IL algorithm. The main innovations and contributions of DWE-IL are summarized as follows:

• a) DWE-IL can basically ignore the internal changes of NS-TS and provides a general on-line forecasting framework for NS-TSP tasks. Besides, it provides an effective processing mechanism for the periodicity of NS-TS.

• b) DWE-IL updates the data weights according to the performance of the current ensemble model on the latest dataset. The updated data weights are used for building the new base model, which helps to improve the generalization performance and robustness of the final ensemble model.

• c) DWE-IL uses a double IL mechanism to train the base model, that is, it trains the base model based on old knowledge and new data blocks at the same time, which strengthens the connection between old and new knowledge. While increasing the diversity of base models, it further improves the prediction performance of the final ensemble model.

• d) DWE-IL uses a double dynamically weighting mechanism to obtain the comprehensive performance of each base model and updates the weight of the base model according to the comprehensive performance dynamically. In this process, the performance of the base model in a newer moment receives more attention. This move eliminates the influence of noise in NS-TS, maintains the stability of DWE-IL, and improves its plasticity.

The rest of this paper is organized as follows. In Section 2, the theoretical knowledge of ELM and ELMK is described in detail. In Section 3, the details of the proposed DWE-IL algorithm are described. The experimental results of the DWE-IL algorithm on six non-stationary time series datasets are reported in Section 4. Finally, in Section 5, the conclusions and future works are given.

2 Theoretical basis

2.1 Extreme learning machine (ELM)

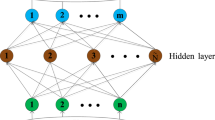
Extreme Learning Machine (ELM) is a specific Single-hidden Layer Feedforward Neural Network [29] (SLFN) model proposed by Guang-Bin Huang in 2004. Its innovations: (1) the connection weights between the input layer and the hidden layer, and the bias of the hidden layer can be generated randomly or set manually; (2) the connection weights between the hidden layer and the output layer do not need to be adjusted repeatedly through iteration, but are directly determined by solving the equations by least square method. Its contributions: compared with SLFNs and SVM, it greatly improves the learning speed and reduces the computational complexity, on the premise of guaranteeing the generalization performance. The block diagram of the ELM algorithm is presented in Fig. 1.

Fig. 1

Block diagram of the ELM algorithm

Assume that there are N training samples(x_i, t_i), i = 1, 2, …N, where x_i = [x_i1, x_i2, ⋯, x_in]^T ∈ Rⁿ and t_i = [t_i1, t_i2, ⋯, t_im]^T ∈ R^m. If any training sample is represented as (x, t), then ELM can be represented as follows:

$$ \boldsymbol{y}={f}_L\left(\boldsymbol{x}\right)={\sum}_{i=1}^L{\boldsymbol{\beta}}_i{h}_i\left(\boldsymbol{x}\right)=\boldsymbol{h}\left(\boldsymbol{x}\right)\boldsymbol{\beta} $$

(1)

where β = [β₁^T, β₂^T, ⋯, β_L^T]^T ∈ R^L × m and β_i ∈ R^m is the connection weight vector between the i^th node in the hidden layer and each node in the output layer, h(x) = [h₁(x), h₂(x), ⋯, h_L(x)] is the output vector of the hidden layer for specific samples.

h(x) can be expressed as follows:

$$ \boldsymbol{h}\left(\boldsymbol{x}\right)={\sum}_{i=1}^Lg\left({\boldsymbol{w}}_i\cdotp \boldsymbol{x}+{b}_i\right)=g\left(\boldsymbol{W}\cdotp \boldsymbol{x}+b\right) $$

(2)

where W = [w₁, w₂, ⋯, w_L] ∈ R^n × L is the weight vector between the input layer and the hidden layer, b = [b₁, b₂, ⋯, b_L] ∈ R^L is the bias vector of the nodes in the hidden layer.

The target function of ELM is as follows:

$$ {\sum}_{i=1}^N\left\Vert {\boldsymbol{y}}_i-{\boldsymbol{t}}_i^T\right\Vert =0 $$

(3)

We can convert this to solving for Y = Hβ = T, where:

$$ \boldsymbol{Y}={\left[\begin{array}{c}{\boldsymbol{y}}_1\\ {}{\boldsymbol{y}}_{\mathbf{2}}\\ {}\vdots \\ {}{\boldsymbol{y}}_N\end{array}\right]}_{N\times m}\mathrm{and}\kern0.5em \boldsymbol{T}={\left[\begin{array}{c}{{\boldsymbol{t}}_1}^T\\ {}{{\boldsymbol{t}}_2}^T\\ {}\vdots \\ {}{{\boldsymbol{t}}_N}^T\end{array}\right]}_{N\times m} $$

(4)

The ultimate goal of ELM is to find the least square solution with the minimum norm for Hβ = T. The solution that satisfies this condition is β = H⁺T, where H⁺ represents the Moore-Penrose generalized inverse of H.

2.2 Extreme learning machine with kernels (ELMK)

ELM can effectively overcome the inherent defects of traditional neural networks [30, 31]. ELM has a parameter that is very important to the generalization performance of the model, namely, the number of nodes in the hidden layer. For each task, it usually needs a certain time and method to determine [32]. ELMK does not need to determine the number of nodes in the hidden layer, only requiring to select the appropriate kernel function and regularization factor. Because of this property, ELMK avoids the randomness of ELM effectively.

ELMK is defined as follows:

$$ {K}_{ELM}=\boldsymbol{H}{\boldsymbol{H}}^T:{K}_{ELM\left(i,j\right)}=\varphi \left({\boldsymbol{x}}_i\right)\cdotp \varphi \left({\boldsymbol{x}}_j\right)=K\left({\boldsymbol{x}}_i,{\boldsymbol{x}}_j\right) $$

(5)

where K_ELM represents ELMK and φ(·) represents an unknown feature map.

Then the output function can be defined as follows:

$$ f\left(\boldsymbol{x}\right)=\varphi \left(\boldsymbol{x}\right){\boldsymbol{H}}^T{\left(\boldsymbol{H}{\boldsymbol{H}}^T+\frac{1}{C}\right)}^{-1}\kern3pt t=\left[\begin{array}{c}K\left(\boldsymbol{x},{\boldsymbol{x}}_1\right)\\ {}\vdots \\ {}K\left(\boldsymbol{x},{\boldsymbol{x}}_N\right)\end{array}\right]{\left({K}_{ELM}+\frac{1}{C}\right)}^{-1}t $$

(6)

If the training dataset is represented as (x_i, t_i), i = 1, …, N, where ${\boldsymbol{x}}_i\in {\mathfrak{R}}^P$ and ${\boldsymbol{t}}_i\in \mathfrak{R}$, then the initial optimization problem of ELMK can be written as:

$$ {\displaystyle \begin{array}{c}\operatorname{Min}\kern0.50em {L}_P=\frac{1}{2}{\left\Vert \boldsymbol{w}\right\Vert}^2+\frac{C}{2}{\sum}_{i=1}^N{\xi_i}^2\\ {}\kern4.5em \mathrm{s}.\mathrm{t}.\varphi {\left({\boldsymbol{x}}_i\right)}^T\boldsymbol{w}={t}_i-{\xi}_i\end{array}} $$

(7)

where w is the connection weight vector between the hidden layer and the output layer, C is the regularization parameter, and ξ_i is the error of (x_i, t_i).

Convert the above equation into Lagrange duality problem:

$$ {L}_D=\frac{1}{2}{\left\Vert \boldsymbol{w}\right\Vert}^2+\frac{C}{2}{\sum}_{i=1}^N{\xi_i}^2-{\sum}_{i=1}^N{\theta}_i\left(\varphi {\left({\boldsymbol{x}}_i\right)}^T\boldsymbol{w}-{t}_i+{\xi}_i\right) $$

(8)

where θ_i, i = 1, …, N are the Lagrange multipliers. The KKT conditions corresponding to the above equation are as follows:

$$ \frac{\partial {L}_D}{\partial \boldsymbol{w}}=\boldsymbol{w}-{\sum}_{i=1}^N{\theta}_i\left(\varphi \left({\boldsymbol{x}}_i\right)=0\to \boldsymbol{w}={\sum}_{i=1}^N{\theta}_i\right(\varphi \left({\boldsymbol{x}}_i\right) $$

(9)

$$ \frac{\partial {L}_D}{\partial {\xi}_i}=C{\xi}_i-{\theta}_i=0\to {\theta}_i=C{\xi}_i,i=1,\dots, N $$

(10)

$$ \frac{\partial {L}_D}{\partial {\theta}_i}=\varphi {\left({\boldsymbol{x}}_i\right)}^T\boldsymbol{w}-{t}_i+{\xi}_i=0,i=1,\dots, N $$

(11)

3 The proposed incremental learning algorithm via dynamically weighting ensemble learning (DWE-IL)

As an IL algorithm based on dynamically weighting ensemble scheme, the DWE-IL algorithm proposed in this paper can effectively NS-TSP problems. When it comes to EL, we have to consider the choice of base model. For the reasons analyzed above, ELMK is selected as the base model for the DWE-IL algorithm. In the experiments conducted in Section 4, we also select ELM as the base model and compare the result of two models to reveal the characteristics of the DWE-IL algorithm.

The basic idea of the DWE-IL algorithm is described as follows. Each data subset generates a base model, and build the base model set in a double incremental manner. Then, the performance of all existing base models on the latest dataset is measured. If the weighted sum of the relative errors of the new base model is greater than 1/2, it proves that it cannot correctly reflect the current environment, so it must be discarded, and a new base model must be regenerated. If the weighted sum of the relative errors of the old base model is greater than 1/2, it proves that the knowledge it has learned is not suitable for the current environment, and it should be temporarily discarded. DWE-IL sets the weighted sum of the relative errors of such old base models to 1/2, so that the weight in the final ensemble is equal to 0, so as to achieve the purpose of temporary discarding. However, it is worth noting that when the historical environment where the old base model is trained reappears, its weight is updated, and it is remembered again. Next, evaluate the overall performance of all base models in the past period of time, so that each base model has a greater weight in the newer environment. Finally, a new ensemble model is obtained by the weighted median method, and the data distribution is updated for the next training according to the performance of the ensemble model on the next dataset.

In Algorithm 1, the specific pseudo-code of the DWE-IL algorithm is presented.

To better demonstrate the process of the DWE-IL algorithm, we present the block diagram of the DWE-IL algorithm in Fig. 2.

Fig. 2

Block diagram of the DWE-IL algorithm

The following is a detailed description of the DWE-IL algorithm:

• A) Input:

• a) The original time series DATA = {d₁, d₂, …, d_N}.

• b) Time window size tw, which is an important super-parameter in TSP and determines the dimension of sample eigenspace. A too large or too small value of tw directly affects the generalization performance of the algorithm.

• c) The number of data subsets T. Divide training dataset Train into Train^t, t = 1, 2, …, T, is for better implementation of IL and EL. A too large value of T makes IL no sense, while a too small value of T results in poor EL performance.

• d) The base model τ, which can have many choices, such as SVR, ELM, and decision tree, etc. Considering that ELMK performs better than ELM in generalization, and possesses, simultaneously, lower computation complexity than SVM and decision tree, we choose ELMK as the base model in this work.

• B) Pretreatment:

First, in order to improve the accuracy and convergence speed of the model, we normalize original time series DATA to DATA′. This paper uses Min-max normalization to normalize the data into the interval [0, 1]. The normalization formula is as follows:

$$ {d_i}^{\prime }=\frac{d_i-{d}_{min}}{d_{max}-{d}_{min}} $$

(12)

where d_i^′ is the normalized value, d_i is the initial value, d_min and d_max are the minimum and maximum values of the original data.

Next, tw is used to convert DATA′ into the training dataset Train and testing dataset Test required by the prediction task, as shown in Fig. 3.

Fig. 3

The translation of time series to training dataset and testing dataset

Finally, divide Train into T subsets ${\boldsymbol{Train}}^t=\left\{\Big({\boldsymbol{x}}_1,{y}_1\right),\left({\boldsymbol{x}}_2,{y}_2\right),\dots, \left({\boldsymbol{x}}_{m^t},{y}_{m^t}\right),t=1,2,\dots, T$, randomly, where ${\sum}_{t=1}^T\ {m}^t=N$.

• C) Procedure:

• a) Initializing D^t, t = 1, 2, …, T to a uniform distribution. In the next step, different from AdaBoost, which updates the samples weights based on the base model, this work updates the samples weights based on the error of the existing ensemble model H^t − 1 on the new dataset Train^t. H^t − 1 is obtained by dynamically integrating each base model generated by Train^k, k = 1, 2, …, t − 1.

• b) Step 1: Calculating the error E^t of H^t − 1 on Train^t. E^t, t = 1, 2, …, T is obtained by summing the product of the relative error of samples in Train^t and the initial weights of samples. The initial weights of samples $\frac{1}{m^t},t=1,2,\dots, T$ can ensure 0 ≤ E^t ≤ 1.

• c) Step 2: Updating the sample weights w^t based on E^t, t = 1, 2, …, T. The formula for updating the samples weights is as follows:

  $$ {w}^t(i)=\frac{1}{m^t}\times {E^t}^{{\left\{1-\left\{ abs\left({H}^{t-1}\left({\boldsymbol{x}}_i\right)-{y_i}^t\right)/ errormax\right\}\right\}}^2},i=1,2,\dots, {m}^t $$

  (13)

  Then, normalizing w^t to ensure that D^t is a distribution. It can be seen from Step 4 and Step 5 that, the updated samples distribution D^t affects the weight of h_k, k = 1, 2, …, t in the ensemble model H^t by affecting the error of h_k on the latest dataset.

• d) Step 3: Training a base model h_k as a new ensemble member with H_k − 1 and Train^t. Note that, when the first data subset comes, the algorithm execution process will skip step 1 and step 2, and jump directly to step 3, because there is no existing ensemble model to update the sample distribution. When the second data subset Train² arrives, h₁ is the ensemble model H¹ at this time.

• e) Step 4: Evaluating the performance of all base models h_k, k = 1, 2, …, t on Train^t. Since the base models are generated at different times, the number of evaluations received by each base model is different. That is, when the latest dataset is Train^t, h_k = t obtains the first error, and h_k, k = 1, 2, …, t − 1 obtains the (t − k + 1)^th error. We use ${\varepsilon}_k^t$ to represent the error of the k^th base model on Train^t.${\varepsilon}_k^t$ can be expressed as follows:

  $$ {\varepsilon}_k^t={\sum}_{i=1}^{m^t}{D}^t(i)\cdotp {\left\{ abs\left({h}_k\left({\boldsymbol{x}}_i\right)-{y_i}^t\right)/ errormax\right\}}^2,k=1,2,\dots, t $$

  (14)

  If ${\varepsilon}_{k=t}^t$ is greater than 1/2, then we discard the base model h_t, and generate a new base model h_t, instead of directly interrupting the training process. If ${\varepsilon}_{k<t}^t$ is greater than 1/2, ${\varepsilon}_{k<t}^t$ is set to 1/2, instead of discarding the base model directly. This is because, if the environment changes dramatically, it is reasonable that the base model does not perform well, and this does not mean that the base model will never be useful again in the future. If the environment reappears, the base model error will become smaller, and the model will again contribute to the current overall decision.

  As mentioned in Section 1, it is a several conditions need to be met by IL algorithms for non-stationary environment prediction, one of which is that there should be a mechanism to coordinate the contradiction between old and new knowledge. The above formula embodies this idea that, allow the ensemble model to strengthen the original knowledge while learn new knowledge.

• f) Step 5: Calculating the weights of all base models h_k, k = 1, 2, …, t on Train^t. First, calculate the average weighted error of each base model, so that the performance of the base model in the latest environment gets more attention. The process is as follows:

  $$ \left[\begin{array}{ccc}{\omega}_1^1& \cdots & {\omega}_1^t\\ {}\vdots & \ddots & \vdots \\ {}0& \cdots & {\omega}_t^t\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{1+{e}^0}& \cdots & \frac{1}{1+{e}^{-\left(t-1\right)}}\\ {}\vdots & \ddots & \vdots \\ {}0& \cdots & \frac{1}{1+{e}^0}\end{array}\right] $$

  (15)

where ${\omega}_k^t$ is the weight of ${\varepsilon}_k^t$.

Row k, 1 < k < t satisfies the following conditions:

$$ {\omega}_k^k=\frac{1}{1+{e}^0}<{\omega}_k^{k+1}=\frac{1}{1+{e}^{-1}}<\cdots <{\omega}_k^t=\frac{1}{1+{e}^{-\left(t-k\right)}} $$

(16)

then normalize ${\omega}_k^t,k=1,2,\dots t$.

The average weighted error of the base model h_k, k = 1, 2, …, t on Train^t can be computed as:

$$ {\displaystyle \begin{array}{l}\overline{\beta_k^t}={\sum}_{j=0}^{t-k}{\omega}_k^{t-j}\left({\varepsilon}_k^{t-j}/\left(1-{\varepsilon}_k^{t-j}\right)\right)\\ {}\kern4em ={\omega}_k^t\frac{\varepsilon_k^t}{1-{\varepsilon}_k^t}+\cdots +{\omega}_k^{t-q}\frac{\varepsilon_k^{t-q}}{1-{\varepsilon}_k^{t-q}}+\dots +{\omega}_k^k\frac{\varepsilon_k^k}{1-{\varepsilon}_k^k}\end{array}} $$

(17)

The weight of h_k is obtained by normalizing the logarithm of the reciprocal of the average weighted error, i.e., ${W}_k^t=\log \left(1/\overline{\beta_k^t}\right)$, ${W}_k^t={W}_k^t/{\sum}_{k=1}^t{W}_k^t$. If the knowledge of the base model h_k does not match the current environment, ${W}_k^t$ will be very small or even zero, thereby achieving the purpose of temporarily “discarding”. If its knowledge becomes relevant again, ${\varepsilon}_k^t$ will be smaller, so that h_k will get a higher weight in the current environment and will be remembered again. This feature is especially useful in periodic environments.

• g) Step 6: All base models are weighted dynamically to get the latest ensemble model as follows:

  $$ {H}^t(i)=\arg\ {\min}_{h_{k\left({\boldsymbol{x}}_i\right)}}{\sum}_{h_{j\left({\boldsymbol{x}}_i\right)}<{h}_{k\left({\boldsymbol{x}}_i\right)}}{W}_k^t\kern0.75em \ge \frac{1}{2}\kern0.5em {\sum}_{j=1}^t{W}_j^t $$

  (18)

  Note that each new data subset generates a new base model and a new ensemble model. At this time, the generated ensemble model influences the weight of the new base model by influencing the next samples update in step 1.

  From the perspective of the whole algorithm description, the DWE-IL algorithm uses IL and EL technologies to realize the on-line forecasting process of NS-TS. Ideally, as long as the data input is uninterrupted, DWE-IL will continue to iteratively update the on-line forecasting model to adapt to the changing non-stationary environment.

4 Experiments

In this paper, six time series datasets are used to evaluate the performance of DWE-IL, including three financial datasets, Sunspot dataset, Mackey-Glass dataset and Lorenz dataset. The reasons why we consider these datasets are explained as follows: (1) These datasets involve finance, astronomy and other fields, and they are classic datasets in the corresponding fields. These fields are closely related to human life and are worthy of our study; (2) These datasets include both real datasets and artificial datasets, which can more comprehensively demonstrate the performance of the proposed DWE-IL algorithm; (3) These datasets are verified to be non-stationary, which is consistent with the topic of our paper. Accordingly, the three financial datasets and another three datasets are selected for the reasons mentioned above, and they are indeed representative.

4.1 Datasets

4.1.1 Three financial time series datasets

Since its birth, stock has been widely valued by people and has a significant impact on the financial market of a country or even the whole world. Therefore, this paper studies three classic stock index datasets, namely Dow Jones Industrial Average Index (DJI), Nikkei 225 Index (N225) and Shanghai Stock Exchange Composite Index (SSE) datasets, all of them are obtained from Yahoo Finance [33].

DJI dataset is composed of monthly samples of Dow Jones Industrial Average Index from February 1985 to March 2015, having a total of 352 data points. N225 dataset is composed of samples of the monthly Nikkei Index from April 1988 to March 2015, containing 324 data points. SSE dataset is composed of monthly samples of Shanghai Stock Exchange Index from December 1990 to January 2015, having a total of 290 data points.

4.1.2 Sunspot dataset

Sunspot is one of the most basic and obvious activities on the solar photosphere, which can reflect the solar activity level in this period, and it is an important index to study the solar cycle. Sunspot data is of great significance for studying space physics, space environment, earth climate and satellite operation. Predicting sunspots is not only significant but also challenging.

4.1.3 Mackey-glass dataset

Mackey-Glass time series, as one of the classical non-stationary chaotic time series, originates from the physiological control system and represents the typical feedback system [34]. It is generated by the following nonlinear differential equation:

$$ \frac{dx}{dt}=\frac{\alpha x\left(t-\delta \right)}{1+{x}^c\left(t-\delta \right)}- bx(t) $$

(19)

If δ > 16.8, then the time series generated by Eq. (17) is chaotic. We set the parameters to:α = 0.2, b = 0.1, c = 10, δ = 10, and x(0) = 1.2.

4.1.4 Lorenz dataset

Lorenz time series is widely used as a classical three-dimensional dynamic system for studying chaotic time series. It is generated by the famous Lorenz equation:

$$ \frac{dx(t)}{dt}=\alpha \left[y(t)-x(t)\right] $$

(20)

$$ \frac{dy(t)}{dt}=x(t)\left[\beta -z(t)\right]-y(t) $$

(21)

$$ \frac{dz(t)}{dt}=x(t)y(t)-\gamma z(t) $$

(22)

We set the parameters to: α = 10, β = 28, and γ = 8/3.

Since not all time series is non-stationary, for rigorous considerations, before the experiment, we use Autocorrelation Function [35] (ACF) test and Augmented Dickey-Fuller [36] (ADF) test to verify the non-stationarity of the six experimental datasets.

The ACF test judges the stationarity of the time series through the attenuation of the autocorrelation coefficient. The autocorrelation coefficient γ_k is calculated as follows:

$$ {\gamma}_k=\frac{\sum_{t=1}^{n-k}\left({X}_t-\overline{X}\right)\left({X}_{t+k}-\overline{X}\right)}{\sum_{t=1}^n{X}_t-{\overline{X}}^2} $$

(23)

where n is the size of the time series, k is the lag period, and $\overline{X}$ is the mean of the time series.

According to Eq. (23), the autocorrelation coefficient γ_k is a decreasing function of the lag period k, which means that with the increase of k, γ_k decreases and gradually tends to 0. Stationary time series have the short-term correlation, that is, usually only the recent value has a significant effect on the current value, while the farther value has a smaller effect on the current value. Therefore, the value of γ_k of stationary time series drops much faster than that of NS-TS.

Figure 4 shows the ACF test result of each experimental dataset. The ACF image shows the value of γ_k corresponding to each k, and the approximate upper and lower autocorrelation confidence bounds with γ_k = 0 represented by two horizontal lines. As mentioned above, if γ_k rapidly drops to 0, fluctuates around 0, and gradually converges to 0, it is considered that the time series is very likely to be stationary. As can be seen from Fig. 4, the autocorrelation coefficient γ_k for each one of the six time series does not conform to the above characteristics. Therefore, we have sufficient reasons to believe that all six experimental datasets are non-stationary.

Fig. 4

ACF image of six experimental datasets. (a) DJI, (b) N225, (c) SSE, (d) Sunspot, (e) Mackey-Glass, (f) Lorenz

Unlike the subjectivity of the ACF test, ADF test judges the stationarity of the time series by the existence of the unit root. If the unit root exists, then the time series is non-stationary. We rigorously prove the non-stationarity of each time series using ADF test and give the corresponding results in Table 1. The ADF test has four basic indicators, the test value pValue, the critical value cValue, the significance level α, and the test result h. The null hypothesis H0 of ADF test is that the time series has a unit root, that is, it is non-stationary. The test result h = 1 indicates that hypothesis H0 is rejected at the 5% significance level. As can be seen from Table 1 that each time series dataset satisfies h = 0 and pValue > α, so it can be concluded that the above six experimental datasets are non-stationary.

Table 1 The results of ADF test on six datasets

4.2 Experimental setup

4.2.1 Parameters setup

The DWE-IL algorithm mainly involves three parameters, namely the time window size tw, the size of the data subsets K, the option of the kernel function Kernel in the base learning algorithm ELMK.

• a) The time window size tw is a very important parameter for addressing TSP issues. A time series is a string of numbers that we need to refactor to convert it into data which is similar to that required for supervised learning, i.e., input variables and output variables, to be predicted using machine learning algorithms. While the time window size tw is the basis for this transformation operation. The value of tw corresponds to the feature size of samples in supervised learning. Too large or small values of tw has a negative impact on the generalization performance of the algorithm.

• b) Data subset size K is also a key parameter in TSP. If K is too large, the meaning of incremental learning will be lost. In contrast, if K is too small, underlearning can occur, and the generalization performance of the basic model trained based upon each data subset will be poor. Therefore, it is necessary to choose an appropriate K value. For better representation and analysis of K, as described in Algorithm 1, we use the number of data subsets T to laterally reflect the importance of K. And $T=\frac{n}{K}$ should balance these two situations, where n represents the size of the non-stationary dataset.

• c) We have four choices for the Kernel function Kernel in the base learning algorithm ELMK, namely, RBF Kernel, Linear Kernel, Polynomial Kernel, and Wavelet Kernel. Each kernel function has its own parameters. Besides, a regularization coefficient C is employed to balance the model complexity and predictive error. In this work, Cross-Validation method [37] is utilized to select the optimal values for the parameters.

4.2.2 Comparative algorithms setup

In order to evaluate the performance of DWE-IL, we compare it with some excellent classic algorithms in recent years and the comparison of experimental results is reported in Section 4.3. The comparative algorithms include: 1) Online Sequential Improved Error Minimized ELM (OSIEM-ELM) [38]; 2) Double Incremental Learning (DIL) [39]; 3) ELMK; 4) DWE-IL (ELM); 5) Temporal Convolutional Network (TCN) [40]; 6) New Online Sequential Learning Algorithm for KELM (NOS-KELM) [41]; 7) Neuron Model based on the Dendritic Mechanism(NBDM) [42]; 8) a new hybrid TSP algorithm, which integrates dynamic ensemble pruning (DEP), IL and kernel density estimation (KDE) (EnsP^KDE&IncL^KDE) [43]; 9) Competitive Two-Island CC (CICC-two-island) [44]; 10) Adaptive Neuro-Fuzzy Inference System (ANFIS) [45]; 11) Evaluation of co-evolutionary neural network architectures (CCRNN-NL) [46].

OSIEM-ELM is an online learning extreme learning machine that can learn data piece by piece or block by block. The DIL algorithm is similar to the DWE-IL algorithm proposed in this paper. They are all IL and EL algorithms. The base model of DIL algorithm is Incremental Support Vector Machine (I-SVM) [47]. Compared with DIL algorithm, it can be verified that, whether the way of using average weighted error of each base model to calculate its weight in the DWE-IL algorithm has a significant effect. The DWE-IL (ELM) algorithm employs ELM as its base model instead of ELMK. Compared with the DWE-IL (ELM) algorithm and ELMK algorithm, it can be verified that, whether the IL framework based on dynamically weighting ensemble scheme proposed in DWE-IL has a significant effect.

TCN is a novel temporal convolutional network, which has received widespread attention since it was proposed. Researchers have done some studies on time series prediction and classification tasks using TCN, such as [48]. These studies show that TCN has excellent performance. NOS-KELM is an NS-TSP method that combines the sparsification rule and the adaptive regularization scheme based on KB-IELM, which has excellent performance in artificial and real-world NS-TS.

NBDM is a neuron model based on dendritic mechanism and phase space reconstruction (PSR). It has excellent performance on Non-Stationary Financial Time Series (NS-FTS) datasets. EnsP^KDE&IncL^KDE benefits from the advantages of integrated DEP scheme, IL paradigm and KDE. It has superior prediction performance in TSP tasks. CICC-two-island is a competitive method used to train recurrent neural networks for chaotic time series prediction. ANFIS is designed based on FL and has good performance on non-stationary artificial and real-world datasets.

4.2.3 Performance measures setup

In order to evaluate the generalization performance of the DWE-IL algorithm and better compare it with the comparative algorithms mentioned in 4.2.2, we need some performance measures to evaluate each algorithm. In this paper, we use four performance measures, i.e., Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Absolute Error (Error), and Standard deviation (Std). They are calculated as follows:

$$ RMSE=\sqrt{\frac{1}{n}{\sum}_{i=1}^n{\left({x}_i-\hat{x_i}\right)}^2} $$

(24)

$$ MAE=\frac{\sum_{i=1}^n\mid {x}_i-\hat{x_i}\mid }{n} $$

(25)

$$ Error={x}_i-\hat{x_i} $$

(26)

$$ Std=\sqrt{\frac{1}{Q-1}{\sum}_{i=1}^Q{\left({RMSE}_i-\overline{RMSE}\right)}^2} $$

(27)

where x_i, i = 1, 2, …, n is the real value of i^th sample, $\hat{x_i},i=1,2,\dots, n$ is the predictive value of i^th sample, n is the size of the dataset, RMSE_i, i = 1, 2, …, Q is the RMSE value of i^th independent repeated experiment, $\overline{RMSE}$ is the mean of RMSEs of all the independent repeated experiments and Q is the number of independent repeated experiments.

In addition, in order to reduce the influence of error caused by accidental factors in the experiments on the algorithm performance evaluation, twenty independent repeated experiments are performed for each algorithm on each dataset, and the average result of twenty experimental results is taken as the final result.

4.3 Experimental results

This section presents the experimental parameters and the corresponding experimental results of the DWE-IL algorithm obtained with these parameters on the six datasets given in Section 4.1, and the comparison results of the DWE-IL algorithm and other excellent algorithms on each dataset. In order to make the experimental comparison of algorithm performances fair and reasonable, experimental settings and conditions of the DWE-IL algorithm and the comparative algorithms are the same.

An algorithm that is verified based on the optimal hyperparameters may result in overfitting to out-of-sample data. In our work, we tackle this problem from two aspects: 1) From the theoretical aspect, the whole principle of DWE-IL helps to solve the problem of overfitting to out-of-sample data. DWE-IL introduces the ideas of ​​EL and IL, which combines multiple base models to obtain more stable and better prediction performance. The risk of overfitting to out-of-sample data of the final ensemble model is much smaller than that of a single base model; 2) From the experimental aspect, we use the Cross-Validation method to determine the optimal hyperparameters. In the experiment, the original dataset is randomly divided into the training dataset and test dataset. The training dataset is used to train the model, and the test dataset is used to determine the optimal hyperparameters and evaluate the generalization performance.

There are many parameters in the DWE-IL algorithm, among which the time window size tw, the data subset size K, and the kernel function Kernel in ELMK are the three most important parameters. In our experiments, we set Kernel = RBF Kernel. As mentioned in Section 4.2.1, we use the number of data subsets T to analyze K laterally.

Table 2 shows the detailed parameters of DWE-IL and the other three competitors on the six experimental datasets. The NOS-KELM algorithm has four main parameters, which are the regularization factor vector γ, the learning rate η, the kernel width σ and algorithm termination threshold δ. The DIL algorithm has three main parameters, which are the time window size tw, the number of subsets K, and the number of iterations T_k. The DWE-IL (ELM) algorithm and DWE-IL’s main parameters and value range are similar, which are the time window size tw, data subset size T, and the number of iterations ActivationFunction. In our experiments, we set ActivationFunction = Sigmode.

Table 2 Experimental parameters of DWE-IL and other three competitors

As described in Section 4.2.1, a too large or too small value of tw affects the generalization performance of the DWE-IL algorithm, as shown in Tables 3, 4 and 5 in the form of data. Of course, tw is judged too big or too small depending on the particular dataset. Due to the large span of tw, the six datasets are divided into two groups for the convenience of expression to present the influence of tw’s different values on the generalization performance of DWE-IL. The generalization performance measure utilized here is RMSE.

Table 3 The average values of RMSEs obtained by DWE-IL with different values of parameter tw on DJI, N225 and Sunspot datasets

Table 4 The average values of RMSEs obtained by DWE-IL with different values of parameter tw on SSE and Lorenz datasets

Table 5 The average values of RMSEs obtained by DWE-IL with different values of parameter tw on Mackey-Glass datasets

Table 6 shows the influence of the number of data subsets T on the generalization performance of the algorithm. It can be seen from Table 6 that T satisfies 2 ≤ T ≤ 6, and different T obtains different experimental results. Therefore, we can verify the conclusion mentioned in Section 4.2.1 from the side, that is, too large or small K affects the performance of the algorithm, so we need to choose an appropriate K value.

Table 6 The average values of RMSEs obtained by DWE-IL with different values of parameter T on six datasets

Table 7 shows the maximum, minimum and average values of RMSEs and MAEs obtained by DWE-IL under optimal parameter combination in twenty independent repeated experiments on each dataset and the average running time (TIME) of each independent repeated experiment. It can be seen from Table 7 that DWE-IL algorithm can train and predict samples better for each dataset in a short time. In addition, it can be seen from Table 7 that, except Sunspot and Lorenz datasets, the generalization performance of the DWE-IL algorithm on the other four datasets is stable but fluctuates within a small range. Due to the interference of some noise data and the complex characteristics of data itself, the generalization performance of the DWE-IL algorithm on Sunspot and Lorenz datasets fluctuates greatly, but it is also within the acceptable range.

Table 7 The maximum, minimum and average values of RMSEs, MAEs and TIMEs obtained by DWE-IL on six datasets

Tables 8, 9 show the comparison results of RMSEs and MAEs of six algorithms including DWE-IL on each dataset. It can be seen from Tables 8, 9 that, the generalization performance of the DWE-IL algorithm on each dataset is better than other algorithms. This reflects that DWE-IL has good plasticity on NS-TSP. DIL and DWE-IL are both IL and EL algorithms. Unlike DWE-IL, DIL updates the weights only based on the performance of each base model. Therefore, we could infer that the double dynamically weighting mechanism of DWE-IL is more suitable to deal with NS-TSP. OSIEM-ELM and TCN are classic and novel examples, respectively, of computational intelligence methods. The reason why their predictive performance and stability are inferior to those of DWE-IL might be that the combination prediction model usually has better performance than a single model. This has been demonstrated by many researchers in their state-of-the-art research works. Although it may cost additional space, however, it is worth it.

Table 8 The average values of RMSEs obtained by different algorithms on six datasets

Table 9 The average values of MAEs obtained by different algorithms on six datasets

Also, worth noting in Tables 8 and 9 is the comparison of the three algorithms DWE-IL, DWE-IL (ELM) and ELMK. It can be seen from the experimental results that, the RMSEs of the DWE-IL algorithm and the DWE-IL (ELM) algorithm are closer to each other and significantly smaller than those of the ELMK. It can be concluded that, the IL framework based on dynamically weighting ensemble scheme proposed in DWE-IL has a significant effect and is more conducive to the performance improvement of the algorithm than the contribution of the base model.

Table 10 shows the standard deviations (Stds) of RMSEs of six algorithms including DWE-IL on each dataset. It is known that the lower value of Std means the lower degree of dispersion and the higher stability. As can be seen from Table 10 that, on five out of six datasets, DWE-IL has the smallest Stds, compared to the other algorithms. This is because the double dynamically weighting mechanism improves the robustness of DWE-IL. And the selected base model ELMK has high learning efficiency and low randomness, compared with some computational algorithms. Therefore, we can conclude that DWE-IL has good stability while having good plasticity.

Table 10 The standard deviations of RMSE obtained by different algorithms on six datasets

Table 11 and Table 12 show the RMSE and MAE t-test results between the DWE-IL algorithm and other algorithms, respectively. From the last column of Table 11 and Table 12, we can see that DWE-IL has no significant improvement over DWE-IL (ELM) on some datasets. This problem can be explained by the previous conclusion that, compared with the choice of the base model, the IL framework based on dynamically weighting ensemble scheme proposed in DWE-IL is more conducive to the improvement of the performance of the algorithm. The choice of the base model is relatively less important.

Table 11 RMSE t-test results between DWE-IL and other comparative algorithms

Table 12 MAE t-test results between DWE-IL and other comparative algorithms

From Table 13 we can see that, the time spent by DWE-IL are relatively short. This is because the computational complexity of DWE-IL is relatively low, and the selected base model ELMK has a simpler structure and faster training speed. Due to these reasons, DWE-IL responds to data changes in NS-TS in a timely manner.

Table 13 The average values of TIME spent by different algorithms on six datasets

In order to show and analyze the prediction performances of DWE-IL and those of all the comparative algorithms more clearly and intuitively, the predictive results and predictive errors obtained by DIL, DWE-IL (ELM) and DWE-IL on the six experimental datasets are shown in Figs. 5, 6, 7, 8, 9, 10, respectively. Among the comparative algorithms, DWE-IL (ELM) and DIL have the first-best and second-best prediction performance, respectively, on the six experimental datasets. Therefore, we think that DWE-IL (ELM) and DIL can represent all the comparative algorithms well. Besides, if the experimental results of all the algorithms are presented, the predicted results and predictive errors shown in the figures will be difficult to be clearly observed.

Fig. 5

Predictive results and Predictive errors of different algorithms on DJI dataset. (a) Predictive results, (b) Predictive errors

Fig. 6

Predictive results and Predictive errors of different algorithms on N225 dataset. (a) Predictive results, (b) Predictive errors

Fig. 7

Predictive results and Predictive errors of different algorithms on SSE dataset. (a) Predictive results, (b) Predictive errors

Fig. 8

Predictive results and Predictive errors of different algorithms on Sunspot dataset. (a) Predictive results, (b) Predictive errors

Fig. 9

Predictive results and Predictive errors of different algorithms on Mackey-Glass dataset. (a) Predictive results, (b) Predictive errors

Fig. 10

Predictive results and Predictive errors of different algorithms on Lorenz dataset. (a) Predictive results, (b) Predictive errors

Figure 5(a) - Fig. 10(a) show the predictive results of DIL, DWE-IL (ELM), and DWE-IL on six NS-TS datasets, respectively, and all the predictive results are compared to the real values. It can be seen from the six figures that the predictive trends of the six algorithms are basically consistent with the real trend, and the predictive trend of the DWE-IL algorithm is the closest to the real trend.

Figure 5(b) - Fig. 10(b) show the predictive errors of DIL, DWE-IL (ELM), and DWE-IL on six NS-TS datasets, respectively. Compared to other algorithms, predictive error curve of the DWE-IL algorithm is the smoothest one on each dataset. However, if only the predictive errors of the DWE-IL algorithm are considered, the stability of the DWE-IL algorithm is not very satisfactory. This also proves the conclusion drawn in Table 7 that, due to the interference of some noise data and the complex nature of the data itself, the generalization performance of the DWE-IL algorithm on some datasets fluctuates greatly, but it is also within the acceptable range. In addition, in order to more clearly observe the results of each algorithm, we use the logarithmic scale to represent the predictive error.

Table 14 shows the comparison results of RMSEs of NBDM, EnsP^KDE&IncL^KDE, ANFIS, and DWE-IL on three NS-FTS datasets. It can be perceived from Table 14 that, DWE-IL provides a good solution to the prediction of the NS-FTS and has significantly superior performance over other comparative algorithms.

Table 14 The average values of RMSEs obtained by different algorithms on DJI, N225, and SSE datasets

Table 15 shows the comparison results of RMSEs of NOS-KELM, CICC-two-island, CCRNN-NL, and DWE-IL on three NS-TS datasets. It can be concluded that, DWE-IL provides a general prediction framework for NS-TSP tasks and has excellent generalization performance.

Table 15 The average values of RMSEs obtained by different algorithms on Sunspot, Mackey-Glass, and Lorenz datasets

From Section 3, we can know that the computational complexity of DWE-IL is O(TkC_h), where T represents the number of data subsets, k represents the number of current base models, and C_h represents the number of base models that are discarded in this iteration. We choose four algorithms mentioned in Section 4.2.2, analyze their computational complexities, and compare their computational complexities with that of DWE-IL.

The first chosen comparative algorithm is DIL, and its computational complexity is O(KT_k(C_h + C_H)), where K represents the number of divided data subsets, T_k represents the number of iterations, C_h and C_H represent the number of base models and ensemble models that are discarded in the process of an iteration, respectively. The second chosen comparative algorithm is CICC-two-island, and its computational complexity is O(T₁T₂D(S + N)), where T₁ represents the global evolution time, T₂ represents the island evolution time, D represents the depth of generations, S and N represent the number of subgroups of the synaptic level and the neuron level, respectively.

The third chosen comparative algorithm is CCRNN-NL, and its computational complexity is O(ckm), where c represents the number of cycles, k represents the total number of neurons in the hidden layer and output layer, and m represents the number of offspring. The fourth chosen comparative algorithm is NOS-KELM, and its computational complexity consists of three parts: 1) the sparse dictionary selection part, and the computational complexity of this part is O(m + 1); 2) the adaptive regularization scheme part, and the computational complexity of this part is O(m²) or O(lm) (when l > m); 3) the kernel weight coefficient update part, and the computational complexity of this part is O(m²). In the above three parts, m represents the number of samples, and l represents the number of iterations of the optimization process.

It can be seen that the computational complexity of DWE-IL is similar to that of CCRNN-NL, and lower than that of DIL and CICC-two-island. According to [41], although each part of NOS-KELM has the lowest computational complexity, its overall running time is no less than that of DWE-IL. In addition, according to the previous experimental results, the prediction performance of DWE-IL is the best among these five algorithms. Therefore, we can conclude that DWE-IL has superior generalization efficiency and generalization performance on the NS-TSP tasks.

5 Conclusions and future works

This paper proposes a novel Incremental Learning Algorithm via Dynamically Weighting Ensemble Learning (DWE-IL), which provides a general framework for solving NS-TSP tasks. The basic principle of DWE-IL is to track real-time data changes by dynamically establishing and maintaining a knowledge base composed of multiple basic models. It trains basic models for each subset of NS-TS, and finally combines each basic model with dynamic weighting rules. In the DWE-IL algorithm, the most critical components are the update of data weights and base model weights and the training of the base model. According to the characteristics of NS-TS, this paper proposes corresponding weight update methods and base model training methods. Experiments prove that the DWE-IL algorithm provides a good solution to the NS-TSP problem and has significantly better performance than other comparative algorithms.

Although the DWE-IL algorithm has shown good results for NS-TSP, there are still some problems to be studied. For example, DWE-IL can only achieve single-step prediction and univariate prediction for NS-TS. In future work, we will try to further expand the DWE-IL algorithm to solve multi-step advance NS-TSP and multivariate NS-TSP problem.