DEP-TSP^meta: a multiple criteria Dynamic Ensemble Pruning technique ad-hoc for time series prediction

Abstract

Time series prediction (TSP) is a process of using data collected at different times in the past for statistical analysis, so as to speculate on the trend of things, where the non-stationary and non-linear characteristics of data portray a hard setting for predictive tasks. Obviously, there will be no single model that could perform the best for all TSP issues. Dynamic Ensemble Selection (DES) technique achieves more accurate and robust performance than a single model, due to that it aims to select an ensemble of the most competent models in a dynamic fashion according to each test sample. A variety of DES approaches have been proposed to address pattern classification problems, but little work has been conducted on the research of TSP adopting the DES paradigm. Commonly, the DES approaches work by the definition of a single criterion to evaluate the capability of base classifiers. However, only one criterion is often inadequate for the comprehensive evaluation of classifier power. Thus, in this paper, a multiple criteria Dynamic Ensemble Pruning (DEP) technique exploiting meta-learning ad-hoc for TSP, termed DEP-TSP^meta, based on the inspiration from a state-of-the-art META-DES framework specifically presented for classification tasks, is developed. Within DEP-TSP^meta, Extreme Learning Machines (ELMs) and Hierarchical Extreme Learning Machines (H-ELMs) are integrated as the base models, and four distinct meta-attributes collections, i.e., hard prediction, local accuracy, global accuracy, and prediction confidence, are presented. Each set of meta-attributes corresponds to a specific assessment criterion, i.e., the prediction accuracy in local area of the eigenspace, the overall local accuracy, the prediction accuracy in global area of the decision space, and the confidence level of predictor. A desirable meta-predictor, obtained by training on the strength of these meta-attributes, is the key to deciding whether a base predictor is capable of predicting the unseen instance well or not. Those incapable base predictors determined by the meta-predictor will be pruned and the capable predictors will be expanded into the final dynamic ensemble system. The size of the sets of meta-attributes is specified dynamically by genetic algorithm for different time series benchmark datasets. Empirical results on eight benchmark datasets with different time granularities have verified that, the proposed DEP-TSP^meta algorithm possesses dramatically improved prediction performance at different granularities, when compared against three other DES approaches and four static selective ensemble learning methods.

1 Introduction

A time series is an assemblage of data points acquired by sampling at equal intervals. Time series prediction (TSP) is a process to predict data future values exploiting knowledge learned from past and current values of data associated with a particular phenomenon [1]. In the digital information age, TSP algorithms have been extensively adopted in various data mining fields, including economics [2, 3], physical sciences [4, 5], and engineering [6].

TSP methods can be divided into traditional linear models, e.g., Auto Regressive (AR) and Auto Regressive Moving Average (ARMA), and nonlinear models, e.g., neural networks (NNs). Some restrictive assumptions are required by these linear models, such as linearity, smoothness and normality, which are rarely satisfied, due to the characteristics of nonlinearity and chaos in time series. Though NNs are more effective than traditional linear models, NNs still have their own demerits, including time-consuming learning process, slow convergence, and being prone to get into local minima [7].

Huang et al. [8] proposed a learning scheme called extreme learning machine (ELM), which is a special case of Single-hidden Layer Feedforward Neural Networks (SLFNs), to improve the above mentioned disadvantages of NNs. For an ELM model, it is not necessary to set stopping criteria, learning rate, and learning epochs. ELM can offer good generalization performance with fast learning speed. Many research works [9,10,11] have proved that ELM is suitable for addressing various types of classification and regression issues. However, when handling natural scenes or practical applications, due to its shallow architecture, feature representation learning using ELM may not be effective. Huang et al. [12] further extended ELM and proposed a Hierarchical ELM (H-ELM) framework for Multi-Layer Perceptrons (MLPs). H-ELM reserves ELM’s advantage of training efficiency, while possessing superior generalization performance to the classical ELM, simultaneously.

What’s more, NNs might be somewhat unstable with randomicity. Ensemble learning paradigm is thus proposed to utilize the unique capability of each component model for better capturing different characteristics in data, which brings remarkable advancements in NNs. Numerous theoretical analysis and experimental results [13,14,15] have shown that the combination of different models can significantly improve the predictive performance of a single model, particularly in the cases that the base learners in an ensemble are adequately complementary and diverse [16, 17]. Diversified ensembles could be generated by utilizing diversified initial weight matrices, variable numbers of hidden nodes, or various activation functions [18]. In this work, both shallow learning models, i.e., ELMs, and deep learning models, i.e., H-ELMs, will be integrated together to form the original ensemble. The original ensembles built in this way are compounded, and possess relatively high complementarity and diversity intuitively.

However, an initial ensemble of base learners is certainly not always optimal for its prediction or classification tasks, while removing the incompetent base learners from an initial ensemble can improve its predictive or classification performance in many cases. In view of that each base learner has its own unique capabilities, it is unreasonable to always underestimate or deny one specific learner, which may have poor performance on some samples, but good performance on the other ones.

To address the above issues, the Dynamic Ensemble Selection (DES) paradigm is proposed for pattern classification tasks. With DES, only the classifiers obtaining a certain competence level for the given test sample, according to a selection criterion or several selection criteria, are dynamically selected into the ensemble currently constructed for the given test sample. Recently, many remarkable achievements and breakthroughs have been made. In [19], a novel probabilistic model for dynamic ensemble selection is proposed. In this model, an optimal subset is obtained by simultaneously measuring diversity and classifier competence. In [20], a creative approach, called dynamic multistage organization (DMO), is proposed by Cavalin et al. It is based on multistage organizations and respectively designs the optimal multistage structure for each unseen sample. In [21], to alleviate the problem of selecting classifiers which overfit the local region in typical DES, new modifications are proposed to improve the generalization performance of DES methods.

Motivated by its preferable performance on pattern recognition, we carry out research on applying the DES paradigm to time series prediction. However, the measure criteria of classifier competence in the above methods are not equally applicable to predictor. With TSP, the key point of the DES is how to evaluate the capability of a base predictor. According to our previous work [22], three novel DES algorithms have been proposed for TSP, including the DES algorithm based on Predictor Accuracy over the Local Region (DES-PALR), the DES algorithm based on the Consensus of Predictors (DES-CP), and the Dynamic validation set determination algorithm based on the similarity between the Output profile of the test sample and the Output profile of each training sample (DVS-OpOp).

All of the above algorithms define only one criterion, such as the local precision in the feature space or the global precision in the decision space, to measure the capability of a base predictor or ensembles of predictors (EoPs) to implement DES tasks. However, it is not sufficient to comprehensively evaluate the competence level of a base predictor merely by utilizing one criterion. Using a single standard to estimate the competence level of a base predictor is one-sided, and thus error prone. Therefore, multiple criteria to measure the competence of a base predictor should be considered in order to achieve a more robust DES technique.

In [23], an updated taxonomy of dynamic selection systems for classification problem is presented. A comparative study shows that the algorithms designed based on meta-learning can generally achieve favorable classification performance. One DES framework using meta-learning, called META-DES, is proposed in [24], where a meta-classifier is trained with multiple criteria to predict whether a base classifier is sufficient to classify a test sample. So even though one criterion does not work well, the framework can still get desirable capability, as the other criteria are also taken into consideration. Then, the authors of [25] assessed the influence of the meta-classifier and an extension algorithm of META-DES. The experimental results demonstrate that the performance of the meta-classifier and the classification accuracy of the DES system are strongly correlated. Moreover, in [26], more meta-features are considered, and a meta-feature selection scheme using a Binary Particle Swarm Optimization (BPSO) is applied, in order to improve the performance of the meta-classifier. It is believed that, the whole capability of the framework will be improved, when the identification ability of the meta-classifier is improved by choosing more suitable sets of meta-features or classifier models to train the meta-classifier.

Enlightened by the researches on the META-DES framework [24,25,26] for classification tasks introduced above, we construct our own multiple criteria Dynamic Ensemble Pruning technique based on the meta-learning paradigm, specifically for solving TSP problems, called the DEP-TSP^meta technique. The key point of the DEP-TSP^meta technique is to construct a meta-predictor, which is responsible for determining whether a base predictor has the ability to predict an unseen instance well or not. The unqualified base predictors will be pruned, while the eligible base predictors will be extended to the final dynamic ensemble system.

The motivations behind the development of DEP-TSP^meta, and simultaneously, the contributions of this work for TSP tasks, as well as the essential differences between META-DES [24,25,26] and our proposed DEP-TSP^meta technique, are summarized as follows.

Firstly, as is known to all that, the more diverse and informative become the generated base models, the more successful the ensemble system will be. Hence, in the ensemble initialization stage of DEP-TSP^meta, ELMs and H-ELMs, as base predictors, which are complementary and diverse, constitute the initial collection of predictors for TSP problems. Both shallow models, i.e., ELMs, and deep models, i.e., H-ELMs, are combined together to establish the initial ensemble. In this sense, the initial ensemble is diversified, which might contribute to the predictive performance advancement acquired by the final dynamically pruned ensemble.

Secondly, in the meta-predictor construction stage of DEP-TSP^meta, we design four groups of meta-attributes, instead of only consider a single criterion, that have proven effective respectively in our previous research results [22]. These newly formed four groups of meta-attributes are entirely different from the meta-features in META-DES [24,25,26]. Besides, ELM is employed as the meta-predictor model, given its good generalization performance, the ability of fast learning and effective avoidance of local minima issues.

Thirdly, the ensemble pruning process within DEP-TSP^meta is implemented dynamically by a meta-predictor trained on basis of the meta-attributes, instead of probabilistic-based approaches or data handling-based approaches.

Fourthly, the parameters utilized in the meta-predictor learning procedure of DEP-TSP^meta are adapted dynamically by genetic algorithm, which markedly boosts its predictive performance.

Fifthly, in the prediction stage of DEP-TSP^meta, based on the data characteristic of time series, the average of the predicted values produced by the selected predictors, rather than the results obtained by using the majority voting rule for classification problem in META-DES, is taken as the final algorithm output.

Last but not least, the DEP-TSP^meta technique proposed in the work is developed specifically for TSP application scenarios, significantly differing from the META-DES framework presented in [24,25,26], which is focused on the problem of pattern classification. The effectiveness of DEP-TSP^meta in handling with TSP problems has been proven by the empirical results conducted based upon eight TSP benchmark datasets with distinct time granularities, such as year, month, quarter, and so on. In comparison with three DES approaches and four Static Ensemble Selection (SES) ones, DEP-TSP^meta achieves superior forecasting performance at various levels of granularities.

The remaining of this paper is arranged as follows. Section 2 presents some important principles of the ELM algorithm and H-ELM algorithm. Section 3 discusses the notion of predictor competence for DES. Section 4 describes the details of the proposed DEP-TSP^meta technique. The experimental investigation is carried out in Sect. 5. Finally, the conclusion and prospect of future work are presented in Sect. 6.

2 Preview of ELM and H-ELM

This section will briefly review the ELM and H-ELM algorithms, which will be utilized in the proposed DEP-TSP^meta technique as the base predictors.

2.1 Extreme Learning Machine (ELM)

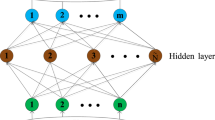
This section describes the background knowledge of ELM (Fig. 1). The ELM model proposed by Huang et al. [8] can be built by using randomly or artificially given hidden node parameters that do not need to be further adjusted. The training dataset is denoted as ${\{ (}\varvec{x}_{i} ,\varvec{t}_{i} \text{)}|\varvec{x}_{i} \in R^{d} \text{,}\;\varvec{t}_{i} \in R^{m} \text{,}\;i = \text{1,} \ldots \text{,}\;N{\} }$, where $\varvec{x}_{i}$ is the feature vector of the i-th training sample, $\varvec{t}_{i}$ denotes the target value of $\varvec{x}_{i}$, and $L$ is the number of hidden neurons. The principle of ELM is devoted to reaching the smallest both training error and the norm of output weights, simultaneously, namely,

Fig. 1

The overview of ELM

$$ {\text{Minimize}}:\;\;\left\|\varvec{\beta}\right\|_{\mu }^{{\sigma_{\text{1}} }} + \lambda \left\| {\varvec{H\beta } - \varvec{T}} \right\|_{\nu }^{{\sigma_{\text{2}} }} $$

(1)

where $\sigma_{1} > 0$, $\sigma_{2} > 0$, $u,v = 0,(1/2), \ldots , + \infty$, $\varvec{H}$ represents the output matrix of the hidden layer, as shown below:

$$ \varvec{H} = \left[ {\begin{array}{*{20}c} {h(\varvec{x}_{\text{1}} )} \\ \cdot \\ \cdot \\ \cdot \\ {h\text{(}\varvec{x}_{N} \text{)}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {h_{\text{1}} \text{(}\varvec{x}_{\text{1}} \text{)}\; \ldots \;h_{L} \text{(}\varvec{x}_{\text{1}} \text{)}} \\ { \cdot \;\;\;\; \cdot \;\;\;\; \cdot } \\ { \cdot \;\;\;\; \cdot \;\;\;\; \cdot } \\ { \cdot \;\;\;\; \cdot \;\;\; \cdot } \\ {h_{\text{1}} \text{(}\varvec{x}_{N} \text{)} \ldots h_{L} \text{(}\varvec{x}_{N} \text{)}} \\ \end{array} } \right]\sin^{ - 1} \theta $$

(2)

and the target matrix $\varvec{T}$ of training data is defined as:

$$ \varvec{T} = \left[ {\begin{array}{*{20}c} {\varvec{t}_{\text{1}}^{T} } \\ . \\ . \\ . \\ {\varvec{t}_{N}^{T} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {t_{{\text{11}}} \; \ldots \;t_{{\text{1}m}} } \\ {.\;\;\;.\;\;\;.} \\ {.\;\;\;.\;\;\;.} \\ {.\;\;\;.\;\;\;.} \\ {t_{{N\text{1}}} \; \ldots \;t_{Nm} } \\ \end{array} } \right] $$

(3)

The ELM training process has the following steps.

(1) Set the hidden neuron parameters at random.

(2) Compute the output matrix $\varvec{H}$ of the hidden layer.

(3) Attain the weight vector of output layer as below:

$$ \varvec{\beta}= \varvec{H}^{\dag } \varvec{T} $$

(4)

where $\varvec{H}^{\dag }$ represents the Moore–Penrose (MP) generalized inverse of matrix $\varvec{H}$.

The MP generalized inverse of matrix $\varvec{H}$ can be computed by utilizing the vertical project approach, namely, $\varvec{H}^{{^{\dag } }} = (\varvec{H}^{T} \varvec{H})^{{ - \text{1}}} \varvec{H}^{T}$. In accordance with the ridge regression theory [27, 28], a positive value $(1/\lambda )$ can be added to the computation of the weight vector $\varvec{\beta}$. The solution is equivalent to the ELM optimal solution with $\sigma_{\text{1}} = \sigma_{\text{2}} = \mu = \nu = \text{2}$, which possesses favorable generalization capability and high stabilization. There is:

$$ \varvec{\beta}= \varvec{H}^{T} \left( {\frac{\text{1}}{\lambda } + \varvec{HH}^{T} } \right)^{{ - \text{1}}} \varvec{T} $$

(5)

and then the output of ELM will be computed as:

$$ f\text{(}\varvec{x}\text{)} = h\text{(}\varvec{x}\text{)}\varvec{\beta}= h\text{(}\varvec{x}\text{)}\varvec{H}^{T} \left( {\frac{\text{1}}{\lambda } + \varvec{HH}^{T} } \right)^{{ - \text{1}}} \varvec{T} $$

(6)

or there is:

$$ \varvec{\beta}= \left( {\frac{\text{1}}{\lambda } + \varvec{HH}^{T} } \right)^{{ - \text{1}}} \varvec{H}^{T} \varvec{T} $$

(7)

and then the corresponding output of ELM will be calculated as:

$$ f\text{(}\varvec{x}\text{)} = h\text{(}\varvec{x}\text{)}\varvec{\beta}= h\text{(}\varvec{x}\text{)}\left( {\frac{\text{1}}{\lambda } + \varvec{HH}^{T} } \right)^{{ - \text{1}}} \varvec{H}^{T} \varvec{T} $$

(8)

2.2 Hierarchical Extreme Learning Machine (H-ELM)

It could be observed from Fig. 2 that, differing from traditional DL frameworks in [29] and [30], the H-ELM system [12] can be partitioned into two independent subframeworks. In the first subframework, a new ELM-based autoencoder is used to obtain multilayer sparse features of the input sample. In the latter subframework, the original ELM is implemented to make final decisions.

Fig. 2

The framework of H-ELM. a General frame of H-ELM, which is partitioned into two subframes: the frame of multilayer forward encoding and the frame of original ELM. b Layout of one single layer inside H-ELM

The principles and merits of H-ELM are described detailedly below. In order to mine latent knowledge within the training instances, the raw data entered is converted into an ELM random eigenspace. High-level sparse features will be acquired through an N-layers unsupervised learning. The output of each hidden layer can be expressed in mathematical formula as follows:

$$ \varvec{H}_{i} = g\text{(}\varvec{H}_{{i - \text{1}}} \cdot\varvec{\beta}\text{)} $$

(9)

where $\varvec{H}_{i}$ and $\varvec{H}_{i - 1}$ are the output matrices of the i-th layer and (i-1)-th layer, respectively, $g\text{(} \cdot \text{)}$ represents the hidden layers activation function, and $\varvec{\beta}$ denotes the output weight vector. It is noteworthy that, when the features of the former hidden layer are extracted, the parameters of the current hidden layer will be determined and do not need to be further adjusted. The more layers, the more compact the feature are generated. Therefore, each function can be regarded as a parted feature extractor, and each hidden layer of H-ELM can be identified as a self-contained module. However, within the classical DL models [29,30,31,32,33], all of their hidden layers are organized as an integral. And Back-Propagation (BP) algorithm is exploited to retrain the integral model iteratively. Consequently, compared to most of the classic DL frameworks, H-ELM possesses a faster learning speed.

As stated earlier, the second subframe of the entire H-ELM framework is implemented by the original ELM, thus we will focus on the first subframe. As is well-known, an autoencoder attempts to make the reconstructed outputs resemble the input data as far as possible, so as to effectively approximate input data [34]. Owing to its universal approximation ability, ELM is employed to develop the autoencoder. In the mean time, sparsity constraint is implemented on the optimization of autoencoder, forming the ELM sparse autoencoder. According to the principle of ELM, the optimization approach of this autoencoder can be formulated as Eq. (10).

$$ O_{\varvec{\beta}} = \text{argmin}\left\{ {\;\left\| {\varvec{H\beta } - \varvec{X}} \right\|^{\text{2}} + \left\|\varvec{\beta}\right\|_{{\ell_{\text{1}} }} } \right\} $$

(10)

where $\varvec{X}$ represents the input samples, $\varvec{H}$ denotes the output matrix of random mapping, which is not required to be optimized, and $\varvec{\beta}$ is weight matrix of the hidden layer to be obtained.

Hereinafter, the $\ell_{\text{1}}$ optimization algorithm is described. For more concise and clear expression, Eq. (10) is rewritten as:

$$ O_{\varvec{\beta}} = p\text{(}\varvec{\beta}\text{)} + q\text{(}\varvec{\beta}\text{)} $$

(11)

where $p\text{(}\varvec{\beta}\text{)} = \left\| {\varvec{H\beta } - \varvec{X}} \right\|^{\text{2}}$, and $q\text{(}\varvec{\beta}\text{)} = \left\|\varvec{\beta}\right\|_{{\ell_{\text{1}} }}$ is the $\ell_{\text{1}}$ penalty term of the model.

A fast iterative shrinkage-thresholding algorithm (FISTA) is employed to tackle with the problem in Eq. (8). The implementation process of FISTA is listed out as below [35].

• (1) Compute the Lipschitz constant $\gamma$ of the gradient of smooth convex function $\nabla p$.

• (2) Start the iteration with $\varvec{y}_{\text{1}} =\varvec{\beta}_{\text{0}} \in {\mathbf{R}}^{n}$, $t_{1} = 1$, initially. For the $j$-th iteration, the below holds.

  • (a) $\varvec{\beta}_{j} = s_{\gamma } \text{(}\varvec{y}_{j} \text{)}$, where $s_{\gamma }$ is given by

    $$ s_{\gamma } = \mathop {\arg \hbox{min} }\limits_{\varvec{\beta}} \left\{ {\frac{\gamma }{2}\left\| {\varvec{\beta}- \left( {\varvec{\beta}_{j - 1} - \frac{1}{\gamma }\nabla p\left( {\varvec{\beta}\left( {j - 1} \right)} \right)} \right)} \right\|^{2} + q\left(\varvec{\beta}\right)} \right\}. $$
  • (b)
    $$ t_{{j + 1}} = \frac{{1 + \sqrt {1 + 4t_{j}^{2} } }}{2} $$

    (12)

  • (c) $y_{{j + 1}} =\varvec{\beta}_{j} + \left( {\frac{{t_{j} - 1}}{{t_{j} + 1}}} \right)\text{(}\varvec{\beta}_{j} -\varvec{\beta}_{{j - 1}} ).$

By computing the iterative steps above, the data from the corrupted ones can be perfectly recovered. The $\ell_{\text{1}}$ optimization has been proved to be a better solution for data recovery and other applications [36].

3 The measure of predictor competence for dynamic ensemble selection

The key of DES is how to measure the predictive power of a predictor for a given unseen sample. Since that the predictive complexities of different test samples dramatically differ from each other, it could be naturally thought of that, a sample will be predicted well if it is fed to the predictors which are good at forecasting it. In our previous work [22], three DES algorithms are proposed, i.e., DES-PALR, DES-CP and DVS-OpOp. They all design a measurement to estimate the predictive power of a base predictor to consider what information can obtain better predictive performance. However, in this paper, through considering multiple criteria, we present a new Dynamic Ensemble Pruning technique, i.e., the DEP-TSP^meta technique, and compare its forecasting performance with that of the previously proposed algorithms in Sect. 5. The three algorithms are described succinctly in the following subsections.

3.1 The DES algorithm based on Predictor Accuracy over the Local Region (DES-PALR)

Predictor precision is the most universal measurement for the implementation of DES. In DES-PALR, predictor precision is calculated based on a small area within the training dataset embracing the prescribed test sample. This area can be determined by implementing clustering algorithms, e.g., K-nearest-neighbor (KNN) algorithm [37]. Specifically, the local region would have a more similar distribute to the unseen instance than the other areas in the training set, so that the predictors which perform well on the local region are selected into the final ensemble system for the unseen sample.

The most important issue existing in DES-PALR is that, the predictive performance of this algorithm is closely related to the definition of local region. Besides, some abnormal samples around the unseen sample will have remarkable influence on the performance of this algorithm. Therefore, only using predictors that perform well on local regions is not enough to make the predicted values close to the true values. Consequently, in order to obtain better predictive performance, more information should be considered.

3.2 The DES algorithm based on the Consensus of Predictors (DES-CP)

Different from DES-PALR, DES-CP considers the extent of consensus of a pool of EoPs rather than a pool of predictors as a criterion. In this algorithm, a population of EoPs is first generated using genetic algorithm, i.e., Genetic Algorithm based Selective Ensemble (GASEN) [38]. The higher the extent of consensus of predictors, the better the predictive performance of the EoP is expected. Then, for each unseen sample, the EoP possessing the maximum consensus will act as the decision maker. Two variant algorithms based on this generated EoPs are proposed in [22]: DES-CP-Var and DES-CP-Clustering. The former assesses the consensus of EoP by calculating the variance of the predicted values of all predictors in each EoP. EoP with lower variance possesses higher consensus. The latter measures the extent of consensus of EoP by the difference between the scale of the cluster comprising the most and the second most predictive values. The bigger the difference is, the higher the consensus of EoP will be regarded.

The most difference between DES-PALR and DES-CP lies in that, DES-CP does not need to extract information from local regions. Therefore, the performance of this algorithm will not be influenced by the manner of local region definition. However, the computational costs would be increased for DES-CP, due to its requirement of generating a group of predictor ensembles.

3.3 The dynamic validation set determination algorithm based on the similarity between the Output profile of the test sample and the output profile of each training sample (DVS-OpOp)

DVS-OpOp is somewhat similar to DES-PALR, where the goal of both of them is to select samples which are close to the unseen sample to form the validation set. However, with DVS-OpOp, the similarity is calculated based on space of decisions rather than eigenspace. What’s more, the similarity is measured by combining the output profile of the unseen sample and the output profiles of training set. The output profile of one sample is a vector that consists of the predicted values obtained by the base predictors for that sample.

The principle merit of this algorithm lies in that, it is not restricted by the definition of the local region in feature space. However, DVS-OpOp only considers the global knowledge of the unseen sample, while ignores its local information. Hence, we can simultaneously consider the local and the global knowledge and other features to measure competence of the base predictor in this work.

4 The proposed technique: DEP-TSP^meta

Aiming at addressing TSP problems, we specifically construct a dynamic ensemble pruning technique, i.e., DEP-TSP^meta, as shown in Fig. 3, which is partitioned into the following three stages. Moreover, to clearly describe our proposed technique, symbols frequently used in this paper is summarized in Table 1.

Fig. 3

Overview of the proposed DEP-TSP^meta technique

Table 1 Definitions of the major mathematical symbols used in our paper

• (a) Ensemble initialization stage, in which a preliminary collection of predictors using the training sample set $T_{\lambda }$ is generated, denoted by $P = \left\{ {p_{1} ,p_{2} , \ldots ,p_{M} } \right\}$.

• (b) Meta-predictor construction stage, given each instance $\left( {\varvec{x}_{j} ,y_{j} } \right)$ from the training dataset $T_{\ell }$ and each predictor $p_{i}$, the meta-attribute vector $\left( {\theta_{i,j} ,\varvec{m}_{i,j} } \right)$ is extracted and put into $T^{ * }$ that is later used to build several candidates and select the most competent one as the meta-predictor $\ell$. A different training dataset is used at this stage to prevent overfitting.

• (c) Prediction stage, for an unseen instance $\left( {\varvec{x}_{test\_j} ,y_{test\_j} } \right)$, the meta-information $\varvec{m}_{i,test\_j}$ is extracted based on dynamic pruning dataset $D_{pru}$ is fed to the meta-predictor $\ell$, which determines several excellent predictors to constitute the final dynamic ensemble $P^{\prime}$, so as to make the final predictive decision for this instance.

4.1 Ensemble initialization

During the ensemble initialization stage, the goal is to produce a diversified and informative collection of predictors, as it makes no sense to integrate predictors that always render duplicate outputs. The method of integrating varying predictor types and different learning parameters is utilized in this stage. Specifically, two types of base learners, i.e., ELMs and H-ELMs, with different numbers of hidden neurons layers, disparate hidden neurons quantities, and diversified activation functions are employed to generate the collection of base predictors, using the training samples from the dataset $T_{\lambda }$. The detailed settings of these generated base predictors $P = \left\{ {p_{1} ,p_{2} , \ldots ,p_{M} } \right\}$ are shown in Table 3 of Sect. 5.2.

4.2 Meta-predictor construction

As displayed in Fig. 3, this stage mainly includes three procedures: the instances adoption procedure, the meta-attributes extraction procedure, and the meta-predictor learning procedure. The crucial parameters existing in the meta-predictor training procedure are specifically introduced in the dynamic parameters adjustment procedure at last. The details of each procedure are described as follows.

4.2.1 Instances adoption

In order to solve the problem of low degree of consensus, we determine to focus the training of meta-predictor $\ell$ to specifically handle the case where the extent of consensus among the collection of predictors is low. Each instance $\left( {\varvec{x}_{j} ,y_{j} } \right)$ is first estimated by the whole ensemble of predictors to obtain $P\left( {\varvec{x}_{j} } \right) = \left( {p_{1} \left( {\varvec{x}_{j} } \right),p_{2} \left( {\varvec{x}_{j} } \right), \ldots ,p_{M} \left( {\varvec{x}_{j} } \right)} \right)$, which denotes the predicted values of all predictors in the ensemble $P$. Then, the consensus of the ensemble $P$ is evaluated by calculating the variance of the predicted values made by its constituent predictors. The prediction variance of instance $\left( {\varvec{x}_{j} ,y_{j} } \right)$ among the collection of predictors is calculated as below:

$$ var\left( {P\left( {\varvec{x}_{j} } \right)} \right) = \frac{{\sum\nolimits_{i = 1}^{M} {\left( {p_{i} \left( {\varvec{x}_{j} } \right) - \frac{{\sum\nolimits_{a = 1}^{M} {p_{a} \left( {\varvec{x}_{j} } \right)} }}{M}} \right)} }}{M} $$

(13)

The smaller the variance is, the higher the consensus will be. Thus, the degree of consensus is computed as:

$$ con\left( {\left( {\varvec{x}_{j} ,y_{j} } \right),P} \right){ = }\frac{1}{{var\left( {P\left( {\varvec{x}_{j} } \right)} \right)}} $$

(14)

To judge whether the extent of consensus is low, a minimum acceptable consensus needs to be defined, i.e., the consensus threshold $\varOmega_{1}$. If the consensus $con\left( {\left( {\varvec{x}_{j} ,y_{j} } \right),P} \right)$ falls below the threshold $\varOmega_{1}$, the instance $(\varvec{x}_{j} ,y_{j} )$ will be selected to extract meta-attributes for training meta-predictor $\ell$.

Before meta-attributes are extracted, the local area of the instance $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$ is calculated by using the KNN algorithm, which is composed of its K most similar instances, and is represented by $L_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}} = {\{ (}\varvec{x}_{\text{1}} \text{,}y_{\text{1}} \text{),(}\varvec{x}_{\text{2}} \text{,}y_{\text{2}} \text{),} \ldots \text{,(}\varvec{x}_{K} \text{,}y_{K} {)\} }$. Next, the instance $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$ and all the instances in the training set ${\rm T}_{\ell }$ are transformed into their corresponding output property files. The output property file of the instance $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$ is denoted as $\tilde{y}_{j} = (\tilde{y}_{j,1} ,\tilde{y}_{j,2} , \ldots ,\tilde{y}_{j,M} )$, where $\tilde{y}_{j,i}$ is the predictive result generated by the base predictor $p_{i}$ for the instance $(\varvec{x}_{j} ,y_{j} )$. Furthermore, the similarity is computed between the output property file of the instance $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$ and the output property files of all the instances in training set ${\rm T}_{\ell }$ by utilizing the KNN algorithm. The outcome of this procedure will guide us to select instances, that are most similar to $(\varvec{x}_{j} \text{,}y_{j} )$, to constitute $G_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}} = {\{ (}\varvec{x}_{\text{1}} \text{,}y_{\text{1}} \text{),(}\varvec{x}{}_{\text{2}}\text{,}y_{\text{2}} \text{),} \ldots \text{,(}\varvec{x}_{Kp} \text{,}y_{Kp} {)\} }$.

Finally, by employing each $p_{i}$ in the collection of predictors $P$, together with the instance $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$, the local area $L_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}}$ and the global area $G_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}}$, one meta-attribute vector $\varvec{m}_{{i\text{,}j}}$ can be extracted.

4.2.2 Meta-attributes extraction

In one of our previous research works [22], we use one single criterion to estimate the capability of a predictor. While in this work, we take into consideration the data characteristics of TSP problems, further proposing four different sets of meta-attributes. Each attribute set, i.e., $\varvec{f}_{\text{1}}$, $f_{\text{2}}$, $\varvec{f}_{\text{3}}$ and $f_{\text{4}}$, reflects a characteristic about the behavior of a base predictor, and can be regarded as a criterion, such as the prediction performance estimated in the local area, and the predictor confidence for the prediction of an unseen instance. Utilizing four different sets of meta-attributes, even if one criterion does not work owing to the inaccuracy in the local areas or the results with low confidence, the system can still accomplish favorable predictive performance, because other criteria are taken into account in the algorithm implementation.

The two attribute sets $\varvec{f}_{\text{1}}$ and $f_{\text{2}}$ are calculated employing the information drawn from the local area of capacity $L_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}}$. The attribute set $\varvec{f}_{\text{3}}$ uses information obtained from the global area of capacity $G_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}}$. And $f_{\text{4}}$ is computed directly from the instance $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$, which shows the level of confidence of $p_{i}$ for the accurate prediction for $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$. The details of the four sets of meta- attributes are described in the following.

The criterion of the neighbor’s hard prediction is denoted by $\varvec{f}_{\text{1}}$. Firstly, a vector with $K$ elements is set up, where $K$ denotes the size of the local area. For each element $\text{(}\varvec{x}_{\sigma }^{{c_{\text{1}} }} \text{,}y_{\sigma }^{{c_{\text{1}} }} \text{)}$, $\sigma \in \text{[1,}\;K\text{]}$, belonging to the local area of the input instance $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$, where $c_{\text{1}}$ represents the first criterion, if the Root Mean Square Error (RMSE) of the prediction made by $p_{i}$ is less than the preset threshold, the $\sigma$-th element of the vector is assigned to 1, otherwise it is assigned to 0.

$$ D_{\sigma }^{{c_{\text{1}} }} = \left\{ \begin{aligned} \text{1,}\;\;\;RMSE\text{(}p_{i} \text{,(}\varvec{x}_{\sigma }^{{c_{\text{1}} }} \text{,}y_{\sigma }^{{c_{\text{1}} }} \text{))} < threshold \hfill \\ \text{0,}\;\;\;{\text{otherwise}} \hfill \\ \end{aligned} \right. $$

(15)

$$ \varvec{f}_{\text{1}} = \text{(}D_{\text{1}}^{{c_{\text{1}} }} \text{,D}_{\text{2}}^{{c_{\text{1}} }} \text{,} \ldots \text{,}D_{K}^{{c_{\text{1}} }} \text{)} $$

(16)

where $\varvec{f}_{\text{1}}$ is a vector of $D_{\sigma }^{{c_{\text{1}} }} \text{,}\;\upsigma \in \text{[1,}\;\text{K]}$, and $D_{\sigma }^{{c_{\text{1}} }}$ represents the performance of $p_{i}$ when implemented on $\text{(}\varvec{x}_{\sigma }^{{c_{\text{1}} }} \text{,}y_{\sigma }^{{c_{\text{1}} }} \text{)}$.

The criterion of the overall local accuracy is denoted by $f_{\text{2}}$. The RMSE of the prediction made by $p_{i}$ on the entire area of capacity $L_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}}$ is calculated, denoted by $RMSE\text{(}p_{i} \text{,}L_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}} \text{)}$ and the reciprocal of $RMSE\text{(}p_{i} \text{,}L_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}} \text{)}$ is encoded as $f_{\text{2}}$.

$$ f_{\text{2}} = \frac{\text{1}}{{RMSE\text{(}p_{i} \text{,}L_{{\text{(}\varvec{x}_{j} \text{,}y{}_{j}\text{)}}} \text{)}}} $$

(17)

The criterion of global area accuracy is denoted by $\varvec{f}_{\text{3}}$. Similar to $\varvec{f}_{\text{1}}$, first, a vector with $Kp$ elements is set up, where $Kp$ denotes the size of the global area. Then, for each element $\text{(}\varvec{x}_{\sigma }^{{c_{\text{3}} }} \text{,}y_{\sigma }^{{c_{\text{3}} }} \text{)}$ in $G_{{\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}}}$, $\sigma \in \left[ {1,Kp} \right]$, where $c_{\text{3}}$ represents the third criterion, belonging to the global area decided by output property file, if difference between the RMSE obtained by $p_{i}$ on $\text{(}\varvec{x}_{\sigma }^{{c_{\text{3}} }} \text{,}y_{\sigma }^{{c_{\text{3}} }} \text{)}$ and the RMSE obtained by $p_{i}$ on $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$ is less than the threshold, the $\sigma$-th element of the vector is assigned to 1, otherwise it is assigned to 0.

$$ D_{\sigma }^{{c_{\text{3}} }} = \left\{ \begin{aligned} & \text{1,}\;\;\;\left| {RMSE\text{(}p_{i} \text{,(}\varvec{x}_{j} \text{,}y_{j} \text{))} - RMSE\text{(}p_{i} \text{,(}\varvec{x}_{\sigma }^{{c_{\text{3}} }} \text{,}y_{\sigma }^{{c_{\text{3}} }} \text{))}} \right| < threshold \hfill \\& \text{0,}\;\;\;{\text{otherwise}} \hfill \\ \end{aligned} \right. $$

(18)

$$ \varvec{f}_{\text{3}} = \text{(}D_{\text{1}}^{{c_{\text{3}} }} \text{,}D_{\text{2}}^{{c_{\text{3}} }} \text{,} \ldots \text{,}D_{Kp}^{{c_{\text{3}} }} \text{)} $$

(19)

where $f_{3}$ is a vector of $D_{\sigma }^{{c_{3} }} ,\;\sigma \in [1,\;Kp]$, and $D_{\sigma }^{{c_{3} }}$ represents the consensus of the decisions of $p_{i}$ when implemented on $\text{(}\varvec{x}_{\sigma }^{{c_{\text{3}} }} \text{,}y_{\sigma }^{{c_{\text{3}} }} \text{)}$ and $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$.

The criterion of predictor’s confidence is denoted by $f_{\text{4}}$. The predicted value of $p_{i}$ on $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$ is added to the set of predicted values, with the scale of the set being equal to the scale of the initial collection of predictors. Then, all the deviations between the predicted values and the true value are calculated. Finally, the min–max normalization approach is utilized to normalize all the deviations to the interval $\text{[0,}\;\text{1]}$. Each of deviation value $d_{i}$ is normalized by the min–max normalization formula, which is shown as below:

$$ d_{i}^{new} = \frac{{d_{i} - d^{min} }}{{d^{max} - d^{min} }} $$

(20)

where $d_{i}^{new}$ is the normalized value, $d_{i}^{\hbox{min} }$ and $d_{i}^{\hbox{max} }$ represent the minimum and maximum value of all deviations, respectively.

$$ f_{\text{4}} = \frac{\text{1}}{{d_{i}^{new} }} $$

(21)

A vector $\varvec{m}_{{i\text{,}j}} = \text{(}\varvec{f}_{\text{1}} ,f_{\text{2}} ,\varvec{f}_{\text{3}} ,f_{\text{4}} \text{)}$ can be constructed at the end of meta-attributes extraction procedure (Fig. 4), where $\varvec{m}_{{i\text{,}j}}$ represents the meta-knowledge that extracted by $p_{i}$ from $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$, with the size of $\varvec{m}_{{i\text{,}j}}$ being $K + Kp + 2$. If the psredicted value of $p_{i}$ on $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$ is very close to the true value, the class label of $\varvec{m}_{{i\text{,}j}}$, i.e., $\theta_{{i\text{,}j}}$, is set to 1; otherwise, it is set to 0.This class label indicates whether $p_{i}$ possesses good enough performance on $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$ or not. $\text{(}\theta_{{i\text{,}j}} \text{,}\varvec{m}_{{i\text{,}j}} \text{)}$ is stored into the meta-attributes dataset ${\rm T}^{*}$.

Fig. 4

Attribute vector contains the meta-knowledge about the behavior of the base predictor. The class label indicates whether $p_{i}$ possesses good enough performance on $\text{(}\varvec{x}_{j} \text{,}y_{j} \text{)}$ or not

Each predictor in the collection of predictors can extract a meta-attribute from each instance. There are $N$ instances belonging to $T_{\ell }$, whose consensus $E\left( {\left( {\varvec{x}_{j} ,y_{j} } \right),P} \right)$ is less than $\varOmega_{1}$. In this way, the size of the meta-attributes dataset ${\rm T}^{*}$ equals $M \times N$ ($M$ is the size of the collection of predictors). Hence, we can address the small sample size prediction issue, due to the lack of training data, by the increasement to the scale of the collection of predictors.

4.2.3 Learning of meta-predictor

The purpose of this procedure is to train the meta-predictor $\ell$. In this work, we use 75 percent of the dataset ${\rm T}^{*}$ for learning and the remaining 25 percent for validation. ELM is employed as the base model for the meta-predictor. Ten ELMs are trained, using {10, 20, …, 100} as the set of the numbers of hidden neurons, and the sigmoid transfer function as the activation function. The criterion utilized to evaluate the performance of the ten meta-predictors is RMSE. That is to say, the meta-predictor achieving the minimum RMSE over the validation set is chosen to be the decisive meta-predictor $\ell$.

The whole meta-predictor construction stage is formalized in Algorithm 1.

4.2.4 The dynamic adjustment of parameters

There exist three crucial parameters for the successful implementation of the proposed technique: the consensus threshold $\varOmega_{1}$, the local area size $K$, and the global area size $Kp$. For different datasets, the most appropriate parameters should be dynamically adapted to apply to the DEP-TSP^meta technique. Here, genetic algorithm (GA) [39,40,41] is applied to find the optimal parameters for each dataset.

GA is a searching algorithm designed on basis of biological evolutionary principle. It is a mathematical model for simulating Darwin’s genetic selection and natural elimination. As an effective global parallel optimization search tool, GA is simple, universal, robust and fit for concurrent processing.

In our paper, the three parameters are optimized by GA, including the following several basic steps:

Step 1: The three parameters are encoded into binary format and an initialized population of size 20 is generated. And the maximal generation epoch of GA is set to 20.

Step 2: The initialized population of size 20 is used in the proposed technique for evaluating the performance of DEP-TSP^meta. RMSE is employed as the measurement for the fitness value.

Step 3: The “roulette” is set to be the selection function. Roulette is the conventional selection function with the survival probability equal to the fitness of $i/sum$ of all the individuals.

Step 4: The “simpleXover” is set to be the crossover function. According to the results obtained by using trial and error method, the probability of crossover operators is assigned to be 0.6. According to the crossover probability, the individuals in the population are randomly matched and the parameters of different positions are changed.

Step 5: The “binaryMutation” is set to be the mutation function. The probability of mutation operators is set to be 0.005. The “binaryMutation” function varies each bit of the parent on basis of the mutation probability.

According to the literature [42], it is proved by means of homogeneous finite Markov chain analysis that GA does not converge to the global optimum. However, as the number of iterations increases, GA can guarantee to find an approximate optimal solution. Moreover, a more practical question regards the time complexity of the algorithm to achieve the optimal solution. Thus, by using the trial-and-error method, a sufficient and acceptable initialized population size and generation epoch are set to ensure that the appropriate values of the three parameters are acquired by searching. Specifically, when the maximal generation epoch is reached, the individual with the maximum fitness function value is the output of the final solution and the algorithm is terminated.

Just as the “No Free Lunch” theorem declares [43], there exists no algorithm that is superior to any other ones among all the probable problems. Therefore, it is necessary that GA is utilized to adjust the three crucial parameters dynamically, i.e., $\varOmega_{1}$, $K$, $Kp$. It is found through our experiments that, dynamic adjustments to the values of the crucial parameters significantly boost the predictive performance of the proposed technique.

4.3 Prediction

The prediction stage is described in Algorithm 2. Given the test instance $\text{(}\varvec{x}_{test\_j} \text{,}y_{test\_j} \text{)}$, in this stage, the local area of capacity $L_{{\left( {\varvec{x}_{test\_j} ,y_{test\_j} } \right)}}$ having $K$ most similar instances is defined with the instances from the dynamic pruning dataset $D_{pru}$. Next, the output property files of all the instances in $D_{pru}$ and $\text{(}\varvec{x}_{test\_j} \text{,}y_{test\_j} \text{)}$ are computed, and the most $Kp$ similasr instances are determined as the global area of capacity $G_{{\left( {\varvec{x}_{test\_j} ,y_{test\_j} } \right)}}$, accosrding to the similarity between the output property files of all the instances in the dynamic pruning dataset and the output property file of the test instance.

Then, for each predictor $p_{i}$ in the initial collection of predictors $P$, the meta-attributes extraction procedure is the same as that described in Sect. 4.2.2, and the vector $\varvec{m}_{{i\text{,}test{\_}j}}$ is extracted. Next, $\varvec{m}_{{i\text{,}test{\_}j}}$ will be fed into the meta-predictor $\ell$. If the output $\theta_{i,test\_j}$ of $\ell$ equals 0 (i.e., $p_{i}$ is incapable for the test instance), $p_{i}$ will be pruned; otherwise if the output $\theta_{{i\text{,}test\_j}}$ of $\ell$ equals 1 (i.e., $p_{i}$ is capable for the test instance), $p_{i}$ will be added into the ensemble $P^{\prime}$. When each predictor in the collection of predictors is estimated, the final ensemble $P^{\prime}$ is obtained. The averaged predicted values made by the predictors in the ensemble $P^{\prime}$ is taken as the final decision for $\text{(}\varvec{x}_{test\_j} \text{,}y_{test\_j} \text{)}$.

Detailed pseudocode of DEP-TSP^meta is described in the following Algorithm 2.

4.4 A summary of the proposed DEP-TSP^meta technique

The contents of this section could be divided into three parts: (1) reorganizing and summarizing the core idea of the DEP-TSP^meta technique; (2) discussing advantages and disadvantages of the proposed technique; (3) analyzing the computational complexity of the proposed technique and making comparison to previous algorithms.

As stated in the “No Free Lunch” (NFL) theorem, without a prior assumption about specific problems, no algorithm could be expected to perform more superior than any other. There does not exist a universal optimal algorithm [44]. However, we believe that using one single criterion to estimate an algorithm performance is biased. It would be comprehensive and reasonable to consider more measurement criteria. In this work, a multiple criteria Dynamic Ensemble Pruning technique exploiting meta-learning specialized for TSP, i.e., the DEP-TSP^meta technique, is presented. The meta-attributes employed by meta-learning are the distinct criteria applied to evaluate the competence of base predictors from different angles.

In our proposed DEP-TSP^meta technique, both shallow models, i.e., ELMs, and deep models, i.e., H-ELMs, with varying predictor types and different learning parameters are combined together to constitute the initial ensemble. Four meta-attributes representing different criteria for evaluating base predictors capacities are developed, including the prediction performance of a predictor in a local area, the prediction confidence of a predictor on every instance in a local area, the predictive performance of a predictor in the global area, and the prediction confidence of a predictor on the current test instance. The meta-attributes extracted from the training dataset are utilized to build one meta-predictor, and this meta-predictor will be responsible for selecting the most appropriate base predictors to construct the final ensemble for making the predictive decision. The crucial parameters of the meta-attributes are adjusted by genetic algorithm for matching the current dataset dynamically.

In summary, DEP-TSP^meta possesses the following three advantages:

• It is developed based upon four different meta-attributes, therefore, it is robust even though some base predictors do not perform well on one or two of the meta-attributes.

• The ensemble within DEP-TSP^meta is constructed employing ELM and H-ELM as its base learners. Consequently, the technique not only inherits the merit of the former in its fast running speed, but also inherits the advantage of the latter in its adequate extraction of data features.

• The dynamic ensemble pruning paradigm employed within DEP-TSP^meta can improve its generalization performance, while reducing its scale, simultaneously.

In contrast with the above summarized advantages, DEP-TSP^meta possesses two obvious disadvantages:

• Genetic algorithm employed within DEP-TSP^meta results in its relatively high computational complexity;

• The structure of DEP-TSP^meta is relatively complex.

The computational complexities of the DEP-TSP^meta training and testing phases are, respectively, $O\left( {N\left( {M + M\left( {N\log K + 2M + N\log K_{p} } \right)} \right)gM^{2} \left( {1.5r + rf} \right)} \right)$ and $O\left( {M + M\left( {N\log K + 2M + N\log K_{p} } \right)} \right)$, where $N$ represents the scale of training dataset, $M$ denotes the number of predictors in the initial ensemble collection, $K$ and $K_{p}$ represent the scales of global area and local area, respectively, $g$ denotes the amount of generations, $r$ denotes the scale of population, and $f$ represents the chromosome length. Because the proposed DEP-TSP^meta technique is constructed based upon four meta-attributes extracted from DES-PALR, DES-CP, and DES-OpOp, the computational complexities of the proposed technique in training and testing phases become larger compared to previous algorithms. However, this construction scheme brings higher prediction accuracy and stronger robustness to the DEP-TSP^meta technique, accordingly.

5 Experiments

5.1 Datasets

We carry out empirical study based upon eight one-dimensional time series datasets selected from Time Series Data Library (TSDL) [45] and Yahoo Finance [46]. The key information of the eight benchmark datasets is presented, respectively, in Table 2. The eight datasets are drawn from diverse real-world domains, with different numbers of data points, different time granularities, different time ranges, different domains, and different types of data, which guarantee the diversity of experimental samples.

Table 2 Crucial information of the eight experimental datasets

It is required to regulate the domain value of each attribute into the interval [0, 1], due to the different scopes of dataset attributes. This operation of normalization guarantees that the data attributes with greater values do not overwhelm the smaller ones, so that predictive performance could be enhanced. Each value in the whole dataset is normalized by min–max normalization.

5.2 Experimental setup

MAE [47] and RMSE [48] are employed as the evaluation measurements of prediction errors in this work, with the definitions being presented as below:

$$ MAE = \frac{\text{1}}{N}\sum\limits_{{i = \text{1}}}^{N} {\left| {y{}_{i} - \tilde{y}_{i} } \right|} $$

(22)

$$ RMSE = \sqrt {\frac{\text{1}}{N}\sum\limits_{{i = \text{1}}}^{N} {\text{(}y_{i} - \tilde{y}_{i} \text{)}^{\text{2}} } } $$

(23)

here $y_{i}$ is the true value, $\tilde{y}_{i}$ denotes the predicted value, and N is the number of samples.

Experiments are carried out with the system configuration as follows: 2.6 GHz PC with 1 GB of RAM using Windows XP operating system, MATLAB language source code.

Then, as base models, 50 well-trained ELMs and 50 well-trained H-ELMs constitute the initial collection of predictors. And the settings of these base models are shown in the following Table 3.

Table 3 The exhaustive information of base models used in experiments

The definitions of the six activation functions are shown as below:

$$ f\text{(}x\text{)} = \frac{\text{1}}{{\text{1} + e^{ - x} }} $$

(24)

$$ f\text{(}x\text{)} = sin\text{(}x\text{)} $$

(25)

$$ f\text{(}x\text{)} = \left\{ \begin{aligned}& \text{1,}\;\;{\text{if}}\;\;x > \text{0} \hfill \\& \text{0,}\;\;{\text{otherwise}} \hfill \\ \end{aligned} \right. $$

(26)

$$ f\text{(}x\text{)} = \left\{ \begin{aligned} &\text{1} - \left| x \right|\text{,}\;\;{\text{if}}\;\; - \text{1} \le x \le \text{1} \hfill \\& \text{0,}\;\;\;\;\;\;\;\;{\text{otherwise}} \hfill \\ \end{aligned} \right. $$

(27)

$$ f\text{(}x\text{)} = e^{{ - x^{\text{2}} }} $$

(28)

$$ f\text{(}x\text{)} = \frac{\text{2}}{{\text{1} + e^{{ - \text{2}x}} }} - \text{1} $$

(29)

Each experiment is repeated for 10 times, and all the reported experimental results are the average of these 10 repetitive runs. By using the trial-and-error method, and taking into account the dataset scale, simultaneously, the time window size (TWS) is set to five. For each repetition, the datasets are divided into: 50% for the training dataset, 25% for the dynamic pruning dataset, and 25% for the test dataset. For the proposed DEP-TSP^meta technique, 50% of the training dataset is used to generate the initial collection of predictors, and the other 50% is used for meta-predictor construction. According to the literature [49], this procedure used in our experiments is actually one kind of cross validation procedures, i.e., hold-out cross validation, which is a technique that relies on a single split of data. The data is divided into two non-overlapping parts and these two parts are used for training and testing respectively. Therefore, in our experiment, the samples that test the performance of the proposed algorithm do not appear in the training dataset, there will not yield an overoptimistic result.

For each dataset, the specific values of GA parameters are listed out in Table 4.

Table 4 Genetic algorithm parameters

GA determines the most appropriate values of the three parameters for each dataset, as shown in Table 5.

Table 5 The parameters values determined by genetic algorithm

We compare the predictive accuracy of the proposed DEP-TSP^meta technique, against seven current techniques. The seven comparative algorithms used in this study are: DES-PALR, DES-CP-Clustering, DVS-OpOp, Genetic Algorithm based on Selective Ensemble (GASEN), Averaging All (AA), Best Single ELM (BS-ELM), and Best Single H-ELM (BS-H-ELM), respectively. The first three algorithms belong to the category of DES techniques, while the others are part of the static ensemble selection techniques.

The objective of the comparative study is mainly to test and verify three research questions: (1) Does the ensemble of predictors outperform the best single model? (2) Does the DEP paradigm outperform the state-of-the-art static ensemble selection one, especially GASEN? (3) Whether the implementation of multiple DEP criteria as meta-attributes leads to a more robust performance or not, even when it is confronted with ill-defined problems?

5.3 Experimental results

We spilt the experimental results into two tables: Table 6 shows the detailed RMSE performance on the eight benchmark time series datasets compared with the seven techniques, including three DES algorithms and four static ensemble selection rules. And Table 7 shows the corresponding comparisons based on the detailed MAE performance.

Table 6 The detailed RMSE performance of corresponding algorithms on the eight benchmark time series datasets

Table 7 The detailed MAE performance of corresponding algorithms on the eight benchmark time series datasets

It is clearly shown from the results reported in Table 6 that, the proposed technique has the best RMSE performance on the QIS, ITD, DJI, and Odonovan datasets, and obtains the second best RMSE performance on the IAP, DSA, and Montgome datasets. That is to say, for 7 out of the 8 RMSE results, the proposed algorithm performs significantly better than the comparative algorithms. In contrast, BS-H-ELM yields the worst results on all the datasets, which could be explained by the lack of training samples. However, the proposed algorithm could overcome this difficulty well. For example, if there are 30 training instances in the meta-predictor construction stage and the collection of predictors consists of 100 base models, then the number of training instances will reach 3,000. Thus, enough learning instances are gotten for training the meta-predictor. In this manner, the performance of the proposed technique will not be limited by the lack of training instances.

It could be observed from the results shown in Table 7 that, the proposed DEP-TSP^meta technique achieves results that are superior to other algorithms on almost all the datasets in terms of MAE, except for the DSA and Montgome datasets. While on the DSA and Montgome datasets, DEP-TSP^meta acquires the second best MAE performance. Since, in DEP-TSP^meta, four different criteria, designed to measure the capacity of base predictors, are employed as the meta-attributes, even though one or two of them do not work well, the integral framework can still achieve excellent performance. In this sense, our framework is a more robust prediction technique than the comparative algorithms considering only one single criterion.

In addition, the algorithms achieving best performances on the datasets are all some ensemble selection methods rather than the method of selecting the best single model, which demonstrates the superiority of ensemble selection paradigm in prediction performance. At the same time, although the DES methods can achieve the best performances on most datasets, static ensemble selection methods, especially GASEN, sometimes have better performance than the DES methods, including the proposed technique, which shows that dynamic ensemble selection algorithms are not always better than static ensemble selection algorithms in any situation. This observation also proves the “No Free Lunch” (NFL) theorem [44].

Next, to make sure whether the proposed DEP-TSP^meta technique is superior to the three DES algorithms and other comparative algorithms in a statistic sense, it is necessary to perform t-tests on the RMSE and MAE results obtained by all the algorithms on the eight time series benchmark datasets.

Then, when the t-tests are performed, the significance level ALPHA is set to 0.05 and TAIL is set to left. The results are shown in Tables 8 and 9. The items displayed in bold and with H = 1 indicate that hypothesis H0 is rejected, i.e., Model A significantly improves the predictive performance of Model B, at 5% significance level (t-value $\le$− 1.8331). Conversely, the items in normal font and with H = 0 manifest that hypothesis H0 cannot be rejected, i.e., there is no significant difference between the predictive performance of Model A and Model B at 5% significant level.

Table 8 T-test results on RMSE between DEP-TSP^meta and other comparative algorithms on the eight benchmark time series datasets

Table 9 T-test results on MAE between DEP-TSP^meta and other comparative algorithms on the eight benchmark time series datasets

As shown in Tables 8 and 9, for 70 out of the 112 t-tests (62.5%), the proposed DEP-TSP^meta technique achieves significant improvements over comparative algorithms at 5% significance level in terms of RMSE and MAE. When applied to the ITD and Odonovan time series datasets, DEP-TSP^meta is far better than all other compared algorithms, including three DES algorithms and four static ensemble selection techniques. At the same time, DEP-TSP^meta achieves significant improvements over BS-H-ELM in terms of RMSE and MAE on all the datasets. These results clearly show that, the proposed technique based on meta-learning is applicable to tackle with the TSP problems with small sample datasets.

STAC [50], which is a web platform that provides a more appropriate statistical test, is used, in this work, to determine whether the superiority of our algorithm is accidental. The statistical test results are shown in Tables 10 and 11. Specifically, the Friedman test [51], a nonparametric statistical test, is used to test differences across multiple algorithms based on the rankings of the algorithms on multiple datasets in terms of RMSE and MAE values. For each dataset, the Friedman test ranks each algorithm, where the best performing algorithm is ranked the first, the next best one is ranked the second, and so on. And then, the average ranking of each algorithm on all the datasets is computed. The best algorithm is the one with the lowest average ranking. The null hypothesis for the Friedman test is that the predictive performances of all the algorithms are equivalent or similar. We set the level of significance $\alpha = 0.1$, i.e., 90% confidence. The Friedman test results show that the null hypotheses are rejected with extremely low p-values, and it can be concluded that the predictive performances of at least two of the algorithms are significantly different from each other.

Table 10 Friedman test and post hoc Finner test based on RMSE values (significance level of 0.1)

Table 11 Friedman test and post hoc Finner test based on MAE values (significance level of 0.1)

Then, a post hoc Finner test [52] with the level of significance $\alpha = 0.1$ is conducted for a pairwise comparison between the rankings achieved by each algorithm, so as to check whether the performance differences between the proposed DEP-TSP^meta algorithm and those comparative algorithms on multiple datasets are statistically significant. In terms of MAE values, DEP-TSP^meta obtains the lowest average ranking of 1.25, followed by the DES-CP-Clustering technique, presenting an average ranking of 3.25. From the Finner test results, the performance of DEP-TSP^meta is significantly better when compared to the majority of the DES techniques and four static ensembles selection techniques. Only DES-CP-Clustering obtains a statistically equivalent performance. Moreover, as shown in Tables 10 and 11, for 9 out of the 14 Finner tests (64.3%), the predictive performance of the proposed DEP-TSP^meta technique is significantly superior with a 90% confidence, when compared to other comparative algorithms, on the eight benchmark datasets, in terms of RMSE and MAE values.

Finally, Figs. 5, 6, 7, 8, 9, 10, 11, 12 display, respectively, the absolute values of the prediction errors obtained by the proposed technique, DES-PALR and BS-ELM on the eight benchmark time series datasets.

Fig. 5

The absolute values of the prediction errors obtained by DEP-TSP^meta, DES-PALR and BS-ELM on the IAP time series

Fig. 6

The absolute values of the prediction errors obtained by DEP-TSP^meta, DES-PALR and BS-ELM on the QIS time series

Fig. 7

The absolute values of the prediction errors obtained by DEP-TSP^meta, DES-PALR and BS-ELM on the DHA time series

Fig. 8

The absolute values of the prediction errors obtained by DEP-TSP^meta, DES-PALR and BS-ELM on the DSA time series

Fig. 9

The absolute values of the prediction errors obtained by DEP-TSP^meta, DES-PALR and BS-ELM on the ITD time series

Fig. 10

The absolute values of the prediction errors obtained by DEP-TSP^meta, DES-PALR and BS-ELM on the DJI time series

Fig. 11

The absolute values of the prediction errors obtained by DEP-TSP^meta, DES-PALR and BS-ELM on the Odonovan time series

Fig. 12

The absolute values of the prediction errors obtained by DEP-TSP^meta, DES-PALR and BS-ELM on the Montgome time series

From the above comparisons, it can be concluded that the proposed technique has better generalization performance and smaller prediction errors than DES-PALR and BS-ELM on the six benchmark TSP problems, except for the DSA and the Montgome datasets. In addition, the proposed DEP-TSP^meta technique obtains the prediction values approximating the real values. It is worth mentioning that, the proposed technique achieves results close to the Oracle [53] performance on the ITD dataset. The Oracle expresses an almost perfect pruning scheme and its error rate is approximately zero.

The above reported experimental results are based upon the results of 10 repetitive runs. The primary reason for implementing repeated experiments is to reduce the impact of random factors, such as the random initialization of weights in neural networks, on the performance of the algorithms, and to decrease the influence of accidental errors on performance evaluation. In order to further explore whether the number of repetitions have an effect on the experimental results, we have added a series of controlled experiments with different repetitions, i.e., 5, 10, 15, 20, on the Odonovan dataset. The detailed RMSE and MAE performances with different repetitions of experiments on the Odonovan dataset are, respectively, presented in Tables 12 and 13.

Table 12 The detailed RMSE performance of corresponding algorithms on the Odonovan dataset

Table 13 The detailed MAE performance of corresponding algorithms on the Odonovan dataset

From Tables 12 and 13, it is not hard to see that, whether the number of repetitions is set as 5, 10, 15, or 20, the proposed DEP-TSP^meta technique consistently obtains the best performances on the Odonovan dataset, in terms of RMSE and MAE, compared with the other seven techniques, including the three DES algorithms and the four static ensemble selection rules. Therefore, it could be concluded that the number of repetitions is changed or dynamic, the comparative experiment results will not change, and the proposed technique still can achieve optimal performance on the Odonovan dataset. When the number of repetitions increases, the performance of our algorithm tends to be more stable. Thus, a rough conclusion could be drawn that, the more numbers of repetitive experiments are conducted, the more reliable the experimental results will be. However, considering the efficiency, ten repetitive experiments are enough to obtain relatively reliable results for analysis.

6 Conclusion and future work

In this paper, a multiple criteria Dynamic Ensemble Pruning technique dedicated to Time Series Prediction applying the meta-learning paradigm, namely the DEP-TSP^meta technique, is proposed. Four sets of meta-attributes are designed, with each set of meta-attribute corresponding to a specific DEP criterion for evaluating the capacity of each predictor in the initial collection of predictors, such as the predictor accuracy in the local area computed over the feature space, the predictor accuracy in the global area computed over the decision space, and the predictor’s confidence. These meta-attributes are utilized to train a meta-predictor. The meta-predictor will be responsible to evaluate whether or not one predictor is capable for predicting the unseen sample. Those incapable predictors determined by the meta-predictor will be pruned, while, in contrast, the capable predictors will be selected to constitute the final dynamic ensemble system.

For different TSP datasets, the size of the local area and global area, and the extent of consensus are totally different, which entails these crucial parameters to be adapted dynamically. After exploiting genetic algorithm to dynamically adjust these key parameters, significant improvement to the prediction accuracy of DEP-TSP^meta is obtained.

Experiments are conducted on eight benchmark TSP datasets coming from different fields, including transport, tourism, finance, crime, and labor market, etc. And DEP-TSP^meta is compared against three DES techniques (each technique measures the competence level of a base predictor based on a single criterion), as well as four static ensemble selection techniques. Empirical results demonstrate that DEP-TSP^meta has better predictive precision than other techniques on most of the eight datasets. These results may benefit from its designing scheme, the advantages of which are summarized as follows: (1) It dynamically provides the most qualified ensemble system for distinct test instances; (2) It devises four distinct DEP criteria to evaluate the competence of base predictors from different angles. Even if one or two criteria might lose efficacy, it can still keep its validity due to the consideration of other criteria; (3) It automatically generates more meta-knowledge to train the meta-predictor and consequently achieves significant performance gains even though the size of the training dataset is small. These characteristics yield the proposed DEP-TSP^meta technique with relatively high effectiveness and robustness.

Furthermore, numerous meta-attribute vectors generated by training instances can be used to train the meta-predictor, consequently, the problem of lack of training instances for meta-predictor could be overcome.

Also, some limitations exist in the proposed DEP-TSP^meta algorithm. Firstly, a desirable meta-predictor, obtained by training on the strength of four distinct meta-attributes, is the key to determine whether a base predictor is capable of predicting an unseen instance well or not. However, there are more criteria than just four sets of meta-attributes, which are worth considering for training a meta-predictor. Secondly, multiple DEP criteria are embedded in the proposed DEP-TSP^meta algorithm encoded as different sets of meta-attributes. However, some DEP criteria are not suitable for every TSP problem. Different prediction problems may require distinct sets of meta-attributes and the meta-predictor training process should be optimized for each specific prediction problem. As such, in our future work, we will work on the following aspects for time series prediction: (1) designing novel criteria to evaluate the capacity of the base predictors more effectively, such as the ranking information based on the number of consecutive correct predictions made by the base predictors; (2) developing a new meta-attributes selection scheme based on optimization algorithms, and selecting adaptively an appropriate set of meta-attributes for specific prediction problems, so as to improve the performance of the meta-predictor, and consequently, the predictive accuracy of the algorithm.