1 Introduction

Feature extraction is a fundamental and challenging problem in the area of computer vision and pattern recognition [1,2,3]. In many existing feature extraction algorithms, principal components analysis (PCA) [4] and linear discriminant analysis (LDA) [5] are the two classical linear feature extraction methods and have been widely used in many practical applications. PCA attempts to project the data along an optimal direction by maximizing the variance matrix of data. Unlike PCA, LDA is a supervised method that seeks to find a projection direction by maximizing the inter-class scatter when minimizing the inner-class scatter. Because the label information is fully exploited, LDA has been proven more efficient than PCA for the classification tasks [5]. To further improve the discriminant ability of feature extraction, some LDA variants have also been proposed, such as Enhanced Fisher Discriminant Criterion (EFDC) [6], Maximum Margin Criterion (MMC) [7], EMKFDA [8], and Orthogonal LDA (OLDA) [9].

To our best knowledge, linear feature extraction methods may fail to discover the underlying nonlinear structure hidden in high-dimensional data. To remedy this deficiency, a large number of manifold learning algorithms have been proposed. The representative manifold learning algorithms include locally linear embedding (LLE) [10], isometric feature mapping (ISOMAP) [11], and Laplacian eigenmaps (LE) [12]. Unfortunately, these manifold learning methods usually suffer from the out-of-sample problem [13]. This is because they fail to construct explicit maps over new measurements. To address this problem, locality preserving projection (LPP) [14] tries to seek a linear approximation to the eigen-functions of Laplace–Beltrami operator on the manifold derived from LE. Neighborhood preserving embedding (NPE) [15] tries to find a linear subspace which preserves the local structure based on the same principle of LLE. To construct an optimal graph for the later feature extraction, discriminative unsupervised dimensionality reduction (DUDR) [16] was proposed. Yan et al. [17] introduced a general framework for feature extraction, called graph embedding. A large number of methods, e.g., LPP, DUDR and OLMGMP [3] can all be considered as the special cases within this framework. Recently, many other methods have been explored in [18,19,20], and as expected, they have achieved good performance in the classification tasks.

However, a common problem with current subspace learning methods is that they only character the locality of samples such that they cannot guarantee a good projection for the classification purposes. To address this problem, Yang et al. [21] proposed unsupervised discriminant projection (UDP). UDP introduces the concept of non-locality and learns the low-dimensional representation of data by maximizing the ratio of nonlocal scatter to local scatter. Nie et al. [22] proposed neighborhood min–max projections (NMMP) by introducing discriminant information into the local structure. Zhang et al. [23] proposed complete global–local LDA (CGLDA) to incorporate three kinds of local information into LDA. Gao et al. [24] proposed joint global and local structure discriminant analysis (JGLDA), which used two quadratic functions to characterize the geometric properties of similarity and diversity of data. In the literature [25], the authors proposed elastic preserving projections (EPP) which considers both the local structure and the global information of data. Luo et al. [26] added the discriminant information and orthogonal constraint into EPP, and proposed discriminant orthogonal elastic preserving projections (DOEPP). To overcome the singular problem of EPP, exponential EPP (EEPP) [27] was proposed. These methods usually share underlying commonality that they integrate both the nonlocal (global) and local structure into the objective function of feature extraction.

Sparse representation has received considerable interest in recent years, especially in image recognition [28,29,30]. The main idea of sparse representation is that a given sample can be represented as a linear combination of the others. The coefficients obtained by sparse representation reflect the contributions of the samples to reconstruct the given sample. The most popular feature extraction methods based on sparse representation include sparsity preserving projection (SPP) [31], discriminant sparse neighborhood preserving embedding (DSNPE) [32], and discriminant sparse local spline embedding (D-SLSE) [33]. In general, they have achieved better performance than the conditional methods. But, all of them must solve the L1-norm minimization problem to construct the sparse weight matrix, so that their computational complexity is excessively high [34]. Recently, objective functions based on complex-norm have been explored, and they are widely used in different fields [35,36,37,38].

Motivated by the above works, we propose a novel supervised feature extraction algorithm called sparsity regularization discriminant projection (SRDP). Specially, SRDP first constructs a concatenated dictionary through the class-wise PCA decompositions and learns the sparse representation structure of each sample. Then SRDP utilizes the learned sparse representation structure as an additional regularization term of UDP so as to construct a new discriminant function. Finally, SRDP is transformed into a generalized eigenvalue problem. Our primary contributions can be summarized as follows:

  1. 1.

    We proposed a novel feature extraction algorithm, called SRDP, to learn the discriminant features of data. SRDP considers both the nonlocal and local structure of data, and simultaneously preserves the sparse representation structure.

  2. 2.

    Compared to UDP, SRDP is a supervised method and can alleviate the small sample size problem (SSS) by introducing the sparse regularization term.

  3. 3.

    Under the concatenated dictionary constructed by class-wise PCA decom-positions, the sparse coefficient in SRDP can be obtained quckly via matrix–vector multiplication. So, its computational complexity is significantly less than other algorithms based on sparse representation via L1-norm optimization, such as SPP and DSNPE.

  4. 4.

    Unlike LPP, EPP, and DOEPP, SRDP considers the local structure twice. The first time is in learning the sparse representation. This is because the sparse representation can implicitly discover the local structure of data. The second time is in constructing the adjacency graph by K nearest neighbors. This adjacency graph also characterizes the locality of samples.

The rest of this paper is organized as follows. We briefly review the SPP and UDP algorithm in Sect. 2. In Sect. 3, we introduce the proposed SRDP algorithm in detail. In Sect. 4, extensive experiments are carried out to demonstrate the effectiveness of the proposed method. Finally, Sect. 5 concludes the paper.

2 Review of the Related Work

2.1 Sparsity Preserving Projections

SPP [31] attempts to preserve the sparse reconstruction relationship of samples. Given a sample set \( {\mathbf{X}} = \left\{ {\varvec{x}_{1} ,\varvec{x}_{2} , \ldots ,\varvec{x}_{N} } \right\} \in\mathbb{R}^{D \times N} \), where D is the number of features and N is the number of samples. SPP first learns the sparse coefficient vector \( {\mathbf{s}}_{\text{i}} \) for each sample \( \varvec{x}_{i} \) by solving the following L1-norm minimization problem:

$$ \begin{aligned} & \hbox{min} \left\| \varvec{s}_{i} \right\|_{1} \\ & {\text{s}} . {\text{t}} .\quad \varvec{x}_{i} = \varvec{Xs}_{i} , 1 { = 1}^{\text{T}} \varvec{s}_{i} \\ \end{aligned} $$
(1)

where \( \left\| \cdot \right\|_{1} \) is the L1-norm and \( \varvec{1} \in\mathbb{R}^{N} \) is a vector of all ones. Once all the coefficient vectors \( {\mathbf{s}}_{\text{i}} ({\text{i}} = 1,2, \ldots ,{\text{N}}) \) are computed, the sparse reconstruction weight matrix S can be obtained by

$$ {\mathbf{S}} = \left[ {{\mathbf{s}}_{ 1} ,{\mathbf{s}}_{ 2} , \ldots ,{\mathbf{s}}_{\text{N}} } \right] $$
(2)

Finally, based on the weight matrix S, the objective function of SPP can be represented as:

$$ { \hbox{min} }_{\varvec{w}} \frac{{{\mathbf{w}}^{\text{T}} {\mathbf{X}}\left( {{\mathbf{I}} - {\mathbf{S}} - {\mathbf{S}}^{T} + {\mathbf{S}}^{T} {\mathbf{S}}} \right){\mathbf{X}}^{\text{T}} {\mathbf{w}}}}{{{\mathbf{w}}^{\text{T}} {\mathbf{XX}}^{\text{T}} {\mathbf{w}}}} $$
(3)

The optimal projection vector w can be obtained by solving for the eigenvector corresponding to the smallest eigenvalue in the generalized eigenvalue equation:

$$ {\mathbf{X}}\left( {{\mathbf{I}} - {\mathbf{S}} - {\mathbf{S}}^{T} + {\mathbf{S}}^{T} {\mathbf{S}}} \right){\mathbf{X}}^{\text{T}} {\mathbf{w}} = \lambda {\mathbf{XX}}^{\text{T}} {\mathbf{w}} $$
(4)

Seen from Eqs. (1) and (2), SPP has to resolve N time-consuming L1-norm minimization problems to obtain the sparse weight matrix S, such that its computational complexity reaches up to \( O\left( {N^{4} } \right) \), which is excessively high in real applications. Besides, the matrix \( {\mathbf{XX}}^{\text{T}} \) is always singular since the training sample size is much smaller than the feature dimensions.

2.2 Unsupervised Discriminant Projection

UDP [21] incorporates the advantage of both the locality and nonlocality of samples. A concise criterion for feature extraction can be obtained by maximizing the ratio of nonlocal scatter to local scatter. The local scatter matrix is defined by

$$ {\mathbf{S}}_{L} = \frac{1}{2}\mathop \sum \limits_{i,j} \left( {\varvec{x}_{i} - \varvec{x}_{j} } \right)\left( {\varvec{x}_{i} - \varvec{x}_{j} } \right)^{T} H_{ij} $$
(5)

where \( H_{ij} \) is defined as

$$ H_{ij} = \left\{ {\begin{array}{*{20}c} {1, } & { if \varvec{x}_{j} \in O\left( {K,\varvec{x}_{i} } \right)} \\ {0,} & {otherwise} \\ \end{array} } \right. $$
(6)

where \( {\text{O}}\left( {K,\varvec{x}_{i} } \right) \) denotes the set of K nearest neighbors of \( \varvec{x}_{i} \).

Similarly, the nonlocal scatter matrix can be defined by

$$ {\mathbf{S}}_{N} = \frac{1}{2}\mathop \sum \limits_{i,j} \left( {\varvec{x}_{i} - \varvec{x}_{j} } \right)\left( {\varvec{x}_{i} - \varvec{x}_{j} } \right)^{T} (1 - H_{ij} ) $$
(7)

UDP then optimizes:

$$ { \hbox{max} }_{\varvec{w}} \frac{{{\mathbf{w}}^{\text{T}} {\mathbf{S}}_{N} {\mathbf{w}}}}{{{\mathbf{w}}^{\text{T}} {\mathbf{S}}_{L} {\mathbf{w}}}} $$
(8)

Generally, the number of training samples is always less than their features. This results in that UDP suffers from the SSS problem. In addition, UDP does not exploit the sparse representation structure of data, which is important for improving classification tasks.

3 Sparsity Regularization Discriminant Projection

In this section, we introduce the proposed SRDP in detail. SRDP can be regarded as the combiner of sparse representation and UDP. But differing from UDP, it considers the sparse representation structure of data, and avoids the SSS problem by introducing the sparse regularization term. And differing from sparse representation based methods, such as SPP and DSNPE, SRDP significantly reduces the computational complexity of learning the sparse representation structure via a concatenated dictionary rather than solving the L1-norm optimization.

3.1 Constructing the Concatenated Dictionary and Learning the Sparse Representation Structure

Given a set of training samples \( {\mathbf{X}} = \left[ {\varvec{x}_{1} ,\varvec{x}_{2} , \ldots ,\varvec{x}_{N} } \right] \), where \( \varvec{x}_{i} \in\mathbb{R}^{D} \). Now, we categorize the samples as \( {\mathbf{X}} = \left[ {\varvec{X}_{1} ,\varvec{X}_{2} , \ldots ,\varvec{X}_{C} } \right] \), where C is the number of classes, and \( \varvec{X}_{i} \in\mathbb{R}^{{D \times N_{i} }} \) contains the samples from class i. For the convenience of relevant calculations, we first center the samples from each class at the origin, \( \bar{\varvec{X}}_{\text{i}} = \left[ {\varvec{x}_{1} - \mu_{i} ,\varvec{x}_{2} - \mu_{i} , \ldots ,\varvec{x}_{{N_{i} }} - \mu_{i} } \right] \) (i = 1, 2,…,C), where \( \mu_{i} \) is mean of samples belonging to class i. Then we conduct PCA decomposition for each class \( \varvec{X}_{i} \), whose objective function is

$$ \mathop {\hbox{max} }\nolimits_{{{\left\| \mathbf{d} \right\|} = 1}} {\mathbf{d}}^{T} {\varvec{\Phi}}_{i} {\mathbf{d}} $$
(9)

where \( {\varvec{\Phi}}_{i} \) is the covariance matrix of \( \bar{\varvec{X}}_{\text{i}} \). For each class i, \( N_{i} \) principal components are selected to construct \( {\mathbf{D}}_{i} = \left[ {\varvec{d}_{1} ,\varvec{d}_{2} , \ldots ,\varvec{d}_{{N_{i} }} } \right] \). Thus, a sample \( \varvec{x} \) from class i can be represented by

$$ \varvec{x} = {\mathbf{D}}_{i} {\mathbf{s}}_{i} = \left[ {\varvec{D}_{1} ,\varvec{D}_{2} , \ldots ,{\mathbf{D}}_{i - 1} ,{\mathbf{D}}_{i} ,{\mathbf{D}}_{i + 1} , \ldots ,\varvec{D}_{C} } \right]{\tilde{\mathbf{s}}} = {\mathbf{D}\tilde{\mathbf{s}}} $$
(10)

where D is the concatenated dictionary constructed by PCA decompositions, and it consists of all \( {\mathbf{D}}_{i} \left( {{\text{i}} = 1,2, \ldots ,C} \right) \). \( {\tilde{\mathbf{s}}} = \left[ {0^{T} ,0^{T} , \ldots ,0^{T} ,{\mathbf{s}}_{i}^{T} ,\varvec{ }0^{T} , \ldots ,0^{T} } \right]^{T} \) is the sparse co-efficient vector under the concatenated dictionary D.

According to the previous procedure, each sample corresponds to a sparse coefficient vector. From Eq. (10), we find that the computation of \( {\tilde{\mathbf{s}}} \) involves only \( {\mathbf{D}}_{i} \), which is also column orthogonal, so that the sparse coefficient vector \( {\tilde{\mathbf{s}}} \) of any training sample from class i can be quickly learned by matrix–vector multiplication, i.e.

$$ {\tilde{\mathbf{s}}} = \left[ {0^{T} ,0^{T} , \ldots ,0^{T} ,\;\left( {{\mathbf{D}}_{i}^{T} \varvec{x}} \right)^{T} ,\;\varvec{ }0^{T} , \ldots ,0^{T} } \right]^{T} $$
(11)

3.2 Preserving Sparse Representation Structure

As can be seen from Sect. 3.1, the sparse representation structure well encodes the local information of the training samples. It is expected that the sparse representation structure in the original high-dimensional space can be preserved in the low-dimensional projective subspace. Thus, the following objective function is defined to seek a projection that preserves the sparse representation structure:

$$ {\text{J}}_{s} \left( \varvec{w} \right) = { \hbox{min} }_{\varvec{w}} \mathop \sum \limits_{i} \varvec{w}^{T} \varvec{x}_{i} - \varvec{w}^{T} \left. {{\mathbf{D}\tilde{\mathbf{s}}}} \right\|_{{{\text{i}}_{\text{F}} }}^{2} $$
(12)

where \( {\tilde{\mathbf{s}}}_{{i}} \) is the sparse coefficient vector corresponding to \( \varvec{x}_{i} \). With some algebraic operations, Eq. (12) can be rewritten as

$$ \begin{aligned} {\text{J}}_{s} \left( \varvec{w} \right) & = { \hbox{min} }_{\varvec{w}} \mathop \sum \limits_{i} \varvec{w}^{T} \varvec{x}_{i} - \varvec{w}^{T} {\mathbf{D}\tilde{\mathbf{s}}}_{{{\text{i}}_{\text{F}} }}^{2} \\ & = { \hbox{min} }_{\varvec{w}} \varvec{w}^{T} \left( {\mathop \sum \limits_{i = 1}^{N} \left( {\varvec{x}_{i} - {\mathbf{D}\tilde{\mathbf{s}}}_{\text{i}} } \right)\left( {\varvec{x}_{i} - {\mathbf{D}\tilde{\mathbf{s}}}_{\text{i}} } \right)^{T} } \right)\varvec{w} \\ & = { \hbox{min} }_{\varvec{w}} \varvec{w}^{T} \left( {{\mathbf{XX}}^{T} - {\mathbf{XS}}^{T} {\mathbf{D}}^{T} - {\mathbf{DSX}}^{\text{T}} + {\mathbf{DSS}}^{T} {\mathbf{D}}^{T} } \right)\varvec{w} \\ \end{aligned} $$
(13)

where \( {\mathbf{S}} = \left[ {{\tilde{\mathbf{s}}}_{ 1} ,\varvec{ }{\tilde{\mathbf{s}}}_{ 2} , \ldots ,{\tilde{\mathbf{s}}}_{\text{N}} } \right]. \)

3.3 Sparsity Regularization Discriminant Projection

The goal of proposed SRDP aims to find the optimal projections that can, on the one hand, preserve the sparse representation structure, on the other hand, maximize the ratio of nonlocal scatter to local scatter. To this end, we choose to maximize the following criterion:

$$ { \hbox{max} }_{\varvec{w}} \frac{{{\mathbf{w}}^{\text{T}} {\mathbf{S}}_{N} {\mathbf{w}}}}{{\alpha {\mathbf{w}}^{\text{T}} {\mathbf{S}}_{L} {\mathbf{w}} + \left( {1 - \alpha } \right)J_{s} \left( \varvec{w} \right)}} $$
(14)

where \( \alpha (0 < \alpha < 1) \) is a parameter that controls the trade-off between the two terms in numerator, and it can be adjusted if balancing is needed. \( {\mathbf{S}}_{N} \) and \( {\mathbf{S}}_{L} \) are the nonlocal scatter matrix and the local scatter matrix, respectively.

Substituting Eq. (13) into (14), we have

$$ \begin{aligned} & { \hbox{max} }_{\varvec{w}} \frac{{{\mathbf{w}}^{\text{T}} {\mathbf{S}}_{N} {\mathbf{w}}}}{{\alpha {\mathbf{w}}^{\text{T}} {\mathbf{S}}_{L} {\mathbf{w}} + \left( {1 - \alpha } \right)J_{s} \left( \varvec{w} \right)}} \\ & = { \hbox{max} }_{\varvec{w}} \frac{{{\mathbf{w}}^{\text{T}} {\mathbf{S}}_{N} {\mathbf{w}}}}{{\alpha {\mathbf{w}}^{\text{T}} {\mathbf{S}}_{L} {\mathbf{w}} + \left( {1 - \alpha } \right){\mathbf{w}}^{T} \left( {{\mathbf{XX}}^{T} - {\mathbf{XS}}^{T} {\mathbf{D}}^{T} - {\mathbf{DSX}}^{\text{T}} + {\mathbf{DSS}}^{T} {\mathbf{D}}^{T} } \right){\mathbf{w}}}} \\ & = { \hbox{max} }_{\varvec{w}} \frac{{{\mathbf{w}}^{\text{T}} {\mathbf{XS}}_{N} {\mathbf{X}}^{\text{T}} {\mathbf{w}}}}{{{\mathbf{w}}^{\text{T}} \left[ {\alpha {\mathbf{S}}_{L} + \left( {1 - \alpha } \right)\left( {{\mathbf{XX}}^{T} - {\mathbf{XS}}^{T} {\mathbf{D}}^{T} - {\mathbf{DSX}}^{\text{T}} + {\mathbf{DSS}}^{T} {\mathbf{D}}^{T} } \right)} \right]{\mathbf{w}}}} \\ \end{aligned} $$
(15)

Let

$$ {\varvec{\Psi}} = \alpha {\mathbf{S}}_{L} + \left( {1 - \alpha } \right)\left( {{\mathbf{XX}}^{T} - {\mathbf{XS}}^{T} {\mathbf{D}}^{T} - {\mathbf{DSX}}^{\text{T}} + {\mathbf{DSS}}^{T} {\mathbf{D}}^{T} } \right) $$

Then the optimization problem in Eq. (15) can be converted to the following generalized eigenvalue problem:

$$ {\mathbf{S}}_{N} {\mathbf{w}} = \lambda \boldsymbol{\Psi}{\mathbf{w}} $$
(16)

The projection matrix \( \varvec{W} = \left[ {{\mathbf{w}}_{1} ,{\mathbf{w}}_{2} , \ldots ,{\mathbf{w}}_{d} } \right] \) consists of the eigenvectors corresponding to the d largest eigenvalues.

The algorithmic procedure of SRDP can be formally summarized as follows:

  • Input: Training set \( {\mathbf{X}} = \left[ {\varvec{x}_{1} ,\varvec{x}_{2} , \ldots ,\varvec{x}_{N} } \right],\;\varvec{x}_{i}\, \in\mathbb{R}^{D} \left( {i = 1,2, \ldots ,N} \right) \) and the balance parameter \( \alpha \).

  • Output: The projection matrix W

  • Step 1: Calculate \( {\mathbf{S}}_{L} \) and \( {\mathbf{S}}_{N} \) by Eq. (5) and Eq. (7), respectively;

  • Step 2: Conduct PCA decompositions to construct the concatenated dictionary D by Eq. (9);

  • Step 3: Learn the sparse coefficient vector \( {\tilde{\mathbf{s}}} \) for every sample by Eq. (11), and then calculate the sparse reconstruction weight matrix S;

  • Step 4: Calculate \( {\varvec{\Psi}} \), and solve the generalized eigenvalue problem in Eq. (16).

3.4 Computational Complexity Analysis

The computational complexity of SRDP includes four parts: the scatter matrices, concatenated dictionary, sparse coefficient vector, and generalized eigenvalue. The computation of scatter matrices requires \( {\text{O}}\left( {N^{2} *D + D^{2} *N} \right) \). The complexity to construct concatenated dictionary via PCA decompositions is \( {\text{O}}\left( {{\text{D}}^{2} *\mathop \sum \nolimits_{i}^{C} m_{i} } \right) \). The complexity of calculating the sparse coefficient vectors for all samples is \( {\text{O}}\left( {{\text{D*}}\mathop \sum \nolimits_{i}^{C} m_{i} N_{i} } \right) \), where \( N_{i} \) denotes the number of samples in class i. In general,\( C \ll N, m_{i} \ll {\text{N}}, N_{i} \ll N \), so \( {\text{O}}\left( {{\text{D*}}\mathop \sum \nolimits_{i}^{C} m_{i} N_{i} } \right) \ll O\left( {N^{4} } \right) \). This means that the computational complexity of learning the sparse weight matrix in SRDP is much less than that in the algorithms based on sparse representation via L1-norm optimization, such as SPP, DSNPE, and D-SLSE. The complexity for solving the generalized eigenvalue is \( {\text{O}}\left( {{\text{D}}^{3} } \right) \). Finally, we can conclude that the computational complexity of SRDP is \( {\text{O}}\left( {{\text{N}}^{2} *D + D^{2} *N + {\text{D}}^{2} *\mathop \sum \nolimits_{i}^{C} m_{i} + {\text{D*}}\mathop \sum \nolimits_{i}^{C} m_{i} N_{i} + {\text{D}}^{3} } \right) \).

4 Experimental Results

In this section, we make a set of experiments to evaluate the effectiveness of the proposed SRDP for feature extraction, and compare it with several popular algorithms, including LPP, UDP, EPP, DOEPP, and SPP. Five benchmark databases are used in our experiments: ORL database [39], Yale database, CMU PIE database [40], FERET database [41] and LFW database [42]. Note that, to overcome the SSS problem, LPP, UDP, EPP, and SPP all involve a PCA phase. In this phase, we keep 98% data energy. For LPP, UDP, EPP, DOEPP, and SRDP, the K-nearest neighborhood parameter K is set to l − 1, where l denotes the number of training samples per class. In DOEPP, we set α = 0.5 and β = 1, respectively. The value of \( \alpha \) in SRDP is empirically set to be 0.1 in all experiments. After all the methods have been adopted to extract low-dimensional feature, the nearest neighbor classifier with Euclidean matrix is employed to perform classification task.

4.1 Experiments on ORL Database

The ORL database contains 400 images of 40 individuals, and each individual has ten images. The face images are captured at different times and have different variations including illumination, expressions (open or closed eyes, smiling or non-smiling) and facial details (glasses or no glasses). In our experiments, each image was resized to 32 × 32. Some samples from this database are shown in Fig. 1.

Fig. 1
figure 1

Ten sample images of one person in ORL database

Full size image

First, in order to demonstrate the performance of each method with varying number of training samples, we randomly selected l (l = 4, 5, 6, 7) images per person for training, and the rest images for testing. For each giving l, the experiments are independently performed 20 times. Table 1 presents the best average recognition results and the corresponding dimensions for each method. As can be seen from Table 1, SRDP can get the best recognition rates in all experiments.

Table 1 The best average recognition accuracy (%) and the corresponding dimension on ORL database
Full size table

Second, to report the computational time (C-T) of different methods on ORL database, the first five images per person are selected for training and the remaining images are used for testing. The C-T is represented by the whole operation time for training and classification. The results are shown in Table 2. From the results, we can see three main points. First, LPP is the fastest in all methods. Second, SPP is slower than all other methods. This is probably because it needs to learn the sparse weight matrix by L1-norm optimization, which is time-consuming. Third, SRDP and UDP are comparable in C-T.

Table 2 Comparison of computational time (s) on ORL database
Full size table

4.2 Experiments on Yale Database

The Yale database contains 165 gray scale face images from 15 individuals. The images demonstrate variations in lighting condition and facial expression (happy, normal, sad, sleepy, surprised, and wink). In the experiments, each image was resized to \( 32 \times 32 \). Figure 2 shows the sample images of one individual.

Fig. 2
figure 2

Sample images of one individual in Yale database

Full size image

First, the projected subspaces learned by LPP, EPP, DOEPP, SPP, UDP, and SRDP are different. Thus, all images in the Yale database are used to learn such spaces spanned by the eigenvectors of the corresponding algorithms. The first eight basis vectors of different algorithms are presented in Fig. 3. It can be seen that SRDP learns a set of basis images that are different from those of the other algorithms.

Fig. 3
figure 3

First eight basis images of different methods: a LPP, b EPP, c DOEPP, d SPP, e UDP, and f SRDP

Full size image

In the next experiments, we randomly select l (l = 5, 8) images per person to form the training set, and the rest are used for testing. Note that there is no overlap between the training and test sets. For each l, we average the results over 20 random splits. The performances of each method are shown in Table 3. The recognition curves versus the dimension of reduced space for each algorithm are shown in Fig. 4. From Fig. 4, we find that, when the dimension is very low, DOEPP performs better than SRDP. This is because forcing an orthogonal relationship between the projection vectors is useful for preserving the structure of data. But with the increase of dimension, SRDP becomes superior to DOEPP. This is probably due to the fact that when the number of projection vector turns to be larger, sparsity representation has an apparent advantage over orthogonal relationship. In general, SRDP can obtain the best recognition rates in the recognition tasks.

Table 3 The optimal recognition accuracy (%) and the corresponding dimension on Yale database
Full size table
Fig. 4
figure 4

Recognition accuracy versus feature dimension on Yale database for (left) 5 train and (right) 8 train

Full size image

4.3 Experiments on CMU PIE Database

The CMU PIE face database contains more than 40,000 face images of 68 individuals. The face images were captured under varying pose, illumination and expression. In our experiments, a subset (C27) which contains about 3329 images of 68 individuals was used. Similarly, all the images were cropped to the solution of \( 32 \times 32 \) in our experiments. Some image samples are shown in Fig. 5.

Fig. 5
figure 5

Sample images of one person in CMU PIE database

Full size image

In the experiments, l (l = 5, 10) images per person are selected for training and the rest are used for testing. For each l, we average the results over 20 random splits. To be fair, the reduced feature dimension is searched from 1 to 40. The best average recognition results and the corresponding dimensions for each method are shown in Table 4. The recognition curves versus the dimension of reduced space for each algorithm are shown in Fig. 6. It can be found that, SRDP and SPP perform better than other methods. This is because sparse representation can improve the robustness to illumination. On the other hand, with the increase of dimension, SRDP tends to be more stable than SPP. This is induced by considering the local and non-local structure of data.

Table 4 The optimal recognition accuracy (%) and the corresponding dimension on CMU PIE database
Full size table
Fig. 6
figure 6

Average recognition rate versus the dimension of reduced space on CMU PIE database for (left) 5 train and (right) 10 train

Full size image

4.4 Experiments on FERET Database

The FERET database comprises a total of 11,338 facial images of 994 distinct individuals. The size of the images is of 512 × 768 pixels. In our experiments, we select a subset which includes 1200 images of 200 different subjects from the FERET face database. Figure 7 shows the samples of two subjects in the FERET subset. The images named “a” are frontal view. The images named “b”, “c”, “d”, and “e”, denote the variation of face in view. The images named “f” are smiling and frontal view. For the sake of efficient computation, each image was manually cropped and scaled to \( 40 \times 40 \) pixels.

Fig. 7
figure 7

Sample images of two subjects in the FERET subset

Full size image

To evaluate the performance of different methods, we design two tests called Test #1 and Test #2. In Test #1, the training set contains “a”, “b”, and “d”, and the test set contains “c”, “e”, and “f”. In Test #2, the training set contains “b”, “c”, “d”, and “e”, and the test set contains “a” and “f”. Table 5 gives the optimal correct recognition rates of each method in two tests.

Table 5 The optimal recognition accuracy (%) and the corresponding dimension on FERET database
Full size table

4.5 Experiments on LFW Database

The LFW (Labeled faces in the Wild) database is designed for studying the problem of the unconstrained face verification task. It contains more than 13,000 images from 5749 people. All the images are collected from web, and the image number of each subject is different. Our experiments are made on a set of 600 images referring to 60 subjects (10 images for each subject). For each image, we first extract the face area, and then resize it to 32 × 32 pixels. Figure 8 shows some sample images and the extracted face area from LFW database. In the experiments, 50% of the images of each subject are used for training and the rest for testing. Table 6 gives the recognition accuracy and the corresponding dimension of different methods. As shown in Table 6, the recognition accuracies of all methods are relatively low. This is because the images have great variations in age, pose, lighting and expression. But SRDP has an apparent advantage.

Fig. 8
figure 8

Sample images in LWF database and the face area is in the red bounding box

Full size image
Table 6 Performance of different methods on LFW database
Full size table

4.6 Discussion

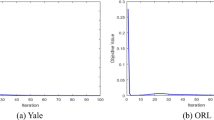
To further explore the influence of \( \alpha \) in SRDP, we conduct experiments on ORL and Yale databases. To be fair, the reduced dimension is set to 40. \( \alpha \) is searched from 0.1 to 0.9. Figure 9 presents the recognition accuracy of SRDP under different values of \( \alpha \). As seen from Fig. 9, the value of \( \alpha \) takes influence on the performance of SRDP. Moreover, it can be seen that the results in the case of \( \alpha = 0.1 \) is usually comparable to the best result among other values.

Fig. 9
figure 9

Recognition accuracy of SRDP for varying \( \alpha \) on ORL and Yale databases

Full size image

From the experiments above, the following observations are obtained:

  1. 1.

    Seen from Table 2, SRDP is faster than SPP. This is because SRDP learns the sparse structure through matrix–vector multiplication rather than solving the L1-norm optimization.

  2. 2.

    From Table 4, it can be found that, sparse representation based feature extraction methods, i.e. SPP and SRDP, performs better than other methods in the experiments on CMU PIE database, where there are variations in illumination. This is because the sparse representation structure can improve the robustness to illumination.

  3. 3.

    SRDP can obtain the best results in most experiments. This is probably because SRDP well encodes the local, non-local, and sparse representation structure.

5 Conclusions

In this paper, we propose a novel feature extraction algorithm, called sparsity regularization discriminant projection (SRDP). SRDP first uses the class-wise PCA decompositions to construct a concatenated dictionary under which the sparse representation structure of each sample can be learned. Then SRDP regards the sparse representation structure as an additional regularization term so as to construct a new discriminant function. Finally, SRDP is transformed into a generalized eigenvalue problem. The experimental results on five real datasets have demonstrated the effectiveness of the proposed method.