1 Introduction

Feature selection and extraction, which have received extensive attention in recent years, play an important role in pattern classification [10, 14, 41]. However an image raw data contains a large number of redundant features and noise, which make difficult for image recognition and image analysis. [18, 19, 27]. In this case, for classification tasks, how to select and extract the different categories of the most significant features in the whole exercise is among the most difficult. It has proven that feature selection and extraction are effective tools in the field of machine learning and pattern classification. They can reduce the complexity, increase the efficiency and enhance the classification performance [20, 25, 26].

Whether it is feature selection or feature extraction, to a certain extent, they both are subspace learning methods [2, 11, 13]. They have common goal in finding a low-dimensional representation of the original high-dimensional data in a new learning space [28, 30, 33].

Various methods of feature extraction have been proposed in the past few decades. In this branch, principal component analysis (PCA) [38] is one of the most famous method, its main idea is to try to learn a projection that can preserve the main energy of the original data. Local preserving projection (LPP) [7], sparse preserving projection (SPP) [24] and neighborhood preserving embedding (NPE) [8] which they learn their projections are also feature extraction methods, these methods consider the local manifold geometry of the original data and try to preserve the local information in the projection space [4, 16, 29]. Subsequently, classifiers, such as K Nearest Neighbor (KNN) [42] and Support Vector Machine (SVM) [3], are usually used for classification. Although the above methods don’t use the label information of the data, have different advantages, the classification performance of these algorithms are not good enough to some extent.

In fact, we hope that dimensionality reduction can be achieved for data with category labels (supervised), and each category can be better distinguished after dimensionality reduction. At this time, another classic feature extraction algorithm-linear discriminant analysis (LDA) appeared [43]. LDA is a classic linear learning method. The idea of linear discrimination is simple but very effective. LDA can greatly expand the distance between classes and reduce the distance within classes. And through the use of label information to learn discriminant projection, which improves the classification accuracy [9, 17, 40].To enhance performance and efficiency, many variants based on LDA are proposed [5, 12, 15] such as orthogonal LDA (OLDA) [31], unrelevant LDA (ULDA) [32]. OLDA and ULDA transform the image into a vector for learning projection, which aim to solve the problem of small LDA sample size. However, these methods, which based on LDA in the calculation of the L2 norm scatter matrix, may cause the error seriously, and these methods are sensitive to outliers [1, 34, 44]. Later, sparse linear discriminant analysis (SLDA) [23] and sparse uncorrelated linear discriminant analysis (SULDA) [39] are proposed to learn sparse discriminant subspace for feature extraction. Robust Adaptive Linear Discriminant Analysis (RALDA) [6] method achieved an appropriate latent subspace for data representation where L2,1 norm is adopted in the formulations of loss function,which the regularization term can reduce the impact of outliers and noise and predict the select discriminative features. Later, Ning et.al. proposed a method named BULDP: Biomimetic Uncorrelated Locality Discriminant Projection for Feature Extraction in Face Recognition, it is based on unsupervised discriminating projection and two human bionic where in: homologous and isomeric principle of continuity principle of similarity [21]. Later, Ning et.al. proposed Real-time 3D Face Alignment Using an Encoder-Decoder Network with an Efficient Deconvolution Layer [22]. Zhang et.al. proposed a new iterative reweight-based log-sum constraint channel estimation scheme. it used the structure sparsity of the mmWave channels by formulating the channel estimation problem as an objective optimization problem. [35].Later, Zhang et.al. proposed Block-Sparsity Log-Sum-Induced Adaptive Filter for Cluster Sparse System Identification The main idea of the proposed scheme is to add a new block-sparsity induced term into the cost function of the LMS algorithm [36]. In addition, he proposed Block-Sparsity Log-Sum-Induced Adaptive Filter for Cluster Sparse System Identification [37] . The main idea is to add a sparsity lp norm penalty cost function of the LMS algorithm.

However, LDA has some obvious disadvantages. Firstly, each new feature combined with others, which the most of projection coefficients are not zero. The learned projection matrix cannot explain the features well. This also shows that LDA cannot select the most useful function from redundant data. Secondly, LDA selects k feature vectors as the projection of feature extraction, and the selected k feature vectors will have a one-to-one correspondence with the first k smallest feature values, and the number of k is related to the data. For dimensionality reduction, this makes the choice of the classification accuracy of linear discriminant analysis sensitive. Thirdly, LDA, and many methods based on linear discriminant analysis are sensitive to noise.

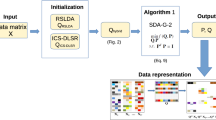
In order to overcome this problem, a new robust sparse manifold discriminant analysis (RSMDA) algorithm is proposed for dimension reduction. Especially, the proposed RSMDA method uses L2,1 norm based sparse constraint to choose the important feature. At the same time, the manifold based local discrimination information is added on the basis of the original linear discrimination analysis. The innovations of this article mainly include the following aspects.

  1. (1)

    The most useful and discriminative features can be selected by introducing the L2,1 norm.

  2. (2)

    Compared with other methods based on linear discriminant analysis, the proposed method is more robust to noise.

  3. (3)

    By introducing the local discriminative information, the sparse projection can use the local identification information to enhance the discrimination of projection.

The remaining chapters of this article are specifically arranged as follows. Section 2 mainly reviews some related work. The third part describes the robust discriminant analysis of sparse manifolds in detail and gives the optimal iterative scheme of RSMDA. In Section 4, There are a large number experiments on different libraries to prove the good performance. Section 5 gives the corresponding conclusion.

2 Related work

In this section, we will briefly review the research work, which mainly includes LDA and manifold based local discriminant information learning. For convenience, Table 1 introduce some notations used through the paper.

Table 1 Significant Notations Annotated in This Paper
Full size table

2.1 Linear discriminant analysis (LDA)

Suppose there are c pattern classes, ni represents the number of samples of the ith class, \( \mathrm{n}={\sum}_{i=1}^c \) is the total number of all samples, column vector \( {x}_j^i\in {R}_m \) denotes the jth sample of the ith class. LDA tries to find a projection matrix, which makes the samples in the same category as close as possible, and makes the samples in different categories are as far away as possible. LDA uses the following fisher to obtain this projection vector.

$$ \mathrm{a}=\arg \kern0.33em \underset{a}{\max}\frac{a^T{S}_ba}{a^T{S}_wa} $$
(1)

where Sb is the inter-class scatter matrix, and Sw is the intra-class scatter matrix. Sb and Sw are calculated as following.

$$ {S}_b=\frac{1}{n}{\sum}_{i=1}^c{n}_i\left({u}_i-u\right){\left({u}_i-u\right)}^T $$
(2)
$$ {S}_w=\frac{1}{n}{\sum}_{i=1}^c{n}_i{\sum}_{j=1}^{n_i}\left({x}_j^i-{u}_i\right){\left({x}_j^i-{u}_i\right)}^T $$
(3)

where \( {u}_i=\frac{1}{n_i}{\sum}_{j=1}^{n_i}{x}_j^i \) is the mean feature of samples of the ith class, \( {u}_i=\frac{1}{n_i}{\sum}_{i=1}^c{\sum}_{j=1}^{n_i}{x}_j^i \) is the mean feature of all samples. Generally, problem (1) is equivalent to the following optimization problem .

$$ {\displaystyle \begin{array}{c}a=\mathrm{argmin}{a}^T\left({S}_w-\mu {S}_b\right)a\\ {}s.t.\kern0.33em {a}^Ta=I\end{array}} $$
(4)

where μ is a small positive constant.

By solving Eq.(4), we can observe that the optimal projection vector a, it is the eigenvector corresponding to the minimum eigenvalue of Swa = μSba. Generally, a single projection vector is not enough to distinguish multiple classes. In real world applications, we usually select a set of projection vectors which satisfy the optimal Fisher criterion \( A=\arg \kern0.33em \underset{A^TA=1}{\min }T\mathrm{r}\left({A}^T\left({S}_{\mathrm{w}}-\mu {S}_b\right)A\right) \) for multiclass classification. The projection matrix X is selected as a set of eigenvectors corresponding to the first k smallest eigenvalues of SwA = λSbA. Let A = [a1, a2, .., ak] ∈ Rm × k be the set of the selected k eigenvectors, we can obtain discriminative feature vector \( {y}_j^i\in {R}^k \) of each sample by \( {y}_j^i={A}^T{x}_j^i \).

2.2 Local manifold learning

The nearest neighbor graph G is first constructed and its weight matrix is defined as follows:

$$ {W}_{ij}=\left\{\begin{array}{c}1,\kern0.66em if\kern0.33em {x}_i\in N\left({x}_j\right)\kern0.33em or\kern0.33em {x}_j\in N\left({x}_i\right)\\ {}0,\kern0.66em otherwise\end{array}\right. $$
(5)

where N(∙) is a set of k nearest neighbors, the nearest neighbor graph G is divided into two graphs, i.e., within-class graph Gw and between-class graph Gb for extracting local discriminant information of samples. For each sample xi, its k nearest neighbors are split into two subsets, Nw(xi) and Nb(xi). Nw(xi) contains the neighbors sharing the same label with xi, whereas Nb(xi) contains the neighbors that have different labels. Let Ww and Wb be the weight matrices of Gw and Gb, respectively. Let Ww and Wb be the weight matrices of Gw and Gb, respectively. In each of the graphs defined above, if two samples have a nonzero weight, then they are referred to as connected samples. It is clear to see that W = Ww + Wb. In this way, the conversion matrix A can map samples from the original sample space to the label space.The result is that the connected samples of Gw stay as close together as possible, while the connected samples of Gb stay as far as possible. Given a map as fi = xiA (i = 1, …, n), it should satisfy the following objective functions:

$$ \min \sum \limits_{ij}{\left\Vert {f}_i-{f}_j\right\Vert}^2{W}_{ij}^w $$
(6)
$$ \max \sum \limits_{ij}{\left\Vert {f}_i-{f}_j\right\Vert}^2{W}_{ij}^b $$
(7)

In Eq. (6), if xi and xj are close and have the same label, then fi and fj should be close as well. In Eq. (7), if xi and xj are close but have different labels, then fi and fj should be far from each other. (6) and (7) can be converted into

$$ \kern0.99em \min \sum \limits_{ij}{\left\Vert {f}_i-{f}_j\right\Vert}^2{W}_{ij}^w=\min Tr\left({A}^T{X}^T{L}_w XA\right) $$
(8)
$$ \kern0.99em \max \sum \limits_{ij}{\left\Vert {f}_i-{f}_j\right\Vert}^2{W}_{ij}^b=\max Tr\left({A}^T{X}^T{L}_b XA\right) $$
(9)

where Lw and Lb are the Laplacian matrix of Gw and Gb. They are defined as Lw = Dw − Ww, Lb = Db − Wb. Dw and Db are diagonal matrices, which their diagonal entries are \( {D}_{ii}^w={\sum}_j{W}_{ij}^w \) and \( {D}_{ii}^b={\sum}_j{W}_{ij}^b \).

Finally, the Eqs. (8) and (9) can be rewritten as

$$ {\displaystyle \begin{array}{c}\underset{\mathrm{A}}{\min}\left( Tr\left({A}^T{X}^T{L}_w XA\right)- Tr\left({A}^T{X}^T{L}_b XA\right)\right)\\ {}=\underset{\mathrm{A}}{\min } Tr\left({A}^T{X}^T\left( Lw-{L}_b\right) XA\right)\end{array}} $$
(10)

3 Robust sparse manifold discriminant analysis (RSMDA)

In this section, the motivation of our RSMDA is firstly introduced. Then the optimization solution of RSMDA is given.

3.1 The motivation of RSMDA

The main object of LDA is projection. The advantage of this algorithm is that the projection, it shortens the projection distance of the same type of sample, and it can also increase the distance of different types of samples. But the LDA also has its design defects. Most of the projection coefficients are non-zero, and the new feature samples are linear combinations of all sample features, which leads to the lack of good explanatoryness of the projective matrix to the characteristics, which is reflected in the following aspects. First of all, LDA does not have a good explanation for matrix features, but it cannot select the most suitable function in a large amount of redundant data. Second, when LDA selects k eigenvector corresponding to the first k minimum eigenvalue as a feature extraction projection, it is greatly affected by the data, and the LDA data classification varies greatly. This leads to great differences in LDA classification accuracy of different sizes. Third, most LDA-based implementation methods cannot be ignored by external environmental impacts, such as many methods that are vulnerable to noise. In this paper, we propose a robust sparse manifold discriminant analysis (RSMDA) to solve the above problems.

At the same time, in practical applications, the acquired data is generally high-dimensional. Data contains a large amount of redundant information, and some noise can corrupt data or images. Therefore, the choice of those essential features from the original complex data discriminant analysis in the whole learning process is vital, because it can effectively reduce the negative impact caused by redundant features. Applying a sparse norm constraint projection allows the model to perform feature selection, such as the L2,1 norm. The L2,1 norm has good line sparsity compared with the L1 norm, precisely because of its property, which makes it easier for the projection to interpret elements. Sparse projection discrimination information can grasp the local identification of the projection to extend. At the same time, we are concerned about the situation of random noise. We use this term to compensate for the noise sparse so that can reduce the negative impact to some extent. Inspired by this motive, we recommend learning more powerful by using the following constraints discrimination subspace

$$ {\displaystyle \begin{array}{c}\underset{P,Q,E}{\min }T\mathrm{r}\left({Q}^T\left({S}_w-\mu {S}_b\right)Q\right)\kern0.33em +{\lambda}_1{\left\Vert Q\right\Vert}_{2,1}+{\lambda}_2{\left\Vert E\right\Vert}_1\\ {}s.t.X=P{Q}^TX+E,{P}^TP=I\end{array}} $$
(11)

where Q ∈ Rm × d(d < m) is divided into scattering matrices between different classes and within the same class. λ1 and λ2 are trade-off parameters, μ is a small positive constant used to balance the importance of Sb and Sw. LDA realizes maximizing the interclass scattering matrix Sw and minimizing the internal class scattering matrix Sb according to the balanced optimization projection matrix. E represents errors and it is used to simulate random noise. ‖⋅‖1 is the L1 norm. In some cases, X = PQTX and PTP = I can be regarded as variants of PCA, which has the advantage that the original data can be recovered well. P ∈ Rm × d is an orthogonal reconstruction matrix. By reconfiguring the relationship between the sample and the original sample that is considering conversion, on a reduced dimension, the transformed data can be retained as much as possible the main energy of the original data. In this way, RSMDA not only learn discriminant subspace, but also learn optimization framework with the minimum loss of information, it is possible to perform better.

The research shows that the discriminant analysis method based on global structure information ignores the local information of the image. On the basis of manifold technology, the original image is reduced and dimensionally processed, the local data manifold structure in the nonlinear sub-manifold can be better maintained. By introducing the manifold based local discriminative information, the objective function of the proposed RSMDA can be rewritten as follows.

$$ {\displaystyle \begin{array}{c}\underset{P,Q,E}{\min }T\mathrm{r}\left({Q}^T\left({S}_w-\mu {\mathrm{S}}_b\right)Q\right)+T\mathrm{r}\left({Q}^T{X}^T\left({L}_w-{L}_b\right) XQ\right)\\ {}+{\lambda}_1{\left\Vert Q\right\Vert}_{2,1}+{\lambda}_2{\left\Vert E\right\Vert}_1\\ {}s.t.X=P{Q}^TX+E,\kern0.43em {P}^TP=I\end{array}} $$
(12)

3.2 Optimization of RSMDA

In this section, we propose an iterative algorithm to update the rules to solve the optimal solution in eq. (12). Since the objective function is non-convex and contains four different variables. It’s difficult for us to get the global optimal solution. Therefore, we can obtain the local optimal solution through continuous iteration. First of all, we use the Lagrange function to convert the problem (12) to the following form.

$$ {\displaystyle \begin{array}{c}L\left(P,Q,E,Y\right)= Tr\left({Q}^T\left( Sw-\mu {\mathrm{S}}_b\right)Q\right)+ Tr\left({Q}^T{X}^T\left({L}_w-{L}_b\right) QX\right)\\ {}+{\lambda}_1{\left\Vert Q\right\Vert}_{2,1}\kern0.33em +{\lambda}_2{\left\Vert E\right\Vert}_1+\left\langle Y,X-{Q}^TX-E\right\rangle \\ {}+\frac{\beta }{2}{\left\Vert X-P{Q}^TX-E\right\Vert}_F^2\\ {}= Tr\left({Q}^T\left({S}_w-\mu {\mathrm{S}}_b\right)Q\right)+ Tr\left({Q}^T{X}^T\left({L}_w-{L}_b\right) QX\right)\\ {}+{\lambda}_1{\left\Vert Q\right\Vert}_{2,1}\kern0.66em +{\lambda}_2{\left\Vert E\right\Vert}_1-\frac{1}{2\beta }{\left\Vert Y\right\Vert}_F^2\\ {}+\frac{\beta }{2}{\left\Vert X-P{Q}^TX-E+\frac{Y}{\beta}\right\Vert}_F^2\\ {}\kern0.99em \end{array}} $$
(13)

where β is a penalty parameter, Y is the Lagrangian multiplier.Then P, Q, E can be alternately solved by minimizing the Lagrangian function L with other variables fixed. The solution scheme is as follows.

  • Fix other variables to update Q

we fix P, E and update Q by solving the following problem

$$ {\displaystyle \begin{array}{c}L(Q)= Tr\left({Q}^T\left({S}_w-\mu {S}_b\right)Q\right)+ Tr\left({Q}^T{X}^T\left({L}_w-{L}_b\right) QX\right)\\ {}+{\lambda}_1{\left\Vert Q\right\Vert}_{2,1}+\frac{\beta }{2}{\left\Vert X-{Q}^TX-E+\frac{Y}{\beta}\right\Vert}_F^2\end{array}} $$
(14)

Define \( X-E+\frac{Y}{\beta }=M \), Q can be calculated by the derivative of L(Q) with respect to Q

$$ \frac{\partial L(Q)}{\partial Q}=2\left( Sw-\mu S\mathrm{b}\right)+{\lambda}_1 DQ+\beta \left(X{X}^TQ-X{M}^T\right) $$
(15)

where D is defined as qi the ith row of Q and \( Q=\left[\begin{array}{c}{q}_1\\ {}\kern0.33em \vdots \\ {}{q}_m\end{array}\right] \). Let ∂L(Q)/∂Q = 0, then we obtain

$$ Q={\left(2\left({S}_w-\mu {S}_b\right)+{\lambda}_1D+\beta X{X}^T\right)}^{-1}\left(\beta X{M}^T\right) $$
(16)

  • Fix other variables to update P

We fix Q E and update P by minimizing the following problem

$$ \underset{P^TP=I}{\min }{\left\Vert X-P{Q}^TX-E+\frac{Y}{\beta}\right\Vert}_F^2 $$
(17)

Let \( X-E+\frac{Y}{\beta }=M \). The optimization (17) is converted to

$$ {\displaystyle \begin{array}{c}\kern0.99em \underset{P^TP=I}{\min }{\left\Vert M-P{Q}^TX\right\Vert}_F^2\\ {}=\underset{P^TP=I}{\min } Tr\left({M}^TM-2{M}^TP{Q}^TX\right)\\ {}=\underset{P^TP=I}{\min } Tr\left({M}^TP{Q}^TX\right)\\ {}=\underset{P^TP=I}{\min } Tr\left({P}^TM{X}^TQ\right)\end{array}} $$
(18)

Problem (18) is an Orthogonal Procrustes problem and it can be simply solved. Suppose SVD(MXTQ) = USVT, then P is obtained as P = UVT, where SVD represents the singular value decomposition operation.

  • Fix other variables to update E

We fix P, Q and update E by solving the following problem.

$$ \underset{E}{\min }{\lambda}_2{\left\Vert E\right\Vert}_1\kern0.33em +\frac{\beta }{2}{\left\Vert X-P{Q}^TX-E+\frac{Y}{\beta}\right\Vert}_F^2 $$
(19)

If we define \( \varepsilon =\frac{\lambda_2}{\beta } \) and \( {E}_0=X-{Q}^TX+\frac{Y}{\beta } \), in according to shrinkage calculator, problem (19) has the closed solution as follows.

$$ E= shrink\left({E}_0,e\right) $$
(20)

where shrink means the shrinkage calculator.

  • Fix other variables to update Lagrange multiplier

Y and β are respectively updated by using the following formulas

$$ Y=Y+\beta \left(X-P{Q}^TX-E\right) $$
(21)
$$ \beta =\min \left(\rho \beta, {\beta}_{\mathrm{max}}\right) $$
(22)

where ρ and βmax are the constant.

3.3 Computational complexity and convergence analysis of RSMDA

We analyze the computational complexity of RSMDA. the major computational cost is the matrix inverse operation. For a m × m matrix, the computational complexity of inverse operation is O(m3). The whole computational complexity of the proposed method is O(τ(m2n + m3 + 2 max(m2; mn)d + d3)), where τ is the iteration number. For simplicity, we suppose that m ≫ n, thus the computational complexity of the proposed method is O(τ(m2n + m3 + 2m2d + d3)).

In this section, two databases are selected to analyze the convergence of the proposed RSMDA. The optimization solution process of RSMDA is realized by iteratively updating three variables. It can be seen from the experimental results in Fig. 1 that the RSMDA algorithm is convergent and converges to the local optimal solution.

Fig. 1
figure 1

The convergence curve of the proposed NMF_ASGR on the two data sets. (a) Yale, (b) ORL

Full size image

4 Experiments

Some experiments have been carried out in this section to prove the good performance of the proposed RSMDA algorithm. This includes classification accuracy, convergence to global optimality, and the effectiveness of high-dimensional image maintenance. In this section, five public image databases are selected to evaluate the effectiveness of the proposed method, KNN and some supervised learning methods, including SVM, LDA, SLDA, OLDA, ULDA, SULDAare chose to compare with the proposed method. At the same time, the accuracy of all test results (AC) is used as a unified evaluation standard. The standard is based on the percentage and actual results of the correct classification results.

4.1 Experiments on the Yale B face database

There are 2432 face images from 38 subjects in the Expanded Yale B Face database. 64 images of faces under different lighting conditions were provided for each subject, and we manually converted each image to a 32 × 32 Gy scale image. One experiment, as show in Fig. 2. which 10, 15, 20 and 25 samples were randomly selected as training samples and the rest as test samples was repeated 10 times, and the classification accuracy of each algorithm was show in Table 2.

Fig. 2
figure 2

Some typical images of the Extended Yale B face database

Full size image
Table 2 Classification accuracy (%) of different methods on the Yale B database
Full size table

Table 2 shows the experimental results obtained by different methods on the extended Yale B database. It can be seen that the proposed RSMDA method has better performance than other supervised learning methods, especially KNN, SVM and LDA.

4.2 Experiments on the CMU PIE face database

There are 41,368 face images from 38 subjects in the CMU PIE face database. These facial images were obtained from 68 subjects in different poses and different lighting conditions. In this experiment, we used a subset of the CMU PIE face database, which contains 11,554 images from 68 subjects. We manually convert each image into a 32 × 32 Gy scale image. Figure 3 shows the sample image of one of them. In this experiment, the training set was the first 10, 15, 20, and 25 images of each person, and the test set was the remaining images. Repeat the algorithm 10 times. The classification accuracy of each algorithm is shown in Table 3.

Fig. 3
figure 3

Some faces images one object from CMU PIE database

Full size image
Table 3 Classification accuracy (%) of different methods on the CMU PIE database
Full size table

It can be seen from Table 3 that as the number of training samples increases, the recognition rates of KNN, SVM, LDA, SLDA, OLDA, ULDA, SULDA and the proposed RSMDA are steadily increasing. Still, no matter how many samples are, the proposed methods perform better than other contrast algorithms. This proves that RSMDA can capture as much discriminative information as possible, which is better than these comparison methods to some extent.

4.3 Experiments on the AR face database

The AR face database contains color face images of 120 people, and the total number of face images exceeds 4000. Among them, 120 subjects were photo graphed twice with different facial expressions, light conditions and shade, with a 14-day interval, and each person produced 26 images. In our experiment, out of 26 facial images of 120 people, seven were selected from each stage, or 14 face images per person. We manually converted each image to 50 by 40 pixels. Figure 4. shows the sample image of one of them. In this experiment, the training set is the first 4, 6, 8, and 12 images of each person, and the test set is the remaining images. Repeat the algorithm 10 times. The classification accuracy of each algorithm is shown in Table 4.

Fig. 4
figure 4

Sample faces images from AR database

Full size image
Table 4 Classification accuracy (%) of different methods on the AR database
Full size table

Table 4 shows the experimental results of different methods on the AR face database. It is clear from the Table 4 that when the number of training samples increases from 6 to 8, the classification accuracy of ULDA and SULDA is decreasing, while the classification accuracy of RSMDA is steadily improving, and no matter how the number of training samples changes, this method achieves the best performance in many methods.

4.4 Experiments on ORL database

The ORL database includes a total of 400 facial images, collected from 40 people, and each person provides 10 facial images. And the images were taken at different times and under a different light. The image content includes different facial expressions and facial details. Figure 5. below shows a sample image of one of them. In this experiment, the training set is the first 3, 4, 5, and 6 images of each person, and the test set is the remaining images. Repeat the algorithm 10 times. The classification accuracy of each algorithm is shown in Table 5.

Fig. 5
figure 5

Sample faces images from ORL face database

Full size image
Table 5 Classification accuracy (%) of different methods on the ORL database
Full size table

We can clearly see from Table 5 that the proposed RSMDA is superior to KNN, SVM, LDA, SLDA, OLDA,ULDA and SULDA.

4.5 Experiments on Georgia Tech database

The Georgia tech face database contains photos of 50 people taken during two or three sessions. The faces in these pictures may be front and tilted, or they may be front or tilted. These images include different expression, illumination and proportion. Each image is manually cropped to 60 by 50 pixels. Be converted to grayscale images. Figure 6 shows the sample image of one of them. In this experiment, the training set was the first 5, to 8 images of each person, and the test set is the remaining images. Repeat the algorithm 10 times. The classification accuracy of each algorithm is shown in Table 6.

Fig. 6
figure 6

Sample faces images from Georgia Tech face database

Full size image
Table 6 Classification accuracy (%) of different methods on the Georgia Tech database
Full size table

Table 6 shows the RSMDA method has better performance than KNN, LDA, OLDA and ULDA, and the recognition rate is higher. Compared with SULDA, the classification accuracy of RSMDA steadily increases with the increase in the number of training samples.This also shows that RSMDA is more stable than SULDA to a certain extent.

4.6 Parameters selection

There are two regularization parameters, which can affect the performance of RSMDA. In the following, we examine the effects of these two parameters λ1 and λ2 on the proposed algorithm by examining the changes in the recognition performance of RSMDA under different parameter values. We choose two databases as the test set, they are CMU PIE and Yale B databases. The experimental results of the algorithm are shown in Fig. 7. We take (10−5,10−4, 10−3,10−2,10−1,1, 101, 102, 103, 104, 105) as the value range of the two regularization parameters λ1 and λ2, then execute the proposed method RSMDA. As can be seen from the Fig. 7, the proposed method performs best when the value λ1 and λ2 are close to 0.0001. Differences in the classification results show that the two parameters for the identification and classification of learning and performance projection algorithm has an important influence.

Fig. 7
figure 7

The Classification accuracy (%) of the proposed method versus parameters λ1 and λ2. on the Yale B database, CMU PIE database and AR database

Full size image

5 Conclusion

In this paper, we propose a novel supervised feature extraction method termed robust sparse manifold discriminant analysis (RSMDA), in which the global discriminative information, local manifold discriminative information and sparse representation are integrated into a framework. By using the L2,1 sparse norm to limit the discriminative projection matrix, the proposed method can perform feature selection and feature extraction at the same time, and these features are more suitable for classification tasks because they have the most discriminative information. This reconstruction constraint minimizes the loss of difference information, thereby improving the accuracy of classification. In addition, the local identification information is introduced, which further enhances the discrimination of the extracted projection matrix. The experimental results on six five databases all show that this method performs better than other competing methods.