1 Introduction

Feature extraction plays a critical role in a lot of pattern recognition and machine learning problems [8, 10,11,12,13, 32, 42]. A main goal of feature extraction is to find some low-dimensional expressive or discriminative features for high-dimensional data. Many feature extraction techniques have been proposed in the literatures [14]. Among them, principal component analysis (PCA) [8, 9] and linear discriminant analysis (LDA) [4, 8, 9] may be two of the most well-known linear ones.

PCA is an unsupervised feature extraction method. It aims to seek a set of orthogonal projection vectors to maximize the variance of the given data. To improve the performance of PCA, some supervised PCA methods have been proposed. Bair et al. [2] and Barshan et al. [3], respectively, proposed the supervised principal component (SPCA) method which can be applied to regression problems where the number of features greatly exceeds the number of samples. Xia et al. [33]proposed a supervised probabilistic principal component analysis (SPPCA) which has successfully been used for feature extraction in hyperspectral remote sensing imagery. By generating face relevance maps, Kawulok et al. [16] improves the discriminating capability of Eigenfaces, which is based on PCA. Different from conventional PCA, LDA is a supervised feature extraction method. It aims to seek a projection transformation matrix on which the given data of the same class are as near as possible to each other while the given data of the different classes are as far as possible from each other. Generally, LDA is superior to PCA for classification problems. Recently, researchers proposed some other feature extraction methods which need not to be trained in advance. In [21], Leng et al. proposed a method called two-directional two-dimensional random projection ((2D)2RP) for feature extraction of biometrics. (2D)2RP can avoid the problem of small sample size (SSS) and overfitting. Dynamic weighted DPA (DWDPA) is proposed in [19, 20] to improve the discrimination power of the selected discrete cosine transform coefficients without premasking window.

Although PCA and LDA have been widely used in many fields, they are sensitive to outliers since their objective functions are based on L2-norm in which the square operation exaggerates the effect of outliers [18]. Generally, L1-norm is more robust to outliers than L2-norm. Therefore, some L1-norm-based feature extraction techniques, e.g. robust PCA [7, 17, 18, 26, 27, 34] and robust LDA [24, 30, 31, 38, 39], are developed to address the drawback of L2-norm-based feature extraction methods.

By using maximum likelihood estimation to the given data, Ke et al. [17] proposed L1-PCA. The objective function of L1-PCA is solved via convex programming techniques. However, L1-PCA is not rotational invariant. R1-PCA [7], in which the rotational invariant L1-norm is used, is rotational invariant and can combine the advantages of PCA and L1-PCA. However, due to the absolute operator, the optimizations of L1-PCA and R1-PCA are more difficult than the conventional PCA.

Recently, to address the drawbacks of L1-PCA and R1-PCA, Kwak [18] proposed the PCA-L1 method, which is rotational invariant and can be solved by a greedy iteration algorithm. PCA-L1 is computational efficiently. Experiments on some face databases demonstrate that PCA-L1 can obtain much lower reconstruction error than L1-PCA and R1-PCA. To obtain much better projection matrix of PCA-L1, Nie et al. [26] proposed a non-greedy strategy to solve PCA-L1 which can obtain all the projection vectors simultaneously. Motivated by PCA-L1 and 2DPCA [36], Li et al. [34] proposed the L1-norm-based 2DPCA method (2DPCA-L1). Further, Pang et al. [27] proposed L1-norm-based tensor PCA (TPCA-L1).

Similar to conventional PCA, L1-norm-based PCA is also unsupervised and cannot find the optimal discriminative projection vectors. Then for object recognition problems, LDA, which is a supervised feature extraction method, may be a better choice. Motivated by R1-PCA and maximum margin criterion (WMMC) [22, 23], Li et al. [24] proposed a new rotational invariant L1-norm based MMC (R1-MMC). The iterative algorithm for solving R1-MMC is based on eigenvalue decomposition, and then R1-MMC is computational expensive. Recently, Wang et al. [30] proposed a robust version of common spatial patterns (CSP), i.e., L1-norm-based CSP (CSP-L1), which replace L2-norm in CSP with L1-norm. An efficient iterative algorithm for solving CSP-L1 is also proposed. Similar ideas are also appeared in [31, 38, 39] where L2-norm is replaced with L1-norm in the LDA objection function and LDA-L1 is proposed.

However, the projection vectors learned by the above L1-norm-based PCA and LDA are still dense, which makes it hard to explain the obtained features. To address this problem, sparse feature extraction methods have been developed in recent years. Zou et al. [40] proposed sparse PCA (SPCA), where PCA is firstly reformulated as a regression problem and then the elastic net is used to regularize the bases obtained by PCA. Jenatton et al. [15] further proposed the structured sparse PCA algorithm, which is a generalization of SPCA. Motivated by the graph embedding framework [35], Cai et al. [5, 6] proposed a unified sparse subspace learning (USSL) framework with spectral regression. Similarly, Tao et al. [41] proposed so-called manifold elastic net, which is also a unified sparse dimension reduction framework with patch alignment technique. Wang [28] proposed structured sparse linear graph embedding (SSLGE), which use the structured sparsity-inducing norm to regularize the bases obtained by linear graph embedding. However, the objective function of the above sparse learning methods is still based on L2-norm with certain sparsity constraint, which makes these methods prone to the influence of noises. In [25], Meng et al. extended PCA-L1 with sparsity (PCA-L1S). In PCA-L1S, the objective function is based on L1-norm. Besides, the project vectors are also regularized with L1-norm. Similarly, Wang et al. [29] extended 2DPCA-L1 with sparsity (2DPCA-L1S).

In order to improve the robustness of LDA-L1 and interpretability of the vectors obtained by LDA-L1 further, in this paper, we propose a novel sparse L1-norm-based linear discriminant analysis (SLDA-L1) which not only replace L2-norm in conventional LDA with L1-norm, but also use the elastic net to regularize the basis vectors. Then L1-norm used in SLDA-L1 is for both robust and sparse modeling simultaneously. An efficient iterative algorithm to solve SLDA-L1, which is theoretically shown to arrive at a locally maximal point, is also proposed.

To show the robustness of SLDA-L1, here, we will presents an experiment on artificial dataset. Two Gaussian classes with covariance matrices being [0.05 0; 0 2] and means being [−2 0] and [2 0] respectively. Each class consists of 20 2D samples as depicted in Fig. 1a and Fig. 1b, respectively, where two classes are respectively specified by “o” and “x”. Firstly, we extract the projection vectors using LDA-L2, R1-MMC, LDA-L1 and SLDA-L1 on the above data without any outlier. The obtained projection vectors are shown in Fig. 1a. We can find that the obtained projection vectors are very similar. In order to compare the robustness of different methods, an additional outlier, i.e. [4] specified by red “o” is introduced in Fig. 1b. The projection vectors extracted by different methods are also shown in Fig. 1b. From Fig. 1b, we can know the projection vectors obtained by SLDA-L1 is better than the other three methods.

Fig. 1
figure 1

Projection vectors learned by different methods on an artificial dataset

Full size image

It is worth highlighting the novelty of our proposed SLDA-L1 method.

  1. 1)

    We propose a novel sparse L1-norm-based linear discriminant analysis (SLDA-L1), in which L1-norm is for both robust and sparse modeling simultaneously.

  2. 2)

    We also propose an efficient iterative algorithm to solve SLDA-L1, which is theoretically shown to arrive at a locally maximal point.

The remainder of the paper is organized as follows. In section 2, we review briefly the conventional LDA technique. In Section 3, we propose the SLDA-L1 method, including its objective function and algorithmic procedure. Section 4 is devoted to the experiments. Finally, we conclude the paper in Section 5.

2 Related work

Let \( X=\left\{{\mathbf{x}}_j^i,j=1,2,\dots, {n}_i;i=1,2,\dots, k\right\} \) be a d-dimensional real sample set with n elements, where k is the number of the classes, n i is the number of the samples of ith class, \( n={\sum}_{i=1}^k{n}_i \) is the number of the data set, and \( {\mathbf{x}}_j^i \) is the jth samples of the ith class. In LDA (termed as LDA-L2), between-class scatter matrix and within-class scatter matrix, are respectively defined as follows:

$$ {S}_b=\sum_{i=1}^k{n}_i\left({\mathbf{m}}_i-\mathbf{m}\right){\left({\mathbf{m}}_i-\mathbf{m}\right)}^T $$
(1)
$$ {S}_w=\sum_{i=1}^k\sum_{j=1}^{n_i}\left({\mathbf{x}}_j^i-{\mathbf{m}}_i\right){\left({\mathbf{x}}_j^i-{\mathbf{m}}_i\right)}^T $$
(2)

where \( {\mathbf{m}}_i=\left(1/{n}_i\right){\sum}_{j=1}^{n_i}{\mathbf{x}}_j^i \) is the mean of the ith class and \( \mathbf{m}=\left(1/n\right){\sum}_{i=1}^k{\sum}_{j=1}^{n_i}{\mathbf{x}}_j^i \) is the global mean of the data set.

Define the matrices

$$ {H}_b=\left[\sqrt{n_1}\left({\mathbf{m}}_1-\mathbf{m}\right),\kern0.5em \sqrt{n_2}\left({\mathbf{m}}_2-\mathbf{m}\right),\kern0.5em \cdots, \kern0.5em \sqrt{n_k}\left({\mathbf{m}}_k-\mathbf{m}\right)\right] $$
(3)
$$ {H}_w=\left[{\mathbf{x}}_1^1-{\mathbf{m}}_1,\kern0.5em \cdots \kern0.5em {\mathbf{x}}_{n_1}^1-{\mathbf{m}}_1,\kern0.5em \begin{array}{ccc}\hfill \cdots, \hfill & \hfill {\mathbf{x}}_1^k-{\mathbf{m}}_k,\hfill & \hfill \begin{array}{cc}\hfill \cdots, \hfill & \hfill {\mathbf{x}}_{n_k}^k-{\mathbf{m}}_k\hfill \end{array}\hfill \end{array}\right] $$
(4)

The optimal projection vector w ∈ R dof LDA can be obtained by maximizing the following so-called Fisher criterion:

$$ J\left(\mathbf{w}\right)=\frac{{\mathbf{w}}^T{S}_b\mathbf{w}}{{\mathbf{w}}^T{S}_w\mathbf{w}} $$
(5)

The projection vector wis the leading generalized eigenvector of S b w = λS w w.

3 Sparse L1-norm-based linear discriminant analysis (SLDA-L1)

3.1 Problem formulation

In this subsection, we will present our proposed sparse L1-norm-based linear discriminant analysis. By simply transforming, Eq. (5) can be reformulated as

$$ J\left(\mathbf{w}\right)=\frac{{\left\Vert {\mathbf{w}}^T{H}_b\right\Vert}_2^2}{{\left\Vert {\mathbf{w}}^T{H}_w\right\Vert}_2^2} $$
(6)

where ‖⋅‖2 denotes L2-norm. Obviously, the objective function of LDA-L2 is based on L2-norm. It is generally believed that L1-norm based feature extraction methods are more robust to outliers than L2-norm based feature extraction methods [31, 39]. Besides, in the sparsity-inducing modeling, L1-norm is often used to regularize the bases obtained by the feature extraction methods. Then, the objective function of SLDA-L1 is defined as follows:

$$ F\left(\mathbf{w}\right)=\frac{{\left\Vert {\mathbf{w}}^T{H}_b\right\Vert}_1}{{\left\Vert {\mathbf{w}}^T{H}_w\right\Vert}_1}-\lambda {\left\Vert \mathbf{w}\right\Vert}_1-\frac{\eta }{2}{\left\Vert \mathbf{w}\right\Vert}_2^2 $$
(7)

where λ > 0 and η > 0 are tuning parameters. The first term in Eq. (7) is the robust design of the objective function of LDA-L2. The second and the third terms in Eq. (7) are the elastic net, which can circumvent potential limitations of lasso [40]. That is, it can not only result in sparsity, but also can improve the grouping effectiveness in regression. The optimal w can be obtained by maximizing Eq. (7). It, however, is difficult to obtain the global optimal solution of variable of w since the absolute value operation in Eq. (7) is not differentiable. In the following subsection, we will propose an iterative algorithm to find a local optimal w.

3.2 Algorithm of finding the projection vector w

We firstly introduce the following notations.

Let w(t) be the basis vector in the t-th iteration. Remove the zero entries of w(t) and denote the new vector as \( \underline {\mathbf{w}}(t) \). Remove the entries of A whose indices is the indices of the zero entries of w(t) and the new vector is denoted as \( \underline{A} \). For example, let w(t) = (2, 0, 0, 3, 0, 5)Tand \( {\mathbf{x}}_j^i={\left(1,3,2,6,8,4\right)}^T \). Then \( \underline {\mathbf{w}}(t)={\left(2,3,5\right)}^T \) and \( {\underline {\mathbf{x}}}_j^i={\left(1,6,4\right)}^T \). Letw(t + 1) be the vector which is formed by inserting zero entries into \( \underline {\mathbf{w}}\left(t+1\right) \) and the indices of the inserted zero entries of w(t + 1) are just the indices of the zero entries of \( \underline {\mathbf{w}}(t) \). For example, if \( \underline {\mathbf{w}}\left(t+1\right)=\left(3,5,4\right) \), then w(t + 1) = (3, 0, 0, 5, 0, 4).

Now the iterative algorithm of SLDA-L1 is stated as follows.

figure e

The convergence of the above iterative algorithm is theoretically justified by the following Theorem 1.

Theorem 1

With the above iterative procedure of SLDA-L1, the objective function of F(w) is nondecreasing with each iteration.

Proof

At each iteration t, we have

$$ F\left(\mathbf{w}(t)\right)=\frac{{\left\Vert \mathbf{w}{(t)}^T{H}_b\right\Vert}_1}{{\left\Vert \mathbf{w}{(t)}^T{H}_w\right\Vert}_1}-\lambda {\left\Vert \mathbf{w}(t)\right\Vert}_1-\frac{\eta }{2}{\left\Vert \mathbf{w}(t)\right\Vert}_2^2 $$
(12)

Obviously Eq. (12) can be rewritten as

$$ F\left(\mathbf{w}(t)\right)=\frac{{\left\Vert \underline {\mathbf{w}}{(t)}^T{\underline{H}}_b\right\Vert}_1}{{\left\Vert \underline {\mathbf{w}}{(t)}^T{\underline{H}}_w\right\Vert}_1}-\lambda {\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1-\frac{\eta }{2}{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_2^2 $$
(13)

The denominator of the first term in Eq. (13) can be rewritten as

$$ {\displaystyle \begin{array}{l}{\left\Vert \underline {\mathbf{w}}{(t)}^T{\underline{H}}_w\right\Vert}_1=\frac{1}{2}\underline {\mathbf{w}}{(t)}^T\left(\sum \limits_{i=1}^k\sum \limits_{j=1}^{n_i}\frac{\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right){\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right)}^T}{\left|\underline {\mathbf{w}}{(t)}^T\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right)\right|}\right)\underline {\mathbf{w}}(t)+\frac{1}{2}{\left\Vert \underline {\mathbf{w}}{(t)}^T{\underline{H}}_w\right\Vert}_1\\ {}=\frac{1}{2}\underline {\mathbf{w}}{(t)}^T\underline{V}(t)\underline {\mathbf{w}}(t)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1\end{array}} $$
(14)

where

$$ \underline{V}(t)=\sum_{i=1}^k\sum_{j=1}^{n_i}\frac{\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right){\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right)}^T}{\left|{\underline{z}}_j^i(t)\right|} $$
(15)

\( {\underline{z}}_j^i(t)=\underline {\mathbf{w}}{(t)}^T\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right) \) and \( \underline {\mathbf{z}}(t) \) is the vector having the elements \( {\left\{{\underline{z}}_j^i(t)\right\}}_{j=1,\dots, {n}_i;i=1,\dots, k} \).

The numerator of the first term in Eq. (13) can be rewritten as

$$ {\displaystyle \begin{array}{l}{\left\Vert \mathbf{w}{(t)}^T{H}_b\right\Vert}_1={\left\Vert \underline {\mathbf{w}}{(t)}^T{\underline{H}}_b\right\Vert}_1=\underline {\mathbf{w}}{(t)}^T\sum \limits_{i=1}^k\sqrt{n_i}{p}_i(t)\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right)\\ {}=\underline {\mathbf{w}}{(t)}^T\underline {\mathbf{u}}(t)\end{array}} $$
(16)

where

$$ \underline {\mathbf{u}}(t)=\sum_{i=1}^k\sqrt{n_i}{p}_i(t)\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right) $$
(17)

The second term of Eq. (13) can be rewritten as

$$ {\left\Vert \mathbf{w}(t)\right\Vert}_1=\frac{1}{2}\underline {\mathbf{w}}{(t)}^T\underline{U}(t)\underline {\mathbf{w}}(t)+\frac{1}{2}{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1 $$
(18)

where \( \underline{U}(t)=\mathit{\operatorname{diag}}\left({\left|{\underline{w}}_1(t)\right|}^{-1},\dots, {\left|{\underline{w}}_p(t)\right|}^{-1}\right) \) is a diagonal matrix.

Combining Eq. (14), Eq. (16), Eq. (18) and Eq. (13), we have

$$ F\left(\mathbf{w}(t)\right)=\frac{\underline {\mathbf{w}}{(t)}^T\underline {\mathbf{u}}(t)}{\frac{1}{2}\underline {\mathbf{w}}{(t)}^T\underline{V}(t)\underline {\mathbf{w}}(t)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1}-\frac{\lambda }{2}\left(\underline {\mathbf{w}}{(t)}^T\underline{U}(t)\underline {\mathbf{w}}(t)+{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1\right)-\frac{\eta }{2}{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_2^2 $$
(19)

Since it is intractable to derive the function F(w(t)) directly, we introduce a surrogate function as follows:

$$ L\left(\xi \right)=\frac{\xi^T\underline {\mathbf{u}}(t)}{\frac{1}{2}{\xi}^T\underline{V}(t)\xi +\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1}-\frac{\lambda }{2}\left({\xi}^T\underline{U}(t)\xi +{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1\right)-\frac{\eta }{2}{\left\Vert \xi \right\Vert}_2^2 $$
(20)

Note that only ξ is the variable while \( \underline {\mathbf{u}}(t) \), \( \underline{V}(t) \), \( \underline {\mathbf{z}}(t) \), \( \underline{U}(t) \) and \( \underline {\mathbf{w}}(t) \) are all fixed values in the function L(ξ). Compute the gradient of Eq. (20) as follows:

$$ {\displaystyle \begin{array}{l}g\left(\xi \right)=\frac{\partial L\left(\xi \right)}{\partial \xi}\\ {}=\frac{\left(\frac{1}{2}{\xi}^T\underline{V}(t)\xi +\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1\right)\underline {\mathbf{u}}(t)-\left({\xi}^T\underline {\mathbf{u}}(t)\right)\underline{V}(t)\xi }{{\left(\frac{1}{2}{\xi}^T\underline{V}(t)\xi +\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1\right)}^2}-\lambda \left(\underline{U}(t)\xi \right)-\eta \xi \\ {}=\frac{\underline {\mathbf{u}}(t)}{\frac{1}{2}{\xi}^T\underline{V}(t)\xi +\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1}-\frac{\left({\xi}^T\underline {\mathbf{u}}(t)\right)\underline{V}(t)\xi }{{\left(\frac{1}{2}{\xi}^T\underline{V}(t)\xi +\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1\right)}^2}-\lambda \left(\underline{U}(t)\xi \right)-\eta \xi \end{array}} $$
(21)

From Eq. (21), we can obtain the gradient at point \( \underline {\mathbf{w}}(t) \):

$$ {\displaystyle \begin{array}{l}g\left(\underline {\mathbf{w}}(t)\right)=\frac{\underline {\mathbf{u}}(t)}{\frac{1}{2}\underline {\mathbf{w}}{(t)}^T\underline{V}(t)\underline {\mathbf{w}}(t)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1}-\frac{\left(\underline {\mathbf{w}}{(t)}^T\underline {\mathbf{u}}(t)\right)\underline{V}(t)\underline {\mathbf{w}}(t)}{{\left(\frac{1}{2}\underline {\mathbf{w}}{(t)}^T\underline{V}(t)\underline {\mathbf{w}}(t)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1\right)}^2}\\ {}-\lambda \left(\underline{U}(t)\underline {\mathbf{w}}(t)\right)-\eta \underline {\mathbf{w}}(t)\end{array}} $$
(22)

Substituting \( \underline {\mathbf{u}}(t) \), \( \underline{V}(t) \), \( {\underline{z}}_j^i(t) \) and \( \underline{U}(t) \) into Eq. (22), we have

$$ {\displaystyle \begin{array}{l}g\left(\underline {\mathbf{w}}(t)\right)\\ {}=\frac{\sum \limits_{i=1}^k\sqrt{n_i}{p}_i(t)\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right)}{{\left\Vert \underline {\mathbf{w}}{(t)}^T{\underline{H}}_w\right\Vert}_1}-\frac{\left(\sum \limits_{i=1}^k\sqrt{n_i}\left|\underline {\mathbf{w}}{(t)}^T\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right)\right|\right)\sum \limits_{i=1}^k\sum \limits_{j=1}^{n_i}{q}_j^i(t)\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right)}{{\left({\left\Vert \underline {\mathbf{w}}{(t)}^T{\underline{H}}_w\right\Vert}_1\right)}^2}\\ {}-\lambda \left(\mathit{\operatorname{sign}}\left({\underline{w}}_1(t)\right),\dots, \mathit{\operatorname{sign}}\left({\underline{w}}_p(t)\right)\right)-\eta \underline {\mathbf{w}}(t)\\ {}=\underline {\mathbf{d}}(t)\end{array}} $$
(23)

Obviously, \( \underline {\mathbf{d}}(t) \)is the vector which points to the ascending direction of g(ξ) at point \( \underline {\mathbf{w}}(t) \). Let

$$ \underline {\mathbf{w}}\left(t+1\right)=\underline {\mathbf{w}}(t)+\beta \underline {\mathbf{d}}(t) $$
(24)

Then according to Eq. (21), we have

$$ L\left(\underline {\mathbf{w}}\left(t+1\right)\right)\ge L\left(\underline {\mathbf{w}}(t)\right) $$
(25)

That is

$$ {\displaystyle \begin{array}{l}\frac{\underline {\mathbf{w}}{\left(t+1\right)}^T\underline {\mathbf{u}}(t)}{\frac{1}{2}\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{V}(t)\underline {\mathbf{w}}\left(t+1\right)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1}-\frac{\lambda }{2}\left(\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{U}(t)\underline {\mathbf{w}}\left(t+1\right)+{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1\right)-\frac{\eta }{2}{\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_2^2\\ {}\ge \frac{\underline {\mathbf{w}}{(t)}^T\underline {\mathbf{u}}(t)}{\frac{1}{2}\underline {\mathbf{w}}{(t)}^T\underline{V}(t)\underline {\mathbf{w}}(t)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1}-\frac{\lambda }{2}\left(\underline {\mathbf{w}}{(t)}^T\underline{U}(t)\underline {\mathbf{w}}(t)+{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1\right)-\frac{\eta }{2}{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_2^2=F\left(\mathbf{w}(t)\right)\end{array}} $$
(26)

In the following we will prove the following inequality

$$ {\displaystyle \begin{array}{l}\frac{{\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_b\right\Vert}_1}{{\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_w\right\Vert}_1}-\lambda {\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_1-\frac{\eta }{2}{\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_2^2\\ {}\ge \frac{\underline {\mathbf{w}}{\left(t+1\right)}^T\underline {\mathbf{u}}(t)}{\frac{1}{2}\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{V}(t)\underline {\mathbf{w}}\left(t+1\right)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1}-\frac{\lambda }{2}\left(\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{U}(t)\underline {\mathbf{w}}\left(t+1\right)+{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1\right)-\frac{\eta }{2}{\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_2^2\end{array}} $$
(27)

Before proving Eq. (27), we firstly introduce the following lemma.

Lemma [15]

For any vector a = (a 1,  … , a n )T ∈ R n, the following equality hold:

$$ {\left\Vert \mathbf{a}\right\Vert}_1={\mathrm{min}}_{\varsigma \in {R}_{+}^n}\frac{1}{2}\sum_{j=1}^n\frac{a_j^2}{\varsigma_j}+\frac{1}{2}{\left\Vert \varsigma \right\Vert}_1 $$
(28)

and the minimum is uniquely reached at ς = |a j |, j = 1 ,  …  , n where ς = (ς 1,  … , ς n )T.

Considering the denominator of the first term of the right hand of Eq. (27), we have

$$ \frac{1}{2}\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{V}(t)\underline {\mathbf{w}}\left(t+1\right)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1=\frac{1}{2}\sum_{i=1}^k\sum_{j=1}^{n_i}\frac{{\left(\underline {\mathbf{w}}{\left(t+1\right)}^T\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right)\right)}^2}{\left|{\underline{z}}_j^i(t)\right|}+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1\ge {\mathrm{min}}_{\varsigma \in {R}_{+}^n}\frac{1}{2}\sum_{i=1}^k\sum_{j=1}^{n_i}\frac{{\left(\underline {\mathbf{w}}{\left(t+1\right)}^T\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right)\right)}^2}{\varsigma_j}+\frac{1}{2}{\left\Vert \varsigma \right\Vert}_1=\sum_{i=1}^k\sum_{j=1}^{n_i}\left|\underline {\mathbf{w}}{\left(t+1\right)}^T\left({\underline {\mathbf{x}}}_j^i-{\underline {\mathbf{m}}}_i\right)\right|={\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_w\right\Vert}_1\ge 0 $$
(29)

Considering the numerator of the first term of the right hand of Eq. (27), we have

$$ {\displaystyle \begin{array}{l}\underline {\mathbf{w}}{\left(t+1\right)}^T\underline {\mathbf{u}}(t)=\underline {\mathbf{w}}{\left(t+1\right)}^T\sum \limits_{i=1}^k\sqrt{n_i}{p}_i(t)\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right)\\ {}\le \underline {\mathbf{w}}{\left(t+1\right)}^T\sum \limits_{i=1}^k\sqrt{n_i}{p}_i\left(t+1\right)\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right)=\sum \limits_{i=1}^k\sqrt{n_i}\left|\underline {\mathbf{w}}{\left(t+1\right)}^T\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right)\right|\\ {}={\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_b\right\Vert}_1\end{array}} $$
(30)

In Eq. (30), the equality is due to the fact that \( {p}_i\left(t+1\right)\underline {\mathbf{w}}{\left(t+1\right)}^T\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right) \), i = 1 , 2 ,  …  , k, is always nonnegative since p i (t + 1) is the polarity of \( \underline {\mathbf{w}}{\left(t+1\right)}^T\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right) \) while \( {p}_i(t)\underline {\mathbf{w}}{\left(t+1\right)}^T\left({\underline {\mathbf{m}}}_i-\underline {\mathbf{m}}\right) \), i = 1 , 2 ,  …  , k may be negative for some i.

Since \( {\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_b\right\Vert}_1\ge 0 \), then from Eq. (29) and Eq. (30) we have

$$ \frac{{\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_b\right\Vert}_1}{{\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_w\right\Vert}_1}\ge \frac{\underline {\mathbf{w}}{\left(t+1\right)}^T\underline {\mathbf{u}}(t)}{\frac{1}{2}\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{V}(t)\underline {\mathbf{w}}\left(t+1\right)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1} $$
(31)

Considering the second term of the right hand of Eq. (27), we have

$$ {\displaystyle \begin{array}{l}\frac{1}{2}\left(\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{U}(t)\underline {\mathbf{w}}\left(t+1\right)+{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1\right)=\frac{1}{2}\left(\sum \limits_{i=1}^p\frac{{\underline{w}}_i{\left(t+1\right)}^2}{\left|{\underline{w}}_i(t)\right|}+{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1\right)\\ {}\ge \frac{1}{2}\left(\sum \limits_{i=1}^p\frac{{\underline{w}}_i{\left(t+1\right)}^2}{\left|{\underline{w}}_i\left(t+1\right)\right|}+{\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_1\right)={\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_1\end{array}} $$
(32)

Then from Eq. (32) we have

$$ -\lambda {\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_1\ge -\frac{\lambda }{2}\left(\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{U}(t)\underline {\mathbf{w}}\left(t+1\right)+{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1\right) $$
(33)

Combining Eq. (31) and Eq. (33), we have

$$ {\displaystyle \begin{array}{l}\frac{{\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_b\right\Vert}_1}{{\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_w\right\Vert}_1}-\lambda {\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_1-\frac{\eta }{2}{\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_2^2\\ {}\ge \frac{\underline {\mathbf{w}}{\left(t+1\right)}^T\underline {\mathbf{u}}(t)}{\frac{1}{2}\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{V}(t)\underline {\mathbf{w}}\left(t+1\right)+\frac{1}{2}{\left\Vert \underline {\mathbf{z}}(t)\right\Vert}_1}-\frac{\lambda }{2}\left(\underline {\mathbf{w}}{\left(t+1\right)}^T\underline{U}(t)\underline {\mathbf{w}}\left(t+1\right)+{\left\Vert \underline {\mathbf{w}}(t)\right\Vert}_1\right)-\frac{\eta }{2}{\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_2^2\end{array}} $$
(34)

We also have

$$ {\displaystyle \begin{array}{l}F\left(\mathbf{w}\left(t+1\right)\right)=\frac{{\left\Vert \mathbf{w}{\left(t+1\right)}^T{H}_b\right\Vert}_1}{{\left\Vert \mathbf{w}{\left(t+1\right)}^T{H}_w\right\Vert}_1}-\lambda {\left\Vert \mathbf{w}\left(t+1\right)\right\Vert}_1-\frac{\eta }{2}{\left\Vert \mathbf{w}\left(t+1\right)\right\Vert}_2^2\\ {}=\frac{{\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_b\right\Vert}_1}{{\left\Vert \underline {\mathbf{w}}{\left(t+1\right)}^T{\underline{H}}_w\right\Vert}_1}-\lambda {\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_1-\frac{\eta }{2}{\left\Vert \underline {\mathbf{w}}\left(t+1\right)\right\Vert}_2^2\end{array}} $$
(35)

Combining Eq. (35), Eq. (34) and Eq. (26), we have

$$ F\left(\mathbf{w}\left(t+1\right)\right)\ge F\left(\mathbf{w}(t)\right) $$
(36)

3.3 Extension to multiple basis vectors

In subsection 3.2, we have shown how to obtain one optimal projection vector. Generally, one projection vectors is not enough. In the following, we will introduce how to learn multiple projection vectors. The deflation technique is used to extract the other projection vectors. If the first r-1 projection vectors w 1 , w 2 ,  …  , w r − 1 have been obtained, then the rth projection vector w r is calculated by using the deflated data

$$ {\left({\mathbf{x}}_j^i\right)}^{deflated}={\mathbf{x}}_j^i-\sum_{l=1}^{r-1}{\mathbf{w}}_l\left({\mathbf{w}}_l^T{\mathbf{x}}_j^i\right) $$
(37)

After \( {\left({\mathbf{x}}_j^i\right)}^{deflated} \) is obtained, we will use \( {\left({\mathbf{x}}_j^i\right)}^{deflated} \) to compute H b and H w . Then the procedure in subsection 3.2 is used to compute w r .

4 Experiments and results

In this section, we will compare our proposed SLDA-L1 with LDA-L2 [4], LDA-L1 [31, 39] and R1-MMC [24] on artificial datasets and some image databases, e.g. Yale, FERET, FRGC and COIL-20. In order to overcome the singularity problem of LDA-L2, we use PCA to reduce the dimension of training sample before the use of LDA. In the PCA phase, we keep nearly 98% image energy. For SLDA-L1, the parameters λ and η are determined by cross-validation. In order to select λ and η conveniently, we assign λ and η as the same value. The learning rate β in SLDA-L1 and LDA-L1 is tried from the set [0.01, 0.03, 0.05, 0.07, 0.09] and the value, which can produce the largest objective function value, is selected. The initial projection vectors of LDA-L1 and SLDA-L1 are set as the projection vectors of LDA-L2. In the experiments, we firstly use the compared methods, i.e., SLDA-L1, LDA-L1, LDA-L2 and R1-MMC, to extract the features of intensity images. Then the nearest neighbor classifier (1-NN) with Euclidean distance is used for classification. The programming environment is MATLAB 2008.

4.1 Experiments on Yale face database

The Yale face database contains 165 Gy scale images of 15 individuals, each individual has 11 images. The images demonstrate variations in lighting condition, facial expression (normal, happy, sad, sleepy, surprised, and wink). In our experiments, each image in Yale database was cropped and resized to 64 × 64.

In the experiments, we randomly choose i (i = 4,5) samples of each person for training, and the remaining ones are used for testing. The procedure is repeated 10 times and the average recognition rates as well as the standard deviation are reported in Table 1. To test the robustness of the proposed SLDA-L1 against outliers, we contaminate each image independently with the probability of 0.5 by rectangle noise. The rectangle noise takes white or black dots, its location in face image is random and its size is 40 × 40. Some face images with or without rectangle noise are shown in Fig. 2. Similarly, the procedure is also repeated 10 times and the average recognition rates as well as the standard deviation are reported in Table 2. We also illustrate the plot of recognition rate vs. the dimension of reduced space for different methods in Fig. 3.

Table 1 Comparison of recognition rates for the different methods on Yale database without noise
Full size table
Fig. 2
figure 2

Some face images with/without occlusion in Yale database

Full size image
Table 2 Comparison of recognition rates for the different methods on Yale database with noise
Full size table
Fig. 3
figure 3

Recognition rate vs. dimension of reduced space on the Yale database. (a) 4 Train, (b) 5 Train

Full size image

4.2 Experiments on FERET face database

The FERET face database contains 14,126 images from 1199 individuals. In our experiments, we select a subset which contains 1400 images of 200 individuals (each individual has seven images). The subset involves variations in facial expression, illumination and pose. In our experiments, each image in FERET database was cropped and resized to 80 × 80.

In the experiments, we randomly choose i (i = 3,4) samples of each person for training, and the remaining ones are used for testing. The procedure is repeated 10 times and the average recognition rates as well as the standard deviation are reported in Table 3. To test the robustness of the proposed SLDA-L1 against outliers, we contaminate each image independently with the probability of 0.5 by rectangle noise. The rectangle noise takes white or black dots, its location in face image is random and its size is 50 × 50. Some face images with or without rectangle noise are shown in Fig. 4. Similarly, The procedure is also repeated 10 times and the average recognition rates as well as the standard deviation are reported in Table 4. We also illustrate the plot of recognition rate vs. the dimension of reduced space for different methods in Fig. 5.

Table 3 Comparison of recognition rates for the different methods on FERET database without noise
Full size table
Fig. 4
figure 4

Some face images with/without occlusion in FERET database

Full size image
Table 4 Comparison of recognition rates for the different methods on FERET database with noise
Full size table
Fig. 5
figure 5

Recognition rate vs. dimension of reduced space on the FERET database. (a) 3 Train, (b) 4 Train

Full size image

4.3 Experiments on FRGC face database

The FRGC version 2 database contains 12,776 training images, 16,028 controlled target images, and 8014 uncontrolled query images for the FRGC Experiment 4. The controlled images have good image quality, while the uncontrolled images display poor image quality, such as large illumination variations, low resolution of the face region, and possible blurring. It is the uncontrolled factors that pose the grand challenge to face recognition performance. In our experiments, 100 people, each with 24 images, were chosen in the experiments. In the experiments, the first 12 samples of each person for training, and the remaining ones are used for testing. Each image was cropped to the size of 60 × 60. The maximal recognition rates of each method are listed in Table 5 and the recognition rates vs. the variations of the dimensions is shown in Figs. 6 and 7. To test the robustness of the proposed SLDA-L1 against outliers, we contaminate each image independently with the probability of 0.5 by rectangle noise. Some face images with or without rectangle noise are shown in Fig. 6. The rectangle noise takes white or black dots, its location in face image is random and its size is 25 × 25. The maximal recognition rates of each method are listed in Table 6.

Table 5 Comparison of recognition rates for the different methods on FRGC database without noise
Full size table
Fig. 6
figure 6

Some face images with/without occlusion in FRGC database

Full size image
Table 6 Comparison of recognition rates for the different methods on FRGC database with noise
Full size table
Fig. 7
figure 7

Recognition rate vs. dimension of reduced space on the FRGC database

Full size image
Fig. 8
figure 8

Some images with/without occlusion in COIL-20 database

Full size image
Fig. 9
figure 9

Recognition rate vs. dimension of reduced space on the COIL-20 database

Full size image
Fig. 10
figure 10

The recognition performance on Yale database by varying λ and η

Full size image

4.4 Experiments on COIL-20 image database

The COIL-20 data set contains 1440 images of 20 objects. For each object, 72 images were captured with a black background from varying angles. The moving interval of the camera is five degrees. Each image is resized to 32 × 32 in our experiment.

In the experiments, we randomly choose ten images of each object for training, and the remaining ones are used for testing. The procedure is repeated 10 times and the average recognition rates as well as the standard deviation are reported in Table 7.To test the robustness of the proposed SLDA-L1 against outliers, we contaminate each image independently with the probability of 0.5 by rectangle noise. The rectangle noise takes white or black dots, its location in face image is random and its size is 16 × 16. Some images with or without rectangle noise are shown in Fig. 8. Similarly, the procedure is repeated 10 times and the average recognition rates as well as the standard deviation are reported in Table 8. We also illustrate the plot of recognition rate vs. the dimension of reduced space for different methods in Fig. 9.

Table 7 Comparison of recognition rates for the different methods on COIL-20 database without noise
Full size table
Table 8 Comparison of recognition rates for the different methods on COIL-20 database with noise
Full size table

4.5 Experiments based on LBP descriptor

In order to further evaluate the recognition performance of the SLDA-L1 method, we use the method of applying the LBP descriptor [1, 37] to Yale face database. We firstly add noises to Yale face images as in Section 4.1. Then the \( {LBP}_{8,2}^{u2} \) operator is applied to extract the features of images. Finally, the same experiment procedures as those in Section 4.1 are conducted. The average recognition rates as well as the standard deviation are reported in Table 9.

Table 9 Comparison of recognition rates on Yale database based on LBP descriptor
Full size table

4.6 Parameter sensitiveness

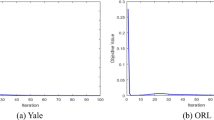
In SLDA-L1, we use the elastic net to regularize the projection vector, and then there are two parameters, i.e., λ and η, to be tuned. In this subsection, we investigate how the recognition rates of the SLDA-L1 method depends on λ and η. λ and η are selected from [0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.06, 0.08, 0.09, 0.10, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.19, 0.20]. Fig. 10 shows the recognition performance of SLDA-L2 on the Yale database w.r.t. λ and η when four samples of each person are used for training.

4.7 Discussions

From the experiment results we can find that L1-norm-based algorithms, i.e., LDA-L1, R1-MMC and SLDA-L1, can achieve higher classification rates than their L2-norm-based counterpart, i.e., LDA-L2. The reason is that L1-norm embedded in the objective function can suppress the negative effects of outliers. Besides, the recognition rates of SLDA-L1 are higher than those of LDA-L1 and R1-MMC, which suggests that introducing the elastic net regularization term into LDA-L1 could improve the recognition performance further. From the experiments in Section 4.5, we can find that using the LBP descriptor can improve the recognition rates of all the algorithms. However, the recognition performance of SLDA-L1 are still higher than those of the other algorithms. Besides, from the experiments in Section 4.6 we can find that the recognition performance of SLDA-L1 depend on the tuning of λ and η. However, when λ and η varies from 0.01 to 0.2, the recognition performance of SLDA-L1 is relatively stable.

5 Conclusions

In this paper, we proposed a novel feature extraction method, called sparse L1-norm-based linear discriminant analysis (SLDA-L1), of subspace based on the L1-norm. First, the proposed SLDA-L1 method seeks projection vectors to maximize the between-class scatter matrix and meanwhile minimized the within-class scatter matrix, both of which are based on L1-norm instead of the conventional L2-norm. Secondly, L1-norm is also used in SLDA-L1 to regularize the basis vectors. Then, L1-norm used in SLDA-L1 is for both robust and sparse modelling simultaneouslyThe experiment results on some image databases show the effectiveness of the proposed SLDA-L1. In the future, we will investigate nonlinear feature extraction methods based on L1-norm.