Dynamical Behavior of Complex-Valued Hopfield Neural Networks with Discontinuous Activation Functions

Abstract

This paper presents some theoretical results on dynamical behavior of complex-valued neural networks with discontinuous neuron activations. Firstly, we introduce the Filippov differential inclusions to complex-valued differential equations with discontinuous right-hand side and give the definition of Filippov solution for discontinuous complex-valued neural networks. Secondly, by separating complex-valued neural networks into real and imaginary part, we study the existence of equilibria of the neural networks according to Leray–Schauder alternative theorem of set-valued maps. Thirdly, by constructing appropriate Lyapunov function, we derive the sufficient condition to ensure global asymptotic stability of the equilibria and convergence in finite time. Numerical examples are given to show the effectiveness and merits of the obtained results.

1 Introduction

As applications of neural networks spread more widely, developing neural networks models that can deal with complex numbers is desired in various fields, such as optoelectronics, remote sensing, quantum devices, signal processing and electromagnetic [1,2,3,4]. Compared with real-valued neural networks, complex-valued neural networks can explore new capabilities and higher performance. For example, as Chakravarthy point out in [5], a complex-valued Hopfield neural networks can exist in both fixed point and oscillatory modes. In the fixed-point mode, complex-valued neural network is similar to a continuous-time Hopfield network. In oscillatory mode, when multiple patterns are stored, the network wanders chaotically among patterns. On the other aspect, in the real-valued neural network, the activation function is usually chosen to be a smooth and bounded analytic function such as sigmoid function. However, in the complex-valued domain, such condition is not suitable for complex-valued activation function because of the Liouville’s theorem, which says every bounded and analytic function in complex domain must be a constant function. In place of analytic function, discontinuous complex-valued function becomes an important choice when we design complex-valued neural networks.

In recent years, researchers have paid more attention on the dynamics of complex-valued neural networks. To study the dynamical behavior, many methods are proposed, such as Lyapunov method, synthesis method and matrix measure method [7,8,9,10,11,12]. In [7], the authors studied the existence of energy function for complex-valued Hopfield neural networks and proposed the stability condition using Lyapunov method. Based on delta differential operator, global stability of complex-valued neural networks on time scales is studied using Lyapunov method in [8, 9]. The stability criteria of discrete complex-valued neural networks are derived in [10] using synthesis method. In [11, 12], the stability of complex-valued neural networks is studied based on matrix measure theory. Compared with the above three methods, Lyapunov method is easier to understand, but it is difficult to construct a Lyapunov function, especially for discontinuous complex-valued neural networks. Synthesis method is usually used to analyze discrete neural networks. The advantage of matrix measure method is to avoid constructing Lyapunov function, but the proposed condition is difficult to verify. As time delay is inevitable in real applications, the dynamics of complex-valued neural networks with time delay have attracted many researchers’ interest [13,14,15,16,17,18,19,20,21,22,23,24,25]. The stability and bifurcation set in parameter plane for first-order complex delayed differential equations are studied in [13]. The stability conditions of complex-valued recurrent neural networks with time delay are derived in [14], and the stability of equilibria is further studied in [15] by separating the real and imaginary parts. In [16], the authors improved the results in [14, 15] using complex-valued Lyapunov function. In [17, 18], the authors researched the global stability and boundedness for complex-valued recurrent neural networks on time scales. The authors studied the exponential stability for delayed complex-valued neural networks in [23,24,25]. However, all these results are required the activation function satisfying Lipschitz condition or its real part and imaginary part have bounded partial derivatives. Obviously, these assumptions are very strict in real application. As Hopfield point out in [26], discontinuous character of activation function can not be negligible when we consider the dynamics of neural networks.

As far as we know, there are few results on dynamics analysis of complex-valued neural networks with discontinuous activation functions [27,28,29,30]. In [27], the multistability of complex-valued recurrent neural networks with real–imaginary-type activation functions is studied. In [28], the author studied the multiple $\mu$-stability of complex-valued neural networks. The author studied the dissipativity, passivity and passification condition of memristor-based complex-valued recurrent neural net works in terms of LMIs in [29, 30]. However, all the above results did not consider the dynamical behavior caused by discontinuous character. If the equilibria are located on the boundaries of activation functions, the methods in [27,28,29,30] can not used to analyze the dynamics of discontinuous complex-valued neural networks.

In the past decades, real-valued neural networks with discontinuous activation functions have been extensively studied via differential inclusion theory [31,32,33,34,35,36,37,38,39], which can analyze the dynamical behavior of discontinuous neural networks successfully. However, the analysis of stability issues of discontinuous complex-valued neural networks is not a simple task and there still lacks effect analysis methods. Such dynamical behavior analysis is faced with three difficulties as follows:

• (1) How to define Filippov differential inclusions and Filippov solution of discontinuous complex-valued differential equation?

• (2) How to ensure the existence of Filippov solution and equilibrium point for complex-valued Hopfield neural networks with discontinuous activation functions?

• (3) How to propose some sufficient conditions to ensure the stability and convergence of equilibria for discontinuous complex-valued Hopfield neural networks?

As far as we know, the result on dynamics of discontinuous complex-valued neural networks using complex differential inclusion theory are not yet available. Motivated by the above discussion, we study the dynamical behavior of discontinuous complex-valued Hopfield neural networks in this paper. The structure of this paper is outlined as follows. In Sect. 2, we introduce the Filippov differential inclusions for complex-valued differential equations with discontinuous right-hand side and give some preliminaries and lemmas. Section 3 presents the main results, including the existence and uniqueness of equilibria, global asymptotic stability and convergence in finite time. Numerical examples are given in Sect. 4 and some concluding remarks are made in Sect. 5.

Notation throughout this paper, R and C show the set of real numbers and the set of complex numbers, respectively. $R^{n}$ and $C^n$ show, respectively, the n-dimensional Euclidean space and the n-dimensional unitary space. $R^{n\times n}$ and $C^{n\times n}$ are, respectively, the set of all $n\times n$ real matrixes and the set of all $n\times n$ complex matrices. $\Vert \cdot \Vert$stands for the Euclidean vector norm or the induced matrix 2-norm. If $A\in R^{n\times n},\,A^{\mathrm{T}}$ shows the transpose of $A,\,A>0\, (A<0)$ means that A is positive definite (negative definite), and $\lambda _{M}(A)$ $(\lambda _{m}(A))$ shows the maximum (minimum) eigenvalue of A. Given a set $Q\in C^{n}\,(Q\in R^{n}),\,K[Q]$ denotes the closure of the convex hull of $Q.\,I$ is used to denote an identity matrix.

2 Problem Description and Some Preliminaries

Let us consider the following complex-valued Hopfield neural networks

$$\begin{aligned} {\dot{z}}_{i}(t)={-}d_{i}z_{i}(t)+\sum \limits _{j=1}^{n}a_{ij}f_{j}\left( z_{j}(t)\right) +u_{i},\quad i=1,\,2,\ldots ,n, \end{aligned}$$

or

$$\begin{aligned} {\dot{z}}(t)={-}Dz(t)+Af(z(t))+u, \end{aligned}$$

(2.1)

where $z(t)=[z_{1}(t),\,z_{2}(t),\ldots ,z_{n}(t)]^{\mathrm{{T}}}\in C^{n}$ is the state vector, $D=\mathrm{diag}\{d_{1},\,d_{2},\ldots ,d_{n}\}$ with $d_{i}>0$ is self-feedback connection weight matrix, $A=[a_{ij}]_{n\times n}\in C^{n\times n}$ means the feedback connection weight matrix, $f(z(t))=[f_{1}(z_{1}(t)),\,f_{2}(z_{2}(t)),\ldots ,f_{n}(z_{n}(t))]^{\mathrm{{T}}}\in C^{n}$ denotes the complex-valued vector activation function and $u=[u_{1},\, u_{2},\ldots ,u_{n}]^{\mathrm{T}}\in C^{n}$ means the vector of constant neuron inputs.

The discontinuous neuron activations $f_{i}(z_{i})$ are assumed to satisfy the following properties.

A(1) For each $i=1,\,2,\ldots ,n,\, f_{i}(z_{i})$ is continuous in finite open domains $G_{k}$ and discontinuous at the boundary of $G_{k},$ which is composed by finite smooth curves. $G_{k},\, k=1,\,2,\ldots ,s$ satisfies $\bigcup \nolimits _{k=1}^{s}(G_{k}\bigcup \partial G_{k})=C$ and $G_{l}\bigcap G_{K}=\emptyset$ for $1\leqslant l\ne k\leqslant s.$

A(2) For every $k=1,\,2,\ldots ,s,$ the limitation $\lim \nolimits _{z\rightarrow z_{0},z\in G_{k}}f_{i}(z)$ exists, where $z_{0}\in \partial G_{k}.$

A(3) There exist two nonnegative constants $\alpha _{i}$ and $\beta _{i}$ such that

$$\begin{aligned} \left\| f_{i}\left( z_{i}(t)\right) \right\| \leqslant \alpha _{i}\left\| z_{i}(t)\right\| +\beta _{i}. \end{aligned}$$

(2.2)

Remark 1

According to the Liouville’s theorem [6], every bounded entire function must be a constant in the complex domain, that is to say, if f(z) is bounded and analytic for all $z\in C,\,f(z)$ is a constant function. When we design a complex-valued neural network model, how to choose activation function becomes an important issue. Since the discontinuity of complex-valued functions means non-analytic, discontinuous activation functions are very useful in constructing complex-valued neural networks.

Remark 2

Though the activation functions are discontinuous in [27, 28], the authors did not consider the case which the equilibria of neural networks are located on the boundaries of discontinuous complex-valued activation functions. In this paper, we analyze the existence and uniqueness of equilibria and study the dynamical behavior under the framework of Filippov differential inclusion.

Remark 3

The assumption A(3) is less conservative than the existing results. If $\beta _{i}=0,$ assumption A(3) plays a similar role with Lipschitz condition, which is needed in [14,15,16]. If $\alpha _{i}=0,$ this means $f_{i}$ is a bounded function, which is required in [27].

Before giving the main results, we introduce the Filippov differential inclusions for complex-valued differential equations with discontinuous right-hand side. Consider the following autonomous complex-valued differential equation:

$$\begin{aligned} {\dot{z}}(t)=f(z(t)), \end{aligned}$$

(2.3)

where $f{\text {:}}\,C^{n}\mapsto C^{n}$ is measurable and essentially locally bounded.

Definition 2.1

Let $E\in C^{n},\,z\mapsto F(z)$ is called a set-valued map from $E \mapsto C^{n}$ if to each point z of a set $E\in C^{n},$ there corresponds a nonempty set $F(z)\in C^{n}.$ A set-valued map F with nonempty values is said to be upper semi-continuous at $z_{0}\in E$ if for any open set N containing $F(z_{0}),$ there exists a neighborhood M of $z_{0}$ such that $F(M)\subset N,$ where $F(M)=\bigcup \nolimits _{y\in M}F(y).\, F(z)$ is said to have a closed (convex, compact) image if for each $z\in E;\, F(z)$ is closed (convex, compact).

Definition 2.2

For system (2.3) with discontinuous right-hand side, a set-valued map $F{\text {:}}\, C^{n}\mapsto F(z)$ follows

$$\begin{aligned} F(z)=\bigcap \limits _{\delta >0}\bigcap \limits _{\mu (\mathcal {N})=0}K[f(B(z,\,\delta )\backslash {\mathcal {N}})], \end{aligned}$$

(2.4)

where K(E) denotes the closure of the convex hull of set $E,\, f(B(z,\,\delta ) \backslash {\mathcal {N}})=\bigcup \nolimits _{y\in (B(z,\delta )\backslash {\mathcal {N}})}f(y),\, B(z,\,\delta )=\{y|\Vert y-z\Vert \le \delta \}$ is the ball with center at x and radius $\delta ,$ and $\mu ({\mathcal {N}})$ is Lebesgue measure of set ${\mathcal {N}}\in C^{n}.$ A solution in the sense of Filippov (or Filippov solution) of Eq. (2.3) with initial condition $z(t_{0})=z_{0}$ is an absolutely continuous vector-value function z(t) on any compact subinterval of $[t_{0},\,T),$ which satisfies $z(t_{0})=z_{0}$ and differential inclusions:

$$\begin{aligned} {\dot{z}}(t)\in F(z), \quad a.e.\quad t\in \left[ t_{0},\,T\right) . \end{aligned}$$

$z(t)=z^{*}$ is called an equilibria of system (2.3) if $0\in F(z^{*})$ holds for any $t\in R.$

Remark 4

According to the definition of absolutely continuity for real function, we can define the absolutely continuity for complex variable function as follows. Suppose $z(t){\text {:}}\,t\mapsto C$ is complex-valued function defined on $[a,\,b].\,z(t)$ is said to be absolutely continuous on $[a,\,b]$ if for any positive number $\varepsilon >0,$ there exist $\delta >0,$ such that for any finite open intervals $(a_{i},\,b_{i}),\,i=1,\,2,\ldots ,n$ satisfying $\sum \nolimits _{i=1}^{n}(b_{i}-a_{i})<\delta ,\, \sum \nolimits _{i=1}^{n}\Vert z(b_{i})-z(a_{i})\Vert <\varepsilon$ holds. It is obvious that the absolutely continuity of z(t) on $[a,\,b]$ is equivalent to that both x(t) and y(t) are absolutely continuous on $[a,\,b],$ where x(t) and y(t) are the real and imaginary part of z(t),  respectively.

Remark 5

The complex set-valued map $F{\text {:}}\,[a,\,b]\rightarrow P_{f}(C^{n})$ is said to be measurable, if for any $z\in C^{n},$ the $R_{+}-$valued function $t\mapsto \mathrm{dist}(z,\,F(z))=\inf \{\Vert z-v\Vert ,\,v\in F(t)\}$ is measurable.

Definition 2.3

A vector function $z(t)=[z_1(t),\,z_2(t),\ldots ,z_n(t)]^{\mathrm{T}}$ is a state solution of discontinuous system (2.1) on $[t_{0},\,T)$ if z(t) is absolutely continuous on any subinterval $[t_1,\,t_2]$ of $[t_{0},\,T)$ and there exists a measurable function $\gamma (t)=[\gamma _1(t),\,\gamma _2(t),\ldots ,\gamma _n(t)]^{\mathrm{T}}$ such that $\gamma _j(t)\in K[f_{j}(z_{j}(t))]$ for a.e. $t\in [t_{0},\,T)$ satisfies:

$$\begin{aligned} \dot{z_i}(t)={-}d_iz_i(t)+\sum \limits _{j=1}^{n}a_{ij}\gamma _j(t)+u_{i},\quad \mathrm{for}\quad a.e. t\in \left[ t_{0},\,T\right) . \end{aligned}$$

(2.5)

The measurable $\gamma (t)$ which satisfies (2.5) is called an output solution associated with state solution z(t). With this definition, it turns out that the sate z(t) is a solution of system (2.1) in sense of Filippov since it satisfies:

$$\begin{aligned} \dot{z_i}(t) \in {-}d_iz_i(t)+\sum \limits _{j=1}^{n}a_{ij}K\left[ f_{j}\left( z_{j}(t)\right) \right] +u_{i},\quad \mathrm{for}\quad a.e. t\in \left[ t_{0},\,T\right) . \end{aligned}$$

For an initial value problem (IVP) associated to the complex-valued neural networks model (2.1), we give the following definition.

Definition 2.4

A absolutely continuous function $z(t)=[z_1(t),\,z_2(t),\ldots ,z_n(t)]^{\mathrm{T}}$ associated with a measurable function $\gamma (t)=[\gamma _1(t),\,\gamma _2(t),\ldots ,\gamma _n(t)]^{\mathrm{T}}$ is said to be a solution of the IVP for system (2.1) on $[t_{0},\,T)$ with initial value $z(t_0)=z_0,$ if the following condition holds for all $i=1,\,2,\ldots ,n,$

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{z_i}(t)={-}d_iz_i(t)+\sum \nolimits _{j=1}^{n}a_{ij}\gamma _j(t)+u_{i}, &{} \mathrm{for}\, a.e.\, t\in [t_{0},\,T),\\ \gamma _j(t)\in K[f_{j}(z_{j}(t))],&{} \mathrm{for}\, a.e.\, t\in [t_{0},\,T).\\ \end{array} \right. \end{aligned}$$

Definition 2.5

$z^{*}$ is said to be an equilibrium point of set-valued map F(z) if $0\in F(z^{*}).$ Particulary, $z^{*}$ is said to be an equilibrium of system (2.1) if there exists $\gamma ^{*}\in K[f(z^{*})]$ such that

$$\begin{aligned} {-}Dz^{*}+A\gamma ^{*}+u=0, \end{aligned}$$

and $\gamma ^{*}$ is said to be an output equilibrium point of system (2.1) corresponding to $z^{*}.$

Definition 2.6

Assume $z^{*}$ is an equilibrium point of system (2.1). $z^{*}$ is said to be globally asymptotically stable if it is stable in the sense of Lyapunov and global attractive, where global attractiveness means that every trajectory z(t) tends to $z^{*}$ as $t\rightarrow \infty .$

Definition 2.7

If $\gamma {\text {:}}\,[a,\,+\infty )\mapsto C^{n}$ is a measurable function, $\gamma ^{*}$ is said to be a limit of $\gamma (t)$ in measure if $\forall \varepsilon>0,\, \exists t_{\varepsilon }>0$ such that $\mu \{t\in [t_{\varepsilon },\,+\infty ){\text {:}}\,\Vert \gamma (t)-\gamma ^{*}\Vert >\varepsilon \}<\varepsilon$ as $t\rightarrow +\infty .$ In this case, we write $\mu -\lim \nolimits _{t\rightarrow +\infty }\gamma (t)=\gamma ^{*},$ i.e., output solution $\gamma (t)$ converge to $\gamma ^{*}$ in measure.

Definition 2.8

The system (2.1) is said to be globally convergent in finite time if the following conditions hold,

• (i) Discontinuous system (2.1) has a unique equilibrium point $z^{*}$ and a unique corresponding output equilibrium point $\gamma ^{*},$

• (ii) For each $z_{0}\in C^{n}$ and any solution z(t) of system (2.1) with $z(t_{0})=z_{0},$ there exists ${\tilde{t}}>0,$ such that $z(t)=z^{*}$ for $t>{\tilde{t}}.$

In this paper, as in [12, 17, 21, 27], we choose the following real–imaginary-type function as activation functions in system (2.1),

$$\begin{aligned} f_{i}\left( z_{i}\right) =f^{R}_{i}\left( \mathrm{Re}\left( z_{i}\right) \right) +f^{I}_{i}\left( \mathrm{Im}\left( z_{i}\right) \right) , \end{aligned}$$

(2.6)

where $f^{R}_{i}(\mathrm{Re}(z_{i}))$ and $f^{I}_{i}(\mathrm{Im}(z_{i}))$ are discontinuous functions. In order to study the stability of system (2.1), we separate it into its real and imaginary parts. Let $z_{i}(t)=x_{i}(t)+\mathbf{i }y_{i}(t),\, a_{ij}=a_{ij}^{R}+\mathbf{i }a_{ij}^{I},\, f_{i}(z_{i}(t))=f_{i}^{R}(x_{i}(t))+\mathbf{i }f_{i}^{I}(y_{i}(t))$ and $u=u^{R}+\mathbf{i }u^{I},$ where $\mathbf{i }$ shows the imaginary unit, i.e., $\mathbf{i }=\sqrt{-1}.$ Denote $x=[x_{1},\,x_{2},\ldots ,x_{n}]^{\mathrm{T}}\in R^{n}$ and $y=[y_{1},\,y_{2},\ldots ,y_{n}]^{\mathrm{T}}\in R^{n},$ then system (2.1) can be separated into its real and imaginary parts as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}={-}Dx+A^{R}f^{R}(x)-A^{I}f^{I}(y)+u^{R},\\ {\dot{y}}={-}Dy+A^{I}f^{R}(x)+A^{R}f^{I}(y)+u^{I},\\ \end{array} \right. \end{aligned}$$

(2.7)

where $A^{R}=[a^{R}_{ij}],\, A^{I}=[a^{I}_{ij}],\, f^{R}(x)=[f_{1}^{R}(x_{1}),\,f_{2}^{R}(x_{2}),\ldots ,f_{n}^{R}(x_{n})]^\mathrm{T},\, u^{R}=[u_{1}^{R},\,u_{2}^{R},\,\ldots ,u_{n}^{R}]^{\mathrm{T}},\, f^{I}(x)=[f_{1}^{I}(y_{1}),\,f_{2}^{I}(y_{2}),\ldots ,f_{n}^{I}(y_{n})]^\mathrm{T}$ and $u^{I}=[u_{1}^{I},\,u_{2}^{I},\ldots ,u_{n}^{I}]^{\mathrm{T}}.$

From A(1) and A(2),  it is easy to know that $f^{R}_{i}(x_{i})$ is discontinuous with some points $x^{k}_{i}$ and $f^{I}_{i}(y_{i})$ is discontinuous with some points $y^{k}_{i}.$ According to A(2),  for every $i=1,\,2,\ldots ,n,$ the limitations $\lim \nolimits _{x\rightarrow x_{0}}f_{i}^{R}(x)=f_{i}^{R}(x_{0})$ and $\lim \nolimits _{y\rightarrow y_{0}}f_{i}^{I}(y)=f_{i}^{I}(y_{0})$ exist where $(x,\,y)\in {\bar{G}}_{k}$ and $(x_{0},\,y_{0})\in \partial {\bar{G}}_{k}.$ Based on above analysis and real-valued set value mapping, we can choose a special way to define the complex set valued maps for (2.6) as follows:

$$\begin{aligned} F(z)=\bigcap \limits _{\delta>0}\bigcap \limits _{\mu ({\mathcal {N}})=0}K\left[ f^{R}(B(x,\,\delta )\backslash \mathcal {N})\right] +\mathbf{i }\bigcap \limits _{\delta >0}\bigcap \limits _{\mu (\mathcal {N})=0}K\left[ f^{I}(B(y,\,\delta )\backslash {\mathcal {N}})\right] , \end{aligned}$$

(2.8)

where $f^R(B(x,\,\delta )\backslash \mathcal {N})=\bigcup \nolimits _{{\bar{x}}\in (B(x,\,\delta )\backslash \mathcal {N})}f^{R}({\bar{x}}),\, B(x,\,\delta )=\{{\bar{x}}|\Vert {\bar{x}}-x\Vert \le \delta \}$ is the ball with center at x and radius $\delta ,\, f^I(B(y,\,\delta )\backslash {\mathcal {N}})=\bigcup \nolimits _{{\bar{y}}\in (B(y,\,\delta )\backslash {\mathcal {N}})}f^{I}({\bar{y}}),\, B(y,\,\delta )=\{{\bar{y}}|\Vert {\bar{y}}-y\Vert \le \delta \}$ is the ball with center at y and radius $\delta$ and $\mu ({\mathcal {N}})$ is Lebesgue measure of set ${\mathcal {N}}\in R^{n}.$

Remark 6

Compared with Definition 2.2, it follows that

$$\begin{aligned}&\bigcap \limits _{\delta>0}\bigcap \limits _{\mu (\mathcal {N})=0}K[f(B(z,\,\delta )\backslash {\mathcal {N}})]\subseteq \bigcap \limits _{\delta>0}\bigcap \limits _{\mu (\mathcal {N})=0}K\left[ f^{R}(B(x,\,\delta )\backslash \mathcal {N})\right] \nonumber \\&\quad +\,\mathbf{i }\bigcap \limits _{\delta >0}\bigcap \limits _{\mu (\mathcal {N})=0}K\left[ f^{I}(B(y,\,\delta )\backslash {\mathcal {N}})\right] , \end{aligned}$$

(2.9)

where $f(z)=f^{R}(x)+\mathbf{i }f^{I}(y).$ For example, let

$$\begin{aligned} f(z)=\left\{ \begin{array}{ll} -0.2-0.1\mathbf{i },&{} x<0 \,\mathrm{and} \, y<0, \\ -0.1+0.1\mathbf{i },&{} x<0 \,\mathrm{and} \, y>0,\\ 0.1-0.1\mathbf{i }, &{} x>0 \,\mathrm{and} \, y<0,\\ 0.2+0.1\mathbf{i }, &{} x>0 \,\mathrm{and} \, y>0.\\ \end{array} \right. \end{aligned}$$

$\bigcap \nolimits _{\delta >0}\bigcap \nolimits _{\mu (\mathcal {N})=0}K[f(B(z,\,\delta )\backslash {\mathcal {N}})]$ and $\bigcap \nolimits _{\delta>0}\bigcap \nolimits _{\mu (\mathcal {N})=0}K[f^{R}(B(x,\,\delta ) \backslash \mathcal {N})]+\mathbf{i }\bigcap \nolimits _{\delta >0}\bigcap \nolimits _{\mu (\mathcal {N})=0}K[f^{I}(B(y,\,\delta )\backslash {\mathcal {N}})]$ at point $z=0$ are shown in Figs. 1 and 2, respectively. It is easy to see the correction of formula (2.9).

Fig. 1

Complex differential inclusion of $f(\cdot )$ at $z=0$ in Definition 2.2

Fig. 2

Complex differential inclusion of $f(\cdot )$ at $z=0$ in the special way of (2.7)

According to A(3),  there exist $\alpha ^{R}_{i},\,\eta ^{R}_{i}$ and $\alpha ^{I}_{i},\,\eta ^{I}_{i}$ satisfying

$$\begin{aligned} \left\{ \begin{array}{l} \sup \nolimits _{\gamma ^{R}_{i}\in K[f^{R}_{i}(x_{i})]}|\gamma ^{R}_{i}|\le \alpha ^{R}_{i}|x_{i}|+\eta ^{R}_{i},\\ \sup \nolimits _{\gamma ^{I}_{i}\in K[f^{I}_{i}(y_{i})]}|\gamma ^{I}_{i}|\le \alpha ^{I}_{i}|y_{i}|+\eta ^{I}_{i}, \end{array} \right. \end{aligned}$$

(2.10)

where

$$\begin{aligned} K\left[ f^{R}_{i}\left( x_{i}\right) \right] =\left[ \mathrm{min}\left\{ f^{R-}_{i}\left( x_{i}\right) ,\,f^{R+}_{i}\left( x_{i}\right) \right\} ,\,\mathrm{max}\left\{ f^{R-}_{i}\left( x_{i}\right) ,\,f^{R+}_{i}\left( x_{i}\right) \right\} \right] , \end{aligned}$$

and

$$\begin{aligned} K\left[ f^{I}_{i}\left( y_{i}\right) \right] = \left[ \mathrm{min}\left\{ f^{I-}_{i}\left( y_{i}\right) ,\, f^{I+}_{i}\left( y_{i}\right) \right\} ,\,\mathrm{max}\left\{ f^{I-}_{i}\left( y_{i}\right) ,\,f^{I+}_{i}\left( y_{i}\right) \right\} \right] . \end{aligned}$$

According to Definition 2.3, that $z(t)=x(t)+\mathbf{i }y(t)$ is a solution of system (2.1) is equivalent to that $[x^\mathrm{T}(t),\,y^{\mathrm{T}}(t)]^{\mathrm{T}}$ is a solution of system (2.7), i.e.,

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}(t)\in {-}Dx(t)+A^{R}K[f^{R}(x)]-A^{I}K[f^{I}(y)]+u^{R},\\ {\dot{y}}(t)\in {-}Dy(t)+A^{I}K[f^{R}(x)]+A^{R}K[f^{I}(y)]+u^{I}.\\ \end{array} \right. \end{aligned}$$

(2.11)

Now denote

$$\begin{aligned} \begin{array}{lll} w(t)=\left[ \begin{array}{c} x(t)\\ y(t)\\ \end{array} \right] ,&{} {\bar{D}}=\left[ \begin{array}{cc} D&{} 0 \\ 0&{} D\\ \end{array} \right] ,&{} {\bar{A}}=\left[ \begin{array}{cc} A^{R}&{} -A^{I}\\ A^{I}&{} A^{R}\\ \end{array} \right] , \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{ll} K[f(w(t))]=\left[ \begin{array}{c} K[f^{R}(x(t))]\\ K[f^{I}(y(t))]\\ \end{array} \right] ,&{} {\bar{u}}=\left[ \begin{array}{c} u^{R}\\ u^{I}\\ \end{array} \right] . \end{array} \end{aligned}$$

Equation (2.11) can be rewritten as

$$\begin{aligned} {\dot{w}}\in {-}{\bar{D}}w+{\bar{A}}K[f(w(t))]+{\bar{u}}. \end{aligned}$$

(2.12)

According to Definition 2.4, we can give the definition of the IVP associated to system (2.7) as follows.

Definition 2.9

A absolutely continuous functions $[x^{\mathrm{T}},\,y^{\mathrm{T}}]^{\mathrm{T}}$ associated with a measurable functions $[(\gamma ^{\mathrm{R}})^\mathrm{T},\,(\gamma ^{\mathrm{I}})^{\mathrm{T}}]^{\mathrm{T}}$ is said to be a solution of the IVP for system (2.7) on $[t_{0},\,T)$ with initial value $x(t_0)=x_0,\, y(t_0)=y_0,$ if the following condition holds,

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}(t)= {-}Dx(t)+A^{R}\gamma ^{\mathrm{R}}(t)-A^{I}\gamma ^\mathrm{I}+u^{R},\quad \mathrm{for}\, a.e.\, t\in [t_{0},\,T),\\ {\dot{y}}(t)= {-}Dy(t)+A^{I}\gamma ^{\mathrm{R}}(t)+A^{R}\gamma ^\mathrm{I}+u^{I},\quad \mathrm{for}\, a.e.\, t\in [t_{0},\,T),\\ \gamma ^{R}_j(t)\in K[f^{R}(x)],\quad \mathrm{for}\, a.e.\, t\in [t_{0},\,T),\\ \gamma ^{I}_j(t)\in K[f^{I}(x)],\quad \mathrm{for}\, a.e.\, t\in [t_{0},\,T), \end{array} \right. \end{aligned}$$

where $x(t)=[x_1(t),\,x_2(t),\ldots ,x_n(t)]^{\mathrm{T}},\, y(t)=[y_1(t),\,y_2(t),\ldots ,y_n(t)]^{\mathrm{T}},\, \gamma ^{R}(t)=[\gamma ^{\mathrm{R}}_1(t),\,\gamma ^{\mathrm{R}}_2(t),\ldots ,\gamma ^{\mathrm{R}}_n(t)]^{\mathrm{T}}$ and $\gamma ^{R}(t)=[\gamma ^{\mathrm{I}}_1(t),\,\gamma ^\mathrm{I}_2(t),\ldots ,\gamma ^{\mathrm{I}}_n(t)]^{\mathrm{T}}.$

According to Definition 2.5, $z^{*}=x^{*}+\mathbf{i }y^{*}$ is an equilibrium point of system (2.1) if and only if $[(x^{*})^{\mathrm{T}},\,(y^{*})^{\mathrm{T}}]^{\mathrm{T}}$ is an equilibrium point of system (2.7). That is to say, there exist $\gamma ^{R^{*}}=[\gamma ^{R^{*}}_{1},\,\gamma ^{R^{*}}_{2},\ldots ,\gamma ^{R^{*}}_{n}]^\mathrm{T}$ and $\gamma ^{I^{*}}=[\gamma ^{I^{*}}_{1},\,\gamma ^{I^{*}}_{2},\ldots ,\gamma ^{I^{*}}_{n}]^\mathrm{T},$ such that

$$\begin{aligned} \left\{ \begin{array}{l} 0={-}Dx^{*}+A^{R}\gamma ^{R^{*}}-A^{I}\gamma ^{I^{*}}+u^{R},\\ 0={-}Dy^{*}+A^{I}\gamma ^{R^{*}}+A^{R}\gamma ^{I^{*}}+u^{I},\\ \end{array} \right. \end{aligned}$$

(2.13)

holds, where $\gamma ^{R^{*}}_{i}\in K[f_{i}^{R}(x_{i}^{*})]$ and $\gamma ^{I^{*}}_{i}\in K[f_{i}^{I}(y^{*}_{i})].$ Therefore, we can analyze the existence and global stability of equilibrium point for system (2.7) through analyzing the equilibrium point of (2.12).

Before giving the stability analysis on the equilibrium point of system (2.1), we present four important lemmas, which will be used later.

Lemma 2.10

(Leray–Schauder alternative theorem [40]) If X is a Banach space, $E\subset X$ is nonempty convex with $0\in E$ and $G{\text {:}}\,E\mapsto P_{kc}(E)$ is an upper semi-continuous multifunction which maps bounded set into relatively compact sets, then one of the following statements is true:

• (i) the set $\Gamma =\{x\in E{\text {:}}\,x\in \lambda G(x),\,\lambda \in (0,\,1)\}$ is unbounded;

• (ii) the $G(\cdot )$ has a fixed point in E,  i.e., there exists $x\in E$ such that $x\in G(x).$ Here $P_{kc}(E)$ denotes the collection of all nonempty, compact, convex subset of E.

Lemma 2.11

[31, 33] If $V(x){\text {:}}\, R^{n}\rightarrow R$ is C-regular, and x(t) is absolutely continuous on any compact subinterval of $[0,\,{+}\infty ).$ Then, x(t) and $V(x(t)){\text {:}}\,[0,\,{+}\infty )\rightarrow R$ are differentiable for a.a. $t\in [0,\,{+}\infty )$ and

$$\begin{aligned} \frac{d}{dt}V(x(t))=\gamma (t)^{\mathrm{{T}}}{\dot{x}}(t), \quad \forall t\in \partial _{c}V(x(t)), \end{aligned}$$

where $\partial _{c}V(x(t))$ is the Clark generalized gradient of V at x(t) and $\gamma (t)$ is an measurable function.

Lemma 2.12

[41] Assume that there exists a continuous, differentiable almost everywhere, positive definite and radially unbounded function $V{\text {:}}\,R^{n}\mapsto R,$ such that:

• (i) ${\dot{V}}\le 0$ for all $x\in R^{n};$

• (ii) The origin is the only invariant subset of the set $E=\{x\in R^{n}{\text {:}}\,{\dot{V}}=0\}.$

Then the equilibrium $x=0$ of system (2.1) is globally asymptotically stable on $R^{n}.$

Lemma 2.13

[14] For any vectors $x,\,y\in R^m$ and positive matrix $P\in R^{m\times m},$ the following matrix inequality holds:

$$\begin{aligned} 2x^{\mathrm{T}}y\le x^{\mathrm{T}}Qx+y^{\mathrm{T}}Q^{-1}y. \end{aligned}$$

3 Dynamical Behavior Analysis

The goal of this section is to investigate the dynamical behavior of system (2.1). Firstly, we investigate the viability, namely, there exists at least one solution of system (2.1) on $[0,\,{+}\infty ].$

Lemma 3.1

[36] If a set-valued map $F{\text {:}}\, E\mapsto R^{n},\,(E\in R^{n})$ is upper semi-continuous in $R^{n}$ with nonempty bounded closed convex values and there exist nonnegative constants p and q such that $\Vert F(x)\Vert \le p\Vert x\Vert +q,$ then the maximal interval of existence of each solution with initial condition $x(t_{0})=x_{0}$ of the differential inclusion ${\dot{x}}\in F(x)$ is $[t_{0},\,{+}\infty ).$

Theorem 3.2

Suppose A(1)–A(3) are satisfied, then system (2.1) with initial value $z(0)=z_0$ has at least a solution z(t) on $[0,\,{+}\infty ).$

Proof

Based on the detailed discussions in Sect. 2 and formula (2.12), the set-valued map $w(t)\mapsto -{\bar{D}}w(t)+{\bar{A}}K[f(w(t))]+{\bar{u}}$ is upper-semi-continuous with nonempty compact convex values, and the local existence of a solution w(t) of system (2.12) can be guaranteed [37].

From A(3) and formula (2.10), there exist two nonnegative constants ${\bar{\alpha }},\,{\bar{\beta }}$ satisfying

$$\begin{aligned} \Vert K[f(w(t))]\Vert \le {\bar{\alpha }}\Vert w(t)\Vert +{\bar{\beta }}. \end{aligned}$$

(3.1)

It follows that

$$\begin{aligned} \begin{array}{ll} &{}\Vert -{\bar{D}}w(t)+{\bar{A}}K[f(w(t))]+{\bar{u}}\Vert \\ &{}\quad \le \Vert {\bar{D}}\Vert \Vert w(t)\Vert +\Vert {\bar{A}}\Vert ({\bar{\alpha }}\Vert w(t)\Vert +{\bar{\beta }})+\Vert {\bar{u}}\Vert \\ &{}\quad =(\Vert {\bar{D}}\Vert +{\bar{\alpha }}\Vert {\bar{A}}\Vert )\Vert w(t)\Vert +({\bar{\beta }}\Vert {\bar{A}}\Vert +\Vert {\bar{u}}\Vert )\\ &{}\quad =\bar{{\bar{\alpha }}}\Vert w(t)\Vert +\bar{{\bar{\beta }}}, \end{array} \end{aligned}$$

(3.2)

where $\bar{{\bar{\alpha }}}=\Vert {\bar{D}}\Vert +{\bar{\alpha }}\Vert {\bar{A}}\Vert$ and $\bar{{\bar{\beta }}}={\bar{\beta }}\Vert {\bar{A}}\Vert +\Vert {\bar{u}}\Vert .$

According to (2.12), for the fixed w,  we have

$$\begin{aligned} w(t)\in w(0)+\int _{0}^{t}[-{\bar{D}}w(s)+{\bar{A}}K[f(w(s))]+{\bar{u}}]\mathrm{d}s. \end{aligned}$$

It follows that

$$\begin{aligned} \Vert w(t)\Vert\le & {} \Vert w(0)\Vert +\int _{0}^{t}\Vert -{\bar{D}}w(s)+{\bar{A}}K[f(w(s))]+{\bar{u}}\Vert \mathrm{d}s\\\le & {} (\Vert w(0)\Vert +\bar{{\bar{\beta }}}t)+\bar{{\bar{\alpha }}}\int _{0}^{t}\Vert w(s)\Vert \mathrm{d}s.\\ \end{aligned}$$

By the Gronwall inequality, one obtains

$$\begin{aligned} \Vert w(t)\Vert \le (\Vert w(0)\Vert +\bar{{\bar{\beta }}}t)e^{\bar{{\bar{\alpha }}} t}. \end{aligned}$$

Hence, since w(t) remains bounded for positive times, it is defined on $[0,\,{+}\infty ),$ i.e., x(t) and y(t) are existed on $[0,\,{+}\infty ).$ Let $z(t)=x(t)+\mathbf{i }y(t),$ then z(t) exists on $[0,\,{+}\infty )$ and satisfies:

$$\begin{aligned} {\dot{z}}(t)\in {-}Dz(t)+AK[f(z)]+u. \end{aligned}$$

This completes the proof of Theorem 3.2. $\square$

Theorem 3.3

There exists at least one equilibrium of system (2.1) if A(1)–A(3) are satisfied and the following two assumptions hold

A(4) For any $(u_{1},\,v_{1})\in R^{2}$ and $(u_{2},\,v_{2})\in R^{2},$ there exist two constant numbers $L_{i}^{R}$ and $L_{i}^{I},$ such that

$$\begin{aligned} \frac{\gamma ^{R}_{i}-\zeta ^{R}_{i}}{u_{1}-u_{2}}\ge {-}L^{R}_{i}\quad \frac{\gamma ^{I}_{i}-\zeta ^{I}_{i}}{v_{1}-v_{2}}\ge {-}L^{I}_{i}, \end{aligned}$$

(3.3)

for $\forall \gamma ^{R}_{i}\in K[f_{i}^{R}(u_{1})],\,\zeta ^{R}_{i}\in K[f_{i}^{R}(u_{2})],\,\gamma ^{I}_{i}\in K[f_{i}^{I}(v_{1})]$ and $\zeta ^{I}_{i}\in K[f_{i}^{I}(v_{2})].$

A(5) There exists $P=\mathrm{diag}\{p_{1},\,p_{2},\ldots ,p_{n}\}$ with $p_{i}>0$ such that $PA^{I}=(A^{I})^{\mathrm{T}}P,\, PA^{R}+(A^{R})^\mathrm{T}P<0,$ and

$$\begin{aligned} \frac{L_{i}p_{i}(\Vert A^{R}(A^{R})^{\mathrm{T}}+A^{I}(A^{I})^\mathrm{T}\Vert )}{d_{m}\lambda _{m}}< \frac{1}{4}, \end{aligned}$$

(3.4)

where $d_{m}=\min \nolimits _{1\le i\le n}\{d_{i}\},\, \lambda _{m}={-}\lambda _{M}\{PA^{R}+(A^{R})^{\mathrm{T}}P\}$ and $L_{i}=\max \{L_{i}^{R},\,L_{i}^{I}\}.$

Proof

Let $\Phi (w)=w-{\bar{D}}w+{\bar{A}}K[f(w)]+{\bar{u}},$ then that $w^{*}$ is an equilibrium of (2.12) is equivalent to say that $w^{*}$ is a fixed point of $\Phi (\cdot ),$ i.e., $w^{*}\in \Phi (w^{*}).$ It is clear that $\Phi {\text {:}}\,R^{2n}\mapsto P_{kc}(R^{2n})$ is an upper semi-continuous multifunction which maps bounded sets into relatively compact sets under the assumptions A(1)–A(3). In order to solve the fixed point problem $w^{*}\in \Phi (w^{*}),$ it is sufficient to show that the set $\Gamma =\{w\in R^{2n}{\text {:}}\,w\in \theta \Phi (w),\,\theta \in (0,\,1)\}$ is bounded. Let

$$\begin{aligned} \Phi (w,\,\theta )={-}(1-\theta )w+\theta [-{\bar{D}}w+{\bar{A}}K[f(w)]+{\bar{u}}], \end{aligned}$$

(3.5)

then $\Gamma =\{w\in R^{2n}{\text {:}}\,0\in \Phi (w,\,\theta ),\theta \in (0,\,1)\}.$ Rewrite (3.5) as

$$\begin{aligned} \Phi (w,\,\theta )={-}(1-\theta )w+\theta [-{\bar{D}}w+{\bar{A}}K[{\tilde{f}}(w)]+\tilde{{\bar{u}}}], \end{aligned}$$

(3.6)

where ${\tilde{f}}(w)=f(w)-{\tilde{\eta }},\, {\tilde{\eta }}\in K[f(0)]$ is a constant vector, and $\tilde{{\bar{u}}}={\bar{A}}{\tilde{\eta }}+{\bar{u}}.$

From A(5),  if $L_{i}>0,$ we can choose a positive number c such that

$$\begin{aligned} \frac{2\Vert (A^{R})^{\mathrm{T}}A^{R}+(A^{I})^\mathrm{T}A^{I}\Vert }{d_{m}\lambda _{m}}<c< \frac{1}{2L_{i}p_{i}}. \end{aligned}$$

(3.7)

If $L_{i}<0,$ we can choose a positive number c such that

$$\begin{aligned} \frac{2\Vert (A^{R})^{\mathrm{T}}A^{R}+(A^{I})^\mathrm{T}A^{I}\Vert }{d_{m}\lambda _{m}}<c. \end{aligned}$$

(3.8)

For any $s\in \Phi (w,\,\theta ),$ there exits ${\hat{\gamma }}\in K[{\tilde{f}}(w)]$ such that $s={-}(1-\theta )w+\theta [-{\bar{D}}w+{\bar{A}}{\hat{\gamma }}+\tilde{{\bar{u}}}],$ where ${\hat{\gamma }}=[({\hat{\gamma }}^{R})^\mathrm{T},\,({\hat{\gamma }}^{I})^{\mathrm{T}}]^{\mathrm{T}},\, {\hat{\gamma }}^{R}\in K[{\tilde{f}}^{R}(x)],\, {\tilde{f}}^{R}(x)=f^{R}(x)-{\tilde{\eta }}^{R},\, {\tilde{\eta }}^{R}\in K[f^{R}(0)]$ and ${\hat{\gamma }}^{I}\in K[{\tilde{f}}^{I}(y)],\, {\tilde{f}}^{I}(y)=f^{I}(y)-{\tilde{\eta }}^{I},\, {\tilde{\eta }}^{I}\in K[f^{I}(0)].$ From the assumption A(4),  we can obtain that for any $(x_{i},\,y_{i})\in R^{2}$ and ${\hat{\gamma }}_{i}^{R}\in K[{\tilde{f}}_{i}^{R}(x_{i})],\, {\hat{\gamma }}_{i}^{I}\in K[{\tilde{f}}_{i}^{I}(y_{i})],$ it follows that

$$\begin{aligned} \frac{{\hat{\gamma }}^{R}_{i}}{x_{i}}\ge -L^{R}_{i}\ge -L_{i}\quad \frac{{\hat{\gamma }}^{I}_{i}}{y_{i}}\ge -L^{I}_{i}\ge -L_{i}.\nonumber \\ \end{aligned}$$

(3.9)

Therefore,

$$\begin{aligned} x_{i}^{2}+2c\left( {\hat{\gamma }}_{i}^{R}\right) p_{i}x_{i}\ge \left( 1-2cp_{i}L_{i}\right) x_{i}^{2},\quad y_{i}^{2}+2c\left( {\hat{\gamma }}_{i}^{I}\right) p_{i}y_{i}\ge \left( 1-2cp_{i}L_{i}\right) y_{i}^{2}.\nonumber \\ \end{aligned}$$

(3.10)

Since $d_i>0,$ one obtains

$$\begin{aligned} d_{i}x_{i}^{2}+2c\left( {\hat{\gamma }}_{i}^{R}\right) p_{i}d_{i}x_{i}\ge & {} \left( 1-2cp_{i}L_{i}\right) d_{i} x_{i}^{2},\quad d_{i}y_{i}^{2}+2c\left( {\hat{\gamma }}_{i}^{I}\right) p_{i}d_{i}y_{i}\nonumber \\\ge & {} \left( 1-2cp_{i}L_{i}\right) d_{i}y_{i}^{2}.\nonumber \\ \end{aligned}$$

(3.11)

It follows that

$$\begin{aligned}&{-}\left( x^{\mathrm{T}}Dx+2c\left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}PDx\right) \le {-}\varepsilon d_{m}x^{\mathrm{T}}x,\nonumber \\&\quad {-}\left( y^{\mathrm{T}}Dy+2c\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}PDy\right) \le {-}\varepsilon d_{m}y^{\mathrm{T}}y, \end{aligned}$$

(3.12)

where $\varepsilon =\min \nolimits _{1\le i\le n}(1-2cp_{i}L_{i})>0.$

Since $PA^{I}=(A^{I})^{\mathrm{T}}P,$ it is easy to get $({\hat{\gamma }}^{R})^\mathrm{T}PA^{I}{\hat{\gamma }}^{I}=({\hat{\gamma }}^{I})^\mathrm{T}PA^{I}{\hat{\gamma }}^{R},$ which will be used in (3.13).

Note that for any $s\in \Phi (w,\,\theta ),$

$$\begin{aligned}&(2w+2cP{\hat{\gamma }})^{\mathrm{T}}s=(2w+2cP{\hat{\gamma }})^\mathrm{T}[-(1-\theta )w+\theta (-{\bar{D}}w+{\bar{A}}{\hat{\gamma }}+\tilde{{\bar{u}}})]\nonumber \\&\quad ={-}2(1-\theta ) x^{\mathrm{T}}x-2(1-\theta )c\left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}Px -2\theta x^{\mathrm{T}}Dx-2c\theta \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}PDx\nonumber \\&\qquad +\,\theta \left[ 2x^\mathrm{T}\left( A^{R}{\hat{\gamma }}^{R}-A^{I}{\hat{\gamma }}^{I}\right) \right] +2\theta c\left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}P\left( A^{R}{\hat{\gamma }}^{R}-A^{I}{\hat{\gamma }}^{I}\right) \nonumber \\&\qquad +\,\theta \left( 2x+2cP{\hat{\gamma }}^{R}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{R}-2(1-\theta ) y^\mathrm{T}y-2(1-\theta )c\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}Py \nonumber \\&\qquad -\,2\theta y^{\mathrm{T}}Dy-2c\theta \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}PDy+\theta \left[ 2y^\mathrm{T}\left( A^{R}{\hat{\gamma }}^{I}+A^{I}{\hat{\gamma }}^{R}\right) \right] \nonumber \\&\qquad +\,2\theta c\left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}P\left( A^{I}{\hat{\gamma }}^{R}+A^{R}{\hat{\gamma }}^{I}\right) +\theta \left( 2y+2cP{\hat{\gamma }}^{I}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{I}\nonumber \\&\quad \le {-}\,2(1-\theta ) x^{\mathrm{T}}x-2(1-\theta )c\left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}Px -\theta x^{\mathrm{T}}Dx-2c\theta \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}PDx\nonumber \\&\qquad -\,\theta \left[ \left( \frac{D^{\frac{1}{2}}x}{\sqrt{2}}-\sqrt{2}D^{-\frac{1}{2}}A^{R}{\hat{\gamma }}^{R}\right) ^\mathrm{T}\left( \frac{D^{\frac{1}{2}}x}{\sqrt{2}}-\sqrt{2}D^{-\frac{1}{2}}A^{R}{\hat{\gamma }}^{R}\right) \right] \nonumber \\&\qquad -\,\theta \left[ \left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}x+\sqrt{2}D^{-\frac{1}{2}}A^{I}{\hat{\gamma }}^{I}\right) ^\mathrm{T}\left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}x+\sqrt{2}D^{-\frac{1}{2}}A^{I}{\hat{\gamma }}^{I}\right) \right] \nonumber \\&\qquad +\,2\theta \left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}\left( A^{R}\right) ^\mathrm{T}D^{-1}A^{R}{\hat{\gamma }}^{R}+2\theta \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}\left( A^{I}\right) ^{\mathrm{T}}D^{-1}A^{I}{\hat{\gamma }}^{I}\nonumber \\&\qquad -\,\theta c\left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}\left( P\left( -A^{R}\right) +\left( -A^{R}\right) ^\mathrm{T}P\right) {\hat{\gamma }}^{R}-2(1-\theta ) y^\mathrm{T}y\nonumber \\&\qquad -\,2(1-\theta )c\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}Py -\theta y^\mathrm{T}Dy-2c\theta \left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}PDy\nonumber \\ \end{aligned}$$

$$\begin{aligned}&\quad \qquad -\,\theta \left[ \left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}y-\sqrt{2}D^{-\frac{1}{2}}A^{R}{\hat{\gamma }}^{I}\right) ^\mathrm{T}\left( \frac{D^{\frac{1}{2}}y}{\sqrt{2}}-\sqrt{2}D^{-\frac{1}{2}}A^{R}{\hat{\gamma }}^{I}\right) \right] \nonumber \\&\quad \qquad -\,\theta \left[ \left( \frac{D^{\frac{1}{2}}x}{\sqrt{2}}-\sqrt{2}D^{-\frac{1}{2}}A^{I}{\hat{\gamma }}^{I}\right) ^\mathrm{T}\left( \frac{D^{\frac{1}{2}}y}{\sqrt{2}}-\sqrt{2}D^{-\frac{1}{2}}A^{I}{\hat{\gamma }}^{R}\right) \right] \nonumber \\&\quad \qquad +\,2\theta \left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}\left( A^{R}\right) ^\mathrm{T}D^{-1}A^{R}{\hat{\gamma }}^{I}+2\theta \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}\left( A^{I}\right) ^{\mathrm{T}}D^{-1}A^{I}{\hat{\gamma }}^{R}\nonumber \\&\quad \qquad -\,\theta c\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}\left( P \left( -A^{R}\right) +\left( -A^{R}\right) ^\mathrm{T}P\right) {\hat{\gamma }}^{I}\nonumber \\&\quad \qquad +\,\theta \left( 2x+2cP{\hat{\gamma }}^{R}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{R}+\theta \left( 2y+2cP{\hat{\gamma }}^{I}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{I}\nonumber \\&\quad \quad \le {-}\,(1-\theta ) x^{\mathrm{T}}x-2(1-\theta )c\left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}Px -\theta x^{\mathrm{T}}Dx-2c\theta \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}PDx\nonumber \\&\quad \qquad +\,\theta \left( 2x+2cP{\hat{\gamma }}^{R}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{R}-\theta \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}\left[ c\lambda _{m}-\frac{2\Vert (A^{I})^{\mathrm{T}}A^{I}+(A^{R})^\mathrm{T}A^{R}\Vert }{d_{m}}\right] {\hat{\gamma }}^{R}\nonumber \\&\quad \qquad -\,2(1-\theta ) y^{\mathrm{T}}y-(1-\theta )c\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}Py -\theta y^{\mathrm{T}}Dy-2c\theta \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}PDy\nonumber \\&\quad \qquad +\,\theta \left( 2y+2cP{\hat{\gamma }}^{I}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{I}-\theta \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}\left[ c\lambda _{m}-\frac{2\Vert (A^{I})^{\mathrm{T}}A^{I}+(A^{R})^\mathrm{T}A^{R}\Vert }{d_{m}}\right] {\hat{\gamma }}^{I}\nonumber \\&\quad \quad \le {-}\,(1-\theta )\varepsilon x^{\mathrm{T}}x-\theta \varepsilon d_{m} x^{\mathrm{T}}x -(1-\theta )\varepsilon y^\mathrm{T}y-\theta \varepsilon d_{m} y^{\mathrm{T}}y\nonumber \\&\quad \qquad +\,\theta \left( 2x+2cP{\hat{\gamma }}^{R}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{R}+\theta \left( 2y+2cP{\hat{\gamma }}^{I}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{I}\nonumber \\&\quad \quad ={-}(1-\theta )\varepsilon w^{\mathrm{T}}w-\theta \varepsilon d_{m} w^{\mathrm{T}}w-2\theta (2w+2cP{\hat{\gamma }})^{\mathrm{T}}\tilde{{\bar{u}}}\nonumber \\&\quad \quad \le {-}(1-\theta )\varepsilon w^{\mathrm{T}}w-\theta \varepsilon d_{m} w^{\mathrm{T}}w+2\left( 1+cp_{M}{\bar{\alpha }}\right) \Vert \tilde{{\bar{u}}}\Vert \Vert w\Vert +2cp_{M}{\bar{\beta }}\Vert \tilde{{\bar{u}}}\Vert \nonumber \\&\quad \quad \le {-}\alpha \Vert w\Vert ^{2}+M\Vert w\Vert +N, \end{aligned}$$

(3.13)

where $\alpha =\min \{\varepsilon ,\,\varepsilon d_{m}\},\, M=2(1+cp_{M}{\bar{\alpha }})\Vert \tilde{{\bar{u}}}\Vert ,\, N=2cp_{M}{\bar{\beta }}\Vert \tilde{{\bar{u}}}\Vert$ and $p_{M}=\max \nolimits _{1\le i\le n}\{p_{i}\}.$

If $R_{0}$ is big enough, then

$$\begin{aligned} (2w+2cP{\hat{\gamma }})^{\mathrm{T}}s<0, \end{aligned}$$

(3.14)

for $\Vert w\Vert >R_{0},$ which means that $0\not \in \Phi (w,\,\theta )$ as $\Vert w\Vert >R_{0},$ i.e., $0\in \Phi (w,\,\theta )$ only if $\Vert w\Vert \le R_{0},$ so $\Gamma$ is bounded. According to Lemma 2.10, there exists $w^{*}\in R^{2n}$ such that $w^{*}\in \Phi (w^{*}).$ By Definition 2.2 in [34], $w^{*}$ is an equilibrium of system (2.12), i.e., $w^{*}=[(x^{*})^{\mathrm{T}},\,(y^{*})^\mathrm{T}]^{\mathrm{T}}$ is an equilibrium of system (2.7). From (2.13), we can obtain the existence of an output equilibrium $[(\gamma ^{R^{*}})^{\mathrm{T}},\,(\gamma ^{I^{*}})^{\mathrm{T}}]^{\mathrm{T}}$ corresponding to $[(x^{*})^{\mathrm{T}},\,(y^{*})^{\mathrm{T}}]^{\mathrm{T}}.$ Let $z^{*}=x^{*}+\mathbf{i }y^{*}$ and $\gamma ^{*}=\gamma ^{R^{*}}+\mathbf{i }\gamma ^{I^{*}},$ then $z^{*}$ is an equilibrium of system (2.1) and $\gamma ^{*}$ is an output equilibrium corresponding to $z^{*}.$ $\square$

Remark 7

In many papers, such as [14, 21, 24, 25], the activation functions are assumed to satisfy Lipschitz condition. In this paper, this assumption is removed. Since the continuity of the activation function implies the assumption A(4),  our result is less conservative.

To simplify the proof of global stability of system (2.1), we shall shift the equilibrium point $z^{*}=x^{*}+\mathbf{i }y^{*}$ of (2.1) to the origin. Let ${\tilde{z}}=z-z^{*}$ and ${\tilde{\gamma }}=\gamma -\gamma ^{*}.$ Then we have

$$\begin{aligned} \dot{{\tilde{z}}}={-}D{\tilde{z}}+A{\tilde{\gamma }}, \end{aligned}$$

(3.15)

where ${\tilde{\gamma }}\in K[{\tilde{f}}(z(t))]$ and ${\tilde{f}}_{i}(z_{i}(t))=f_{i}({\tilde{z}}_{i}(t)+z_{i}^{*}),\, i=1,\,2,\ldots ,n.$ Obviously, ${\tilde{f}}$ satisfies A(1)–A(3) and $0\in K[{\tilde{f}}(0)].$ Separated (3.15) with its real and imaginary part, it follows that

$$\begin{aligned} \left\{ \begin{array}{l} \dot{{\tilde{x}}}={-}D{\tilde{x}}+A^{R}{\tilde{\gamma }}^{R}-A^{I}{\tilde{\gamma }}^{I},\\ \dot{{\tilde{y}}}={-}D{\tilde{y}}+A^{I}{\tilde{\gamma }}^{R}+A^{R}{\tilde{\gamma }}^{I},\\ \end{array} \right. \end{aligned}$$

(3.16)

where ${\tilde{x}}=x-x^{*},\,{\tilde{y}}=y-y^{*},\, {\tilde{\gamma }}^{R}\in K[{\tilde{f}}^{R}(x)],\, {\tilde{f}}_{i}^{R}(x_{i})=f_{i}^{R}(x_{i}^{*}+{\tilde{x}}_{i})$ and ${\tilde{\gamma }}^{I}\in K[{\tilde{f}}^{I}(y)],\, {\tilde{f}}_{i}^{I}(y_{i})=f_{i}^{I}(y_{i}^{*}+{\tilde{y}}_{i}).$ Clearly, from the assumption A(4),  we can obtain that for any $(\tilde{x_{i}},\,{\tilde{y}}_{i})\in R^{2}$ and ${\tilde{\gamma }}_{i}^{R}\in K[{\tilde{f}}_{i}^{R}({\tilde{x}}_{i})],\, {\tilde{\gamma }}_{i}^{I}\in K[{\tilde{f}}_{i}^{I}({\tilde{y}}_{i})],$ it follows that

$$\begin{aligned} \frac{{\tilde{\gamma }}^{R}_{i}}{{\tilde{x}}_{i}}\ge {-}L^{R}_{i}\quad \frac{{\tilde{\gamma }}^{I}_{i}}{{\tilde{y}}_{i}}\ge {-}L^{I}_{i}. \end{aligned}$$

(3.17)

Theorem 3.4

(Global Asymptotic Stability) Assume the assumptions A(1)–A(5) are satisfied, then for any input vector $u\in C^{n},$ system (2.1) has a unique equilibrium point $z^{*},$ which is globally asymptotically stable.

Proof

Let us consider the Lyapunov function

$$\begin{aligned} V[{\tilde{z}},\,{\tilde{\gamma }}]={\tilde{x}}^\mathrm{T}{\tilde{x}}+{\tilde{y}}^\mathrm{T}{\tilde{y}}+2c\sum \limits _{i=1}^{n}p_{i}\int _{0}^{{\tilde{x}}_{i}}{\tilde{f}}_{i}^{R}(\rho )\mathrm{d}\rho +2c\sum \limits _{i=1}^{n}p_{i}\int _{0}^{{\tilde{y}}_{i}}{\tilde{f}}_{i}^{I}(\rho )\mathrm{d}\rho , \end{aligned}$$

(3.18)

where c is defined in (3.7) or (3.8).

From (3.16) and with the similar analysis in [38], it is easy to obtain $V[{\tilde{z}},\,{\tilde{\gamma }}]\ge 0,\,V(0)=0.$ In addition, it is obvious that $V[{\tilde{z}},\,{\tilde{\gamma }}]$ is C-regular, continuous, positive definite, and radially unbounded.

By Lemma 2.11, we calculate and estimate the derivative along system (3.16) as follows

$$\begin{aligned} {\dot{V}}[{\tilde{z}},\,{\tilde{\gamma }}]= & {} \left( 2{\tilde{x}}+2cP{\tilde{\gamma }}^{R}\right) ^\mathrm{T}\left[ -D{\tilde{x}}+A^{R}{\tilde{\gamma }}^{R}-A^{I}{\tilde{\gamma }}^{I}\right] \nonumber \\&\quad +\left( 2{\tilde{y}}+2cP{\tilde{\gamma }}^{I}\right) ^\mathrm{T}\left[ -D{\tilde{y}}+A^{R}{\tilde{\gamma }}^{I}+A^{I}{\tilde{\gamma }}^{R}\right] \nonumber \\\le & {} {-} {\tilde{x}}^{\mathrm{T}}D{\tilde{x}}-2c\left( {\tilde{\gamma }}^{R}\right) ^\mathrm{T}PD{\tilde{x}}-{\tilde{y}}^\mathrm{T}D{\tilde{y}}-2c\left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}PD{\tilde{y}}\nonumber \\&\quad -\left[ \left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}{\tilde{x}}-\sqrt{2}D^{-\frac{1}{2}}A^{R}{\tilde{\gamma }}^{R}\right) ^\mathrm{T}\left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}{\tilde{x}}-\sqrt{2}D^{-\frac{1}{2}}A^{R}{\tilde{\gamma }}^{R}\right) \right] \nonumber \\&\quad -\left[ \left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}{\tilde{x}}+\sqrt{2}D^{-\frac{1}{2}}A^{I}{\tilde{\gamma }}^{I}\right) ^\mathrm{T}\left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}{\tilde{x}}+\sqrt{2}D^{-\frac{1}{2}}A^{I}{\tilde{\gamma }}^{I}\right) \right] \nonumber \\&\quad +\,2\left( {\tilde{\gamma }}^{R}\right) ^{\mathrm{T}}\left( A^{R}\right) ^\mathrm{T}D^{-1}A^{R}{\tilde{\gamma }}^{R}+2\left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}\left( A^{I}\right) ^{\mathrm{T}}D^{-1}A^{I}{\tilde{\gamma }}^{I}\nonumber \\&\quad -\,c\left( {\tilde{\gamma }}^{R}\right) ^{\mathrm{T}}\left( P\left( -A^{R}\right) +\left( -A^{R}\right) ^\mathrm{T}P\right) {\tilde{\gamma }}^{R}\end{aligned}$$

(3.19)

$$\begin{aligned}&\quad -\left[ \left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}{\tilde{y}}-\sqrt{2}D^{-\frac{1}{2}}A^{R}{\tilde{\gamma }}^{I}\right) ^\mathrm{T}\left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}{\tilde{y}}-\sqrt{2}D^{-\frac{1}{2}}A^{R}{\tilde{\gamma }}^{I}\right) \right] \nonumber \\&\quad -\left[ \left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}{\tilde{x}}-\sqrt{2}D^{-\frac{1}{2}}A^{I}{\tilde{\gamma }}^{I}\right) ^\mathrm{T}\left( \frac{1}{\sqrt{2}}D^{\frac{1}{2}}{\tilde{y}}-\sqrt{2}D^{-\frac{1}{2}}A^{I}{\tilde{\gamma }}^{R}\right) \right] \nonumber \\&\quad +\,2\left( {\tilde{\gamma }}^{I}\right) ^{\mathrm{T}}\left( A^{R}\right) ^\mathrm{T}D^{-1}A^{R}{\tilde{\gamma }}^{I}+2\left( {\tilde{\gamma }}^{R}\right) ^\mathrm{T}\left( A^{I}\right) ^{\mathrm{T}}D^{-1}A^{I}{\tilde{\gamma }}^{R}\nonumber \\&\quad -\,c\left( {\tilde{\gamma }}^{I}\right) ^{\mathrm{T}}\left( P\left( -A^{R}\right) +\left( -A^{R}\right) ^\mathrm{T}P\right) {\tilde{\gamma }}^{I}\nonumber \\\le & {} {-} {\tilde{x}}^{\mathrm{T}}D{\tilde{x}}-2c\left( {\tilde{\gamma }}^{R}\right) ^\mathrm{T}PD{\tilde{x}}-{\tilde{y}}^\mathrm{T}D{\tilde{y}}-2c\left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}PD{\tilde{y}}\nonumber \\&\quad -\left( {\tilde{\gamma }}^{R}\right) ^{\mathrm{T}}\left[ c\lambda _{m}-\frac{2\Vert (A^{I})^\mathrm{T}A^{I}+(A^{R})^\mathrm{T}A^{R}\Vert }{d_{m}}\right] {\tilde{\gamma }}^{R}-\left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}\nonumber \\&\quad \times \left[ c\lambda _{m}-\frac{2\Vert (A^{I})^{\mathrm{T}}A^{I}+(A^{R})^\mathrm{T}A^{R}\Vert }{d_{m}}\right] {\tilde{\gamma }}^{I}\nonumber \\\le & {} {-}\varepsilon d _{m}{\tilde{x}}^{\mathrm{T}}{\tilde{x}}-\varepsilon d _{m}{\tilde{y}}^{\mathrm{T}}{\tilde{y}}-\rho \left( {\tilde{\gamma }}^{R}\right) ^\mathrm{T}{\tilde{\gamma }}^{R} -\rho \left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}{\tilde{\gamma }}^{I} \end{aligned}$$

(3.20)

where $\rho =c \lambda _{m}-\frac{2\Vert (A^{R})^{\mathrm{T}}A^{R}+(A^{I})^\mathrm{T}A^{I}\Vert }{d_{m}}>0.$ Therefore, ${\dot{V}}$ is negative definite. From Lemma 2.12, it follows that 0 is globally asymptotically stable, i.e., 0 is an equilibrium point of (3.15). Therefore, the equilibrium $z^{*}=x^{*}+\mathbf{i }y^{*}$ of system (2.1) is globally asymptotically stable. From (3.20), there exists exactly one equilibrium $z^{*}$ of system (2.1). $\square$

From (3.20), we have ${\dot{V}}[{\tilde{z}},\,{\tilde{\gamma }}]\le -\rho ({\tilde{\gamma }}^{I})^{\mathrm{T}}{\tilde{\gamma }}^{I}$ and ${\dot{V}}[{\tilde{z}},\,{\tilde{\gamma }}]\le -\rho ({\tilde{\gamma }}^{R})^{\mathrm{T}}{\tilde{\gamma }}^{R}.$ It follows that

$$\begin{aligned} V[{\tilde{z}},\,{\tilde{\gamma }}](t)-V[{\tilde{z}},\,{\tilde{\gamma }}](0)\le {-}\rho \int _{0}^{t}\left( {\tilde{\gamma }}^{R}(s)\right) ^\mathrm{T}{\tilde{\gamma }}^{R}(s)\mathrm{d}s \end{aligned}$$

and

$$\begin{aligned} V[{\tilde{z}},\,{\tilde{\gamma }}](t)-V[{\tilde{z}},\,{\tilde{\gamma }}](0)\le -\rho \int _{0}^{t}\left( {\tilde{\gamma }}^{I}(s)\right) ^\mathrm{T}{\tilde{\gamma }}^{I}(s)\mathrm{d}s. \end{aligned}$$

Therefore, one obtains $\int _{0}^{t}({\tilde{\gamma }}^{R}(s))^\mathrm{T}{\tilde{\gamma }}^{R}(s)\mathrm{d}s\le \frac{V[{\tilde{z}},\,{\tilde{\gamma }}](0)}{\rho }$ and $\int _{0}^{t}({\tilde{\gamma }}^{I}(s))^\mathrm{T}{\tilde{\gamma }}^{I}(s)\mathrm{d}s\le \frac{V[{\tilde{z}},\,{\tilde{\gamma }}](0)}{\rho }.$

For any $\sigma >0,$ let $E^{R}_{\sigma }=\left\{ t\in [0,\,{+}\infty ){\text {:}}\,\Vert {\tilde{\gamma }}^{R}(t)\Vert >\frac{\sigma }{\sqrt{2}}\right\}$ and $E^{I}_{\sigma }=\big \{t\in [0,\,{+}\infty ){\text {:}}\,\Vert {\tilde{\gamma }}^{I}(t)\Vert >\frac{\sigma }{\sqrt{2}}\big \},$ we have

$$\begin{aligned}&\frac{V[{\tilde{z}},\,{\tilde{\gamma }}](0)}{\rho }\ge \int _{0}^{t}\left( {\tilde{\gamma }}^{R}(s)\right) ^\mathrm{T}{\tilde{\gamma }}^{R}(s)\mathrm{d}s\ge \int _{E^{R}_{\sigma }}\left( {\tilde{\gamma }}^{R}(s)\right) ^\mathrm{T}{\tilde{\gamma }}^{R}(s)\mathrm{d}s\ge \frac{\sigma ^{2}}{2}\mu \left( E^{R}_{\sigma }\right) ,\nonumber \\&\frac{V[{\tilde{z}},\,{\tilde{\gamma }}](0)}{\rho }\ge \int _{0}^{t}\left( {\tilde{\gamma }}^{I}(s)\right) ^\mathrm{T}{\tilde{\gamma }}^{I}(s)\mathrm{d}s\ge \int _{E^{I}_{\sigma }}\left( {\tilde{\gamma }}^{I}(s)\right) ^\mathrm{T}{\tilde{\gamma }}^{I}(s)\mathrm{d}s\ge \frac{\sigma ^{2}}{2}\mu \left( E^{I}_{\sigma }\right) .\nonumber \\ \end{aligned}$$

Therefore, $\mu (E^{R}_{\sigma })<\infty$ and $\mu (E^{I}_{\sigma })<\infty .$ Since $E_{\sigma }=\{t\in [0,\,{+}\infty ){\text {:}}\,\Vert {\tilde{\gamma }} (t)\Vert>\sigma \}\subseteq \left\{ t\in [0,\,{+}\infty ){\text {:}}\,\Vert {\tilde{\gamma }}^{R}\Vert>\frac{\sigma }{\sqrt{2}}\right\} \bigcup \left\{ t\in [0,\,{+}\infty ){\text {:}}\,\Vert {\tilde{\gamma }}^{I}(t)\Vert >\frac{\sigma }{\sqrt{2}}\right\} ,$ where ${\tilde{\gamma }}={\tilde{\gamma }}^{R}+\mathbf{i }{\tilde{\gamma }}^{I}.$ Therefore, $\mu (E_{\sigma })<\infty .$ From Proposition 2 in [31], one can see that ${\tilde{\gamma }}(t)$ converge to zero in measure, that is to say $\mu -\lim \nolimits _{t\rightarrow \infty }{\tilde{\gamma }}(t)=0$ and $\mu -\lim \nolimits _{t\rightarrow \infty }\gamma (t)=\gamma ^{*}.$ In view of Definition 2.7, the output solution $\gamma (t)=\gamma ^{R}(t)+\mathbf{i }\gamma ^{I}(t)$ of system (2.1) converges to $\gamma ^{*}=\gamma ^{R^{*}}+\mathbf{i }\gamma ^{I^{*}}.$

If we let the imaginary parts of all the variables and parameters be zero, system (2.1) becomes the neural network model in [39], which can be described as follows

$$\begin{aligned} {\dot{x}}(t)={-}Dx(t)+Af(x(t))+u. \end{aligned}$$

(3.21)

With the similar analysis, we can get the following corollary, which is the result of Theorem 2 in paper [39].

Corollary 3.5

Suppose the following assumptions are satisfied:

$A^{\prime }(1)$ :

For each $i=1,\,2,\ldots ,n,\, f_{i}(x_{i})$ is continuous at finite points $x^{k}_{i},\,k=1,\,2,\ldots ,s.$

$A^{\prime }(2)$ :

For every $k=1,\,2,\ldots ,s,$ the limitations $\lim \nolimits _{x\rightarrow x^{k+}_{i}}f_{i}(x)=f_{i}(x^{k+}_{i})$ and $\lim \nolimits _{x\rightarrow x^{k-}_{i}}f_{i}(x)=f_{i}(x^{k-}_{i})$ exist.

$A^{\prime }(3)$ :

For each $i=1,\,2,\ldots ,n,$ there exist nonnegative constants $\alpha _{i}$ and $\beta _{i}$ such that

$$\begin{aligned} \left\| f_{i}\left( x_{i}(t)\right) \right\| \leqslant \alpha _{i}\left\| x_{i}(t)\right\| +\beta _{i}. \end{aligned}$$

$A^{\prime }(4)$ :

For each $i=1,\,2,\ldots ,n,$ there exists a constant number $L_{i},$ such that for any $u\in R$ and $v\in R,\, \forall \gamma _{i}\in K[f_{i}(u)],\, \zeta \in K[f_{i}(v)],$

$$\begin{aligned} \frac{\gamma _{i}-\zeta _{i}}{u-v}\ge -L_{i}. \end{aligned}$$

$A^{\prime }(5)$ :

There exists $P=\mathrm{diag}\{p_{1},\,p_{2},\ldots ,p_n\}$ with $p_{i}>0$ such that $PA+A^{\mathrm{T}}P<0$ and

$$\begin{aligned} \frac{L_{i}p_{i}\Vert A^{\mathrm{T}}A\Vert }{d_{m}\lambda _{m}}< \frac{1}{4}, \end{aligned}$$

where $d_{m}=\min \nolimits _{1\le i\le n}\{d_{i}\},\, \lambda _{m}={-}\lambda _{M}\{PA+A^{\mathrm{T}}P\}.$

Then there exists at least one equilibrium of system (3.21). Furthermore, the equilibrium point is globally asymptotically stable.

In Theorems 3.3 and 3.4, the condition of $PA^{I}=(A^{I})^{\mathrm{T}}P$ is not satisfied for many complex-valued neural networks. Therefore, we proposed the following theorem.

Theorem 3.6

Suppose A(1)–A(4) are satisfied and the following assumption holds: ${\bar{A}}(5)$ There exists $P=\mathrm{diag}\{p_{1},\,p_{2},\ldots ,p_n\}$ with $p_{i}>0$ such that $Q=PA^{R}+(A^{R})^{\mathrm{T}}P+P+(A^{I})^\mathrm{T}PA^{I}<0$ and

$$\begin{aligned} \frac{L_{i}p_{i}\Vert (A^{R})^{\mathrm{T}}A^{R}+(A^{I})^\mathrm{T}A^{I}\Vert }{d_{m}\lambda _{m}}< \frac{1}{4}, \end{aligned}$$

(3.22)

where $d_{m}=\min \nolimits _{1\le i\le n}\{d_{i}\},\, \lambda _{m}={-}\lambda _{M}\{Q\}$ and $L_{i}=\max \{L_{i}^{R},\,L_{i}^{I}\}.$

Then system (2.1) has an unique equilibrium point $z^{*}.$ Moreover, $z^{*}$ is globally asymptotically stable and the output solution $\gamma$ converge to $\gamma ^{*}$ in measure.

Proof

Since $\theta >0$ and $c>0,$ using Lemma 2.13, one obtains

$$\begin{aligned} \theta c \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}PA^{I}{\hat{\gamma }}^{I}\le \theta c\left( \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}P{\hat{\gamma }}^{R}+\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}\left( A^{I}\right) ^\mathrm{T}PA^{I}{\hat{\gamma }}^{I}\right) \end{aligned}$$

and

$$\begin{aligned} \theta c \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}PA^{R}{\hat{\gamma }}^{I}\le \theta c\left( \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}P{\hat{\gamma }}^{I}+\left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}\left( A^{I}\right) ^\mathrm{T}PA^{I}{\hat{\gamma }}^{R}\right) . \end{aligned}$$

Submitting the above inequalities into (3.13) and (3.20), we can get

$$\begin{aligned}&(2w+2cP{\hat{\gamma }})^{\mathrm{T}}s \le -2(1-\theta ) x^\mathrm{T}x-2(1-\theta )c\left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}Px -\theta x^\mathrm{T}Dx-2c\theta \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}PDx\nonumber \\&\qquad +\,2\theta \left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}\left( A^{R}\right) ^\mathrm{T}D^{-1}A^{R}{\hat{\gamma }}^{R}+2\theta \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}\left( A^{I}\right) ^{\mathrm{T}}D^{-1}A^{I}{\hat{\gamma }}^{I}\nonumber \\&\qquad +\,\theta c\left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}\left( PA^{R}+\left( A^{R}\right) ^\mathrm{T}P\right) {\hat{\gamma }}^{R}+\theta c\left( \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}P{\hat{\gamma }}^{R}+\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}\left( A^{I}\right) ^\mathrm{T}PA^{I}{\hat{\gamma }}^{I}\right) \nonumber \\&\qquad -\,2(1-\theta ) y^{\mathrm{T}}y-2(1-\theta )c\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}Py -\theta y^{\mathrm{T}}Dy-2c\theta \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}PDy\nonumber \\&\qquad +\,2\theta \left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}\left( A^{R}\right) ^\mathrm{T}D^{-1}A^{R}{\hat{\gamma }}^{I}+2\theta \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}\left( A^{I}\right) ^{\mathrm{T}}D^{-1}A^{I}{\hat{\gamma }}^{R}\nonumber \\&\qquad +\,\theta c\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}\left( PA^{R}+\left( A^{R}\right) ^\mathrm{T}P\right) {\hat{\gamma }}^{I}+\theta c\left( \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}P{\hat{\gamma }}^{I}+\left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}\left( A^{I}\right) ^\mathrm{T}PA^{I}{\hat{\gamma }}^{R}\right) \nonumber \\&\qquad +\,\theta \left( 2x+2cP{\hat{\gamma }}^{R}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{R}+\theta \left( 2y+2cP{\hat{\gamma }}^{I}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{I}\nonumber \\&\quad \le {-}(1-\theta ) x^{\mathrm{T}}x-2(1-\theta )c\left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}Px -\theta x^{\mathrm{T}}Dx-2c\theta \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}PDx\nonumber \\&\qquad +\,\theta \left( 2x+2cP{\hat{\gamma }}^{R}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{R}-\theta \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}\left[ c\lambda _{m}-\frac{2\Vert (A^{I})^{\mathrm{T}}A^{I}+(A^{R})^\mathrm{T}A^{R}\Vert }{d_{m}}\right] {\hat{\gamma }}^{R}\nonumber \\&\qquad -\,2(1-\theta ) y^{\mathrm{T}}y-(1-\theta )c\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}Py -\theta y^{\mathrm{T}}Dy-2c\theta \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}PDy\nonumber \\&\qquad +\,\theta \left( 2y+2cP{\hat{\gamma }}^{I}\right) ^\mathrm{T}\tilde{{\bar{u}}}^{I}-\theta \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}\left[ c\lambda _{m}-\frac{2\Vert (A^{I})^{\mathrm{T}}A^{I}+(A^{R})^\mathrm{T}A^{R}\Vert }{d_{m}}\right] {\hat{\gamma }}^{I}\nonumber \\&\quad \le {-}\alpha \Vert w\Vert ^{2}+M\Vert w\Vert +N, \end{aligned}$$

and

$$\begin{aligned}&{\dot{V}}[{\tilde{z}},\,{\tilde{\gamma }}]\le {-} {\tilde{x}}^\mathrm{T}D{\tilde{x}}-2c\left( {\tilde{\gamma }}^{R}\right) ^\mathrm{T}PD{\tilde{x}}-{\tilde{y}}^\mathrm{T}D{\tilde{y}}-2c\left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}PD{\tilde{y}}\nonumber \\&\qquad +\,2\left( {\tilde{\gamma }}^{R}\right) ^{\mathrm{T}}\left( A^{R}\right) ^\mathrm{T}D^{-1}A^{R}{\tilde{\gamma }}^{R}+2\left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}\left( A^{I}\right) ^{\mathrm{T}}D^{-1}A^{I}{\tilde{\gamma }}^{I}\nonumber \\&\qquad +\,c\left( {\tilde{\gamma }}^{R}\right) ^{\mathrm{T}}\left( PA^{R}+\left( A^{R}\right) ^\mathrm{T}P\right) {\tilde{\gamma }}^{R}+\left( \left( {\hat{\gamma }}^{R}\right) ^\mathrm{T}P{\hat{\gamma }}^{R}+\left( {\hat{\gamma }}^{I}\right) ^{\mathrm{T}}\left( A^{I}\right) ^\mathrm{T}PA^{I}{\hat{\gamma }}^{I}\right) \nonumber \\&\qquad +\,2\left( {\tilde{\gamma }}^{I}\right) ^{\mathrm{T}}\left( A^{R}\right) ^\mathrm{T}D^{-1}A^{R}{\tilde{\gamma }}^{I}+2\left( {\tilde{\gamma }}^{R}\right) ^\mathrm{T}\left( A^{I}\right) ^{\mathrm{T}}D^{-1}A^{I}{\tilde{\gamma }}^{R}\nonumber \\&\qquad +\,c\left( {\tilde{\gamma }}^{I}\right) ^{\mathrm{T}}\left( PA^{R}+\left( A^{R}\right) ^\mathrm{T}P\right) {\tilde{\gamma }}^{I}+\left( \left( {\hat{\gamma }}^{I}\right) ^\mathrm{T}P{\hat{\gamma }}^{I}+\left( {\hat{\gamma }}^{R}\right) ^{\mathrm{T}}\left( A^{I}\right) ^\mathrm{T}PA^{I}{\hat{\gamma }}^{R}\right) \nonumber \\&\quad \le {-} {\tilde{x}}^{\mathrm{T}}D{\tilde{x}}-2c\left( {\tilde{\gamma }}^{R}\right) ^\mathrm{T}PD{\tilde{x}}-{\tilde{y}}^\mathrm{T}D{\tilde{y}}-2c\left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}PD{\tilde{y}}\nonumber \\&\qquad -\,\left( {\tilde{\gamma }}^{R}\right) ^{\mathrm{T}}\left[ c\lambda _{m}-\frac{2\Vert (A^{I})^\mathrm{T}A^{I}+(A^{R})^\mathrm{T}A^{R}\Vert }{d_{m}}\right] {\tilde{\gamma }}^{R}-\left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}\nonumber \\&\qquad \times \left[ c\lambda _{m}-\frac{2\Vert (A^{I})^{\mathrm{T}}A^{I}+(A^{R})^\mathrm{T}A^{R}\Vert }{d_{m}}\right] {\tilde{\gamma }}^{I}\nonumber \\&\quad \le {-}\varepsilon d _{m}{\tilde{x}}^{\mathrm{T}}{\tilde{x}}-\varepsilon d _{m}{\tilde{y}}^{\mathrm{T}}{\tilde{y}}-\rho \left( {\tilde{\gamma }}^{R}\right) ^\mathrm{T}{\tilde{\gamma }}^{R} -\rho \left( {\tilde{\gamma }}^{I}\right) ^\mathrm{T}{\tilde{\gamma }}^{I}. \end{aligned}$$

The rest proof are same with that in Theorems 3.3 and 3.4. $\square$

Theorem 3.7

(Convergence in Finite Time) Suppose the assumptions of Theorem 3.3 and the assumption A(6) below are satisfied:

A(6) $z_{i}^{*}=x_{i}^{*}+\mathbf{i }y_{i}^{*}$ is a discontinuous point of $f_{i}$ and $f_{i}^{R-}(x_{i}^{*})-\gamma ^{R^{*}}<0<f_{i}^{R+}(x_{i}^{*})-\gamma ^{R^{*}}$ and $f_{i}^{I-}(y_{i}^{*})-\gamma ^{I^{*}}<0<f_{i}^{I+}(y_{i}^{*})-\gamma ^{I^{*}},$ where $z^{*}=[z_{1}^{*},\,z_{2}^{*},\ldots ,z_{n}^{*}]^{\mathrm{T}}$ is an equilibrium of system (2.1).

Then, for each solution of system (2.1) with initial condition $z(t_0)=z_{0},$ there exists $t_{f}>0$ such that $z(t)=z^{*}$ for $t\ge t_{f},$ i.e., z(t) converges to the equilibrium $z^{*}$ in finite time $t_{f}.$

Proof

Let us define $\Delta _{i}^{R-}=\gamma ^{R^{*}}-f_{i}^{R-}(x_{i}^{*}),\, \Delta _{i}^{R+}=f_{i}^{R+}(x_{i}^{*})-\gamma ^{R^{*}},\, \Delta _{i}^{I-}=\gamma ^{I^{*}}-f_{i}^{I-}(x_{i}^{*}),\, \Delta _{i}^{I+}=f_{i}^{I+}(x_{i}^{*})-\gamma ^{I^{*}}$ and $\Delta =\min \nolimits _{i=1,2,\ldots ,n}\{\min \{\Delta _{i}^{R-},\,\Delta _{i}^{R+},\,\Delta _{i}^{I-},\,\Delta _{i}^{I+}\}\}.$

Since $\lim \nolimits _{\rho \rightarrow 0^{-}} {\tilde{f}}^{R}_{i}(\rho )\le -\Delta$ and $\lim \nolimits _{\rho \rightarrow 0^+} {\tilde{f}}^{R}_{i}(\rho )\ge \Delta ,\, \lim \nolimits _{\rho \rightarrow 0^{-}} {\tilde{f}}^{I}_{i}(\rho )\le -\Delta$ and $\lim \nolimits _{\rho \rightarrow 0^+} {\tilde{f}}^{I}_{i}(\rho )\ge \Delta ,$ there exists a sufficient small positive constant $\delta$ such that

$$\begin{aligned} \begin{array}{cc} \Vert {\tilde{f}}^{R}_{i}(x_{i})\Vert>\Delta , &{} \forall 0<\Vert x\Vert<\delta ,\\ \Vert {\tilde{f}}^{I}_{i}(y_{i})\Vert >\Delta , &{} \forall 0<\Vert y\Vert <\delta .\\ \end{array} \end{aligned}$$

Note that the equilibrium point $z^*$ of system (2.1) is globally asymptotically stable, thus for each solution z(t) of (2.1) with initial condition $z(t_0)=z_{0},$ there exists $t_{\delta }>0$ such that $\Vert x\Vert \le \delta$ and $\Vert y\Vert \le \delta$ for $t>t_{\delta }.$

Performing similar estimates as in the proof of Theorem 3.4, we get ${\dot{V}}[{\tilde{z}},\,{\tilde{\gamma }}]\le {-}\rho ({\tilde{\gamma }}^{I})^{\mathrm{T}}{\tilde{\gamma }}^{I}\le {-}\rho \Delta ^{2}$ and ${\dot{V}}[{\tilde{z}},\,{\tilde{\gamma }}]\le -\rho ({\tilde{\gamma }}^{R})^{\mathrm{T}}{\tilde{\gamma }}^{R}\le -\rho \Delta ^{2}.$ It is easy to get $V[{\tilde{z}},\,{\tilde{\gamma }}](t)\le 0$ for $t\ge \frac{V[{\tilde{z}},\,{\tilde{\gamma }}](0)}{\rho \Delta ^{2}}.$ It follows that $x(t)=x^{*}$ and $y(t)=y^{*}$ for $t\ge \frac{V[{\tilde{z}},\,{\tilde{\gamma }}](0)}{\rho \Delta ^{2}}+t_{\delta }.$ This implies that there exists a positive constant $t_{f}=\frac{V[{\tilde{z}},\,{\tilde{\gamma }}](0)}{\rho \Delta ^{2}}+t_{\delta }>0$ such that $z(t)=z^{*}$ for $t>t_{f}.$ $\square$

4 Numerical Examples

In this section, we will give two examples to demonstrate the above results.

Example 4.1

Consider a two-neuron complex-valued neural network described as follows:

$$\begin{aligned} {\dot{z}}={-}Dz+Af(z)+u, \end{aligned}$$

(4.1)

where

$$\begin{aligned} D=\left[ \begin{array}{cc} 2&{}0\\ 0&{}2\\ \end{array}\right] ,\quad A=\left[ \begin{array}{cc} -\frac{1}{10}+\frac{1}{20}\mathbf{i }&{}\frac{1}{5}+\frac{1}{10}\mathbf{i }\\ {-}\frac{1}{5}+\frac{1}{10}\mathbf{i }&{}{-}\frac{1}{10}+\frac{1}{20}\mathbf{i }\\ \end{array}\right] ,\quad u=\left[ \begin{array}{c} 1+0.5\mathbf{i }\\ 0.5+\mathbf{i }\\ \end{array}\right] . \end{aligned}$$

We choose the real part and imaginary part of discontinuous complex-valued activation functions as the same with functions in [33], that is

$$\begin{aligned} f(s)=\left\{ \begin{array}{ll} -(\mathrm{Re}(s)+1)+(\mathrm{Im}(s)+1)\mathbf{i }, &{} \mathrm{Re}(s)<0\, \mathrm{and}\,\mathrm{Im}(s)<0, \\ -(\mathrm{Re}(s)+1)-(\mathrm{Im}(s)+1)\mathbf{i }, &{}\mathrm{Re}(s)<0\, \mathrm{and} \, \mathrm{Im}(s)>0,\\ (\mathrm{Re}(s)+1)+(\mathrm{Im}(s)+1)\mathbf{i }, &{}\mathrm{Re}(s)>0\, \mathrm{and} \,\mathrm{Im}(s)<0,\\ (\mathrm{Re}(s)+1)-(\mathrm{Im}(s)+1)\mathbf{i }, &{} \mathrm{Re}(s)>0\, \mathrm{and} \,\mathrm{Im}(s)>0,\\ \end{array} \right. \end{aligned}$$

where $s\in C$ and $i=1,\,2.$ It is obvious that the activation function $f(z)=[f_{1}(z_{1}),\,f_{2}(z_{2})]^{\mathrm{T}}$ is discontinuous on the complex domain $C^{2},$ and $f_{i}(z_{i})$ is satisfying A(4) with $L^{R}_{i}=L_{i}^{I}=1,$ which is unbounded in $C^{2}.$

Fig. 3

Time responses for the real part and imaginary part of $z_{1},\, z_{2}$ in Example 4.1 and trajectories of states $x_1,\, x_2$ in system (4.2)

Now take $P=I,$ where I is the unit matrix. Then it is easy to get $PA^{I}=(A^{I})^{\mathrm{T}}P,\, PA^{R}+(A^{R})^{\mathrm{T}}P<0$ and $d_{m}=1.$ Through simple computation, we obtain $\Vert A^{R}(A^{R})^{\mathrm{T}}+A^{I}(A^{I})^{\mathrm{T}}\Vert =0.0725,\, \lambda _{m}=1/5,$ and

$$\begin{aligned} \frac{L_{i}p_{i}(\Vert A^{R}(A^{R})^{\mathrm{T}}+A^{I}(A^{I})^\mathrm{T}\Vert )}{d_{m}\lambda _{m}}=\frac{29}{160}<\frac{1}{4}. \end{aligned}$$

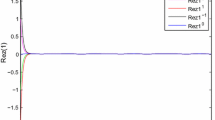
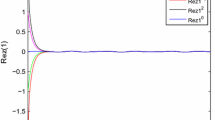
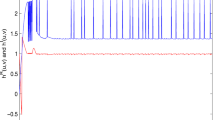
According to Theorem 3.4, the equilibrium $z^{*}=(0.65+0.23\mathbf{i },\,0.14+0.83\mathbf{i })$ is unique and globally asymptotically stable. The output solution $\gamma (t)$ of system (4.1) convergence to $\gamma ^{*}=(1.65-1.23\mathbf{i },\,1.14-1.83\mathbf{i })$ in measure. According to Theorem 3.7, the trajectories of z(t) convergence to $z^{*}$ in finite time. Consider the IVP of system (4.1) with the initial condition $z_0=[2-\mathbf{i },\,1-2\mathbf{i }]^{\mathrm{T}},$ the time response of the real part and imaginary part for $z_{1},\,z_{2}$ and $\gamma _{1}(t),\,\gamma _{2}(t)$ are shown in Figs. 3 and 4, respectively. The trajectories of $z_{1},\,z_{2}$ and output solution $\gamma _1(t),\,\gamma _2(t)$ in complex domain are shown in Figs. 5 and 6.

Fig. 4

Time responses for the real part and imaginary part of output solutions in Example 4.1 and trajectories of output solutions in system (4.2)

Fig. 5

Phase plane behavior of the state variables $z_{1}$ and $z_{2}$ in complex domain C in Example 4.1

Fig. 6

Phase plane behavior of the state variables $\gamma _{1}$ and $\gamma _{2}$ in complex domain C in Example 4.1

Fig. 7

Time responses for the real part and imaginary part of the variables $z_{1}$ and $z_{2}$ in Example 4.2

Fig. 8

Phase plane behavior of the state variables $z_{1}$ and $z_{2}$ in complex domain C in Example 4.2

Remark 8

Let the imaginary parts of all the variables and parameters be zero, the system (4.1) becomes:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x_1}={-}2x_1-\frac{1}{10}f_1(x_1)+\frac{1}{5}f_2(x_2)+1,\\ \dot{x_2}={-}2x_2-\frac{1}{5}f_1(x_1)-\frac{1}{10}f_2(x_2)+0.5,\\ \end{array} \right. \end{aligned}$$

(4.2)

where $f_i(x)=(x+1)\mathrm{sign(x)}$ for $i=1,\,2.$ From Fig. 3, we can see that the equilibrium point of system (4.2) is different from the equilibrium point of real part of z in system (4.1). This is because the imaginary part of system can affect the equilibrium point definitely. On the other aspect, system (4.1) has four equilibrium points while system (4.2) has two equilibrium points, this manifests that complex-valued neural networks can enhance the capacity compared with the same dimensional real-valued neural networks, which has been reported in [10].

Example 4.2

Consider a two-neuron complex-valued neural network described as follows:

$$\begin{aligned} {\dot{z}}={-}Dz+Af(z), \end{aligned}$$

(4.3)

where

$$\begin{aligned} D=\left[ \begin{array}{cc} 9&{}0\\ 0&{}8.5\\ \end{array}\right] ,\quad A=\left[ \begin{array}{cc} -1+0.5\mathbf{i }&{}0.25+0.25\mathbf{i }\\ -0.25-0.25\mathbf{i }&{}-1+0.5\mathbf{i }\\ \end{array}\right] , \end{aligned}$$

and $f(s)=(\mathrm{Re}(s)+0.2)\mathrm{sign}(\mathrm{Re}(s))+\mathbf{i }(\mathrm{Im}(s)+0.1)\mathrm{sign}(\mathrm{Im}(s))$ for any $s\in C$ and $i=1,\,2.$ It is clear that the activation function $f(z)=[f_{1}(z_{1}),\,f_{2}(z_{2})]^{\mathrm{T}}$ is discontinuous on the complex domain $C^{2},$ and $f_{i}(z_{i})$ is satisfying A(4) with $L^{R}_{i}=L_{i}^{I}=1.$ According to Definition 2.5, $z^*=[0,\,0]^{\mathrm{T}}$ is an equilibrium point of system (4.3).

Now take $P=I,$ it is easy to get $Q=\mathrm {diag}\{-11/16,\,-11/16\}$ and $(A^{R})^{\mathrm{T}}A^{R}+(A^{I})^{\mathrm{T}}A^{I}=\mathrm {diag}\{ 11/8,\,11/8\}.$ Therefore, we obtain $\Vert (A^{R})^{\mathrm{T}}(A^{R})+(A^{I})^\mathrm{T}(A^{I})\Vert =11/8,\, \lambda _{m}=11/16$ and

$$\begin{aligned} \frac{L_{i}p_{i}\Vert (A^{R})^{\mathrm{T}}A^{R}+(A^{I})^\mathrm{T}A^{I}\Vert }{d_{m}\lambda _{m}}=\frac{4}{17}< \frac{1}{4}. \end{aligned}$$

According to Theorem 3.6, the equilibrium $z^*=[0,\,0]^{\mathrm{T}}$ is unique and globally asymptotically stable. We choose the initial value $z(0)=[2-\mathbf{i },\,1-2\mathbf{i }]^{\mathrm{T}},$ then time response of the real part and imaginary part of $z_{1},\,z_{2}$ is shown in Fig. 7. Figure 8 shows the trajectories of $z_{1},\,z_{2}$ in complex domain.

Remark 9

It can be seen that $[0,\,0]^{\mathrm{T}}$ is a discontinuous point of activation function f(z) and $K[f(0)]=[-0.2,\,0.2]+\mathbf{i }[-0.1,\,0.1],$ which is shown in Fig. 2. The stability problem can not be studied by methods proposed in [27, 28]. In this paper, we can analyze the stability of the equilibria under the framework of Filippov differential inclusion.

5 Conclusion

In this paper, we introduced the Filippov differential inclusions for complex differential equations with discontinuous right-hand side. Dynamical behavior of complex-valued Hopfield neural networks, including global asymptotic stability, output solution convergence in measure and convergence in finite time was studied in this paper based on differential inclusion theory and generalized Lyapunov stability theory. Numerical simulations are given to show the effectiveness and correction of our results. We think it would be interesting to investigate the possibility of extending the results to more complex discontinuous complex-valued neural network system with time varying and distributed delays.