1 Introduction

In the past decades, in order to process information intelligently, people set up artificial neural networks to simulate the functions of human brain. Traditional artificial neural network has been implemented with circuit, and the connection between neural processing units is realized with resistor. The resistance is equal to the strength of synapses between neurons. The strength of synapses is variable while the resistance is invariable. Combining the memory characteristic and nanometer dimensions of memristor, the resistor is replaced by memristor in order to simulate the artificial neural network of human brain better. And the memristor eventually may have the potential to be used in artificial neural networks. With the development of applications, memristive nanodevices as synapses and conventional CMOS technology as neurons are widely adopted in order to design brain-like processing systems. Recently, the authors in Refs. [1–6] have concentrated on the dynamical nature of memristor-based neural networks in order to use it in applications, such as pattern recognition, associative memories and learning, in a way that mimics the human brain.

The stability issue for neural networks with stochastic perturbations has attracted a lot of attention. In real nervous systems, because of random fluctuations from the release of neurotransmitters and other probabilistic causes, the synaptic transmission is indeed an noisy process. Therefore, in Refs. [7–11] authors have studied stochastic perturbations on neural networks. In addition, anti-synchronization control of neural networks plays important roles in many potential applications, e.g., non-volatile memories, neuromorphic devices to simulate learning, adaptive and spontaneous behavior. Moreover, the authors in Ref. [12] have studied the anti-synchronization control of memristive neural networks. However, the memristor-based neural networks models proposed and studied in the literature are deterministic. Therefore, it is of practical importance to study the stochastic memristor-based neural networks. To the authors’ best knowledge, there are few results about the anti-synchronization control of memristive neural networks with stochastic perturbations.

Moreover, most literatures regarding the stability of neural networks with stochastic perturbations are based on the convergence time being large enough, even though we require the states of neural networks become stable as quickly as possible in practical applications. In order to achieve faster convergent speed and complete stabilization in finite time rather than merely asymptotically, an effective method is to use finite-time techniques which have demonstrated better robustness and disturbance rejection properties. Finite-time synchronization control of complex networks has been investigated in Refs. [13, 14]. Unfortunately, few papers in the open literature considered the finite-time synchronization control of memristive neural networks, let alone finite-time anti-synchronization of memristive neural networks with stochastic perturbations.

In this paper, our aim is to shorten such a gap by making the attempt to deal with the anti-synchronization problem for memristive neural networks with stochastic perturbations in finite time. The difference of this paper lies in three aspects. First, we studied the anti-synchronization control problem about the memristive neural networks with stochastic perturbations. Moreover, based on the differential inclusions theory and the finite-time stability theorem, we proposed a nonlinear controller to ensure the stability of memristive neural networks with stochastic perturbations in finite-time. Finally, according to two kinds of memductance functions, finite-time stability criteria are obtained for memristive neural networks. Two numerical examples are provided to show the effectiveness of the proposed theorems.

2 Preliminaries

We describe a general class of recurrent neural networks, and we give its circuit in Fig. 1. The Kirchoff’s current law of its \(i\hbox {th}\) subsystem in Ref. [12] has been proposed by the following equation:

$$\begin{aligned} \dot{x}_{i}(t)&= -\frac{1}{\mathbb {C}_{i}} \left[ \sum _{j=1}^{n}\frac{1}{\mathbb {R}_{ij}}\times sgin_{ij}+\frac{1}{\mathcal {R}_{i}} \right] x_{i}(t)\nonumber \\&+\frac{1}{\mathbb {C}_{i}}\sum _{j=1}^{n}\frac{g_{j}(x_{j}(t))}{\mathbb {R}_{ij}}\times sgin_{ij},\nonumber \\&\quad t\ge 0, i=1,2,\ldots , n, \end{aligned}$$
(1)

where \(x_{i}(t)\) is the voltage of the capacitor \(\mathbb {C}_{i}\); \(\mathbb {R}_{ij}\) denotes the resistor through the feedback function \(g_{i}(x_{i}(t))\) and \(x_{i}(t)\). \(\mathcal {R}_{i}\) represents the parallel-resistor corresponding the capacitor \(\mathbb {C}_{i}\). And

$$\begin{aligned} sgin_{ij}=\left\{ \begin{array}{r@{\quad }l} 1,&{} i\ne j,\\ -1, &{}i=j.\\ \end{array} \right. \end{aligned}$$

From (1), we have

$$\begin{aligned} \begin{aligned}&\dot{x}_{i}(t)=-\tilde{a}_{i}x_{i}(t)+ \sum _{j=1}^{n}\tilde{b}_{ij} g_{j}(x_{j}(t)),\\&\quad t\ge 0, i=1,2,\ldots , n, \end{aligned} \end{aligned}$$
(2)

where

$$\begin{aligned}&\displaystyle \tilde{a}_{i} = \frac{1}{\mathbb {C}_{i}} \left[ \sum _{j=1}^{n}\frac{1}{\mathbb {R}_{ij}}\times sgin_{ij}+\frac{1}{\mathcal {R}_{i}} \right] ,&\\&\displaystyle \tilde{b}_{ij} = \frac{1}{\mathbb {C}_{i}\mathbb {R}_{ij}}\times sgin_{ij}.&\end{aligned}$$

By replacing the resistor \(\mathbb {R}_{ij}\) and \(\mathcal {R}_{i}\) in the primitive neural networks (1) with memristor whose memductance are \(W_{ij}\) and \(P_{i}\), we can construct the memristive neural networks of the following form

$$\begin{aligned} \begin{aligned}&\dot{x}_{i}(t)=-a_{i}(x_{i}(t))x_{i}(t)+ \sum _{j=1}^{n}b_{ij}(x_{i}(t)) g_{j}(x_{j}(t)),\\&\quad t\ge 0, i=1,2,\ldots , n, \end{aligned} \end{aligned}$$
(3)

where

$$\begin{aligned} a_{i}(x_{i}(t))&= \frac{1}{\mathbb {C}_{i}} \left[ \sum _{j=1}^{n}W_{ij}\times sgin_{ij}+P_{i} \right] , \\ b_{ij}(x_{i}(t))&= \frac{W_{ij}}{\mathbb {C}_{i}}\times sgin_{ij}, \end{aligned}$$

Combining the physical structure of a memristor device, one can see that

$$\begin{aligned} W_{ij}&= \frac{dq_{ij}}{d\sigma _{ij}}, \\ P_{i}&= \frac{dp_{i}}{d\chi _{i}}, \end{aligned}$$

where \(q_{ij}\) and \(\sigma _{ij}\) denote charge and magnetic fluxes corresponding to the memristor \(\mathbb {R}_{ij}\), and \(p_{i}\) and \(\chi _{i}\) denote charge and magnetic fluxes corresponding to the memristor \(\mathcal {R}_{i}\).

Fig. 1
figure 1

(Color online) The circuit of recurrent neural networks in model (1)

Full size image

As we know that the pinched hysteresis loop is due to the nonlinearity of memductance function. Based on two typical memductance functions, in this paper, we discuss the following two cases which are proposed in Ref. [4].

Case 1: The memductance function \(W_{ij}\), \(P_{i}\) are given by

$$\begin{aligned} W_{ij}&= \left\{ \begin{array}{r@{\quad } l} \xi _{ij},&{} \mid \sigma _{ij}\mid < l_{ij},\\ \eta _{ij},&{} \mid \sigma _{ij}\mid > l_{ij},\\ \end{array} \right. \\ P_{i}&= \left\{ \begin{array}{r@{\quad }l} \phi _{i},&{} \mid \chi _{i}\mid < T_{i},\\ \varphi _{i},&{} \mid \chi _{i}\mid >T_{i},\\ \end{array} \right. \end{aligned}$$

where \(\xi _{ij}, \eta _{ij},\phi _{i},\varphi _{i}\) and \(l_{ij}, T_{i}\) are constants.

Case 2: The memductance function \(W_{ij}\) is given by

$$\begin{aligned} W_{ij}&= c_{ij}+3d_{ij}\sigma _{ij}^{2}, \\ P_{i}&= \alpha _{i}+3\beta _{i}\chi _{i}^{2}, \end{aligned}$$

where \(c_{ij} , \, d_{ij}, \, \alpha _{i}, \, \beta _{i}\) are constants, \(i,j=1,2,\ldots , n.\)

We give some definitions which are needed in the following.

Definition 1

(See [15]) Suppose \(E\subseteq R^{n}\), then \(x\rightarrow F(x)\) is called a set-valued map from \(E\rightarrow R^{n}\), if for each point \(x\epsilon E\), there exists a nonempty set \(F(x)\subseteq R^{n}\). A set-valued map \(F\) with nonempty values is said to be upper semi-continuous at \(x_{0}\epsilon E\), if for any open set \(N\) containing \(F(x_{0})\), there exists a neighborhood \(M\) of \(x_{0}\) such that \(F(M)\subseteq N\). The map \(F(x)\) is said to have a closed (convex, compact) image if for each \(x\epsilon E, F(x)\) is closed (convex, compact).

Definition 2

(See [16]) For the system \(\dot{x}(t)=f(x), \, x\epsilon R^{n}\), with discontinuous right-hand sides, a set-valued map is defined as

$$\begin{aligned} F(t,x)=\bigcap _{\delta >0}\bigcap _{\mu (N)=0}co[f(B(x,\delta )\setminus N)], \end{aligned}$$

where \(co[E]\) is the closure of the convex hull of set \(E, \, B(x,\delta )=\{y:\Vert y-x\Vert \le \delta \}\) and \(\mu (N)\) is Lebesgue measure of set \(N\). A solution in Filippov’s sense of Cauchy problem for this system with initial condition \(x(0)=x_{0}\) is an absolutely continuous function \(x(t)\), which satisfies \(x(0)=x_{0}\) and differential inclusion

$$\begin{aligned} \dot{x}(t)\,\epsilon \, F(t,x). \end{aligned}$$

In order to establish our main results, it is necessary to give the following assumptions and Lemmas.

Assumption 1

The function \(g_{i}\) is odd function and bounded, and satisfies the Lipschitz condition with a Lipschitz constants \(Q_{i}\), i.e.,

$$\begin{aligned} \mid \! g_{i}(x)-g_{i}(y)\! \mid \,\le Q_{i}\mid \! x-y\!\mid , \end{aligned}$$
(4)

where \(Q_{i}\) is a positive constant for \(i=1,2,\ldots ,n\). We let \(Q=diag\{Q_{1},Q_{2},\ldots ,Q_{n}\}\).

Assumption 2

For \(i,j=1,2,\ldots ,n\),

$$\begin{aligned} \begin{aligned}&co\{\hat{a}_{i},\check{a}_{i}\}x_{i}(t)+co\{\hat{a}_{i},\check{a}_{i}\}y_{i}(t)\subseteq co\{\hat{a}_{i},\check{a}_{i}\}e_{i}(t),\\&co\{\hat{b}_{ij},\check{b}_{ij}\}g_{j}(x_{i}(t))+co\{\hat{b}_{ij},\check{b}_{ij}\}g_{j}(y_{i}(t))\\&\quad \subseteq co\{\hat{b}_{ij},\check{b}_{ij}\}(g_{j}(x_{i}(t))+g_{j}(y_{i}(t))),\\ \end{aligned} \end{aligned}$$

Lemma 1

([17]) If \(a_{1}, a_{2}, \ldots , a_{n}\) are positive numbers and \(0<r<p\), then

$$\begin{aligned} \left( \sum _{i=1}^{n}a_{i}^{p} \right) ^{\frac{1}{p}}\le \left( \sum _{i=1}^{n}a_{i}^{r} \right) ^{\frac{1}{r}}. \end{aligned}$$
(5)

Lemma 2

([18]) If \(\mu , \nu (t),\) and \(\omega \) are real matrices of appropriate dimension with \(\vartheta \) satisfying \(\vartheta =\vartheta ^{T}\), then

$$\begin{aligned} \vartheta +\mu \nu (t)\omega +\omega ^{T}\nu ^{T}(t)\mu ^{T}<0 \end{aligned}$$
(6)

for all \(\nu (t)\nu ^{T}(t)\le I\), if and only if there exists a positive constant \(\lambda \) such that

$$\begin{aligned} \vartheta +\lambda ^{-1}\mu \mu ^{T}+\lambda \omega ^{T}\omega <0. \end{aligned}$$
(7)

According to the features of memristor given in Case 1 and Case 2, the following two cases can happen.

Case \(1'\): In case 1, according to the work in Ref. [19], we get

$$\begin{aligned} co(a_{i}(x_{i}(t))&= \left\{ \begin{array}{l@{\quad }l@{\quad }l} \hat{a}_{i}, &{}-\dot{f}_{i}(x_{i}(t))-\dot{x}_{i}(t)<0,\\ {[}\underline{a}_{i}, \overline{a}_{i}{]}, &{}-\dot{f}_{i}(x_{i}(t))-\dot{x}_{i}(t)=0,\\ \check{a}_{i}, &{}-\dot{f}_{i}(x_{i}(t))-\dot{x}_{i}(t)> 0,\\ \end{array} \right. \\ co(b_{ij}(x_{i}(t))&= \left\{ \begin{array}{l@{\quad }l@{\quad }l} \hat{b}_{ij}, &{}sgin_{ij}\frac{df_{j}(x_{j}(t))}{dt}-\frac{dx_{i}(t)}{dt}<0,\\ {[}\underline{b}_{ij}, \overline{b}_{ij}{]}, &{}sgin_{ij}\frac{df_{j}(x_{j}(t))}{dt}-\frac{dx_{i}(t)}{dt}=0,\\ \check{b}_{ij},&{} sgin_{ij}\frac{df_{j}(x_{j}(t))}{dt}-\frac{dx_{i}(t)}{dt} > 0,\\ \end{array} \right. \end{aligned}$$

for \(i,j=1,2,\ldots ,n\), where \(\hat{a}_{i}, \, \check{a}_{i} \, \hat{b}_{ij}\) and \(\check{b}_{ij}\) are constants, and \(\bar{a}_{i}=\max \{\hat{a}_{i}, \check{a}_{i}\}, \, \underline{a}_{i}=\min \{\hat{a}_{i}, \check{a}_{i}\}\). \(\bar{b}_{ij}=\max \{\hat{b}_{ij}, \check{b}_{ij}\}, \, \underline{b}_{ij}=\min \{\hat{b}_{ij}, \check{b}_{ij}\}\). Solutions of all the systems considered in this paper are intended in the Filippov’s sense. \([\cdot ,\cdot ]\) represents the interval. co\(\{\tilde{\varDelta },\hat{\varDelta }\}\) denotes the closure of the convex hull of \(R^{n}\) generated by real numbers \(\tilde{\varDelta }\) and \(\hat{\varDelta }\).

The system (3) is a differential equation with discontinuous right-hand sides, and based on the theory of differential inclusion, if \(x_{i}(t)\) is a solution of (3) in the sense of Filippov, then system (3) can be modified by the following

$$\begin{aligned} \begin{aligned}&\dot{x}_{i}(t)\epsilon -co\{a_{i}(x_{i}(t))\}x_{i}(t)+\sum _{j=1}^{n}co\{b_{ij}(x_{i}(t))\} g_{j}(x_{j}(t)),\\&\quad t\ge 0, i=1,2,\ldots , n, \end{aligned} \end{aligned}$$
(8)

or equivalently, there exist \(a_{i}(t)\epsilon co(a_{i}(x_{i}(t)))\) and \(b_{ij}(t)\epsilon co(b_{ij}(x_{i}(t)))\), such that

$$\begin{aligned} \begin{aligned}&\dot{x}_{i}(t)= -a_{i}(t)x_{i}(t)+\sum _{j=1}^{n}b_{ij}(t) g_{j}(x_{j}(t)),\quad t\ge 0,\\&\quad i=1,2,\ldots , n, \end{aligned} \end{aligned}$$
(9)

where \(a_{i}(t)\) and \(b_{ij}(t)\) depend on the state \(x_{i}(t)\) and time \(t\).

In this paper, we consider system (8) or (9) as the drive system and the corresponding response system is:

$$\begin{aligned} \begin{aligned}&\dot{y}_{i}(t)\epsilon -co\{a_{i}(y_{i}(t))\}y_{i}(t)+\sum _{j=1}^{n}co\{b_{ij}(y_{i}(t))\} g_{j}(y_{j}(t)), \\&\quad t\ge 0, i=1,2,\ldots , n, \end{aligned} \end{aligned}$$
(10)

or equivalently, there exist \(a_{i}(t)\epsilon co(a_{i}(y_{i}(t)))\) and \(b_{ij}(t) \epsilon co(b_{ij}(y_{i}(t)))\), such that

$$\begin{aligned} \begin{aligned}&\dot{y}_{i}(t)= -a_{i}(t)y_{i}(t)+\sum _{j=1}^{n}b_{ij}(t) g_{j}(y_{j}(t)),\quad t\ge 0,\\&\quad i=1,2,\ldots , n. \end{aligned} \end{aligned}$$
(11)

Let \(e(t)=(e_{1}(t),e_{2}(t),\ldots , e_{n}(t))^{T}\) be the anti-synchro- nization error, where \(e_{i}(t)=x_{i}(t)+y_{i}(t)\), using the theories of set-valued maps and differential inclusions, then we can get the anti-synchronization error system in the following. Since there exist environmental noises in real neural networks, stochastic perturbations should be considered in neural networks models. According to Assumption 2, we get

$$\begin{aligned} \begin{aligned}&de_{i}(t)\, \epsilon \left[ -co\{a_{i}(e_{i}(t))\}e_{i}(t) +\sum _{j=1}^{n}co\{b_{ij}(e_{i}(t))\} f_{j}(e_{j}(t)) \right] dt\\&\quad +h(t,e_{i}(t))dw_{i}(t),\quad t\ge 0,\\&\qquad i=1,2,\ldots , n, \end{aligned} \end{aligned}$$
(12)

or equivalently, there exist \(a_{i}(t)\epsilon co(a_{i}(e_{i}(t)))\) and \(b_{ij}(t) \epsilon co(b_{ij}(e_{i}(t)))\), such that

$$\begin{aligned} \begin{aligned}&de_{i}(t)= \left[ -a_{i}(t)e_{i}(t)+\sum _{j=1}^{n}b_{ij}(t) f_{j}(e_{j}(t)) \right] dt\\&\quad +h(t,e_{i}(t))dw_{i}(t),\quad t\ge 0,\\&\qquad i=1,2,\ldots , n, \end{aligned} \end{aligned}$$
(13)

where \(f_{j}(e_{j}(t))=g_{j}(x_{j}(t))+g_{j}(y_{j}(t))\), and the white noise \(dw_{i}(t)\) is independent of \(dw_{j}(t)\) for \(i\ne j\). \(w(t)=(w_{1}(t), w_{2}(t), \ldots , w_{n}(t))^{T}\epsilon R^{n}\) is an \(n\)-dimensional Brownian motion. The intensity function \(h\) is the noise intensity function matrix satisfying the following condition:

$$\begin{aligned} trace[h^{T}(t,e(t))\cdot h(t,e(t))]\le \parallel M e(t)\parallel ^{2}, \end{aligned}$$
(14)

where \(M\) is a known constant matrix with compatible dimensions, and \(e(t)=(e_{1}(t), e_{2}(t), \ldots , e_{n}(t))\).

Let \(A(t)=(a_{i}(t))_{n\times n}, \, \hat{A}=(\hat{a}_{i})_{n\times n},\check{A}=(\check{a}_{i})_{n\times n}, \, co\{\hat{A}, \check{A}\}=[\underline{A},\bar{A}]\), where \(\underline{A}=(\underline{a}_{i})_{n\times n}, \bar{A}=(\bar{a}_{i})_{n\times n}\) and \(B(t)=(b_{ij}(t))_{n\times n}, \, \hat{B}=(\hat{b}_{ij})_{n\times n},\check{B}=(\check{b}_{ij})_{n\times n}, \, co\{\hat{B}, \check{B}\}=[\underline{B},\bar{B}]\), where \(\underline{B}=(\underline{b}_{ij})_{n\times n}, \bar{B}=(\bar{b}_{ij})_{n\times n}\), then Eq. (13) can be written in the compact form:

$$\begin{aligned} de(t)= [-A(t)e(t)+B(t)f(e(t))]dt+h(t,e(t))dw(t), \end{aligned}$$
(15)

Case \(2'\): \(a_{i}(x_{i}(t))\) and \(b_{ij}(x_{i}(t))\) are continuous functions, and \(\underline{\varPsi }_{i}\le a_{i}(x_{i}(t))\le \overline{\varPsi }_{i}\) where \(\underline{\varPsi }_{i}\) and \(\overline{\varPsi }_{i}\) are constants. \(\underline{\varLambda }_{ij}\le b_{ij}(x_{i}(t))\le \overline{\varLambda }_{ij}\) where \(\underline{\varLambda }_{ij}\) and \(\overline{\varLambda }_{ij}\) are constants.

Similar to the case \(1'\), let \(\varPsi (t)=(\varPsi _{i}(t))_{n\times n}\), where \(\underline{\varPsi }=(\underline{\varPsi }_{i})_{n\times n}, \bar{\varPsi }=(\bar{\varPsi }_{i})_{n\times n}, \, \varLambda (t)=(\varLambda _{i}(t))_{n\times n}\), and \(\underline{\varLambda }=(\underline{\varLambda }_{i})_{n\times n}, \bar{\varLambda }=(\bar{\varLambda }_{i})_{n\times n}\). By adding the drive system and the response system, the error system can be written in the compact form as follows:

$$\begin{aligned} de(t)= [-\varPsi (t)e(t)+\varLambda (t) f(e(t))]dt+h(t,e(t))dw(t). \end{aligned}$$
(16)

3 Main Results

In this section, according to two cases of memductance functions, discrete and continuous finite-time synchronization criteria are given for memristive neural networks, respectively. Two corollaries are derived for the memristive neural networks without stochastic perturbations.

3.1 Finite-Time Synchronization Criteria in Case \(1'\)

Theorem 1

If there exists a constant \(\varepsilon \) and a positive-definite matrix \(Z\epsilon R^{n\times n}\) which satisfy that

$$\begin{aligned} \begin{aligned}&-\,Z\underline{A}-\underline{A}^{T}Z-2\underline{K}_{1}Z+\varepsilon ^{-1}Z\bar{B} \bar{B}^{T}Z+\varepsilon Q^{T}Q\\&\quad +\lambda _{\max }(Z)M^{T}M <0, \end{aligned} \end{aligned}$$
(17)

then the system (15) under the following controller \(u_{i}(t)\) can achieve the finite-time synchronization,

$$\begin{aligned} u_{i}(t)=-k_{i1}e_{i}(t)-k_{i2}sgn(e_{i}(t))\mid e_{i}(t)\mid ^{\alpha }, \end{aligned}$$
(18)

where \(0<\alpha <1, \, k_{i1}\) and \(k_{i2}\) are positive constants.

And

$$\begin{aligned} sgn(e_{i}(t))=\left\{ \begin{array}{l@{\qquad }l} -1,&{} \mid e_{i}(t)\mid < 0,\\ 0, &{}\mid e_{i}(t)\mid =0,\\ 1,&{} \mid e_{i}(t)\mid > 0.\\ \end{array} \right. \end{aligned}$$

The upper bound of its convergent time is

$$\begin{aligned} \frac{\lambda _{max}(Z)}{\lambda _{min}(Z)}\cdot \frac{\parallel e(0)\parallel ^{1-\alpha }}{\underline{K}_{2}(1-\alpha )}, \end{aligned}$$
(19)

where

$$\begin{aligned} K_{1}&= (k_{11},k_{21},\ldots ,k_{n1})^{T},\\ K_{2}&= (k_{12},k_{22},\ldots ,k_{n2}(t))^{T},\\ \underline{K}_{1}&= min(\underline{k}_{11},\underline{k}_{21},\ldots ,\underline{k}_{n1})^{T},\\ \underline{K}_{2}&= min(\underline{k}_{12},\underline{k}_{22},\ldots ,\underline{k}_{n2})^{T}. \end{aligned}$$

Proof

The system (15) under the controller \(u(t)\) can be written as

$$\begin{aligned} de(t)=[-A(t)e(t)+B(t)f(e(t))+u(t)]dt+h(t,e(t))dw(t), \end{aligned}$$
(20)

where

$$\begin{aligned} e(t)&= (e_{1}(t),e_{2}(t),\ldots ,e_{n}(t))^{T}, \\ u(t)&= (u_{1}(t),u_{2}(t),\ldots ,u_{n}(t))^{T}, \\ f(e(t))&= (f_{1}(e_{1}(t)),f_{2}(e_{2}(t)),\ldots ,f_{n}(e_{n}(t)))^{T}, \end{aligned}$$

Transform (18) into the compact form as follows:

$$\begin{aligned} u(t)=-K_{1}e(t)-K_{2}sgn(e(t))\mid e(t)\mid ^{\alpha }. \end{aligned}$$
(21)

Consider the controlled system (20) with controller (21), we have

$$\begin{aligned} \begin{aligned} de(t)&= \big [-A(t)e(t)+B(t)f(e(t))-K_{1}e(t)\\&\quad -K_{2}sgn(e(t))\mid \!e(t)\!\mid ^{\alpha } \big ]dt+h(t,e(t))dw(t). \end{aligned} \end{aligned}$$
(22)

\(\square \)

We construct the Lyapunov function as follows:

$$\begin{aligned} V(e(t))=e^{T}(t)Ze(t), \end{aligned}$$
(23)

then we calculate the time derivative of \(V(e(t))\) along the trajectories of the system (22). By the Itô’s formula in Ref. [20], we obtain the stochastic differential as

$$\begin{aligned} dV(e(t))=LV(e(t))dt+2e^{T}(t)Zh(t,e(t))dw(t), \end{aligned}$$
(24)

where

$$\begin{aligned} LV(e(t))&= 2e^{T}(t)Z \big [(-A(t)-K_{1})e(t)+B(t)f(e(t))\nonumber \\&\quad -K_{2}sgn(e(t))\mid e(t)\mid ^{\alpha } \big ]+trace \big [h^{T}(t)Zh(t)\big ]\nonumber \\&= 2e^{T}(t)Z(-A(t)-K_{1})e(t)+2e^{T}(t)ZB(t)f(e(t))\nonumber \\&\quad +trace \big [h^{T}(t)Zh(t) \big ]-2K_{2}e^{T}(t)Z sgn(e(t))\mid e(t)\mid ^{\alpha }. \end{aligned}$$
(25)

According to Lemma 2 and Assumption 1, we have

$$\begin{aligned} \begin{aligned} 2e^{T}(t)ZB(t)f(e(t))&\le \varepsilon ^{-1}e^{T}(t)ZB(t)B^{T}(t)Ze(t)+\varepsilon f^{T}(e(t))f(e(t))\\&\le \varepsilon ^{-1}e^{T}(t)ZB(t)B^{T}(t)Ze(t) +\varepsilon e^{T}(t)Q^{T}Qe(t), \end{aligned} \end{aligned}$$
(26)

where \(\varepsilon >0\) is an arbitrary positive constant.

Combining (25)–(26) results in

$$\begin{aligned} \begin{aligned} LV(e(t))&\le e^{T}(t)\Big [-Z\underline{A}-\underline{A}^{T}Z-2\underline{K}_{1}Z+\varepsilon ^{-1}Z\bar{B} \bar{B}^{T}Z\\&\quad +\varepsilon Q^{T}Q+\lambda _{\max }(Z)M^{T}M \Big ]\times e(t)-2\underline{K}_{2}\lambda _{min}(Z)\sum _{i=1}^{n}\mid \! e_{i}(t)\!\mid ^{\alpha +1}. \end{aligned} \end{aligned}$$
(27)

According to \(0<\alpha <1\) and Lemma 1, we get

$$\begin{aligned} \left( \sum _{i=1}^{n}\mid \! e_{i}(t)\!\mid ^{\alpha +1} \right) ^{\frac{1}{\alpha +1}}\ge \left( \sum _{i=1}^{n}\mid e_{i}(t)\mid ^{2} \right) ^{\frac{1}{2}}, \end{aligned}$$
(28)

then,

$$\begin{aligned} \sum _{i=1}^{n}\mid e_{i}(t)\mid ^{\alpha +1}\ge \left( \sum _{i=1}^{n}\mid e_{i}(t)\mid ^{2} \right) ^{\frac{\alpha +1}{2}}= \left[ e^{T}(t)e(t) \right] ^{\frac{\alpha +1}{2}}. \end{aligned}$$
(29)

Thus, based on (17), taking the expectations on both sides of (27), we have

$$\begin{aligned} \begin{aligned} E\{dV(e(t))\}&\le -2\underline{K}_{2}\lambda _{min}(Z)E \left\{ \Big [e^{T}(t)e(t)\Big ]^{\frac{\alpha +1}{2}} \right\} \\&\le -2\underline{K}_{2}\lambda _{min}(Z)[\lambda _{max}(Z)]^{\frac{-(\alpha +1)}{2}}E \left\{ V(e(t))^{\frac{(\alpha +1)}{2}} \right\} \\&\le -2\underline{K}_{2}\lambda _{min}(Z)[\lambda _{max}(Z)]^{\frac{-(\alpha +1)}{2}}E \left\{ V(e(t))^{\frac{(\alpha +1)}{2}} \right\} . \end{aligned} \end{aligned}$$
(30)

And

$$\begin{aligned} E \left\{ V^{\frac{(\alpha +1)}{2}}(e(0)) \right\} = \Big (E\{V(e(0))\} \Big )^{\frac{(\alpha +1)}{2}}. \end{aligned}$$

By the finite-time stabilization theory in [21], \(V(e(t))\) stochastically converges to zero in finite time, whose upper bound is

$$\begin{aligned} \begin{aligned} T&=\frac{[\lambda _{max}(Z)]^{\frac{(\alpha +1)}{2}}[V(e(0))]^{\frac{(1-\alpha )}{2}}}{2\underline{K}_{2}\lambda _{min}(Z)\frac{(1-\alpha )}{2}}\\&\le \frac{[\lambda _{max}(Z)]^{\frac{(\alpha +1)}{2}}[\lambda _{max}(Z)]^{\frac{(1-\alpha )}{2}}\parallel e(0)\parallel _{2}^{1-\alpha }}{\lambda _{min}(Z)\underline{K}_{2}(1-\alpha )}\\&\le \frac{\lambda _{max}(Z)}{\lambda _{min}(Z)}\cdot \frac{\parallel e(0)\parallel ^{1-\alpha }}{\underline{K}_{2}(1-\alpha )}. \end{aligned} \end{aligned}$$
(31)

Thus we complete the proof.

Corollary 1

In case \(1'\), if there exist a constant \(\varepsilon \) and a positive-definite matrix \(Z\epsilon R^{n\times n}\) which satisfy

$$\begin{aligned} -Z\underline{A}-\underline{A}^{T}Z-2\underline{K}_{1}Z+\varepsilon ^{-1}Z\bar{B}\bar{B}^{T}Z+\varepsilon Q^{T}Q <0, \end{aligned}$$
(32)

then when the system (15) without stochastic perturbations via the controller (18) will achieve the synchronization in finite-time and the upper bound of its synchronization time is the same as (31).

3.2 Finite-Time Synchronization Criteria in Case \(2'\)

Theorem 2

Under the case \(2'\), the system (16) under the controller (18) will achieve the finite-time synchronization, if there exist a constant \(\varepsilon \) and a positive-definite matrix \(Z\epsilon R^{n\times n}\) which satisfy that

$$\begin{aligned} \begin{aligned}&-Z\underline{\varPsi }-\underline{\varPsi }^{T}Z-2\underline{K}_{1}Z+\varepsilon ^{-1}Z\bar{\varLambda }\bar{\varLambda }^{T}Z+\varepsilon Q^{T}Q\\&\quad +\lambda _{\max }(Z)M^{T}M<0. \end{aligned} \end{aligned}$$
(33)

The upper bound of its convergence time is the same as that in Theorem 1.

Proof

By Eq. (16), it is easy to know

$$\begin{aligned} de_{i}(t)\le \Bigg [-\varPsi _{i}(t)e_{i}(t)+\sum _{j=1}^{n}\varLambda _{ij}(t)f_{j}(e_{j}(t)) +u_{i}(t) \Bigg ]dt+h(t,e_{i}(t))dw_{i}(t), \end{aligned}$$
(34)

Transform (34) into the compact form as follows:

$$\begin{aligned} \begin{aligned} de(t)&= \big [-\varPsi (t)e(t)+\varLambda (t) f(e(t))-K_{1}e(t)\\&-K_{2}sign(e(t))\mid e(t)\mid ^{\alpha } \big ]dt+h(t,e(t))dw(t), \end{aligned} \end{aligned}$$
(35)

We construct the Lyapunov function as follows:

$$\begin{aligned} V(e(t))=e^{T}(t)Ze(t). \end{aligned}$$
(36)

Then we calculate the time derivative of \(V(e(t))\) along the trajectories of system (35). By It\(\hat{o}\)’s formula, we obtain the following stochastic differential as

$$\begin{aligned} dV(e(t))=LV(e(t))dt+2e^{T}(t)Zh(t,e(t))dw(t), \end{aligned}$$
(37)

where

$$\begin{aligned} \begin{aligned} LV(e(t))&=2e^{T}(t)Z \big [(-\varPsi (t)-K_{1})e(t)+\varLambda (t) f(e(t))\\&\quad -K_{2}sign(e(t))\mid \! e(t)\!\mid ^{\alpha } \big ]+trace \big [h^{T}(t)Zh(t) \big ]\\&=2e^{T}(t)Z(-\varPsi (t)-K_{1})e(t)+2e^{T}(t)Z\varLambda (t) f(e(t))\\&\quad +trace \big [h^{T}(t)Zh(t) \big ] -2K_{2}e^{T}(t)Z sign(e(t))\mid e(t)\mid ^{\alpha }\!. \end{aligned} \end{aligned}$$
(38)

\(\square \)

According to Lemma 2 and Assumption 1, we have

$$\begin{aligned} \begin{aligned}&2e^{T}(t)Z\varLambda (t) f(e(t))\\&\quad \le \varepsilon ^{-1}e^{T}(t)Z\bar{\varLambda }\bar{\varLambda }^{T}Ze(t)+\varepsilon f^{T}(e(t))f(e(t))\\&\quad \le \varepsilon ^{-1}e^{T}(t)Z\bar{\varLambda }\bar{\varLambda }^{T}Ze(t)+\varepsilon e^{T}(t)Q^{T}Qe(t), \end{aligned} \end{aligned}$$
(39)

where \(\varepsilon >0\) is an arbitrary positive constant.

Combining (38)–(39) results in

$$\begin{aligned} \begin{aligned} LV(e(t))&\le e^{T}(t)\big [-Z\underline{\varPsi }-\underline{\varPsi }^{T}Z-2\underline{K}_{1}Z+\varepsilon ^{-1}Z\bar{\varLambda }\bar{\varLambda }^{T}Z\\&\quad +\varepsilon Q^{T}Q+\lambda _{\max }(Z)M^{T}M \big ]\times e(t)-2\underline{K}_{2}\lambda _{min}(Z)\sum _{i=1}^{n}\mid e_{i}(t)\mid ^{\alpha +1}. \end{aligned} \end{aligned}$$
(40)

According to \(0<\alpha <1\) and Lemma 1, we get

$$\begin{aligned} \left( \sum _{i=1}^{n}\mid e_{i}(t)\mid ^{\alpha +1} \right) ^{\frac{1}{\alpha +1}}\ge \left( \sum _{i=1}^{n}\mid e_{i}(t)\mid ^{2} \right) ^{\frac{1}{2}}, \end{aligned}$$
(41)

then,

$$\begin{aligned} \sum _{i=1}^{n}\mid e_{i}(t)\mid ^{\alpha +1}\,\ge \left( \sum _{i=1}^{n}\mid e_{i}(t)\mid ^{2} \right) ^{\frac{\alpha +1}{2}}= \left[ e^{T}(t)e(t) \right] ^{\frac{\alpha +1}{2}}\!. \end{aligned}$$
(42)

Thus, based on Eq. (33), taking the expectations on both sides of Eq. (40), we have

$$\begin{aligned} \begin{aligned} E\{dV(e(t))\}&\le -2\underline{K}_{2}\lambda _{min}(Z)E \left\{ \Big [e^{T}(t)e(t)\Big ]^{\frac{\alpha +1}{2}} \right\} \\&\le -2\underline{K}_{2}\lambda _{min}(Z)[\lambda _{max}(Z)]^{\frac{-(\alpha +1)}{2}}E \left\{ V(e(t))^{\frac{(\alpha +1)}{2}} \right\} \\&\le -2\underline{K}_{2}\lambda _{min}(Z)[\lambda _{max}(Z)]^{\frac{-(\alpha +1)}{2}}E \left\{ V(e(t))^{\frac{(\alpha +1)}{2}} \right\} \!. \end{aligned} \end{aligned}$$
(43)

And

$$\begin{aligned} E \Big \{V^{\frac{(\alpha +1)}{2}}(e(0)) \Big \}= \Big (E\{V(e(0))\} \Big )^{\frac{(\alpha +1)}{2}}\!. \end{aligned}$$

By the finite-time stabilization theory , \(V(e(t))\) stochastically converges to zero in finite time. The upper bound of its convergent time is

$$\begin{aligned} \begin{aligned} T&=\frac{[\lambda _{max}(Z)]^{\frac{(\alpha +1)}{2}}[V(e(0))]^{\frac{(1-\alpha )}{2}}}{2\underline{K}_{2}\lambda _{min}(Z)\frac{(1-\alpha )}{2}}\\&\le \frac{[\lambda _{max}(Z)]^{\frac{(\alpha +1)}{2}}[\lambda _{max}(Z)]^{\frac{(1-\alpha )}{2}}\parallel e(0)\parallel _{2}^{1-\alpha }}{\lambda _{min}(Z)\underline{K}_{2}(1-\alpha )}\\&\le \frac{\lambda _{max}(Z)}{\lambda _{min}(Z)}\cdot \frac{\parallel e(0)\parallel ^{1-\alpha }}{\underline{K}_{2}(1-\alpha )}. \end{aligned} \end{aligned}$$
(44)

Thus we complete the proof.

Remark 1

This paper fills the gap of finite-time control of memristive neural networks. According to two kinds of memductance functions, discrete and continuous finite-time stability criteria are obtained for memristive neural networks, respectively.

Remark 2

In this paper, the proposed two synchronization criteria not only ensure the neural networks with stochastic perturbations can achieve stabilization, but also can estimate the upper bound of the convergence time. The proposed theoretical results provide the convenience for related applications of memristive neural networks.

Corollary 2

Under Case \(2'\), the system (16) without stochastic perturbations under controller (18) will achieve finite-time synchronization, if there exist a constant \(\varepsilon \) and a positive-definite matrix \(Z\epsilon R^{n\times n}\) which satisfy that

$$\begin{aligned} -Z\underline{\varPsi }-\underline{\varPsi }^{T}Z-2\underline{K}_{1}Z+\varepsilon ^{-1}Z\bar{\varLambda }\bar{\varLambda }^{T}Z+\varepsilon Q^{T}Q<0. \end{aligned}$$
(45)

The upper bound of its converge time is the same as Eq. (44).

4 Illustrative Example

In this section, two numerical examples are given to illustrate the effectiveness of the results obtained above.

Example 1

In Case \(1'\), we consider the two-dimensional memristive neural network with stochastic perturbations as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{1}(t)=-a_{1}(x_{1}(t))x_{1}(t)+b_{11}(x_{1}(t))f(x_{1}(t))\\ \qquad \qquad +\, b_{12}(x_{1}(t))f(x_{2}(t))+h(t,x_{1}(t))dw_{1}(t),\\ \dot{x}_{2}(t)=-a_{2}(x_{2}(t))x_{2}(t)+b_{21}(x_{2}(t))f(x_{1}(t))\\ \qquad \qquad +\, b_{22}(x_{2}(t))f(x_{2}(t))+h(t,x_{2}(t))dw_{2}(t),\\ \end{array} \right. \end{aligned}$$

where \(f(x(t))=tanh(x(t))\), and

$$\begin{aligned} a_{1}(x_{1}(t))&= \left\{ \begin{array}{l@{\quad }l@{\quad }l} 1,&{}-\dot{f}_{i}(x_{1}(t))-\dot{x}_{1}(t)\le 0,\\ 1.4,&{}-\dot{f}_{i}(x_{1}(t))-\dot{x}_{1}(t)> 0,\\ \end{array} \right. \\ a_{2}(x_{2}(t))&= \left\{ \begin{array}{l@{\quad }l@{\quad }l} 1.7,&{}-\dot{f}_{i}(x_{2}(t))-\dot{x}_{2}(t)\le 0,\\ 1,&{}-\dot{f}_{i}(x_{2}(t))-\dot{x}_{2}(t)> 0,\\ \end{array} \right. \\ b_{11}(x_{1}(t))&= \left\{ \begin{array}{l@{\quad }l@{\quad }l} 0.3,&{}-\frac{df(x_{1}(t))}{dt}-\frac{dx_{1}(t)}{dt}\le 0,\\ 0.4,&{}-\frac{df(x_{1}(t))}{dt}-\frac{dx_{1}(t)}{dt}> 0,\\ \end{array} \right. \\ b_{12}(x_{1}(t))&= \left\{ \begin{array}{l@{\quad }l@{\quad }l} 0.2,&{}\frac{df(x_{2}(t))}{dt}-\frac{dx_{1}(t)}{dt}\le 0,\\ 0.3,&{}\frac{df(x_{2}(t))}{dt}-\frac{dx_{1}(t)}{dt}> 0,\\ \end{array} \right. \\ b_{21}(x_{2}(t))&= \left\{ \begin{array}{l@{\quad }l@{\quad }l} 0.2,&{}\frac{df(x_{1}(t))}{dt}-\frac{dx_{2}(t)}{dt}\le 0,\\ 0.3,&{}\frac{df(x_{1}(t))}{dt}-\frac{dx_{2}(t)}{dt}> 0,\\ \end{array} \right. \\ b_{22}(x_{2}(t))&= \left\{ \begin{array}{l@{\quad }l@{\quad }l} 0.3,&{}-\frac{df(x_{2}(t))}{dt}-\frac{dx_{2}(t)}{dt}\le 0,\\ 0.5,&{}-\frac{df(x_{2}(t))}{dt}-\frac{dx_{2}(t)}{dt}> 0.\\ \end{array} \right. \end{aligned}$$

So we get

$$\begin{aligned} \underline{B}=\left( \begin{array}{c@{\quad }c} 0.3&{}0.2\\ 0.2&{}0.3\\ \end{array} \right) , \bar{B}=\left( \begin{array}{c@{\quad }c} 0.4&{}0.3\\ 0.3&{}0.5\\ \end{array} \right) . \end{aligned}$$

And \(h(t,x(t))=diag(tanh(x_{1}(t)), tanh(x_{2}(t)))\). Then \(Q=M\) is a \(2\times 2\) identity matrix. The initial values of the error system are \(e(0)=[1,-1]^{T}\), then we get \(\parallel e(0)\parallel =1.414\). We choose \(\alpha =0.5\). If \(Z\) is an identity matrices, and \(\varepsilon =1, \, \underline{K}_{1}=2\), then we get

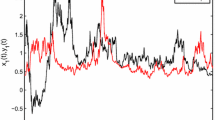
$$\begin{aligned} \begin{aligned}&-Z\underline{A}-\underline{A}^{T}Z-2\underline{K}_{1}Z+\varepsilon ^{-1}Z\bar{B}\bar{B}^{T}Z+\varepsilon Q^{T}Q\\&\quad +\lambda _{\max }(Z)M^{T}M <0. \end{aligned} \end{aligned}$$

By choosing an arbitrary gain and the upper bound \(\underline{K}_{2}=0.6\), the system in Example 1 is stabilized in finite time. The upper bound of its convergence time is \(T=\frac{\parallel e(0)\parallel ^{0.5}}{0.6\times 0.5}=3.9637\). The simulation results are depicted in Fig. 2, which shows the evolutions of the errors \(e_{1}(t),e_{2}(t)\) for the controlled system in Example 1. The simulation results have confirmed the effectiveness of Theorem 1.

Fig. 2
figure 2

(Color online) The error curves of the system in Example 1 via the controller (18), the upper bound of its convergence time is 3.9637

Full size image

Example 2

In Case \(2'\), we consider the following two-dimensional memristive neural network with stochastic perturbations

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{1}(t)=-a_{1}(x_{1}(t))x_{1}(t)+b_{11}(x_{1}(t))f(x_{1}(t))\\ \qquad \qquad +\, b_{12}(x_{1}(t))f(x_{2}(t))+h(t,x_{1}(t))dw_{1}(t),\\ \dot{x}_{2}(t)=-a_{2}(x_{2}(t))x_{2}(t)+b_{21}(x_{2}(t))f(x_{1}(t))\\ \qquad \qquad +\, b_{22}(x_{2}(t))f(x_{2}(t))+h(t,x_{2}(t))dw_{2}(t),\\ \end{array} \right. \end{aligned}$$

where \(f(x(t))=tanh(x(t))\), and \(a_{1}(x_{1}(t))=1+0.3sin(x_{1}(t)), \, a_{2}(x_{2}(t))=1+0.6cos(x_{2}(t)), \, b_{11}(x_{1}(t))=0.6sin(x_{1}(t)), \, b_{12}(x_{1}(t))=0.8sin(x_{1}(t)), \, b_{21}(x_{2}(t))=0.8cos(x_{2}(t)), \, b_{22}(x_{2}(t))=0.6cos(x_{2}(t)), \, \underline{K}_{1}=0.5\), and the values of other parameters are as the same as those in Example 1. Then we have

$$\begin{aligned} \bar{\varLambda }=\left( \begin{array}{c@{\quad }c} 0.6&{}0.8\\ 0.8&{}0.6\\ \end{array} \right) , \end{aligned}$$

and we verified that

$$\begin{aligned} \begin{aligned}&-Z\underline{\varPsi }-\underline{\varPsi }^{T}Z-2\underline{K}_{1}Z+\varepsilon ^{-1}Z\bar{\varLambda }\bar{\varLambda }^{T}Z\\&\quad +\varepsilon Q^{T}Q+\lambda _{\max }(Z)M^{T}M<0. \end{aligned} \end{aligned}$$
(46)

From Fig. 3, we can see that the error curves become convergent. The upper bound of the convergence time is \(T=\frac{\parallel e(0)\parallel ^{0.5}}{0.5\times 0.5}=2.3782\), which verified the effectiveness of Theorem 2.

Fig. 3
figure 3

(Color online) The error curves of the system in Example 2 with the controller (18), its upper bound of the convergence time is 2.3782

Full size image

5 Conclusion

This paper studied finite-time anti-synchronization control of memristive neural network with stochastic perturbations. According to two kinds of memductance functions, finite-time stability criteria are obtained for memristive neural networks. It can well mimic the human brain in many applications, such as pattern recognition and associative memories. Finally, two numerical examples are given to illustrate the effectiveness of the proposed results.