Ensemble particle swarm optimization and differential evolution with alternative mutation method

Abstract

This paper presents a new ensemble algorithm which combines two well-known algorithms particle swarm optimization (PSO) and differential evolution (DE). To avoid the suboptimal solutions occurring in the previous hybrid algorithms, in this study, an alternative mutation method is developed and embedded in the proposed algorithm. The population of the proposed algorithm consists of two groups which employ two independent updating methods (i.e. velocity updating method from PSO and mutative method from DE). By comparing with the previously generated population at the last generation, two new groups are generated according to the updating methods. Based on the alternative mutation method, the population is updated by the alternative selection according to the evaluation functions. To enhance the diversity of the population, the strategies of re-mutation, crossover, and selection are conducted throughout the optimization process. Each individual conducts the correspondent mutation and crossover strategies according to the parameter values randomly selected, and the parameter values of scaling factor and crossover probability will be updated accordingly throughout the iterations. Numerous simulations on twenty-five benchmark functions have been conducted, which indicates the proposed algorithm outperforms some well-exploited algorithms (i.e. inertia weight PSO, comprehensive learning PSO, and DE) and recently proposed algorithms (i.e. DE with the ensemble of parameters and mutation strategies and ensemble PSO).

1 Introduction

Particle swarm optimization (PSO) (Kennedy and Eberhart 1995) is known for its fast convergence, fewer initialization parameters, and easy to implement in complex optimization problems, which has been widely applied to many practical problems such as sampling-based image matting problem (Mohapatra et al. 2017), radial basis function networks problem (Alexandridis et al. 2016) and constrained non-convex and piecewise optimization problem (Chen et al. 2017). However, the main drawback associated with PSO and its variants is easily to fall into the local optima in comparison to other evolutionary algorithms. Different from the PSO method, differential evolution (DE) (Storn and Price 1997) is famous for its superior exploration capability using the strategies such as mutation, crossover and selection. Currently, DE has shown the great success in engineering applications such as economic or emission dispatch problem (Jebaraj et al. 2017), circuit designs problem (Zheng et al. 2017), and flood classification problem (Liao et al. 2013). Even so, the convergence speed of DE seems to be rather slow in the late optimization stage, which leads to the local optimum like PSO.

To overcome the limitation associated with PSO methods and DE methods, various strategies (Cheng et al. 2014; Guo et al. 2015; Juang et al. 2015; Niu et al. 2014, 2017) are used in the improvements of PSO and DE method. For example, some methods [e.g. integrating a unification factor (Tsai 2017), incorporating the individual particles memories (Guedria 2016) and improving the particles’ collision and “territories” (Arani et al. 2013)] were applied in the independent PSO to avoid the premature convergence. Additionally, to encourage broader exploration, some strategies were also introduced in the independent DE, such as, the combination of Taguchi method with sliding levels (Tsai 2015), the introduction of fuzzy selection method (Pandit et al. 2015) and the application of restricting the discrete variables (Ho-Huu et al. 2015). In recent years, the hybrid DE and PSO have been verified the superior performance on practical problems. In (Ma et al. 2015), a hierarchical hybrid algorithm, adopting the velocity and position method in PSO and a mutation strategy in DE, has been proposed and applied to solving the bi-level programming problem (BLPP). With equal sub lots method, a proposed hybrid algorithms of PSO and DE (Vijay Chakaravarthy et al. 2013) was used for scheduling m-machine flow shops with lot streaming. A hybrid method of PSO and DE integrating fuzzy c-means clustering algorithm had good performance on image segmentation (Liu and Qiao 2015).

Although the combination strategies can improve the effectiveness of global capability of DE or PSO, they generally have to burden larger computational complexity. To address this drawback, many improvements of hybrid PSO and DE have been proposed. In (Mao et al. 2017), combined the DE with the acceleration factors updating strategy in PSO, a global optimization method was developed to reduce the computational complexity. The updated mutation and crossover strategies were introduced in the novel hybrid DE and PSO algorithm (DE-PSO) (Xu et al. 2016) to make use of the shared resources, i.e. location and time. In (Tang et al. 2016), a novel hybrid PSO and DE algorithm, with the nonlinear time-varying PSO (NTVPSO) and the ranking-based self-adaptive DE (RBSADE), was developed to avoid stagnation and enhance the convergence speed. With the strategies of making uses of the population diversity of DE and the convergence ability of PSO, a multi-objective hybrid algorithm (Ma et al. 2015) integrating DE and PSO is designed to quickly produce the satisfactory solutions. In addition, some strategies have been presented in the hybrid DE and PSO methods to enhance the global search ability, such as the aging leader and challenger strategy (Moharam et al. 2016), population reduction strategy (Ali and Tawhid 2016), and hybrid operator and a multi-population strategy (Zuo and Xiao 2014). Though those hybrid methods can improve the performance of the original algorithms of the PSO and DE, premature stagnation is still a major problem.

In this study, based on an alternative mutation method, a combination of PSO and DE with ensemble strategies (EPSODE) is proposed to address the problem of premature convergence in original PSO and DE. Unlike previous combination algorithms of DE and PSO, this proposed EPSODE algorithm is a hierarchical method, which includes the alternative mutation method, the novel mutation and crossover strategies. Different mutation strategies of DE algorithm can achieve more accurate results than a unique mutation strategy. The ensemble mutation and crossover strategies have the characteristics of fast convergence and easy to jump out of the local optimal situation. To enhance population diversity, in the alternative mutation strategy, the population is separated into two groups generated by two different methods (i.e. velocity updating strategy of PSO and mutation strategy of DE). Additionally, those two new generated groups are updated by making the comparison with the previous population. The population at the next generation is obtained by intentionally selecting from two separated groups.

Thus, the main contributions of this paper are as follows:

• A new combination of PSO and DE is proposed with ensemble strategies to address the problem of premature convergence;

• The ensemble mutation and crossover strategies are developed to ensure the diversity of the population and the convergence speed of the optimization;

• The population of the proposed method is separately updated using velocity updating strategy of PSO and mutation strategy of DE to increase the disturbances between individuals;

• Compared with three well-exploited algorithms and two recently proposed PSO and DE algorithms, the new proposed combination algorithm is demonstrated to be superior by demonstrating on twenty-five benchmark functions.

The remaining paper is organized as follows. Section 2 provided a brief introduction of PSO algorithm and DE algorithm. In Sect. 3, the ensemble algorithm of PSO and DE with alternative mutation method is presented. Section 4 gives experimental results of the simulations on benchmark functions. Finally, Sect. 5 gives the conclusion remarks.

2 Description of algorithms

In this Section, the particle swarm optimization (PSO) method and differential evolution (DE) method are introduced, separately.

2.1 Particle swarm optimization

Inspired by the behavior of birds flocking, PSO (Kennedy and Eberhart 1995) is proposed as one of the intelligent optimization methods. In the simulation of PSO algorithm, a group of particles without quality and volume flies in the search space to find the optimal location. Each particle represents a potential solution to the problem under analysis. All particles are given random positions x and velocities v at the initial state. At each generation, the best position of ith particle is represented by p best_i and the best position of all particles is denoted by gbest. By learning from them, the particles gradually approach to their optimal position. Equations (1)–(2) are the update equation:

$$v_{i}^{G + 1} = \omega v_{i}^{G} + c_{1} rand(0,1)(pbest_{i}^{G} - x_{i}^{G} ) + c_{2} rand(0,1)(gbest^{G} - x_{i}^{G} )$$

(1)

$$x_{i}^{G + 1} = x_{i}^{G} + v_{i}^{G + 1}$$

(2)

where N is the number of particles, D is the dimension of search space, and G is the number of generation, $x_{i} \left( {i = 1, \, 2, \, \ldots , \, N} \right)$ denotes the ith particle, $v_{i} (i = 1,2, \ldots , \, N)$ is the velocity (i.e. the rate of change of position) of the ith particle. c₁ and c₂ are acceleration factors. Finally, the value of inertia weight represented by ω plays an important role in the search ability of PSO algorithm.

In addition to giving a fixed inertia weight, Shi and Eberhart (1998) proposed a linearly decreasing strategy for inertia weight [i.e. Eq. (3)] to improve the premature convergence in 1999. In the early part of the optimization, larger inertia weight can enhance the global exploration. While a smaller inertia weight in the later part of the generation can enable the local exploitation.

$$\omega = \omega_{\hbox{max} } - (\omega_{\hbox{max} } - \omega_{\hbox{min} } )*G/G_{\hbox{max} }$$

(3)

where ω_max and ω_min are the maximum and minimum values of inertia weight respectively. Gis the current number of generation and G_max is the maximum number of generation.

2.2 Differential evolution algorithm

Proposed by Storn and Price (1997), DE is a well-known evolutionary optimization algorithm, which generally includes three basic operators including mutation, crossover, and selection. In DE algorithm, each candidate solution is encoded as $x_{i} = \left\{ {x_{i1} ,x_{i2} , \ldots ,\left. {x_{iD} } \right\}} \right.$, i = 1, 2, …, N. The initial population should be distributed throughout the whole search space. The lower limit and the upper limit of the search space are $x_{\hbox{min} } = \left\{ {x_{\hbox{min} 1} ,x_{\hbox{min} 2} , \ldots ,\left. {x_{\hbox{min} D} } \right\}} \right.$ and $x_{\hbox{max} } = \left\{ {x_{\hbox{max} 1} ,x_{\hbox{max} 2} , \ldots ,\left. {x_{\hbox{max} D} } \right\}} \right.$, respectively. In general, the initial population is generated by using the following equation [i.e. Eq. (4)].

$$x_{ij} = x_{\hbox{min} j} + rand(1,0) \cdot (x_{\hbox{max} j} - x_{\hbox{min} j} ) \quad j = (1,2, \ldots ,D)$$

(4)

where N is the number of individuals and D is the search space’s dimension.

Mutation: In order to avoid the local optima, the offspring of DE algorithm is produced by using mutation operation (Salman et al. 2007), and most frequently used mutation strategies are shown as follows:

$${\text{DE}}/{\text{rand}}/1 \, \left( {{\text{Storn }}1996} \right):\quad V_{\text{i}}^{G} = x_{r1}^{G} + F \cdot (x_{r2}^{G} - x_{r3}^{G} )$$

(5)

$${\text{DE}}/{\text{rand}}/2 \, \left( {{\text{Qin et al}}. \, 2009} \right):\quad V_{\text{i}}^{G} = x_{r1}^{G} + F \cdot (x_{r2}^{G} - x_{r3}^{G} ) + F \cdot (x_{r4}^{G} - x_{r5}^{G} )$$

(6)

$${\text{DE}}/{\text{best}}/1 \, \left( {{\text{Storn }}1996} \right):\quad V_{\text{i}}^{G} = x_{best}^{G} + F \cdot (x_{r1}^{G} - x_{r2}^{G} )$$

(7)

$${\text{DE}}/{\text{best}}/2 \, \left( {{\text{Storn}}\;1996} \right):\quad V_{\text{i}}^{G} = x_{best}^{G} + F \cdot (x_{r1}^{G} - x_{r2}^{G} ) + F \cdot (x_{r3}^{G} - x_{r4}^{G} )$$

(8)

$${\text{DE}}/{\text{rand}-\text{to}-\text{best}}/1 \, \left( {{\text{Storn}}\;1996} \right)\;{\text{or}}\;{\text{DE}}/{\text{target}-\text{to}-\text{best}}/1 \, \left( {{\text{Price}}\;{\text{et}}\;{\text{al}}.\;2005} \right):\quad V_{\text{i}}^{G} = x_{i}^{G} + K \cdot (x_{best}^{G} - x_{i}^{G} ) + F \cdot (x_{r1}^{G} - x_{r2}^{G} )$$

(9)

$${\text{DE}}/{\text{rand}-\text{to}-\text{best}}/2 \, \left({{\text{Qin}}\;{\text{et}}\;{\text{al}}.\;2009} \right):\quad V_{\text{i}}^{G} = x_{i}^{G} + K \cdot (x_{best}^{G} - x_{i}^{G} ) + F \cdot (x_{r1}^{G} - x_{r2}^{G} + x_{r3}^{G} - x_{r4}^{G} )$$

(10)

$${\text{DE}}/{\text{current}-\text{to}-\text{rand}}/1 \, \left( {{\text{Iorio}}\;{\text{and}}\;{\text{Li}}\;2004} \right):\quad u_{\text{i}}^{G} = x_{i}^{G} + K \cdot (x_{r1}^{G} - x_{i}^{G} ) + F \cdot (x_{r2}^{G} - x_{r3}^{G} )$$

(11)

where G is the current generation, the scaling factor F plays an important role in disturbing the previous vectors. Larger scaling factor is useful for obtaining more potential solutions while smaller scaling factor facilitates to enhance the speed of convergence. K is a random number selected from 0 to 1. r1, r2, r3, r4 and r5 not equal to each other are randomly selected from 1 to N, and also different to i. V_i is the updated ith vector through mutating. $x_{best}^{G}$ is the optimal individual at the Gth generation.

Though the single mutation strategy obtains good performance in DE, many limitations still exist. In terms of search accuracy, DE/rand/1 (Storn 1996) is widely used in the intelligence optimization field while it does not obtain the better solution relative to the DE/rand-to-best/1 (Storn 1996, Price et al. 2005). DE/rand/2 (Qin et al. 2009) increases the diversity relative to the DE/rand/1 (Storn 1996). DE/best/1 (Storn 1996, DE/rand-to-best/1 (Storn 1996, Price et al. 2005), DE/rand-to-best/2 (Qin et al. 2009) and DE/current-to-rand/1 (Iorio and Li 2004) all have certain limitations in high dimension and multi-model. Additionally, the speed of the DE/rand-to-best/1 (Storn 1996) is faster on easier optimization problems, and DE/current-to-rand/1 (Iorio and Li 2004) is superior to the other strategies for solving the rotated problems. Therefore, in order to integrate the advantages of those mutation strategies, the strategies of DE/rand-to-best/1 [i.e. Equation (9)] and DE/current-to-rand/1 [i.e. Eq. (11)] are employed in the proposed EPSODE algorithm.

Crossover: In DE algorithm, crossover operation is used for increasing the diversity of the population. The number of the alternative population is determined by the crossover probability CR. Smaller CR preserves the stability of the population during the evolution procedure, and larger CR enhances the diversity of the population. Equations (12)–(13) are the formulas of crossover:

$$u_{{_{ij} }}^{G} = \left\{ {\begin{array}{*{20}l} {V_{{_{ij} }}^{G} } \hfill & {if(rand_{j} (0,1) \le CR)or j = j_{rand} } \hfill \\ {x_{{_{ij} }}^{G} } \hfill & {otherwise} \hfill \\ \end{array} } \right., \, j = 1 \ldots D$$

(12)

$$u_{{_{ij} }}^{G} = \left\{ {\begin{array}{*{20}l} {V_{{_{ij} }}^{G} } \hfill & {ij = \left\langle {j_{rand} } \right\rangle_{D} ,\left\langle {j_{rand} + 1} \right\rangle_{D} , \ldots ,\left\langle {j_{rand} + L - 1} \right\rangle_{D} } \hfill \\ {x_{{_{ij} }}^{G} } \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(13)

where u_ij is the trial vector, j_rand is a randomly selected index in the range of[1, D], rand_j is a random number in the range of [0, 1], $\left\langle l \right\rangle_{D}$ represents the modulo operation for D, and L is an integer between 1 to D. To enhance the diversity of the population, the binomial crossover and exponential crossover [i.e. Eq. (13)] (Zaharie 2009) are applied in the proposed algorithm (Mallipeddi and Suganthan 2010).

Selection: Following the crossover process, every trial vectoru_iwill be compared with the individual vectorx_iin terms of the fitness value, and the vectors corresponding to the better fitness values will be preserved to the next generation. The greedy algorithm [i.e. Eq. (14)] is used to select individuals for the next generation process.

$$x_{i}^{G + 1} = \left\{ {\begin{array}{*{20}l} {u_{i}^{G} } \hfill & {if \, f(u_{i}^{G} ) \le f(x_{i}^{G} )} \hfill \\ {x_{i}^{G} } \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(14)

3 Ensemble particle swarm optimization and differential evolution (EPSODE)

The superior characteristics of PSO are fast convergence speed and fewer initial parameters. However, due to insufficient information search, the suboptimal solutions might be more frequently obtained by PSO. Different from PSO, the population of DE tends to be more diverse as the number of generations increases but the computational complexity is greater. To take advantages of those two algorithms, in this paper, a new ensemble PSO and DE method (EPSODE) is proposed to improve the search capability of particles. The description of the proposed EPSODE algorithm is as follows.

3.1 Alternative mutation method

At the beginning of each generation, two subpopulation groups (i.e. P₁ and P₂) are generated by PSO and DE. Considering that PSO is easy to implement and has fewer parameters, one group (i.e., P₁) is produced by the PSO with the inertial weight of linearly decreasing strategy to reduce computational complexity [i.e. Eqs. (1)–(3)]. In order to disrupt the original movement direction, another group P₂is renewed by the mutation method [i.e. Eq. (15)].

$$x_{i} = K_{1} \cdot (x_{pbest} - x_{i} ) + K_{2} \cdot (x_{a} - x_{b} ), \, i = 1 \ldots N$$

(15)

where N is the individuals’ number, K₁ and K₂ are randomly selected from [0, 1], x_idonates the ith individual. x_pbest is the optimal population, a and bare indexes selected from 1 to N, but different from the i.

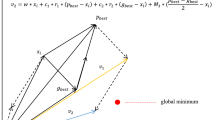
The mutation method is proposed to break the rules of the original particle movement. For example, as shown in Fig. 1, if the initial directions of x_i, x_pbest, x_a and x_b are given, the directions of x_best − x_i and x_a − x_b are also determined. K₁ and K₂play the role in regulating the direction. If the value of K₁and K₂ are the same, the direction of the individual is the same of $(x_{pbest} - x_{i} ) + (x_{a} - x_{b} )$. If not, it will be updated.

Fig. 1

Disturbance map of the improved mutation method

After updating the two subpopulation groups, the two updated groups (i.e. P₁ and P₂) are compared with the initial population or reserved population at the last generation according to the fitness value. The better individuals are preserved to update the new P₁andP₂again.

The individuals of two new groups (i.e. new P₁ and P₂) are sorted in accordance with the fitness value, and the sorted groups are also compared to retain the superior individuals. The new group P₃ is consist of the superior individuals, and served as the basic population in the next simulation experiment. The flowchart of the alternative mutation method is shown in Fig. 2.

Fig. 2

The flowchart of the alternative mutation method

3.2 Ensemble strategy of mutation and crossover

The selection method of mutation and crossover strategies plays an important role in the simulation process of DE. The suitable strategy can make the algorithm more efficient in solving the diffident types of functions, such as unimodal function, multimodal function, continuous functions, and discrete functions and so on. The recently proposed algorithm (Mallipeddi and Suganthan 2010) obtains superior offspring by employing the multi-strategies of mutation and crossover successfully. Based on the superior performance of multi-strategies, the ensemble of mutation and crossover strategy is employed in the proposed EPSODE algorithm.

In order to improve the global search ability of the proposed algorithm, DE/rand-to-best/1 [i.e. Eq. (9)] and DE/current-to-rand/1 [i.e. Eq. (11)] are applied in the proposed EPSODE algorithm. Getting information from the best individual of the whole group (i.e. DE/rand-to-best/1), the proposed EPSODE is easier to obtain the optimal value relative to other mutation strategies (i.e. DE/rand/1 and DE/rand/2). Obtaining information from neighbor individuals (i.e. DE/current-to-rand/1), the disturbance between individuals can be increased. Binomial crossover [i.e. Eq. (12)] and exponential crossover [i.e. (13)] (Wong et al. 2016) are applied in EPSODE to enhance population diversity.

In the ensemble method of mutation and crossover strategies, mutation crossover strategies are randomly selected according to the following pattern. The pattern is as follows: the scaling factorFis given two values (i.e. 0.5 and 0.9) and the crossover probability CR is also given three values (i.e. 0.1, 0.5, and 0.9). Each individual will be given a randomFandCR during each iteration. T₁ and T₂ are the test labels, and the value is 0 or 1 (the two value can be selected arbitrarily). Each individual of the population P3 is given random T₁ and T₂. If $T_{1} { = 0}$, the DE/rand-to-best/1 is selected as the mutation strategy according to the corresponding F. Otherwise, DE/current-to-rand/1 is used in EPSODE. To improve population diversity, the individuals which obtain information from the best individual of the whole group, are employed in the crossover strategy. If $T_{1} = 0$ and $T_{ 2} = 0$, the exponential crossover is selected as the crossover strategy according to the corresponding CR. If $T_{1} = 0$ and $T_{2} = 1$, binomial crossover is used for the crossover strategy. If the trial vector is not superior to the individual of populationP₃, the parameters (i.e. F, CR, T₁ and T₂) are updated again. The flowchart of the ensemble method of mutation and crossover strategies is shown in Fig. 3.

Fig. 3

The flowchart of the ensemble strategy of mutation and crossover

3.3 The pseudo-code of EPSODE

Effective termination criteria can save a lot of computation time while achieving superior solutions (Wong et al. 2016). In general, if the maximum number of generations is satisfied or the best value of fitness is found, the simulation process of this algorithm terminates. In EPSODE, the function evaluations have been performed more than once. Therefore, the original termination condition is prone to consume excessive computation because of the repeated fitness evaluation. To reduce computational complexity, the maximum number of function evaluations FESis employed as the termination criteria (Lynn and Suganthan 2017). The pseudo-code of EPSODE is given in Table 1.

Table 1 The pseudo-code of EPSODE

As displayed in Table 1, in the simulation of EPSODE, the initial individual, generated using Eq. (4), is described as the initial target individualx. Based on the alternative mutation method, the population is updated using the updated velocity strategy of PSO and the modified mutation method of DE. The new trial individual u is generated according to the ensemble strategy of mutation and crossover. In order to obtained optimal generation, the function evaluation value of new trial individualu is compared with the function evaluation value of target individualx. If the new trial individualu is better than the target individualx, the trial individualu is regarded as an updated target vector. Otherwise, the target vector xis reserved as the target individual of the next generation [i.e. Eq. (14)].

4 Experiments and analyses

4.1 Benchmark functions and algorithms

Twenty-five benchmark functions (Suganthan et al. 2005) are applied to test the performance of the proposed EPSODE algorithm. According to the CEC2005 benchmark competition (Suganthan et al. 2005), those twenty-five functions can be divided into two categories: unimodal functions(i.e. functions F1–F5)and multimodal functions (F6–F25). Multimodal functions contain basic multimodal functions (i.e. functions F6–F12), expanded functions (i.e. functions F13–F14) and hybrid composition functions (i.e. functions F15–F25). The initialization ranges, search ranges and bias values of these benchmark functions are given in Table 2. The initialization range is set in accordance with CEC2005 (Suganthan et al. 2005).

Table 2 CEC 2005 test functions

To verify the performance of the proposed algorithm, some classic algorithms [i.e. PSO, DE and comprehensive learning PSO (CLPSO) (Liang et al. 2006)] and recently proposed algorithms [e.g. differential evolution algorithm with ensemble of parameters and mutation strategies (EPSDE) and ensemble PSO (EPSO) (Lynn and Suganthan 2017)] are introduced.

• Inertia weight PSO (PSO) (Shi and Eberhart 1998).

• Differential evolution algorithm (DE) (Storn and Price 1997).

• Differential evolution algorithm with ensemble of parameters and mutation strategies(EPSDE) (Mallipeddi and Suganthan 2010).

• Comprehensive learning PSO (CLPSO) (Liang et al. 2006).

• Ensemble particle swarm optimizer (EPSO) (Lynn and Suganthan 2017).

The first three algorithms are the original algorithms and have been used in the proposed EPSODE algorithm. In CLPSO algorithm, the historical best information of all other particles is applied to update the velocity. The CLPSO algorithm obtains good performances in dealing with the multimodal problem (Liang et al. 2006). EPSO algorithm, combined with a variety of PSO strategies, has been demonstrated to be superior in dealing with real-parameter optimization problems (Lynn and Suganthan 2017). All experiments are conducted through MATLAB R2014a software.

The same parameters of the six algorithms are described in detail (Lynn and Suganthan 2017). The maximum number of the generation (G_max) is a constant value i.e. $G_{\hbox{max} } = 7500$. The maximum number of function evaluations (FES) varies with the population size Nand the maximum number of the generation G_max, i.e. $FES = N *G_{\hbox{max} }$ (Lynn and Suganthan 2017). Therefore, $FES = 300{,}000$ and N  = 40 are used in the simulation of 30-dimensional problems. When the problem dimension is 50, FES is 600,000 and N is 80. If the maximum number of the generation G_max is satisfied while the maximum number of function evaluations (FES) is not satisfied, the current number of generation would decrease in order. Other parameters of all algorithms are shown as follow:

• In CLPSO (Liang et al. 2006), inertia weightωis also from 0.9 to 0.2, (i.e. ω_max = 0.9 and ω_min = 0.2), and acceleration coefficient c is from 3 to 1.5.

• In inertia weight PSO (Shi and Eberhart 1998), inertia weightωis from 0.9 to 0.2,$\begin{array}{*{20}l} {c_{1} = \, 2, \, c_{2} = \, 2} \hfill \\ \end{array}$.

• In EPSO, some parameters of the integrated inertia weight PSO and CLPSO such as inertia weight ω and acceleration coefficient c, are same as above. Other parameters are from the literature (Lynn and Suganthan 2017).

• In DE (Storn and Price 1997), mutation factorFis 0.9, and crossover probability CR is 0.5.

• In EPSDE (Mallipeddi and Suganthan 2010), mutation factors F are 0.5 and 0.9, and crossover probabilities CR are 0.1, 0.5 and 0.9.

• In the EPSODE, mutation factors F are also 0.5 and 0.9, and crossover probabilities CR are 0.1, 0.5 and 0.9. Inertia weight ω is also from 0.9 to 0.2, $\begin{array}{*{20}l} {c_{1} = \, 2, \, c_{2} = \, 2} \hfill \\ \end{array}$.

4.2 Experiment results and discussion

The mean fitness and the standard deviation obtained by six algorithms are given in Tables 3 and 4. The best results among these optimization algorithms are highlighted in italics. Figure 4 shows the convergence curves of different test functions with the dimension 50. In order to make the graphical curve clear, the graphical interpretation labels are provided only in the first and last functions (i.e.F1 and F25). The legends in remaining subfigures are the same to F1 and F25.

Table 3 Experiment results on benchmark functions with dimensionality 30

Table 4 Experiment results on benchmark functions with dimensionality 50

Fig. 4

The generation process of the algorithms when dimensionality = 50

The maximum number of function evaluations (FES) 300,000 and population size 40 are used in the simulation of 30-dimensional problems (Lynn and Suganthan 2017). Experiment results are illustrated in Table 3. For unimodal functions, EPSODE obtains the best results on functions F1–F4, and the second-best result on the function F5. EPSODE performs well as the EPSDE on functions F1 and F2. For basic multimodal functions, EPSODE performs best on functions F6–F9. EPSDE algorithm yields the best results on functionF10. For the remaining basic multimodal functions (i.e. functions F11 and F12), inertial weight PSO and EPSO respectively get the best results. The proposed EPSODE algorithm dedicates the best results on the function F13 while inertial weight PSO complies the best on functionF14. For hybrid composition functions, the proposed EPSODE algorithm implements the superior results on functions F15–F16, F18–F21 and F23–F24. EPSO algorithm performs the best on F17 and F22. EPSODE algorithm and EPSDE algorithm obtain the same fitness values on functions F19, F21 and F23, but the standard deviations of EPSODE are better than EPSDE except the function F23. Therefore, the proposed algorithm obtains good performance in most functions whether the function is unimodal or multimodal.

The experiment results in 50-dimensional problems are shown in Table 4. The number of function evaluations (FES) is 600,000 and population size is 80. EPSODE implements the best results on the functions F1 and F3–F4 while EPSO and EPSDE respectively perform the best on functions F2 and F5. For basic multimodal functions, EPSODE, EPSO, CLPSO, DE and EPSDE obtain the same best results on functions F7. The performances of EPSODE algorithm are significantly better than other algorithms on function F9–F10 and F12. For expanded functions (i.e. functions F13–F14), the proposed EPSDE successes to maintain its good performance on functions F13. For hybrid composition functions, DE and EPSDE comply the same best results on function F15. EPSODE obtains the best results on functions F16–F20 and F22–F23. Inertia weight PSO algorithm gets the best results on function F21. The proposed EPSODE gets the same performances as well as inertial weight PSO on function F24, but the convergence speed of EPSODE is evidently superior to the inertial weight PSO in Fig. 4. Therefore, EPSODE algorithm successful remained its superior performance in higher dimension problems.

As shown in Fig. 4, the convergence speed of EPSODE is faster than other algorithms on functions F1, F7, F10 and F24. The convergence solutions are closer to optimal values on most functions e.g., F1, F3, F10, F13, F16, F24 and so on. Altogether, the superior performance of EPSODE algorithm can still be seen from the convergence curves.

In summary, the proposed algorithm is more powerful than the other algorithms (i.e. inertial weight PSO, CLPSO, EPSO, DE and EPSDE) in terms of the search ability. Though EPSDE, and inertial weight PSO algorithm can obtain the similar solutions on some benchmark functions (e.g., functions F1 and F24), the convergence speed is not better than the proposed EPSODE algorithms. In terms of dimensionality, the proposed EPSODE algorithm performs better than other algorithms when the dimension increases. The main reasons of the superiority are as follows:

• One group uses the updating method of PSO to carry out more in-depth exploration in the alternative mutation method of EPSODE.

• The other group applies the mutative method of DE to disturb the original direction in the alternative mutation method of EPSODE.

• Hence, the new population is given a deeper ability to explore and is different from the original updating direction.

• Additionally, the non-single and fixed mutation crossover strategy contributes to increasing the diversity of the population.

5 Conclusion

An ensemble PSO and DE algorithm (EPSODE), based on the alternative mutation method, is proposed for solving different types of functions. Modified DE algorithm are the main program and PSO algorithm is the subprogram in the proposed algorithm. The velocity update strategy of PSO combined with the modified mutation method is the key of the proposed algorithm, which can avoid the premature convergence and improve the search capability. Meanwhile, the strategies of multiple mutation and crossover can improve convergence speed. Experiment results show that EPSODE algorithm outperforms other algorithms in terms of mean and standard deviation. Thus, the proposed alternative mutation method can enhance the performance of EPSODE algorithm, which has been verified by testing on the benchmark functions. In our future studies, the proposed algorithm will be developed and applied to solving the real-world problems.