Hybrid particle swarm optimization and differential evolution algorithm for bi-level programming problem and its application to pricing and lot-sizing decisions

Abstract

This paper proposes a hierarchical hybrid particle swarm optimization (PSO) and differential evolution (DE) based algorithm (HHPSODE) to deal with bi-level programming problem (BLPP). To overcome the shortcomings of basic PSO and basic DE, this paper improves PSO and DE, respectively by using a velocity and position modulation method in PSO and a modified mutation strategy in DE. HHPSODE employs the modified PSO as a main program and the modified DE as a subprogram. According to the interactive iterations of modified PSO and DE, HHPSODE is independent of some restrictive conditions of BLPP. The results based on eight typical bi-level problems demonstrate that the proposed algorithm HHPSODE exhibits a better performance than other algorithms. HHPSODE is then adopted to solve a bi-level pricing and lot-sizing model proposed in this paper, and the data is used to analyze the features of the proposed bi-level model. Further tests based on the proposed bi-level model also exhibit good performance of HHPSODE in dealing with BLPP.

Introduction

Bi-level programming techniques aim to deal with decision problems involving two decision makers with a hierarchical structure (Calvete and Galé 2011). Both of these two decision makers seek to optimize their individual objective functions and control their own set of decision variables. The leader at the upper level of the hierarchy first specifies a strategy, and then the follower at the lower level of the hierarchy specifies a strategy so as to optimize the objective functions with full knowledge of the action of the leader. Bi-level programming techniques have been successfully applied to many different areas (Gao et al. 2011), such as mechanics, decentralized resource planning, electric power markets, logistics, civil engineering, and road network management and so on.

Bi-level programming problem (BLPP) has been proved to be a NP-hard problem (Jeroslow 1985) which is very difficult to solve. However, the bi-level programming is used so widely that there are many researchers focusing on BLPP, and several different kinds of methods have been developed to solve this problem. The main methods for solving linear bi-level programming problems can be divided into the following four categories (Hejazia et al. 2002): Methods based on vertex enumeration; methods based on Kuhn–Tucker conditions; fuzzy approach and methods based on meta-heuristics, such as genetic algorithm based approaches, simulated annealing based approaches, and so on. It needs to be pointed out that methods based on vertex enumeration and Kuhn–Tucker conditions have some limitations for solving BLPPs as they rely on the differentiability of the objective function, the convexity of search space, etc. Methods based on meta-heuristics, however, are independent of these limiting conditions and are suitable for solving highly complex nonlinear problems which traditional search algorithms cannot solve. In reality, most BLPPs are not merely linear problems. There are much more complex bi-level programming problems: nonlinear bi-level decision problems, multi-leader bi-level decision problems, multi-follower decision bi-level problems, multi-objective bi-level decision problems, fuzzy bi-level decision problems (Gao et al. 2011), and so on. Thus, it is important to develop effective and efficient methods to solve these problems.

Because of their inherent merits, meta heuristics have been widely applied to solve BLPPs. Genetic algorithms have been developed in Calvete et al. (2008), Hejazia et al. (2002), Li et al. (2010), tabu search is applied in Lukač et al. (2008), Rajesh et al. (2003), Wen and Huang (1996), simulated annealing is applied in Sahin and Ciric (1998) and neural network approach is proposed in Lan et al. (2007), Shih et al. (2004). Bi-level differential evolution algorithms are developed in Vincent et al. (2012). Particle swarm optimization algorithm is developed for solving bi-level programming problem in Gao et al. (2011), Kuo and Huang (2009), Li et al. (2006).

Supply chain is a complex hierarchical system, which contains many different interest participants, such as suppliers, manufacturers, distributors, retailers and end customers. These members compose a long and hierarchical chain. Each of the members in the chain independently controls a set of decision variables, disjoint from the others, and need to make decisions based on their own interests, while still considering the choice of the others, as the others’ decisions will have an influence on their own interests. Therefore, it is especially suitable to adopt BLPP to deal with supply chain management (SCM) problems. As two of the most important problems in SCM, the decision of pricing and lot-sizing play important roles in optimizing profits in a supply chain. There are many studies that have focused on pricing and lot-sizing problems (Abad 2003; Guan and Liu 2010; Kébé et al. 2012; Li and Meissner 2011; Lu and Qi 2011; Raa and Aghezzaf 2005; Yıldırmaz et al. 2009). The literature considers pricing and lot-sizing problems by using the traditional modeling methods, which may neglect the fact that a supply chain is a hierarchical system, and there is little literature on pricing and lot-sizing policies based on BLPP. Marcotte et al. (2009) considered the characterization of optimal strategies for a service firm acting in an oligopolistic environment, and the decision problem is formulated as a leader-follower game played on a transportation network. Dewez et al. (2008) and Gao et al. (2011) also established bi-level models for pricing problems.

This paper proposes a hierarchical hybrid particle swarm optimization (PSO) and differential evolution (DE) based algorithm (HHPSODE) to deal with BLPP. Unlike most problem-dependent algorithms designed for specific versions or based on specific assumptions, the proposed algorithm HHPSODE is a hierarchical algorithm, which solves BLPP iteratively by a modified PSO and a modified DE. On the one hand, in each iterative process of PSO, the particles sometimes may move too far away from the problem’s feasible region, and this may lead to a local optimal solution. In the modified PSO, a velocity and position modulation method is applied to the movement of particles in order to guide them within the region of interest, which can help the PSO maintain a faster convergence speed and global convergence. On the other hand, to overcome the shortcomings of basic DE, this paper adopts a modified mutation strategy. Combining the advantages of DE/rand and DE/best, the modified mutation strategy has the properties of fast convergence property and not falling easily into premature convergence. According to the interactive iterations of the modified PSO algorithm and DE algorithm, HHPSODE can solve the BLPP without any specific assumption or any transformation of the objective or constraints functions. Then eight benchmark bi-level problems from the related literature are employed to test the performance of the proposed algorithm HHPSODE, and the results demonstrate that the proposed algorithm HHPSODE shows better performance than other algorithms.

Because there is little literature on pricing and lot-sizing policies based on BLPP, this paper establishes a bi-level pricing and lot-sizing model. Then HHPSODE is employed to solve the bi-level model, and the features of the model are analyzed based on the data solved by HHPSODE. Finally, based on the proposed bi-level model, we do a further test to illustrate the performance of HHPSODE, and the results also exhibit good performance of HHPSODE in dealing with BLPP.

Following the introduction in “Introduction” section, the rest of this paper is organized as follows. “Background” section briefly describes the basic concept of BLPP, PSO and DE. “Algorithm design” section develops a hybrid algorithm HHPSODE for solving BLPP. Numerical experiments are shown in “Numerical experiments” section to demonstrate the performance of HHPSODE. “An application on pricing and lot-sizing decisions” section gives an application of BLPP on SCM and also analyzes the features of the proposed bi-level model. Finally, the conclusions are given in “Conclusion” section.

Background

Basic model of BLPP

In the BLPP, two decision makers are involved. The lower level decision maker optimizes his objective function under the given parameters from the upper level decision maker. General model of BLPP can be formulated as follows:

$$\begin{aligned}&\mathop {\min }\limits _{x\in X} \;f_1 (x,y) \nonumber \\&\quad s.t.\;\;\;G(x,y)\le 0 \nonumber \\&\text{ where, }\;\text{ for }\;\text{ given }\;x,\;\text{ the } \;\text{ vector }\;y\;\text{ solves }\nonumber \\&\quad \mathop {\min }\limits _{y\in Y} \;f_2 (x,y) \nonumber \\&\qquad s.t.\;g(x,y)\le 0 \end{aligned}$$

(1)

where, $x\in X\subset R^{n_1},\;y\in Y\subset R^{n_2}$. $x$ is the vector of variables controlled by the leader (upper level variables), and $y$ is the vector of variables controlled by the follower (lower level variables). $f_1 (x,y)$ and $f_2 (x,y)$ are the leader’s and the follower’s objective functions, respectively. $G(x,y)\le 0$ and $g(x,y)\le 0$ are corresponding constraints of the upper and lower level problems.

In formal terms, the bi-level programming problems are mathematical programs in which the subset of variables $y$ is required to be an optimal solution of another mathematical program parameterized by the remaining variables $x$.

Basic PSO

As a typical model of swarm intelligence (SI) and a new evolutionary algorithm based on SI, PSO has gained wide attention among SI researchers since it was proposed by Kennedy and Eberhart (1995). Because PSO is easy to implement with only a few parameters to adjust, it has been applied successfully to many different areas, such as combinatorial problems (Belmecheri et al. 2012), electric power systems (Sadeghierad et al. 2010), neural network systems (Gaitonde and Karnik 2012), fuzzy systems control (Bingül and Karahan 2011), industry fields (Chu and Hsieh 2012) and many other various applications (Chan and Tiwari 2007).

Particle swarm optimization consists of a swarm of particles without quality and volume. Each particle represents a candidate solution. In each iteration, the particle will track two extreme values: One is the best solution of each particle gained so far, which represents the each particle’s cognition level; the other is the overall best solution gained by any particle in the population so far, which represents society’s cognition level. PSO supposes that there are $N$ particles in the $D$ dimensions. $x_i =(x_{i1} ,x_{i2} ,\ldots ,x_{iD} )$ and $v_i =(v_{i1} ,v_{i2} ,\ldots ,v_{iD} )$ represent the particle’s position and velocity, respectively. $p_i =(p_{i1} ,p_{i2} ,\ldots ,p_{iD} )$ denotes the best position that the particle has visited.$p_g =(p_{g1} ,p_{g2} ,\ldots ,p_{gD} )$ denotes the best position that the swarm has visited. The particles are manipulated according to the equations below:

$$\begin{aligned} v_{id} (t+1)&= wv_{id} (t)+c_1 r_1 (p_{id} (t)-x_{id} (t))\nonumber \\&\quad +c_2 r_2 (p_{gd} (t)-x_{id} (t))\end{aligned}$$

(2)

$$\begin{aligned} x_{id} (t+1)&= x_{id} (t)+v_{id} (t+1) \end{aligned}$$

(3)

where, $1\le d \le D, 1\le i \le N, c_{1}$ and $c_{2}$ are non-negative constants, which are called the cognitive and social parameter. $r_{1}$ and $r_{2}$ are two random numbers, which are uniformly distributed in the range (0,1). $w$ denotes the inertia weight, which plays an important role in balancing global search ability and local search ability of PSO.

Shi and Eberhart (1999) proposed the linearly decreasing strategy as follows:

$$\begin{aligned} w(t)=w_{\min } +(w_{\max } -w_{\min } )\cdot \left( {\frac{T_{\max } -t}{T_{\max } }} \right) \end{aligned}$$

(4)

where, the superscript $t$ denotes the $t \text{ th }$ iteration, and $T_\mathrm{max}$ denotes the iteration’s maximum number. $w_\mathrm{min}$ and $w_\mathrm{max}$, respectively denote the minimum and maximum of original inertia weight.

Basic DE

Differential evolution algorithm, proposed by Storn and Price (1997), has become a popular and effective algorithm for its many attractive characteristics, such as compact structure, ease of use, fast convergence speed and robustness. Thanks to these features, DE has been applied to solve problems in many scientific and engineering fields (Plagianakos et al. 2008), such as technical system design (Storn 1999), scheduling problem (Vincent et al. 2012), pattern recognition (Ilonen et al. 2003) and so on.

Assume that the population of the standard DE algorithm contains $N D$-dimensional vectors. Then the $i\text{ th }$ individual in the population could be presented with a $D$-dimensional vector. The basic operators in classical DE include the following five steps (Price et al. 2005):

• 1. Initialization: Input the population size $N$, the scaling factor $F\in [0,2]$ and the crossover rate $CR\in [0,1]$. Then individuals in first generation are generated randomly:

  $$\begin{aligned} y_i (0)=(y_{i1} (0),y_{i2} (0),\ldots ,y_{iD} (0)) \end{aligned}$$

• 2. Evaluation: For each individual $y_{i}(t)$, evaluate its fitness value $fit(y_{i}(t))$.

• 3. Mutation: The most frequently used mutation strategies implemented in the basic DE are (Zhao et al. 2011):

  $$\begin{aligned}&\text{ DE }/\text{ rand }/1:v_{yid} (t)=y_{r_1 d} (t)+F\cdot (y_{r_2 d} (t)\\&\quad -y_{r_3 d} (t))\\&\text{ DE }/\text{ best }/1:v_{yid} (t)=y_{bestd} (t)+F\cdot (y_{r_1 d} (t)\\&\quad -y_{r_2 d} (t))\\&\text{ DE }/\text{ rand }-\text{ to }-\text{ best }/1:v_{yid} (t)=y_{r_1 d} (t)\\&\quad +F\cdot (y_{bestd} (t)-y_{r_2 d} (t)) +F\cdot (y_{r_3 d} (t)-y_{r_4 d} (t))\\&\text{ DE }/\text{ best }/2:v_{yid} (t)=y_{bestd} (t)+F\cdot (y_{r_1 d} (t)\\&\quad -y_{r_2 d} (t)) +F\cdot (y_{r_3 d} (t)-y_{r_4 d} (t))\\&\text{ DE }/\text{ rand }/2:v_{yid} (t)=y_{r_1 d} (t)+F\cdot (y_{r_2 d} (t)\\&\quad -y_{r_3 d} (t))+F\cdot (y_{r_4 d} (t)-y_{r_5 d} (t)) \end{aligned}$$

  where, $d=1,2,\ldots ,D$. The indices $r_{1},r_{2},r_{3},r_{4},r_{5}\in \{1,2,{\ldots },N\}$ are mutually exclusive integers randomly generated, which are also different from the index $i$.

• 4. Crossover: Crossover operator is designed to increase the diversity of the population. First, an integer $d_{rand}\in \{1,2,{\ldots },D\}$ is generated randomly. Then, we have the trail vector $u_{yi} (t)=(u_{yi1} (t),u_{yi2} (t),\ldots ,u_{yiD} (t))$ by the following equation:

  $$\begin{aligned} \begin{array}{ll} u_{yid} (t)&{}=\!\left\{ \! {\begin{array}{l} v_{yid} (t),\quad \text{ if }\;\text{ rand }[0,1]\le CR\;\text{ or }\;d=d_{rand} \\ y_{id} (t),\quad \text{ otherwise } \\ \end{array}} \right. \\ d&{}=1,2,\ldots ,D \\ \end{array} \end{aligned}$$

  (5)

• 5. Selection: Selection operates by comparing the individuals’ fitness value to generate the next generation population:

  $$\begin{aligned} y_i (t+1)=\left\{ {\begin{array}{l} y_i (t),\quad \text{ if }\;fit(y_i (t))<fit(u_{yi} (t)) \\ u_{yi} (t),\quad \text{ otherwise } \\ \end{array}} \right. \end{aligned}$$

  (6)

Algorithm design

Similar to other intelligent algorithms, both basic PSO and DE have some shortcomings: stagnation and premature convergence. Therefore, one of the most important topics is to design more effective search strategies to enhance the performance of basic PSO and DE. Many researchers have made many attempts to solve these problems. For PSO, Janson and Middendorf (2005) arranged the particles in a dynamic hierarchy according to the quality of their so-far best-found solution, and the result was improved performance on most of the benchmark problems considered. García-Nieto and Alba (2011) proposed a velocity modulation method and a restarting mechanism to enhance scalability of PSO. Belmecheri et al. (2012) proposed a PSO with a local search strategy, and the approach has shown its effectiveness on several combinatorial problems. For DE, Zhao et al. (2011) proposed an improved self-adaptive DE to solve large-scale continuous optimization problems. Vincent et al. (2012) developed different variants of the bi-level differential evolution (BiDE) algorithms. Cai et al. (2012) proposed a learning-enhanced DE (LeDE) that encourages individuals to exchange information systematically.

In this section, we introduce a modified velocity and position modulation of PSO and a modified mutation strategy of DE to improve performance of basic PSO and DE. Then, a constraint handling mechanism is presented. Lastly, the framework of HHPSODE for solving BLPP is given. Note that all the pseudo-codes used in the following algorithms are designed for the minimization problem.

A modified PSO

This section employs a velocity and position modulation method to guide the particles within the region of interest (García-Nieto and Alba 2011). In each iterative process of PSO, the particles sometimes move too far away from the problem’s feasible region, and this may lead to a local optimal solution. To enhance scalability and ensure global convergence of PSO, this paper restricts the particle’s movement to the feasible region of the problem by using velocity and position modulation as shown in Algorithm 1.

In Algorithm 1, $x_{dlow}$ and $x_{dupp}$ denote the $d\text{ th }$ dimension lower and upper bound of the decision variable $x$. $v_{idnew}$ and $x_{idnew}$ denote the new velocity value and the new position of $i\text{ th }$ particle in $d\text{ th }$ dimension.

The procedure can be explained as follows:

After calculating the new velocity value $v_{idnew}$ according to Eqs. (2) and (4) in “Basic PSO” section, the velocity vector magnitude is bounded (line 2–6), which prevents the given particle from moving far from the area of interest. Then, once the new velocity $v_{id }(t+1)$ is obtained, the new particle position $x_{idnew}$ is calculated according to Eq. (3) in “Basic PSO” section, and the new position $x_{idnew}$ should not exceed the problem limits $(x_{dlow}, x_{dupp})$. If $x_{idnew}$ exceeds ($x_{dlow}, x_{dupp})$, the new position is recalculated by subtracting the new velocity from the old particle position (line 7–12).

A modified mutation in DE

The most frequently used mutation strategies implemented in the basic DE have some shortcomings. For example, DE/rand may have slower convergence than DE/best, while DE/best may fall easily into premature convergence. For this reason, this paper adopts a modified mutation strategy named ”DE/rand-to-best” by combining the advantages of DE/rand and DE/best, which has a fast convergence property and does not easily fall into premature convergence. The proposed modified mutation strategy first establishes an archive in the operation process of DE (Zhao et al. 2011). The archive is initiated as empty, then, after each generation, the parent solutions that fail in the selection process are added to the archive. If the archive size exceeds the population size $N$, then some solutions are randomly removed from the archive to keep the archive size at $N$. The archive provides information about the evolution path and improves the diversity of the population. Compared with DE/rand and DE/best, DE/rand-to-best benefits from its fast convergence and strong global search ability by incorporating best solution information in the evolutionary search and keeping the diversity of the population. The proposed mutation strategy is generated as follows:

$$\begin{aligned} v_{yid} (t)&= y_{r_1 d} (t)+F\cdot (y_{bestd} (t)-y_{r_2 d} (t))\nonumber \\&\quad +F\cdot (y_{r_3 d} (t)-\tilde{y}_{r_4 d} (t)) \end{aligned}$$

(7)

where, $y_{r_1 d}, y_{r_2 d}$ and $y_{r_3 d}$ are individuals randomly selected from the current population, $y_{bestd}$ is the best individual of the current population. $\tilde{y}_{r_4 d}$ is randomly chosen from the union of the current population and the archive. The pseudo-code of the modified mutation strategy is below:

Constraint handling mechanism

For BLPP (1), both the upper and the lower level programming problems are standard constraint optimization problems without considering the information interaction between the leader and the follower. However, the constraint handling mechanism is very important for the constraint optimization problem. To this end, we adopt a penalty function based technique to deal with the constraints.

Considering the constraint optimization problem below:

$$\begin{aligned}&\min f(x) \\&s.t.\;g_i (x)\le 0,\quad i=1,2,\ldots p \end{aligned}$$

where, $S$ denotes search space, $x\in S, S\subseteq R^{\pi }$.

By using a penalty factor, the above problem can be transformed into the following problem:

$$\begin{aligned} \min \;F(x)=f(x)+M\cdot \sum \limits _{i=1}^p {(\max \{g_i (x),0\})^{2}} \end{aligned}$$

where, $M$ is a pre-set and sufficiently large positive constant called penalty factor.

Without loss of generality, we take the lower level programming problem as a single independent constraint optimization problem to describe the constraint handling technique. We suppose that there are $p$ inequality constraints in the lower level programming problem, and the decision variable of the upper level programming problem, $x$, is given. In the search space, a particle which satisfies the constraints is called a feasible particle, otherwise it is called an infeasible particle. In this condition, we can calculate all particles’ fitness according to the following equations

$$\begin{aligned} \text{ fit }(x,y)&= \left\{ {{\begin{array}{l} {f(x,y),\;\text{ if }\;y\in \Omega (x)} \\ {F(x,y),\;\text{ if }\;y\in S\backslash \Omega (x)} \\ \end{array} }} \right. \end{aligned}$$

(8)

$$\begin{aligned} F(x,y)&= f(x,y)+M\cdot \sum \limits _{i=1}^p {(\max \{g_i (x,y),0\})^{2}} \end{aligned}$$

(9)

where, $S$ is the search space, and $\Omega (x)$ is the feasible set of the lower level programming problem.

The steps of HHPSODE to solve BLPP

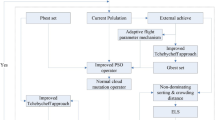
This section presents the solution procedure of HHPSODE for solving BLPP. HHPSODE is consisted of a modified PSO algorithm based main program and a modified DE algorithm based subprogram. Algorithm 2 and Algorithm 3 are the main program and the subprogram. In addition, Fig. 1 is a flow chart of the main program to illustrate HHPSODE intuitively. Details are shown below.

Fig. 1

Flow chart of HHPSODE

Example

To explain the hybrid algorithm HHPSODE, we have chosen to apply HHPSODE on an example (take the test problem T5 for example) where the data are presented in Tables 6 and 7. The details of solving process are as follows:

Numerical experiments

To illustrate the performance of HHPSODE, we adopt eight typical bi-level problems including four bi-level linear programming problems (Kuo and Huang 2009) and four bi-level nonlinear programming problems (Li et al. 2006) to test the algorithm HHPSODE, and then we compare HHPSODE with other algorithms.

Parameters setting of HHPSODE: Iterations $T_\mathrm{max1}=T_\mathrm{max2}=100$; population size $N_{1}=N_{2}=20$; learning factors $c_{1}=c_{2}=2.0$; maximum inertia weight $w_\mathrm{max}=0.9$ and minimum inertia weight $w_\mathrm{min}=0.4$; scaling factor $F=0.5$; crossover rate CR=0.9; penalty factor $M$ = 100,000. The parameters setting of related algorithms proposed in the literature (Kuo and Huang 2009; Li et al. 2006) are given in Table 1.

Table 1 Parameters setting of GA, PSO and HPSOBLP (Kuo and Huang 2009; Li et al. 2006)

GA and PSO are different algorithms mentioned in Kuo and Huang (2009). HPSOBLP, TRM (trust region method) and Original are different algorithms mentioned in Li et al. (2006). All computational experiences for the examples were implemented on the IBM E420 laptop with Windows 7 ($\text{ Intel }^\circledR \text{ Core }^{\mathrm{TM}}$ i3 Duo CPU, 2 GB of RAM).

For each BLPP, we execute HHPSODE 20 times independently, and record the best and the average results. Note that BLPPs always take the leader’s interest as a priority. In addition, the goals of the four linear BLPPs (T1–T4) are to maximize their objective functions, and the goals of the four non-linear BLPPs (T5–T8) are to minimize their objective functions. Thus for T1–T4, the larger realization of $f_{1}$ (the upper level objective function) the better results we have, and for T5–T8, the smaller realization of $f_{1}$ (the upper level objective function) the better results we have.

Comparisons of the best and average-found results of T1–T4 based on three different algorithms (HHPSODE, GA, PSO) are respectively given in Tables 2 and 3. Corresponding best and average decision variables’ solutions are given in Tables 4 and 5, respectively.

Table 2 Comparisons of the best-found results of T1–T4 based on three different algorithms

Table 3 Comparisons of the average-found results of T1–T4 based on three different algorithms

Table 4 Corresponding best-found solutions of decision variables based on three algorithms

Table 5 Corresponding average solutions of decision variables based on three algorithms

Tables 2 and 3 show that, compared with GA and PSO, HHPSODE shows higher accuracy on the best and the average results of T1–T4. Take T1 for example, the best-found value of $f_{1}$(upper level objective) based on HHPSODE, 85.6727, is larger than that of GA and PSO which are 85.0551 and 85.0700, respectively. In addition, the average-found values of $f_{1}$ based on HHPSODE are also larger than the average-found values of $f_{1}$ based on GA and PSO. Similarly, for T2 and T4, the best values of $f_{1}$ based on HHPSODE are larger than the best values of $f_{1}$ based on GA and PSO, and the average values of $f_{1}$ based on HHPSODE are larger than the average values of $f_{1}$ based on GA. For T3, the best value of $f_{1}$ solved by HHPSODE is slightly less than the best value of $f{1}$ solved by PSO, but larger than that of GA.

Table 6 shows the best and average-found results of T5–T8 based on HHPSODE. Table 7 gives corresponding decision variables’ solutions of T5–T8. Comparisons of the best-found results of T5–T8 based on HHPSODE and the other three algorithms are shown in Table 8.

Table 6 The best and average-found results of T5–T8 based on HHPSODE

Table 7 Corresponding solutions of decision variables based on HHPSODE

Table 8 Comparisons of the best-found results based on four different algorithms

From Table 8 we can see that, for T5, although there are slight gaps between HHPSODE and HPSOBLP for the best-found value of $f_{1}$, HHPSODE exhibits higher accuracy than TRM and Original. For T6 and T8, the best-found results of $f_{1}$ solved by HHPSODE are much better than the results solved by HPSOBLP, TRM and Original. For T7, the best-found value of $f_{1}$ based on HHPSODE, 2.000, is equal to that of the other three algorithms. Additionally, for the best-found values of $f_{2}$ of T5–T8, HHPSODE also outperforms HPSOBLP, TRM and Original.

The test problems’ average computation time based on HHPSODE are given in Table 9. From Table 9 we can see that the maximum average computation time of T1–T8 is less than 28 s, and this indicates that the average time spent to find the solutions is acceptable. Note that we do not compare the computation time based on HHPSODE with other algorithms. This is because different authors may code their algorithms in different structures and implement their algorithms on different computers. In a word, for most of the test problems, HHPSODE outperforms other algorithms.

An application on pricing and lot-sizing decisions

As an application of the proposed HHPSODE, we provide a bi-level pricing and lot-sizing model in a single manufacturer-single retailer system facing retail price-sensitive market demand in this section. The pricing and lot-sizing model derives from the model developed by Yıldırmaz et al. (2009), but differs from the model in the literature. In this system, the manufacturer, as the leader, first purchases raw materials from the supplier, and then the raw materials are transformed into end products. Finally, the end products are sold from the manufacturer to the retailer. As a follower, the retailer reacts, bearing in mind the selection of the manufacturer, making a decision after the manufacturer.

Model formulation

To formulate the mathematical bi-level model, some assumptions are given: The demand of the market is a monotonic decreasing function of the retail price; both manufacturer and retailer are aiming to maximize their own profits, and both of them have the right to make decisions; one unit of product is produced by one unit of raw material; and a 1 year planning horizon is considered.

Table 9 Average computation time based on HHPSODE

The following symbols are used to model the problem:

Decision variables are as follows:

$p_{m}$::

Retailer’s unit purchase cost (or wholesale price).

$p_{r}$::

Product selling price to end customer (or retail price).

$\alpha$::

Number of retailer’s lot size.

$Q$::

Retailer’s lot size.

Other related parameters are as follows:

$C$::

Maximum load that can be placed in a truck.

$D(p_{r})$::

Annual demand for the product, $D(p_{r})=b- a\cdot p_{r}$.

$h_{m}$::

Manufacturer’s annual holding cost rate.

$h_{r}$::

Retailer’s annual holding cost rate.

$M_{c}$::

Production cost of unit product.

$O_{m}$::

Manufacturer’s ordering cost per order.

$O_{r}$::

Retailer’s ordering cost per order.

$p_{s}$::

Manufacturer’s purchase cost.

$R$::

Truckload charge

The manufacturer’s annual revenue, holding cost and ordering cost are denoted by $R_{m}, H_{m}$ and $C_{m}$ as follows:

$$\begin{aligned} \left\{ {{\begin{array}{l} {R_m =(p_m -p_s -M_c )D} \\ {H_m =h_m \cdot (p_s +M_c )\cdot \frac{Q(\alpha -1)}{2}=\frac{(p_s +M_c )(\alpha -1)h_m Q}{2}} \\ {C_m =\frac{O_m }{\alpha Q}} \\ \end{array} }} \right. \end{aligned}$$

The manufacturer’s annual profit is denoted by $\Pi _{m}$ as follows:

$$\begin{aligned} \Pi _m&= R_m -H_m -C_m =(p_m -p_s -M_c )D\nonumber \\&\quad -\frac{(p_s +M_c )(\alpha -1)h_m Q}{2}-\frac{O_m D}{\alpha Q}\nonumber \\ \end{aligned}$$

(10)

The retailer’s annual revenue, holding cost and ordering cost are denoted by $R_{r}, H_{r}$ and $C_{r}$ as follows:

$$\begin{aligned} \left\{ {{\begin{array}{l} {R_r =\left( {p_r -p_m -\frac{F(Q)}{Q}} \right) D} \\ {H_r =h_r \left( {p_m +\frac{F(Q)}{Q}} \right) \cdot \frac{Q}{2}=\frac{h_r (p_m Q+F(Q))}{2}} \\ {C_r =\frac{(O_r +F(Q))D}{Q}} \\ \end{array} }} \right. \end{aligned}$$

The retailer’s annual profit is denoted by $\Pi _{r}$ as follows:

$$\begin{aligned} \prod \limits _r&= R_r -H_r -C_r =\left( {p_r -p_m -\frac{F(Q)}{Q}} \right) D\nonumber \\&\quad -\frac{h_r (p_m Q+F(Q))}{2}-\frac{(O_r +F(Q))D}{Q} \end{aligned}$$

(11)

We suppose that the retail price is a multiple of the wholesale price, that is

$$\begin{aligned} p_r =kp_m \end{aligned}$$

(12)

where, $k$ denotes the ratio of the retail price to the wholesale price, and $k\ge 1$.

The relationship between the lot size and the number of deliveries is

$$\begin{aligned} Q=\frac{D}{\alpha } \end{aligned}$$

(13)

To compute $F(Q)$, we assume that the transportation cost is determined in terms of truck loads; therefore freight cost is computed as (Yıldırmaz et al. 2009):

$$\begin{aligned} F(Q)=\left\lceil {\frac{Q}{C}} \right\rceil R=\left\lceil {\frac{D}{\alpha C}} \right\rceil R \end{aligned}$$

(14)

By combining Eqs. (10) and (11), and substituting Eqs. (12)–(14) into (10) and (11), we establish a bi-level joint pricing and lot-sizing model guided by the manufacturer as follows:

$$\begin{aligned}&\mathop {\max }\limits _{p_m } \Pi _m =(p_m -p_s -M_c )D-\frac{(p_s +M_c )(\alpha -1)h_m D}{2\alpha }-O_m \nonumber \\&s.t.\quad p_s +M_c <p_m \le p^{*} \nonumber \\&\mathop {\max }\limits _{\alpha ,k} \Pi _r =\left( {kp_m -p_m -\frac{\alpha \left\lceil {\frac{D}{\alpha C}} \right\rceil R}{D}} \right) D\nonumber \\&\qquad \qquad \quad \;-\frac{h_r \left( {p_m D+\alpha } \right) \left\lceil {\frac{D}{\alpha C}} \right\rceil R}{2\alpha }-\alpha \left( {O_r +\left\lceil {\frac{D}{\alpha C}} \right\rceil R} \right) \nonumber \\&s.t.\quad \alpha \in N^{+},1<k\le k^{*} \end{aligned}$$

(15)

where, $p^{*}$ and $k^{*}$, respectively represent upper bounds of $p_{m}$ and $k$. Because the above bi-level model is a NP-hard problem, for which there is no solution in the classical method, we will adopt the proposed algorithm HHPSODE to deal with this problem in the next section.

Model evaluation and analysis

In this section, we will adopt HHPSODE to solve the bi-level model (15) proposed in “Model formulation” section. The parameters in model (15) are set as follows: $h_{m}= h_{r} =0.01; O_{m}=2000; O_{r}=200; p_{s}=4; M_{c}=1; C=200; R=100$. These parameter values are randomly produced and used to analyze features of the proposed model.

In reality, the wholesale price and retail price should not be too high, and they should have upper limits. To analyze the model, two upper bound groups of $k^{*}$ (the upper bound of the ratio of the retail price to the wholesale price) and $p^{*}$(the upper bound of the wholesale price) are separately considered: $k^{*}=2, p^{*}=10; k^{*}=4, p^{*}=10$. The parameter settings of HHPSODE are the same as in “Numerical experiments” section, and the results are shown in Tables 10 and 11.

Table 10 Different results based on different combinations of demand coefficients ($k^{*}=2, p^{*}=10$)

Table 11 Different results based on different combinations of coefficients ($k^{*}=4, p^{*}=10$)

The demand function proposed in this paper is a linear decreasing function of retail price. $a$ denotes price elastic coefficient, and $b$ represents maximum market demand. In the following numerical simulation, we fix $b$ (the maximum market demand) and change $a$ (the price elastic coefficient) from a lower price sensitivity to a higher price sensitivity to investigate variations of the manufacturer and the retailer’s profits when demand’s sensitivity to the retail price changes.

Tables 10 and 11 denote the profits of the manufacturer and the retailer under different upper bounds of the retail price and the wholesale price. From these two tables we can see that the higher demand’s sensitivity to the price, the less profits earned by the manufacturer and the retailer. In other words, demand’s sensitivity to price is negatively correlated with the profits of the manufacturer and the retailer, and this condition abides by the market’s rule.

Finally, we do a further test to verify the good performance of HHPSODE, using the following two steps:

• (1) On the one hand, without loss of generality, Figs. 2 and 3 are drawn based on condition of $a$ = 2, $b$ = 1,000. In these two figurers, Pm (the blue curves) and Pr (the red curves), respectively represent the profits of the manufacturer and the retailer. In Fig. 2, we fix two parameters: $p_{m}=10$ and $\alpha =2$. We then draw the profits curves of the manufacturer and the retailer when $k^{*}\in [1, 50]$. From Fig. 2 we can see that when $k^{*}$ lies nearby 25, the retailer’s profit reaches its maximum value. In Fig. 3, we fix two parameters: $k=2$ and $\alpha =2$. Then we draw the profits curves of the manufacturer and the retailer when $p^{*}\in [1, 250]$. From Fig.  3 we can see that when $p^{*}$ is sited near 125, the manufacturer and the retailer’s profits reach their maximum values.

  Fig. 2

  

  The profit curves of the manufacturer and the retailer under the condition of $a$ = 2, $b$ = 1,000; $\alpha =2; p_{m}=10; k^{*}\in [1, 50]$ (Color figure online)

• (2) On the other hand, we employ HHPSODE to solve the model under the same condition as in Figs. 2 and 3. Firstly, we set $p_{m}\in [5, 10]$ and $k^{*}\in [1, 50]$; secondly, we set $p^{*}\in [1, 250]$ and $k\in [1, 2]$. Then HHPSODE is executed to solve the proposed bi-level model under the two situations. The results of these two conditions are shown in Table 12. From Table 12 we can see that for the first condition, the best-found solution based on HHPSODE of $p_{m}$ is 10, which is equal to the preset value of $p_{m}$ in Fig. 2; the best-found solution based on HHPSODE of $k^{*}$ is 25.3514, which is nearby 25. For the second condition, the best-found solution based on HHPSODE of $k$ is 2, which is equal to the pre-set value of $k$ in Fig.3; the best-found solution of $p^{*}$ is 127.5041, which is nearby 125. This shows that the quasi-optimal solutions obtained by HHPSODE are very close to the optimal solution of the bi-level model. Therefore, it also illustrates that HHPSODE is effective and efficient in solving the model.

Fig. 3

The profit curves of the manufacturer and the retailer under the condition of $a$ = 2, $b$ = 1,000; $\alpha =2; k=2; p^{*}\in [1{,}250]$ (Color figure online)

Table 12 Best found-results based on HHPSODE ($a$ = 2, $b$ = 1,000)

Conclusion

This paper proposes a hierarchical hybrid PSO and DE based algorithm (HHPSODE) to deal with BLPP. To overcome the shortcomings of basic PSO and basic DE, this paper improve PSO and DE, respectively by using a velocity and position modulation method in PSO and a modified mutation strategy in DE. HHPSODE employs the modified PSO as a main program and the modified DE as a subprogram. Unlike most problem-dependent algorithms designed for specific versions or based on specific assumptions, such as the gradient information of objective functions, the convexity of constraint regions and so on, HHPSODE has solved different classes of BLPPs directly. The performance of HHPSODE has been verified by eight benchmark test bi-level problems. According to results compared with other algorithms, HHPSODE exhibits a better performance.

Additionally, we employ HHPSODE to solve a bi-level pricing and lot-sizing model proposed in this paper. By analyzing the data, some managerial insights which abide by market rule are derived. This demonstrates that the proposed bi-level model is able to deal with pricing and lot-sizing problems in a manufacturer-guided supply chain system. Further tests of the proposed model also exhibit that HHPSODE is an effective and efficient algorithm to deal with BLPP. Therefore, HHPSODE is recommended for further application.

In reality, there many problems that are much more complex, such as multi-objective BLPP, multi-level programming problem and so on. Therefore, future work will focus on extending the proposed algorithm for solving multi-objective BLPP and multi-level programming problem. In addition, some improvements, such as combining PSO or DE with other intelligent algorithms, or modifying the constraint handling mechanism, could be applied to improve the calculation accuracy of the algorithm.

Appendix

Test problems

T1	T 2
$\begin{array}{l} \max \;f_1 =-2x_1 +11x_2 \;\text{ where }\;x_2 \;\text{ solves } \\ \text{ max }\;f_2 =-x_1 -3x_2 \\ \text{ s.t. } x_1 -2x_2 \le 4 \\ \quad \,2x_1 -x_2 \le 24 \\ \quad \,3x_1 +4x_2 \le 96 \\ \quad \,x_1 +7x_2 \le 126 \\ \quad \,-4x_1 +5x_2 \le 65, \\ \quad \,x_1 +4x_2 \ge 8 \\ \quad \,x_1 \ge 0,x_2 \ge 0 \\ \end{array}$	$\begin{array}{l} \max \;f_1 =x_2 \;\text{ where }\;x_2 \;\text{ solves } \\ \text{ max }\;f_2 =x_2 \\ \text{ s.t. } -x_1 -2x_2 \le 10 \\ \quad \,x_1 -2x_2 \le 6 \\ \quad \,2x_1 +x_2 \le 21 \\ \quad \,x_1 +2x_2 \le 38, \\ \quad \,-x_1 +2x_2 \le 18, \\ \quad \,x_1 \ge 0,x_2 \ge 0 \\ \end{array}$
T3	T4
$\begin{array}{l} \max \;f_1 =3x_2 \;\text{ where }\;x_2 \;\text{ solves } \\ \text{ max }\;f_2 =-x_2 \\ \text{ s.t. } -x_1 +x_2 \le 3 \\ \quad \,x_1 -2x_2 \le 12 \\ \quad \,4x_1 +x_2 \le 12 \\ \quad \,x_1 \ge 0,x_2 \ge 0 \\ \end{array}$	$\begin{array}{l} \max \;f_1 =8x_1 +4x_2 -4y_1 +40y_2 +4y_3 \\ \text{ where }\;y\;\text{ solves } \\ \text{ max }\;f_2 =-x_1 -2x_2 -y_1 -y_2 -2y_3 \\ \text{ s.t. } y_1 -y_2 -y_3 \ge -1 \\ \quad \,-2x_1 +y_1 -2y_2 +0.5y_3 \ge -1 \\ \quad \,-2x_1 -2y_1 +y_2 +0.5y_3 \ge -1 \\ \quad \,x_1 ,x_2 ,y_1 ,y_2 ,y_3 \ge 0 \\ \end{array}$
T5	T6
$\begin{array}{l} \min \;f_1 =-x_1^2 -3x_2 -4y_1 y_2^2 \\ \text{ s.t. } x_1^2 +2x_2 \le 4,x_1 \ge 0,x_2 \ge 0 \\ \text{ where }\;y\;\text{ solves } \\ \text{ min }\;f_2 =2x_1^2 +y_1^2 -5y_2 \\ \text{ s.t. } x_1^2 -2x_1 +x_2^2 -2y_1 +y_2 \ge -3 \\ \quad \, x_2 +3y_1 -4y_2 \ge -4,y_1 \ge 0,y_2 \ge 0 \\ \end{array}$	$\begin{array}{l} \min \;f_1 =x^{2}+(y-10)^{2} \\ \text{ s.t. } x+2y-6\le 0,-x\le 0 \\ \text{ where }\;y\;\text{ solves } \\ \text{ min }\;f_2 =x^{3}+2y^{3}+x-2y-x^{2} \\ \text{ s.t. } -x-2y-3\le 0,-y\le 0 \\ \end{array}$
T7	T8
$\begin{array}{l} \min \;f_1 =(x-5)^{4}+(2y+1)^{4} \\ \text{ s.t. } x+y-4\le 0,-x\le 0 \\ \text{ where }\;y\;\text{ solves } \\ \text{ min }\;f_2 =e^{-x+y}+x^{2}+2xy+y^{2}+2x+6y \\ \text{ s.t. } -x+y-2\le 0,-y\le 0 \\ \end{array}$	$\begin{array}{l} \min \;f_1 =(x_1 -y_2 )^{4}+(y_1 -1)^{2}+(y_1 -y_2 )^{2} \\ \text{ s.t. } -x_1 \le 0 \\ \text{ where }\;y\;\text{ solves } \\ \text{ min }\;f_2 =2x_1 +e^{y_1 }+y_1^2 +4y_1 +2y_2^2 -6y_2 \\ \text{ s.t.6 }x_1 +2y_1^2 +e^{y_2 }-15\le 0,-y_1 \le 0,y_1 -4\le 0 \\ \quad \,5x_1 +y_1^4 +y_2 -25\le 0,-y_2 \le 0,y_2 -2\le 0 \\ \end{array}$