Keywords

1 Introduction

Particle Swarm Optimization (PSO), proposed by Kennedy and Eberhart [1], is a well-known global intelligence optimization algorithm. On the basis of individual perception and social perception, the particles of PSO are replaced to enhance the speed of convergence and search accuracy in every iteration. Since then, many modifications have been developed. A recent version of modification was to update the particle positions by using two selected functions and combining individual experiences to avoid getting into the local optimum [2]. A fitness function was defined in [3] to identify the parameters of nonlinear dynamic hysteresis model. To a certain extent, the algorithm improves the convergence of the progress. However, a common problem occurring in the simulation experiments is still the premature clustering in the early part of iteration procedure.

Differential Evolution (DE) [4] is a population-based method of function optimization like Genetic algorithm (GA), including mutation, crossover, and selection. In DE, new individuals are generated from the information of multiple previous individuals to get out of stagnation. Hence, some improved DE algorithms are proposed for getting better consequents. An improvement of DE with Taguchi method of sliding levers had the powerful ability of global search and obtained a better solution [5]. The fuzzy selection operation was used in an improved DE to reduce the complexity of multiple attribute decisions and enhance population diversity [6]. Though the DE has some advantages in global optimization, there is a dependency on controlling parameters which are not easy to decide when confronting high-dimensional complex problems.

In view of the advantages and disadvantages of PSO and DE, many hybrid algorithms of PSO and DE are described to combine the advantages of both and better solve various practical problems. The hybrid PSO and DE with population size reduction (HPSODEPSR) [7] can achieve optimal or near optimal solution faster than other comparison algorithms. The Bacterial Foraging Optimization (BFO) hybridized [8] with PSO and DE was introduced to effectively handle the dynamic economic dispatch problem. In order to improve the diversity and make each subgroup achieve a different optimal solution in the range of fitness values, Zuo and Xiao [9] used a hybrid operator and multi-population strategy performing the PSO and DE operation in turn. A novel hybrid algorithm PSO-DE [10] jumped out of stagnation, increased the speed of convergence and improved the algorithm’s performance. A modified algorithm hybridizing PSO and DE with an aging leader and challengers was advanced to find the optimal parameters of PID controller quickly [11]. Though those hybrid algorithms improve the performance of the original algorithms (i.e. PSO and DE), premature stagnation is still a major problem.

This paper presents a novel hybrid algorithm of PSO and DE (DEPSO) with alternative replication strategy to overcome the above-mentioned problems. In the proposed algorithm, population is separated into two groups which are generated by two different methods, i.e. velocity updating strategy of PSO and mutative strategy of DE. A novel population are produced according to alternative replication strategy. The poor half of the population is eliminated while the other half is reproduced for the new evolution. In order to enhance the diversity of the population, the scaling factor of DEPSO is adjusted according to the linear decreasing rule.

The remaining paper is organized as follows. A brief introduction of PSO algorithm and DE algorithm is provided in Sect. 2. In Sect. 3, the hybrid algorithm of PSO and DE with alternative and replication strategy is described in detail. Section 4 gives experimental results of the Simulations on benchmark functions. Finally, the conclusion is presented in Sect. 5.

2 Description of Algorithms

2.1 Particle Swarm Optimization

In standard PSO algorithm, a group of particles flies in the search space to find the optimal location. The particles are given random positions x and velocities v in the initiate progress. In each iteration, the best position of each particle pbest id and the best position of global gbest id are learnt, which leads the particle to the new position. Equations (1)–(2) are the updated rule [1]:

$$ v_{id}^{G + 1} = \omega v_{id}^{G} + c_{1} rand(0,1)(pbest_{id}^{G} - x_{id}^{G} ) + c_{2} rand(0,1)(gbest_{id}^{G} - x_{id}^{G} ) $$
(1)
$$ x_{id}^{G + 1} = x_{id}^{G} + v_{id}^{G + 1} ,i = 1,..,N,d = 1, \ldots ,D $$
(2)
$$ \omega = \omega_{\hbox{max} } - (\omega_{\hbox{max} } - \omega_{\hbox{min} } )*G/G_{\hbox{max} } $$
(3)

where x id and v id are the position and velocity of the ith particle, respectively, N is the number of particles, and D is the dimensions of search space, c 1 and c 2 are acceleration factors. Finally, ω is the inertia weight adjusted by Eq. (3) in [12], ω max and ω min are the maximum and the minimum value of inertia weight, respectively. G and G max are the current number of iteration and the maximum number of iteration, separately.

2.2 Differential Evolution Algorithm

DE, proposed by Storn and Price [4], has the significant effect on solving application problems. The outline of DE can be described as follows:

  • Step 1: initialize individuals according to the upper and lower bounds of search space, and evaluate the fitness of each individual.

  • Step 2: compare the fitness of every individual and record the best individual.

  • Step 3: generate new vectors through mutation process. The mutation rule is as follows Eq. (4):

  • $$ v_{i} = x_{r1} + F(x_{r2} - x_{r3} ),i = 1,..,N $$
    (4)

where N is the number of individuals, x i is the ith individual and v i is the updated ith vector through mutating. F is the scaling factor, r 1 , r 2 and r 3 not equal to each other are randomly selected from [1, N].

  • Step 4: cross populations and mutant vectors to get a trial vector. Equation (5) is the crossover formula:

  • $$ u_{ij} = \left\{ {\begin{array}{*{20}l} {v_{ij} } \hfill & {if(rand_{j} (0,1) \le CR)\,or \,j = j_{rand} } \hfill \\ {x_{ij} } \hfill & {otherwise} \hfill \\ \end{array} } \right., \, j = 1 \ldots D $$
    (5)

where D is the number of parameters, while u ij represents the ith individual at the jth search space after crossing operation. CR is the crossover probability, and j rand is a randomly selected index in the range of [0, D].

  • Step 5: The greedy algorithm (i.e. Eq. (6)) is used to select individuals for the next iteration process.

  • $$ x_{i} = \left\{ {\begin{array}{*{20}l} {u_{i} } \hfill & {if\;f(u_{i} ) \le f(x_{i} )} \hfill \\ {x_{i} } \hfill & {otherwise} \hfill \\ \end{array} } \right. $$
    (6)

3 DEPSO Algorithm with Alternative Replication Strategy

Due to rapid information search, the suboptimal solutions might be more frequently obtained by PSO. Different from the PSO, population of DE tends to be more diversity as the number of iterations increases but consumes more computational complexity. To take advantages of those two algorithms, in this paper, a new hybrid DEPSO method is proposed to improve the search capability of particles with smaller computational time.

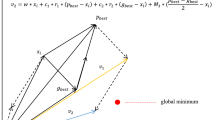
For the purpose of preventing individuals from sinking into suboptimal solution, we use the following alternative replication strategy to optimize the initial particles of each iteration.

At the beginning of each iteration, a new group P 1 is generated by PSO algorithm (i.e. Eqs. (1)–(2)). Considering the optimal value of every individual x pbest , another group P 2 is renewed by the mutation process of DE algorithm (i.e. Eq. (7)). Based on the fitness value, we compare the updated groups (i.e. P 1 and P 2 ) with the initial group P 0 and preserve the better individuals to form new P 1 and P 2 .

$$ x_{i} = F(x_{pbest} - x_{i} ) + F(x_{r4} - x_{r5} ), \, i = 1 \ldots N $$
(7)

where N is individuals’ number, x i is the i individuals, F is the scaling factor, and r 4 and r 5 are indexes selected from [1, N].

Sort the individuals of new groups (i.e. P 1 and P 2 ) according to the fitness values, and the sorted groups are also compared to retain the superior individuals constituting a group P 3 . The new group P 3 eliminates half of the individuals with poor fitness values, and the rest of the individuals are reproduced to keep the number of individuals.

In order to overcome the shortcoming of population reduction, the mutation factor decreases linearly with the number of iterations increasing in the mutation procedure. The scaling factor is controlled in Eq. (8).

$$ F = F_{\hbox{max} } - (F_{\hbox{max} } - F_{\hbox{min} } )*G/G_{\hbox{max} } $$
(8)

where F max , F min , G, and G max are the maximum mutation factor, minimum mutation factor, the current number of iteration and the maximum number of iteration, respectively.

Finally, DE algorithm is re-simulated based on the group which is obtained using the alternative replication strategy. The scheme of DEPSO is described as follows in detail:

Step 1::

initialize the position and velocity of every individual, and generate initial group P 0 .

Step 2::

calculate the fitness of each individual, and evaluate the best solution of each individual pbest and the best solution of all individuals gbest.

Step 3::

update the position and velocity of individuals using Eqs. (1)–(2), and generate new group P 1 .

Step 4::

mutate the initial individuals (i.e. Eq. (7)) and introduce a new group P 2 .

Step 5::

calculate the fitness of two groups (i.e. P 1 and P 2 ), and compare the fitness with the initial group P 0 to update the groups P 1 and P 2 , respectively.

Step 6::

P 1 and P 2 are sorted based on the fitness. A new group P 3 is constituted of the superb individuals in the comparison of the sorted groups. The group P 3 is updated by alternative replication strategy.

Step 7::

new vectors are formed by the group P 3 in the light of mutation process (i.e. Eq. (4)).

Step 8::

Equation (5) is applied to get trial vectors through the crossover of individuals and mutant vectors in DE algorithm.

Step 9::

select the best individuals using Eq. (6) and new offspring P 0 are introduced to execute the iterative procedure. Figure 1 presents the flowchart of DEPSO.

Fig. 1.
figure 1

Flowchart of DEPSO

Full size image

4 Experiments and Analysis

4.1 Benchmark Functions and Algorithms

To verify the performance of the proposed DEPSO algorithm, eight benchmark functions [13] (i.e. Sphere f1, SumPowers f2, Rosenbrock f3, Quartic f4, Rastrigin f5, Griewank f6, Ackley f7, Schwefel2.22 f8) are applied to test the improved algorithm. One important reason for choosing these eight functions is that they contain unimodal functions (i.e. f1, f2, f3, and f4) and multimodal functions (i.e. f5, f6, f7, and f8). Additionally, these functions are minimum problems and the minimum value is known to be zero. The performance of DEPSO is demonstrated through eight benchmark functions and compared with some classic algorithms, i.e. PSO, DE, Genetic algorithm (GA) [14], Artificial Bee Colony algorithm (ABC) [15, 16], and Bacterial Foraging Optimization (BFO) [17]. All functions are tested on these optimization algorithms through MATLAB R2014a software.

4.2 Experimental Parameters

The similar parameters of six optimization algorithms are set as follows: the size of the population is 50, the maximum iterative number is set to 5000. Each function is run 30 times with the search space dimension 30, 50, and 80. The parameters of GA, ABC and BFO are from [18] except the reproduction’s number of BFO is 25. More parameters setting of PSO, DE and DEPSO are shown as follows: In PSO, c 1 = c 2 = 2, ω max = 0.9, and ω min = 0.4; In DE, CR = 0.5, and F ranges from 0.4 to 0.9; In DEPSO, c 1 , c 2 , ω max and ω min are the same as PSO. CR and F are the same as DE. The values are the results of multiple simulations.

4.3 Experiment Results and Discussion

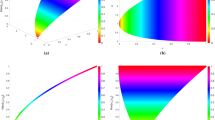
To get experiment results, all benchmark functions are executed by coding these search methods. The mean fitness value and the standard deviation obtained by six optimization algorithms are displayed in Table 1. The bold type is used to underline the best of all the numerical results attained by comparing six optimization algorithms. Figure 2 lists the convergence curves of different test functions gotten by all the algorithms with the dimension 50. In Fig. 2, in order to make the curves clear, the results are the logarithm with base 10.

Table 1. Experiment results on benchmark functions
Full size table
Fig. 2.
figure 2

The iteration process of the algorithms when the dimensionality is 50

Full size image

As shown in Table 1, DEPSO algorithm almost gets the optimal mean and standard deviation among all the algorithms for the eight benchmark functions. It means that the hybrid DEPSO algorithm is better than other algorithms in terms of search accuracy. Additionally, the proposed algorithm obtains the minimum values (i.e. zero) on functions of Sphere, SumPowers, Quartic, Rastrigin, Griewank, and Schwefel2.22. It means that the convergence precision of the DEPSO algorithm is high in the selected functions.

In terms of dimensionality, the DEPSO can perform better than other algorithms when the dimension is increasing. From Fig. 2, we can conclude the convergent speed of DEPSO algorithm is significantly faster than other algorithms and the convergent results are closer to optimal values. Altogether, the performance of DEPSO algorithm performs better whether in unimodal functions or in multimodal functions.

5 Conclusion

A hybrid algorithm integrating the advantages of PSO and DE is proposed in this paper. The results show that the DEPSO algorithm outperforms other algorithms in terms of mean and standard deviation. Though DE with nonlinearly decreasing mechanism of scaling factor can obtain the similar solutions on some benchmark functions (e.g., Rosenbrock and Rastrigin), the convergence speed is not good than the proposed DEPSO method. Thus, the proposed alternative replication strategy can enhance the performance of the hybrid algorithm. Our future study will focus on the application of the proposed algorithm to solve the real-world problems and more hybrid methods will be developed to obtain better solutions.