An efficient methodology to estimate the parameters of a two-dimensional chirp signal model

Abstract

In various capacities of statistical signal processing two-dimensional (2-D) chirp models have been considered significantly, particularly in image processing—to model gray-scale and texture images, magnetic resonance imaging, optical imaging etc. In this paper we address the problem of estimation of the unknown parameters of a 2-D chirp model under the assumption that the errors are independently and identically distributed (i.i.d.). The key attribute of the proposed estimation procedure is that it is computationally more efficient than the least squares estimation method. Moreover, the proposed estimators are observed to have the same asymptotic properties as the least squares estimators, thus providing computational effectiveness without any compromise on the efficiency of the estimators. We extend the propounded estimation method to provide a sequential procedure to estimate the unknown parameters of a 2-D chirp model with multiple components and under the assumption of i.i.d. errors we study the large sample properties of these sequential estimators. Simulation studies and two synthetic data analyses have been performed to show the effectiveness of the proposed estimators.

1 Introduction

A two-dimensional (2-D) chirp model has the following mathematical expression:

$$\begin{aligned} \begin{aligned} y(m,n)&= \sum _{k=1}^{p} \{A_k^0 \cos (\alpha _k^0 m + \beta _k^0 m^2 + \gamma _k^0 n + \delta _k^0 n^2) \\&\quad + B_k^0 \sin (\alpha _k^0 m + \beta _k^0 m^2 + \gamma _k^0 n + \delta _k^0 n^2)\} + X(m,n);\\&\qquad m = 1, \ldots , M; n = 1, \ldots , N. \end{aligned} \end{aligned}$$

(1)

Here, y(m, n) is the observed signal data, and the parameters $A_k^0$s, $B_k^0$s are the amplitudes, $\alpha _k^0$s, $\gamma _k^0$s are the frequencies and $\beta _k^0$s, $\delta _k^0$s are the frequency rates. The random component X(m, n) accounts for the noise component of the observed signal. In this paper, we assume that X(m, n) is an independently and identically distributed (i.i.d.) random field.

It can be seen that the model admits a decomposition of two components—the deterministic component and the random component. The deterministic component represents a gray-scale texture and the random component makes the model more realistic for practical realisation. For illustration, we simulate data with a fixed set of model parameters. Figure 1 represents the gray-scale texture corresponding to the simulated data without the noise component and Fig. 2 represents the contaminated texture image corresponding to the simulated data with the noise component. This clearly suggests that the 2-D chirp signal models can be used effectively in modelling and analysing black and white texture images.

Fig. 1

Original texture

Fig. 2

Noisy texture

Apart from the applications in image analysis, these signals are commonly observed in mobile telecommunications, surveillance systems, in radars and sonars etc. For more details on the applications, one may see the works of Francos and Friedlander (1998, 1999), Simeunović and Djurović (2016) and Zhang et al. (2008) and the references cited therein.

Parameter estimation of a 2-D chirp signal is an important statistical signal processing problem. Recently Zhang et al. (2008), Lahiri et al. (2013) and Grover et al. (2018) proposed some estimation methods of note. For instance, Zhang et al. (2008) proposed an algorithm based on the product cubic phase function for the estimation of the frequency rates of the 2-D chirp signals under low signal to noise ratio and the assumption of stationary errors. They conducted simulations to verify the performance of the proposed estimation algorithm, however there was no study of the theoretical properties of the proposed estimators. Lahiri et al. (2015) suggested the least squares estimation method. They observed that the least squares estimators (LSEs) of the unknown parameters of this model are strongly consistent and asymptotically normally distributed under the assumption of stationary additive errors. The rates of convergence of the amplitude estimates were observed to be $M^{-1/2}N^{-1/2}$, of the frequencies estimates, they are $M^{-3/2}N^{-1/2}$ and $M^{-1/2}N^{-3/2}$ and of the frequency rate estimates, they are $M^{-5/2}N^{-1/2}$ and $M^{-1/2}N^{-5/2}$. Grover et al. (2018) proposed the approximate least squares estimators (ALSEs), obtained by maximising a periodogram-type function and under the same stationary error assumptions, they observed that ALSEs are strongly consistent and asymptotically equivalent to the LSEs.

A chirp signal is a particular case of the polynomial phase signal when the phase is a quadratic polynomial. Although work on parameter estimation of the aforementioned 2-D chirp model is rather limited, several authors have considered the more generalised version of this model—the 2-D polynomial phase signal model. For references, see Djurović et al. (2010), Djurović (2017), Francos and Friedlander (1998, 1999), Friedlander and Francos (1996), Lahiri and Kundu (2017), Simeunović et al. (2014), Simeunović and Djurović (2016) and Djurović and Simeunović (2018).

In this paper, we address the problem of parameter estimation of a one-component 2-D chirp model as well as the more general multiple-component 2-D chirp model. We put forward two methods for this purpose. The key characteristic of the proposed estimation method is that it reduces the foregoing 2-D chirp model into two 1-D chirp models. Thus, instead of fitting a 2-D chirp model, we are required to fit two 1-D chirp models to the given data matrix. For the fitting of 1-D models, one may use any efficient algorithm to estimate the parameters of the obtained 1-D chirp models. Due to widespread applicability, a lot of work has been done in literature on the parameter estimation of a 1-D chirp model. For references, one may see the works of Abatzoglou (1986), Djuric and Kay (1990), Peleg and Porat (1991), Wood and Barry (1994), Barbarossa (1995), Friedlander and Francos (1995), Xia (2000), Saha and Kay (2002), Wang et al. (2010) and the references cited therein.

The proposed algorithm is numerically more efficient than the usual least squares estimation method proposed by Lahiri (2013). For instance, for a one-component 2-D chirp model, to estimate the parameters using these algorithms, we need to solve two 2-D optimisation problems as opposed to a 4-D optimisation problem in the case of finding the LSEs. This also leads to curtailment of the number of grid points required to find the initial values of the non-linear parameters as the 4-D grid search required in case of the computation of the usual LSEs or ALSEs, reduces to two 2-D grid searches. Therefore, instead of searching along a grid mesh consisting of $M^3N^3$ points, we need to search among only $M^3 + N^3$ points, which is much more feasible to execute computationally. In essence, the contributions of this paper are three-fold:

• 1. We put forward a computationally efficient algorithm for the estimation of the unknown parameters of 2-D chirp signal models as a practical alternative to the usual least squares estimation method.

• 2. We examine the asymptotic properties of the proposed estimators under the assumption of i.i.d. errors and observe that the proposed estimators are strongly consistent and asymptotically normally distributed. In fact, they are observed to be asymptotically equivalent to the corresponding LSEs. When the errors are assumed to be Gaussian, the asymptotic variance-covariance matrix of the proposed estimators coincides with asymptotic Cramér-Rao lower bound.

• 3. We conduct simulation experiments and analyse a synthetic texture (see Fig. 2) to assess the effectiveness of the proposed estimators.

The rest of the paper is organised as follows. In the next section, we provide some preliminary results required to study the asymptotic properties of the proposed estimators. In Sect. 2, we consider a one-component 2-D chirp model and state the model assumptions, some notations and present the proposed algorithms along with the asymptotic properties of the proposed estimators. In Sect. 3, we extend the algorithm and develop a sequential procedure to estimate the parameters of a multiple-component 2-D chirp model. We also study the asymptotic properties of the proposed sequential estimators in this section. We perform numerical experiments for different model parameters in Sect. 4 and analyse synthetic data for illustration in Sect. 5. Finally, we conclude the paper in Sect. 6 and we provide the proofs of all the theoretical results in the appendices.

2 One-component 2-D chirp model

In this section, we provide the methodology to obtain the proposed estimators for the parameters of a one-component 2-D chirp model, mathematically expressed as follows:

$$\begin{aligned} \begin{aligned} y(m,n)&=A^0 \cos (\alpha ^0 m + \beta ^0 m^2 + \gamma ^0 n + \delta ^0 n^2) \\&\quad + B^0 \sin (\alpha ^0 m + \beta ^0 m^2 + \gamma ^0 n + \delta ^0 n^2) + X(m,n);\\&\qquad m = 1, \ldots , M; n = 1, \ldots , N. \end{aligned} \end{aligned}$$

(2)

Here y(m, n) is the observed data and the parameters $A^0$, $B^0$ are the amplitudes, $\alpha ^0$, $\gamma ^0$ are the frequencies and $\beta ^0$, $\delta ^0$ are the frequency rates of the signal model. As mentioned in the introduction, X(m, n) accounts for the noise present in the signal.

We will use the following notations: $\varvec{\theta } = (A, B, \alpha , \beta , \gamma , \delta )$ is the parameter vector, $\varvec{\theta }^0 = (A^0, B^0, \alpha ^0, \beta ^0, \gamma ^0, \delta ^0)$ is the true parameter vector and $\varvec{\Theta }_1$ = $[-K, K] \times [-K, K] \times [0, \pi ] \times [0, \pi ]\times [0, \pi ] \times [0, \pi ]$ is the parameter space.

2.1 Preliminary results

In this section, we provide the asymptotic results obtained for the usual LSEs of the unknown parameters of a 1-D chirp model by Lahiri et al. (2015). These results are later exploited to prove the asymptotic normality of the proposed estimators.

2.1.1 One-component 1-D chirp model

Consider a 1-D chirp model with the following mathematical expression:

$$\begin{aligned} y(n) = A^0 \cos (\alpha ^0 n + \beta ^0 n^2) + B^0 \sin (\alpha ^0 n + \beta ^0 n^2) + X(n). \end{aligned}$$

(3)

Here y(n) is the observed data at time points $n = 1, \ldots , N$, $A^0$, $B^0$ are the amplitudes and $\alpha ^0$ is the frequency and $\beta ^0$ is the frequency rate parameter. $\{X(n)\}_{n=1}^{N}$ is the sequence of error random variables.

The LSEs of $\alpha ^0$ and $\beta ^0$ can be obtained by minimising the following reduced error sum of squares:

$$\begin{aligned} R_{N}(\alpha , \beta ) = Q_N({\hat{A}}, {\hat{B}}, \alpha , \beta ) = {{\varvec{Y}}}_{N \times 1}^{\top }({{\varvec{I}}} - {{\varvec{P}}}_{{{\varvec{Z}}}_N}(\alpha , \beta )){{\varvec{Y}}}_{N \times 1} \end{aligned}$$

where,

$$\begin{aligned} Q_N(A, B, \alpha , \beta ) = ({{\varvec{Y}}}_{N \times 1} - {{\varvec{Z}}}_N(\alpha , \beta )\varvec{\phi })^{\top }({{\varvec{Y}}}_{N \times 1} - {{\varvec{Z}}}_N(\alpha , \beta )\varvec{\phi }), \end{aligned}$$

is the error sum of squares, ${{\varvec{P}}}_{{{\varvec{Z}}}_N}(\alpha , \beta ) = {{\varvec{Z}}}_N(\alpha , \beta )({{\varvec{Z}}}_N(\alpha , \beta )^{\top }{{\varvec{Z}}}_N(\alpha , \beta ))^{-1}{{\varvec{Z}}}_N(\alpha , \beta )^{\top }$ is the projection matrix on the column space of the matrix ${{\varvec{Z}}}_N(\alpha , \beta )$,

$$\begin{aligned} {{\varvec{Z}}}_N(\alpha , \beta ) = \begin{bmatrix} \cos (\alpha + \beta ) &{}\quad \sin (\alpha + \beta ) \\ \vdots &{}\quad \vdots \\ \cos (N\alpha + N^2\beta ) &{}\quad \sin (N\alpha + N^2\beta ) \\ \end{bmatrix}, \end{aligned}$$

(4)

${{\varvec{Y}}}_{N \times 1} = \begin{bmatrix} y(1),\ \ldots ,\ y(N) \end{bmatrix}^{\top }$ is the observed data vector and $\varvec{\phi } = \begin{bmatrix} A,\ B \end{bmatrix}^{\top }$ is the the vector of linear parameters.

Following are the assumptions, we make on the error component and the parameters of model (3):

Assumption P1

X(n) is a sequence of i.i.d. random variables with mean zero, variance $\sigma ^2$ and finite fourth order moment.

Assumption P2

$(A^0, B^0, \alpha ^0, \beta ^0)$ is an interior point of the parameter space $\varvec{\Theta } = [-K, K] \times [-K, K] \times [0, \pi ] \times [0, \pi ],$ where K is a positive real number and ${A^0}^2 + {B^0}^2 > 0.$

Theorem P1

Let us denote ${{\varvec{R}}}'_{N}(\alpha , \beta )$ as the gradient vector and ${{\varvec{R}}}''_{N}(\alpha , \beta )$ as the Hessian matrix of the function $R_{N}(\alpha , \beta )$. Then, under the assumptions P1 and P2, we have:

$$\begin{aligned}&-{{\varvec{R}}}'_{N}(\alpha ^0, \beta ^0)\varvec{\Delta } \xrightarrow {d} \varvec{{\mathcal {N}}}_2(\mathbf{0 }, 2\sigma ^2 \varvec{\Sigma }^{-1})\ as\ N \rightarrow \infty , \end{aligned}$$

(5)

$$\begin{aligned}&\varvec{\Delta }{{\varvec{R}}}''_{N}(\alpha ^0, \beta ^0)\varvec{\Delta } \xrightarrow {a.s.} \varvec{\Sigma }^{-1} \ as\ N \rightarrow \infty . \end{aligned}$$

(6)

Here, $\varvec{\Delta } = \text {diag}(\frac{1}{N\sqrt{N}}, \frac{1}{N^2\sqrt{N}})$,

$$\begin{aligned} \varvec{\Sigma }= & {} \frac{2}{{A^0}^2 + {B^0}^2} \begin{bmatrix} 96 &{} -90 \\ -90 &{} 90 \\ \end{bmatrix} \text { and } \end{aligned}$$

(7)

$$\begin{aligned} \varvec{\Sigma }^{-1}= & {} \begin{bmatrix} \frac{{A^0}^2 + {B^0}^2}{12} &{} \frac{{A^0}^2 + {B^0}^2}{12} \\ \frac{{A^0}^2 + {B^0}^2}{12} &{} \frac{4({A^0}^2 + {B^0}^2)}{45} \\ \end{bmatrix}. \end{aligned}$$

(8)

The notation $\varvec{{\mathcal {N}}}_2(\varvec{\mu }, \varvec{{\mathcal {V}}})$ means bivariate normally distributed random variable with mean vector $\varvec{\mu }_{2 \times 1}$ and variance-covariance matrix $\varvec{{\mathcal {V}}}_{2 \times 2}$.

Proof

This proof follows from Theorem 2 of Lahiri et al. (2015). $\square$

As mentioned in the introduction, any efficient algorithm can be used to estimate the parameters of a 1-D chirp model, once we reduce the dimension of the underlying model. Although the main aim of the paper is not the estimation of parameters of 1-D chirp model, but the efficient estimation of a 2-D chirp model by reducing it into 1-D models to save time. We choose to estimate the parameters of the reduced models using the LSEs as they have optimal convergence rates. For details, one may refer to Lahiri et al. (2015).

2.2 Proposed methodology

Let us consider the above-stated 2-D chirp signal model (2) with one-component. Suppose we fix $n = n_0$, then (2) can be rewritten as follows:

$$\begin{aligned} \begin{aligned} y(m,n_0)&= A^0 \cos (\alpha ^0 m + \beta ^0 m^2 + \gamma ^0 n_0 + \delta ^0 n_0^2) \\&\quad + B^0 \sin (\alpha ^0 m + \beta ^0 m^2 + \gamma ^0 n_0 + \delta ^0 n_0^2) + X(m,n_0)\\&= A^0(n_0) \cos (\alpha ^0 m + \beta ^0 m^2) + B^0(n_0) \sin (\alpha ^0 m + \beta ^0 m^2) \\&\quad + X(m,n_0);\ \ m = 1, \cdots , M, \end{aligned} \end{aligned}$$

(9)

which represents a 1-D chirp model with $A^0(n_0)$, $B^0(n_0)$ as the amplitudes, $\alpha ^0$ as the frequency parameter and $\beta ^0$ as the frequency rate parameter. Here,

$$\begin{aligned} \begin{aligned}&A^0(n_0) = \ \ A^0 \cos (\gamma ^0 n_0 + \delta ^0 n_0^2) + B^0 \sin (\gamma ^0 n_0 + \delta ^0 n_0^2), \text { and} \\&B^0(n_0) = -A^0 \sin (\gamma ^0 n_0 + \delta ^0 n_0^2) + B^0 \cos (\gamma ^0 n_0 + \delta ^0 n_0^2). \end{aligned} \end{aligned}$$

Thus for each fixed $n_0$ $\in$ $\{1,\ \ldots ,\ N\}$, we have a 1-D chirp model with the same frequency and frequency rate parameters, though different amplitudes. This 1-D model corresponds to a column of the 2-D data matrix.

Our aim is to estimate the non-linear parameters $\alpha ^0$ and $\beta ^0$ from the columns of the data matrix and one of the most reasonable estimators for this purpose are the least squares estimators. Therefore, the estimators of $\alpha ^0$ and $\beta ^0$ can be obtained by minimising the following function:

$$\begin{aligned} \begin{aligned} R_M(\alpha , \beta , n_0)&= {{{\varvec{Y}}}^{\top }_{n_0}}({{\varvec{I}}} - {{\varvec{P}}}_{{{\varvec{Z}}}_M}(\alpha , \beta )){{\varvec{Y}}}_{n_0} \end{aligned} \end{aligned}$$

for each $n_0$. Here, ${{\varvec{Y}}}_{n_0} = \begin{bmatrix} y[1,n_0],\ \ldots ,\ y[M,n_0] \end{bmatrix}^{\top }$ is the $n_0$th column of the original data matrix, ${{\varvec{P}}}_{{{\varvec{Z}}}_M}(\alpha , \beta ) = {{\varvec{Z}}}_M(\alpha , \beta )({{\varvec{Z}}}_M(\alpha , \beta )^{\top }{{\varvec{Z}}}_M(\alpha , \beta ))^{-1}{{\varvec{Z}}}_M(\alpha , \beta )^{\top }$ is the projection matrix on the column space of the matrix ${{\varvec{Z}}}_M(\alpha , \beta )$ and the matrix ${{\varvec{Z}}}_M(\alpha , \beta )$ can be obtained by replacing N by M in (4). This process involves minimising N 2-D functions corresponding to the N columns of the matrix. Thus, for computational efficiency, we propose to minimise the following function instead:

$$\begin{aligned} \begin{aligned} R^{(1)}_{MN}(\alpha , \beta )&= \sum _{n_0 = 1}^{N}R_M(\alpha , \beta , n_0) = \sum _{n_0 = 1}^{N} {{\varvec{Y}}}^{\top }_{n_0}({{\varvec{I}}} - {{\varvec{P}}}_{{{\varvec{Z}}}_M}(\alpha , \beta )){{\varvec{Y}}}_{n_0} \end{aligned} \end{aligned}$$

(10)

with respect to $\alpha$ and $\beta$ simultaneously and obtain ${\hat{\alpha }}$ and ${\hat{\beta }}$ which reduces the estimation process to solving only one 2-D optimisation problem. Note that since the errors are assumed to be i.i.d. replacing these N functions by their sum is justifiable.

Similarly, we can obtain the estimates, ${\hat{\gamma }}$ and ${\hat{\delta }}$, of $\gamma ^0$ and $\delta ^0$, by minimising the following criterion function:

$$\begin{aligned} \begin{aligned} R^{(2)}_{MN}(\gamma , \delta )&= \sum _{m_0 = 1}^{M}R_N(\gamma , \delta , m_0) = \sum _{m_0 = 1}^{M} {{\varvec{Y}}}^{\top }_{m_0}({{\varvec{I}}} - {{\varvec{P}}}_{{{\varvec{Z}}}_N}(\gamma , \delta )){{\varvec{Y}}}_{m_0} \end{aligned} \end{aligned}$$

(11)

with respect to $\gamma$ and $\delta$ simultaneously. The data vector ${{\varvec{Y}}}_{m_0} = \begin{bmatrix} y[m_0,1],\ \ldots ,\ y[m_0,N] \end{bmatrix}^{\top }$, is the $m_0$th row of the data matrix, $m_0 = 1, \ldots , M$, ${{\varvec{P}}}_{{{\varvec{Z}}}_N}(\gamma , \delta )$ is the projection matrix on the column space of the matrix ${{\varvec{Z}}}_N(\gamma , \delta )$ and the matrix ${{\varvec{Z}}}_{N}(\gamma , \delta )$ can be obtained by replacing $\alpha$ and $\beta$ by $\gamma$ and $\delta$ respectively in the matrix ${{\varvec{Z}}}_N(\alpha , \beta )$, defined in (4).

Once we have the estimates of the non-linear parameters, we estimate the linear parameters by the usual least squares regression technique as proposed by Lahiri et al. (2015):

$$\begin{aligned} \begin{bmatrix} {\hat{A}} \\ {\hat{B}} \end{bmatrix} = [{{\varvec{W}}}({\hat{\alpha }}, {\hat{\beta }}, {\hat{\gamma }}, {\hat{\delta }})^{\top } {{\varvec{W}}}({\hat{\alpha }}, {\hat{\beta }}, {\hat{\gamma }}, {\hat{\delta }})]^{-1}{{\varvec{W}}}({\hat{\alpha }}, {\hat{\beta }}, {\hat{\gamma }}, {\hat{\delta }})^{\top }{{\varvec{Y}}}_{M N \times 1}. \end{aligned}$$

Here, ${{\varvec{Y}}}_{M N \times 1} = \begin{bmatrix} y(1, 1),\ \ldots ,\ y(M, 1),\ \ldots ,\ y(1, N),\ \ldots ,\ y(M, N)\end{bmatrix}^{\top }$ is the observed data vector, and

$$\begin{aligned} {{\varvec{W}}}(\alpha , \beta , \gamma , \delta )_{M N \times 2} = \left[ \begin{array}{cc}\cos (\alpha + \beta + \gamma + \delta ) &{} \sin (\alpha + \beta + \gamma + \delta ) \\ \cos (2\alpha + 4\beta + \gamma + \delta ) &{} \sin (2\alpha + 4\beta + \gamma + \delta ) \\ \vdots &{} \vdots \\ \cos (M \alpha + M^2 \beta + \gamma + \delta ) &{} \sin (M \alpha + M^2 \beta + \gamma + \delta ) \\ \vdots &{} \vdots \\ \cos (\alpha + \beta + N \gamma + N^2 \delta ) &{} \sin (\alpha + \beta + N \gamma + N^2 \delta ) \\ \cos (2\alpha + 4\beta + N \gamma + N^2 \delta ) &{} \sin (2\alpha + 4\beta + N \gamma + N^2 \delta )\\ \vdots &{} \vdots \\ \cos (M \alpha + M^2 \beta + N \gamma + N^2 \delta ) &{} \sin (M \alpha + M^2 \beta + N \gamma + N^2 \delta )\end{array}\right] . \end{aligned}$$

(12)

We make the following assumptions on the error component and the model parameters before we examine the asymptotic properties of the proposed estimators:

Assumption 1

X(m,n) is a double array sequence of i.i.d. random variables with mean zero, variance $\sigma ^2$ and finite fourth order moment.

Assumption 2

The true parameter vector $\varvec{\theta }^0$ is an interior point of the parametric space $\varvec{\Theta }_1$, and ${A^0}^2 + {B^0}^2 > 0$.

2.3 Consistency

The results obtained on the consistency of the proposed estimators are presented in the following theorems:

Theorem 1

Under Assumptions 1 and 2, ${\hat{\alpha }}$ and ${\hat{\beta }}$ are strongly consistent estimators of $\alpha ^0$ and $\beta ^0$ respectively, that is,

$$\begin{aligned} \begin{aligned}&{\hat{\alpha }} \xrightarrow {a.s.} \alpha ^0 \text { as } M \rightarrow \infty .\\&{\hat{\beta }} \xrightarrow {a.s.} \beta ^0 \text { as } M \rightarrow \infty . \end{aligned} \end{aligned}$$

Proof

See “Appendix A”. $\square$

Theorem 2

Under Assumptions 1 and 2, ${\hat{\gamma }}$ and ${\hat{\delta }}$ are strongly consistent estimators of $\gamma ^0$ and $\delta ^0$ respectively, that is,

$$\begin{aligned} \begin{aligned}&{\hat{\gamma }} \xrightarrow {a.s.} \gamma ^0 \text { as } N \rightarrow \infty .\\&{\hat{\delta }} \xrightarrow {a.s.} \delta ^0 \text { as } N \rightarrow \infty . \end{aligned} \end{aligned}$$

Proof

This proof follows along the same lines as the proof of Theorem 1. $\square$

2.4 Asymptotic distribution

The following theorems provide the asymptotic distributions of the proposed estimators:

Theorem 3

If the Assumptions 1 and 2 are satisfied, then

$$\begin{aligned}\begin{aligned} \begin{bmatrix} ({\hat{\alpha }} - \alpha ^0),\ ({\hat{\beta }} - \beta ^0) \end{bmatrix}{{\varvec{D}}}_1^{-1} \xrightarrow {d} \varvec{{\mathcal {N}}}_2(\mathbf{0 }, 2\sigma ^2 \varvec{\Sigma }) \text { as } M \rightarrow \infty .\\ \end{aligned} \end{aligned}$$

Here, ${\mathbf {D}}_1 = \text {diag}(M^{\frac{-3}{2}}N^{\frac{-1}{2}}, M^{\frac{-5}{2}}N^{\frac{-1}{2}})$ and $\varvec{\Sigma }$ is as defined in (7).

Proof

See “Appendix A”. $\square$

Theorem 4

If the Assumptions 1 and 2 are satisfied, then

$$\begin{aligned}\begin{aligned} \begin{bmatrix} ({\hat{\gamma }} - \gamma ^0),\ ({\hat{\delta }} - \delta ^0) \end{bmatrix}{{\varvec{D}}}_2^{-1} \xrightarrow {d} \varvec{{\mathcal {N}}}_2(\mathbf{0 }, 2\sigma ^2 \varvec{\Sigma }) \text { as } N \rightarrow \infty .\\ \end{aligned} \end{aligned}$$

Here, ${\mathbf {D}}_2 = \text {diag}( M^{\frac{-1}{2}}N^{\frac{-3}{2}}, M^{\frac{-1}{2}}N^{\frac{-5}{2}})$ and $\varvec{\Sigma }$ is as defined in (7).

Proof

This proof follows along the same lines as the proof of Theorem 3. $\square$

The asymptotic distributions of $({\hat{\alpha }}, {\hat{\beta }})$ and $({\hat{\gamma }}, {\hat{\delta }})$ are observed to be the same as those of the corresponding LSEs. Thus, we get the same efficiency as that of the LSEs without going through the process of actually computing the LSEs.

3 Multiple-component 2-D chirp model

In this section, we consider the multipl-component 2-D chirp model with p number of components, with the mathematical expression of the model as given in (1). Although estimation of p is an important problem and will be under our future research, in this paper we deal with the estimation of the other important parameters characterising the observed signal, the amplitudes, the frequencies and the frequency rates, assuming p to be known. We propose a sequential procedure to estimate these parameters. The main idea supporting the proposed sequential procedure is same as that behind the ones proposed by Prasad et al. (2008) for a sinusoidal model and Lahiri et al. (2015) for a chirp model—the orthogonality of different regressor vectors. Along with the computational efficiency, the sequential method provides estimators with the same rates of convergence as the LSEs.

We use the following notation hereafter: For $k = 1,\ \ldots ,\ p$, $\varvec{\theta }_k = (A_k,\ , B_k,\ , \alpha _k,\ \beta _k,\ \gamma _k,\ \delta _k)$ is the parameter vector, $\varvec{\theta }_k^0 = (A_k^0,\ , B_k^0,\ , \alpha _k^0,\ \beta _k^0,\ \gamma _k^0,\ \delta _k^0)$ is the true parameter vector.

3.1 Preliminary results

3.1.1 Multiple-component 1-D chirp model

Now we consider a 1-D chirp model with multiple components, mathematically expressed as follows:

$$\begin{aligned} y(n) = \sum _{k=1}^{p} \{A_k^0 \cos (\alpha _k^0 n + \beta _k^0 n^2) + B_k^0 \sin (\alpha _k^0 n + \beta _k^0 n^2)\} + X(n); \ n = 1, \ldots , N. \end{aligned}$$

Here, $A_k^0$s, $B_k^0$s are the amplitudes, $\alpha _k^0$s are the frequencies and $\beta _k^0$ are the frequency rates, the parameters that characterise the observed signal y(n) and X(n) is the random noise component.

Lahiri et al. (2015) suggested a sequential procedure to estimate the unknown parameters of the above model. We discuss in brief, the proposed sequential procedure and then state some of the asymptotic results they established, germane to our work.

Step 1:

The first step of the sequential method is to obtain the estimates, ${\hat{\alpha }}_1$ and ${\hat{\beta }}_1$, of the non-linear parameters of the first component, $\alpha _1^0$ and $\beta _1^0$, by minimising the following reduced error sum of squares:

$$\begin{aligned} R_{1,N}(\alpha _1, \beta _1) = {{\varvec{Y}}}^{\top }_{N \times 1}({{\varvec{I}}} - {{\varvec{P}}}_{{{\varvec{Z}}}_N}(\alpha _1, \beta _1)){{\varvec{Y}}}_{N \times 1} \end{aligned}$$

with respect to $\alpha$ and $\beta$ simultaneously.

Step 2:

Then the first component linear parameter estimates, ${\hat{A}}_1$ and ${\hat{B}}_1$ are obtained using the separable linear regression of Richards Richards (1961) as follows:

$$\begin{aligned} \begin{bmatrix} {\hat{A}}_1 \\ {\hat{B}}_1 \end{bmatrix} = [{{\varvec{Z}}}_N({\hat{\alpha }}_1, {\hat{\beta }}_1)^{\top }{{\varvec{Z}}}_N({\hat{\alpha }}_1, {\hat{\beta }}_1)]^{-1}{{\varvec{Z}}}_N({\hat{\alpha }}_1, {\hat{\beta }}_1)^{\top }{{\varvec{Y}}}_{N \times 1}. \end{aligned}$$

Step 3:

Once we have the estimates of the first component parameters, we take out its effect from the original signal and obtain a new data vector as follows:

$$\begin{aligned} {{\varvec{Y}}}_1 = {{\varvec{Y}}}_{N \times 1} - {{\varvec{Z}}}_N({\hat{\alpha }}_1, {\hat{\beta }}_1)\begin{bmatrix} {\hat{A}}_1 \\ {\hat{B}}_1 \end{bmatrix}. \end{aligned}$$

Step 4:

Then the estimates of the second component parameters are obtained by using the new data vector and following the same procedure and the process is repeated p times.

Under the Assumption P1 on the error random variables and the following assumption on the parameters:

Assumption P3

$(A_k^0, B_k^0, \alpha _k^0, \beta _k^0)$ is an interior point of $\varvec{\Theta }$, for all $k = 1, \ldots , p$ and the frequencies and the frequency rates are such that $(\alpha _i^0, \beta _i^0) \ne (\alpha _j^0, \beta _j^0)$ $\forall \ i \ne j\ i,\ j = 1,\ \ldots ,\ p$.

Assumption P4

$A_k^0$s and $B_k^0$s satisfy the following relationship:

$$\begin{aligned} K^2> {A_{1}^{0}}^2 + {B_{1}^{0}}^2> {A_{2}^{0}}^2 + {B_{2}^{0}}^2> \cdots> {A_{p}^{0}}^2 + {B_{p}^{0}}^2 > 0, \end{aligned}$$

we have the following results.

Theorem P2

Let us denote ${{\varvec{R}}}'_{k,N}(\alpha , \beta )$ as the gradient vector and ${{\varvec{R}}}''_{k,N}(\alpha , \beta )$ as the Hessian matrix of the function $R_{k,N}(\alpha , \beta )$, $k = 1, \ldots , p$. Then, under the Assumptions P1, P3 and P4:

$$\begin{aligned}&-\frac{1}{\sqrt{N}}{{\varvec{R}}}'_{k,N}(\alpha ^0, \beta ^0)\varvec{\Delta } \xrightarrow {a.s.} 0\ as \ N \rightarrow \infty , \end{aligned}$$

(13)

$$\begin{aligned}&-{{\varvec{R}}}'_{k,N}(\alpha ^0, \beta ^0)\varvec{\Delta } \xrightarrow {d} \varvec{{\mathcal {N}}}_2(\mathbf{0 }, 2\sigma ^2 \varvec{\Sigma }_k^{-1})\ as \ N \rightarrow \infty , \end{aligned}$$

(14)

$$\begin{aligned}&\varvec{\Delta }{{\varvec{R}}}''_{k,N}(\alpha ^0, \beta ^0)\varvec{\Delta } \xrightarrow {a.s.} \varvec{\Sigma }_k^{-1}\ as \ N \rightarrow \infty . \end{aligned}$$

(15)

Here, $\varvec{\Delta }$ is as defined in Theorem P1,

$$\begin{aligned} \varvec{\Sigma }_k= & {} \frac{2}{{A_k^0}^2 + {B_k^0}^2} \begin{bmatrix} 96 &{} -90 \\ -90 &{} 90 \end{bmatrix} \text { and } \end{aligned}$$

(16)

$$\begin{aligned} \varvec{\Sigma }_k^{-1}= & {} \begin{bmatrix} \frac{{A_k^0}^2 + {B_k^0}^2}{12} &{} \frac{{A_k^0}^2 + {B_k^0}^2}{12} \\ \frac{{A_k^0}^2 + {B_k^0}^2}{12} &{} \frac{4({A_k^0}^2 + {B_k^0}^2)}{45} \end{bmatrix}. \end{aligned}$$

(17)

Proof

The proof of (13) follows along the same lines as proof of Lemma 4 of Lahiri et al. (2015) and that of (14) and (15) follows from Theorem 2 of Lahiri et al. (2015). Note that Lahiri et al. (2015) showed that the sequential LSEs have the same asymptotic distribution as the usual LSEs based on a number theory conjecture. $\square$

3.2 Proposed sequential algorithm

The following algorithm is a simple extension of the method proposed to obtain the estimators for a one-component 2-D model in Sect. 2.2:

Step 1:

Compute ${\hat{\alpha }}_1$ and ${\hat{\beta }}_1$ by minimising the following function:

$$\begin{aligned} R^{(1)}_{1, MN}(\alpha _1, \beta _1) = \sum _{n_0 = 1}^{N} {{\varvec{Y}}}^{\top }_{n_0}({{\varvec{I}}} - {{\varvec{P}}}_{{{\varvec{Z}}}_M}(\alpha _1, \beta _1)){{\varvec{Y}}}_{n_0} \end{aligned}$$

with respect to $\alpha _1$ and $\beta _1$ simultaneously.

Step 2:

Compute ${\hat{\gamma }}_1$ and ${\hat{\delta }}_1$ by minimising the function:

$$\begin{aligned} R^{(2)}_{1,MN}(\gamma _1, \delta _1) = \sum _{m_0 = 1}^{M} {{\varvec{Y}}}^{\top }_{m_0}({{\varvec{I}}} - {{\varvec{P}}}_{{{\varvec{Z}}}_N}(\gamma _1, \delta _1)){{\varvec{Y}}}_{m_0} \end{aligned}$$

with respect to $\gamma _1$ and $\delta _1$ simultaneously.

Step 3:

Once the nonlinear parameters of the first component of the model are estimated, estimate the linear parameters $A_1^0$ and $B_1^0$ by the usual least squares estimation technique:

$$\begin{aligned} \begin{bmatrix} {\hat{A}}_1 \\ {\hat{B}}_1 \end{bmatrix} = [{{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)^{\top } {{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)]^{-1}{{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)^{\top }{{\varvec{Y}}}_{M N \times 1}. \end{aligned}$$

Here, ${{\varvec{Y}}}_{M N \times 1} = \begin{bmatrix} y(1, 1),\ \ldots ,\ y(M, 1),\ \ldots ,\ y(1, N),\ \ldots ,\ y(M, N)\end{bmatrix}^{\top }$ is the observed data vector, and the matrix ${{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)$ can be obtained by replacing $\alpha$, $\beta$, $\gamma$ and $\delta$ by ${\hat{\alpha }}_1$, ${\hat{\beta }}_1$, ${\hat{\gamma }}_1$ and ${\hat{\delta }}_1$ respectively in (12).

Step 4:

Eliminate the effect of the first component from the original data and construct new data as follows:

$$\begin{aligned} \begin{aligned} y_1(m,n)&= y(m,n) - {\hat{A}}_1 \cos ({\hat{\alpha }}_1 m + {\hat{\beta }}_1 m^2 + {\hat{\gamma }}_1 n + {\hat{\delta }}_1 n^2) \\&\quad - {\hat{B}}_1 \sin ({\hat{\alpha }}_1 m + {\hat{\beta }}_1 m^2 + {\hat{\gamma }}_1 n + {\hat{\delta }}_1 n^2); \\&\qquad m = 1, \ldots , M;\ n = 1, \ldots , N. \end{aligned} \end{aligned}$$

(18)

Step 5::

Using the new data, estimate the parameters of the second component by following the same procedure.

Step 6::

Continue this process until the parameters of all the p components are estimated.

In the following sections, we examine the asymptotic properties of the proposed estimators under the Assumptions 1, P4 and the following assumption on the parameters:

Assumption 3

$\varvec{\theta }_{k}^{0}$ is an interior point of $\varvec{\Theta }_1$, for all $k = 1, \ldots , p$ and the frequencies $\alpha _{k}^0s$, $\gamma _{k}^0s$ and the frequency rates $\beta _{k}^0s$, $\delta _{k}^0s$ are such that $(\alpha _i^0, \beta _i^0) \ne (\alpha _j^0, \beta _j^0)$ and $(\gamma _i^0, \delta _i^0)$ $\ne$ $(\gamma _j^0, \delta _j^0)$ $\forall \ i \ne j,\ i,\ j = 1,\ \ldots ,\ p$.

3.3 Consistency

Through the following theorems, we proclaim the consistency of the proposed estimators when the number of components, p is unknown.

Theorem 5

If Assumptions 1, 3 and P4 are satisfied, then the following results hold true for $1 \leqslant k \leqslant p$:

$$\begin{aligned} \begin{aligned}&{\hat{\alpha }}_k \xrightarrow {a.s.} \alpha _k^0 \text { as } M \rightarrow \infty , \\&{\hat{\beta }}_k \xrightarrow {a.s.} \beta _k^0 \text { as } M \rightarrow \infty . \end{aligned} \end{aligned}$$

Proof

See “Appendix B”. $\square$

Theorem 6

If Assumptions 1, 3 and P4 are satisfied, then the following results hold true for $1 \leqslant k \leqslant p$:

$$\begin{aligned} \begin{aligned}&{\hat{\gamma }}_k \xrightarrow {a.s.} \gamma _k^0 \text { as } N \rightarrow \infty , \\&{\hat{\delta }}_k \xrightarrow {a.s.} \delta _k^0 \text { as } N \rightarrow \infty . \end{aligned} \end{aligned}$$

Proof

This proof can be obtained along the same lines as proof of Theorem 5. $\square$

Theorem 7

If the Assumptions 1, 3 and P4 are satisfied, and if $\hat{A_k}$, $\hat{B_k}$, $\hat{\alpha _k}$, $\hat{\beta _k}$, $\hat{\gamma _k}$ and $\hat{\delta _k}$ are the estimators obtained at the k-th step, then for $1 \leqslant k \leqslant p$,

$$\begin{aligned} \begin{aligned}&\hat{A_k} \xrightarrow { a.s } A_k^0 \text { as } \text {min}\{M, N\} \rightarrow \infty \\&\hat{B_k} \xrightarrow { a.s } B_k^0 \text { as } \text {min}\{M, N\} \rightarrow \infty , \end{aligned} \end{aligned}$$

and for $k > p$,

$$\begin{aligned} \begin{aligned}&\hat{A_k} \xrightarrow { a.s } 0 \text { as } \text {min}\{M, N\} \rightarrow \infty \\&\hat{B_k} \xrightarrow { a.s } 0 \text { as } \text {min}\{M, N\} \rightarrow \infty . \end{aligned} \end{aligned}$$

Proof

See “Appendix B”. $\square$

From the above theorem, it is clear that if the number of components of the fitted model is less than or same as the true number of components, p, then the amplitude estimators converge to their true values almost surely, else if it is more than p, then the amplitude estimators upto the p-th step converge to the true values and past that, they converge to zero almost surely. Thus, this result can be used as a criterion to estimate the number p. However, this might not work in low signal-to-noise ratio scenarios.

3.4 Asymptotic distribution

Theorem 8

If Assumptions 1, 3 and P4 are satisfied, then for $1 \leqslant k \leqslant p:$

$$\begin{aligned}\begin{aligned}&\begin{bmatrix} ({\hat{\alpha }}_k - \alpha _k^0),\ ({\hat{\beta }}_k - \beta _k^0) \end{bmatrix}{{\varvec{D}}}_1^{-1} \xrightarrow {d} \varvec{{\mathcal {N}}}_2(\mathbf{0 }, 2\sigma ^2 \varvec{\Sigma }_{k}) \text { as } M \rightarrow \infty .\\ \end{aligned} \end{aligned}$$

Here ${{\varvec{D}}}_1$ is as defined in Theorem 3 and $\varvec{\Sigma }_{k}$ is as defined in (16).

Proof

See “Appendix B”. $\square$

Theorem 9

If the Assumptions 1, 3 and P4 are satisfied, then

$$\begin{aligned}\begin{aligned} \begin{bmatrix} ({\hat{\gamma }}_k - \gamma _k^0),\ ({\hat{\delta }}_k - \delta _k^0) \end{bmatrix}{{\varvec{D}}}_2^{-1} \xrightarrow {d} \varvec{{\mathcal {N}}}_2(\mathbf{0 }, 2\sigma ^2 \varvec{\Sigma }_k) \text { as } N \rightarrow \infty .\\ \end{aligned} \end{aligned}$$

Here ${{\varvec{D}}}_2$ is as defined in Theorem 4 and $\varvec{\Sigma }_{k}$ is as defined in (16).

Proof

This proof follows along the same lines as the proof of Theorem 8. $\square$

4 Numerical experiments

We perform simulations to examine the performance of the proposed estimators. We consider the following two cases:

Case I:

When the data are generated from a one-component model (2), with the following set of parameters:

$A^0 = 2$, $B^0 = 3$, $\alpha ^0 = 1.5$, $\beta ^0 = 0.5$, $\gamma ^0 = 2.5$ and $\delta ^0 = 0.75$.

Case II:

When the data are generated from a two components model (1), with the following set of parameters:

$A_1^0 = 5$, $B_1^0 = 4$, $\alpha _1^0 = 2.1$, $\beta _1^0 = 0.1$, $\gamma _1^0 = 1.25$ and $\delta _1^0 = 0.25$, $A_2^0 = 3$, $B_2^0 = 2$, $\alpha _2^0 = 1.5$, $\beta _2^0 = 0.5$, $\gamma _2^0 = 1.75$ and $\delta _2^0 = 0.75$.

The noise used in the simulations is generated from Gaussian distribution with mean 0 and variance $\sigma ^2$. Also, different values of the error variance, $\sigma ^2$ and sample sizes, M and N are considered. We estimate the parameters using the proposed estimation technique as well as the least squares estimation technique for Case I and for Case II, the proposed sequential technique and the sequential least squares technique proposed by Lahiri et al. (2015) are employed for comparison. For each case, the procedure is replicated 1000 times and the average values of the estimates, the average biases and the mean square errors (MSEs) are reported. The collation of the MSEs and the theoretical asymptotic variances exhibits the efficacy of the proposed estimation method.

4.1 One-component simulation results

4.1.1 Estimation performance versus sample size

In this section, we show how the proposed estimators perform in comparison with the usual LSEs (in this particular case, the usual LSEs are the MLEs as the noise is Gaussian) as well as the asymptotic CRLBs, as the sample size varies. We vary M and N from 50 to 100 each. In Fig. 3, we plot the MSEs of both the estimators along with the asymptotic CRLBs. As can be seen from this figure, the MSEs of the propounded estimates as well as the least squares estimates are well-matched with the corresponding theoretical asymptotic variances. This verifies consistency of the proposed estimators.

Fig. 3

MSEs of the proposed estimates (solid lines) along with the MSEs of the LS estimates (dashed lines) and the corresponding CRLBs (dashed-dotted lines) of the estimators of the parameters of the one-component simulated model versus sample size

4.1.2 Estimation performance versus signal-to-noise ratio (SNR)

Here we study the performance of the proposed estimates, again in comparison with the usual LSEs and the corresponding CRLBs, but as the SNR varies. The SNR Stoica et al. (1997) is defined as follows:

$$\begin{aligned} {\text {SNR} = 10 \log _{10}\bigg (\frac{{A^0}^2 + {B^0}^2}{\sigma ^2}\bigg )} \end{aligned}$$

Figure 4 displays this comparison. It can be seen from the figure that for each of the cases, the MSEs of the proposed estimates almost coincides with the corresponding asymptotic CRLBs, particularly for increasing values of SNR and the dimensions of the data matrix.

Fig. 4

MSEs of the proposed estimates (solid lines) along with the MSEs of the LS estimates (dashed lines) and the corresponding CRLBs (dashed-dotted lines) of the estimators of the parameters of the one-component simulated model versus SNR

4.1.3 Comparison of computational complexity

The efficient method in this paper is proposed to reduce the computational burden involved in finding the usual LSEs of the parameters of model (1). In the above sections, we see that the proposed estimators perform nearly as accurately as the usual LSEs. Here we demonstrate how the computational complexity is reduced significantly through the following example.

We consider the following model:

$$\begin{aligned} \begin{aligned} y(m,n)&= 2 \cos (1.5 m + 0.5 m^2 + 2.5 n + 0.75 n^2) \\&\quad + 3 \sin (1.5 m + 0.5 m^2 + 2.5 n + 0.75 n^2) + X(m,n);\\&\qquad m = 1, \ldots , 10, n = 1, \ldots , 10. \end{aligned} \end{aligned}$$

As explained in the introduction, finding the initial values to compute the proposed estimators involves two 2-D searches which means precisely $2 \times 9 \times 99 = 1782$ evaluations of the objective function to be minimised. The time taken for the computation of these initial values is 0.81 seconds. On the other hand, to compute the initial guesses for the usual LSEs of the non-linear parameters of the above model, we perform a 4D fine grid search in the parameter space. This requires $9 \times 99 \times 9 \times 99 = 793881$ computations of the least squares objective function and the time taken for this search is 196.61 s. This gives us a clear idea of the significant time savings if we use the proposed method rather than the least squares estimation method. Moreover, using the usual least squares method increases the computational load exponentially as the dimensions of the data matrix increase. This experiment is performed using $\hbox {Intel}^\circledR$ $\hbox {Core}^{TM}$i7-2600 @ 3.4 GHz, 4 GB RAM machines, the program codes are written in R software (3.3.0).

4.2 Two component simulation results

In this section, we present the simulation results for Case II. In the interest of brevity, we present the results only for the second component of the model. The estimates of the first component behave in the same manner and as they are obtained by minimising the same functions as for the one component model, we omit these results.

4.2.1 Estimation performance versus sample size

We first study the performance of the proposed estimators and compare it with the corresponding sequential LSEs and the asymptotic CRLBS versus the dimensions of the simulated data matrix.

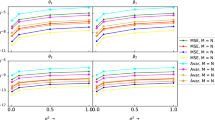
Figure 5 show the results obtained for the parameters of the second component of the underlying two-component model. These results verify consistency of the proposed sequential estimators. It is also observed that the MSEs of the obtained parameter estimates have exactly the same order as the corresponding asymptotic variances.

Fig. 5

MSEs of the proposed estimates(solid lines) along with the MSEs of the LS estimates (dashed lines) and the corresponding CRLBs (dashed-dotted lines) of the estimators of the parameters of the second component of the two-component simulated model versus sample size

4.2.2 Estimation performance versus SNR

Next we study the performance of the proposed estimators as the SNR varies. For the multiple component model, SNR is defined as follows:

$$\begin{aligned} \text {SNR}_k = 10 \log _{10}\bigg (\frac{{A_k^0}^2 + {B_k^0}^2}{\sigma ^2}\bigg ) \end{aligned}$$

The MSEs of the proposed estimators are plotted along with those of the sequential LSEs and the respective asymptotic CRLBs in Fig. 6.The results show that the MSEs of both types the estimates practically coincide with the corresponding CRLBs.

Fig. 6

MSEs of the proposed estimates (solid lines) along with the MSEs of the LS estimates (dashed lines) and the corresponding CRLBs (dashed-dotted lines) of the estimators of the parameters of the second component of the two-component simulated model versus SNR

It can be concluded that the simulations validate the accuracy of the proposed estimators. Also, as discussed in Sect. 4.1.3, the proposed estimators are much faster to compute than the sequential LSEs. Therefore the proposed estimators achieve computational simplicity along with an excellent estimation accuracy.

5 Simulated data analyses

In this section, we assess the performance of the proposed algorithm by analysing two symmetric gray-scale textures, one generated using a one-component 2-D chirp model and the other using a multiple-component 2-D chirp model.

5.1 When the data set is generated from a one-component 2-D chirp model

First, we consider a one-component 2-D chirp model defined as follows:

$$\begin{aligned} \begin{aligned} y(m,n)&= \cos (0.45 m + 0.0015 m^2 + 0.82 n + 0.0025 n^2) \\&\quad + \sin (0.45 m + 0.0015 m^2 + 0.82 n + 0.0025 n^2)\\&\quad + X(m,n); m = 1, \ldots , M, n = 1, \ldots , N. \end{aligned} \end{aligned}$$

(19)

We begin by generating data from the above defined model structure. Here, X(m, n) are i.i.d. Gaussian errors with mean 0 and variance 1. Figures 7 and 8 represent the true and the noisy image corresponding to the generated data.

Fig. 7

Original texture corresponding to model (19)

Fig. 8

Noisy texture corresponding to model (19)

We estimate the parameters of the underlying model using the proposed algorithm for the one-component model parameter estimation in Sect. 2.2. Figure 9 shows the estimated gray-scale image. It is evident that the the proposed method provides an accurate estimation of the original texture.

Fig. 9

Estimated texture corresponding to model (19)

5.2 When the data set is generated from a multiple-component 2-D chirp model

We also analyse a synthetic texture data using model (1) to demonstrate how the proposed parameter estimation method works for a 2-D chirp signal with multiple chirp components. The signal data are generated using the following model structure and parameters:

$$\begin{aligned} \begin{aligned} y(m,n)&= \sum _{k=1}^{5}\left\{ A_k^0 \cos (\alpha _k^0 m {+} \beta _k^0 m^2 {+} \gamma _k^0 n + \delta _k^0 n^2) + B_k^0 \sin (\alpha _k^0 m {+} \beta _k^0 m^2 + \gamma _k^0 n {+} \delta _k^0 n^2)\right\} \\&\quad + X(m,n) \end{aligned}\nonumber \\ \end{aligned}$$

(20)

The true parameter values are provided in Table 1. The errors X(m, n)s are i.i.d. Gaussian random variables with mean 0 and variance 100. Figure 1 represents the original texture without any contamination and Fig. 2 represents the noisy texture. Our purpose is to extract the original gray-scale texture from the one which is contaminated.

Table 1 True parameters values of the synthetic data

We estimate the parameters of model (20) using the proposed sequential procedure and the estimated texture is plotted in Fig. 10. It is clear that the estimated texture and the original texture look extremely well-matched.

Fig. 10

Estimated texture for the synthetic data

6 Concluding remarks

In this paper, we have considered the estimation of unknown parameters of a 2-D chirp model under the assumption of i.i.d. additive errors. The main idea is to reduce the computational complexity involved in finding the LSEs of these parameters. The proposed estimators minimise the computations to a great extent and are observed to be strongly consistent and asymptotically equivalent to the LSEs. For a 2-D chirp model with p number of components, we have proposed a sequential procedure which reduces the problem of estimation of the parameters to solving p number of 2-D optimisation problems. Moreover, the propounded sequential estimators are observed to be strongly consistent and asymptotically equivalent to the usual LSEs.

The numerical experiments—the simulations and the data analysis, show that the proposed estimation technique provides as accurate results as the least squares estimation method with the additional advantage of being computationally more efficient. Thus to summarise, the proposed estimators seem to be the method of choice as their performance is satisfactory and as efficient as the LSEs, both numerically and analytically.

Appendices

Appendix A

Henceforth, we will denote $\varvec{\theta }(n_0) = (A(n_0), B(n_0), \alpha , \beta )$ as the parameter vector and $\varvec{\theta }^0(n_0) = (A^0(n_0), B^0(n_0), \alpha ^0, \beta ^0)$ as the true parameter vector of the 1-D chirp model (9).

To prove Theorem 1, we need the following lemma:

Lemma 1

Consider the set $S_c = \{(\alpha , \beta ) : |\alpha - \alpha ^0| \geqslant c \text { or } |\beta - \beta ^0| \geqslant c\}$. If for any c > 0,

$$\begin{aligned} \liminf \inf \limits _{(\alpha , \beta ) \in S_c} \frac{1}{M N}\bigg [R^{(1)}_{MN}(\alpha , \beta ) - R^{(1)}_{MN}(\alpha ^0, \beta ^0)\bigg ] > 0 \ a.s. \end{aligned}$$

(21)

then, ${\hat{\alpha }}$ $\rightarrow$ $\alpha ^0$ and ${\hat{\beta }}$ $\rightarrow$ $\beta ^0$ almost surely as $M \rightarrow \infty$. Note that $\liminf$ stands for limit infimum and $\inf$ stands for the infimum.

Proof

This proof follows along the same lines as that of Lemma 1 of Wu (1981). $\square$

Proof of Theorem 1:

Let us consider the following:

$$\begin{aligned}&\liminf \inf \limits _{(\alpha , \beta ) \in S_c} \frac{1}{M N}\bigg [R^{(1)}_{MN}(\alpha , \beta ) - R^{(1)}_{MN}(\alpha ^0, \beta ^0)\bigg ]&\\&\quad = \liminf \inf \limits _{(\alpha , \beta ) \in S_c} \frac{1}{M N}\bigg [\sum _{{n_0} = 1}^{N}R_{M}(\alpha , \beta , n_0) - \sum _{{n_0} = 1}^{N} R_{M}(\alpha ^0, \beta ^0, n_0)\bigg ]&\\&\quad = \liminf \inf \limits _{(\alpha , \beta ) \in S_c} \frac{1}{M N}\bigg [\sum _{{n_0} = 1}^{N}Q_{M}({\hat{A}}(n_0), {\hat{B}}(n_0), \alpha , \beta ) - \sum _{{n_0} = 1}^{N} Q_{M}({\hat{A}}(n_0), {\hat{B}}(n_0), \alpha ^0, \beta ^0)\bigg ]&\\&\quad \geqslant \liminf \inf \limits _{(\alpha , \beta ) \in S_c} \frac{1}{M N}\bigg [\sum _{{n_0} = 1}^{N}Q_{M}({\hat{A}}(n_0), {\hat{B}}(n_0), \alpha , \beta ) - \sum _{{n_0} = 1}^{N} Q_{M}(A^0(n_0) , B^0(n_0), \alpha ^0, \beta ^0)\bigg ]&\\&\quad \geqslant \liminf \inf \limits _{ \varvec{\theta }(n_0) \in M_c^{n_0}} \frac{1}{M N}\bigg [\sum _{{n_0} = 1}^{N}Q_{M}(A(n_0), B(n_0), \alpha , \beta ) - \sum _{{n_0} = 1}^{N} Q_{M}(A^0(n_0) , B^0(n_0), \alpha ^0, \beta ^0)\bigg ]&\\&\quad \geqslant \frac{1}{N}\sum _{n_0 = 1}^{N} \liminf \inf \limits _{\varvec{\theta }(n_0) \in M_c^{n_0}} \frac{1}{M}\bigg [Q_M(\varvec{\theta }(n_0)) - Q_M(\varvec{\theta }^0(n_0))\bigg ] > 0.&\end{aligned}$$

This follows from the proof of Theorem 1 of Kundu and Nandi (2008). Here, $Q_{M}(A(n_0), B(n_0), \alpha , \beta ) = {{\varvec{Y}}}^{\top }_{n_0}({{\varvec{\textit{I}}}} - {{\varvec{Z}}}_M(\alpha , \beta )({{\varvec{Z}}}_M(\alpha , \beta )^{\top }{{\varvec{Z}}}_M(\alpha , \beta ))^{-1}{{\varvec{Z}}}_M(\alpha , \beta )^{\top }){{\varvec{Y}}}_{n_0}$. Also note that the set $M_c^{n_0}$ = $\{\varvec{\theta }(n_0) : |A(n_0) - A^0(n_0)| \geqslant c \text { or } |B(n_0) - B^0(n_0)| \geqslant c \text { or } |\alpha - \alpha ^0| \geqslant c \text { or } |\beta - \beta ^0| \geqslant c\}$ which implies $S_c \subset M_c^{n_0}$, for all $n_0 \in \{1, \ldots , N\}$. Thus, using Lemma 1, ${\hat{\alpha }} \xrightarrow {a.s.} \alpha ^0$ and ${\hat{\beta }} \xrightarrow {a.s.} \beta ^0$. $\square$

Proof of Theorem 3:

Let us denote $\varvec{\xi } = (\alpha , \beta )$ and $\hat{\varvec{\xi }} = ({\hat{\alpha }}, {\hat{\beta }})$, the estimator of $\varvec{\xi }^0 = (\alpha ^0, \beta ^0)$ obtained by minimising the function $R_{MN}^{(1)}(\varvec{\xi }) = R_{MN}^{(1)}(\alpha , \beta )$ defined in (10).

Using multivariate Taylor series, we expand the $1 \times 2$ gradient vector ${{\varvec{R}}}_{MN}^{(1)'}(\hat{\varvec{\xi }})$ of the function $R_{MN}^{(1)}(\varvec{\xi })$, around the point $\varvec{\xi }^0$ as follows:

$$\begin{aligned} {{\varvec{R}}}_{MN}^{(1)'}(\hat{\varvec{\xi }}) - {{\varvec{R}}}_{MN}^{(1)'}(\xi ^0) = (\hat{\varvec{\xi }} - \varvec{\xi }^0){{\varvec{R}}}_{MN}^{(1)''}(\bar{\varvec{\xi }}), \end{aligned}$$

where $\bar{\varvec{\xi }}$ is a point between $\hat{\varvec{\xi }}$ and $\varvec{\xi }^0$ and ${{\varvec{R}}}_{MN}^{(1)''}(\bar{\varvec{\xi }})$ is the $2 \times 2$ Hessian matrix of the function $R_{MN}^{(1)}(\varvec{\xi })$ at the point $\bar{\varvec{\xi }}$. Since $\hat{\varvec{\xi }}$ minimises the function $R_{MN}^{(1)}(\varvec{\xi })$, ${{\varvec{R}}}_{MN}^{(1)'}(\hat{\varvec{\xi }}) = 0$. Thus, we have

$$\begin{aligned} (\hat{\varvec{\xi }} - \varvec{\xi }^0) = - {{\varvec{R}}}_{MN}^{(1)'}(\varvec{\xi }^0)[{{\varvec{R}}}_{MN}^{(1)''}(\bar{\varvec{\xi }})]^{-1}. \end{aligned}$$

Multiplying both sides by the diagonal matrix ${{\varvec{D}}}_1^{-1} = \text {diag}(M^{\frac{-3}{2}}N^{\frac{-1}{2}}, M^{\frac{-5}{2}}N^{\frac{-1}{2}})$, we get:

$$\begin{aligned} (\hat{\varvec{\xi }} - \varvec{\xi }^0){{\varvec{D}}}_1^{-1} = - {{\varvec{R}}}_{MN}^{(1)'}(\varvec{\xi }^0){{\varvec{D}}}_1[{{\varvec{D}}}_1R_{MN}^{(1)''}(\bar{\varvec{\xi }}){{\varvec{D}}}_1]^{-1}. \end{aligned}$$

(22)

Consider the vector,

$$\begin{aligned} {{\varvec{R}}}_{MN}^{(1)'}(\varvec{\xi }^0){{\varvec{D}}}_1 = \begin{bmatrix} \frac{1}{M^{3/2}N^{1/2}}\frac{\partial R_{MN}^{(1)}(\varvec{\xi }^0)}{\partial \alpha },&\frac{1}{M^{5/2}N^{1/2}}\frac{\partial R_{MN}^{(1)}(\varvec{\xi }^0)}{\partial \beta } \end{bmatrix}. \end{aligned}$$

On computing the elements of this vector and using preliminary result (5) (see Sect. 2.1) and the definition of the function:

$$\begin{aligned} R_{MN}^{(1)}(\alpha , \beta ) = \sum \limits _{{n_0} = 1}^{N}R_M(\alpha , \beta , n_0) \end{aligned}$$

we obtain the following result:

$$\begin{aligned} -{{\varvec{R}}}_{MN}^{(1)'}(\varvec{\xi }^0){{\varvec{D}}}_1 \xrightarrow {d} \varvec{{\mathcal {N}}}_2(\mathbf{0 }, 2\sigma ^2\varvec{\Sigma }) \text { as } M \rightarrow \infty . \end{aligned}$$

(23)

Since $\hat{\varvec{\xi }} \xrightarrow {a.s.} \varvec{\xi }^0$, and as each element of the matrix ${{\varvec{R}}}_{MN}^{(1)''}(\varvec{\xi })$ is a continuous function of $\varvec{\xi }$, we have

$$\begin{aligned} \lim _{M \rightarrow \infty }{{\varvec{D}}}_1{{\varvec{R}}}_{MN}^{(1)''}(\bar{\varvec{\xi }}){{\varvec{D}}}_1 = \lim _{M \rightarrow \infty }{{\varvec{D}}}_1{{\varvec{R}}}_{MN}^{(1)''}(\varvec{\xi }^0){{\varvec{D}}}_1. \end{aligned}$$

Now using preliminary result (6) (see Sect. 2.1), it can be seen that:

$$\begin{aligned} \lim _{M \rightarrow \infty }{{\varvec{D}}}_1{{\varvec{R}}}_{MN}^{(1)''}(\varvec{\xi }^0){{\varvec{D}}}_1 \rightarrow \varvec{\Sigma }^{-1}. \end{aligned}$$

(24)

On combining (22), (23) and (24), we have the desired result. $\square$

Appendix B

To prove Theorem 5, we need the following lemmas:

Lemma 2

Consider the set $S_c^{1}$ = $\{(\alpha , \beta ) : |\alpha - \alpha _1^0| \geqslant c \text { or } |\beta - \beta _1^0| \geqslant c\}$.If for any c > 0,

$$\begin{aligned} \liminf \inf \limits _{(\alpha , \beta ) \in S_c^{1}} \frac{1}{M N}[R^{(1)}_{1,MN}(\alpha , \beta ) - R^{(1)}_{1,MN}(\alpha _1^0, \beta _1^0)] > 0 \ a.s. \end{aligned}$$

(25)

then, ${\hat{\alpha }}_1$ $\rightarrow$ $\alpha _1^0$ and ${\hat{\beta }}_1$ $\rightarrow$ $\beta _1^0$ almost surely as $M \rightarrow \infty$.

Proof

This proof follows along the same lines as proof of Lemma 1. $\square$

Lemma 3

If Assumptions 1, 3 and P4 are satisfied then:

$$\begin{aligned}\begin{aligned}&M({\hat{\alpha }}_1 - \alpha _1^0) \xrightarrow {a.s.} 0,\\&M^2({\hat{\beta }}_1 - \beta _1^0) \xrightarrow {a.s.} 0. \end{aligned} \end{aligned}$$

Proof

Let us denote ${{\varvec{R}}}_{1, MN}^{(1)'}(\varvec{\xi })$ as the $1 \times 2$ gradient vector and ${{\varvec{R}}}_{1, MN}^{(1)''}(\varvec{\xi })$ as the $2 \times 2$ Hessian matrix of the function $R_{1, MN}^{(1)}(\varvec{\xi })$. Using multivariate Taylor series expansion, we expand the function ${{\varvec{R}}}_{1, MN}^{(1)'}(\hat{\varvec{\xi }}_1)$ around the point $\varvec{\xi }_1^0$ as follows:

$$\begin{aligned} {{\varvec{R}}}_{1, MN}^{(1)'}(\hat{\varvec{\xi }}_1) - {{\varvec{R}}}_{1, MN}^{(1)'}(\varvec{\xi }_1^0) = (\hat{\varvec{\xi }}_1 - \varvec{\xi }_1^0){{\varvec{R}}}_{1, MN}^{(1)''}(\bar{\varvec{\xi }}_1) \end{aligned}$$

where $\bar{\varvec{\xi }}_1$ is a point between $\hat{\varvec{\xi }}_1$ and $\varvec{\xi }_1^0$. Note that ${{\varvec{R}}}_{1, MN}^{(1)'}(\hat{\varvec{\xi }}_1) = 0$. Thus, we have:

$$\begin{aligned} (\hat{\varvec{\xi }}_1 - \varvec{\xi }_1^0) = - {{\varvec{R}}}_{1, MN}^{(1)'}(\varvec{\xi }_1^0)[{{\varvec{R}}}_{1, MN}^{(1)''}(\bar{\varvec{\xi }}_1)]^{-1}. \end{aligned}$$

(26)

Multiplying both sides by $\frac{1}{\sqrt{MN}}{{\varvec{D}}}_1^{-1}$, we get:

$$\begin{aligned} (\hat{\varvec{\xi }}_1 - \varvec{\xi }_1^0)(\sqrt{MN}{{\varvec{D}}}_1)^{-1} = - \frac{1}{\sqrt{MN}}{{\varvec{R}}}_{1, MN}^{(1)'}(\varvec{\xi }_1^0){{\varvec{D}}}_1[{{\varvec{D}}}_1{{\varvec{R}}}_{1, MN}^{(1)''}(\bar{\varvec{\xi }}_1){{\varvec{D}}}_1]^{-1}. \end{aligned}$$

(27)

Since each of the elements of the matrix ${{\varvec{R}}}_{1, MN}^{(1)''}(\varvec{\xi })$ is a continuous function of $\varvec{\xi },$

$$\begin{aligned} \lim _{M \rightarrow \infty } {{\varvec{D}}}_1{{\varvec{R}}}_{1, MN}^{(1)''}(\bar{\varvec{\xi }}_1){{\varvec{D}}}_1 = \lim _{M \rightarrow \infty } {{\varvec{D}}}_1{{\varvec{R}}}_{1, MN}^{(1)''}(\varvec{\xi }_1^0){{\varvec{D}}}_1. \end{aligned}$$

By definition,

$$\begin{aligned} R_{1, MN}^{(1)}(\varvec{\xi }) = \sum _{{n_0} = 1}^{N} R_{1,M}(\varvec{\xi }, n_0). \end{aligned}$$

(28)

Using this and the preliminary result (13) and (15) (see Sect. 3.1), it can be seen that:

$$\begin{aligned}&- \frac{1}{\sqrt{MN}}{{\varvec{R}}}_{1, MN}^{(1)'}(\varvec{\xi }_1^0){{\varvec{D}}}_1 \xrightarrow {a.s.} 0 \text { as } M \rightarrow \infty . \end{aligned}$$

(29)

$$\begin{aligned}&{{\varvec{D}}}_1{{\varvec{R}}}_{1, MN}^{(1)''}(\varvec{\xi }_1^0){{\varvec{D}}}_1 \xrightarrow {a.s.} \varvec{\Sigma }_1^{-1} \text { as } M \rightarrow \infty . \end{aligned}$$

(30)

On combining (27), (29) and (30), we have the desired result. $\square$

Proof of Theorem 5:

Consider the left hand side of (25), that is,

$$\begin{aligned}&\liminf \inf \limits _{(\alpha , \beta ) \in S_c^{1}} \frac{1}{M N}\left[ R^{(1)}_{1,MN}(\alpha , \beta ) - R^{(1)}_{1,MN}(\alpha _1^0, \beta _1^0)\right]&\\&\quad = \liminf \inf \limits _{(\alpha , \beta ) \in S_c^{1}} \frac{1}{M N}\left[ \sum _{{n_0} = 1}^{N}Q_{1,M}({\hat{A}}_1(n_0), {\hat{B}}_1(n_0), \alpha , \beta ) - \sum _{{n_0} = 1}^{N} Q_{1,M}({\hat{A}}_1(n_0), {\hat{B}}_1(n_0), \alpha _1^0, \beta _1^0)\right]&\\&\quad \geqslant \liminf \inf \limits _{(\alpha , \beta ) \in S_c^{1}} \frac{1}{M N}\left[ \sum _{{n_0} = 1}^{N}Q_{1,M}({\hat{A}}_1(n_0), {\hat{B}}_1(n_0), \alpha , \beta ) - \sum _{{n_0} = 1}^{N} Q_{1,M}(A_1^0(n_0) , B_1^0(n_0), \alpha _1^0, \beta _1^0)\right]&\\&\quad \geqslant \liminf \inf \limits _{ \varvec{\theta }_1(n_0) \in M_c^{1,n_0}} \frac{1}{M N}\left[ \sum _{{n_0} = 1}^{N}Q_{1,M}(A_1(n_0), B_1(n_0), \alpha , \beta ) - \sum _{{n_0} = 1}^{N} Q_{1,M}(A_1^0(n_0) , B_1^0(n_0), \alpha _1^0, \beta _1^0)\right]&\\&\quad \geqslant \frac{1}{N}\sum _{n_0 = 1}^{N} \liminf \inf \limits _{\varvec{\theta }_1(n_0) \in M_c^{1,n_0}} \frac{1}{M}\bigg [Q_{1,M}(\varvec{\theta }_1(n_0)) - Q_{1,M}(\varvec{\theta }_1^0(n_0))\bigg ] > 0.&\end{aligned}$$

Here, $Q_{1,M}(A(n_0), B(n_0), \alpha , \beta ) = {{\varvec{Y}}}^{\top }_{n_0}({{\varvec{\textit{I}}}} - {{\varvec{Z}}}_M(\alpha , \beta )({{\varvec{Z}}}_M(\alpha , \beta )^{\top }{{\varvec{Z}}}_M(\alpha , \beta ))^{-1}{{\varvec{Z}}}_M(\alpha , \beta )^{\top }){{\varvec{Y}}}_{n_0}$ and $M_c^{1,n_0}$ can be obtained by replacing $\alpha ^0$ and $\beta ^0$ by $\alpha _1^0$ and $\beta _1^0$ respectively, in the set $M_c^{n_0}$ defined in Lemma 1. The last step follows from the proof of Theorem 2.4.1 of Lahiri et al. (2015). Thus, using Lemma 2, ${\hat{\alpha }}_1 \xrightarrow {a.s.} \alpha _1^0$ and ${\hat{\beta }}_1 \xrightarrow {a.s.} \beta _1^0$ as $M \rightarrow \infty$.

Following similar arguments, one can obtain the consistency of ${\hat{\gamma }}_1$ and ${\hat{\delta }}_1$ as $N \rightarrow \infty$. Also,

$$\begin{aligned} \begin{aligned}&N({\hat{\gamma }}_1 - \gamma _1^0) \xrightarrow {a.s.} 0,\\&N^2({\hat{\delta }}_1 - \delta _1^0) \xrightarrow {a.s.} 0. \end{aligned} \end{aligned}$$

The proof of the above equations follows along the same lines as the proof of Lemma 3. From Theorem 7, it follows that as min$\{M, N\} \rightarrow \infty$:

$$\begin{aligned} \begin{aligned}&({\hat{A}}_1 - A_1^0) \xrightarrow {a.s.} 0,\\&({\hat{B}}_1 - B_1^0) \xrightarrow {a.s.} 0. \end{aligned} \end{aligned}$$

Thus, we have the following relationship between the first component of model (1) and its estimate:

$$\begin{aligned} \begin{aligned}&{\hat{A}}_1 \cos ({\hat{\alpha }}_1 m + {\hat{\beta }}_1 m^2 + {\hat{\gamma }}_1 n + {\hat{\delta }}_1 n^2) + {\hat{B}}_1 \sin ({\hat{\alpha }}_1 m + {\hat{\beta }}_1 m^2 + {\hat{\gamma }}_1 n + {\hat{\delta }}_1 n^2) \\&\quad = A_1^0 \cos (\alpha _1^0 m + \beta _1^0 m^2 + \gamma _1^0 n + \delta _1^0 n^2) + B_1^0 \sin (\alpha _1^0 m + \beta _1^0 m^2 + \gamma _1^0 n + \delta _1^0 n^2) + o(1). \end{aligned} \end{aligned}$$

(31)

Here a function g is o(1), if $g \rightarrow 0$ almost surely as min$\{M, N\} \rightarrow \infty$.

Using (31) and following the same arguments as above for the consistency of ${\hat{\alpha }}_1$, ${\hat{\beta }}_1$, ${\hat{\gamma }}_1$ and ${\hat{\delta }}_1$, we can show that, ${\hat{\alpha }}_2$, ${\hat{\beta }}_2$, ${\hat{\gamma }}_2$ and ${\hat{\delta }}_2$ are strongly consistent estimators of $\alpha _2^0$, $\beta _2^0$, $\gamma _2^0$ and $\delta _2^0$ respectively. And the same can be extended for $k \leqslant p.$ Hence, the result. $\square$

Proof of Theorem 7:

We will consider the following two cases that will cover both the scenarios—underestimation as well as overestimation of the number of components:

• Case 1 When $k = 1$:

  $$\begin{aligned} \begin{aligned} \begin{bmatrix} {\hat{A}}_1 \\ {\hat{B}}_1 \end{bmatrix} = [{{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)^{\top }{{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)]^{-1}{{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)^{\top } {{\varvec{Y}}}_{MN \times 1} \end{aligned} \end{aligned}$$

  (32)

  Using Lemma 1 of Lahiri et al. (2015), it can be seen that:

  $$\begin{aligned} \frac{1}{MN}[{{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)^{\top }{{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)] \rightarrow \frac{1}{2}{{\varvec{\textit{I}}}}_{2 \times 2} \text { as } \min \{M, N\} \rightarrow \infty . \end{aligned}$$

  Substituting this result in (32), we get:

  $$\begin{aligned}\begin{aligned} \begin{bmatrix} {\hat{A}}_1 \\ {\hat{B}}_1 \end{bmatrix}&= \frac{2}{MN}{{\varvec{W}}}({\hat{\alpha }}_1, {\hat{\beta }}_1, {\hat{\gamma }}_1, {\hat{\delta }}_1)^{\top } {{\varvec{Y}}}_{MN \times 1} + o(1)\\&= \begin{bmatrix} \frac{2}{MN}\sum \limits _{n=1}^{N}\sum \limits _{m=1}^{M}y(m,n)\cos ({\hat{\alpha }}_1 m + {\hat{\beta }}_1 m^2 + {\hat{\gamma }}_1 n + {\hat{\delta }}_1 n^2) + o(1) \\ \frac{2}{MN}\sum \limits _{n=1}^{N}\sum \limits _{m=1}^{M}y(m,n)\sin ({\hat{\alpha }}_1 m + {\hat{\beta }}_1 m^2 + {\hat{\gamma }}_1 n + {\hat{\delta }}_1 n^2) + o(1) \end{bmatrix}. \end{aligned} \end{aligned}$$

  Now consider the estimate ${\hat{A}}_1$. Using multivariate Taylor series, we expand the function $\cos ({\hat{\alpha }}_1 m + {\hat{\beta }}_1 m^2 + {\hat{\gamma }}_1 n + {\hat{\delta }}_1 n^2)$ around the point $(\alpha _1^0, \beta _1^0, \gamma _1^0, \delta _1^0)$ and we obtain:

  $$\begin{aligned} \begin{aligned}&{\hat{A}}_1 \\&\quad = \frac{2}{MN}\sum \limits _{n=1}^{N}\sum \limits _{m=1}^{M}y(m,n)\bigg \{\cos (\alpha _1^0 m + \beta _1^0 m^2 + \gamma _1^0 n + \delta _1^0 n^2) \\&\qquad - m ({\hat{\alpha }}_1 - \alpha _1^0)\sin (\alpha _1^0 m + \beta _1^0 m^2 + \gamma _1^0 n \\&\qquad + \delta _1^0 n^2) - m^2({\hat{\beta }}_1 - \beta _1^0)\sin (\alpha _1^0 m + \beta _1^0 m^2 + \gamma _1^0 n + \delta _1^0 n^2) \\&\qquad - n ({\hat{\gamma }}_1 - \gamma _1^0)\sin (\alpha _1^0 m + \beta _1^0 m^2 + \gamma _1^0 n \\&\qquad + \delta _1^0 n^2) - n^2({\hat{\delta }}_1 - \delta _1^0)\sin (\alpha _1^0 m + \beta _1^0 m^2 + \gamma _1^0 n + \delta _1^0 n^2) \bigg \} \\&\qquad \rightarrow 2 \times \frac{A_1^0}{2} = A_1^0 \text { almost surely as } \min \{M, N\} \rightarrow \infty , \end{aligned} \end{aligned}$$

  using (1) and Lemma 1 and Lemma 2 of Lahiri et al. (2015). Similarly, it can be shown that ${\hat{B}}_1 \rightarrow B_1^0$ almost surely as $\min \{M, N\} \rightarrow \infty$.

  For the second component linear parameter estimates, consider:

  $$\begin{aligned}\begin{aligned} \begin{bmatrix} {\hat{A}}_2 \\ {\hat{B}}_2 \end{bmatrix} = \begin{bmatrix} \frac{2}{MN}\sum \limits _{n=1}^{N}\sum \limits _{m=1}^{M}y_1(m,n)\cos ({\hat{\alpha }}_2 m + {\hat{\beta }}_2 m^2 + {\hat{\gamma }}_2 n + {\hat{\delta }}_2 n^2) + o(1)\\ \frac{2}{MN}\sum \limits _{n=1}^{N}\sum \limits _{m=1}^{M}y_1(m,n)\sin ({\hat{\alpha }}_2 m + {\hat{\beta }}_2 m^2 + {\hat{\gamma }}_2 n + {\hat{\delta }}_2 n^2) + o(1) \end{bmatrix}. \end{aligned} \end{aligned}$$

  Here, $y_1(m,n)$ is the data obtained at the second stage after eliminating the effect of the first component from the original data as defined in (18). Using the relationship (31) and following the same procedure as for the consistency of ${\hat{A}}_1$, it can be seen that:

  $$\begin{aligned} {\hat{A}}_2 \xrightarrow {a.s.} A_2^0 \quad \text {and} \quad {\hat{B}}_2 \xrightarrow {a.s.} B_2^0 \text { as } \min \{M, N\} \rightarrow \infty . \end{aligned}$$

  (33)

  It is evident that the result can be easily extended for any $2 \leqslant k \leqslant p$.

• Case 2 When $k = p+1$:

  $$\begin{aligned} \begin{aligned} \begin{bmatrix} {\hat{A}}_{p+1} \\ {\hat{B}}_{p+1} \end{bmatrix} = \begin{bmatrix} \frac{2}{MN}\sum \limits _{n=1}^{N}\sum \limits _{m=1}^{M}y_p(m,n)\cos ({\hat{\alpha }}_{p+1} m + {\hat{\beta }}_{p+1} m^2 + {\hat{\gamma }}_{p+1} n + {\hat{\delta }}_{p+1} n^2) + o(1)\\ \frac{2}{MN}\sum \limits _{n=1}^{N}\sum \limits _{m=1}^{M}y_p(m,n)\sin ({\hat{\alpha }}_{p+1} m + {\hat{\beta }}_{p+1} m^2 + {\hat{\gamma }}_{p+1} n + {\hat{\delta }}_{p+1} n^2) + o(1) \end{bmatrix}, \end{aligned} \end{aligned}$$

  (34)

  where

  $$\begin{aligned} \begin{aligned}&y_p(m,n)\\&\quad = y(m,n) - \sum \limits _{j=1}^{p}\bigg \{{\hat{A}}_j \cos ({\hat{\alpha }}_j m + {\hat{\beta }}_j m^2 + {\hat{\gamma }}_j n + {\hat{\delta }}_j n^2) \\&\qquad + {\hat{B}}_j \sin ({\hat{\alpha }}_j m + {\hat{\beta }}_j m^2 + {\hat{\gamma }}_j n + {\hat{\delta }}_j n^2) \bigg \} \\&\quad = X(m,n) + o(1), \text { using }(31) \text { and case 1 results.} \end{aligned} \end{aligned}$$

  From here, it is not difficult to see that (34) implies the following result:

  $$\begin{aligned} {\hat{A}}_{p+1} \xrightarrow {a.s.} 0 \quad \text {and} \quad {\hat{B}}_{p+1} \xrightarrow {a.s.} 0 \text { as } \min \{M, N\} \rightarrow \infty . \end{aligned}$$

  This is obtained using Lemma 2 of Lahiri et al. (2015). It is apparent that the result holds true for any $k > p.$

$\square$

Proof of Theorem 8:

Consider (26) and multiply both sides of the equation with the diagonal matrix, ${{\varvec{D}}}_1^{-1}$:

$$\begin{aligned} (\hat{\varvec{\xi }}_1 - \varvec{\xi }_1^0){{\varvec{D}}}_1^{-1} = - {{\varvec{R}}}_{1, MN}^{(1)'}(\varvec{\xi }_1^0){{\varvec{D}}}_1[{{\varvec{D}}}_1{{\varvec{R}}}_{1, MN}^{(1)''}(\bar{\varvec{\xi }}_1){{\varvec{D}}}_1]^{-1}. \end{aligned}$$

(35)

Computing the elements of the vector $- {{\varvec{R}}}_{1, MN}^{(1)'}(\varvec{\xi }_1^0){{\varvec{D}}}_1$ and using definition (28) and the preliminary result (14) (Sect. 3.1), we obtain the following result:

$$\begin{aligned} - {{\varvec{R}}}_{1, MN}^{(1)'}(\varvec{\xi }_1^0){{\varvec{D}}}_1 \xrightarrow {d} \varvec{{\mathcal {N}}}_2(\mathbf{0 }, 2\sigma ^2 \varvec{\Sigma }_1^{-1}) \text { as } M \rightarrow \infty . \end{aligned}$$

(36)

On combining (35), (36) and (30), we have:

$$\begin{aligned} (\hat{\varvec{\xi }}_1 - \varvec{\xi }_1^0){{\varvec{D}}}_1^{-1} \xrightarrow {d} \varvec{{\mathcal {N}}}_2(\mathbf{0 }, 2\sigma ^2 \varvec{\Sigma }_1) \end{aligned}$$

This result can be extended for $k = 2$ using the relation (31) and following the same argument as above. Similarly, we can continue to extend the result for any $k \leqslant p$. $\square$