On a Chirp-Like Model and Its Parameter Estimation Using Periodogram-Type Estimators

Abstract

Parametric modelling of physical phenomena has received a great deal of attention in the signal processing literature. Different models like ARMA models, sinusoidal models, harmonic models, models with amplitude modulation, models with frequency modulation and their different versions and combinations have been used to describe natural and synthetic signals in a wide range of applications. Two of the classical models that were considered by Professor C. R. Rao were one-dimensional superimposed exponential model and two-dimensional superimposed exponential model. In this paper, we consider parameter estimation of a newly introduced but related model, called a chirp-like model. This model was devised as an alternative to the more popular chirp model. A chirp-like model overcomes the problem of computational difficulty involved in fitting a chirp model to data to a large extent and at the same time provides visually indistinguishable results. We search the peaks of a periodogram-type function to estimate the frequencies and chirp rates of a chirp-like model. The obtained estimators are called approximate least squares estimators (ALSEs). We also put forward a sequential algorithm for the parameter estimation problem which reduces the computational load of finding the ALSEs significantly. Large-sample properties of the proposed estimators are investigated and the results indicate strong consistency and asymptotic normality of the ALSEs as well as the sequential ALSEs. The performance of the estimators is analysed in an extensive manner both on synthetic as well as real world signals and the results indicate that the proposed methods of estimation provide reasonably accurate estimates of frequencies and frequency rates.

1 Introduction

The most conventional way of modelling a periodic signal is using a sinusoidal model. A generic form of this model is expressed mathematically as follows:

$$\begin{aligned} y(t) = \sum _{j=1}^{p}\{A_j^0 \cos (\alpha _j^0 t) + B_j^0 \sin (\alpha _j^0 t)\} + X(t); \ t = 1, \ldots , N. \end{aligned}$$

(1)

Here, y(t) represents the observed signal at discrete time points $1, \ldots , N$, p is the number of sinusoids present in the model, $A_j^0$s and $B_j^0$s are the amplitudes and $\alpha _j^0$s are the frequencies of the signal. The non-sinusoidal part of the signal X(t) accounts for the noise present in the signal. An entire body of scientific literature has been developed to describe signals exhibiting periodic behaviour in different areas of science and engineering such as audio and speech processing, seismology, electrocardiography, astronomy to mention a few.

Professor C. R. Rao and his collaborators mainly worked on the sinusoidal signal models in their analytic form which is complex valued. These are also known as complex exponential models and can be mathematically expressed as follows:

$$\begin{aligned} y(t) = \sum _{j=1}^{p}A_j^0 e^{i\alpha _j^0 t} + X(t); \ t = 1, \ldots , N. \end{aligned}$$

(2)

Here, $A_j^0$s are complex-valued amplitudes, $\alpha _j^0 \in (0, \pi )$ are frequencies and $i = \sqrt{-1}$. Although the signals observed are real-valued, sometimes it can be useful to consider their complex counterpart for ease in analytical derivations. Professor Rao along with his collaborators treated the problem of estimation of the above model as a non-linear regression problem. He considered the LSEs for the estimation of the unknown parameters of model (2) and established their asymptotic properties in an unconventional manner. This was motivated by the fact that the underlying model did not satisfy common sufficient conditions of Jennrich [1] or Wu [2], and therefore, the asymptotic properties were not immediate to follow. Their work led to an elegant way of deriving these statistical properties. Their approach of dealing with this problem has been adapted in this paper as well. For a detailed review on his work in this area, we invoke the interested reader to the recent article on Professor C. R. Rao’s contributions to Statistical Signal Processing by the first author [3].

In many practical scenarios, the signals are not exactly periodic and a sinusoidal model may not be the “best” to model such signals. A popular alternative is the more flexible chirp model, where the frequencies are linear functions of time. Following is the mathematical expression of a chirp model:

$$\begin{aligned} y(t) = \sum _{j=1}^{p}\{A_j^0 \cos (\alpha _j^0 t + \beta _j^0 t^2) + B_j^0 \sin (\alpha _j^0 t + \beta _j^0 t^2)\} + X(t); \ t = 1, \ldots , N. \end{aligned}$$

(3)

Here, as before, $A_j^0$s, $B_j^0$s are the amplitudes and $\alpha _j^0$s are the frequencies of the observed signal y(t)s, however, the frequencies are not constant anymore and $\beta _j^0$s are the frequency rates. This model has been applied to natural as well as man-made signals such as bird songs, music, ultrasonic sounds made by bats, whales, biomedical signals like electrencephalography (EEG), electromyography (EMG) and in quantum optics. The reader is referred to Flandrin [4] and the references cited therein for more applications of the model. Taking off from the initial works of Bello [5], Kelly [6] and Abatzoglou [7], quite a lot of estimation methods have been proposed for the parameter estimation of this model such as rank reduction method [8], phase unwrapping technique [9], FFT based method [10], quadratic phase transform [11], non-linear least squares [12] and Monte Carlo importance sampling [13] to name a few. However, they suffer from a high computational cost.

In this paper, we consider a practical alternative to a chirp model called a chirp-like model. It has been observed that the two models have almost identical performance. Despite their similar behaviour, there is a huge difference in the computational load that is involved in the fitting of these two models to real world signals. Therefore, it is advantageous from a computational and algorithmic point of view to use a chirp-like model rather than a chirp model in practice. Mathematically, a generic form of a chirp-like model is given by:

$$\begin{aligned} \begin{aligned} y(t) =&\sum _{j=1}^{p}\{A_j^0 \cos (\alpha _j^0 t) + B_j^0 \sin (\alpha _j^0 t)\} \\&+ \sum _{k=1}^{q}\{C_k^0 \cos (\beta _k^0 t^2) + D_k^0 \sin (\beta _k^0 t^2)\} + X(t);\ \ \ \ \ \ t = 1, \ldots , N. \end{aligned} \end{aligned}$$

Here, y(t) is the data observed at discrete time points 1 through N. It is decomposed as the sum of a deterministic component and an additive noise component X(t). p and q are the number of sinusoids and the number of chirp components present in the signal respectively. $A_j^0$s, $B_j^0$s, $C_k^0$s, $D_k^0$s, $\alpha _j^0$s and $\beta _j^0$s are the unknown parameters that characterise the deterministic part of the signal. Note that the signal is a linear function of the amplitudes $A_j^0$s, $B_j^0$s, $C_k^0$s and $D_k^0$s but a non-linear function of the frequencies $\alpha _j^0$s and the chirp rates $\beta _j^0$s.

Given the data, the problem of describing it using the above model reduces to the estimation of its unknown parameters. The intent of this paper is three-fold:

• to motivate the chirp-like model as a proxy to the well-established chirp model in the context of different applications,

• to introduce a computationally efficient and theoretically optimal method of estimation of the parameters of a chirp-like model, and

• to demonstrate the effectiveness of the proposed methodology in practice.

The paper is organised as follows. The motivation behind the model is presented in the next section. Section 3 outlines the methodology to obtain periodogram-type estimators of the unknown parameters of a chirp-like model and a theoretical analysis of their properties. A computationally efficient sequential method for the underlying parameter estimation problem is suggested in Sect. 4. In this section, we also state large-sample properties of the sequential estimators. We assess the accuracy of the proposed estimators through extensive simulation and the results are reported in Sect. 5. The performance of the model and the proposed estimators is evaluated on real world signals in Sect. 6 and the paper is concluded in Sect. 7. The lemmas required to prove the theoretical results are in “Appendix A” and the proofs of these results are in the rest of the appendices.

2 Motivation Behind the Chirp-Like Model

The main motivation behind using a chirp-like model as a surrogate for a chirp model is its ability to envelop a chirp signal completely. We illustrate this on two different chirp signals. These signals are synthesised with one and multiple components present in the chirp model.

The data for the one component chirp model are generated using the following model equation:

$$\begin{aligned} y(t) = 4 \cos (0.05 t + 0.005 t^2) + 4 \sin (0.05 t + 0.005 t^2);\ t = 1, \ldots , 50. \end{aligned}$$

(4)

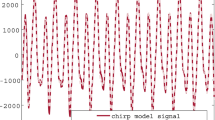
Here, we consider only the true model without any contamination. To the generated data set we fit a chirp-like model using the sequential method we propose later in this paper. The fitted chirp-like signal is plotted overlapping the synthesised chirp signal in Fig. 1.

Fig. 1

Synthesised chirp signal using model equation (4) and fitted chirp-like signal

Clearly, the above graphical representation of two signals running together reveals that a chirp-like signal is able to clone a chirp signal quite effectively. We consider a more general case as well, where we generate data from a chirp model with more than one component. We sample data from a chirp model with three components for illustration. The mathematical descriptions of this models is given below.

$$\begin{aligned} y(t)&= 4 \cos (0.05 t + 0.005 t^2) + 4 \sin (0.05 t + 0.005 t^2) + 3 \cos (0.01 t + 0.001 t^2) \nonumber \\&\quad +\, 3 \sin (0.01 t + 0.001 t^2) + 2 \cos (0.15 t + 0.0045 t^2) \nonumber \\&\quad +\, 2 \sin (0.15 t + 0.0045 t^2);\ t = 1, \ldots , 50. \end{aligned}$$

(5)

As before, we generate data from this model without any noise and a chirp-like model is fitted to the simulated data. The estimated fitting along with the synthesised signal simulated from model (5) are plotted in Fig. 2. It is evident from these figures that a chirp-like model can replace a chirp model accurately. In the later sections, we will also see that using a chirp-like model is computationally more efficient than fitting a chirp model to an observed set of data. This icentivizes the use of chirp-like model instead of a chirp model in practice.

Fig. 2

Synthesised chirp signal using model equation (5) and fitted chirp-like signal

3 Periodogram Type-Estimators and Their Properties

Periodogram is one conventional approach to estimate the frequencies of a sinusoidal model. A periodogram function is mathematically expressed as follows:

$$\begin{aligned} I_1(\alpha ) = \frac{1}{N}\bigg |\sum _{t=1}^{N} y(t) e^{-i\alpha t}\bigg |^2. \end{aligned}$$

(6)

The estimators of the frequencies can be obtained by maximising this periodogram function. It has been observed that asymptotically the periodogram function has local maximums at the true frequencies (see Nandi and Kundu [14]). Therefore, the periodogram estimators of frequencies of a p component sinusoidal model are simply the p largest peaks of this periodogram function. To illustrate this, we consider a two-component chirp-like model defined as follows:

$$\begin{aligned} \begin{aligned} y(t) =&4 \cos (2.5 t) + 4 \sin (2.5 t) + 2 \cos (1.5 t) + 2 \sin (1.5 t) + 4 \cos (0.001 t^2) \\&+ 4 \sin (0.001 t^2) + 2 \cos (0.005 t^2) + 2 \sin (0.005 t^2) + X(t). \end{aligned}\end{aligned}$$

(7)

Here X(t)s are i.i.d. normal random variables with mean 0 and variance 0.1. In Fig. 3, the periodogram function of the simulated signal y(t) is shown. In this case, the frequency estimates are the locations of the two prominent peaks of the periodogram function, that clearly are the argument maximisers of $I_1(\alpha )$.

Fig. 3

Periodogram plot of the signal generated using model (7)

In this paper, we consider the approximate least squares estimators (ALSEs) of the unknown parameters of the underlying model. The ALSEs of the frequencies are obtained by maximising the usual periodogram function as defined in (6) continuously over the interval $[0,\pi ]$. To find the ALSEs of the chirp rates, we define a periodogram-type function as follows:

$$\begin{aligned} I_2(\beta ) = \frac{1}{N}\bigg |\sum _{t=1}^{N} y(t) e^{-i\beta t^2}\bigg |^2 \end{aligned}$$

(8)

The Fig. 4 shows the plot of a periodogram-type function of the simulated signal (7). Although one can see sharp peaks around the true values of the chirp rates of the synthesised signal, it is important to note that there are several local maxima present in this plot. And this problems gets even worse for large number of components in the model.

Fig. 4

A magnified view of the plot of periodogram-type function (8) of the signal generated using model (7)

Once the non-linear parameter estimates are found, the linear parameters estimates can be worked out using simple linear regression techniques. Unfortunately the periodogram-type surface is not smooth and has several local maxima. Therefore, numerical methods have to be employed to find the proposed estimators and the performance of these methods depends heavily on the choice of initial values. To find the initial values, traditionally a fine grid search is carried out. For the frequencies, the usual way is to search the periodogram function over the Fourier frequencies $\displaystyle {\frac{\pi j}{N}}$, $j = 1, \ldots , N-1$. Analogous to the Fourier grid, the periodogram-type function is evaluated at $\displaystyle {\frac{\pi k}{N^2}}$, $k = 1, \ldots , N^2-1$.

The problem of estimating the non-linear parameters is more complex for large number of components in the model. We propose a sequential algorithm for this estimation problem in the next section. The proposed method is computationally modest and has optimal statistical properties. We derive large-sample properties of these estimators as well as perform numerical studies to examine their performance in the subsequent sections.

4 Sequential Algorithm to Find Periodogram-Type Estimators

In this section, we put forward a sequential method to estimate the parameters of a chirp-like model assuming we know the number of components, p and q. We will come back to the matter of choosing p and q later. It is important to note that the proposed algorithm is justified by the fact that different sinusoids are asymptotically orthogonal for any set of distinct frequencies and the same result hold for different chirp components for distinct chirp rates. The orthogonality of these components is a direct result of Lemma 1 and Lemma 2 in “Appendix A”. Also, from Lemma 3, it can be seen that the sinusoids and chirplets are orthogonal to each other. Exploiting this special structure of the regressors present in the model, we lower the computational load involved in calculating the least squares estimators (LSEs) to a great extent, but get the same efficiency as that of LSEs.

In the proposed algorithm, assuming that we have p sinusoids and q chirp components, we first estimate the first sinusoid component from the observed or simulated data. At the next step, we eliminate the effect of the estimated sinusoid, and obtain a new data: $y(t) - {\hat{A}}_1 \cos ({\hat{\alpha }}_1 t) - {\hat{B}}_1 \sin ({\hat{\alpha }}_1 t)$. Using this new data, we estimate the first chirplet. We alternately fit a sinusoid component and a chirp component to the data and continue to do so until all the p sinusoids and q chirp components are estimated. The sequential algorithm is presented in detail below. All the three cases: $p = q$, $p <q$ and $p> q$ are considered, while explaining the method. We also investigate the properties of the sequential estimators in this section and examine their numerical performance in the subsequent sections. These properties are derived under the following assumptions:

Assumption 1

Let Z be the set of integers. $\{X(t)\}$ is a stationary linear process of the form:

$$\begin{aligned} X(t) = \sum _{j = -\infty }^{\infty } a(j)e(t-j), \end{aligned}$$

(9)

where $\{e(t); t \in Z\}$ is a sequence of independently and identically distributed (i.i.d.) random variables with $E(e(t)) = 0$, $V(e(t)) = \sigma ^2$, and a(j)s are real constants such that

$$\begin{aligned} \sum \limits _{j= - \infty }^{\infty }|a(j)| < \infty . \end{aligned}$$

(10)

Assumption 2

The true parameters $0< \alpha _1^0, \ldots , \alpha _p^0, \beta _1^0, \ldots , \beta _q^0 < \pi$. The frequencies $\alpha _{j}^0s$ are distinct for $j = 1, \ldots p$ and so are the frequency rates $\beta _{k}^0s$ for $k = 1, \cdots q$.

Assumption 3

The amplitudes, $A_j^0$s and $B_j^0$s satisfy the following relationship:

$$\begin{aligned} \infty> {A_{1}^{0}}^2 + {B_{1}^{0}}^2> {A_{2}^{0}}^2 + {B_{2}^{0}}^2> \cdots> {A_{p}^{0}}^2 + {B_{p}^{0}}^2 > 0. \end{aligned}$$

Similarly, $C_k^0$s and $D_k^0$s satisfy the following relationship:

$$\begin{aligned} \infty> {C_{1}^{0}}^2 + {D_{1}^{0}}^2> {C_{2}^{0}}^2 + {D_{2}^{0}}^2> \cdots> {C_{q}^{0}}^2 + {D_{q}^{0}}^2 > 0. \end{aligned}$$

The following theorems provide the statistical properties of the proposed sequential ALSEs. We observe that under the assumption of stationary errors these estimators are strongly consistent as well as asymptotically normally distributed. Additionally, the derived asymptotic distribution of the sequential ALSEs coincides with that of the LSEs. Thus, with Algorithm 1 we obtain computational efficiency without any compromise on the statistical properties as they remain optimal.

Theorem 1

If Assumptions 1, 2and 3are satisfied, the following are true:

• (a)
  $$\begin{aligned} ({\hat{A}}_j, {\hat{B}}_j, {\hat{\alpha }}_j) \xrightarrow {a.s.} (A_j^0, B_j^0, \alpha _j^0) \text{ as } N \rightarrow \infty , \text{ for } \text{ all } j = 1, \cdots , p, \end{aligned}$$
• (b)
  $$\begin{aligned} ({\hat{C}}_k, {\hat{D}}_k, {\hat{\beta }}_k) \xrightarrow {a.s.} (C_k^0, D_k^0, \beta _k^0) \text{ as } N \rightarrow \infty , \text{ for } \text{ all } k = 1, \cdots , q. \end{aligned}$$

Proof

See “Appendix  B”. $\square$

Theorem 2

If Assumptions 1, 2and 3are true, then the following are true:

• (a)
  $$\begin{aligned} {\hat{A}}_{p+k} \xrightarrow {a.s.} 0, \quad {\hat{B}}_{p+k} \xrightarrow {a.s.} 0 \text { for } k = 1,2, \ldots , \text { as } N \rightarrow \infty , \end{aligned}$$
• (b)
  $$\begin{aligned} {\hat{C}}_{q+k} \xrightarrow {a.s.} 0, \quad {\hat{D}}_{q+k} \xrightarrow {a.s.} 0 \text { for } k = 1,2, \ldots , \text { as } N \rightarrow \infty . \end{aligned}$$

Proof

See “Appendix  B”. $\square$

Theorem 3

If Assumptions 1, 2and 3are satisfied and presuming Conjecture 1holds true, then for all $j = 1, \ldots , p$ and $k = 1, \ldots , q$:

• (a)
  $$\begin{aligned} (({\hat{A}}_j - A_j^0), ({\hat{B}}_j - B_j^0), ({\hat{\alpha }}_j - \alpha _j^0)) {\mathbf{D} }_1^{-1} \xrightarrow {d} {\mathcal {N}}_3(0, c \sigma ^2 {\varvec{\varSigma }^{(1)}_j}^{-1}) \text{ as } N \rightarrow \infty , \end{aligned}$$
• (b)
  $$\begin{aligned} (({\hat{C}}_k - C_k^0), ({\hat{D}}_k - D_k^0), ({\hat{\beta }}_k - \beta _k^0))\mathbf{D }_2^{-1} \xrightarrow {d} {\mathcal {N}}_3(0, c \sigma ^2 {\varvec{\varSigma }^{(2)}_k}^{-1}) \text{ as } N \rightarrow \infty . \end{aligned}$$

with $\varvec{\varSigma }^{(1)}_j = \left( {\begin{array}{*{20}l} \frac{1}{2} &{} 0 &{} \frac{B_j^0}{4} \\ 0 &{} \frac{1}{2} &{} \frac{-A_j^0}{4} \\ \frac{B_j^0}{4} &{} \frac{-A_j^0}{4} &{} \frac{{A_j^0}^2 + {B_j^0}^2}{6} \end{array} } \right) ,\ j = 1, \ldots , p$ and $\varvec{\varSigma }^{(2)}_k = \left( {\begin{array}{*{20}l} \frac{1}{2} &{} 0 &{} \frac{D_k^0}{6} \\ 0 &{} \frac{1}{2} &{} \frac{-C_k^0}{6} \\ \frac{D_k^0}{6} &{} \frac{-C_k^0}{6} &{} \frac{{C_k^0}^2 + {D_k^0}^2}{10} \end{array} } \right) ,\ k = 1, \ldots , q.$ Also, $\mathbf{D }_1 = diag(\frac{1}{\sqrt{N}}, \frac{1}{\sqrt{N}}, \frac{1}{N\sqrt{N}})$, $\mathbf{D }_2 = diag(\frac{1}{\sqrt{N}}, \frac{1}{\sqrt{N}}, \frac{1}{N^2\sqrt{N}})$ and $c = \sum \limits _{j=-\infty }^{\infty }a(j)^2$.

Proof

See “Appendix C”. $\square$

In order to compare the theoretical results with those obtained for the chirp model parameter estimates, we consider a one-component chirp model and a chirp-like model with the following mathematical expresssions:

$$\begin{aligned}&A^0 \cos (\alpha ^0 t + \beta ^0 t^2) + B^0 \sin (\alpha ^0 t + \beta ^0 t^2) + X(t), \text{ and } \\&A^0 \cos (\alpha ^0 t) + B^0 \sin (\alpha ^0 t) + A^0 \cos (\beta ^0 t^2) + B^0 \sin (\beta ^0 t^2) + X(t), \end{aligned}$$

respectively. Note that the amplitude parameters of the chirp model and those of the sinusoidal and chirp component of the chirp-like model are set to be equal to make the asymptotic variances of the non-linear parameters comparable. Now from Theorem 3, it can be seen that the asymptotic variance of estimator of the frequency parameter is $\displaystyle {\frac{24 c \sigma ^2}{N^3 ({A^0}^2 + {B^0}^2)}}$ and that of the estimator of the frequency rate parameter is $\displaystyle {\frac{45 c \sigma ^2}{2N^5({A^0}^2 + {B^0}^2)}}$. On the other hand, for the above chirp model, the asymptotic variance of estimator of the frequency parameter is $\displaystyle {\frac{384 c \sigma ^2}{N^3 ({A^0}^2 + {B^0}^2)}}$ and that of the estimator of the frequency rate parameter is $\displaystyle {\frac{360 c \sigma ^2}{2 N^5({A^0}^2 + {B^0}^2)}}$. For these results, one may refer to Lahiri [15]. From here, we can conclude that the the estimators of frequencies of both the models have the same rate of convergence to the true value. The same result holds true for the frequency rate parameter. Moreover, the asymptotic variances of the estimators of both the non-linear parameters of a chirp-like model are much lower than those of the chirp model.

5 Performance Assessment of the Proposed Estimators

In this section, several numerical experiments for various choices of sample size N and standard deviation $\sigma$ are performed. The accuracy of the sequential ALSEs is evaluated for a multiple component chirp model with two sinusoids and twp chirp components. We generate the data using the following model equation:

$$\begin{aligned} \begin{aligned} y(t) =&6 \cos (1.5 t) + 6 \sin (1.5 t) + 6 \cos (0.1 t^2) + 6 \sin (0.1 t^2) \\&+ 4 \cos (t) + 4 \sin (t) + 4 \cos (0.05 t^2) + 4 \sin (0.05 t^2) + X(t);\ t = 1, \ldots , N. \end{aligned}\end{aligned}$$

(11)

Here, X(t) is from an MA(1) process with $\rho = 0.5$, that is,

$$\begin{aligned} X(t) = e(t) + 0.5 e(t-1), \end{aligned}$$

(12)

where

$$\begin{aligned} e(t) \sim {\mathcal {N}}(0, \sigma ^2). \end{aligned}$$

To evaluate the accuracy of the proposed estimators, we simulate the data from the above model for varying sample sizes, that is, $N = 100, 500$ and 1000 and for varying error standard deviation, $\sigma = 0.5$ and 1. For every N and $\sigma$, 1000 realisations are generated and estimates are obtained. For optimisation of the periodogram-type function at each stage of the sequential algorithm as described in Section, Nelder-Mead method is used. The initial values of the frequency and chirp rate are set to the true values for use in the optimisation method. Based on these simulations, we calculate average value of the estimates, their average bias and mean squares error (MSE). In the tables to follow, we summarise these results. The theoretical asymptotic variances (Avar) are also reported as a benchmark for the MSEs.

Table 1 Average (Avg), Bias and MSE of the sequential ALSEs of frequency and chirp rate parameters of model (11) for error standard deviation $\sigma = 0.50$ and for different choices of sample size N

Table 2 Average (Avg), Bias and MSE of the sequential ALSEs of frequency and chirp rate parameters of model (11) for error standard deviation $\sigma = 1.00$ and for different choices of sample size N

Some noteworthy deductions from the table are enumerated below:

• 1. The biases of the estimates are small and therefore the average estimates are close to the true values.

• 2. The MSEs of the estimates are well-matched with the theoretically computed asymptotic variances.

• 3. The performance of the sequential ALSEs becomes better as N is increased.

• 4. Another interesting observation is that the second component parameter estimates have lower biases and MSEs than those of the first component parameter estimates.

It is clear from the results, that the sequential ALSEs are quite accurate. When the sample size is increased, the biases and the MSEs get smaller, thereby validating the consistency property of the proposed estimators. The MSEs match well with the theoretical asymptotic variances and the difference is minimal when N is large. In conclusion as exemplified in Tables 1 and 2 , the simulations indicate that the proposed method yields satisfactory results.

6 Analyses of Real World Signals

In this section, we demonstrate the applicability of chirp-like model to describe some real world signals. We consider segments of observations originating from an EEG signal and a bat signal. The original signals are shown in the Figs. 5 and 6 .

Fig. 5

EEG data: reference and details

Fig. 6

Bat data: reference and details

We first consider the EEG signal segment which has 256 data points. We fit a chirp-like model to this data using the proposed sequential algorithm. For estimating the model order, we use the following form of Bayesian information criterion (BIC):

$$\begin{aligned} BIC[p,q] = N log_e(SS_{Res}[p,q]) + \frac{1}{2} (5p + 7q + arma_{a,b} + 1) log_e(N) \end{aligned}$$

Here, $\text{ SS}_{res}[p,q]$ is the residuals sum of squares when p number of sinusoidal components and q number of chirp components are fitted to the data. This is based on the assumption that the maximum number of sinusoids is P and the maximum number of chirp components present in the model can be Q. Here, we choose $P = Q = 100$. Also, here $arma_{a,b}$ denotes the ARMA model fitted to the residuals with a number of AR parameters and b number of MA parameters. We select $p = 61$ and $q = 3$ corresponding to the minimum value of BIC as the estimate of p and q. In Fig. 7, the plot of fitted values using the selected model along with the original observations is shown. It is evident that the observed signal can be reconstructed using the chirp-like model quite satisfactorily.

Fig. 7

Estimated chirp-like signal along with the observed EEG data

Next using the same algorithm, we fit a chirp-like model to the bat data. An important observation here is that unlike in the previous instance, the BIC does not work well for this data set. However, the fit provided by this model for various p and q, suggests that a chirp-like model can explain the underlying bat signal very well. To illustrate this, in Fig. 8, a chirp-like model fitting using only 2 sinusoidal components, but 100 chirp components is shown. Although the fit looks good for various choices of p and q that we considered, for $q = 100$, the model is able to capture the non-periodic parts of the signal quite effectively.

Fig. 8

Estimated chirp-like signal along with the observed bat data

We can conclude from here that the chirp-like model is able to represent the two data sets reasonably well and the proposed sequential algorithm works well in providing the model fits. However, since the BIC does not always work and can be data driven, a major challenge is to find an appropriate model selection criterion. We believe more work is needed in this area.

We also perform residuals analyses for both the data sets, to test for stationarity assumptions that we make in this paper. We use the traditional tests, namely Augmented Dickey Fuller (ADF) test (Fuller [16] and Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test (Kwiatkowski et al. [17]) for this purpose. The ADF test tests the null hypothesis $H_0:$ a unit root is present in the time series against the alternative $H_1:$ that the series is stationary. And the KPSS test tests the null hypothesis $H_0:$ the series is stationary against the alternative $H_1:$ a unit root is present in the series. We use in-built functions “adf.test” and “kpss.test” in “tseries” package in R software. For both the data sets, the ADF test rejects the null hypothesis and the KPSS test does not reject the null hypothesis. Hence, we may conclude that the residuals are stationary. The residual plots are shown in Figs. 9 and 10 . We also use the inbuilt function “auto.arima” in the “forecast” package in R to find the order of the ARMA process of the residuals. This function selects ARMA(2,2) process for the residuals of the EEG data and ARMA(0,0) process for the residuals of the bat data.

Fig. 9

Residuals plot of the EEG signal

Fig. 10

Residuals plot of the bat signal

7 Conclusion

We have proposed periodogram-type estimators for the parameter estimation of a chirp-like model. These are also called ALSEs as it can be shown that for large sample sizes, the least squares function is equivalent to the periodogram-type function. Theoretically, we derive the large-sample properties of these estimators and we show that they are strongly consistent and asymptotically normally distributed under the assumption of stationary errors. If the noise is white and has normal distribution, the proposed estimators achieve the corresponding CRLBs. Extensive simulation results corroborate our theory and also indicate accuracy of the ALSEs in terms of biases and MSEs. Another main contribution of the paper has been the data analyses of real world signals from different application domains. The analyses of these signals is not only to assess the performance of the proposed estimators but also to gain a new and deeper insight into the behavior of a chirp-like model and how it can be a practical alternative over a chirp model.

Appendices

Appendices

Preliminary Results

In this section, we provide some number theory results and conjectures. These are necessary preliminary for the development of the analytical properties of the proposed sequential estimators.

Lemma 1

If $\phi \in (0, \pi )$, then the following hold true:

• (a) $\lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{t=1}^{N}\cos (\phi t) = \lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{t=1}^{N}\sin (\phi t) = 0.$

• (b) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \cos ^2(\phi t) = \lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \sin ^2(\phi t) = \frac{1}{2(k+1)};\ k = 0, 1, 2, \cdots .$

• (c) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \sin (\phi t) \cos (\phi t) = 0;\ k = 0, 1, 2, \cdots .$

Proof

Refer to Kundu and Nandi [14]. $\square$

Lemma 2

If $\phi \in (0, \pi )$, then except for a countable number of points, the following hold true:

• (a) $\lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{t=1}^{N}\cos (\phi t^2) = \lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{t=1}^{N}\sin (\phi t^2) = 0.$

• (b) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \cos ^2(\phi t^2) = \lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \sin ^2(\phi t^2) = \frac{1}{2(k+1)};\ k = 0, 1, 2, \cdots .$

• (c) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N}t^{k} \sin (\phi t^2) \cos (\phi t^2) = 0;\ k = 0, 1, 2, \ldots .$

Proof

Refer to Lahiri [15]. $\square$

Lemma 3

If $(\phi _1, \phi _2) \in (0, \pi ) \times (0, \pi )$, then except for a countable number of points, the following hold true:

• (a) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\cos (\phi _2 t^2) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\sin (\phi _2 t^2) = 0$

• (b) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\cos (\phi _2 t^2) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\sin (\phi _2 t^2) = 0$

$k = 0, 1, 2, \cdots$

Proof

This proof follows from the number theoretic result proved by Lahiri [15] (see Lemma 2.2.1 of the reference). $\square$

Lemma 4

If X(t) satisfies Assumptions 1, 2and3, then for $k \geqslant 0$:

(a) $\sup \limits _{\phi } \bigg |\frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k X(t)e^{i(\phi t)}\bigg | \xrightarrow {a.s.} 0$            (b) $\sup \limits _{\phi } \bigg |\frac{1}{N^{k+1}} \sum \limits _{t=1}^{N} t^k X(t)e^{i(\phi t^2)}\bigg | \xrightarrow {a.s.} 0$

Proof

These can be obtained as particular cases of Lemma 2.2.2 of Lahiri [15]. $\square$

The following conjecture is derivative of the famous number theory conjecture of Montgomery [18]. One may refer to Lahiri [15] for details. Although these conjectures have not been proved theoretically, extensive numerical simulations indicate their validity.

Conjecture 1

If $(\phi _1, \phi _2) \in (0, \pi ) \times (0, \pi )$, then except for a countable number of points, the following hold true:

• (a) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t^2) = \lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t^2) = 0$

• (b) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\cos (\phi _2 t) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\sin (\phi _2 t) = 0$

• (c) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\sin (\phi _2 t) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\cos (\phi _2 t^2) = 0$

• (d) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k\sqrt{N}} \sum \limits _{t=1}^{N} t^k \cos (\phi _1 t)\sin (\phi _2 t^2) =$ $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k \sqrt{N}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\cos (\phi _2 t^2) = 0$

• (e) $\lim \limits _{N \rightarrow \infty } \frac{1}{N^k \sqrt{N}} \sum \limits _{t=1}^{N} t^k \sin (\phi _1 t)\sin (\phi _2 t^2) = 0\quad k = 0, 1, 2, \ldots$

.

Consistency of the Sequential ALSEs

To prove the consistency of the sequential ALSEs of the non-linear parameters, we need the following two lemmas:

Lemma 5

Consider the set $S_{c_1}^{(j)} = \{\alpha _j: |\alpha _j - \alpha _j^0| > c_1\}$; $j = 1, \ldots , p$. If for any $c_1 > 0$, the following holds true:

$$\begin{aligned} \limsup \sup \limits _{S_{c_1}^{(1)}} \frac{1}{N} (I_{2j-1}(\alpha _j) - I_{2j-1}(\alpha _j^0)) < 0 \text{ a.s., } \end{aligned}$$

(13)

then ${\hat{\alpha }}_j \xrightarrow {a.s.} \alpha _j^0$ as $N \rightarrow \infty$. Note that $I_{2j-1}(\alpha _j)$ can be obtained by replacing y(t) by $y_{2j-1}(t)$ and $\alpha$ by $\alpha _j$ in Eq. (6).

Proof

This proof follows along the same lines as the proof of Lemma 2A.2 in Grover [19]. $\square$

Lemma 6

Consider the set $S_{c_2}^{(k)} = \{\beta _k: |\beta _k - \beta _k^0| > c_2\}$; $k = 1, \ldots , q$. If for any $c_2 > 0$, the following holds true:

$$\begin{aligned} \limsup \sup \limits _{S_{c_2}^{(1)}} \frac{1}{N} (I_{2k}(\beta _k) - I_{2k}(\beta _k^0)) < 0 \text{ a.s., } \end{aligned}$$

then ${\hat{\beta }}_k \xrightarrow {a.s.} \beta _k^0$ as $N \rightarrow \infty$. Note that $I_{2k}(\beta _k)$ can be obtained by replacing y(t) by $y_{2k}(t)$ and $\beta$ by $\beta _k$ in Eq. (8).

Proof

This proof follows along the same lines as the proof of Lemma 2A.2 in Grover [19]. $\square$

Proof of Theorem 1

Here again, for convenience of notation, we assume $p = 2$ and $q = 2$. Now we first prove the consistency of the non-linear parameter ${\hat{\alpha }}_1$. For that we consider the following difference:

$$\begin{aligned}\begin{aligned}&\frac{1}{N} [I_1(\alpha _1) - I_1(\alpha _1^0)] \\&\quad = \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_1(t)\cos (\alpha _1 t)\bigg \}^2 + \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_1(t) \sin (\alpha _1 t)\bigg \}^2 \\&\qquad - \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_1(t)\cos (\alpha _1^0 t)\bigg \}^2- \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_1(t) \sin (\alpha _1^0 t)\bigg \}^2 \\ \end{aligned}\end{aligned}$$

where $y_1(t) = y(t) = \mu (t,\varvec{\theta })$¹$+ X(t)$, the original data.

Using lemmas 1, 2, 3 and 4 , we get:

$$\begin{aligned}&\limsup \sup _{S_{c_1}^{(1)}} \frac{1}{N}[I_1(\alpha _1) - I_1(\alpha _1^0)] = \limsup \sup _{|\alpha _1 - \alpha _1^0|> c} \frac{1}{N}[I_1(\alpha _1) - I_1(\alpha _1^0)] \\&\quad = -\frac{{A_1^0}^2}{4} - \frac{{B_1^0}^2}{4} \end{aligned}$$

From Lemma 5, it follows that:

$$\begin{aligned} {\hat{\alpha }}_1 \xrightarrow {a.s.} \alpha _1^0 \text{ as } N \rightarrow \infty . \end{aligned}$$

Let us recall that the linear parameter estimators of the first sinusoid are given by:

$$\begin{aligned} {\hat{A}}_1 = \frac{2}{N} \sum _{t=1}^{N} y(t) \cos (\hat{\alpha _1} t) \qquad {\hat{B}}_1 = \frac{2}{N} \sum _{t=1}^{N} y(t) \sin (\hat{\alpha _1} t) \end{aligned}$$

To prove the consistency of the estimators of the linear parameters, $A_1^0$ and $B_1^0$, we need the following lemma:

Lemma 7

If ${\hat{\alpha }}_1$ is the sequential ALSE of ${\hat{\alpha }}_1^0$ then

$$\begin{aligned} \begin{aligned} N({\hat{\alpha }}_1 - \alpha _1^0) \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

(14)

Proof

Let us denote $I_1^{\prime }(\alpha _1)$ and $I_1^{\prime \prime }(\alpha _1)$ as the first and second derivatives of the periodogram function $I_1(\alpha _1)$. Consider the Taylor series expansion of the function $I_1^{\prime }({\hat{\alpha }}_1)$ around the point $\alpha _1^0$ as follows:

$$\begin{aligned} I_1^{\prime }({\hat{\alpha }}_1) - I_1^{\prime }(\alpha _1^0) = ({\hat{\alpha }}_1 - \alpha _1^0) I_1^{\prime \prime }({\bar{\alpha }}_1) \end{aligned}$$

(15)

where ${\bar{\alpha }}_1$ is a point between ${\hat{\alpha }}_1$ and $\alpha _1^0$. Since ${\hat{\alpha }}_1$ is the argument maximiser of the function $I_1(\alpha _1)$, it implies that $I_1^{\prime }({\hat{\alpha }}_1) = 0$. Therefore, (15) can be rewritten as follows:

$$\begin{aligned}\begin{aligned}&- I_1^{\prime }(\alpha _1^0) = ({\hat{\alpha }}_1 - \alpha _1^0) I_1^{\prime \prime }({\bar{\alpha }}_1) \\&\quad \Rightarrow ({\hat{\alpha }}_1 - \alpha _1^0) = - I_1^{\prime }(\alpha _1^0)[I_1^{\prime \prime }({\bar{\alpha }}_1)]^{-1} \\&\quad \Rightarrow N({\hat{\alpha }}_1 - \alpha _1^0) = - \frac{1}{N^2}I_1^{\prime }(\alpha _1^0)[\frac{1}{N^3}I_1^{\prime \prime }({\bar{\alpha }}_1)]^{-1} \end{aligned} \end{aligned}$$

Now using simple calculations and number theory results 1, 2 and 3 , one can show that:

$$\begin{aligned}&\frac{1}{N^2}I_1^{\prime }(\alpha _1^0) \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty , \text{ and } \\&\quad \lim _{N \rightarrow \infty }\frac{1}{N^3}I_1^{\prime \prime }({\bar{\alpha }}_1) = \lim _{N \rightarrow \infty }\frac{1}{N^3}I_1^{\prime \prime }(\alpha _1^0) = \frac{-({A_1^0}^2 + {B_1^0}^2)}{24} \text{ as } N \rightarrow \infty . \\ \end{aligned}$$

Combining the above three equations, we have the desired result. $\square$

Now, let us consider ALSE ${\hat{A}}_1$ of $A_1^0$. Using Taylor series expansion, we expand $\cos ({\hat{\alpha }}_1 t)$ around the point $\alpha _1^0$ and get:

$$\begin{aligned}\begin{aligned} {\hat{A}}_1&= \frac{2}{N} \sum _{t=1}^{N} y(t) \cos ({\hat{\alpha }}_1 t) \\&= \frac{2}{N}\sum _{t=1}^{N}\bigg \{\mu (t, \varvec{\theta }) + X(t)\bigg \} \\&\quad \times \bigg \{\cos (\alpha _1^0 t) - t({\hat{\alpha }}_1 - \alpha _1^0) \sin ({\bar{\alpha }}_1 t) \bigg \} \xrightarrow {a.s.} A_1^0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

The convergence in the last step follows on using the results from the preliminary number theory results (see lemmas 1, 2, 3 and 4 ) and Lemma 7.

One can show the consistency of ${\hat{B}}_1$ in the same manner as we proved for ${\hat{A}}_1$. Next, we show the strong consistency of the estimator ${\hat{\beta }}_1$. For that we consider the difference:

$$\begin{aligned}\begin{aligned}&\frac{1}{N} [I_2(\beta _1) - I_2(\beta _1^0)] \\&\quad = \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_2(t)\cos (\beta _1 t^2)\bigg \}^2 + \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_2(t) \sin (\beta _1 t^2)\bigg \}^2 \\&\qquad - \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_2(t)\cos (\beta _1^0 t^2)\bigg \}^2 - \frac{1}{N^2}\bigg \{\sum _{t=1}^{N}y_2(t) \sin (\beta _1^0 t)\bigg \}^2 \\ \end{aligned}\end{aligned}$$

where $y_2(t) = y_1(t) - {\hat{A}}_1 \cos ({\hat{\alpha }}_1 t) - {\hat{B}}_1 \sin ({\hat{\alpha }}_1 t)$. On using lemmas 1, 2, 3 and 4 , we have:

$$\begin{aligned} \limsup \sup _{|\beta _1 - \beta _1^0|> c} \frac{1}{N}[I_2(\beta _1) - I_2(\beta _1^0)] \\ = -\frac{{C_1^0}^2}{4} - \frac{{B_1^0}^2}{4} < 0 \text{ a.s. } \end{aligned}$$

Therefore, ${\hat{\beta }}_1 \xrightarrow {a.s.} \beta _1^0$ as $N \rightarrow \infty$. This follows from Lemma 6.

To prove the consistency of linear parameter estimators of the first chirp component, that is, ${\hat{C}}_1$ and ${\hat{D}}_1$, we need the following lemma

Lemma 8

If ${\hat{\beta }}_1$ is the sequential ALSE of $\beta _1^0$, then

$$\begin{aligned} \begin{aligned} N^2({\hat{\beta }}_1 - \beta _1^0) \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

(16)

Proof

The proof of this lemma follows along the same lines as that of Lemma 7. $\square$

The consistency of linear parameter estimators ${\hat{C}}_1$ and ${\hat{D}}_1$ can now be shown along the same lines as that of ${\hat{A}}_1$ above.

Following the above proof, one can easily show the strong consistency of the second sinusoid component and chirp component parameter estimates. Moreover, the results can be extended for any p and q in general. $\square$

Proof of Theorem 2

Let us first consider the ALSE ${\hat{A}}_{p+1}$ of the linear parameter $A_{p+1}^0$:

$$\begin{aligned} \begin{aligned} {\hat{A}}_{p+1} = \frac{2}{N}\sum _{t=1}^{N} y_{p+q+1}(t) \cos ({\hat{\alpha }}_{p+1} t) \end{aligned}\end{aligned}$$

(17)

Now $y_{p+q+1}(t)$ is the data obtained by eliminating the effect of first p sinusoids and first q chirp components from the original data. It means that

$$\begin{aligned} \begin{aligned} y_{p+q+1}(t)&= y_{1}(t) - \sum _{j=1}^{p}\{{\hat{A}}_j \cos ({\hat{\alpha }}_j t) + {\hat{B}}_j \sin ({\hat{\alpha }}_j t)\} \\&\quad - \sum _{k=1}^{q}\{{\hat{C}}_k \cos ({\hat{\beta }}_k t^2) + {\hat{D}}_k \sin ({\hat{\beta }}_k t^2)\} \\&= X(t) + o(1), \text{ using } \text{ the } \text{ results } \text{ derived } \text{ in } \text{ the } \text{ proof } \text{ of } \text{ Theorem } \text{1 }. \end{aligned} \end{aligned}$$

(18)

Using the above equation, we get:

$$\begin{aligned} \begin{aligned} {\hat{A}}_{p+1}&= \frac{2}{N}\sum _{t=1}^{N} (X(t) + o(1)) \cos ({\hat{\alpha }}_{p+1} t) = \frac{2}{N}\sum _{t=1}^{n} X(t) \cos ({\hat{\alpha }}_{p+1} t) + o(1) \\&\xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

(19)

This follows from Lemma 4. Similarly, we have the following result:

$$\begin{aligned} \begin{aligned} {\hat{B}}_{p+1}&= \frac{2}{N}\sum _{t=1}^{N} y_{p+q+1}(t) \sin ({\hat{\alpha }}_{p+1} t) = \frac{2}{N}\sum _{t=1}^{N} (X(t) + o(1)) \sin ({\hat{\alpha }}_{p+1} t) \\&= \frac{2}{N}\sum _{t=1}^{n} X(t) \sin ({\hat{\alpha }}_{p+1} t) + o(1) \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}\end{aligned}$$

(20)

Analogously one can show that in case of overestimation the sequential ALSEs of the amplitudes of the chirp component converge to 0 as well, that is,

$$\begin{aligned} {\hat{C}}_{q+1} \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty \text{ and } {\hat{D}}_{q+1} \xrightarrow {a.s.} 0 \text{ as } N \rightarrow \infty . \end{aligned}$$

Hence, the result. $\square$

Asymptotic Distribution of the Sequential ALSEs

Proof of Theorem 3

To prove this, theorem we will show asymptotic equivalence between the proposed sequential ALSEs and the sequential LSEs (see Grover [19]). For ease of notation, we assume $p = q = 2$ here, however the result can be extended for any p and q. First consider:

$$\begin{aligned}\begin{aligned}&\frac{1}{N} Q_1(\alpha _1) = \frac{1}{N} \sum _{t=1}^{N} \bigg ( y(t) - A_1 \cos (\alpha _1 t) - B_1 \sin (\alpha _1 t)\bigg )^2 \\&\quad = \frac{1}{N} \sum _{t=1}^{N} y^2(t) - \frac{2}{N} y(t) \bigg \{A_1 \cos (\alpha _1 t) + B_1 \sin (\alpha _1 t)\bigg \} \\&\qquad + \frac{1}{N}\sum _{t=1}^{N} \bigg \{A_1 \cos (\alpha _1 t) + B_1 \sin (\alpha _1 t)\bigg \}^2 \\&\quad = \frac{1}{N} \sum _{t=1}^{N} y^2(t) - \frac{1}{N} J_1(A_1, B_1, \alpha _1) + o(1) \end{aligned}\end{aligned}$$

where,

$$\begin{aligned} \frac{1}{N}J_1(A_1, B_1, \alpha _1) = \frac{2}{N} \sum _{t=1}^{N}y(t) \bigg \{A_1 \cos (\alpha _1 t) + B_1 \sin (\alpha _1 t)\bigg \} - \frac{{A_1}^2 + {B_1}^2}{2} \end{aligned}$$

At $A_1 = {\hat{A}}_1$ and $B_1 = {\hat{B}}_1$, one can show that:

$$\begin{aligned} J_1({\hat{A}}_1, {\hat{B}}_1, \alpha _1) = I_1(\alpha _1) \end{aligned}$$

Therefore, the estimator of $(A_1^0, B_1^0, \alpha _1^0)$ that maximises $J_1(A_1, B_1, \alpha _1)$ is equivalent to the sequential ALSE of $({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1)$. Now expanding ${\mathbf{J }}^{\prime }_1({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1)$ around the point $(A_1^0, B_1^0, \alpha _1^0)$, we have:

$$\begin{aligned}\begin{aligned}&\mathbf{J }^{\prime }_1({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1) - \mathbf{J }^{\prime }_1(A_1^0, B_1^0, \alpha _1^0) = ({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1) - (A_1^0, B_1^0, \alpha _1^0)[\mathbf{J }^{\prime }_1({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1)]^{-1}\\&\quad \Rightarrow - \mathbf{J }^{\prime }_1(A_1^0, B_1^0, \alpha _1^0)[\mathbf{J }^{\prime \prime }_1({\bar{A}}_1, {\bar{B}}_1, {\bar{\alpha }}_1)]^{-1} = ({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1) - (A_1^0, B_1^0, \alpha _1^0) \end{aligned}\end{aligned}$$

Now we compute the elements of first derivative vector $\mathbf{J }^{\prime }_1(A_1^0, B_1^0, \alpha _1^0)$ and using the preliminary lemmas 1, 2 and 3 and the Conjecture 1, we obtain:

$$\begin{aligned}&\begin{aligned} \frac{\partial J_1(A_1^0, B_1^0, \alpha _1^0)}{\partial A_1} = \frac{2}{N} \sum _{t=1}^{N} y(t) \cos (\alpha _1^0 t) - A_1^0 = \frac{2}{N} \sum _{t=1}^{N} X(t) \cos (\alpha _1^0 t) + o(\frac{1}{\sqrt{N}}) \end{aligned}\\&\begin{aligned} \text{ Similarly, } \frac{1}{N}\frac{\partial J_1(A_1^0, B_1^0, \alpha _1^0)}{\partial B_1} = \frac{2}{N} \sum _{t=1}^{N} X(t) \sin (\alpha _1^0 t) + o(\frac{1}{\sqrt{N}})\\ \end{aligned} \end{aligned}$$

Also,

$$\begin{aligned}\begin{aligned} \frac{1}{N}\frac{\partial J_1(A_1^0, B_1^0, \alpha _1^0)}{\partial B_1} = \frac{2}{N} \sum _{t=1}^{N} t X(t) \bigg \{-A_1^0 \sin (\alpha _1^0 t) + B_1^0 \cos (\alpha _1^0 t)\bigg \} + o(\sqrt{N})\\ \end{aligned} \end{aligned}$$

From the above three equations, it is easy to see that:

$$\begin{aligned} \begin{aligned}&\mathbf{Q }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0) = -\mathbf{J }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0) + \left[ {\begin{array}{*{20}l} o(\sqrt{N})&o(\sqrt{N})&o(N\sqrt{N}) \end{array} } \right] \\&\quad \Rightarrow \mathbf{Q }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 = -\mathbf{J }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 + \left[ {\begin{array}{*{20}l} o(1)&o(1)&o(1) \end{array} } \right] \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \lim _{N \rightarrow \infty }\mathbf{Q }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 = - \lim _{N \rightarrow \infty }\mathbf{J }_1^{\prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 \end{aligned}$$

Similarly, on computing the elements of the second derivative matrix, it can be shown that

$$\begin{aligned} \lim _{N \rightarrow \infty }\mathbf{D }_1\mathbf{Q }_1^{\prime \prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 = -\lim _{N \rightarrow \infty }\mathbf{D }_1\mathbf{J }_1^{\prime \prime }(A_1^0, B_1^0, \alpha _1^0)\mathbf{D }_1 \end{aligned}$$

On combining these results, we get the asymptotic equivalence between the sequential ALSE $({\hat{A}}_1, {\hat{B}}_1, {\hat{\alpha }}_1)$ and $({\hat{A}}_{1 LSE}, {\hat{B}}_{1 LSE}, {\hat{\alpha }}_{1 LSE})$. It has been proved in Grover [19] that the sequential LSEs have the same asymptotic distribution as the LSEs of the parameters of a chirp-like model. This implies that $(({\hat{A}}_1 - A_1^0), ({\hat{B}}_1 - B_1^0), ({\hat{\alpha }}_1 - \alpha _1^0)) \mathbf{D }_1^{-1} \xrightarrow {d} {\mathcal {N}}_3(0, c \sigma ^2 {\varvec{\varSigma }^{(1)}_j}^{-1}) \text{ as } N \rightarrow \infty$.

Next to derive the asymptotic distribution of the sequential ALSEs of first chirp component parameters, that is, $({\hat{C}}_1, {\hat{D}}_1, {\hat{\beta }}_1)$, we proceed as before.

$$\begin{aligned} \frac{1}{N}Q_2(C_1, D_1, \beta _1) = \frac{1}{N} \sum _{t=1}^{N}\bigg (y_2(t) - C_1 \cos (\beta _1 t^2) - D_1 \sin (\beta _1 t^2)\bigg )^2. \end{aligned}$$

(21)

Here,

$$\begin{aligned}\begin{aligned}&y_2(t) = y(t) - {\hat{A}}_1 \cos (\alpha _1 t) - {\hat{B}}_1 \sin (\alpha _1 t)\\&\quad = A_2^0 \cos (\alpha _2^0 t) + B_2^0 \sin (\alpha _2^0 t) + \sum _{k=1}^{2}\{C_k^0 \cos (\beta _k^0 t^2) + D_k^0 \sin (\beta _k^0 t^2)\} + o(1) \end{aligned}\end{aligned}$$

Now expanding the right hand side of (21), we get:

$$\begin{aligned}\begin{aligned} \frac{1}{N}Q_2(C_1, D_1, \beta _1) = = \frac{1}{N} \sum _{t=1}^{N}y^2_2(t) - \frac{1}{N}J_2(C_1, D_1, \beta _1) + o(1), \end{aligned}\end{aligned}$$

where

$$\begin{aligned} \frac{1}{N}J_2(C_1, D_1, \beta _1) = \frac{2}{N} \sum _{t=1}^{N} y_2(t) \bigg \{C_1 \cos (\beta _1 t^2) + D_1 \sin (\beta _1 t^2)\bigg \} - \frac{{C_1}^2 + {D_1}^2}{2} \end{aligned}$$

We compute $\frac{1}{N} \mathbf{J }_2^{\prime }(C_1^0, D_1^0, \beta _1^0$ and using Conjecture 1 and lemmas 1, 2 and 3 , we get:

$$\begin{aligned}\begin{aligned}&\frac{1}{N}\frac{\partial J_2(C_1^0, D_1^0, \beta _1^0)}{\partial C_1} = \frac{2}{N} \sum _{t=1}^{N} X(t) \cos (\beta _1^0 t^2) + o(\frac{1}{\sqrt{N}}) \\&\frac{1}{N}\frac{\partial J_2(C_1^0, D_1^0, \beta _1^0)}{\partial D_1} = \frac{2}{N} \sum _{t=1}^{N} X(t) \sin (\beta _1^0 t^2) + o(\frac{1}{\sqrt{N}}) \\&\frac{1}{N}\frac{\partial J_2(C_1^0, D_1^0, \beta _1^0)}{\partial \beta _1} = \frac{2}{N} \sum _{t=1}^{N} t^2 X(t) \{ -C_1^0 \sin (\beta _1^0 t^2) + D_1^0\cos (\beta _1^0 t^2)\} + o({N\sqrt{N}})\\ \end{aligned} \end{aligned}$$

A similar equivalence can now be established between the $\mathbf{Q }_2^{\prime }(C_1^0, D_1^0, \beta _1^0)$ and $\mathbf{J }_2^{\prime }(C_1^0, D_1^0, \beta _1^0)$ and $\mathbf{Q }_2^{\prime \prime }(C_1^0, D_1^0, \beta _1^0)$ and $\mathbf{J }_2^{\prime \prime }(C_1^0, D_1^0, \beta _1^0)$. Procceding exactly the same way as for the first sinusoid estimators, it can be shown that the sequential ALSE $({\hat{C}}_1, {\hat{D}}_1, {\hat{\beta }}_1)$ and the sequential LSE $({\hat{C}}_{1LSE}, {\hat{D}}_{1LSE}, {\hat{\beta }}_{1LSE})$ have the same asymptotic distribution. The asymptotic distribution of the sequential LSE has been derived explicitly by Grover [19] in her thesis. Thus, we have:

$$\begin{aligned} (({\hat{C}}_1 - C_1^0), ({\hat{D}}_1 - D_1^0), ({\hat{\beta }}_1 - \beta _1^0))\mathbf{D }_2^{-1} \xrightarrow {d} {\mathcal {N}}_3(0, c \sigma ^2 {\varvec{\varSigma }^{(2)}_1}^{-1}) \text{ as } N \rightarrow \infty , \end{aligned}$$

the desired result. The result can now be extended for any p and q. $\square$