Spatial locomotion of a metameric earthworm-like robot: generation and analysis of gaits

Abstract

This research aims to advance the current state-of-the-art of earthworm-like robots by extending the gait study from rectilinear and planar locomotion to spatial locomotion. In detail, the following five important but largely unaddressed issues are tackled in this paper, including the multibody kinematic modeling of the robot with spatial locomotion capability, 3D gait generation algorithm, spatial locomotion mode classification, spatial locomotion performance evaluation, and 3D gait planning. Based on the multibody model of the metameric earthworm-like robot and learning from the retrograde peristalsis wave, a gait-generation algorithm is proposed for generating all admissible 3D locomotion gaits. The 3D locomotion can be classified into four major types (rectilinear, sidewinding, circular, and cycloid), and further, ten modes with their defining conditions in terms of the gait parameters being derived. Among them, several spatial locomotion modes, such as the 3D cycloid locomotion, are uncovered for the first time. For each mode, different kinematic indexes, including the average (axial) velocity and the circumradius of the trajectory, are evaluated to comprehensively clarify the relationship between the locomotion performance and the gait parameters. Moreover, aiming at reaching the target both quickly and precisely, 3D gait planning is also studied. With contradictory objectives, the Pareto front is determined via the genetic algorithm so that a trade-off between the proximity and speed to the target can be achieved.

1 Introduction

In the past several decades, there has been a rising demand for locomotion robots that are capable of moving and operating in confined and hazardous spaces, such as navigating in industrial pipelines to clean foreign objects [1], drilling in the seafloor to collect samples [2], and entering in human gastrointestinal tracks to examine and resect lesions [3]. Due to the complex structure and the limited miniaturization capability, conventional wheeled and legged robots often fail to function properly in narrow and vulnerable environments. On the other hand, the crawling robots, by regularly changing their body configurations [4–6], could always move effectively in restricted spaces, without the need for active protruded components (e.g., legs and wheels). As a result, the crawling robots are always simple in structure and small in size, making them become a hotspot of robotic research.

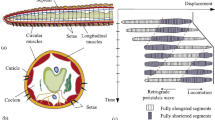
Particularly, the earthworm, due to its extremely soft body and excellent environmental adaptability, has inspired a great number of robot designs [7–9]. Fundamentally, as a locomotion system [10], the earthworm possesses remarkable motion capability originating from its unique morphology characteristics, manifested in three aspects: ($i$) the earthworm’s body is divided into a large number of independently working segments separated by septa (aka “metameric segmentation”) (Fig. 1(a)) [11]; ($ii$) each body segment possesses circular and longitudinal muscles that interact antagonistically to each other, i.e., contraction of the circular muscles will axially elongate and radially contract the body segment, and contraction of the longitudinal muscles will have the opposite effects (Fig. 1(b, c)) [12–15]; (iii) the body segments are equipped with bristle-like setae (Fig. 1(b)) that can stretch out to from temporary anchorage with the environment, thus preventing backward slippage when other segments are moving forward [11]. Based upon these morphological features and with wave-like contraction and relaxation of muscles that propagate backward along the body (aka “the retrograde peristalsis wave” [11, 13]), the earthworm could move effectively in various environments. Note that the retrograde peristalsis wave is the most fundamental mechanism of earthworm locomotion; however, when moving in different media and different safety situations, the earthworm is capable of adjusting its muscular peristalsis wave, manifesting as locomotion gaits, to survive, to adapt to different circumstances, and to move more efficiently [16]. Especially, it has been observed that in addition to rectilinear locomotion, the earthworm could carry out planar and spatial locomotion by bending the body toward one side (Fig. 1(d, e)).

Fig. 1

Morphology characteristics and locomotion capabilities of the earthworm. (a) Schematic illustration of an earthworm. (b) Longitudinal and cross-sections of the earthworm. (c) Axial extension and contraction of the earthworm segment. (d) One-side contraction of the earthworm segment. (e) Rectilinear, planar, and spatial locomotion of the earthworm

Earthworms’ morphological characteristics also provide important guidelines for the design of earthworm-like locomotion robots. For example, many robots are designed to be segmented to mimic the earthworm’s metameric body [2, 9, 17, 18]; each robot segment is equipped with certain actuators to generate antagonistically radial and axial deformations, as the earthworm’s body segment does [2, 9, 17, 18]; the robot segment also possesses active or passive components to acquire anisotropic resistance or anchoring effects for directional locomotion, which reproduces the functions of the earthworm’s setae [19–21]. Such design principles have been implemented for achieving earthworm-like rectilinear locomotion both in pipelines and on the ground. Representative robot prototypes include the origami-based earthworm-like robot actuated by DC motors [22] and magnetic field [23], the mesh-worm actuated by SMA springs [24], and the soft earthworm-like robot actuated by air pressure [25]. In these examples, since the number of robot segments is relatively small and for the purpose of verifying the design rationality, discrete actuation sequences of the robot segments are assigned by roughly mimicking the earthworm’s retrograde peristalsis wave.

In addition to robot design and prototyping, considerable efforts have been devoted to understanding the relationship between the control strategies and the rectilinear locomotion performance. For example, following the mechanism of retrograde peristalsis wave and by establishing the correspondence between binary numbers (‘0’ and ‘1’) and robot segment states (axially-extended and axially-contracted), a generic gait generation algorithm was proposed for a metameric locomotion robot with an arbitrary number of segments [26]. Based on the established multibody kinematic model of the robot, gait optimization was carried out to maximize the average locomotion speed. Moreover, the effects of gaits on anchor slippage were examined both theoretically and experimentally [9], which shows the necessity and importance of considering the dynamics [27, 28] when evaluating the earthworm-like robotic locomotion. Note that a similar gait generation algorithm has also been proposed and implemented in inchworm-like robots [29], and based on the constructed dynamic model [27], gait shift using adaptive control was also demonstrated [30]. From another perspective, without any global prerequisite rules but by optimizing the actuation phases of the robot segments based on symmetry theory, the optimum phase-difference pattern corresponding to the maximum average locomotion speed was identified [31]. Numerical calculations and experiments indicated that the optimized phase-difference pattern could naturally reproduce the peristalsis wave, without global prerequisite wave-like rules. For the continuously deformable earthworm-like robot proposed by Boxerbaum et al., rather than discretely assigning the states of the robot segments, the wave controller [32], stable heteroclinic channel (SHC) controller [33], and neural network controller [34] have been proposed for achieving locomotion, and their effects are evaluated in terms of average locomotion speed and energy efficiency [35]. Although this robot shows obvious continuity in its body, it is still described as a segmented model for examining its locomotion performance.

In nature, the earthworm can also perform planar locomotion, which thus promotes the upgrade from rectilinear locomotion robots to planar locomotion robots. Note that the earthworm achieves turning motion by contracting the longitudinal muscles at one side [12], which indicates the necessity of incorporating additional actuators to the existing earthworm-like rectilinear locomotion robots. For example, by setting two or three independent actuators (e.g., servomotors or solenoid pairs) in each robot segment [7, 8, 36], the robot segment could be effectively contracted, extended, and bent, thus endowing the robots with planar locomotion capability. For continuous earthworm-like robots, additional longitudinal SMA wires [35] or independent servomotors [37] are introduced to bend the robot body to one side.

To achieve earthworm-like planar robotic locomotion, the retrograde peristalsis wave still plays the core role in designing control strategies. For metameric earthworm-like robots, by prescribing the states of the robot segments following the retrograde peristalsis wave, discrete locomotion gaits have been demonstrated to be effective in realizing planar locomotion [7, 38]. Specifically, two additional states of the robot segments are added (i.e., the leftward-contracted and rightward-contracted states) to the existing axially-relaxed and axially-contracted states of the rectilinear locomotion robot. Zhan et al. carried out a comprehensive study on the generation, classification, and characterization of the planar locomotion gaits [36]. By establishing a correspondence between the discrete numbers (‘0’, ‘1’, ‘2’, and ‘3’) and the four states of the robot segments, a generic gait generation algorithm is proposed. Based on an $N$-segment kinematic model of the planar locomotion robot, linear and angular displacements of the robot in a locomotion period can be derived, which can be then used to predict the average locomotion speeds (both linear and angular). Moreover, Zhan et al. found that with different gaits, the robot could exhibit four qualitatively different locomotion modes, namely, the rectilinear, sidewinding, circular, and cycloid locomotion. This has been verified through both numerical simulations and experiments. Based upon these findings, a framework of in-plane gait planning based on the genetic algorithm is proposed to help the robot to choose the optimal gait to reach the target, which is evaluated by two objective functions, namely, the distance to the target position on the plane and the number of locomotion steps the robot taken before reaching the target [39]. For the continuous earthworm-like robot (mesh-worm), based on the retrograde peristalsis wave, Kandhari et al. proposed nonperiodic waveforms for eliminating the undesired slip of the robot [40, 41].

Despite the progress in achieving and understanding the earthworm-like robotic rectilinear and planar locomotion, there is still a significant gap between the current earthworm-like robot technology and what is needed for practical applications. For earthworm-like robots used in complex environments (e.g., unstructured underground space and 3-dimensional (3D) pipelines), spatial (or 3D) locomotion capability is necessary and important for increasing spatial accessibility, improving environmental adaptability, and enriching potential functionality. It is worth remarking here that another type of bio-inspired robot, the snake-like robot, which has similar shape characteristics to the earthworm-like robot, is capable of performing 3D locomotion [42–44]. However, the locomotion mechanisms of snake-like robots and earthworm-like robots are fundamentally disparate. The snake-like robot relies on swinging the active/passive joints between adjacent body segments to acquire forward propulsion[45, 46], which is referred to as lateral undulation [5, 47, 48]; while for the earthworm-like robot, as mentioned above, it relies on axial deformations of robot segments that propagate backward of the body to achieve locomotion, which is referred to as the retrograde peristalsis wave. Actually, developing earthworm-like spatial locomotion robots has become a recent research hotspot, and a few designs and prototypes have been reported. For instance, Yang et al. developed a worm-inspired robot with pneumatic suction cups mounted on the segments; the robot could crawl on horizontal, inclined, or vertical walls [49]. In our previous work, we designed and prototyped a novel earthworm-like spatial locomotion robot based on the Yoshimura-ori structure. Actuated by four independent SMA springs and an inner pneumatic balloon, each robot segment could bend in four directions (i.e., upward, downward, rightward, and leftward), making the robot able to achieve effective rectilinear, turning, and rising locomotion [50]. Note that in these two examples, the robot body is made up of a small number of segments (say, four segments in [49] and five segments in [50]). This, on the one hand, makes it relatively easy to control the robot by directly prescribing the actuation sequence of the robot segments and, on the other hand, severely limits the spatial locomotion performance. Actually, by incorporating more segments into the body, the metameric robot would be more flexible in motion such that rich spatial locomotion modes with qualitatively and quantitatively different characteristics can be expected, but the direct actuation-assignment approach would become tedious and infeasible to acquire all possible gaits. However, aside from the abovementioned case studies, a generic kinematic robot model with an arbitrarily large number of segments has not been established, and a systematic 3D locomotion gait study is still blank. With a large number of robot segments, there is an almost complete lack of knowledge on how to generate and describe the 3D locomotion gaits, and we are completely in the dark about the effects of different gaits on locomotion performance.

The above-mentioned challenging issues constitute the major motivation of this research, i.e., to get profound insights into the spatial locomotion of earthworm-like metameric robots in terms of 3D gait generation and gait analysis. To achieve this goal, the following fundamental but largely undressed issues will be tackled:

• (1) How to build a generic model of the earthworm-like metameric robot that can well capture the 3D deformations of the segments and the overall spatial locomotion of the robot?

• (2) How to generate all admissible 3D locomotion gaits for an arbitrary number of robot segments?

• (3) How to classify the 3D locomotion gaits based on the robot’s locomotion characteristics?

• (4) How different gait parameters would affect the robot’s spatial locomotion performance, both qualitatively and quantitatively?

• (5) How to choose the optimal 3D gait to reach the target position in 3D space, and especially, if both proximity and speed are aimed for?

These questions are all answered in this paper via comprehensive theoretical and numerical investigations. In the 3D scenario, each robot segment needs six states to achieve 3D deformations, which would significantly amplify the library of locomotion gaits. Assuming ideal anchoring and ideal actuation, a multibody kinematic model of an $N$-segment earthworm-like robot is established. Based on the retrograde peristalsis wave, a generic gait generation algorithm is proposed for producing all admissible 3D locomotion gaits. Controlled by different 3D gaits, the robot could exhibit four major types and, further, ten qualitatively different spatial locomotion modes, which completely include the 1D and 2D locomotion modes reported in previous studies [26, 36]. Among them, several spatial locomotion modes, including the 3D sidewinding, 3D circular, and 3D cycloid, are uncovered for the first time. Corresponding to each mode, the robot’s locomotion performances under all admissible gaits are systematically evaluated, and the relationship between the performance indexes and the gait parameters are clarified. Finally, based on the genetic algorithm, a gait planning framework is proposed. To achieve the target in 3D spaces with better proximity and faster speed, bi-objective optimization is carried out to obtain the Pareto front, which helps us to make tradeoffs.

2 Kinematic modeling and gait generation

The earthworm’s morphology characteristics provide important guidelines for modeling the metameric earthworm-like robots with spatial locomotion capability. In this section, by abstracting the deformation characteristics of an origami earthworm-like robot, a kinematic model is developed. The $N$-segment model also holds generality in that it is also applicable to other metameric robots with similar 3D deformation capabilities, and it thus serves as the basis for studying the 3D locomotion gaits.

2.1 Kinematics of a single robot segment

In our previous research [49], we have designed and prototyped a Yoshimura-ori based earthworm-like robot that is able to perform effective 3D locomotion (e.g., rectilinear, turning, and rising, Fig. 2(a)). Specifically, following the morphology characteristics of the earthworm’s body segment, each robot segment is equipped with four SMA springs, a pneumatic balloon, and a pair of electromagnets: the SMA springs are used to bend the segment, the pneumatic balloon is employed for extending and contracting the segment, and the electromagnets are used for anchoring with the working environment. Each robot segment could stay at six states, namely, the axially-relaxed, the axially-contracted, the leftward-contracted, the rightward-contracted, the upward-contracted, and the downward-contracted states (Fig. 2(b)). Considering the generality of the deformation patterns presented by the origami robot segment prototype, they are abstracted and used for robot state description (Fig. 2(c)). Specifically, the six states are respectively denoted by digits ‘1’, ‘2’, ‘3’, ‘5’, ‘4’, and ‘6’ (Table 1). Particularly, when the segment is axially contracted, the electromagnets will be activated to achieve anchoring.

Fig. 2

Kinematic models of the robot segment and the robot as a whole. (a) The snapshot of the Yoshimura-ori based earthworm-like robot under rectilinear, turning, and rising locomotion. (b) The photo of the robot segment staying at six states. (c)The simplified model of six states. (d) Configuration vectors corresponding to the axially-relaxed, axially-contracted, and one-side contracted states. (e) A generic kinematic model of the metameric earthworm-like robot with spatial locomotion capability, which includes six types of segments, and the heading direction is indicated. For each segment, both the configuration vector and its label in the global index system are given

Table 1 Configuration vectors corresponding to the six segment states

To quantify the deformations of the robot segment (Fig. 2(a)), a kinematic model of the robot segment is developed, shown in Fig. 2(d). The posterior and anterior boundaries represent the acrylic plates of the robot segment, which keep rigid during segment deformation. Based upon this model, the spatial position and orientation of each segment can be described by a configuration vector $\mathbf{r}_{i}$ (the subscript $i = 1,\ldots,6$ indicates the segment state), which points from the center of the posterior boundary of a segment to the center of the anterior boundary (Fig. 2(d)). For all six states, the components of the configuration vectors in the $xyz$ coordinate system are listed in Table 1. Specifically, $L_{0}$ and $L_{1}$ represent the lengths of the segment (along the $y$-direction) at the axially-relaxed state and the axially-contracted state, respectively; $L_{2}$, $\alpha$, and $\beta$ are used to quantify the one-side contracted states, with $L_{2}$ denoting the length of the one-side contracted segment, $\alpha$ denoting the intersection angle between the configuration vector and the $y$-axis, and $\beta$ denoting the angular deformation of the segment. In this research, $\beta /\pi$ ($\beta < \pi$) must be rational so that the robot could achieve all possible locomotion modes (the details would be explained in Sect. 3). For the axially-relaxed and axially-contracted segments, $\alpha = \beta = 0$. Considering the geometric relations, the angles $\alpha$ and $\beta$ are not independent; rather, they satisfy

$$ \beta = 2\alpha. $$

(1)

Each segment could switch among the six states by its actuators, and the state transition can be finished within a unit time interval $\Delta t$. Particularly, if the robot segment remains at the axially-contracted state during an interval $\Delta t$, it is assumed to anchor ideally with the working medium. Note that anchoring to the environment is necessary for earthworm-like robots that move in three dimensions in the soil [2, 7], and anchoring is also achieved by radial expansion of the robot segment to increase the normal pressure and friction with the soil. Here, as a generic study of 3D earthworm-like robotic locomotion gait, a kinematic model of a robot segment with 3D deformation capabilities is developed. We do not discuss exactly how anchoring is achieved, but introduce it into the model as an assumption (see the next section for details).

2.2 A generic kinematic model of the robot and the fundamental locomotion mechanism

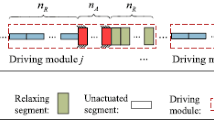
By connecting multiple segments at different states in series under the continuity conditions of displacement and orientation, a generic kinematic model of the metameric earthworm-like robot can be established (Fig. 2(e)). In this model, the number of segments at state ‘$i$’ is denoted by $n_{i}$ ($i = 1,\ldots,6$), which are natural numbers. Without loss of generality, segments of the same states are gathered, and they are organized in the order of axially-relaxed (‘1’), leftward-contracted (‘3’), rightward-contracted (‘5’), upward-contracted (‘4’), downward-contracted (‘6’), and axially-contracted (‘2’), from the tail to the head. With different sort orders of segments, while the robot’s moving direction, velocity, or even the locomotion mode may change, the proposed analysis method remains effective in predicting the locomotion.

To achieve effective earthworm-like spatial locomotion, the fundamental locomotion mechanism of the earthworm, i.e., the retrograde peristalsis wave, is mimicked, from three aspects. First, we assume that the segment states are propagated backward by $n_{p}$ segments in each transition; this constitutes the core of the robotic locomotion mechanism. Second, when the segment states are propagated to the tail of the robot, they will return to the robot head and keep propagating. Third, during each state transition, there should always exist some segments that remain at the axially-contracted (‘2’) state to form an anchor with the working environment so that other segments can lean against it and deform to achieve effective displacements. For achieving steady-state locomotion, the number of anchoring segments should remain unchanged during each transition. To this end, additional $n_{p}$ axially-contracted segments are needed and are placed at the tail of the robot (Fig. 2(c), denoted by subscripts ‘$p$’). Hence, the total number of axially-contracted segments is $n_{2} + n_{p}$,and the robot has ($N_{\mathrm{total}} = n_{1} + n_{3} + n_{5} + n_{4} + n_{6} + n_{2} + n_{p}$) segments in total.

In what follows, to indicate a specific segment in the robot model, the configuration vector $\mathbf{r}_{i}^{j}$ will be cited, where the subscript $i = 1,\ldots,6$ indicates the state of the segment, and the superscript $j = 1,\ldots,n_{i}$ indicates the $j$th segment of state ‘$i$’ in the robot. The segments can also be cited in a global index system, where the tail segment is labeled as #1; numbering the segments in turn from the tail to the head, the head segment is labeled as #$N$_total (Fig. 2(c)). The head point, which is defined as the front boundary center of the head segment, is adopted to represent the spatial position of the robot; and the orientation of the head segment is regarded as the heading direction of the robot. Specifically, as a kinematic model, it is reasonable to propose the following two model assumptions on each segment:

Model ssumption 1

The anchoring segment could provide infinite friction/anchoring force to prevent them from slipping when their adjacent segments are deforming.

Model ssumption 2

The non-anchored segments suffer friction during moving, while the axially-relaxing, axially-contracting, and bending processes are powerful enough to overcome the friction, deform the segment into the assigned state, and pull or push adjacent segments.

We emphasize here again that the kinematic model, although developed based on the Yoshimura-ori robot design, is applicable to other metameric robots with similar 3D deformability. As a result, this model is used as a platform for subsequent generic gait studies.

2.3 Gait parameters, constraints, and gait generation algorithm

Inherited from 1D and 2D earthworm-like locomotion robots [9, 36], the state vector and the locomotion gait are defined below to describe the state of the robot with respect to time.

Definition 1

State vector

The state vector is used to describe the state of each segment in a $N$_total-segment robot, which could be defined as

$$ \mathbf{s}_{t} = (s_{t}^{1},s_{t}^{2},\ldots...s_{t}^{N_{\mathrm{total}}}),s_{t}^{j} \in \{ 1,2,3,4,5,6\}, $$

(2)

where $s_{t}^{j}$ denotes the state of the $j$th ($j = 1,\ldots,N_{\mathrm{total}}$) segment at the time instant $t$.

Definition 2

Locomotion gait

The locomotion gait of an $N$_total-segment robot can be defined as a sequence of the state vectors, which depicts the transitions of the state vector with respect to time

$$ (\mathbf{s}_{t_{0}},\mathbf{s}_{t_{0} + \Delta t},\ldots...\mathbf{s}_{t_{f}}), $$

(3)

where $\mathbf{s}_{t_{0}}$ and $\mathbf{s}_{t_{f}}$ are the state vectors at the initial and final time instants of a period, respectively. To ensure periodicity of the locomotion, $\mathbf{s}_{t_{0}}$ and $\mathbf{s}_{t_{f}}$ are asked to be identical.

In the generic robot model shown in Fig. 2(e), the number of segments at different states ($n_{i}$ ($i = 1,\ldots,6$)) and the number of propagated segments $n_{p}$ are variable. With different assignments of these numbers, the robot would exhibit different spatial locomotion. Hence, in this research, $n_{i}$ ($i = 1,\ldots,6$) and $n_{p}$ serve as the parameters to define the gait, and we use $G = \{ n_{1},n_{3},n_{5},n_{4},n_{6},n_{2} | n_{p}\}$ to denote a group of gait parameters. Among these seven parameters, $n_{1}$ determines the forward thrust, $n_{2}$ determines the anchoring capability, $n_{3}$, $n_{4}$, $n_{5}$, $n_{6}$ determine the spatial turning, and $n_{\mathrm{p}}$ determines the speed for state propagation along the robot body. Note that these seven parameters are not independent of each other; rather, they have to satisfy the following four constraints:

Gait parameter constraint 1

The total number of segments is a constant $N_{\mathrm{total}}$, i.e.,

$$ N_{\mathrm{total}} = n_{1} + n_{3} + n_{5} + n_{4} + n_{6} + n_{2} + n_{p}, $$

(4)

which reduces the number of independent parameters to 6.

Gait parameter constraint 2

During each state transition, the robot should possess at least one anchoring segment, and the segment states should be propagated backward by at least one segment. Hence, $n_{2}$ and $n_{p}$ should satisfy

$$ n_{2} \ge 1, n_{p} \ge 1. $$

(5)

Gait parameter constraint 3

The robot should have enough segments for at least one complete propagation of states without overlap, which calls for

$$ N_{\mathrm{total}} \ge n_{2} + 2n_{p}. $$

(6)

Gait parameter constraint 4

At any time, to avoid the overlapping of the robot’s body, the robot is not allowed to bend over 180°, which requires

$$ n_{3}\beta \le \pi , n_{5}\beta \le \pi ,n_{4}\beta \le \pi ,n_{6}\beta \le \pi . $$

(7)

With the developed robot model (Fig. 2(c)) and a group of prescribed gait parameters, the state vector of the robot at each time instant can be determined, which further constitutes the locomotion gait. According to the retrograde peristalsis wave mechanism, the segment states will propagate backward by $n_{p}$ segments during each transition [36]; when reaching the robot tail, the propagation will continue from the head. Hence, the robot needs $\mathrm{LCM}(N_{\mathrm{total}},n_{p})/n_{p}$ transitions to finish a complete period of steady-state locomotion, and the period yields

$$ T = \left ( \mathrm{LCM}(N_{\mathrm{total}},n_{p})/n_{p} \right )\Delta t, $$

(8)

where $\mathrm{LCM}$ computes the least common multiple of $N_{\mathrm{total}}$ and $n_{p}$. The backward propagation of segment states, which is the essence of the retrograde peristaltic wave, can be expressed by the switch of the state

$$ s_{t_{k}}^{j} = s_{t_{0}}^{\mathrm{Mod}[j - 1 + k \cdot n_{\mathrm{p}},N_{\mathrm{total}}] + 1}, j = 1,2,\ldots,N_{\mathrm{total}},k = 1,2,\ldots,\mathrm{LCM}(N_{\mathrm{total}},n_{p})/n_{p} + 1, $$

(9)

where $\mathrm{Mod}[ \cdot ]$ donates the modulo operation. Based on this, a generic gait generation algorithm can be constructed (Algorithm 1), and all admissible gaits can be generated.

Algorithm 1

Generic Gait Generation

Figure 3 displays an example with gait parameters $G\ = \left \{ 0,1,0,1,0,1\left | 2 \right . \right \}$, initial state vector $\mathbf{s}_{t_{0}} = (2,2,3,4,2)$, and initial heading direction $(0,1,0)^{\mathrm{T}}$. Based on Eq. (8), this 5-segment robot needs five transitions to finish a period of steady-state locomotion. To describe the movement, the center of the posterior boundary of the left-most anchoring segment is selected as the reference point. Figure 3 reveals clearly that in each transition, the states (e.g., characterized by the reference point) are propagated backward by $n_{p} = 2$ segments; moreover, in each transition, there is $n_{2}\ = 1$ axially-contracted segment that anchors with the environment (denoted by red vertical lines) so that the other segments can lean against them and achieve net displacements. After two transitions, the reference point is propagated to the rear part of the robot, and it experiences a rear-front switch to the forepart of the robot during the 3rd transition. Such a rear-front switch is observed again during the 5th transition, which lets the robot return to its initial state. In what follows, the propagation process of the reference point from the forepart to the rear-part, and back to the forepart, is defined as a loop. With given gait parameters $G$, $\mu$ loops are required to finish an entire locomotion period. The number of required loops $\mu$ is given by

$$ \mu = \mathrm{LCM}(N_{\mathrm{total}},n_{p})/N_{\mathrm{total}}. $$

(10)

In particular, if the total number of segments $N_{\mathrm{total}}$ is divisible by $n_{p}$, the number of required loops $\mu \ = 1$. In the $l$th ($l \in \left [ 1,\mu \right ]$) loop, the number of state transitions yields

$$ N_{l} = \left \lceil \frac{M_{l}}{n_{p}} \right \rceil , l = 1,2,\ldots,\mu , $$

(11)

where $\left \lceil . \right \rceil$ donates the ceiling function, and $M_{l}$ is the number of segments passed by in the $l$th loop, given by

$$ \textstyle\begin{array}{l} M_{1} = N_{\mathrm{total}} - (n_{2} - 1), \\ M_{l + 1} = N_{\mathrm{total}} - (N_{l}n_{p} - M_{l}), l = 1,2,..,\mu . \end{array} $$

(12)

Hence, for the example shown in Fig. 3, the number of required loops $\mu \ = 2$. In the first loop, $N_{1} = 3$ transitions are needed and $M_{1} = 5$ segments are passed by; in the second loop, $N_{2} = 2$ transitions are needed and $M_{2} = 4$ segments are passed by. Detailed derivation and interpretations of $N_{l}$ and $M_{l}$ can be found in the Supplementary, Section S1.

Fig. 3

A period of the robot’s steady-state locomotion with gait parameters $G\ = \left \{ 0,1,0,1,0,1\left | 2 \right . \right \}$. The robot needs five transitions to finish a locomotion period. During each transition, the anchoring segments (denoted by oblique lines) remain fixed (denoted by red vertical lines), and the robot states are propagated backward by $n_{p} = 2$ segments. The loops required by a period are also indicated (Color figure online)

2.4 Robot kinematics

Inherited from 2D earthworm-like locomotion robots [36], two kinematic indexes are defined in this research to evaluate the locomotion performance of the $N$_total-segment robot.

Definition 3

Linear displacement vector

The linear displacement vector $\mathbf{D} = (D_{x},D_{y}, D_{z})^{\mathrm{T}}$, which is defined to characterize the spatial motion of the head point in a period. It depends on the configuration vectors of all segments and the gait parameters.

Definition 4

Rotation matrix

The rotation matrix $\boldsymbol{\Theta}$ (a $3 \times 3$ matrix) of the robot [51], which is used to describe the change of the heading direction vector $\mathbf{H}_{t}\ = (H_{t,x},H_{t,y},H_{t,z})^{\mathrm{T}}$ (i.e., the unit outer normal vector of the head segment’s anterior boundary denoted by the blue arrow shown in Fig. 3) in a period. It is closely related to the gait parameters and the angular deformation of a segment $\beta$. Without loss of generality, the robot’s heading direction vector at $t = 0$ is set to be parallel with the $y$-axis, i.e.,

$$ \mathbf{H}_{t = 0} = (0,1,0)^{\mathrm{T}}. $$

(13)

To derive the expression of $\boldsymbol{\Theta}$, the rotation matrices $\mathbf{P}$ and $\mathbf{Q}$ are firstly defined, which depict the rotation of the anterior boundary to the posterior boundary of the one-side contracted segment. Specifically, for the rightward-contracted segment, the rotation matrix $\mathbf{P}$ yields

$$ \mathbf{P} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \cos ( - \beta ) & - \sin ( - \beta ) & 0 \\ \sin ( - \beta ) & \cos ( - \beta ) & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ]. $$

(14)

For the upward-contracted segment, the rotation matrix $\mathbf{Q}$ gives

$$ \mathbf{Q} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 0 & \cos (\beta ) & - \sin (\beta ) \\ 0 & \sin (\beta ) & \cos (\beta ) \end{array}\displaystyle \right ]. $$

(15)

The rotation matrices for the leftward-contracted and downward-contracted segments can be obtained by inverse operation, i.e., $\mathbf{P}^{ - 1}$ for the leftward-contracted segment and $\mathbf{Q}^{ - 1}$ for the downward-contracted segments.

Hence, for given gait parameters $G$ and based on Eq. (11)–(12), the rotation matrix of the robot after the $l$th loop (denoted by $\boldsymbol{\Omega}_{l}$) can be expressed via the rotation matrices of the one-side contracted segments (i.e., $\mathbf{P}$, $\mathbf{Q}$, $\mathbf{P}^{ - 1}$, and $\mathbf{Q}^{ - 1}$)

$$ \boldsymbol{\Omega}_{l} = (\mathbf{P}^{n_{3} - n_{5}}\mathbf{Q}^{n_{4} - n_{6}})^{l}, l = 1,2,\ldots,\mu . $$

(16)

The linear displacement vector after the $l$th loops yields

$$ \boldsymbol{\Psi}_{l} = \sum _{j = 1}^{l} \left ( \boldsymbol{\Omega} {}_{1} \right )^{j - 1} \left [ \textstyle\begin{array}{l} ( - n_{p}N_{j} + n_{p} + n_{2} - N_{\mathrm{total}} - 1 + M_{j})\mathbf{r}_{2} \\ + (N_{\mathrm{total}} + 1 - M_{j + 1})\boldsymbol{\Omega} {}_{1}\mathbf{r}_{2} \\ + \sum _{i = 0}^{n_{3} - 1} \mathbf{P}^{i}\mathbf{r}_{3} + \sum _{i = 0}^{n_{5} - 1} \mathbf{P}^{n_{3} - i}\mathbf{r}_{5} + \sum _{i = 0}^{n_{4} - 1} \mathbf{P}^{n_{3} - n_{5}}\mathbf{Q}^{i}\mathbf{r}_{4} \\ + \sum _{i = 0}^{n_{6} - 1} \mathbf{P}^{n_{3} - n_{5}}\mathbf{Q}^{n_{4} - i}\mathbf{r}_{6} + n_{1}\mathbf{r}_{1} \end{array}\displaystyle \right ]. $$

(17)

Particularly, when $l = \mu$, an entire locomotion period is finished. The rotation matrix $\boldsymbol{\Theta}$ and the linear displacement vector $\mathbf{D}$ of the robot in a period yield

$$ \boldsymbol{\Theta} = \boldsymbol{\Omega}_{\mu}, \mathbf{D} = \boldsymbol{\Psi}_{\mu} . $$

(18)

The heading direction vector of the robot after a locomotion period changes to

$$ \mathbf{H}_{t = T} = \boldsymbol{\Theta} \mathbf{H}_{t = 0}. $$

(19)

Overall, with the defined linear vectors $\mathbf{D}$ and the rotation matrix $\boldsymbol{\Theta}$, the position and heading direction of the robot head are given by stringent mathematical formulations Eq. (17)–(19), which serve as the basis for the subsequent locomotion analysis.

3 Locomotion modes

By varying the gait parameters, the robot is expected to perform various types of locomotion. Previous research has shown that in the 1D scenario, only rectilinear locomotion can be achieved by the metameric earthworm-like robot [2, 9]; in the 2D scenario, four planar locomotion modes, namely, rectilinear, sidewinding, circular, and cycloid locomotion, are possible [36]. Here, we show that in the 3D scenario, ten qualitatively different spatial locomotion modes can be achieved, which completely cover the 1D and 2D cases. Moreover, for the first time, a few spatial locomotion modes, including 3D sidewinding, 3D circular, and 3D cycloid locomotion, etc., are uncovered. Specifically, for each locomotion mode, an example is given and the corresponding trajectory (i.e., the position of the robot head point during each transition) is shown in Fig. 4.

Fig. 4

Trajectories of the ten locomotion modes. The yellow pentacle denotes the initial position of the robot’s head point (i.e., (0, 0, 0) in the $o$-xyz coordinate system), the red circles are the position of the head point after each locomotion period, and the grey circles are passed positions of the head point during each transition. Circles are connected by blue lines, which represent the corresponding net displacement. The red and blue planes indicate that the robot’s trajectory stays within the yoz and the xoy coordinate plane, respectively. (a) rectilinear locomotion; (b)–(c) 2D and 3D sidewinding locomotion; (d)–(e) 2D and 3D circular locomotion; (f)–(g) 2D and 3D cycloid locomotion. (h)–(j) Period-k cycloid locomotion, irrational cycloid locomotion, and ‘bowl’ locomotion (Color figure online)

3.1 Rectilinear locomotion

When the robot does not contain any one-side contracted segments, the trajectory will be a straight line without turning. Such a locomotion mode is the rectilinear locomotion, which has been reported in our previous work [9]. The conditions for achieving rectilinear locomotion yield

$$ n_{3} = 0, n_{5} = 0, n_{4} = 0, n_{6} = 0. $$

(20)

Figure 4(a) displays an example of rectilinear locomotion with gait parameters $G\ = \{ 1,0,0,0,0,1\left | 1 \right .\}$. The robot has three segments in total, and the locomotion is shown in five periods.

3.2 Sidewinding locomotion

When the robot contains the same numbers of leftward-contracted and rightward-contracted segments and the same number of upward-contracted segments and downward-contracted segments, the robot will perform sidewinding locomotion. The characteristic feature of the sidewinding locomotion is that the robot will achieve nonzero linear displacements but restores the heading direction after a locomotion period. Based on whether the trajectory is in-plane or out-of-plane, sidewinding locomotion can be further divided into 2D and 3D types.

3.2.1 2D sidewinding locomotion

If the one-side contracted segments are made up of leftward-contracted and rightward-contracted segments only, the robot will perform 2D sidewinding locomotion in the xoy coordinate plane, which asks the gait parameters to satisfy

$$ n_{3} = 0, n_{5} = 0, n_{4} = 0, n_{6} = 0. $$

(21)

On the other hand, if the one-side contracted segments are of upward-contracted and downward-contracted types, the 2D sidewinding locomotion will stay in the yoz coordinate plane, which is determined by the following condition

$$ n_{4} = n_{6} \ne 0, n_{3} = n_{5} = 0. $$

(22)

Figure 4(b) displays two examples of 2D sidewinding locomotion. The robot has seven segments in total, and four locomotion periods are shown. With $G\ = \{ 1,2,2,0,0,1\left | 1 \right .\}$, the locomotion stays in the xoy coordinate plane (blue plane); and with $G\ = \{ 1,0,0,2,2,1\left | 1 \right .\}$, the locomotion stays in the yoz coordinate plane (red plane).

3.2.2 3D sidewinding locomotion

If all four types of one-side contracted segments are included in the robot, and the following conditions are satisfied

$$ n_{3} = n_{5} \ne 0, n_{4} = n_{6} \ne 0, $$

(23)

the robot will exhibit 3D sidewinding locomotion. Here, the trajectory no longer stays in a plane, while the heading direction can still be restored after a locomotion period. Figure 4(c) shows an example of the 3D sidewinding locomotion with gait parameters $G\ = \{ 1,2,2,2,2,1\left | 1 \right .\}$. The robot has 11 segments in total, and 3 locomotion periods are shown.

3.3 Circular locomotion

In the sidewinding locomotion, due to the same number of leftward/rightward contracted segments ($n_{3} = n_{5}$), and the same number of upward/downward contracted segments ($n_{4} = n_{6}$), the robot can always regain its heading direction after a locomotion period. If $n_{3} \ne n_{5}\ \text{or} n_{4} \ne n_{6}$, the heading direction will experience a change after a locomotion period. Based on (18), the rotation matrix and the linear displacement vector after $k$ locomotion periods can be expressed

$$ \boldsymbol{\Theta}_{k} = \boldsymbol{\Theta}^{k}, \mathbf{D}_{k} = \sum _{i = 1}^{k} \boldsymbol{\Theta}^{i - 1}\mathbf{D} . $$

(24)

If $\boldsymbol{\Theta}_{k}$ and $\mathbf{D}_{k}$ satisfy the following conditions

$$ \boldsymbol{\Theta}_{k} = \mathbf{I}, \mathbf{D}_{k} = \mathbf{0}\ \text{for } k > 1, $$

(25)

the robot’s head point will return its initial position and regain its initial heading direction after $k$ locomotion periods. Such locomotion is named circular locomotion. Equation (25) not only imposes constraints on the gait parameters but also puts requirements on the angular deformation of the segment (i.e., $\beta$). Based on whether the trajectory is in-plane or out-of-plane, circular locomotion can also be divided into 2D and 3D types.

3.3.1 2D circular locomotion

In the 2D scenario, to ensure (25), $\beta$ has to be the rational number multiple of $2\pi$ ($\beta > 0$) [36]. Moreover, if the robot only contains leftward/rightward contracted segments, and their numbers are different, i.e.,

$$ n_{3} \ne n_{5}, n_{4} = n_{6} = 0, \boldsymbol{\Theta}_{k} = \mathbf{I}, \mathbf{D}_{k} = \mathbf{0}\ \text{for } k > 1, $$

(26)

the robot will perform 2D circular locomotion in the xoy coordinate plane; if the robot only contains upward/downward contracted segments, and their numbers are different, i.e., the robot will perform 2D circular locomotion in the xoy coordinate plane; if the robot only contains upward/downward contracted segments, and their numbers are different, i.e.,

$$ n_{4} \ne n_{6}, n_{3} = n_{5} = 0, \boldsymbol{\Theta}_{k} = \mathbf{I}, \mathbf{D}_{k} = \mathbf{0}\ \text{for } k > 1, $$

(27)

the robot will perform 2D circular locomotion in the yoz coordinate plane. Figure 4(d) shows two examples of the 2D circular locomotion. The robot has five segments in total, and eight locomotion periods are shown. With gait parameters $G\ = \{ 1,2,0,0,0,1\left | 1 \right .\}$ and $\{ 1,0,0,2,0,1\left | 1 \right .\}$, the locomotion stays in the xoy plane and yoz plane, respectively.

3.3.2 3D circular locomotion

If the robot contains both leftward/rightward contracted segments or upward/downward contracted segments (i.e., $n_{3}$ and $n_{5}$ cannot all equal to zero, $n_{4}$ and $n_{6}$ cannot all equal to zero), and their numbers satisfy the following conditions

$$ n_{3} \ne n_{5}\ \text{or} n_{4} \ne n_{6}, \boldsymbol{\Theta}_{k} = \mathbf{I}, \mathbf{D}_{k} = \mathbf{0}\ \text{for } k > 1, $$

(28)

the robot will carry out 3D circular locomotion. Figure 4(e) displays an example with gait parameters $G\ = \{ 6,8,0,1,0,1\left | 4 \right .\}$. The robot possesses 20 segments in total, and the robot head can return the initial position and regain the initial heading direction in two locomotion periods.

3.4 Cycloid locomotion

In addition to the above five locomotion modes, the rest locomotion modes are categorized into cycloid locomotion. Considering the characteristics of the linear displacement and the rotation matrix, cycloid locomotion can be further classified into three major types: period-1 cycloid locomotion, period-$k$ cycloid locomotion, and irrational cycloid locomotion.

3.4.1 2D and 3D period-1 cycloid locomotion

If the following conditions are satisfied

$$ \boldsymbol{\Theta}_{k} = \mathbf{I}, \mathbf{D}_{k} \ne \mathbf{0},\ \text{for } k = 1, $$

(29)

the robot will regain its heading direction and acquire a nonzero net displacement after a period of locomotion. Such locomotion is named period-1 cycloid locomotion. Unlike the circular locomotion, the robot will no longer return its initial position, no matter how many locomotion periods are executed. The period-1 cycloid locomotion can be further divided into 2D and 3D types considering the coplanarity of the trajectory. If the gait parameters meet the following conditions

$$ n_{3} \ne n_{5}, n_{4} = n_{6} = 0, \boldsymbol{\Theta}_{k} = \mathbf{I}, \mathbf{D}_{k} \ne \mathbf{0},\ \text{for } k = 1, $$

(30)

or

$$ n_{4} \ne n_{6}, n_{3} = n_{5} = 0, \boldsymbol{\Theta}_{k} = \mathbf{I}, \mathbf{D}_{k} \ne \mathbf{0},\ \text{for } k = 1, $$

(31)

the robot will perform 2D period-1 cycloid locomotion in the xoy or yoz coordinate plane, respectively. Figure 4(f) shows two examples of 2D period-1cycloid locomotion with gait parameters $G\ = \{ 1,0,4,0,0,4\left | 4 \right .\}$ (the trajectory stays in the xoy plane) and $G\ = \{ 1,0,0,0,4,4\left | 4 \right .\}$ (the trajectory stays in the yoz plane). The robot has 13 segments in total, and the trajectories of the head point in 4 periods are characteristic cycloids.

If the following conditions are met

$$ n_{3} \ne n_{5}, n_{4} \ne n_{6}, \boldsymbol{\Theta}_{k} = \mathbf{I}, \mathbf{D}_{k} \ne \mathbf{0},\ \text{for } k = 1, $$

(32)

the robot will perform 3D period-1 cycloid locomotion. With gait parameters $G\ = \left \{ 0,4,0,4,0,2\left | 6 \right . \right \}$, an example is demonstrated in Fig. 4(g), in which the robot has 16 segments in total, and 3 periods of locomotion are demonstrated. Here, the trajectory of the robot’s head point no longer stays in a plane.

3.4.2 Period-k cycloid locomotion

If the robot contains both leftward/rightward contracted segments or upward/downward contracted segments (i.e., $n_{3}$ and $n_{5}$ cannot all equal to zero, $n_{4}$ and $n_{6}$ cannot all equal to zero), and the following conditions are met

$$ n_{3} \ne n_{5}\ \text{or} n_{4} \ne n_{6}, \boldsymbol{\Theta}_{k} = \mathbf{I}, \mathbf{D}_{k} \ne \mathbf{0},\ \text{for } k > 1, $$

(33)

the robot’s head point will regain its initial heading direction and acquire a nonzero displacement after $k$ locomotion periods. This is named period-$k$ cycloid locomotion. Similarly, the robot will no longer return its initial position in period-$k$ cycloid locomotion. An example with gait parameters $G\ = \{ 2,2,1,0,8,1\left | 2 \right .\}$ is demonstrated in Fig. 4(h), in which the robot has 16 segments in total, and 6 locomotion periods are plotted.

3.4.3 Irrational cycloid locomotion

If we cannot find a positive integer $k$ within an upper bound (say, $k < 3000$ in this research) to meet the condition $\boldsymbol{\Theta}_{k} = \mathbf{I}$, the robot’s head point will not return to its initial position or regain its initial heading direction. Figure 4(i) displays an example of irrational cycloid locomotion of a 5-segment robot with gait parameters $G\ = \{ 0,2,0,0,1,1\left | 1 \right .\}$.

Particularly, if the robot’s head point after each locomotion period locates in the same plane, while the head point during a locomotion period locates outside this plane, the trajectory is similar to a ‘bowl’ shape. An example of ‘bowl’ locomotion is shown in Fig. 4(j), in which the robot has eight segments in total, and the gait parameters are $G\ = \{ 2,0,2,1,0,1\left | 2 \right .\}$.

Overall, the metameric earthworm-like robot is capable of exhibiting four major types of locomotion (rectilinear, sidewinding, circular, and cycloid) that are qualitatively different in characteristics. Considering the coplanarity and the shape of the robot’s head-point trajectory, they are further classified into ten locomotion modes. The conditions for these ten modes are specifically derived and are summarized in Table 2; they not only depend on the gait parameters but also relate to the angular deformability of the segment. For each mode, video illustrations are also provided in the Supplementary and are indexed in Table 2. In the next section, the locomotion performance corresponding to these ten modes will be systematically examined.

Table 2 Detailed information of the locomotion modes

4 Locomotion performance

In this section, the following parameters of the robot segment are adopted for examining the locomotion performance: $L_{0} = 15$ cm, $L_{1} = 6$ cm, $L_{2} = 7.13$ cm, $\beta = 22.5^{ \circ}$; the unit time interval for a state switch of the segment is set to be $\Delta t = 1\mathrm{s}$; the initial position of the head point is $(0,0,0)^{\mathrm{T}}$, and the initial heading direction is $\mathbf{H}_{t\ = 0} = (0,1,0)^{\mathrm{T}}$. Considering that the trajectories corresponding to the ten locomotion modes are qualitatively different, different indexes are employed for evaluating the locomotion performance. Note that a systematic study on rectilinear locomotion has been carried out [9, 26], which includes locomotion kinematic and dynamics, gait optimization, and experimental verification. As a result, this research is primarily concerned with spatial locomotion.

4.1 Performance of the sidewinding locomotion

As mentioned above, the robot would only achieve nonzero linear displacement along a specific direction in sidewinding locomotion. Thus, the motion direction vector $\mathbf{e}_{v}$ and the average velocity $\bar{V}$ are sufficient to evaluate the performance of sidewinding locomotion. Note that in sidewinding locomotion, the robot will maintain its heading direction after each period, and the linear displacement is along an oblique line. Hence, the motion direction vector for sidewinding locomotion is defined as

$$ \mathbf{e}_{v} = \mathbf{D}/\left \| \mathbf{D} \right \|, $$

(34)

and the average velocity is defined as

$$ \bar{V} = \frac{\left \| \mathbf{D} \right \|}{(\mathrm{LCM}(N_{\mathrm{total}},n_{p})/n_{p})\Delta t}. $$

(35)

Figure 5(a) shows an example of sidewinding locomotion with gait parameters $G\ = \{ 0,1,1,1,1,1\left | 1 \right .\}$, in which the linear displacement vector and the motion direction vector are denoted.

Fig. 5

Performance of sidewinding locomotion. (a) Locomotion trajectory and the corresponding transition based on gait parameters $G\ = \{ 0,1,1,1,1,1\left | 1 \right .\}$. (b) Distribution of the motion direction vectors in octants I and IV. The blue and red points represent the motion direction vectors in the xoy and yoz planes, respectively. (c) With different arrangements of the one-side contracted segments, the motion direction vectors can point to all the eight octants. (d) Distribution of the average velocity $\bar{V}$ for $N$_total ranging from 4 to 30. The relationship between the maximum average velocity $\bar{V}_{\max}$ and $N$_total is fitted by a linear line (in red); the normalized maximum average velocity $\tilde{\bar{V}}_{\max}$ is denoted by the orange curve. (e) For $N$_total = 30, the relationship between the number of sidewinding gaits corresponding to different ranges of average velocity and the value of $n_{p}$. (f) Distribution of the MAAV with respect to $n_{p}$ and $n_{1}/n_{2}$ (Color figure online)

We first examine the motion direction vector. Note that the robot needs at least four segments to achieve sidewinding locomotion. Based on the arrangement of one-side contracted segments given in Fig. 2(e) (i.e., ‘3-5-4-6’), all the sidewinding gaits for $N_{\mathrm{total}} = 4\sim 30$ (52,577 gaits in total) are traversed, and the terminal points of the motion direction vectors are plotted in Fig. 5(b). It reveals that the motion direction vectors are distributed throughout octants I and IV. Particularly, if conditions (21) or (22) are satisfied, the motion direction vectors will locate in the xoy coordinate plane (blue points) or the yoz coordinate plane (red points), respectively. The motion direction can also point to other octants if the arrangement of one-side contracted segments is changed (Fig. 5(c)). For instance, the robot’s motion direction vector can point to octants II and III if the one-side contracted segments are organized in the order of ‘5-3-4-6’ or ‘4-6-5-3’. In other words, by adjusting the arrangement of one-side contracted segments and the gait parameters, the direction of the robot’s sidewinding locomotion can be effectively tailored to any of the eight octants.

The robot’s average velocity is closely related to the gait parameters. Figure 5(d) displays the distribution of the average velocity with respect to the total number of segments $N_{\mathrm{total}}$. It reveals that the range of achievable average velocity expands significantly as $N_{\mathrm{total}}$ increases, and the maximum average velocity ($\bar{V}_{\max}$) is linearly dependent on $N_{\mathrm{total}}$, which can be approximated by the following linear equation (coefficient of determination $r^{2} = 0.992$, denoted by the red line in Fig. 5(d))

$$ \bar{V}_{\max} = 2.15N_{\mathrm{total}} - 9.37. $$

(36)

Equation (36) could effectively exhibit the upper limit of the reachable average velocity. On the other hand, the maximum average velocity is normalized by the initial length of the robot to quantify the locomotion capability, i.e.,

$$ \tilde{\bar{V}}_{\max} = \bar{V}_{\max} /(N_{\mathrm{total}} \cdot L_{0}), $$

(37)

which is denoted by the orange curve in Fig. 5(d). Rather than a linear relationship with $N_{\mathrm{total}}$, the normalized maximum average velocity increases rapidly when $N_{\mathrm{total}}$ is relatively small, and then gradually saturates when $N_{\mathrm{total}}$ is larger than 20, indicating that the robot’s locomotion capability cannot be increased infinitely by increasing the number of segments.

To further understand the relationship between the average velocity and the gait parameters, the case with $N_{\mathrm{total}} = 30$, which corresponds to a wide range of achievable average velocity, is examined in detail. Here, the gait parameter $n_{p}$ is particularly focused because it determines the speed of state propagation, and thus imposes a strong impact on the average velocity. Figure 5(e) shows the relationship between the number of sidewinding gaits corresponding to different ranges of average velocity and the values of $n_{p}$. From a general view, with the increase of $n_{p}$, the number of sidewinding gaits reduces substantially, but the achievable average velocity range expands. When $n_{p} = 1$, there are 1029 sidewinding gaits, but they all correspond to relatively low average velocities within $(0, 10)(\mathrm{cm}/\mathrm{s})$. When $n_{p}$ is increased to 3, although the number of sidewinding gaits declines to 876, there are 9 gaits that correspond to higher average velocities within $(10, 30)(\mathrm{cm}/\mathrm{s})$. As $n_{p}$ grows, the number of gaits corresponding to low average velocities (within $(0, 10)(\mathrm{cm}/\mathrm{s})$) keeps reducing, while the gaits corresponding to relatively high average velocities become the majority. For example, when $n_{p} = 11$, there are only 2 of 284 gaits that correspond to the low average velocity range $(0, 10)(\mathrm{cm}/\mathrm{s})$; for $n_{p} = 12\sim 14$, all gaits correspond to relatively high average velocities within $(10, 56)(\mathrm{cm}/\mathrm{s})$.

On the other hand, the gait parameters $n_{1}$ and $n_{2}$ also relate to the forward thrusting of the robot, and their effects on average velocity are thus looked into. Considering that for given values of $n_{1}/n_{2}$ and $n_{p}$, multiple gaits are possible; among these gaits, the maximum achievable average velocity (MAAV) is picked out. Figure 5(f) displays the distribution of the MAAV with respect to $n_{1}/n_{2}$ and $n_{p}$. In general, with a fixed $N_{\mathrm{total}}$, the growth of $n_{\mathrm{p}}$ will narrow the admissible range of $n_{1}/n_{2}$ but increase the MAAV. The ratio $n_{1}/n_{2}$ could also affect the MAAV, while the relationship between them is not intuitive or clear. Particularly, for $N_{\mathrm{total}} = 30$, the global maximum average velocity of sidewinding locomotion (55.54 cm/s) is achieved at $n_{1}/n_{2}\ = 13$ and $n_{p}\ = 14$.

4.2 Performance of the circular locomotion

During 2D/3D circular locomotion, the trajectory of the robot is a closed curve, and its circumcircle can be characterized by the radius and the corresponding trajectory plane. Based upon this, three indexes are needed to evaluate the performance of the circular locomotion: the average velocity $\overline{V}$ (defined by Eq. (35)), the normal vector of the trajectory plane $\mathbf{e}_{\mathrm{normal}}$, and the circumradius of the trajectory $R$. Different from the sidewinding locomotion, the position of the head point would return to its initial position after a certain number of periods; and the last position of the head point after each locomotion period stays in the same plane (i.e., the trajectory plane, see the proof in the Supplementary, Section S2). To quantify the trajectory plane, its normal vector is defined

$$ \mathbf{e}_{\mathrm{normal}} = \frac{\mathbf{D}_{1} \times \mathbf{D}_{2}}{\left \| \mathbf{D}_{1} \times \mathbf{D}_{2} \right \|}. $$

(38)

By projecting the whole trajectory onto the trajectory plane, a curved polygon is obtained, and its circumcircle can be determined, whose radius $R$ can be numerically derived. Figure 6(a) and Fig. 6(b) display an example of 3D circular locomotion with gait parameters $G\ = \{ 8,5,1,5,1,1\left | 7 \right .\}$, in which the spatial trajectory, the linear displacement vector, the trajectory plane, and the associated normal vector, and the circumcircle are denoted. As predicted, the initial position and the last position of the head point after each locomotion period stay in the same plane; after three periods, the head point returns to its initial position.

Fig. 6

Performance of circular locomotion. (a) Locomotion trajectory based on gait parameters $G\ = \{ 8,5,1,5,1,1\left | 7 \right .\}$. (b) The circumcircle of the trajectory. (c) Distribution of the normal vectors. The red and blue lines represent the normal vectors of the yoz and xoy planes, respectively. (d) Distribution of the circumradius $R$ for $N$_total ranging from 3 to 30. The relationship between the maximum circumradius $R_{\max}$ and $N$_total is fitted by a linear line (in red); the normalized maximum circumradius $\tilde{R}_{\max}$ is denoted by the orange curve. (e) The trajectories of the head point during a period with gait parameters $G = \{ 5,8,3,0,0,1|12\}$ and $\{ 6,8,3,0,0,1|12\}$. (f) Distribution of the average velocity $\bar{V}$ for $N$_total ranging from 3 to 30. The relationship between the maximum average velocity $\bar{V}_{\max}$ and $N$_total is fitted by a linear line (in red); the normalized maximum average velocity $\tilde{\bar{V}}_{\max}$ is denoted by the orange curve. (g) For $N$_total = 30, the relationship between the number of circular gaits corresponding to different ranges of circumradius and the value of $n_{p}$. (h) For $N$_total = 30, the relationship between the number of circular gaits corresponding to different ranges of average velocity and the value of $n_{p}$ (Color figure online)

Note that the robot needs at least three segments to achieve circular locomotion. Based on the ‘3-5-4-6’ arrangement of the one-side contracted segments (Fig. 2(c)), all circular locomotion gaits for $TN = 3\sim 30$ (207,276 gaits in total) are traversed. Figure 6(c) displays the distribution of the terminal points of the normal vector $\mathbf{e}_{\mathrm{normal}}$, which are sparse in space.

Figure 6(d) demonstrates the distribution of the circumradius with respect to the total number of segments $N_{\mathrm{total}}$. It reveals that with the increase of $N_{\mathrm{total}}$, the range of achievable circumradius expands notably. To better show the upper limit of the reachable circumradius, a linear model is used to approximate the growth of the maximum circumradius $R_{\max}$ (coefficient of determination $r^{2} = 0.925$, denoted by the red line shown in Fig. 6(d))

$$ R_{\max} = 23.15N_{\mathrm{total}} - 63.71. $$

(39)

The normalized maximum circumradius, defined by

$$ \tilde{R}_{\max} = R_{\max} /(TN \cdot L_{0}), $$

(40)

is also evaluated to quantify the robot’s turning capability, shown in Fig. 6(d). It reveals that $\tilde{R}_{\max}$ is not linearly dependent on $N_{\mathrm{total}}$. When $N_{\mathrm{total}}$ is relatively small, $\tilde{R}_{\max}$ climbs rapidly with $N_{\mathrm{total}}$; and when $N_{\mathrm{total}}\ > 10$, the rising tendency gradually slows down.

Note that both $R_{\max}$ and $\tilde{R}_{\max}$ experience an upsurge at $N_{\mathrm{total}}\ = 30$, which is because the locomotion trajectory changes dramatically when the gait parameters are slightly adjusted. Actually, the locomotion trajectory is extremely sensitive to the gait parameters. As an example, the following two gait parameters $G = \{ 5,8,3,0,0,1|13\}$ and $\{ 6,8,3,0,0,1|13\}$ are evaluated, and the corresponding locomotion trajectories in a period are plotted in Fig. 6(e). The only difference between these two groups of gait parameters is the value of $n_{1}$. With gait parameters $G = \{ 5,8,3,0,0,1|12\}$, the robot (with $N_{\mathrm{total}}\ = 30$ segments in total) could achieve a 285.56 cm linear displacement in a period (denoted by bold arrow), and the circumradius is 841.79 cm. If we add another axially-relaxed segment into the robot, the robot would have $N_{\mathrm{total}}\ = 31$ segments in total, and the gait parameters are slightly changed to $G = \{ 6,8,3,0,0,1|13\}$. Intuitively, the robot would attain larger linear displacement in a period due to the increased number of axially-relaxed segments; however, surprisingly, the achieved linear displacement slumps to 42.71 cm, and the circumradius drops to 370.16 cm.

To further understand the effects of the gait parameters on the distribution of the circumradius, the case with $N_{\mathrm{total}}\ = 30$, which corresponds to the widest range of achievable circumradius, is examined in detail. Figure 6(g) shows how $n_{p}$ ($n_{p}$ determines the speed of state propagation) affects the number of circular gaits corresponding to different ranges of circumradius. With the increase of $n_{p}$, the number of circular gaits gradually reduces. For $n_{p} = 1\sim 10$, the gaits corresponding to relatively small circumradii (within $(0, 180)(\mathrm{cm})$) account for the major part. Note that the relationship between the achievable circumradius and the value of $n_{p}$ is not clear. For example, large circumradii within $(720, 842)(\mathrm{cm})$ are achievable for $n_{p} = 13$ (including 64 gaits) but are unachievable for $n_{p} = 14$. Actually, for $n_{p} = 14$, the achievable circumradii do not exceed 360 mm, while for $n_{p} = 1\sim 13$, the range $(360, 540)(\mathrm{cm})$ is achievable, and for $n_{p} = 1\sim 4$, $(540,\ 720)(\mathrm{cm})$ is attainable. It is also worth noting that there is a trough at $n_{p} = 8$, which is because the conditions for period-1 cycloid locomotion are fulfilled by some gait parameters.

We further investigate the distribution of the average velocity with respect to $N_{\mathrm{total}}$, shown in Fig. 6(f). Overall, the maximum average velocity $\bar{V}_{\max}$ increases monotonously with the total number of segments $N_{\mathrm{total}}$, which can be roughly fitted by a linear equation (coefficient of determination $r^{2} = 0.759$, denoted by the red line shown in Fig. 6(f))

$$ \bar{V}_{\max} = 2.44N_{\mathrm{total}} - 8.37. $$

(41)

This curve could effectively show the upper limit of the reachable average velocity with $N_{\mathrm{total}}$ segments. However, fluctuations are significant at some $N_{\mathrm{total}}$ because the locomotion trajectory and linear displacement are highly sensitive to the gait parameters. The maximum normalized average velocity $\tilde{\bar{V}}_{\max}$ (defined in (37)) is also examined (Fig. 6(f)). After a quick monotonous increase for $N_{\mathrm{total}} < 10$, the growth trend of $\tilde{\bar{V}}_{\max}$ gradually slows, and large fluctuations are observed. This manifests that for circular locomotion, enlarging $N$_total has a limited effect on improving the locomotion capability.

Moreover, the case with $N_{\mathrm{total}} = 30$ is exemplified in detail in Fig. 6(h). Similar to Fig. 6(g), the relationship between the number of circular gaits corresponding to different average velocity ranges and the value of $n_{p}$ is unclear. For $n_{p} = 1$, all the 3,050 circular gaits correspond to relatively low average velocities within $(0, 12)\ (\mathrm{cm}/\mathrm{s})$; as $n_{p}$ rises to 4, the number of circular gaits reduces to 2,494, while higher average velocities within $(24, 36)(\mathrm{cm}/\mathrm{s})$ become achievable. The highest average velocity range $(48, 65) (\mathrm{cm}/\mathrm{s})$ is attainable for $n_{p} = 9, 10, 12$. Nevertheless, the average velocity range is narrowed from $(0, 65)(\mathrm{cm}/\mathrm{s})$ to $(0, 24)(\mathrm{cm}/\mathrm{s})$ when $n_{p} = 11$ and 13, and it is expanded to $(0, 48)(\mathrm{cm}/\mathrm{s})$ again when $n_{p} = 14$.

4.3 Performance of the cycloid locomotion

4.3.1 Performance of the period-1 cycloid locomotion

For period-1 cycloid locomotion, the robot regains its heading direction after a period and only achieves a nonzero linear displacement. Therefore, similar to the sidewinding locomotion, two indexes are sufficient to evaluate the period-1 cycloid locomotion, which are the motion direction vector $\mathbf{e}_{v}$ (defined in (34)) and the average velocity $\bar{V}$ (defined in (35)). Figure 7(a) shows an example of the period-1 cycloid locomotion with gait parameters $G\ = \{ 0,0,3,0,8,1\left | 8 \right .\}$, in which the corresponding transitions, linear displacement vector, and the motion direction vector are denoted.

Fig. 7

Performance of the period-1 cycloid locomotion. (a) Locomotion trajectory and the corresponding transitions based on gait parameters $G\ = \{ 0,0,3,0,8,1\left | 8 \right .\}$. (b) Distribution of the motion direction vectors in space. The blue and red points represent the motion direction vectors corresponding to the 2D period-1 cycloid locomotion in the xoy and yoz planes, respectively. (c) Distribution of the average velocity for $N$_total ranging from 9, 11, 13-30. The relationship between the maximum average velocity $\bar{V}_{\max}$ and $N_{\mathrm{total}}$ is fitted by a quadratic curve (in red); the normalized maximum average velocity $\tilde{\bar{V}}_{\max}$ is denoted by the orange curve. (d) For $N_{\mathrm{total}} = 30$, the relationship between the number of period-1 cycloid gaits corresponding to different ranges of average velocity and the value of $n_{p}$ (Color figure online)

Based on the physical parameters of a single segment, the robot needs at least nine segments to fulfill the conditions for period-1 cycloid locomotion (i.e., (29)). For $N_{\mathrm{total}} = 9,11,13\sim 30$ and the ‘3-5-4-6’ arrangement of the one-side contracted segments, all period-1 cycloid locomotion gaits (72,656 in total) are traversed. The distribution of the terminal points of the motion direction vectors $\mathbf{e}_{v}$ is shown in Fig. 7(c), which does not exhibit a dispersive feature. The terminal points of $\mathbf{e}_{v}$ mainly stay on a few circles with origin (0,0,0), including the circles on the xoy and yoz planes (denoted by blue and red points, respectively).

The relationship between the average velocity $\bar{V}$ and the gait parameters is also examined. Figure 7(c) displays the distribution of the average velocity with respect to the total number of segments $N_{\mathrm{total}}$. It shows that the maximum average velocity $\overline{V}_{\max}$ increases monotonously with $N_{\mathrm{total}}$, and the relationship can be approximated by a second-order polynomial (coefficient of determination $r^{2} = \ 0.9924$, denoted by the red line shown in Fig. 7(c))

$$ \overline{V}_{\max} = - 0.041N_{\mathrm{total}}^{2} + 0.57N_{\mathrm{total}} - 7.53. $$

(42)

The fitted curve could effectively show the upper limit of the reachable average velocity. The maximum normalized average velocity $\tilde{\bar{V}}_{\max}$ (defined in (37)) is also plotted in Fig. 7(b). When $N_{\mathrm{total}}$ is relatively small, $\tilde{\bar{V}}_{\max}$ climbs rapidly with significant fluctuations; when $N_{\mathrm{total}}$ is relatively large, being different from the sidewinding and circular locomotion, a flattening trend is not observed, and $\tilde{\bar{V}}_{\max}$ keeps swelling quickly. This indicates that for the period-1 cycloid locomotion, increasing the number of segments is a feasible approach to enhance the robot’s locomotion capability.

With $N_{\mathrm{total}}\ = 30$, the effect of $n_{p}$ on the number of period-1 cycloid gaits corresponding to different ranges of average velocity is further exemplified, shown in Fig. 7(d). Unlike sidewinding and circular locomotion, the conditions for period-1 cycloid locomotion (i.e., conditions given in (29)) can only be satisfied at certain $n_{p}$ ($n_{p}\ = 4, 8, 9, 12$). This explains why the numbers of admissible gaits for $n_{p}\ = 4, 8, 9, 12$ in circular and period-$k$ cycloid locomotion are diminished (see Fig. 6(g), 6(h) and Fig. 8(f), (g)). With larger $n_{p}$, the achievable average velocities can be higher. For example, when $n_{p}\ = 4$, all gaits correspond to relatively low average velocities within $(0, 20)(\mathrm{cm}/\mathrm{s})$, while for $n_{p}\ = 12$, the achievable range becomes $(10, 46)(\mathrm{cm}/\mathrm{s})$.

Fig. 8

Performance of the period-$k$ cycloid locomotion. (a) Locomotion trajectory and the corresponding transition based on gait parameters $G\ = \{ 0,1,1,1,0,1\left | 2 \right .\}$. (b) The circumcircle of the trajectory on the projection plane. (c) Distribution of the direction vectors in space. The blue and red points represent the direction vectors within the xoy and yoz planes, respectively. (d) Distribution of the circumradius for $N_{\mathrm{total}}$ ranging from 3 to 30. The relationship between the maximum circumradius $R_{\max}$ and $N_{\mathrm{total}}$ is fitted by a linear line (in red); the normalized maximum circumradius $\tilde{R}_{\max}$ is denoted by the orange curve. (e) Distribution of the average velocity $\bar{V}$ for $N_{\mathrm{total}}$ ranging from 3 to 30. The relationship between the maximum average axial velocity $\bar{V}_{\max}$ and $N_{\mathrm{total}}$ is fitted by a quadratic curve (in red); the normalized maximum average axial velocity $\tilde{\bar{V}}_{\max}$ is denoted by the orange curve. (f) For $N_{\mathrm{total}}\ = 30$, the relationship between the number of period-$k$ cycloid gaits corresponding to different ranges of circumradius and the value of $n_{p}$.(h) For $N_{\mathrm{total}}\ = 30$, the relationship between the number of period-$k$ cycloid gaits corresponding to different ranges of average axial velocity and the value of $n_{p}$ (Color figure online)

4.3.2 Performance of the period-k cycloid locomotion

For period-$k$ cycloid locomotion, the robot will regain its heading direction and reach a nonzero linear displacement after $k$ periods, and the shape of the corresponding trajectory is similar to a cylinder. Hence, the trajectory can be characterized by the height, the direction of the central axis, and the radius. Based on this, three indexes are proposed to evaluate the performance of period-$k$ cycloid locomotion, which are the direction vector of the cycloid’s central axis $\mathbf{e}_{\mathrm{Axial}}$, the circumradius of the trajectory $R$, and the average axial velocity $\overline{V}_{\mathrm{Axial}}$ along the central axis.

Note that the cycloid’s central axis is parallel to the vector pointing from the initial position to the last position of the head point after $k$ periods. Hence, the direction vector of the cycloid’s central axial can be calculated as

$$ \mathbf{e}_{\mathrm{Axial}} = \mathbf{D}_{k}/\left \| \mathbf{D}_{k} \right \|. $$

(43)

With this direction vector as the projection axis, the projection plane can be determined. By projecting the trajectory to the projection plane, the circumcircle of the projected trajectory with circumradius $R$ can be determined through numerical methods. The average axial velocity is defined as the average velocity of the robot’s head point along the central axis of the cycloidal trajectory in a period. It can be calculated by projecting the linear displacement vector $\mathbf{D}$ in a period onto the central axis $\mathbf{e}_{\mathrm{Axial}}$, and then divided by the period time $\mu (N_{\mathrm{total}}/n_{p})\Delta t$, i.e.,

$$ \bar{V}_{\mathrm{Axial}} = \frac{\left \| \mathbf{D} \cdot \mathbf{e}_{\mathrm{Axial}} \right \|}{(\mathrm{LCM}(N_{\mathrm{total}},n_{p})/n_{p})\Delta t}. $$

(44)

Figure 8(a) shows an example of the period-$k$ cycloid locomotion with gait parameters $G\ = \{ 0,1,1,1,0,1\left | 2 \right .\}$. The corresponding transitions, linear displacement vector, projection plane, and the direction vector of the cycloid’s central axis $\mathbf{e}_{\mathrm{Axial}}$ are denoted. It is worth noting that the projected trajectory after $k$ periods will overlap the previous one (Fig. 8(b)).

Based on the physical parameters of a single segment, the robot needs at least five segments to fulfill the conditions for period-$k$ cycloid locomotion (i.e., (33)). For $N_{\mathrm{total}} = 5\sim 30$ and the ‘3-5-4-6’ arrangement of the one-side contracted segments, all period-$k$ cycloid locomotion gaits (744,392 in total) are traversed, and the terminal points of the direction vector $\mathbf{e}_{\mathrm{Axial}}$ are plotted in Fig. 8(c). Overall, the points are sparse in distribution. The vectors located within the xoy and yoz planes (denoted by blue and red dots, respectively) account for the main part of the points, while the points located outside the xoy and yoz planes are scares.

Figure 8(d) displays the distribution of the circumradius $R$ with respect to $N_{\mathrm{total}}$. Overall, the range of achievable circumradius expands notably with the increase of $N_{\mathrm{total}}$, and the maximum circumradius $R_{\max}$ exhibits an almost linear relationship with $N_{\mathrm{total}}$, which can be approximated by a linear model (coefficient of determination $r^{2} = 0.925$, denoted by the red line shown in Fig. 8(d))

$$ R_{\max} = 23.34N_{\mathrm{total}} - 99.41. $$

(45)

The curve determined by Eq. (45) can effectively show the upper limit of the reachable circumradius. For the normalized radius defined in (40) (orange curve in Fig. 8(d)), rather than linear growth, it will gradually saturate when $N$_total increases. Note that at $N_{\mathrm{total}} = 17,18,22,23,30$ obvious fluctuations can be observed because the locomotion trajectory is highly sensitive to the gait parameters (see examples in Supplementary, Section S3).

Similarly, the case with $N_{\mathrm{total}} = 30$ is examined in detail to understand the effects of the gait parameters on the distribution of the circumradius. Figure 8(f) shows the distribution of the circumradius with respect to $n_{p}$. Overall, the number of period-$k$ cycloid gaits reduces as $n_{p}$ increases. Among the 126,448 admissible gaits, 97.44% correspond to relatively small circumradii ranging between $(0, 300)(\mathrm{cm})$, and only 192 gaits (0.15%) correspond to large circumradii between $(600, 866)(\mathrm{cm})$, which are achieved when $n_{p} = 13$. Also, the number of period-$k$ cycloid gaits experiences troughs at $n_{p} = 4$ and 8, which is because the conditions for period-1 cycloid locomotion are met (see Fig. 7(d)).

The distribution of the average axial velocity for different values of $N_{\mathrm{total}}$ is also examined, shown in Fig. 8(e). The upper limit of the reachable axial velocity (the maximum axial velocity $\overline{V}_{\mathrm{Axial},\max}$) increases monotonously with $N_{\mathrm{total}}$, which can be approximated by a second-order polynomial (coefficient of determination $r^{2} = \ 0.9996$, denoted by the red curve in Fig. 8(e))

$$ \overline{V}_{\mathrm{Axial},\max} = 0.045N_{\mathrm{total}}^{2} + 0.28N_{\mathrm{total}} - 2.45. $$

(46)

The normalized maximum average axial velocity $\tilde{\bar{V}}_{\mathrm{Axial},\max}$ (defined in (37)) is also investigated, shown in Fig. 8(e) with the orange curve. Rather than the saturation phenomena observed in the sidewinding and circular locomotion, $\tilde{\bar{V}}_{\mathrm{Axial},\max}$ keeps increasing with respect to $N_{\mathrm{total}}$ in an almost constant slope.

Considering the case with $N_{\mathrm{total}} = 30$, we also demonstrate the effects of $n_{p}$ on the number of period-$k$ cycloid gaits corresponding to different average axial velocities (Fig. 8(h)). It reveals that when $n_{p} = 1,2$, all period-$k$ cycloid gaits (35,760 in total) correspond to relatively low average axial velocity within $(0, 10)(\mathrm{cm}/\mathrm{s})$. With the increase of $n_{p}$, relatively high velocities become attainable, while the number of gaits is limited. For example, average axial velocities ranging between $(40, 47)(\mathrm{cm}/\mathrm{s})$ are achievable when $n_{p} = 9\sim 11,13,14$, while the number of gaits is only 60, which accounts for 0.047% of the total period-$k$ cycloid gaits.

4.3.3 Performance of the irrational cycloid locomotion

The trajectory of irrational cycloid locomotion is very similar to the period-$k$ cycloid locomotion, whose shape is also similar to a cylinder. As a result, we still choose the direction vector of the cycloid’s central axis $\mathbf{e}_{\mathrm{Axial}}$, the circumradius of the trajectory $R$, and the average axial velocity $\overline{V}_{\mathrm{Axial}}$ along the central axis to evaluate the performance of the irrational cycloid locomotion. Note that for irrational cycloid locomotion, the robot will not regain its initial heading direction within 3,000 periods. Hence, the direction vector of the cycloid’s central axis cannot be expressed by (43) anymore and is re-defined via

$$ \left ( \mathbf{D}_{k + 1} - \mathbf{D}_{k} \right ) \cdot \mathbf{e}_{\mathrm{Axial}} = \left ( \mathbf{D}_{k + 2} - \mathbf{D}_{k + 1} \right ) \cdot \mathbf{e}_{\operatorname{Axial}} ,k > 1. $$

(47)

Equation (47) indicates that the projection of the linear displacement vector onto the central axis keeps constant in each period, and it can be solved via numerical methods. Based on this direction vector, the projection plane can be determined. By projecting the trajectory to the projection plane, the circumcircle of the projected trajectory with circumradius $R$ can be obtained via numerical methods. The average axial velocity can still be calculated by (44). Figure 9(a) shows an example of irrational cycloid locomotion based on gait parameters $G\ = \{ 0,1,0,2,0,1\left | 1 \right .\}$, in which the linear displacement vector and the direction vector of the cycloid’s central axis $\mathbf{e}_{\mathrm{Axial}}$ are denoted. Figure 9(b) displays the projected trajectory in 30 periods and the corresponding circumcircle. Note that the projected trajectory of each period does not overlap, and they will constitute a dense ring when the number of periods increases.

Fig. 9

Performance of the irrational cycloid locomotion. (a) Locomotion trajectory and the corresponding transition based on gait parameters $G\ = \{ 0,1,0,2,0,1\left | 1 \right .\}$. (b) The circumcircle of the trajectory on the projection plane. (c) Distribution of the direction vectors in space. (d) Distribution of the circumradius for $N_{\mathrm{total}}$ ranging from 3 to 30. (e) Distribution of the average velocity $\bar{V}$ for $N_{\mathrm{total}}$ ranging from 3 to 30. The relationship between the maximum average axial velocity $\bar{V}_{\max}$ and $N_{\mathrm{total}}$ is fitted by a quadratic curve (in red); the normalized maximum average axial velocity $\tilde{\bar{V}}_{\max}$ is denoted by the orange curve. (f) For $N_{\mathrm{total}}\ = 30$, the relationship between the number of irrational cycloid gaits corresponding to different ranges of circumradius and the value of $n_{p}$.(h) For $N_{\mathrm{total}}\ = 30$, the relationship between the number of irrational cycloid gaits corresponding to different ranges of average axial velocity and the value of $n_{p}$ (Color figure online)

Based on the physical parameters of a single segment, the robot needs at least four segments to meet the conditions for the irrational cycloid locomotion. For $N_{\mathrm{total}} = 4\sim 30$ and based on the ‘3-5-4-6’ arrangement of one-side contracted segments, 2,783,152 gaits are admissible for the irrational cycloid locomotion, and they are comprehensively analyzed. Specifically, corresponding to these gaits, the terminal points of the direction vector $\mathbf{e}_{\mathrm{Axial}}$ are plotted in Fig. 9(c). It shows that the direction vectors are dense in spatial distribution, indicating that many directions are available for the cycloid’s central axis. However, it is worth noting that, being different from the period-$k$ cycloid locomotion, direction vectors locating within the xoy plane or the yoz plane are not found.

The circumradius of the trajectory is also studied. Figure 9(d) plots the distribution of the circumradius with respect to $N_{\mathrm{total}}$ in logarithmic coordinate. Overall, the achievable circumradii are densely distributed, and the range gradually enlarges as $N_{\mathrm{total}}$ increases. When $N_{\mathrm{total}} \ge 16$, some dispersed large radii (over $10^{3}$ (cm) or even over $10^{4}$ (cm)) are observed, although their quantities are small. In fact, 99.57% of the irrational cycloid locomotion gaits correspond to the circumradius range $(10^{0}, 10^{3})(\mathrm{cm})$.

The case with $N_{\mathrm{total}} = 30$ is also exemplified to uncover the relationship between the number of irrational cycloid gaits corresponding to different ranges of circumradius and the values of $n_{p}$ (Fig. 9(f)). The number of irrational cycloid gaits reduces steadily as $n_{p}$ increases. Among the 452,470 admissible gaits, 93.86% correspond to relatively small circumradii ranging between $(0, 200)(\mathrm{cm})$, while only 0.33% correspond to large circumradii ranging between $(800, 5119)(\mathrm{cm})$. Particularly, the highest circumradius range $(800, 5119)(\mathrm{cm})$ can only be achieved when $n_{p} = 11,13$.

We further investigate the relationship between the average axial velocity and the total number of segments $N_{\mathrm{total}}$, as shown in Fig. 9(e). As $N_{\mathrm{total}}$ increases, the upper limit of reachable average axial velocity (maximal average axial velocity $\bar{V}_{\mathrm{Axial},\max}$) improves significantly, which can be approximated by a second-order polynomial (coefficient of determination $r^{2} = \ 0.9993$, denoted by the red curve in Fig. 9(e))

$$ \bar{V}_{\mathrm{Axial},\max} = 0.052N_{\mathrm{total}}^{2} + 0.14N_{\mathrm{total}} - 1.63. $$

(48)

The maximum normalized average axial velocity $\tilde{\bar{V}}_{\mathrm{Axial},\max}$ (defined in (37)) is also examined, denoted by the orange curve in Fig. 9(e). Similar to the period-$k$ cycloid locomotion, there is an almost linearly increasing relationship between $\tilde{\bar{V}}_{\mathrm{Axial},\max}$ and $N_{\mathrm{total}}$, without a saturation phenomenon.

Taking the case with $N_{\mathrm{total}} = 30$ into consideration, the effects of $n_{p}$ on the number of irrational cycloid gaits corresponding to different average axial velocity ranges are demonstrated (Fig. 9(g)). Overall, the number of irrational cycloid gaits and $n_{p}$ are inversely correlated, while the achievable average axial velocity range expands with $n_{p}$. When $n_{p} = 1$, all the 62,163 irrational cycloid gaits correspond to relatively low average axial velocities ranging between $(0, 10)(\mathrm{cm}/\mathrm{s})$. When $n_{p}$ is increased to 4, the number of admissible gaits is reduced to 47,980, while 28 gaits could achieve higher average axial velocities ranging between $(20, 30)(\mathrm{cm}/\mathrm{s})$. As $n_{p}$ keeps growing, the number of gaits corresponding to relatively low average axial velocities within $(0, 10)(\mathrm{cm}/\mathrm{s})$ keeps reducing but would never decline to zero. When $n_{p}$ takes a value between 10 ∼14, a wide range of the average axial velocity $(0, 49)(\mathrm{cm}/\mathrm{s})$ could be achieved, although the gaits corresponding to the high average axial velocity range $(40, 49)(\mathrm{cm}/\mathrm{s})$ are rare.

In sum, the above investigation systematically uncovers the relationship between the gait parameters (mainly focused on $N_{\mathrm{total}}$ and $n_{p}$) and the locomotion performance. Considering that the trajectories for different locomotion types are qualitatively different in geometric characteristics, different kinematic indexes are examined to evaluate the locomotion performance. The revealed results, demonstrated in Fig. 5–9 and Table 2, could provide useful guidelines for inverse gait design aiming at different tasks.

5 3D gait planning

With the above-mentioned rich locomotion types, we are interested to know how to choose appropriate gait parameters to reach a given goal point in space. This, however, is a tough problem for spatial locomotion because the gait library is vast and expands exponentially as the number of total segments increases (Fig. 10(a)). For example, for $N_{\mathrm{total}}\ = 3\sim 30$, the total number of gaits is 3,862,188. As a result, the 3D gait planning problem is tacked via the genetic algorithm [39] in this research.

Fig. 10

Bi-objective gait planning. (a) The number of gaits increases significantly with $N_{\mathrm{total}}$. The number of gaits corresponding to different locomotion modes are indicated by different colors. (b)–(f) The Pareto fronts (denoted by red points) of the sidewinding, circular, period-1 cycloid, period-$k$ cycloid, and irrational cycloid locomotion. Particularly, the proximity-optimal gait (red triangle) and the speed-optimal gait (red circle) are marked, respectively. (g) The Pareto front of all locomotion modes (Color figure online)

5.1 Problem definition and objectives

The earthworm-like robot is asked to reach the target position in 3D space from the starting position in terms of the head point. Here, we assume that there is no barrier in the robot’s working environment. The path between the starting and target positions is not prescribed but determined by gait parameters. Hence, the aim of gait planning is to determine the optimal gait so that the robot can reach the target position with the best performance. Generally, the robot is expected to reach the target position accurately and quickly. To this end, two objective functions are defined to evaluate the proximity to the target position and the required time to reach the target position.

Specifically, the proximity to the target position is defined as the Euclidean distance between the target position $\mathbf{x}^{ *} = (x^{*},y^{*},z^{*})^{\mathrm{T}}$ and the robot head position $\mathbf{x}^{t} = (x^{t},y^{t},z^{t})^{\mathrm{T}}$ at current time $t$, i.e.,

$$ f_{1}(G,t) = d(\mathbf{x}^{*},\mathbf{x}^{t}) = \left \| \mathbf{x}^{*} - \mathbf{x}^{t} \right \|_{2}. $$

(49)

The robot is closer to the target position if $f_{1}$ is smaller. The required time for reaching the target position is equivalently defined by the number of transitions (denoted by $f_{2}(G)$) the robot undergoes for reaching the target. It quantifies the speed of the robot. A smaller value of $f_{2}$ suggests that the robot reaches the target more quickly. Note that $f_{2}$ is meaningless if the robot cannot reach the target under a certain gait.

The two objective functions are considered simultaneously when planning the gait for improving the locomotion performance. Fundamentally, this is a multi-objective optimization problem. In this research, it is handled by the genetic algorithm, and the gaits are evaluated numerically. Considering the huge gait library and to improve the optimization efficiency, two stopping criteria are set for the numerical simulation process. Before describing the criteria, the neighborhood of the target position $\mathbf{x}^{ *} = (x^{*},y^{*},z^{*})^{\mathrm{T}}$ is defined, which is as an open ball with the center $\mathbf{x}^{\boldsymbol{*}}$ and the radius $\varepsilon$

$$ B(\mathbf{x}^{*},\varepsilon ) = \{ \mathbf{x} \in \mathbb{R}^{3}:d(\mathbf{x}^{*},\mathbf{x}) = \left \| \mathbf{x}^{*} - \mathbf{x} \right \|_{2} < \varepsilon \}. $$

(50)

Hence, the two stopping criteria can be described as follows.

Criteria 1

If the robot head has already been located within the neighborhood $B(\mathbf{x}^{*},\varepsilon )$ at time $t_{s}$, and through the next transition during the interval ($t_{s}$, $t_{s} + \Delta t$), the Euclidean distance between the current position and the target position (i.e., $f_{1}(G,t_{s} + \Delta t)$) increases with respect to the last transition (i.e., $f_{1}(G,t_{s})$), the numerical simulation will be stopped, and the current gait parameters will be output. The aim of this criterion is to prevent the deterioration of an optimized gait.

Criteria 2

If the robot head has not entered the neighborhood $B(\mathbf{x}^{*},\varepsilon )$, and the Euclidean distance between the current position and the target position keeps increasing for $CN$ consecutive state transitions, the numerical simulation will be stopped and the under-investigated gait will be abandoned. The aim of these criteria is to prevent from spending too much simulation time on a bad gait.

If any of the stopping criteria is triggered, the simulation of the current gait will be stopped, and the optimization process will jump out of the current gait and evaluate the next admissible gait.

5.2 3D gait planning

As an example, we consider the 3D gait planning problem of a 30-segment robot, which possesses 2,783,152 admissible gaits in total. The starting position of the robot’s head point is set as $(0,0,0)^{\mathrm{T}}$, the initial heading direction is toward the positive $y$-axis (i.e., the heading direction vector is $\mathbf{H}_{t\ = 0} = (0,1,0)^{\mathrm{T}}$), and the target position is set as $(400,600,20)^{\mathrm{T}}$. The critical values in Criteria 1 and 2 are set as $\varepsilon = 30$ cm, $CN = 480$. Note that the robot will keep moving along the $y$ axis in rectilinear locomotion. Hence, only sidewinding, circular, period-1 cycloid, period-$k$ cycloid, and irrational cycloid locomotion are included in 3D gait planning.

Figure 5–9 have revealed that the gaits with larger $n_{p}$ are more likely to induce a relatively high average velocity of the robot. However, the gaits with larger $n_{p}$ also give rise to larger stride lengths that may keep the robot head from entering the neighborhood of the target position. In other words, the two objective functions may contradict each other, and tradeoffs are needed when searching for the optimal gait. As a result, the Pareto front, which is the set of nondominated solutions [52], is sought so that tradeoffs can be made within this set, rather than considering the full gait library. Figure 10(b) ∼10(f) respectively displays the Pareto front (denoted by the red points) corresponding to the sidewinding, circular, cycloid, period-$k$ cycloid, and irrational cycloid locomotion. The dominated solutions are plotted by the grey point.

For sidewinding locomotion (Fig. 10(b)), the Pareto front consists of four points, which are connected by solid lines. These four solutions are considered as optimal since no objective can be improved without sacrificing at least one other objective. Among them, two gaits are special. The first one $G = \{ 11,5,5,1,1,6|1\}$ (denoted by the red triangle in Fig. 10(b)) is the optimal gait in terms of proximity ($f_{1} = 4.62$ cm), which means that under this gait, the robot can reach the target position more accurately than the other gaits. The second one $G = \{ 7,4,4,0,0,1|14\}$ (denoted by the red circle in Fig. 10(b)) is the optimal gait in terms of the required time, indicating that under this gait, the robot can enter the neighborhood of the target position with the least number of transitions ($f_{2} = 26$). For the other four locomotion modes, the proximity optimal and the required-time optimal gaits can also be identified. Integrating the five cases, the global Pareto front can be obtained, shown in Fig. 10(g). The proximity-optimal ($f_{1} = 4.62$ cm) gait is a sidewinding locomotion gait with parameters $G = \{ 11,5,5,1,1,6|1\}$, while the speed-optimal ($f_{2} = 21$) gait is a circular locomotion gait with parameters $G = \{ 22,1,0,0,0,1|6\}$. Overall, the optimization results, including the global Pareto front and the Pareto front for each locomotion mode, could provide useful guidelines for selecting gait aiming at different objectives.

6 Summary and conclusions

Previous research has uncovered the relationship between the gaits and the locomotion performance of the earthworm-like robot in the 1D and 2D scenarios, while the investigation of spatial locomotion is a complete blank. To advance the state of the art, this research systematically investigates the 3D locomotion of the earthworm-like robot from five aspects: multibody kinematic modeling, 3D gait generation, locomotion classification, spatial locomotion characteristics, and 3D gait planning.

First, a generic $N$-segment multibody kinematic model is developed in this research. The model not only captures the main deformation characteristics of the origami earthworm-like robot prototype, but also applies to other metameric robots with similar 3D deformability. Based on this model and learning from the fundamental locomotion mechanism, i.e., the retrograde peristalsis wave, a generic gait-generation algorithm is proposed, based on which, all admissible locomotion gaits can be generated. By examining the characteristics of the trajectory, the robot’s locomotion is classified into four major types, and further, ten modes, and their defining conditions in terms of the gait parameters are derived. Among these modes, 3D sidewinding, 3D circular, and 3D cycloid locomotion are observed for the first time. For each mode, different indexes, including the average velocity, the direction vector, and the trajectory’s circumradius, are comprehensively evaluated to clarify the relationship between the robotic locomotion performance and the gait parameters.

With a vast gait library for spatial locomotion, the 3D gait planning problem is also tackled in this research. Aiming at reaching the target position both quickly and precisely, a bi-objective optimization of the gait parameters is carried out. Two objective functions are defined to evaluate the proximity to the target position and the required time to reach the target position. Noting that these two objective functions are always contradictory, the Pareto front is determined via the genetic algorithm so that tradeoffs between the accuracy and the speed can be made within this set.

This research is a crucial step toward a generalized 3D gait analysis framework. At the current stage, the proposed gait generation, analysis, and planning algorithms still lack an experimental verification, because a mature robot platform for spatial gait study is not yet available. As a result, this research offers not only important guidelines but also a strong impetus to the design of earthworm-like robots with spatial locomotion capability. Another possible topic for future research is the dynamic analysis of spatial locomotion by considering the actuation force and the environmental contact [53]. In this study, the actuation and the anchoring are all assumed to be ideal, which confines the problem within the kinematic realm. However, the assumptions cannot be always met for a practical robot prototype, and a fine dynamic model by incorporating the limited actuation force and the nonsmooth friction force becomes a necessity. Previous studies on the dynamics of earthworm-like robot rectilinear locomotion [9, 26] and snake-like robot locomotion [54] could provide some reference.