1 General introduction

1.1 Background

In recent years, there is a rising demand for locomotion robots that are capable of moving in confined space and hazardous environment, such as burrowing through rubbles to search for earthquake survivors, navigating in slender industrial pipelines to inspect and clean foreign objects, performing covert action in battlefield to gather information, and entering in human gastrointestinal (GI) tracts to examine and treat diseases. These potential applications fostered a significant amount of research on robot locomotion mechanisms, such as wheeled, legged and crawling mechanisms. For some wheeled and legged robots, the complication in structure, weakness in controllability and difficulty of miniaturization limit their further development for application in restricted environment [1]. On the other hand, crawling robots, by either changing their own configuration or driving internal mass(es) [2–4], can move forward in various media without protruded components for propulsion (e.g., wheels, oars, legs and jets, etc.). They normally possess simpler structure and better controllability, and can be miniaturized more easily than traditional wheeled- and legged-robots.

Biomimetics is one of the most important approaches to promote the state-of-the-art of robotics. Recently, the good locomotion performance of earthworms in various environments (e.g., on dry rocks, on moist earth and in flowing mud) has attracted much attention from researchers. A great number of worm-like robots have been developed and tested from many aspects [5–17], among which most efforts have focused on the design and experimental verification of the appropriate actuation mechanisms [5–12]. In these studies, robots were always modeled as a chain of a few (low and specific number) segments, and only simple gaits were utilized to achieve linear locomotion. A general model with arbitrary number of segments and general issues of gait design and gait analysis were not investigated in [5–12].

As the number of segments in the robot increases, multiple types of gait are possible. Different types of gait could lead to different kinematic and dynamic behaviors, and therefore, understanding the correlation between gaits and locomotion performance becomes crucially important for robot development. However, not much research efforts were devoted to addressing these issues. Steigenberger, Behn and Zimmermann, etc. [13–16] systematically studied a worm-like N-mass-point system interconnected by (N−1) kinematic drivers or viscoelastic force actuators. Considering both kinematics and dynamics, gaits were generated by arranging the resting mass points [15]. Adaptive control of the uncertain system (unknown actuator and environment parameters) was studied in [13, 14] to track a prescribed kinematic gait. For a certain environment-dependent speed of the system, gait shift was also considered to find the optimal gait with respect to low spike forces or actuator forces [16]. Chen, Yeo and Gao [17] studied the gait generation problem for an N-segment inchworm-like robot through exhaustive search in a directed graph. While these studies on gaits initiated some new directions, there still exist many issues to be addressed, which will be stated in Sect. 2.

1.2 Biological inspiration

To better learn from the earthworms, characteristics of earthworms’ morphology structure and locomotion mechanism will be briefly introduced here. Inspiration gained from these characteristics will be presented.

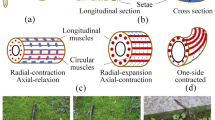
In view of morphology structure, three features deserve our attention [18]. The first one is the metameric segmentation of earthworm. The earthworm’s body is divided into a large number of segments (for some species more than 100 segments) by septa, which mechanically isolate each segment, keeping the volume of coelomic fluid unchanged, as is shown in Fig. 1(a). The metamerism ensures that each segment can work independently, i.e., shortening or elongating of one segment does not influence the state of adjacent segments. The second feature is the muscle layout in individual segment. The muscular system consists of two muscle layers, namely, circular muscles and longitudinal muscles, which can be observed in both Fig. 1(a) and 1(b). Due to the constant-volume of coelomic fluid, these two muscles function antagonistically to each other, forming the hydrostatic skeleton of the earthworm. Contraction of circular muscles will reduce the diameter but extend the length of the segment; while contraction of longitudinal muscles will increase the diameter but shorten the length. Generally, it is believed that the longitudinal muscles play a major role in earthworm’s locomotion [6, 18]. The third feature is the setae, which are connected to the longitudinal muscles. During the contraction of longitudinal muscles, setae are stretched out to form extra contact with the environment, increasing resistance or inducing temporary anchorage with the environment. It is the setae that make the directed locomotion of earthworm possible.

Fig. 1
figure 1

Schematic illustrations of an earthworm’s morphology structure and locomotion mechanism: (a) longitudinal section, (b) cross-section, (c) continuous trace of locomotion, redrawn based on [19]. In (a) and (b), only the hydrostatic skeleton and setae are labeled, all the other internal organs and nervous system are not labeled. In (c), a peristalsis wave travels in the opposite direction to locomotion, indicated by dashed curves

Full size image

In view of locomotion mechanism, there are three features that require our attention [18, 19]. The first one is the temporary anchorage. Figure 1(c) schematically shows a continuous trace of an earthworm’s locomotion on the ground or inside a burrow. The dark-colored segments are at their shortest but widest (fattest) states as the longitudinal muscles are fully contracted. They have additional setae contact with the ground or the burrow, and hence, temporarily anchor themselves to the environment and prevent the earthworm from slipping backwards. The light-colored segments are at their longest but thinnest states as the circular muscles are fully contracted. These segments can be free from any contact with the environment and as a result experience little resistance. The second feature is the waves of muscular contraction. The alternative contraction of circular and longitudinal muscles in each segment (i.e., elongating and shortening of each segment) leads to the forward motion of the earthworm (see the transitions in Fig. 1(c)). The fully shortened segments (dark-colored) move in the opposite direction to the crawling of the earthworm in the form of a peristalsis wave, i.e., retrograde peristalsis wave, which is considered as the most representative feature of the earthworms’ locomotion. The third feature is the adaptability of gaits. Earthworms’ locomotion may differ significantly when they move in different media (on glass or on earth), in different weather conditions (dry or moist) and in different operating situations (safe or dangerous) [20]. They possess the ability to adjust their muscular activities, and hence, the gait, to adapt to the environment, to move efficiently and to preserve themselves.

Overall, the aforementioned characteristics in the earthworms’ muscular structure and locomotion mechanism provide many guidelines for developing an efficient earthworm-like robot. From a structure perspective, the metameric segmentation of the earthworm suggests that the robot could consist of many independent segments. In this way, the robot can have sufficient degrees of freedom to exhibit various gaits. The antagonistic layout of the longitudinal and circular muscles in an earthworm represents a simple mechanism for actuation and anchoring, which can be mimicked in robot design as well. Similar to the setae, the robot surface can also feature anisotropic friction coefficient to enable directed locomotion and improve locomotion efficiency. From the locomotion mechanism perspective, the temporary anchorage and the retrograde peristalsis wave of muscular contraction tell us how to effectively arrange and control the many segments in the robot, i.e., how to construct gaits. The earthworm’s good adaptability of gaits to environments indicates the necessity of having multiple choices on locomotion gaits.

2 Problem statement and research objectives

Based on reviewing the previous work and inspired by the earthworm, three core issues need to be further addressed to advance the state of the art of earthworm-like robot design and locomotion performance optimization: modeling, gait analysis and experiments. These are discussed in detail in Sect. 2.1 through 2.3, respectively. The research objectives will be presented in Sect. 2.4.

2.1 Modeling

The first aspect to be discussed is the kinematic modeling idea of the earthworm-like robots. On the one hand, in many previous built earthworm-like robots [5–12], actuators were separated from the anchors, and in some cases, actuators were separated from the body segments (or mass points). However, considering the real earthworm, almost every segment takes on multiple roles of being both actuator and anchor simultaneously. Recently, several earthworm-like robots based on SMA actuators [5], pneumatic and fluidic actuators [8, 10, 21] and rubber balloons [11] were designed following the idea that both actuator and anchor are integrated into one body segment. Such a modeling idea can significantly reduce the complexity of the robot, and hence, improve the reliability and ease the difficulty for control. On the other hand, with the purpose of designing and experimentally verifying actuation mechanisms for earthworm-like locomotion, most previous research focused on robots consisting of a specific number of segments [5–12]. Robots with general and arbitrary number of segments were studied in [13–16], where, however, actuator, anchor and body segment were separated. Notice that an earthworm possess a large number of segments, and an earthworm-like robot with more segments could have richer locomotion patterns. Therefore, based on the idea of integrating actuator, anchor component and body segment together, building a general kinematic model with large and arbitrary number of segments would greatly contribute to the bio-inspired design of earthworm-like robots.

Another aspect that needs attention is the dynamic modeling of earthworm-like robots. In previous designs, ideal anchorage (no slippage) and ideal actuator (unlimited actuation force) were assumed [5–12]. Such an assumption helps to understand the kinematics of locomotion, but fails to describe the dynamic features. In terms of anchorage, previous work indicated that the experimental achieved stride/speed is always lower than the theoretical prediction, and one of the major reasons is that the anchors fail to work ideally, causing the robot as a whole to slip backward [5, 7, 8, 12]. Besides, notice that active spikes require additional actuators to drive them [22], which may increase the system complexity and decrease the reliability. Moreover, in some sensitive and vulnerable media (e.g., inside human’s GI tracts), spikes/bristles are not suitable because they may damage the media. If spikes/bristles are not present at the surface of the robot, friction forces have to serve the role of the anchoring force (e.g., inside the human GI tracts, the anisotropic friction forces are provided by the microvilli; and in underground burrows, the friction forces are provided by the irregular soil). Hence, instead of ideal spikes/bristles, considering the non-ideal anchoring forces provided by friction in earthworm-like robots is a more general and meaningful task. Similarly, in terms of actuators, they may fail to output enough forces to drive the robot when the number of segments is large. Hence, the ideal-actuator assumption is not suitable for analyzing the dynamics of the robots, and non-ideal actuating forces should be considered in a dynamic model. Consequently, studying a dynamic model with non-ideal actuating force and non-ideal anchoring force can lead to a comprehensive understanding of the dynamic behavior of the earthworm-like robots, thus providing sound knowledge base for future better robot design.

2.2 Gait analysis

Since many previous studies focused on robots with low and specific number of body segments, simple motion gaits (patterns) are enough to achieve effective forward locomotion and to verify actuator performance [5–12]. However, once the number of segments is relatively large, changing of gaits might induce a huge difference in locomotion performance. Noticing that the earthworms can exhibit different gaits in different environment, it makes sense to systematically construct various gaits in an N-segment earthworm-like robot, and further, to study the effects of gaits on the kinematics and dynamics of the robot.

For the inchworm-like robot, single-stride and multiple-stride gaits were constructed through exhaustive search [17]. For the worm-like N-mass-point system, gait construction was also studied [15]. In their constructed gaits, more than one mass point can anchor with the ground, according with the real earthworm situation that several fully-shortened segments act as anchor (see the dark segments in Fig. 1(c)). However, it is assumed that only a pair of actuators can deform simultaneously (one in contracting state and one in relaxing state, locating in front of and behind the anchor, respectively), which is quite different from the real earthworm that multiple segments work at a time (see the transitions between two time instants in Fig. 1(c)). Besides, sometimes in a real earthworm, more than one anchor point can coexist, which has not been considered in previous studies. For these reasons, it is worthwhile to consider a more general problem of gait generation, i.e., how to construct gaits with multiple anchoring segments, multiple pairs of deforming segments, and multiple anchor points in a robot.

The purpose of studying gait is to explore the relationship between the gait design and the locomotion characteristics of the robot. However, only little research has focused in this field. In [16], an interesting topic of gait shift, was first put forward and studied. By shifting gaits according to environment changes, the robot can achieve an optimal speed while maintaining low anchor and/or actuator force requirements. The present research will employ a new philosophy to deal with the gait analysis. First, for the given actuator and working environment, the critical conditions for actuator-overload and anchor-slippage will be explored, respectively. Then, the relationship among physical parameters, gait patterns and locomotion behavior of the robot will be studied. Gait optimization will be carried out to maximize the average speed of the robot. Understanding these issues is important to the gait design and optimal control of the earthworm-like robots.

2.3 Experiments

In previous experimental studies, many earthworm-like robots have been prototyped and tested, with the purpose of verifying the effectiveness of new actuation mechanism or overall-design [5–12], and only simple gaits have been adopted to control these robots. To the authors’ knowledge, there has been no systematic experimental study specifically on locomotion gaits of earthworm-like robots. The experiments to be carried out in this paper aim to verify the results on gait generation and gait analysis, rather than to test a new robot. However, to this end, a robust robot platform is still necessary. The robot prototype should reflect the key characteristics of the constructed models, and at the same time should have simple design, should be easily actuated and should be able to effectively and efficiently perform locomotion. The experimental gait studies and the obtained result would greatly enhance the understanding and utilization of locomotion gaits in earthworm-like robots.

2.4 Research objectives

Based on the above arguments, the objectives of this research are to develop generic models of the earthworm-like robot, to systematically investigate the correlation between the gait and the locomotion characteristics of the earthworm-like robot, and to experimentally investigate the gait and validate the analytical results. The outcome of this research can greatly advance the state-of-the-art of the earthworm-like robots, including robot design and locomotion gait design. To achieve these objectives, several progressive research tasks will be carried out: (a) develop an N-segment kinematic model of the earthworm-like robot based on the idea of integrating actuator and anchor component into an individual body segment; (b) evolve the kinematic model into a dynamic model by incorporating non-ideal anchoring forces and non-ideal actuators, and to derive the critical conditions for actuator-overload and anchor slippage; (c) systematically generate locomotion gaits in a most general pattern; (d) investigate the relationship among physical parameters, gait patterns and locomotion behavior of the robot; (e) optimize the gait design for both kinematic and dynamic models with the purpose of maximizing average speed; (f) experimentally validate the effectiveness of the gait generation algorithm and verify the results of gait analysis via an earthworm-like robot prototype.

The paper will be divided into two parts, Part A and Part B. Part A will mainly discuss the issues of modeling and gait generation (tasks (a) to (c)). Part B will focus on gait analysis and experiments (tasks (d) to (f)).

3 Kinematic model

In this section, a new N-segment kinematic model of the earthworm-like robot, developed based on the inspiration gained from the earthworm and the idea of integrating actuator and anchor into an individual segment, is presented. Kinematics of a single segment as well as the locomotion mechanism and average speed of the robot are derived.

3.1 Kinematics of a single segment

The kinematic model is made up of N identical segments interconnected through non-deformable connectors, as illustrated in Fig. 2(a). Each segment has axisymmetric configuration as a cylinder and works as an actuator with similar characteristics as an earthworm’s segment. Hence, each segment has two states, namely, fully relaxed state and fully contracted state, denoted by binary values ‘0’ and ‘1’, respectively. Segment at state ‘0’ has the longest length l max but the smallest diameter d min; while segment at state ‘1’ has the shortest length l min but the largest diameter d max, as is shown in Fig. 2(b) and 2(c). As a result, during the transitions ‘0→1’ and ‘1→0’, the stroke of a segment is

$$ \Delta l = l_{\max} - l_{\min}. $$
(1)
Fig. 2
figure 2

An N-segment kinematic model of an earthworm-like robot: (a) a line of separated segments from #1 to #N, (b) fully relaxed state ‘0’ of a segment, (c) fully contracted state ‘1’ of a segment

Full size image

Temporary anchorage is a key factor for the earthworm-like locomotion. In this kinematic model, it is assumed that segments at state ‘0’ have no contact with the environment (see Fig. 2(b)), while segments at state ‘1’ have full contact with the environment due to the radial expansion. When the robot moves on the ground or inside a burrow, extra friction will occur at the contact surface between the fully contracted segments (state ‘1’) and the ground or the sidewalls of the burrow, forming a temporary anchorage in a similar way as the earthworm does (see Fig. 2(c)).

During one transition, four actuating actions are possible to take place in a single segment, which are listed in Table 1. Hence, during each transition, segments can be classified into four types based on their current actuating actions, namely, contracting segments, relaxing segments, temporarily anchoring segments (for brevity, anchoring segments) and unactuated segments. Deformation of a segment corresponding to each action is listed in Table 1. It is worth mentioning that each segment can switch its types during different transitions.

Table 1 Four actuating actions of a single segment
Full size table

As a kinematic model, it is reasonable to adopt the following two model assumptions on each segment.

Model Assumption 1

(Ideal anchors)

The friction/anchoring force generated from the anchoring segments are strong enough to prevent them from slipping backward when their adjacent segments are contracting or relaxing.

Model Assumption 2

(Ideal actuators)

The actuating forces generated from the contracting and relaxing segments are large enough to pull/push any number of adjacent segments forward.

3.2 Locomotion mechanism

Similar as the locomotion of the real earthworm, displacement of the robot during one transition is induced by the contracting and relaxing segments, providing that the anchoring segments stay at rest. Hence, we say that the locomotion of the robot is driven by a “driving module”, defined as follows:

Definition 1

(Driving module)

A driving module is a group of segments that actually drive the robot forward. During a transition, a driving module is composed of contiguous contracting segments, anchoring segments and relaxing segments. To ensure a forward locomotion, relaxing segments have to locate in front of the anchoring segments, while contracting segments have to locate behind the anchoring segments. Contracting and relaxing segments are required to deform simultaneously during a transition.

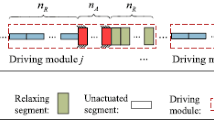
Figure 3 shows a general driving module made up of n C contracting segments, n A anchoring segments and n R relaxing segments. In total, the driving module contains (n C +n A +n R ) segments. Here, n C , n A and n R are all positive integers. At time instant t 0, the leftmost segment in a random jth driving module is labeled as segment (1,j). Other segments in this driving module can be numbered in turn so that the rightmost segment is (n C +n A +n R ,j). Denote the time for one transition as Δt. During the transition from t 0 to (t 0+Δt), the n A anchoring segments temporarily anchor with the environment and keep still, the n C contracting segments pull themselves and the adjacent segments forward, and the n R relaxing segments push themselves and the adjacent segments forward. Based on the model assumptions and kinematics law, the relative displacement of each segment during the transition can be expressed (the front-end position of each segment is used as the location marker of the displacement, sub-indexes (□,j) are the labels of segments in the jth driving module):

(2)
Fig. 3
figure 3

An illustration of a general driving module composed of n C contracting segments, n A anchoring segments and n R relaxing segments. The driving modules at time instants t 0 and (t 0+Δt) are indicated by dashed rectangles. The locomotion direction of the driving module is assumed to be right. Legend will remain in effect in later discussion

Full size image

In order to preserve the configuration of the driving module and obtain a steady-state locomotion, the number of contracting segments has to equal to the number of relaxing segments in a driving module, i.e.,

$$ n_{C} = n_{R}. $$
(3)

As a result, at the time instant (t 0+Δt), the head-end displacement \(x_{2n_{R} + n_{A},j}\) and the tail-end displacement x 0,j of the driving module are the same and equal to Δx, as is marked in Fig. 3,

$$ \Delta x = x_{0,j} = x_{2n_{R} + n_{A},j} = n_{R}\Delta l. $$
(4)

It is worth noting that if condition (3) is satisfied, the driving module as a whole will move backward regularly. As is revealed in Fig. 3, during the transition, the driving module travels backward by n R segments. It can be predicted that during the next transition that begins at time instant (t 0+Δt), the driving module will travel backward by another n R segments. Like the earthworm, such backward traveling of driving module is a reflection of the retrograde peristalsis wave.

As is mentioned in Sect. 2.2, several anchor points, i.e., several driving modules, can coexist and work simultaneously in a robot. To ensure a regular steady-state motion, all the driving modules in the robot are assumed to be identical, i.e., each driving module shares the same configuration of segments. For convenience, we use (n A ,n R ) to denote the configuration of a driving module composed of n A anchoring segments, n R contracting and n R relaxing segments.

Notice that the unactuated segments do not produce any deformation but just play a connecting and transmission role. For convenience, it is assumed that the (N−k(n A +2n R )) unactuated segments are concentrated, and without loss of generality, are located at the head of the sequence at the initial instant. Therefore, a general N-segment kinematic model with k driving modules (n A ,n R ) and (N−k(n A +2n R )) unactuated segments can be built, which is displayed in Fig. 4. In a global numbering system, the very end segment is labeled as #1, and numbering in turn, the very front segment is labeled as #N.

Fig. 4
figure 4

A general N-segment kinematic model of the earthworm-like robot with k driving modules (n A ,n R ) and N−k(n A +2n R ) unactuated segments

Full size image

Next, the average speed of the N-segment robot is derived. As is mentioned earlier, during each transition Δt, the driving module will move backward by n R segments. Keeping moving backward, this driving module needs μ(N/n R ) transitions to return to its original position, where μ>0 is the smallest integer that makes the number of transitions μ(N/n R ) to be an integer. If the quotient (N/n R ) is already an integer, then the coefficient μ=1. As a result, the motion period T of the robot is

$$ T = \mu (N/n_{R})\Delta t. $$
(5)

Notice that the anchoring segments in the additional driving modules will limit the transmission of displacement induced by adjacent driving modules. The very front and very end driving modules, in fact, determine the displacement of the N-segment robot as a whole during a transition. Hence, provided that each driving module is identical, the displacement of the whole robot during a transition is the same with that of a single driving module, i.e., Δx=n R Δl. Then, for the period T, the tolerable displacement of the robot can be obtained as

$$ X_{\mathrm{tolerable}} = \mu (N/n_{R})\Delta x = \mu N\Delta l. $$
(6)

When a driving module moves to the rear part of the system, it will continue propagating to the front part. However, the displacement of the robot will be limited because of the rear-front transition. Figure 5 shows the locomotion of a 6-segment kinematic model with one driving module (n A =2,n R =2). The displacement during each transition is identified, from which, displacement loss induced by rear–front transition can be observed. Generally, for a driving module (n A ,n R ), during a rear–front transition, there will be a displacement loss (n A +n R )Δl due to the re-contracting and re-anchoring of the head segments. Hence, for the period T, the displacement loss of a driving module gives

$$ x_{\mathrm{loss}} = \mu (n_{A} + n_{R})\Delta l. $$
(7)
Fig. 5
figure 5

A 6-segment robot with one driving module (n A =1,n R =2), with displacement loss during the rear–front transition. During the first transition, segments #3, #4 and #5, #6 are contracting and relaxing, respectively, inducing a 2Δl displacement of the robot; during the second transition, although segments #3 and #4 are elongating, the robot only make a global displacement of Δl because of the re-contracting of the head segment #6; during the third transition, segment #6 is anchoring with the environment, and segments #4 and #5 are re-contracting, which completely prevents the robot achieving any global displacement

Full size image

In sum, during a period, the global displacement of the N-segment robot with k driving modules (n A ,n R ) is

$$\begin{aligned} X =& X_{\mathrm{tolerable}} - k \cdot x_{\mathrm{loss}} \\ =& \mu N\Delta l - k \cdot \mu (n_{A} + n_{R})\Delta l = \mu \bigl[N - k(n_{A} + n_{R}) \bigr]\Delta l. \end{aligned}$$
(8)

Then the average speed can be obtained as

$$ \bar{V} = \frac{X}{T} = \frac{\mu [N - k(n_{A} + n_{R})]\Delta l}{\mu (N/n_{R})\Delta t} = \frac{N - k(n_{A} + n_{R})}{N/n_{R}} \frac{\Delta l}{\Delta t}. $$
(9)

For a worm system with kinematic drives, a similar expression of the average speed was given in [23].

4 Gait generation

In this section, gaits are systematically generated for the metameric earthworm-like robot. Definitions, constraints and gait generation algorithm are given, with several gait examples as illustration. It is worth noting that the constructed gaits follow the basic kinematics law, and applies to both the kinematic and dynamic models.

4.1 Definition

To clearly describe the locomotion gait, the following two definitions are given.

Definition 2

(State)

The state of an N-segment earthworm-like robot describes the state of each segment. It is an N-tuple vector \(q = (s_{1}^{t},s_{2}^{t},\ldots,s_{N}^{t})\) with binary numbers \(s_{i}^{t} \in \{ 0,1\}\), where ‘0’ and ‘1’ denote the fully relaxed state and the fully contracted state of a segment, respectively, t is the current time instant.

Definition 3

(Gait)

The gait of an N-segment earthworm-like robot describes the discrete transition of states with respect to time. It is a sequence of states (q 0,q 1,q 2,…,q f ), where q 0 is the initial state, and q f is the final state. To ensure periodicity, it is required that q 0=q f .

As an example, the gait for the locomotion shown in Fig. 5 is (q 0,q 1,q 2,q f ), where q 0=(0,0,0,1,1,1), q 1=(0,1,1,1,0,0), q 2=(1,1,0,0,0,1) and q f =(0,0,0,1,1,1).

4.2 Gait parameters and constraints

According to the N-segment kinematic model in Fig. 4, the construction of locomotion gaits depends on the following four parameters:

  • The total number of segments, N

  • The number of driving modules, k

  • The number of anchoring segments in a driving module, n A

  • The number of relaxing/contracting segments in a driving module, n R

These parameters are all positive integers, and are not independent of each other. Instead, several constraints have to be satisfied to ensure correctness of the kinematics.

First of all, referring to the definition on driving module, we have

$$ k \ge 1,\qquad n_{A} \ge 1,\qquad n_{R} \ge 1. $$
(10)

Secondly, the total number of segments N should not be smaller than the number of segments in k driving modules, i.e.,

$$ N \ge k(n_{A} + 2n_{R}). $$
(11)

For any fixed value of N, conditions (10) and (11) define the region where the gait parameters N, k, n A and n R can locate. As an example, for an 11-segment robot with different number of driving modules, regions of admissible values for n A and n R are displayed in Fig. 6. The dots in the regions represent the integer values that n A and n R can take. Notice that by increasing the number of driving modules, the admissible region for gait n A and n R shrinks considerably, meaning fewer choices for gaits.

Fig. 6
figure 6

Regions of gait parameters n A and n R according to constraints (10) and (11), where the total number of segments N=11, the number of driving modules k=1, 2 and 3. The region for k=3 is included in the region for k=2, which is further included in the region for k=1. The dots stand for the integral values that n A and n R can take

Full size image

4.3 Gait algorithm

Based on the locomotion mechanism, especially the retrograde peristalsis waves, a gait generation algorithm is put forward to construct the locomotion gaits of the metameric earthworm-like robot. Figure 7 shows the routine of the gait generation algorithm.

Fig. 7
figure 7

Routine of the gait generation algorithm

Full size image

The core of this algorithm is the transition \(s_{i}^{t_{h}} = s_{i - n_{R}}^{t_{h - 1}}\), i.e., during each transition, the state of the robot moves backward by n R segments. It is a full reflection of the retrograde peristalsis wave. Following this algorithm, providing that the gait parameters (N,k,n A ,n R ) and the initial state \(q_{t_{0}}\) are eligibly given, all the subsequent states of the robot, and hence, the gait, can be determined. The generated gaits not only work for the kinematic model, but are also valid in the dynamic model to be discussed later. In what follows, for simplicity, we will always use the gait parameters (N,k,n A ,n R ) to denote the gait.

4.4 Gait examples

To demonstrate the gait generation algorithm, for N=6, four gaits (satisfying the constraints (10) and (11)) are illustrated in this subsection as an example. Corresponding to the four gaits, the spatial and temporal distribution of the robot segments as well as the sequence of states are shown in Fig. 8(a) to 8(d), respectively. Peristalsis waves are observed in all gaits (marked by oblique lines). The waves travel in the opposite direction to locomotion, and as a result are retrograde peristalsis waves, which are analogous to those in earthworms.

Fig. 8
figure 8

Four gaits of a 6-segment kinematic model of the earthworm-like robot: (a) k=1, n A =1, n R =1, (b) k=1, n A =3, n R =1, (c) k=1, n A =2, n R =2, (d) k=2, n A =1, n R =1. The spatial and temporal distributions of the robot segments as well as the sequence of states (gaits) are shown. Retrograde peristalsis waves are denoted by oblique lines. Displacements during transitions are labeled

Full size image

Especially, in Fig. 8(d), there are two driving modules in a system, corresponding to two retrograde peristalsis waves.

Figure 8 reveals that the robot’s locomotion varies greatly due to the change of gaits. These changes also lead to the change of global displacement in a specified period of 6Δt, and hence, the change of average speed. It is these phenomena that arouse our interest on the analysis and optimization of the locomotion gaits, which is one of the focuses of Part B.

5 Dynamic model

In the N-segment kinematic model developed in Sect. 3, anchors and actuators are all assumed to be ideal. In this section, these assumptions are relaxed so that an N-segment dynamic model of the earthworm-like robot considering actuator-overload and anchor-slippage can be built.

The definition on driving module (Definition 1) and the configuration of the N-segment kinematic model (Fig. 4) still apply in the N-segment dynamic model. However, Assumptions 1 and 2 are no longer required. For gait design, both the kinematic and dynamic models use the same definitions on state and gait (Definitions 2 and 3) and the same gait generation algorithm shown in Fig. 7.

In what follows, dynamics of a single segment will be studied first. Then, equations for the N-segment dynamic model will be derived, and critical conditions for actuator-overload and anchor-slippage will be studied.

5.1 Dynamics of a single segment

Figure 9 shows the deformation of a contracting segment and an relaxing segment (locating at the left and right side of the anchoring segments, respectively) during a transition from t 0 to (t 0+Δt). The dashed segments represent the configurations at time instant t 0. Notice that during the transition, the length of the contracting segment changes from l max to l min, while the relaxing segment is just the opposite, changing from l min to l max. At a time instant t∈(t 0,t 0+Δt), the lengths of the contracting and relaxing segments are denoted by l C (t) and l R (t), respectively. Hence, the contracting and relaxing velocities \(\dot{x}_{C}, \dot{x}_{R}\), contracting and relaxing accelerations \(\ddot{x}_{C}, \ddot{x}_{R}\) (denoted by the velocities and accelerations at point C and point R, respectively) can be expressed as

$$ \begin{array}{rcl} \dot{x}_{C}(t) &=& - \frac{\mathrm{d} ( l_{C}(t) - l_{\max} )}{\mathrm{d}t} = - \dot{l}_{C}(t),\qquad \dot{x}_{R}(t) = \frac{\mathrm{d} ( l_{R}(t) - l_{\min} )}{\mathrm{d}t} = \dot{l}_{R}(t), \\ \ddot{x}_{C}(t) &=& - \frac{\mathrm{d}^{2} ( l_{C}(t) - l_{\max} )}{\mathrm{d}t^{2}} = - \ddot{l}_{C}(t),\qquad \ddot{x}_{R}(t) = \frac{\mathrm{d}^{2} ( l_{R}(t) - l_{\min} )}{\mathrm{d}t^{2}} = \ddot{l}_{R}(t), \end{array} $$
(12)

where

$$ \begin{array}{l} l_{C}(t) = \bigl( 1 + \varepsilon_{C}(t) \bigr)l_{\max}, \\ l_{R}(t) = \bigl( 1 + \varepsilon_{R}(t) \bigr)l_{\min}. \end{array} $$
(13)

ε C (t) and ε R (t) are the strains of the contracting and relaxing segments, respectively.

Fig. 9
figure 9

Dynamics of a single segment: (a) deformation of a relaxing segment and a contracting segment during a transition (t 0,t 0+Δt); (b)–(d) \(\ddot{\varepsilon} - t\), \(\dot{\varepsilon} - t\) and ε−t relations of the relaxing segment (solid curves) and contracting segment (dotted curves)

Full size image

To ensure the periodicity and continuity, the contracting and relaxing processes should meet the following conditions on displacement and velocity:

$$\begin{aligned} &\begin{array}{l} l_{C}(t_{0}) = l_{\max},\qquad l_{R}(t_{0}) = l_{\min}, \\ l_{C}(t_{0} + \Delta t) = l_{\min},\qquad l_{R}(t_{0} + \Delta t) = l_{\max}. \end{array} \end{aligned}$$
(14)
$$\begin{aligned} &\begin{array}{l} \dot{l}_{C}(t_{0}) = 0,\qquad \dot{l}_{R}(t_{0}) = 0, \\ \dot{l}_{C}(t_{0} + \Delta t)= 0,\qquad \dot{l}_{R}(t_{0} + \Delta t) = 0. \end{array} \end{aligned}$$
(15)

Using Eq. (13), conditions (14) and (15) can be rewritten as

$$\begin{aligned} &\begin{array}{l} \varepsilon_{C}(t_{0}) = 0,\qquad \varepsilon_{R}(t_{0}) = 0, \\ \bigl( 1 + \varepsilon_{C}(t_{0} + \Delta t) \bigr) \bigl( 1 + \varepsilon_{R}(t_{0} + \Delta t) \bigr) = 1. \end{array} \end{aligned}$$
(16)
$$\begin{aligned} &\begin{array}{l} \dot{\varepsilon}_{C}(t_{0}) = 0,\qquad \dot{\varepsilon}_{R}(t_{0}) = 0, \\ \dot{\varepsilon}_{C}(t_{0} + \Delta t) = 0,\qquad \dot{\varepsilon}_{R}(t_{0} + \Delta t) = 0. \end{array} \end{aligned}$$
(17)

Considering the acceleration of strain-change to be piecewise constant and following conditions (16) and (17), the contracting and relaxing processes can be assigned. Analytically, the accelerations of strain-change are given as

$$ \begin{array}{rcl} \ddot{\varepsilon}_{C}(t) &=& \left \{ \begin{array}{l@{\quad }l} - \nu \alpha, & t_{0} \le t \le t_{0} + \xi, \\ \nu \beta, & t_{0} + \xi < t \le t_{0} + \Delta t, \end{array} \right . \\ \ddot{\varepsilon}_{R}(t) &=& \left \{ \begin{array}{l@{\quad }l} \alpha, & t_{0} \le t \le t_{0} + \xi, \\ - \beta, & t_{0} + \xi < t \le t_{0} + \Delta t. \end{array} \right . \end{array} $$
(18)

Here, α and β are positive constants, characterizing the acceleration of strain-change (Fig. 9(b)). ρ,ν and ξ are actuator parameters: ρ denotes the maximal velocity of the strain-change of the relaxing segments; ν denotes the strain ratio of contracting segment to relaxing segment; ξ∈(0,Δt) is the discontinuity point at accelerations. α,β,ρ,ν,Δt and ξ satisfy the following relations: \(\xi = \frac{\rho}{\alpha}\), \(\beta = \frac{\rho}{\Delta t - \xi}\), and \(\nu = ( 1 + \frac{1}{2}\rho \Delta t )^{ - 1}\). Integrating Eq. (18), velocities of strain-change \(\dot{\varepsilon}_{C}(t), \dot{\varepsilon}_{R}(t)\) and strains ε C (t),ε R (t) can be obtained, see Fig. 9(c) and 9(d), respectively.

Based on the accelerations (18) and the derived ε−t, \(\dot{\varepsilon} - t\) relations, and employing Eqs. (12) and (13), the velocities and accelerations for the contracting and relaxing processes yield

$$ \begin{array}{rcl} \dot{x}_{C}(t) &=& \dot{x}_{R}(t) = \left \{ \begin{array}{l@{\quad }l} \alpha l_{\min} (t - t_{0}), & t_{0} \le t \le t_{0} + \xi, \\ - \beta l_{\min} (t - t_{0}) + \beta l_{\min} \Delta t, & t_{0} + \xi < t \le t_{0} + \Delta t, \end{array} \right . \\ \ddot{x}_{C}(t) &=& \ddot{x}_{R}(t) = \left \{ \begin{array}{l@{\quad }l} \alpha l_{\min}, & t_{0} \le t \le t_{0} + \xi, \\ - \beta l_{\min}, & t_{0} + \xi < t \le t_{0} + \Delta t. \end{array} \right . \end{array} $$
(19)

In this dynamic model, it is assumed that the normal force at the contact between the robot segment and the environment is also dependent on the segments’ radial deformation. For the fully relaxed segment (state ‘0’) and the contracting/relaxing segments, due to the small radial dimension, these segments have weak contact with the environment. Radial deformation has no contribution to the normal force, and it gives

$$ P_{0} = mg. $$
(20)

For the fully contracted segment (state ‘1’), i.e., the anchoring segment, the radial expansion squeezes the contacting surface, increases the normal force. Hence, the normal force is assigned as

$$ P_{1} = (1 + \eta )mg, $$
(21)

where η>0 is a positive ratio characterizing the additional pressure induced by the expansion of a segment. Here, the sub-index of P s (s=0,1) stands for the state of a segment, m is the mass of each segment, g is the gravitational acceleration.

In addition, in the dynamic model, each actuator is non-ideal and has a maximum actuating force Q max. In some cases, if Q max is not large enough for an actuator to drive itself and the adjacent segments, this actuator is defined to be overloaded, which may cause some damage to the actuator and even the robot, and should be avoided in practice. In this research, critical condition for actuator-overload will be derived, but the dynamic behavior of the robot when the actuator is overloaded will not be discussed because the overloading characteristics of the actuator are not clear.

5.2 Dynamic equations

Referring to the general driving module depicted in Fig. 3, velocity and acceleration at the front-end position of each segment in a driving module can be expressed:

(22)
(23)

As a general case, the temporarily anchoring segments are assumed to slip with velocity \(\dot{x}_{A}\) and acceleration \(\ddot{x}_{A}\).

To derive the dynamic equations of the model, the velocity and acceleration of mass center of each segment are approximately expressed as

$$ \dot{x}_{ic} = \frac{\dot{x}_{i - 1} + \dot{x}_{i}}{2},\quad \ddot{x}_{ic} = \frac{\ddot{x}_{i - 1} + \ddot{x}_{i}}{2}\quad (i = 1,\ldots,N). $$
(24)

Substituting Eqs. (22) and (23) into (24) yields

(25)
(26)

To perform a steady-state motion, all the driving modules in the dynamic model share the same velocities and accelerations shown in Eqs. (25) and (26). Besides the segments in the driving modules, the velocities and accelerations of mass center of the unactuated segments are \(\dot{x}_{U}\) and \(\ddot{x}_{U}\):

$$ \begin{array}{l} \dot{x}_{(k(n_A + 2n_R)+ 1)c} = \dot{x}_{(k(n_A + 2n_R)+ 2)c} = \cdots = \dot{x}_{Nc} = \dot{x}_{U} = n_{R}\dot{x}_{R} +\dot{x}_{A}, \\ \ddot{x}_{(k(n_A + 2n_R)+ 1)c} = \ddot{x}_{(k(n_A + 2n_R)+ 2)c} = \cdots = \ddot{x}_{Nc} = \ddot{x}_{U} = n_{R}\ddot{x}_{R} +\ddot{x}_{A}. \end{array} $$
(27)

In our dynamic model, the anisotropic Coulomb dry friction is employed, which describes the non-ideal anchoring force as follows:

$$ F(\dot{x}_{ic}) = \left \{ \begin{array}{l@{\quad }l} - P_{s}f_{ +}, & \mbox{if}\ \dot{x}_{ic} > 0, \\ F_{0}, & \mbox{if}\ \dot{x}_{ic} = 0, \\ P_{s}f_{ -} & \mbox{if}\ \dot{x}_{ic} < 0, \end{array} \right . $$
(28)

where F 0 is the static friction force; P s (s=0,1) is the normal force; f + and f − are the coefficients of dry friction corresponding to forward and backward motion, respectively. Both f + and f − are non-negative constants and are assumed to be different. Without loss of generality, it is assumed that

$$ f_{ +} < f_{ -}. $$
(29)

This difference reflects the anisotropy of the interface between the segments and the environment.

Denote R i the resultant of all forces applied to segment #i except the friction force, the static friction force F 0 can then be written as

$$ F_{0} = \left \{ \begin{array}{l@{\quad }l} - P_{s}f_{ +}, & \mbox{if}\ \dot{x}_{ic} = 0\ \mbox{and}\ R_{i} > P_{s}f_{ +}, \\ R_{i}, &\mbox{if}\ \dot{x}_{ic} = 0\ \mbox{and}\ {-}P_{s}f_{ -} \le R_{i} \le P_{s}f_{ +}, \\ P_{s}f_{ -}, &\mbox{if}\ \dot{x}_{ic} = 0\ \mbox{and}\ R_{i} < - P_{s}f_{ -}. \end{array} \right .\quad (s = 0,1) $$
(30)

As long as the magnitude of the resultant force R i does not exceed the given maximal value of the friction force at rest (P s f + or P s f −), segment #i will remain at a static state, i.e., sticking, which is a characteristic feature of dynamic systems with Coulomb dry friction. Otherwise, if the magnitude of the resultant force R i exceeds the maximal friction force at rest, segment #i will slip. In fact, the “temporary anchor” in the dynamic model is a sticking motion.

Considering the dynamics of the whole model and according to Newton’s Second Law, the dynamic equation of the N-segment dynamic model gives

$$ \sum_{i = 1}^{N} m\ddot{x}_{ic} = \sum_{i = 1}^{N} F(\dot{x}_{ic}). $$
(31)

Substituting the velocity (25) and acceleration (26) of each segment and the dry friction force (28) into Eq. (31), one gets

$$\begin{aligned} &Nm\ddot{X}_{c} = k \Biggl[ n_{A}F(\dot{x}_{A}) + 2\sum_{i = 1}^{n_{R}} F \biggl( \dot{x}_{A} + \frac{2i - 1}{2}\dot{x}_{R} \biggr) \Biggr] + \bigl( N - k(n_{A} + 2n_{R}) \bigr)F ( \dot{x}_{A} + n_{R}\dot{x}_{R} ) \end{aligned}$$
(32)

where the mass center of the whole robot is defined as \(X_{c} = \frac{1}{N}\sum_{i = 1}^{N} x_{ic}\), and the symbol \(\sum_{i = 1}^{n_{R}} \square\) sums the object over the n R contracting (or relaxing) segments in a driving module. The velocity of the anchoring segment can be expressed by

$$ \dot{x}_{A} = \dot{X}_{c} - \frac{N - k(n_{A} + n_{R})}{N}n_{R} \dot{x}_{R}. $$
(33)

5.3 Critical conditions for actuator-overload and anchor-slippage

In this section, critical conditions for actuator-overload and anchor-slippage are derived.

First, we study the critical condition for actuator-overload. Note that the actuating force from a contracting/relaxing segment need to assume three functions, the first is to provide acceleration to the segment itself, the second is to provide acceleration to the adjacent segments, and the third is to overcome the friction forces. In each driving module (e.g., the jth driving module), segment #(n R ,j) or #(n R +n A +1,j) have to pull or push the largest number of segments forward (including itself and the adjacent (n R −1) segments in the jth driving module). Especially, segment #(n R +n A +1,k) shown in Fig. 4 has to additionally push the (N−k(n A +2n R )) unactuated segments forward, and as a result, demands the highest actuating force. The contribution of segment #(n R +n A +1,k) to itself and the adjacent segments is shown in Table 2, from which, the required actuating force of segment #(n R +n A +1,k) is obtained as

$$\begin{aligned} Q_{\# (n_{R} + n_{A} + 1,k)} =& m\ddot{x}_{R}/2 + \bigl[ (n_{R} - 1) + \bigl( N - k(n_{A} + 2n_{R}) \bigr) \bigr]m \ddot{x}_{R} \\ &{}+ f_{ +} mg + \bigl( N - k(n_{A} + 2n_{R}) \bigr)f_{ +} mg/n_{R}. \end{aligned}$$
(34)

If the output force \(Q_{\# (n_{R} + n_{A} + 1,k)}\) is larger than the maximal output Q max, segment #(n R +n A +1,k) may fail to push the adjacent segments forward. Note that this is the most conservative estimation. Considering the critical situation that \(Q_{\# (n_{R} + n_{A} + 1,k)}\) takes its maximal value, i.e., \(\ddot{x}_{R} = \alpha l_{\min}\) during (t 0,t 0+ξ), the critical condition for actuator overload yields

$$\begin{aligned} &\frac{m\alpha l_{\min}}{2} + \bigl[ (n_{R} - 1) + \bigl( N - k(n_{A} + 2n_{R}) \bigr) \bigr]m\alpha l_{\min} + f_{ +} mg \\ &\quad {} + \frac{N - k(n_{A} + 2n_{R})}{n_{R}}f_{ +} mg > Q_{\max}. \end{aligned}$$
(35)
Table 2 Contribution of actuating force from segment #(n R +n A +1,k) to itself and the adjacent segments
Full size table

Then we will study the critical conditions for backward and forward slippage of anchoring segments, providing that the actuator-overload does not occur on any segment. Reorganizing Eq. (32), we obtain

$$\begin{aligned} &m \bigl[ N\ddot{x}_{A} + \bigl( N - k(n_{A} + n_{R}) \bigr)n_{R}\ddot{x}_{R} \bigr] - 2k\sum _{i = 1}^{n_{R}} F \biggl( \dot{x}_{A} + \frac{2i - 1}{2}\dot{x}_{R} \biggr) \\ &\quad {}- \bigl( N - k(n_{A} + 2n_{R}) \bigr)F(\dot{x}_{A} + n_{R}\dot{x}_{R}) = kn_{A}F(\dot{x}_{A}), \end{aligned}$$
(36)

where the left side stands for the sum of all the external forces except the friction forces that act on all the anchoring segments, and the right side presents the friction forces on all the anchoring segments. According to the dry friction model in Eqs. (28) and (30), if the external force acting on all the anchoring segments is larger than the maximal static friction force, slippage of the anchoring segments will happen.

Consider the critical situation that the anchoring segments are about to start slipping backward. In such a situation, \(\dot{x}_{A} = 0, \ddot{x}_{A} = 0\), and all the other segments have forward velocities. Based on the dry friction model, all the friction forces can be determined. If the external force during (t 0,t 0+ξ) is larger than the maximal static friction force for backward slippage kn A f − P 1, all the anchoring segments will slip backward. Substituting the acceleration \(\ddot{x}_{R}\), normal pressure P s (s=0,1) and friction forces (28) into Eq. (36), the critical condition for backward anchor-slippage gives

$$ \bigl( N - k(n_{A} + n_{R}) \bigr)n_{R}\alpha l_{\min} + (N - kn_{A})f_{ +} g > kn_{A}(1 + \eta )f_{ -} g. $$
(37)

Consider the other case that the anchoring segments are about to start sliding forward. Here, \(\dot{x}_{A} = 0\), \(\ddot{x}_{A} = 0\), and all the other segments still have forward velocities. During (t 0+ξ,t 0+Δt), if the absolute value of external force is larger than that of the maximal static friction forces for forward slippage −kn A f + P 1, all the anchoring segments will slip forward. Hence, the critical condition for forward anchor-slippage is

$$ - \bigl( N - k(n_{A} + n_{R}) \bigr)n_{R}\beta l_{\min} + (N - kn_{A})f_{ +} g < - kn_{A}(1 + \eta )f_{ +} g. $$
(38)

To verify the derived critical conditions, an 11-segment robot with one driving module is simulated. The physical parameters are shown in Table 3.

Table 3 Parameters of the 11-segment robot example
Full size table

Figure 10(a) shows the critical conditions in the n A −n R plane. The outside rectangle region is determined by constraints (10) and (11). The boundary c.c.1 is the critical condition for actuator overloading, i.e., condition (35). The boundary c.c.2 is the critical condition for backward slippage, i.e., condition (36). In region H 1, actuators are not strong enough to propagate the robot during some transitions. Gaits locating in region H 1 are not considered in this research. In region H 2, actuators can work normally, but the anchor is not strong enough to prevent backward slippage of the anchoring segments. To analyze the dynamic model with gait parameters in this region, numerical simulation on Eq. (32) is required. In region H 3, both actuators and anchors can work normally. The dynamic model in this region degenerates into the kinematic model, therefore, expressions for displacement and average speed in Eqs. (8) and (9) hold valid in this region.

Fig. 10
figure 10

Verification of the critical conditions for actuator-overload and anchor-slippage in an 11-segment robot with one driving module: (a) Region of gait parameters n A and n R , and the two critical conditions c.c.1 and c.c.2, two points O 1 (n A =1,n R =4) and O 2 (n A =2,n R =4) are simulated to verify the critical conditions. (b) Velocity of mass center \(\dot{X}_{c}\) (m/s) and velocity of anchoring segments \(\dot{x}_{A}\) (m/s) corresponding to point O 1; (c) Velocity of mass center \(\dot{X}_{c}\) (m/s) and velocity of anchoring segments \(\dot{x}_{A}\) (m/s) corresponding to point O 2

Full size image

Notice that the critical condition (38) does not appear in this region. This is because the magnitude of the friction forces on other segments (except the anchoring segments) (N−kn A )f + g is much larger than that of the acceleration component −(N−k(n A +n R ))n R βl min, and their sum does not exceed the maximal static friction for forward slippage. However, when increasing the total number of segments N or changing the physical or gait parameters, forward slippage may occur, which will be presented in Part B.

Points O 1 (n A =1,n R =4) and O 2 (n A =2,n R =4) are taken in regions H 2 and H 3, respectively, to verify the critical conditions. Through numerical simulation on Eqs. (32) and (33), velocity of mass center \(\dot{X}_{c}\) and velocity of anchoring segments \(\dot{x}_{A}\) corresponding to points O 1 and O 2 are calculated and shown in Fig. 10(b) and 10(c), respectively. One can read from Fig. 10(b) and 10(c) that at point O 1, obvious backward velocity of anchoring segments exists; while at point O 2, the velocity of anchoring segments \(\dot{x}_{A}\) is always zero, i.e., no slippage occurs. These phenomena agree with our analysis.

6 Summary

In this paper, inspired by the earthworms’ morphology and locomotion mechanism, an N-segment kinematic model of the metameric earthworm-like robot is developed following the idea of integrating ideal actuator and ideal anchor into an individual body segment. The metameric earthworm-like robot belongs to the general class of metastructures, the concept of synthesizing adaptive structures via modular element design and integration. Kinematics of a single segment and the locomotion mechanism of the whole robot are studied. It is shown that with the proposed kinematic model, the metameric earthworm-like robot can perform locomotion in the form of retrograde peristalsis waves, similar to the real earthworm.

The issue of gait generation is then discussed in the most general case. Four gait parameters are identified, and their constraints are given. A gait generation algorithm is put forward based on the mechanism of retrograde peristalsis wave. Following this algorithm, locomotion gaits can be generated if appropriate gait parameters and initial state are assigned. The generated gaits apply to both the kinematic and dynamic models of the earthworm-like robot.

Without the assumptions of ideal anchors and ideal actuators, an N-segment dynamic model is developed. In the dynamic model, the actuator has an upper limit of output force, and the contact between the robot surface and the environment obeys the anisotropic dry friction law. Assuming that the actuating accelerations are piecewise constant, the dynamics of a single segment is studied, based on which, the dynamic equations are derived. Furthermore, it is shown that actuators may fail to drive the robot forward when the required driving force is larger than the maximal output. Slippage of anchoring segment may occur when the external forces exceed the maximal static friction force. Critical conditions for actuator-overload and anchor-slippage are derived.

The kinematic model and dynamic model as well as the gait generation algorithm developed in this research provide a basis for gait analysis and gait optimization that will be performed in Part B. These models also help to guide the design and prototyping of an earthworm-like robot for experimental investigation, which will also be presented in Part B.