Magneto-photo-thermoelastic interaction in a slim strip characterized by hereditary features with two relaxation times

Abstract

This paper is devoted to studying the photo-thermoelastic response of homogeneous and isotropic finite thin slim strip that is exposed to a moving heat source, where both the ends are fixed. The novel thermo-viscoelastic theory is associated with the nonsingular relaxation kernel “Mittag-Leffler relaxation function”. In the context of memory-dependent Moore–Gibson–Thompson (MGT) theory, the heat transport law is framed. Solutions of all the significant physical fields such as the displacement, carrier density, temperature, and thermal stress are evaluated in their dimensionless form in the Laplace transform domain. The distribution of the physical fields are found numerically in the real space-time domain implementing the Riemann-sum approximation technique. From the computational results and the corresponding graphical representations, significant effect of the effective parameters such as the nonlocality parameter, time-delay parameter has been reported. Also, significant effect for different choice of kernel function is indicated. Moreover, it is also proposed how a nonlinear kernel function is more superior compared to linear kernel in context of this new theory.

1 Introduction

Semiconducting materials have been widely applied in modern engineering applications with the recent development of technologies. Basically, the consideration of a semiconductor with band gap energy $E_{g}$ is illuminated by a laser beam with energy $E$ higher than $E_{g}$ and followed by an excitation process of electrons, which will take place. The excited electrons will transfer from the valence band to an energy level with the energy of $(E - E_{g})$ above the conduction band edge. Then these photo-excited free carriers will relax to one of the unfilled levels nearby the bottom of the conduction band (non-radiative transition) (Kumar et al. 2022). After the relaxation process, there is electron and hole plasma, which is followed by the formation of electron-hole pairs through the recombination process. The electronic deformation may cause local tensions in the sample, which can introduce plasma waves that are similar to the heat wave generated by local periodic elastic deformation.

Recently, the problem of wave propagation within a semiconducting medium has become a more important academic and applicable value. Many authors have reported the problem of wave propagation in a semiconducting medium during a photothermal process. Gordon et al. (1965) were the first to discover the photothermal method when they found an intracavity sample. Thereafter, Kreuzer (1971) showed that the photoacoustic spectroscopy can be used for sensitive analysis. After that, photothermal methods have been used to measure temperature, thermal diffusivities, sound velocity, bulk flow velocities, surface thickness, and specific heats (Tam 1983, 1986, 1989). The propagation of a thermal wave causes elastic vibrations in a medium, which is basically thermoelastic (TE) mechanism of photothermal generation. For semiconductor materials, the photoexcited free carriers produce directly a periodic elastic deformation, i.e., the electronic deformation (ED) in the sample (Todorovic et al. 1999). Todorovic (2005) analyzed the system of coupled plasma and elastic and thermal wave equations.

Over the past few decades, theories of thermoelasticity, admitting finite velocity for thermal signals, have received a lot of attention from researchers. Lord and Shulman (1967) were the first to present the first theory of generalized thermoelasticity involving one relaxation time, while Green and Lindsay (1972) obtained the second theory of generalized of thermoelasticity with two relaxation time in contrast to the coupled thermoelasticity theory based on a parabolic heat equation (Biot 1956). In recent years, the area of fluid mechanics (Thompson 1972) has gained a lot of interest for the Moore–Gibson–Thompson (MGT) heat conduction law, which is considered by adjoining the energy equation to the equation (Gupta et al. 2022; Chena and Ikehata 2021; Dell’Oro et al. 2016)

$$ \vec{q}+\tau _{0} \frac{\partial \vec{q}}{\partial t}=-(k \vec{\nabla} T -k^{\star }\vec{\nabla} \nu ), \;\; \dot{\nu}=T, $$

(1)

where $\vec{q}$ is the heat flux vector, $\tau _{0}$ ($>0$) is the relaxation time, $\nu$ is the thermal displacement, $k$ is the thermal conductivity, and $k^{\star}$ is the conductivity rate parameter (Kumar and Mukhopadhyay 2020; Fernández and Quintanilla 2021). Quintanilla (2019), Pellicer and Quintanilla (2020) derived the constitutive equations for coupled thermoelasticity theory based on this MGT theory. The uniqueness of the solution and exponential stability of this new theory were also discussed by Quintanilla (2019), Pellicer and Quintanilla (2020). This new theory can be seen as a fusion of both LS and GN-III (Green and Naghdi 1992a,b, 1993) thermoelasticity theories, and naturally, it has dragged the interest of researchers and prompted them to work in this direction (Tiwari 2023; Aboulregal et al. 2023; Sur 2023). Under the MGT thermoelasticity theory, Pellicer and Quintanilla (2020) proved the uniqueness and instability of some thermomechanical problems. The domain of influence results for MGT theory were recently discussed by Jangid and Mukhopadhyay (2020a,b). Recently Sur (2023) reported the thermo-hydro-mechanical problem due to the vibration of mining vehicle within porous sea sediments in the context of Moore–Gibson–Thompson theory. Also, Othman et al. studied (Othman et al. 2023) the influence of memory dependence for a rotating porous solid medium. Further, the theoretical aspects and some practical applicabilities of the MGT theory can be found in the following literatures (Conti et al. 2020a,b; Bazarra et al. 2021).

For the last few decades, fractional calculus (FC) has drawn increasing attention in various scientific disciplines involving attenuation and dispersion in complex viscoelastic media, nanoprecipitate growth in solids, heat transfer, diffusion and wave propagation, electrical spectroscopy impedance, chaos and fractals, genetic algorithms, percolation, modeling and identification, telecommunications, chemistry, physics, control systems, etc. The previous models have historical challenges in capturing real-world description of properties of various real materials, in particular the description of memory and hereditary properties of various materials and processes. The main advantage of using FC is that it has produced a successful revolution to modify many existing models of physical processes, e.g., the description of rheological properties of rocks as well as mechanical modeling of engineering materials such as polymers over extended ranges of time and frequency (Mainardi 1997, 2022). Fractional-order models in heat transfer and electrochemistry work well; for example, the half-order fractional integral is the natural integral operator connecting the applied gradients with the diffusion of heat (Gorenflo et al. 2007), which is followed by various new mathematical models in thermoelasticity and hereditary thermoelasticity theories.

Wang and Li (2011) introduced the memory-dependent derivative (MDD) of a function $f$ with a “kernel function” $K(t-\xi )$ together with a “delay-time” parameter $\omega$ ($>0$), defined in an integral form as follows:

$$ D_{\omega }f(t)=\frac{1}{\omega}\int _{t-\omega}^{t}K(t-\xi )f'( \xi ) d\xi . $$

(2)

For a variety of reasons, the usage of MDD in the heat transfer laws is regarded as one step forward process beyond fractional laws. The first is that the MDD model has a unique structure, while the fractional model has a variety of configurations. On the other hand, the physical importance of the MDD model is really good in terms of the substance of the MDD description (Sur 2021; Sur et al. 2021, 2022). In addition, the kernel functions of MDD are completely customizable, such as $K(t-\xi )=1$, $1-\frac{t-\xi}{\omega}$, and $\left (1-\frac{t-\xi}{\omega}\right )^{2}$. The kernel function can be understood as the degree of the past effect on the present. As a result, it provides more options to represent the practical reaction of the material. Moreover, if $K(t-\xi )= 1$,

$$ D_{\omega }f(t)=\frac{1}{\omega}\int _{t-\omega}^{t} f'(\xi )d \xi =\dfrac{f(t)-f(t-\omega )}{\omega}\rightarrow f'(t). $$

(3)

So, the common derivative $\frac{d}{dt}$ is being reflected as the limit of $D_{\omega}$ as $\omega \rightarrow 0$.

The basic principles of classical continuum theory assumes that a material is a composition of an infinite number of particles, each of which is a point that can only move and interact with its nearest neighbors (Eringen 2002a,b; Edelen and Laws 1971). This classical theory has limited applications where it fails to describe the discrete structure of the material or to reveal many of the microscopic phenomena, e.g., micro-deformation and micro-dislocation. This observation motivated the need for a general point of view that instills the fact that the material particle is a volume element that would deform and rotate, and the material is generally a multiscale material (Tiwari et al. 2022; Tiwari and Kumar 2022; Tiwari et al. 2021). In addition, the particle’s equilibrium should not be considered in isolation from its nonlocal interactions with other particles of the material. Material models with these features are the nonlocal micro-continuum theories (Karlic̆ić et al. 2016).

To the best knowledge of the author, it is hard to find research works that address the effect of a nonsingular relaxation kernel. However, nonsingularity in the kernel function of the heat transport law seems to be one of significant observations. Also, as recommended by Atangana and Baleanu (2017), “The non-singular kernel in integral operator will be helpful to discuss real world problems and it also will have a great advantage when using the Laplace transform to solve some physical problems with initial conditions and good for describing the dynamics of systems with memory effect for small and large times”. Therefore, the present problem aims to study photo-thermoelastic interaction in a slim strip that is exposed to a moving heat source. The heat conduction law in the present problem is associated with “Mittag-Leffler relaxation function” in the context of MGT theory. The strip is fixed at both ends and is influenced by an induced external magnetic field of constant intensity. Modeling of the problem is performed by adopting the nonlocal theory proposed by Eringen. Incorporating the Laplace transform, the coupled equations have been solved in the transformed domain. Numerical calculations are rendered and graphically displayed (Tzou 1996) for the studied physical fields. The results reveal that there are various effects of the nonlinear kernel functions, time-delay, and nonlocality on the photo-thermoelastic interactions. The significance of the moving heat source speed and the effect of time variable are also reported. It is also addressed from the graphical representation how MGT theory is of more attraction to the researchers compared to the Lord–Shulman theory in the heat transfer problems.

2 Basic equations

For a homogeneous and isotropic elastic solid occupying the region having volume $V$ and surface area $\partial V$, the linear theory is expressed as (Eringen 1983)

$$ t_{ij,j}+\rho (f_{i}-\ddot{u}_{i})=0, $$

(4)

$$ t_{ij}(\textbf{x}')=\int _{\textbf{V}}\alpha (|\textbf{x}'- \textbf{x}|, \chi )\sigma _{ij}(\textbf{x}')dv(\textbf{x}'), $$

(5)

$$ \sigma _{ij}(\textbf{x})=\lambda e_{rr}(\textbf{x}')\delta _{ij}+2\mu e_{ij}( \textbf{x}'), $$

(6)

$$ e_{ij}(\textbf{x}')=\frac{1}{2}\left ( \frac{\partial u_{i}(\textbf{x}')}{\partial x'_{j}}+ \frac{\partial u_{j} (\textbf{x}')}{\partial x'_{i}}\right ), $$

(7)

where $t_{ij}$, $\rho$, $f_{i}$, and $u_{i}$ are respectively the nonlocal stress tensor, the mass density, the body force, and the displacement component at a reference point $\textbf{x}$ within the body at time $t$. However, $\sigma _{ij}(\textbf{x}')$ is the macroscopic (classical) stress tensor at a point $\textbf{x}'$ in the body at time $t$. $\lambda$ and $\mu$ are Lamé constants.

There are different examples of nonlocal modulus $\alpha$, such as (Eringen 1983)

$$ \alpha (|\textbf{x}'-\textbf{x}|, \chi )=\displaystyle \frac{1}{2l\chi}e^{- \frac{|\textbf{x}'-\textbf{x}|}{l\chi}}. $$

(8)

Consider $\alpha$ to be a Green’s function of the linear differential operator (Eringen 1983)

$$ L \alpha (|\textbf{x}'-\textbf{x}|, \chi )=\delta (|\textbf{x}'- \textbf{x}|). $$

(9)

In particular, $L$ is a differential operator satisfying

$$ (Lt_{ij})_{,j}=Lt_{ij,j}. $$

(10)

Moreover, applying $L$ in equation (5) yields

$$ \begin{aligned} Lt_{ij}(\textbf{x}') & = L\int \limits _{\textbf{V}}\alpha (|\textbf{x}'- \textbf{x}|, \chi )\sigma _{ij}(\textbf{x}')dv(\textbf{x}'), \\ & = \int \limits _{\textbf{V}}L\alpha (|\textbf{x}'-\textbf{x}|, \chi ) \sigma _{ij}(\textbf{x}')dv(\textbf{x}'), \\ & =\int \limits _{\textbf{V}}\delta (|\textbf{x}'-\textbf{x}|, \chi ) \sigma _{ij}(\textbf{x}')dv(\textbf{x}'), \\ & = \sigma _{ij}(x). \end{aligned} $$

(11)

Therefore, equation (4) yields

$$ Lt_{ij,j}+L (\rho f_{i}-\rho \ddot{u}_{i})=0. $$

(12)

Using equation (10), the above equation yields

$$ (Lt_{ij})_{,j}+L (\rho f_{i}-\rho \ddot{u}_{i})=0. $$

(13)

In view of equation (11), (12) reduces to

$$ \sigma _{ij,j}+L (\rho f_{i}-\rho \ddot{u}_{i})=0, $$

(14)

where the differential operator $L$ for equation (9) is defined as (Sur 2023)

$$ L\equiv 1-\chi ^{2} l^{2} \nabla ^{2}. $$

(15)

Consider a viscoelastic medium contained within a volume $V$ and bounded by a closed surface $S$. The theoretical analyses of the transport process in a semiconductor polymer nanocomposites medium involve in the consideration coupled plasma waves, thermal waves, and elastic waves simultaneously. The carrier intensity $N(r, t)$, the concentration and temperature distribution $T(r, t)$ are the main variable quantities. The coupled plasma, thermal, and elastic transport equations are given by

$$ \frac{\partial N(r,t)}{\partial t}=D_{e} \nabla ^{2} N(r,t)- \frac{N(r,t)}{\tau}+\kappa T(r,t), $$

(16)

where, with the aim to keep the equations linear in $N$ and $T$, it is assumed that the transport heat coefficients are also dependent on $N$ and $T$. Here the thermal activation parameter $k_{\alpha}=\frac{\partial N_{0}}{\partial T}\frac{T}{\tau}$ is negligible in the case of relatively low temperature. The quantity $\frac{E_{g} }{\tau}N(r,t)$ characterizes the effect of heat generation by the carrier volume and surface de-excitations in the sample.

Define a linear thermo-viscoelastic material for which the component of the stress tensor $\sigma _{ij}(\textbf{x},t)$ and the strain component $e_{ij}(\textbf{x},t)$ are defined in the form of a convolution integral as follows:

$$\begin{gathered} \sigma _{ij}(\textbf{x},t)=\int _{0}^{t}\mathcal{R}_{ijkl}(t- \nu )\frac{\partial e_{kl}(\textbf{x}, \nu )}{\partial \nu}d\nu - \alpha _{N}\int _{0}^{t}\gamma _{ij}(t-\nu ) \frac{\partial N(\textbf{x}, \nu )}{\partial \nu}d\nu \\ {} -\alpha _{T} \int _{0}^{t}\gamma _{ij}(t-\nu ) \frac{\partial T(\textbf{x}, \nu )}{\partial \nu}d\nu , \end{gathered}$$

(17)

where $\mathcal{R}_{ijkl}$ and $\gamma _{ij}$ are the fourth-order and second-order tensorial relaxation functions of the material, respectively. However, it is assumed that the following symmetry relations are satisfied:

$$ \mathcal{R}_{ijkl}=\mathcal{R}_{klij}=\mathcal{R}_{ikjl}=\mathcal{R}_{jlik}, \;\;\; \gamma _{ij}=\gamma _{ji}. $$

Therefore, in the context of nonlocal theory proposed by Eringen, the constitutive equation is given by

$$ [1-(e_{0}a_{0})^{2} \nabla ^{2}]\sigma _{ij}(\textbf{x},t)=\int _{0}^{t}\mathcal{R}_{ijkl}(t-\nu ) \frac{\partial e_{kl}(\textbf{x}, \nu )}{\partial \nu}d\nu - $$

$$ \alpha _{N}\int _{0}^{t}\gamma _{ij}(t-\nu ) \frac{\partial N(\textbf{x}, \nu )}{\partial \nu}d\nu -\alpha _{T} \int _{0}^{t}\gamma _{ij}(t-\nu ) \frac{\partial T(\textbf{x}, \nu )}{\partial \nu}d\nu , $$

(18)

where

$$ \mathcal{R}_{ijkl}=\mathcal{R}_{1} \delta _{ij}\delta _{kl}+ \mathcal{R}_{2}(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}), $$

$$ \gamma _{ij}=(3\mathcal{R}_{1}+2\mathcal{R}_{2})\delta _{ij}, \;\;\; k_{ij}=k \delta _{ij}, $$

(19)

where $\mathcal{R}_{i}(t;\beta )$ $(i=1, \; 2)$ are assumed to be a relaxation function of time.

The relaxation function for the Mittag-Leffler relaxation function is defined as

$$ \mathcal{R}_{i}(t; \beta )=R_{i} \tau ^{\beta }E_{\beta}\left (- \beta \frac{t^{\beta}}{1-\beta}\right ),\;\; t>0, $$

(20)

where $R_{1}$ and $R_{2}$ are the viscoelastic material constants, $\tau$ is a positive constant for the ratio of the shear viscosity to Young’s modulus, and $\beta$ is an arbitrary parameter which represents the order of the time-derivative, $\beta \in (0, \;1)$.

Substituting (19) and (20) in equation (18), the constitutive equation yields

$$ [1-(e_{0}a_{0})^{2} \nabla ^{2}]\sigma _{ij}(\textbf{x},t)=2R_{2}\tau ^{ \beta}\int _{0}^{t}E_{\beta}\left (- \frac{\beta (t-\nu )^{\beta}}{1-\beta}\right ) \frac{\partial e_{ij}(\mathbf{x}, \nu )}{\partial \nu}d\nu $$

$$ +\tau ^{\beta }\delta _{ij}\left [R_{1} \int _{0}^{t} E_{ \beta}\left (-\frac{\beta (t-\nu )^{\beta}}{1-\beta}\right ) \frac{\partial e(\mathbf{x}, \nu )}{\partial \nu}d\nu\right . $$

$$ -(3R_{1}+2R_{2}) \alpha _{N} \int _{0}^{t} E_{\beta}\left (- \frac{\beta (t-\nu )^{\beta}}{1-\beta}\right ) \frac{\partial N(\mathbf{x}, \nu )}{\partial \nu}d\nu $$

$$ \left .-(3R_{1}+2R_{2})\alpha _{T} \int _{0}^{t} E_{\beta} \left (-\frac{\beta (t-\nu )^{\beta}}{1-\beta}\right ) \frac{\partial T(\mathbf{x}, \nu )}{\partial \nu}d\nu \right ], $$

(21)

which can be represented as

$$\begin{gathered}{} [1-(e_{0}a_{0})^{2} \nabla ^{2}]\sigma _{ij}(\textbf{x},t) = \hat{\boldsymbol{R}}_{\beta}\left (2R_{2} e_{ij}+\delta _{ij} \big[R_{1} e-(3R_{1}+2R_{2})\alpha _{N} N \right. \\ \left.{}-(3R_{1}+2R_{2})\alpha _{T} T \big]\right ), \end{gathered}$$

(22)

where $e$ is the cubical dilatation given by $e=e_{kk}$ and the operator $\hat{\boldsymbol{R}}_{\beta}(\cdot )$ is defined for a function $f(\mathbf{x},t)$

$$ \hat{\boldsymbol{R}}_{\beta }[f(\mathbf{x}, t)]=\tau ^{\beta } \int _{0}^{t}E_{\beta}\left (- \frac{\beta (t-\nu )^{\beta}}{1-\beta}\right ) \frac{\partial f(\mathbf{x}, \nu )}{\partial \nu}d\nu . $$

3 Formulation of the problem

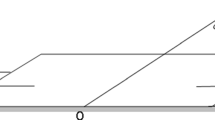
Consider a thermoelastic thin strip that is induced by a magnetic field of constant intensity $\textbf{H}=(0, H_{0}, 0)$ acting perpendicular to the axial direction of the strip, taken as the $x$-axis. It is assumed that the strip is fixed at both ends and subjected to a moving heat source propagating along the $x$-direction as described in Fig. 1. It is further assumed that the length scale along the $x$-axis is much greater than those along the other two directions orthogonal to the $x$-axis; therefore, the problem of the thin slim strip is treated as a one-dimensional problem.

Fig. 1

Geometry of the problem

The constitutive equation is given by

$$\begin{gathered}{} [1-(e_{0}a_{0})^{2} \nabla ^{2}]\sigma _{ij}(\textbf{x},t)= \hat{\boldsymbol{R}}_{\beta}\left (2R_{2} e_{ij}+\delta _{ij} \big[R_{1} e-(3R_{1}+2R_{2})\alpha _{N} N \right. \\ \left.{}-(3R_{1}+2R_{2})\alpha _{T} T \big]\right ). \end{gathered}$$

(23)

The energy equation is given by

$$ q_{i,i}=-\frac{\partial}{\partial t}\left (\rho c_{E} T+(3R_{1}+2R_{2}) \alpha _{T} T_{0}\hat{\boldsymbol{R}}_{\beta }(e)-Q\right ). $$

The heat transport equation in the context of memory-dependent MGT theory is given by

$$ k \nabla ^{2} \dot{T}+k^{\star }\nabla ^{2}T +\frac{E_{g}}{\tau} \dot{N}=\left (1+\tau _{0} D_{\omega}\right )\left [\rho c_{E} \ddot{T}+\gamma _{t}T_{0} \hat{\boldsymbol{R}}_{\beta }\left ( \frac{\partial ^{3}u}{\partial x \partial t^{2}}\right )-\dot{Q} \right ]. $$

(24)

The coupled plasma equation for the present problem is

$$ D_{e} \frac{\partial ^{2} N}{\partial x^{2}}-\frac{N}{\tau}+ \frac{k_{\alpha }T}{\tau} = \frac{\partial N}{\partial t}. $$

(25)

The electromagneto-thermoelastic governing equations are given by

$$ \mathbf{B}=\mu _{0} \mathbf{H}, $$

(26)

$$ \mathbf{J}=\sigma _{0} (\mathbf{E}+\mathbf{\dot{u}}\times \mathbf{B}). $$

(27)

Since no external electric field is applied, and the effect of polarization of the ionized medium can be neglected, it follows that the total $\mathbf{E}$ vanishes identically within the medium. The components are

$$ B_{x}=B_{z}=0, \;\; B_{y}=\mu _{0} H_{0}. $$

The components of the Lorentz force $\mathbf{F}=\mathbf{J}\times \mathbf{B}$ are given by

$$ F_{x}=\sigma _{0} \mu _{0}^{2} H_{0}^{2} \frac{\partial u}{\partial t}, \hspace{.1in} F_{y}=F_{z}=0. $$

The equation of motion for the present problem is given by

$$ \sigma _{ij,j}+ \big[1-(e_{0}a_{0})^{2} \nabla ^{2}\big](\mathbf{J} \times \mathbf{B})_{i}=\rho \big[1-(e_{0}a_{0})^{2} \nabla ^{2}\big] \ddot{u}_{i}. $$

(28)

For the one-dimensional problem, the displacement component and the temperature field are given by

$$ u_{x}=u(x,t), \hspace{.1in} u_{y}=u_{z}=0, \hspace{.1in} \theta =\theta (x,t). $$

The one dimensional basic equations yield the form

$$ \left [1-(e_{0}a_{0})^{2}\frac{\partial ^{2}}{\partial x^{2}}\right ] \sigma =\hat{\boldsymbol{R}}_{\beta }\left ((\lambda +2\mu ) \frac{\partial u}{\partial x}-\gamma _{n}N-\gamma _{t}T\right ), $$

(29)

$$\begin{gathered} \hat{\boldsymbol{R}}_{\beta}\left ((\lambda +2\mu ) \frac{\partial ^{2} u}{\partial x^{2}}-\gamma _{n} \frac{\partial N}{\partial x}-\gamma _{t} \frac{\partial T}{\partial x}\right )-\left (1-(e_{0}a_{0})^{2} \frac{\partial ^{2}}{\partial x^{2}}\right )\sigma _{0} \mu _{0}^{2} H_{0}^{2} \frac{\partial u}{\partial t} \\ = \rho \left [1-(e_{0}a_{0})^{2} \frac{\partial ^{2} }{\partial x^{2}}\right ]\ddot{u}, \end{gathered}$$

(30)

$$ k \frac{\partial ^{2} \dot{T}}{\partial x^{2}}+k^{\star } \frac{\partial ^{2} T}{\partial x^{2}} +\frac{E_{g}}{\tau } \dot{N}= \left (1+\tau _{0} D_{\omega}\right )\left [\rho c_{E} \ddot{T}+ \gamma _{t} T_{0} \hat{\boldsymbol{R}}_{\beta}\left ( \frac{\partial \ddot{u}}{\partial x}\right )-\dot{Q}\right ], $$

(31)

$$ D_{e} \frac{\partial ^{2} N}{\partial x^{2}}-\frac{N}{\tau}+ \frac{k_{\alpha}}{\tau} T=\frac{\partial N}{\partial t}. $$

(32)

Introducing the suitable nondimensional variables

$$ x'=c_{0} \eta x, \hspace{.1in} u'=c_{0} \eta u, \hspace{.1in} t'=c_{0}^{2} \eta t, \hspace{.1in} \tau '=c_{0}^{2} \eta \tau , $$

$$ \tau '_{0} =c_{0}^{2} \eta \tau _{0}, \hspace{.1in} \omega '=c_{0}^{2} \eta \omega , \hspace{.1in} \theta = \frac{T}{T_{0}}, \hspace{.1in} N'=\frac{N}{n_{0}}, $$

$$ \sigma '_{ij}=\frac{\sigma _{ij}}{\mu}, \hspace{.1in} \xi '=(c_{0} \eta )(e_{0} a_{0}), \hspace{.1in} \eta =\frac{\rho c_{E}}{k}, \hspace{.1in} Q'=\frac{Q}{\kappa T_{0} c_{0}^{2} \eta ^{2}}, \hspace{.1in} c_{0}^{2} = \frac{\lambda +2\mu}{\rho}, $$

and after removing primes, the above equations can be written in a nondimensional form as follows:

$$ \left (1-\xi ^{2} \frac{\partial ^{2}}{\partial x^{2}}\right )\sigma = \hat{\boldsymbol{R}}_{\beta }\left (\beta ^{2} \frac{\partial u}{\partial x}-\gamma _{n} N-\gamma _{t} T\right ), $$

(33)

$$ \hat{\boldsymbol{R}}_{\beta}\left ( \frac{\partial ^{2} u}{\partial x^{2}}-\frac{b_{1} }{\beta ^{2}} \frac{\partial N}{\partial x} -\frac{b_{2}}{\beta ^{2}} \frac{\partial T}{\partial x}\right )-\left (1-\xi ^{2} \frac{\partial ^{2}}{\partial x^{2}}\right )\epsilon \frac{\partial u}{\partial t}=\left (1-\xi ^{2} \frac{\partial ^{2}}{\partial x^{2}}\right ) \frac{\partial ^{2} u}{\partial t^{2}}, $$

(34)

$$ \frac{\partial ^{2} \dot{T}}{\partial x^{2}}+c_{T}^{2} \frac{\partial ^{2} T}{\partial x^{2}}+\epsilon _{1} \frac{\partial N}{\partial t}=(1+\tau _{0} D_{\omega})\left [\ddot{T}+g \hat{\boldsymbol{R}}_{\beta }\left ( \frac{\partial \ddot{u}}{\partial x}\right )-\dot{Q}\right ], $$

(35)

$$ \frac{\partial ^{2} N}{\partial x^{2}}=\gamma _{7} \frac{\partial N}{\partial t}+\frac{\gamma _{7}}{\tau}N- \frac{\gamma}{\tau} T, $$

(36)

where

$$ \gamma _{1}=\frac{\gamma _{n} n_{0}}{\mu}, \hspace{.1in} \gamma _{2}=\frac{\gamma _{t} T_{0}}{\mu}, \hspace{.1in} \beta ^{2}=\frac{\lambda +2\mu}{\mu}, \hspace{.1in} \epsilon = \frac{\sigma _{0} \mu _{0}^{2}H_{0}^{2}}{\eta (\lambda +2\mu )}, \hspace{.1in} \epsilon _{1}=\frac{E_{g}n_{0}}{\rho c_{E} T_{0}}, \hspace{.1in} g=\frac{\gamma _{t}}{\rho c_{E}}, $$

$$ c_{T}^{2}=\frac{k^{\star}}{\rho c_{E}c_{0}^{2}}, \hspace{.1in} \gamma =\frac{k_{\alpha }T_{0}}{D_{e} \eta n_{0}}, \hspace{.1in} \gamma _{7}=\frac{1}{D_{e} \eta}. $$

The strip is assumed to be initially at rest at a reference temperature $T_{0}$. Therefore, the initial conditions of the problem are

$$ u(x,0)=\dot{u}(x,0)=0, \hspace{.1in} T(x,0)=\dot{T}(x,0)=0, \hspace{.1in} N(x,0)=\dot{N}(x,0)=0. $$

(37)

Assume that the strip is fixed at both ends with a nondimensional length $l$ and both ends are thermally insulated. Therefore,

$$ u(0,t)=u(l,t)=0, \hspace{.1in} \frac{\partial T(0,t)}{\partial x}=\frac{\partial T(l,t)}{\partial x}=0, \hspace{.1in} \frac{\partial N(0,t)}{\partial x}=\frac{\partial N(l,t)}{\partial x}=0. $$

(38)

The strip is subjected to a moving heat source of constant strength, releasing its energy continuously while moving along the positive direction of the $x$-axis with a constant velocity $v$ given in the following form:

$$ Q=Q_{0} \delta (x-vt), $$

(39)

where $Q_{0}$ is a constant and $\delta (\cdot )$ is the Dirac delta function.

To justify the dependence of memory effect, the kernel function $K(t-\xi )$ in the heat transport law is considered as (Yu et al. 2014; Ezzat et al. 2016; Sur 2022; Ezzat et al. 2016; Mondal et al. 2020)

$$ K(t-\xi )=1-\frac{2f}{\omega}(t-\xi )+\frac{e^{2}}{\omega ^{2}}(t- \xi )^{2}=\left \{ \textstyle\begin{array}{l@{\quad}l@{\ }l} 1, & \text{if} & e=0, \, f=0 \\ 1-\frac{(t-\xi )}{\omega}, & \text{if} & e=0, \, f=\frac{1}{2} \\ \left (1-\frac{t-\xi}{\omega}\right )^{2}, & \text{if} & e=1, \, f= 1 \end{array}\displaystyle \right . $$

where $\omega$ is the delay time and $e$, $f$ are constants.

4 Method of solution

We employ the Laplace transform defined by

$$ \overline{f}(x,p)=\mathscr{L}[f(x,t)]=\int _{0}^{\infty }e^{-pt}f(x,t)dt, \,\, \text{Re}(p)>0, $$

satisfying the operational relationship (Sur 2023)

$$ \mathscr{L}\Big[\int _{t-\omega}^{t}K(t-\xi )f'(x,\xi )d\xi \Big]=\overline{f}(x,p)G_{\omega}(p), $$

where

$$ G_{\omega}(p)=1-\frac{2f}{\omega}+\frac{2e^{2}}{\omega ^{2}}-e^{-p \omega}\left [(1-2f+e^{2})+ \frac{2(e^{2}-f)}{\omega p}+ \frac{2e^{2}}{\omega ^{2}p^{2}}\right ]. $$

The definition of Mittag-Leffler function yields

$$ E_{\alpha}\left (\mu t^{\alpha}\right )=\sum _{n=0}^{\infty } \frac{\left (\mu t^{\alpha}\right )^{n}}{\Gamma (n\alpha +1)}. $$

The Laplace transform of the Mittag-Leffler function is defined as

$$ \mathscr{L}\left [E_{\alpha}\left (\mu t^{\alpha}\right )\right ]= \int _{0}^{\infty }e^{-pt}\sum _{n=0}^{\infty } \frac{\left (\mu t^{\alpha}\right )^{n}}{\Gamma (n\alpha +1)}dt= \frac{s^{\alpha -1}}{s^{\alpha}-\mu}, $$

which is outlined in the Appendix A.

Therefore, equations (33)–(36) yield

$$ \left (1-\xi ^{2} \frac{d^{2}}{dx^{2}}\right )\bar{\sigma}=\Psi \left (\beta ^{2} \frac{d\bar{u}}{dx}-\gamma _{1} \bar{N}-\gamma _{2} \bar{T}\right ), $$

(40)

$$ \left (\Psi +\xi ^{2} p^{2} +\xi ^{2} \epsilon p\right ) \frac{d^{2} \bar{u}}{dx^{2}}-\frac{\Psi b_{1}}{\beta ^{2} } \frac{d\bar{N}}{dx}-\frac{\Psi b_{2}}{\beta ^{2} } \frac{d\bar{T}}{dx}=p(p+\epsilon )\bar{u}, $$

(41)

$$ \frac{d^{2} \bar{T}}{dx^{2}}+a_{3} \bar{N}=a_{4} \left (p^{2} T+gp^{2} \Psi \frac{d\bar{u}}{dx}-pw e^{-(p/v)x}\right ), $$

(42)

$$ \frac{d^{2} \bar{N}}{dx^{2}}=\gamma _{7} a_{5} \bar{N}- \frac{\gamma}{\tau } \bar{T}, $$

(43)

where

$$ \Psi =\frac{\tau ^{\beta }s^{\beta}}{s^{\beta}+\frac{\beta}{1-\beta}}, \hspace{.1in} a_{3}=\frac{\epsilon _{1} p}{p+c_{T}^{2}}, \hspace{.1in} a_{4}=\frac{1+\frac{\tau _{0}}{\omega}G_{\omega}}{p+c_{T}^{2}}, \hspace{.1in} a_{5}= p+\frac{1}{\tau}, $$

$$ c_{41}=\Psi +\xi ^{2} p^{2} +\xi ^{2} p \epsilon , \hspace{.1in} c_{42}=p(p+\epsilon ), \hspace{.1in} w=\frac{Q_{0}}{v}. $$

Eliminating $\bar{N}$ and $\bar{T}$ from equations (41)–(43), the following equation satisfied by $\bar{u}$ yields

$$ \frac{d^{6}\bar{u}}{dx^{6}}-m_{1}\frac{d^{4}\bar{u}}{dx^{4}}+m_{2} \frac{d^{2} \bar{u}}{dx^{2}}-m_{3}\bar{u}=m_{4}e^{-(p/v)x}, $$

(44)

where

$$ \begin{aligned} m_{1} & = \gamma _{7} a_{5}+a_{4}p^{2} +\frac{c_{42}}{c_{41}}- \frac{a_{5} gp^{2}\Psi}{c_{41}\beta ^{2}}, \\ m_{2} & = a_{4}p^{2} \gamma _{7} a_{5} -\frac{a_{3} \gamma}{\tau}+ \frac{c_{42}}{c_{41}}(\gamma _{7} a_{5}+a_{4} p^{2})- \frac{\Psi a_{5} gp^{2}}{c_{41}\beta ^{2} \tau} (\gamma _{7} a_{5} \tau -\gamma ), \\ m_{3} & =\frac{c_{42}}{c_{41}}\left (a_{4}p^{2} \gamma _{7} a_{5} - \frac{a_{3} \gamma}{\tau}\right ), \\ m_{4} & = -\frac{\Psi a_{4} p}{c_{41}\beta ^{2}}w\left (\frac{p}{v} \right )^{3}+\frac{\Psi a_{4} p}{c_{41}\beta ^{2} \tau}\left (\tau \gamma _{7} a_{5} -\gamma \right )w \left (\frac{p}{v}\right ). \end{aligned} $$

The general solution of equation (44) gives

$$ \bar{u}=C_{1}e^{-k_{1} x}+C_{2}e^{k_{1} x}+C_{3}e^{-k_{2} x}+C_{4}e^{k_{2} x}+C_{5}e^{-k_{3} x}+C_{6}e^{k_{3} x}+C_{7}e^{-(p/v)x}, $$

(45)

where $C_{i}$ $(i=1, 2, \ldots , 6)$ are the parameters dependent on the Laplace transform parameter $p$, which are to be determined from the boundary conditions and $C_{7}= \frac{m_{4}}{\left (\frac{p}{v}\right )^{6}-m_{1} \left (\frac{p}{v}\right )^{4}+m_{2} \left (\frac{p}{v}\right )^{2} -m_{3}}$.

Also, $k_{i}$ $(i=1, \; 2, \; 3)$ are the roots with positive real part of the characteristic equation

$$ k^{6}-m_{1}k^{4}+m_{2}k^{2}-m_{3}=0, $$

(46)

given by

$$ \begin{aligned} k_{1} & =\sqrt{\frac{1}{3}\big[2p\sin q+m_{1}\big]}, \\ k_{2} & =\sqrt{\frac{1}{3}\big[m_{1}-p\big(\sqrt{3}\cos q+\sin q\big) \big]}, \\ k_{3} & = \sqrt{\frac{1}{3}\big[m_{1}+p\big(\sqrt{3}\cos q-\sin q \big)\big]}, \end{aligned} $$

where

$$ p=\sqrt{m_{1}^{2}-3m_{2}}, \hspace{.1in} q=\frac{\sin ^{-1}\nu}{3}, \hspace{.1in} \nu =\frac{2m_{1}^{3}-9m_{1}m_{2}+27m_{3}}{2p^{3}}. $$

In a similar fashion, eliminating $\bar{u}$ and $\bar{T}$ between equations (41)–(43) yields the differential equation satisfied by $\bar{N}$ as

$$ \frac{d^{6}\bar{N}}{dx^{6}}-m_{1}\frac{d^{4}\bar{N}}{dx^{4}}+m_{2} \frac{d^{2} \bar{N}}{dx^{2}}-m_{3}\bar{N}=m_{5}e^{-(p/v)x}, $$

(47)

where $m_{5}= -\frac{ a_{4} \gamma p}{\tau}w \left (\frac{p}{v}\right )^{2}+ \frac{c_{42}}{c_{41}}\frac{a_{4} \gamma p}{\tau}w$.

The corresponding general solution of equation (47) yields

$$ \bar{N}=C_{11}e^{-k_{1} x}+C_{22}e^{k_{1} x}+C_{33}e^{-k_{2} x}+C_{44}e^{k_{2} x}+C_{55}e^{-k_{3} x}+C_{66}e^{k_{3} x}+C_{77}e^{-(p/v)x}, $$

(48)

where $C_{ii}$ $(i=1, 2, \ldots , 6)$ are the parameters dependent on $p$, which has to be determined from the boundary conditions and $C_{77}= \frac{m_{5}}{\left (\frac{p}{v}\right )^{6}-m_{1} \left (\frac{p}{v}\right )^{4}+m_{2} \left (\frac{p}{v}\right )^{2} -m_{3}}$.

Substituting (48) and (48) in equation (41) yields

$$ \begin{aligned} C_{11} & = \dfrac{\left [c_{41}k_{1}^{2} -p(p+\epsilon )\right ]}{\frac{\Psi}{\beta ^{2} }\left [\frac{\gamma _{2}\tau}{\gamma}(k_{1}^{2}-\gamma _{7} a_{5})-\gamma _{1} k_{1}\right ]}C_{1} \\ C_{22} & =- \dfrac{\left [c_{41}k_{1}^{2} -p(p+\epsilon )\right ]}{\frac{\Psi}{\beta ^{2} }\left [\frac{\gamma _{2}\tau}{\gamma}(k_{1}^{2}-\gamma _{7} a_{5})-\gamma _{1} k_{1}\right ]}C_{2} \\ C_{33} & = \dfrac{\left [c_{41}k_{2}^{2} -p(p+\epsilon )\right ]}{\frac{\Psi}{\beta ^{2} }\left [\frac{\gamma _{2}\tau}{\gamma}(k_{2}^{2}-\gamma _{7} a_{5})-\gamma _{1} k_{2}\right ]}C_{3} \\ C_{44} & = - \dfrac{\left [c_{41}k_{2}^{2} -p(p+\epsilon )\right ]}{\frac{\Psi}{\beta ^{2} }\left [\frac{\gamma _{2}\tau}{\gamma}(k_{2}^{2}-\gamma _{7} a_{5})-\gamma _{1} k_{2}\right ]}C_{4} \\ C_{55} & = \dfrac{\left [c_{41}k_{3}^{2} -p(p+\epsilon )\right ]}{\frac{\Psi}{\beta ^{2} }\left [\frac{\gamma _{2}\tau}{\gamma}(k_{3}^{2}-\gamma _{7} a_{5})-\gamma _{1} k_{3}\right ]}C_{5} \\ C_{66} & = - \dfrac{\left [c_{41}k_{3}^{2} -p(p+\epsilon )\right ]}{\frac{\Psi}{\beta ^{2} }\left [\frac{\gamma _{2}\tau}{\gamma}(k_{3}^{2}-\gamma _{7} a_{5})-\gamma _{1} k_{3}\right ]}C_{6}. \end{aligned} $$

(49)

To determine the parameters $C_{i}$ and $C_{ii}$ $(i=1, \;2, \; 3, \; 4, \; 5, \;6)$, the boundary conditions yield

$$ C_{1}+C_{2}+C_{3}+C_{4}+C_{5}+C_{6}=-C_{7}, $$

(50)

$$ C_{1} e^{-k_{1} l}+C_{2} e^{k_{1} l}+C_{3} e^{-k_{2} l}+C_{4} e^{k_{2} l}+C_{5} e^{-k_{3} l} +C_{6} e^{k_{3} l}=-C_{7} e^{-(p/v)l}, $$

(51)

$$ -C_{11}k_{1} +C_{22} k_{1} -C_{33}k_{2}+C_{44}k_{2} -C_{55}k_{3}+C_{66}k_{3}= \frac{p}{v}C_{77}, $$

(52)

$$ -C_{11}k_{1}e^{-k_{1} l} +C_{22} k_{1}e^{k_{1} l} -C_{33}k_{2} e^{-k_{2} l}+C_{44}k_{2} e^{k_{2} l} -C_{55}k_{3} e^{-k_{3} l}+$$

$$C_{66}k_{3}e^{k_{3} l}=\frac{p}{v}C_{77}e^{-(p/v)l}, $$

(53)

$$ C_{11}k_{1} (k_{1}^{2} -\gamma _{7}a_{5})-C_{22}k_{1} (k_{1}^{2} - \gamma _{7} a_{5})+C_{33}k_{2} (k_{2}^{2}-\gamma _{7} a_{5})+C_{44}k_{2} (k_{2}^{2}-\gamma _{7} a_{5}) + $$

$$ C_{55}k_{3} (k_{3}^{2}-\gamma _{7} a_{5})-C_{66}k_{3} (k_{3}^{2}-\gamma _{7} a_{5})=-\frac{p}{v}\left ( \frac{p^{2}}{v^{2}}-\gamma _{7} a_{5}\right ), $$

(54)

$$ C_{11}k_{1} (k_{1}^{2} -\gamma _{7}a_{5})e^{-k_{1} l}-C_{22}k_{1} (k_{1}^{2} - \gamma _{7} a_{5})e^{k_{1} l}+C_{33}k_{2} (k_{2}^{2}-\gamma _{7} a_{5})e^{-k_{2} l}+ $$

$$ C_{44}k_{2} (k_{2}^{2}-\gamma _{7} a_{5})e^{k_{2} l} +C_{55}k_{3} (k_{3}^{2}-\gamma _{7} a_{5})e^{-k_{3} l} $$

$$ -C_{66}k_{3} (k_{3}^{2}- \gamma _{7} a_{5})e^{k_{3} l}=-\frac{p}{v}\left (\frac{p^{2}}{v^{2}}- \gamma _{7} a_{5}\right ). $$

(55)

Solving the system of equations (50)–(55) together with the operational relationship (49) yields the unknown parameters $C_{i}$ $(i=1, 2, \ldots , 6)$. The determination of the unknown parameters completes the solution in the Laplace transform domain. However, the solutions corresponding to the absence of nonlocality $(\xi =0)$ in the absence of memory responses for Lord–Shulman theory ($c_{T}=0$) agree with the results of existing literature (He and Cao 2009).

5 Exponential stability in the one-dimensional case

Consider a one-dimensional homogeneous material that deals with the system as laid down in equations (29)–(32). In this section, the objective is to study the exponential stability for the current problem determined by this system subject to the initial conditions

$$ u(x,0)=\dot{u}(x,0)=0, \hspace{.1in} T(x,0)=\dot{T}(x,0)=0, \hspace{.1in} N(x,0)=\dot{N}(x,0)=0. $$

However, the boundary conditions for the present problem are

$$ u(0,t)=u(l,t)=0, \hspace{.1in} \frac{\partial T(0,t)}{\partial x}=\frac{\partial T(l,t)}{\partial x}=0, \hspace{.1in} \frac{\partial N(0,t)}{\partial x}=\frac{\partial N(l,t)}{\partial x}=0. $$

The strip is subjected to a moving heat source of constant strength, releasing its energy continuously while moving along the positive direction of the $x$-axis with a constant velocity $v$ given in the following form:

$$ Q=Q_{0} \delta (x-vt), $$

where $Q_{0}$ is a constant and $\delta (\cdot )$ is the Dirac delta function.

That is, the Dirichlet boundary conditions for the mechanical variable and Neumann conditions for the thermal component. It is worth saying that the boundary conditions are proposed in such a way that it allows the mathematical analysis to be simplified.

The parameters that appear in the system are related to the properties of the material and have to satisfy some thermomechanical restrictions. In particular, it is assumed that $c>0$, $\tau >0$, $\tau _{0}>0$, $k>0$, $k^{\star}>0$ and $k>k^{\star }\tau _{0}$, $\rho >0$, $\gamma _{t}\neq 0$. The assumptions are in agreement with the thermomechanical axioms and the empirical experiments. It is clear that the assumptions concerning the mass density and the thermal capacity are obvious. The conditions on $k$, $k^{\star}$, and $\tau _{0}$ are the natural ones to have dissipation. The assumption on $\gamma _{t}$ is strictly needed to guarantee the coupling between the mechanical and thermal field.

6 Numerical results and discussions

Since it is now a formidable task to interpret the nature of field variables from the closed-form solutions evaluated above, it is mandatory to determine the computational outcomes that describe the nature of the studied fields: displacement, temperature, and thermal stress. Finally, from the numerical results, the critical conclusions about the new theory due to the presence of various forms of kernel function are discussed. The inverse Laplace transformation is a useful tool, but it is challenging to compute analytically for a complex differential equation. Several numerical inverse Laplace transform techniques have been available to tackle Laplace transform inversion difficulties. For the present problem, the author uses the Riemann-sum approximation technique (Tzou 1996) for the numerical inversion of the Laplace transform, which is outlined in the Appendix B and a suitable Mathematica code is adopted. For the purpose of illustration, copper material has been used, and the material parameters are given by He and Cao (2009)

$$ E_{g}=1.11~ (\text{eV}), \hspace{.1in} \rho =8954~\text{kg}/\text{m}^{3}, \hspace{.1in} k=3.86~ \text{W} \text{m}^{-1}\text{K}^{-1}, \hspace{.1in} c_{E}=383.1 \text{J}~\text{kg}^{-1} \text{K}^{-1}, $$

$$ \alpha _{t}=1.78\times 10^{-5}\text{K}^{-1}, \hspace{.1in} d_{N}=-9\times 10^{-31}\text{m}^{3}, \hspace{.1in} \lambda =7.76\times 10^{10} \text{N}/\text{m}^{2}, $$

$$ \mu =3.86\times 10^{10}\text{N}/\text{m}^{2}, \hspace{.1in} T_{0}=293~\text{K}, \hspace{.1in} s_{0}=2~\text{ms}^{-1}, \hspace{.1in} n_{0}=10^{20}\text{m}^{-3}, $$

$$ D_{e}=2.5\times 10^{-3}\text{m}^{2} \text{s}^{-1}, \hspace{.1in} Q_{0}=10, \hspace{.1in} j=10, \hspace{.1in} \mu _{0}=4\pi \times 10^{-7 }\text{H}~ \text{m}^{-1}, $$

$$ \sigma _{0}=5.7\times 10^{7} \Omega ^{-1} \text{m}^{-1}, \hspace{.1in} l=10, \hspace{.1in} \tau _{0}=0.05. $$

Also, the phase lag parameters and the additional material constants taken from (Sherief and Abd El-Latief 2013) satisfy the stability condition for MGT heat conduction (Sur 2023) that the solution will be exponentially stable if $c>0$, $\tau _{0}>0$, $k>0$, $k^{\star}>0$, and $k>k^{\star }\tau _{0}$ is satisfied (Quintanilla 2019, 2020).

Figures 2–4 illustrate the effect of different kernel function in the variation of displacement, temperature, and stress distributions for a nonlocal medium. For the numerical computations, the kernel function is taken as $K(t-\xi )=1$, $1-\frac{t-\xi}{\omega}$, and $\left (1-\frac{t-\xi}{\omega}\right )^{2}$. The computations are carried out at time $t=1$. The nonlocal parameter is taken as $\xi =0.2$, the time-delay parameter is $\omega =0.1$, the magnetic field parameter is $\epsilon =5$, and the velocity of the moving heat source is $v=2$.

Fig. 2

Variation of $u$ vs. $x$ for $t=1$, $v=2$, $\epsilon =5$, and $\xi =0.2$

Figure 2 describes the nature of the displacement $u$ against the distance $x$ for the photo-thermoelastic medium for different kernel function. As seen from the figure, the displacement component is increasing in nature in $0< x<1$ to attain the maximum near $x=1$; thereafter, a decreasing phenomenon is relieved in the nature of the displacement distribution. It is perceived that the magnitude of the profile of $u$ is larger for $K(t-\xi )=1-\frac{t-\xi}{\omega}$ compared to $K(t-\xi )=1$ than that of $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )^{2}$. For a photothermal excitation, the time-delay indicates the difference for laser exposure between any two adjacent points on successive scanning lines of the semiconductor. Therefore, second degree term in the delay time controls the rapid decrease of displacement of the semiconductor.

Figure 3 exhibits the variation of the temperature profile $T$ for different kernel functions. The figure indicates that the differences among the curves are prominent in $0< x<3$ and after that all the curves disappear. Moreover, it is prominent from the graphical representation that the maximum effect of temperature is seen near the plane $x=0$. This is realistic in the sense that the intensity of the moving heat source is active near the bounding plane. The behavior also concludes that the temperature profile decreases more sharply for $K(t-\xi )=1$ compared to the case when $K(t-\xi )=1-\frac{t-\xi}{\omega}$ than that of $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )^{2}$.

Fig. 3

Variation of $T$ vs. $x$ for $t=1$, $v=2$, $\epsilon =5$, and $\xi =0.2$

Figure 4 predicts the variation of the stress distribution within the medium for the same set of parameters as mentioned earlier. As seen from the figure, the stress component $\sigma$ is compressive in nature near the plane of application of the heat source. However, the magnitude of the profile of $\sigma$ is larger for $K(t-\xi )=1$ than that of $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )^{2}$ than $K(t-\xi )=1-\frac{t-\xi}{\omega}$.

Fig. 4

Variation of $\sigma$ vs. $x$ for $t=1$, $v=2$, $\epsilon =5$, and $\xi =0.2$

Figure 5 depicts the variation of the carrier density $(N)$ for a nonlocal medium of the semiconductor for different kernel functions as mentioned above. From the figure, it is seen that the nonlinear kernel function in the modified heat transport can also reduce the carrier density within the medium in the presence of a heat source.

Fig. 5

Variation of $N$ vs. $x$ for $t=1$, $v=2$, $\epsilon =5$, and $\xi =0.2$

Figures 6–8 demonstrate the variation of the thermophysical quantities for different time instants $t=1, \; 2,\; 3$ for a nonlocal medium. The kernel function in the numerical estimates is taken as $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )^{2}$. The nonlocal parameter is taken as $\xi =0.2$, the time-delay parameter is $\omega =0.1$, the magnetic field parameter is $\epsilon =5$, and the velocity of the moving heat source is $v=2$. From these figures, it is noted that the magnitude of the profile of the thermophysical quantities increases within the increase of the time-span. This is realistic in the sense that, as the time of heat distribution increases, the region of heat distribution evolves deeper within the strip. As a consequence, due to the applied heat source, the strip undergoes a thermal deformation, which results in the expansion of the thermal deformation with the increment of time-span.

Fig. 6

$u$ vs. $x$ for $v=2$, $\epsilon =5$, $\xi =0.2$, and $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )^{2}$

Fig. 7

$T$ vs. $x$ for $v=2$, $\epsilon =5$, $\xi =0.2$, and $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )^{2}$

Fig. 8

$\sigma$ vs. $x$ for $v=2$, $\epsilon =5$, $\xi =0.2$, and $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )^{2}$

Figures 9 and 10 exhibit the variation of the displacement and temperature distribution within the medium for kernel function $K(t-\xi )=1-\frac{t-\xi}{\omega}$ for different velocities of the moving heat source in a nonlocal medium. For the numerical estimates, the parameter values have been taken to be the same as mentioned in the previous section. The pattern of variations of the thermophysical quantities shows a similar qualitative behavior as seen from the previous section. However, the increment of the velocity of the heat source has the tendency to decrease the magnitude of the profile of the displacement and temperature distribution. This is realistic in the sense that as the heat source moves with a constant velocity $v$, once the time instant $t$ is assigned, the distance that the heat source traverse across is $x=vt$. Therefore, at the location $x=vt$, the heat source releases its maximum energy, which leads to sharp decay in magnitude near that neighborhood.

Fig. 9

$u$ vs. $x$ for $t=1$, $\epsilon =5$, and $\xi =0.2$ for $K(t-\xi )=1-\frac{t-\xi}{\omega}$

Fig. 10

$T$ vs. $x$ for $t=1$, $\epsilon =5$, and $\xi =0.2$ for $K(t-\xi )=1-\frac{t-\xi}{\omega}$

Figures 11 and 12 depict the variation of the displacement and temperature distribution for the kernel $K(t-\xi )=1$ for the same set of parameters for a nonlocal medium. As seen from the figure, presence of induced magnetic field has the tendency to diminish the magnitude of the displacement component within the body. However, in the variation of the temperature distribution, there is no such effect of the induced magnetic field, which is quite plausible since the magnetic field and the temperature field are mutually independent.

Fig. 11

$u$ vs, $x$ for $t=1$, $v=2$, $\xi =0.2$, and $K(t-\xi )=1$

Fig. 12

$T$ vs, $x$ for $t=1$, $v=2$, $\xi =0.2$, and $K(t-\xi )=1$

Figures 13 and 14 have been plotted to display the effect of nonlocality on the thermophysical quantities. In this case, the kernel function is considered to be $K(t-\xi )=1-\frac{t-\xi}{\omega}$. The graphical representation predicts that compared to a local medium, the magnitude of the thermophysical quantities decreases in case of a nonlocal semiconductor. Since, from the viewpoint of the nonlocal theory proposed by Eringen, it is observed that the stress at a point is assumed to be a function of strains at all other points of the continuum, this observation is realistic because this new theory contains more information about the semiconductor.

Fig. 13

$u$ vs. $x$ for $t=1$, $v=2$, $\epsilon =5$, and $K(t-\xi )=1-\frac{t-\xi}{\omega}$

Fig. 14

$T$ vs. $x$ for $t=1$, $v=2$, $\epsilon =5$, and $K(t-\xi )=1-\frac{t-\xi}{\omega}$

With the aim to draw a comparative study for the variation of displacement and temperature profile for the computed results of Moore–Gibson–Thompson theory (i.e., “Comp”) with the estimated results corresponding to Lord–Shulman theory (“Est”) in existing literature (He and Cao 2009), Figs. 15 and 16 have been plotted. As noticed from these figures, the computed results due to the absence of both nonlocality and memory effect agree with the estimated results of existing literature up to quite satisfactory level. This observation is also demonstrated by the data set as portrayed in Table 1. One might conclude about the validation of the results from the numerical data and the corresponding graphical representations.

Fig. 15

Computed and estimated values of displacement for $\xi =0$, $v=4$, and $t=1$

Fig. 16

Computed and estimated values of temperature for $\xi =0$, $v=4$, and $t=1$

Table 1 Comparison between the computed and estimated results

Figure 17 is now depicted to make a comparative study for the displacement distribution $(u)$ for both LS and MGT theory. For the numerical computation, the kernel function is taken as $K(t-\xi )=1-\frac{t-\xi}{\omega}$ for $\omega =0.1$ in presence of magnetic field $\epsilon =5$ when $v=2$ and $t=1$. As noticed from the figure, for LS theory, the displacement increases within the body abruptly, and a sudden fall in the magnitude of $u$ is seen. Whereas for MGT theory, a prolonged effect of the displacement is noticed. So, for the thermoelastic problems of heat transfer in which a high heat flux is produced for a sufficiently small span of time, it is advantageous to deal with MGT theory.

Fig. 17

Comparative study between LS and MGT theory for $K(t-\xi )=1-\frac{t-\xi}{\omega}$

7 Conclusions

In this work, a magneto-photo-thermoelastic nonlocal heat conduction model has been considered. This novel nonlocal model has been derived on the basis of the concepts investigated by Eringen in addition to the derivative frame based on memory. The medium is influenced under the effect of a moving heat source. From the present investigation, the following conclusions can be revealed.

• 1. Due to the presence of delay-time in the heat transport law, instantaneous change rate depends on the past states and it is possible to classify the materials according to time-delay parameter $\omega$.

• 2. For a nonlinear kernel, the degree of the delay-time influences the heat transport law more compared to the linear kernels; and therefore, as a remark, it might be concluded that for heat transport problems within a sufficiently small-time interval with high heat-flux, it is advantageous to formulate the heat transport law with nonlinear kernel.

• 3. Compared to a local medium, the magnitude of the thermophysical quantities decreases in case of a nonlocal semiconductor since this new theory contains more information about the medium.

• 4. The Mittag-Leffler relaxation function will be helpful to discuss real world problems, and the main advantage of using this method is that it predicts finite speeds of propagation for thermal waves.

• 5. For the heat transfer problems, in which some high heat flux is produced for a sufficiently small span of time or even in delayed intervals of memory responses, it is advantageous to formulate the problem based on MGT theory compared to other generalized theories.

• 6. These theoretical findings will be valuable to experimental scientists and researchers researching this arena. In fact, instead of memory-dependent derivative, the Atangana and Baleanu fractional derivatives might be used as a future scope of the problem. Moreover, some laboratory experiments can also be done for the validation of the theoretical results.

• 7. Changing the thermal properties of a material, such as the coefficient of thermal conductivity and its dependence on temperature change, significantly affects its behavior in different physical domains. However, these modifications would be considered as further scope of the present analysis.

Appendices

Appendix A: Laplace transform of the Mittag-Leffler function

The Laplace inversion of the function $F(s)=\frac{1}{s^{\gamma +1}}$ is $f(t)$ defined as

$$ f(t)=\mathscr{L}^{-1}\big[F(s)\big]=\int _{c-i\infty}^{c+i \infty} \frac{e^{dt}}{s^{\gamma +1}}ds. $$

The only singularity of the function $\frac{e^{dt}}{s^{\gamma +1}}$ is at $s=0$, which is a branch point. To evaluate the integral $\frac{1}{2\pi i }\int _{\Gamma} \frac{e^{dt}}{s^{\gamma +1}} ds$, the contour $\gamma$ is depicted in Fig. 18.

Fig. 18

The contour of the integration

Since there is no singularity of the function inside $\Gamma$, the Cauchy integral formula yields

$$ \frac{1}{2\pi i }\left (\int _{C-iR}^{C+iR}+\int _{C_{R}}+ \int _{CD}+\int _{C_{\rho}}+\int _{D'C'}+ \int _{C_{R}'}\right )\frac{e^{dt}}{s^{\gamma +1}} ds=0. $$

On $C_{R}$, $s=C+Re^{i\theta}$, $\frac{\pi}{2}\leqslant \theta < \pi$. Therefore

$$ \int _{C_{R}} \frac{e^{dt}}{s^{\gamma +1}} ds=\int _{ \pi /2}^{\pi} \frac{e^{(C+Re^{i\theta})t}}{(C+R e^{i\theta})^{\gamma +1}}iR e^{i \theta}d\theta $$

$$ \left |\int _{C_{R}} \frac{e^{dt}}{s^{\gamma +1}} ds\right | \leqslant \frac{e^{Ct}}{R^{\gamma}} \frac{R^{\gamma +1}}{\left (C^{2}+R^{2}+2CR \right )^{\frac{\gamma +1}{2}}} \int _{\pi /2}^{\pi }e^{Rt \cos \theta} d\theta , $$

and using the inequality in $0\leqslant \theta \leqslant \pi /2$, $\frac{2\theta}{\pi}\leqslant \sin \theta \leqslant \theta$ holds. Therefore

$$ \left |\int _{C_{R}} \frac{e^{dt}}{s^{\gamma +1}} ds\right | \leqslant \frac{\pi e^{Ct}}{R^{\gamma +1}2t}\left (1-e^{-Rt}\right ) \rightarrow 0 \;\;\; \text{as}\;\;\; R \rightarrow \infty . $$

Similarly, it can be shown that

$$ \left |\int _{C_{R}'} \frac{e^{dt}}{s^{\gamma +1}} ds\right | \rightarrow 0 \;\;\; \text{as}\;\;\; R \rightarrow \infty . $$

On CD, $s=xe^{i\pi}$. Therefore,

$$ \int _{CD}\frac{e^{dt}}{s^{\gamma +1}} ds=-\int _{ \rho}^{R} \frac{e^{-xt}e^{i\pi}}{\left (xe^{i\pi}\right )^{\gamma +1}}dx $$

$$ \displaystyle \lim _{\substack{\rho \to a \\ R\to \infty}}\int _{CD}\frac{e^{dt}}{s^{\gamma +1}} ds=- \frac{t^{\gamma}}{e^{i\pi \gamma}}\Gamma (-\gamma ). $$

On $D^{\prime }C^{\prime}$, $s=xe^{-i\pi}$. Therefore,

$$ \displaystyle \lim _{\substack{\rho \to 0 \\ R\to \infty}}\int _{D'C'}\frac{e^{dt}}{s^{\gamma +1}} ds=\int _{0}^{ \infty}\frac{e^{-xt}}{x^{\gamma +1}e^{-i\pi \gamma}}dx=e^{i\pi \gamma}t^{ \gamma}\Gamma (-\gamma ) $$

$$ \therefore \int _{CD}\frac{e^{st}}{s^{\gamma +1}}ds+\int _{D'C'}\frac{e^{st}}{s^{\gamma +1}}ds=2i t^{\gamma}\sin \pi \gamma . $$

On $C_{\rho}$, $s=\rho e^{i\theta}$, $\pi <\theta <-\pi$

$$ \therefore \int _{C_{\rho}}\frac{e^{st}}{s^{\gamma +1}}ds= \displaystyle \lim _{\rho \to 0}\int _{\pi}^{-\pi} \frac{e^{\rho e^{i\theta} t}}{\left (\rho e^{i\theta}\right )^{\gamma +1}}i \rho e^{i\theta}\to 0 \hspace{.1in} \text{as} \hspace{.1in} \rho \to 0. $$

Hence,

$$ \frac{1}{2\pi i }\int _{C-i\infty}^{C+i \infty} \frac{e^{st}}{s^{\gamma +1}}ds=\frac{t^{\gamma}}{\Gamma (1+\gamma )}. $$

From this result, the Laplace transform of the Mittag-Leffler function can be derived.

Appendix B: Numerical inversion of the Laplace transform

To determine the temperature, displacement, and stress distributions in a semiconductor material in the space-time domain, we need to apply the Laplace inversion on the field quantities, which we have computed numerically employing the Riemann-sum approximation method. In this method, any function $\overline{f}(x,p)$ in the Laplace transform domain can be inverted to the space-time domain as (Tzou 1996) follows. The required Laplace inversion is obtained by introducing a variable transformation from complex $p$ to real $\omega$ as defined by

$$ f(x,t)= \frac{1}{2 \pi i } \int _{\beta -i \infty}^{\beta + i \infty}\overline{f}(x,p) e^{pt}dp, $$

(A.1)

with

$$ p=\beta +i\omega , \hspace{.1in} i=\sqrt{-1}, $$

(A.2)

where $\beta$ is the real constant specifying the vertical segment in the Bromwich contour. Thus, equation (A.1) reduces to

$$ f(x,t)= \frac{e^{\beta t }}{2 \pi} \int _{-\infty}^{\infty} \overline{f} (x, \beta +i\omega )e^{i \omega t}d \omega . $$

(A.3)

The Fourier integral thus can be approximated by a Riemann-sum (Tzou 1996) denoting $\omega$ as the wave frequency and $\tau$ being the half-period of its oscillation, i.e., $\omega =n \pi / \tau$ for the $n$th wave mode and $\Delta \omega _{n}=\pi /\tau$ for all modes. Therefore

$$ f(x,t)=\frac{e^{\beta t }}{2 \tau} \sum _{n=-\infty}^{\infty} \overline{f} \left (x, p=\beta +\frac{in \pi}{\tau}\right )e^{ \frac{in\pi t }{\tau}}. $$

(A.4)

Noticing further that the wave modes with positive and negative $n$ values appear in pairs and

$$\begin{gathered} \overline{f} \left (x, \beta +\frac{in \pi}{\tau}\right ) e^{i(n \pi t / \tau )}+\overline{f}\left (x, \beta -\frac{i n \pi}{\tau}\right ) e^{-i(n \pi t/\tau )} \\ =2 \text{Re}\left [\overline{f}\left (x, \beta + \frac{i n \pi}{\tau}\right ) e^{i(n \pi t /\tau )}\right ], \end{gathered}$$

(A.5)

equation (A.4) can be further expressed as

$$ f(x,t)=\frac{e^{\beta t }}{\tau}\left [\frac{1}{2}\overline{f}(x, \beta )+\text{Re}\sum _{n=1}^{\infty}\overline{f}\left (x, \beta + \frac{in \pi}{\tau}\right )e^{i(n \pi t )/\tau}\right ], $$

(A.6)

in which $\text{Re}$ represents the real part of the summation. Since the function $e^{i(n \pi t )/\tau}$ has a fundamental period $2 \pi$, the physical domain of $t$ is $0 \leqslant t \leqslant 2 \pi$. At $t =\tau$, we have from Eq. (A.6)

$$ f(x,t)=\frac{e^{\beta t}}{t}\left [\frac{1}{2}\overline{f}(x,\beta )+ \text{Re} \sum _{n=1}^{N} \overline{f}\left (x,\beta + \frac{i n \pi}{t}\right )(-1)^{n}\right ], $$

(A.7)

which is the required inversion formula. The Riemann-sum approximation involved here represents a single summation in the numerical process. The accuracy depends on the value of $\beta$ and the truncation error dictated by $N$. The value of $\beta$ must be selected so that the Bromwich contour encloses all the branch points. Therefore, any positive number can be selected for $\beta$ because the branch points are all negative. For a faster convergence of the scheme, however, numerous numerical experiments have shown that the value of $\beta$ has to satisfy the relation $\beta t \approx 4.7 \approx 2+e$, where $t$ stands for time (Tzou 1996).