1 Introduction

As a fundamental task in the field of the image processing, the aim of the image segmentation is to separate the image domain Ω into K disjoint regions Ωi (i = 2,3,⋯ ,K) according to some characteristics such as the intensity, the color and the texture [19, 30, 31]. According to the characteristics of segmentation, it can be divided into data-driven models and model-driven models. Data-driven models usually require a large amount of image data and strong model support [18, 27]. However, many difficulties such as insufficient data, background noise, local intensity variations and complex segmentation targets render the segmentation problem with the high challenge [23]. When the available data is too small and the model is imperfect, the model-driven models can perfectly solve such problems. Among the model-driven models, active contour models are generally distinguished by a predefined energy functional with the intensity and the gradient information based on the intrinsic properties of images. According to the nature of constraints, active contour models can be roughly categorized into the edge-based models and the region-based models. The edge-based models such as the snake model and the geodesic contour model use edge-detection functions and evolve the curves toward sharp gradients [9, 17]. However, these models are sensitive to the noise. As a comparison, the region-based models are robust to the noise via incorporating region and boundary information [11, 12, 26, 32].

Among region-based models, one of the most fundamental schemes is the Chan-Vese (CV) model [12], which is the simplification of the Mumford-Shah (MS) model [26]. Due to this simplification, the CV model has been applied to many fields of the image segmentation. However, this model is nonconvex and nosmooth. So how to solve it is the key for the actual application. In general, there are two research hotspots such as the Level Set Method (LSM) and the Convex Relaxation Method (CRM). To the LSM, the level set function (LSF) needs to be re-initialized to ensure that the LSF is always a signed distance function [7, 21]. However, this scheme has strong computational difficulties and is quite inefficient due to the complex difference scheme of their PDEs [14, 24]. To the CRM, its objective function is based on the equivalent description of Euler-Lagrangian equation for the CV model, where the binary constraint is relaxed into a closed interval [11]. With this transformation, some efficient numerical methods can be used to solve it [1, 5, 10, 28, 29]. However, the segmentation result depends on the choice of the threshold parameter. Then this method leads to a gap between the sole segmentation result for the real image and the theoretical analysis based on the relaxed model [11, 14, 22]. Different to two kinds of aforementioned methods, this paper tries to propose a new scheme to solve the CV model based on the Lagrangian dual theory [4]. In the proposed scheme, the CV model is first transformed into an equivalent binary optimization problem and then solve this problem through the Lagrangian dual strategy and the alternating direction of method of multipliers (ADMM). Especially, once the value of the dual variable is obtained, the segmentation result can be obtained via using the signum function. Numerical comparisons illustrates that the proposed scheme can improve the segmentation accuracy of segmentation compared with other classic numerical methods.

The rest of the paper is organized as follows. Section 2 first gives some comments of the Lagrangian dual scheme and then uses this scheme to solve the CV model with the help of the ADMM. Some numerical comparisons are arranged in Section 3 and conclusions are given in Section 4.

2 Dual-based scheme to solve the CV model

This section first introduces the Lagrangian dual scheme and an efficient numerical method is then proposed to solve the CV model.

2.1 Lagrangian dual scheme

Among the various dual program formulations, the Lagrangian dual formulation in particular lends to a rich understanding of duality theory in optimization research [4, 16]. Its main motivation is to find a boundary or a solution to the original problem through its dual problem. More specifically, the solution to the dual problem can provide a bound to the primal problem or the same optimal solution to the primal problem, which is useful if the primal problem is harder to be solved than the dual problem. To describe the Lagrangian dual function, we consider the general model as

$$ \begin{array}{@{}rcl@{}} \begin{cases} \displaystyle\min_{\mathrm{y}\in\mathbb{Y}} h(\mathrm{y}),\\ \mathrm{s.t.}r_{i}(\mathrm{y})\leq0,\\ s_{j}(\mathrm{y})=0, \end{cases} \end{array} $$
(1)

where h(y),ri(y) and sj(y) are some suitable functions for i = 1,2,⋯ ,m, j = 1,2,⋯ ,p and \(\mathbb {Y}\subseteq \mathbb {R}^{n}\). It is obvious that the Lagrangian function of the problem (1) can be written as

$$ \begin{array}{@{}rcl@{}} \mathcal{L}(\mathrm{y},\boldsymbol{\mu},\boldsymbol{\nu})=h(\mathrm{y})+\sum\limits_{i=1}^{m}r_{i}(\mathrm{y})\mu_{i}+ \sum\limits_{j=1}^{p}s_{j}(\mathrm{y})\nu_{j}, \end{array} $$
(2)

where μi ≥ 0 and νj are the Lagrange multipliers associated with the inequality constraints and the equality constraints, respectively. In general, we call problem (1) to be the original problem. In the following, we give the definition of the dual objective function.

Definition 1

The dual objective function of the original problem (1) is defined by

$$ \begin{array}{@{}rcl@{}} q(\boldsymbol{\mu},\boldsymbol{\nu})=\min_{\mathrm{y}\in \mathbb{Y}}\mathcal{L}(\mathrm{y},\boldsymbol{\mu},\boldsymbol{\nu}). \end{array} $$
(3)

Furthermore, the Lagrangian dual function is given by

$$ \begin{array}{@{}rcl@{}} q^{*}=\max_{(\boldsymbol{\mu},\boldsymbol{\nu})\in\mathcal{D}} q(\boldsymbol{\mu},\boldsymbol{\nu}), \end{array} $$
(4)

where \(\mathcal {D}=\left \{(\boldsymbol {\mu },\boldsymbol {\nu })\in \mathbb {R}_{+}^{m}\times \mathbb {R}^{p}| q(\boldsymbol {\mu },\boldsymbol {\nu })>-\infty \right \}\).

Based on above definition, it can be easily deduced that the Lagrangian dual function (4) is always convex and it consists of maximizing a concave function over a convex feasible set \(\mathcal {D}\).

Lemma 1

Let \(\bar {\mathrm {y}}\) be a feasible solution to the primal problem (1) and \((\bar {\boldsymbol {\mu }},\bar {\boldsymbol {\nu }})\) be a feasible solution of the dual problem (4), then have

$$ \begin{array}{@{}rcl@{}} h(\bar{\mathrm{y}})\geq q(\bar{\boldsymbol{\mu}},\bar{\boldsymbol{\nu}}). \end{array} $$

Lemma 1 is called the weak duality theorem which shows that the objective value of any feasible solution to the dual problem yields a lower bound on the objective value of any feasible solution to the primal problem. This theorem also implies the saddle point of the Lagrangian function as

$$ \begin{array}{@{}rcl@{}} \mathcal{L}\left( \mathrm{y}^{*},\boldsymbol{\mu},\boldsymbol{\nu}\right)\leq \mathcal{L}\left( \mathrm{y}^{*},\boldsymbol{\mu}^{*},\boldsymbol{\nu}^{*}\right)\leq \mathcal{L}\left( \mathrm{y},\boldsymbol{\mu}^{*},\boldsymbol{\nu}^{*}\right), \end{array} $$

where y∗ is the optimal solution of the primal problem (1) and \(\left (\boldsymbol {\mu }^{*},\boldsymbol {\nu }^{*}\right )\) is the optimal solution of the primal problem (4). A strong duality theorem cannot necessarily be established for a general nonlinear optimization problem without adding assumptions for regarding the convexity such as the Slater’s condition [8].

2.2 Convex relaxation method to solve the CV model

The CV model [12] is the curve evolution implementation of a piecewise-constant case of the Mumford-Shah model [26] and also is applied in many fields of the image segmentation. Assume that \(f:{\varOmega }\rightarrow \mathbb {R}\) is the observed image, the CV model can be formally formulated as

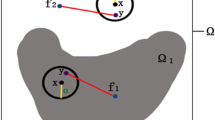
$$ \begin{array}{@{}rcl@{}} \min_{c_{1},c_{2},\mathrm{\Gamma}}{\int}_{{\varOmega}_{1}}|f(\mathrm{x})-c_{1}|^{2}\text{dx}+{\int}_{{\varOmega}_{2}}|f(\mathrm{x})-c_{2}|^{2}\text{dx} +\lambda\text{Length}(\mathrm{\Gamma}), \end{array} $$
(5)

where Ω1 = Ω ∖Ω2 and Ω1 ∩Ω2 = ∅, c1 and c2 denote the average intensity value of the segmentation region, Γ is a closed contour dividing into two regions Ω1 and Ω2 and λ is the regularization parameter.

To solve the CV model (5), the zero level set Γ = {x ∈Ω|ϕ(x) = 0} is used to replace the unknown curve Γ. With this setting, the CV model (5) can be equivalently rewritten in terms of the level set function ϕFootnote 1 as

$$ \underset{c_{1},c_{2},\phi}{\min}{\int}_{{\varOmega}}\left( |f-c_{1}|^{2}\mathrm{H}(\phi)+|f-c_{2}|^{2} (1-\mathrm{H}(\phi))\right)\text{dx}+\lambda{\int}_{{\varOmega}}\delta(\phi)\|\nabla\phi\|\text{dx}, $$
(6)

where \(\|\nabla \phi \|=\sqrt {(\nabla _{x}\phi )^{2}+(\nabla _{y}\phi )^{2}}\), H(⋅) denotes the Heaviside function and δ the Dirac mass, its distributional derivative as

$$ \mathrm{H}(t)=\begin{cases} 1~\text{if}~t\geq0\\ 0~\text{if}~t<0 \end{cases} \text{and}~\delta(t)=\frac{\mathrm{d}}{\mathrm{d}t}\mathrm{H}(t). $$

In the problem (6), the existence of ϕ and the regularity, such as differentiability can be trivially deduced from the proof of existence and regularity for the piecewise constant model in [25]. In order to solve problem (6), Chan and Vese in [12] proposed to alternately obtain the curve Γ and the constant values c1 and c2 by solving the following variational formulation

$$ \left\{ \begin{array}{ll} c_{1}=\frac{{\int}_{{\varOmega}}f\mathrm{H}(\phi)\text{dx}}{{\int}_{{\varOmega}}\mathrm{H}(\phi)\text{dx}}, c_{2}=\frac{{\int}_{{\varOmega}}f(1-\mathrm{H}(\phi))\text{dx}}{{\int}_{{\varOmega}}(1-\mathrm{H}(\phi))\text{dx}},\\ \frac{\partial\phi}{\partial t}=\delta(\phi)\left[\lambda\text{div}\left( \frac{\nabla \phi}{\|\nabla\phi\|}\right)-(f-c_{1})^{2}+(f-c_{2})^{2}\right]. \end{array} \right. $$
(7)

However, this method requires the time step to be small enough and the solution also tends to the unique minimizer as the time increasement. Actually, it is slow due to the Courant-Friedrichs-Lewy (CFL) stability constraint [13], which puts a very tight bound on the time step when the solution develops flat regions. Furthermore, a local gradient flow is used for the minimization and so the result is strongly dependent on the initialization. In particular, no optimality guarantee can be deduced. In addition, the level set approach is very costly due to a gradient descent type minimization.

In order to overcome above drawbacks, Chan et al. in [11] equivalently rewrote the steady equation equation of the CV model as an optimization problem

$$ \underset{\phi\in\{0,1\}}{\min}{\int}_{{\varOmega}}s\phi\text{dx}+\lambda{\int}_{{\varOmega}}\|\nabla\phi\|\text{dx}, $$
(8)

for s = (f − c1)2 − (f − c2)2. The problem (8) is nonconvex due to the binary constraint, so they furthermore relaxed it into the following convex optimization problem

$$ \underset{\phi\in[0,1]}{\min}{\int}_{{\varOmega}}s\phi\text{dx}+\lambda{\int}_{{\varOmega}}\|\nabla\phi\|\text{dx}. $$
(9)

Since the model (9) is convex and nonsmooth, many operator splitting methods such as the alternating direction method of multipliers [5, 28, 29] and the primal dual method [1, 10] can be used to solve it.

2.3 Dual-based ADMM to solve the CV model

In this subsection, a new scheme is considered to solve the NP hard problem (8) based on the dual theory. In order to flexibly use the Lagrangian dual scheme, we first set v = 2ϕ − 1 and it is obvious that v can be equivalently written as v = sign(ϕ) for ϕ ∈{0,1}. Then the problem (8) can be written as

$$ \begin{cases} \underset{v,\phi}{\min}{\int}_{{\varOmega}}sv\text{dx}+\lambda{\int}_{{\varOmega}}\|\nabla v\|\text{dx},\\ \mathrm{s.t.}v= {sign}(\phi), \end{cases} $$
(10)

where v is an auxiliary variable and sign(ϕ) denotes the piecewise signum function. In the following, the average intensity value \(\bar {c}_{1}\) and \(\bar {c}_{2}\) in Ω1 and Ω2 need to be recomputed due to the replacement v = 2ϕ − 1. Specifically, with the simple computation, it can be obtained by

$$ \bar{c}_{1}(v)=\frac{{\int}_{{\varOmega}}f(v+1)\text{dx}}{{\int}_{{\varOmega}}(v+1)\text{dx}} ~\text{and}~ \bar{c}_{2}(v)=\frac{{\int}_{{\varOmega}}f(v-1)\text{dx}}{{\int}_{{\varOmega}}(v-1)\text{dx}}. $$
(11)

The problem (10) is difficultly solved since there couples the gradient operator into the L1-norm. One efficient numerical method is to use some operator splitting schemes such as the primal-dual splitting (PDS) [10] and the ADMM [6]. Here focus on the latter to solve the problem (10). To the ADMM, the basic motivation is to first split the original problem into several easily solvable subproblems by introducing some auxiliary variables, and then solves each subproblem separately by employing some efficient numerical methods. To this end, by introducing two auxiliary variables w and z, the problem (10) can be transformed as

$$ \begin{cases} \underset{v,\textbf{z},w,\phi}{\min}{\int}_{{\varOmega}}sw\text{dx} +\lambda{\int}_{{\varOmega}}\|\textbf{z}\|\text{dx},\\ \text{s.t.} w=v,\textbf{z}=\nabla v~\text{and}~w=\text{sign}(\phi), \end{cases} $$
(12)

where z = (z1,z2) and \(\|\textbf {z}\|:=\sqrt {{z_{1}^{2}}+{z_{2}^{2}}}\). By introducing three Lagrange multipliers for three constraints, the problem (12) can be written as a saddle-point problem

$$ \underset{v,\textbf{z},w,\phi}{\min}\underset{\alpha,\boldsymbol{\beta},\mu}{\max}\mathcal{L}(v,\textbf{z}, w,\phi;\alpha,\boldsymbol{\beta},\mu), $$
(13)

where the augmented Lagrangian function is defined by

$$ \begin{array}{@{}rcl@{}} \mathcal{L}(v,\textbf{z},w,\phi;\alpha,\boldsymbol{\beta},\mu)&=& \lambda{\int}_{{\varOmega}}\|\textbf{z}\|\text{dx}+{\int}_{{\varOmega}}\alpha(v-w) \text{dx}+\frac{\gamma_{1}}{2}{\int}_{{\varOmega}}|v-w|^{2}\text{dx} \\&& +{\int}_{{\varOmega}}sw\text{dx}+{\int}_{{\varOmega}}\boldsymbol{\beta}^{T}(\textbf{z}-\nabla v)\text{dx} +\frac{\gamma_{2}}{2}{\int}_{{\varOmega}}\|\textbf{z}-\nabla v\|^{2}\text{dx}\\ &&+{\int}_{{\varOmega}}\mu(w- {sign}(\phi))\text{dx}. \end{array} $$

Here γ1 and γ2 are the penalty parameters, α, β and μ are the Lagrangian multipliers. Note there is not the penalty term to deal with the third constraint in (12) since we want to use the Lagrangian dual scheme to solve it. To solve the problem (13), the ADMM scheme can be described as

where ρ1 and ρ2 are the weighted parameters. In the following we consider to solve several subproblems (14)–(16).

  • To the subproblem (14), it can be written as

    $$ \begin{array}{@{}rcl@{}} v^{k+1}&=&{argmin}_{v}{\int}_{{\varOmega}}\alpha^{k}\left( v-w^{k}\right) \text{dx}+\frac{\gamma_{1}}{2}{\int}_{{\varOmega}}\left|v-w^{k}\right|^{2}\text{dx} \\&& +{\int}_{{\varOmega}}\left( \boldsymbol{\beta}^{k}\right)^{T}\left( \textbf{z}^{k}-\nabla v\right)\text{dx} +\frac{\gamma_{2}}{2}{\int}_{{\varOmega}}\left\|\textbf{z}^{k}-\nabla v\right\|^{2}\text{dx}. \end{array} $$

    Its Euler-Lagrange equation is

    $$ (\gamma_{1}\mathcal{I}-\gamma_{2}\triangle)v^{k+1}=\gamma_{1}w^{k}-\alpha^{k} -\text{div}\left( \boldsymbol{\beta}^{k}+\gamma_{2}\textbf{z}^{k}\right), $$

    where \(\mathcal {I}\) is an identity operator. It is a linear equation, the numerical method depends on the used boundary condition. By assuming to use the periodic boundary condition of the gradient operator ∇, the solution can be obtained

    $$ \begin{array}{@{}rcl@{}} v^{k+1}=\mathcal{F}^{-1}\left( \frac{\mathcal{F}\left( \gamma_{1}w^{k}-\alpha^{k}-\text{div} \left( \boldsymbol{\beta}^{k}+\gamma_{2}\textbf{z}^{k}\right)\right)} {\gamma_{1}\mathcal{F}(\mathcal{I})-\gamma_{2}\mathcal{F}(\bigtriangleup)}\right) \end{array} $$
    (19)

    by using the fast Fourier transform, where \(\mathcal {F}\) denotes the Fourier transform and \(\mathcal {F}^{-1}\) denotes the inverse of \(\mathcal {F}\).

  • To the subproblem (15), the following lemma need to be arranged.

    Lemma 2

    Assume that \(\textbf {x}=(x_{1},x_{2})\in \mathbb {R}^{2} \) and \(\textbf {y}=(y_{1},y_{2})\in \mathbb {R}^{2}\), then the closed-form solution x∗ of

    $$ \min_{\textbf{x}}\frac{1}{2\tau}\|\textbf{x}-\textbf{y}\|^{2}+\|\textbf{x}\| $$
    (20)

    can be obtained by the following soft-thresholding operator as

    $$ \textbf{x}^{*}=\mathcal{S}(\textbf{y},\tau)=\max\left( \|\textbf{y}\|-\tau,0\right) \frac{\textbf{y}}{\|\textbf{y}\|}. $$
    (21)

    Proof

    For the convenience, we set

    $$F(\textbf{x})=\frac{1}{2\tau}\|\textbf{x}-\textbf{y}\|^{2}+\|\textbf{x}\|.$$

    Based on the Fermat theorem [2], the optimization condition of the problem (20) satisfies that

    $$ 0\in\partial F\left( \textbf{x}^{*}\right):=\frac{1}{\tau} \left( \textbf{x}^{*}-\textbf{y}\right)+\partial(\|\textbf{x}^{*}\|), $$
    (22)

    where ∂(⋅) denotes the subgradient Footnote 2. Specially, ∂(∥x∗∥) has the form as

    $$ \partial(\|\textbf{x}^{*}\|) =\begin{cases} \frac{\textbf{x}^{*}}{\|\textbf{x}^{*}\|}&\text{if}~\textbf{x}^{*}\neq\textbf{0},\\ \textbf{p}&\text{if}~\textbf{x}^{*}=\textbf{0}, \end{cases} $$

    where p satisfies that ∥p∥≤ 1. To the case of x∗≠0, the equation (22) implies that

    $$ \begin{array}{@{}rcl@{}} \textbf{x}^{*}\left( 1+\frac{\tau}{\|\textbf{x}^{*}\|}\right)=\textbf{y}. \end{array} $$
    (23)

    Then, it can be deduced that the vectors x∗ and y have the same direction. That is to say

    $$ \begin{array}{@{}rcl@{}} \frac{\textbf{x}^{*}}{\|\textbf{x}^{*}\|}=\frac{\textbf{y}}{\|\textbf{y}\|}. \end{array} $$
    (24)

    Substituting (24) into (23) deduces that

    $$ \textbf{x}^{*}=(\|\textbf{y}\|-\tau)\frac{\textbf{y}}{\|\textbf{y}\|}. $$
    (25)

    In addition, the formula (25) also implies that ∥y∥≥ τ due to the same direction between x∗ and y. To the case of x∗ = 0, the formula (22) implies that

    $$ \frac{1}{\tau}\textbf{y}=\textbf{p}. $$
    (26)

    Using ∥p∥≤ 1, we have ∥y∥ < τ. As a summarization, above assertion is held. □

    In order to use Lemma 2, the problem (15) needs to be rearranged as

    $$ \textbf{z}^{k+1} ={argmin}_{\textbf{z}}{\int}_{{\varOmega}}\left( \lambda\|\textbf{z}\| +\frac{\gamma_{2}}{2}\left\|\textbf{z}-\left( \nabla v^{k+1}-\frac{\boldsymbol{\beta}^{k}}{\gamma_{2}}\right)\right\|^{2}\right)\text{dx}. $$

    It is the classic L2 − L1 problem, so its closed-form solution can be directly obtained by the following soft-thresholding operator

    $$ \textbf{z}^{k+1}=\mathcal{S}\left( \nabla v^{k+1}-\frac{\boldsymbol{\beta}^{k}}{\gamma_{2}},\frac{\lambda}{\gamma_{2}}\right). $$
    (27)

  • To the subproblem (16), we want to use the Lagrangian dual scheme [3, 16]. So it is rearranged to a compact form as

    $$ \begin{array}{@{}rcl@{}} \left( w^{k+1},\phi^{k+1},\mu^{k+1}\right)=\underset{w,\phi}{\arg\min}~\underset{\mu}{\max} \underbrace{H^{k}(w)+S^{k}(\phi)}_{:=\mathbb{L}\left( w,\phi,\mu\right)}, \end{array} $$
    (28)

    where

    $$ H^{k}(w)=\frac{\gamma_{1}}{2}{\int}_{{\varOmega}}\left|v^{k+1}-w +\frac{\alpha^{k}}{\gamma_{1}}\right|^{2}\text{dx}+{\int}_{{\varOmega}}\left( s+\mu^{k}\right)w\text{dx} $$

    and

    $$ S^{k}(\phi)=-{\int}_{{\varOmega}}\mu~{sign}(\phi)\text{dx}. $$

    In the saddle point (28), if we can define the primal problem as

    $$ \left( w^{k+1},\phi^{k+1}\right)=\underset{w,\phi}{\arg\min}~ \mathbb{L}\left( w,\phi;\mu^{k}\right), $$
    (29)

    its dual problem can be defined by

    $$ \begin{array}{@{}rcl@{}} \mu^{k+1}=\underset{\mu}{\arg\max}\mathbb{~L}\left( w^{k+1},\phi^{k+1},\mu\right). \end{array} $$
    (30)

    To the primal problem (29), the alternating direction of method used in [16] can be employed to solve it as

    $$ \begin{array}{@{}rcl@{}}{} w^{k+1}=\underset{w}{\arg\min}~ H^k(w), \end{array} $$
    (31)
    $$ \begin{array}{@{}rcl@{}} \phi^{k+1}=\underset{\phi}{\arg\min}~ S^k(\phi). \end{array} $$
    (32)

    To the subproblem (31), its solution can be written

    $$ w^{k+1}=v^{k+1}+\frac{\alpha^{k}-\left( \mu^{k}+s\right)}{\gamma_{1}} $$
    (33)

    based on the optimization condition.

    In the following, we mainly discuss the solution of the subproblem (32).

    Theorem 1

    The optimization value of the subproblem (32) can be obtained by

    $$ \begin{array}{@{}rcl@{}} S^{k}(\phi^{k+1})=-{\int}_{{\varOmega}}\left|\mu^{k}\right|\text{dx}. \end{array} $$
    (34)

    Proof

    : To the problem

    $$ \underset{\phi}{\min} -{\int}_{{\varOmega}}\mu^{k}{sign}(\phi)\text{dx}, $$
    (35)

    it is obvious that the solution is not unique. However, it is worth noticing that the minimizer can be obtained by setting ϕ = μk. That is to say \(\mu ^{k}{sign}(\phi )=\mu ^{k}{sign}\left (\mu ^{k}\right )=\left |\mu ^{k}\right |\). Then the assertion is held. □

    By using Theorem 1, the dual problem (32) can be solved by

    $$ \begin{array}{@{}rcl@{}} \mu^{k+1}&=&\underset{\mu}{\arg\max}\mathbb{L}\left( w^{k+1},\phi^{k+1},\mu\right)\\ &=&\underset{\mu}{\arg\max}_-\frac{1}{2\gamma_{1}}{\int}_{{\varOmega}}\left|\mu-B^{k}\right|^{2}\text{dx} -{\int}_{{\varOmega}}|\mu|\text{dx}\\ &=&\underset{\mu}{\arg\min}_{\frac{1}{2\gamma_{1}}}{\int}_{{\varOmega}}\left|\mu-B^{k}\right|^{2}\text{dx} +{\int}_{{\varOmega}}|\mu|\text{dx}\\ &=&\max\left\{\left|B^{k}\right|-\gamma_{1},0\right\} \frac{B^{k}}{\left|B^{k}\right|}, \end{array} $$
    (36)

    where Bk = γ1vk+ 1 + αk − s. Once μk+ 1 is obtained, ϕk+ 1 := μk+ 1 can be set. Furthermore, a binary solution to the problem (12) is obtained as

    $$ \begin{array}{@{}rcl@{}} w^{k+1}={sign}\left( \phi^{k+1}\right). \end{array} $$
    (37)

    Based on above discussion, the dual-based ADMM to solve the problem (10) can be summarized as the following framework.

3 Numerical method

This section mainly arranges some numerical comparisons between our proposed Algorithm 1 (called DADMM) and other classic numerical methods to solve the CV model. These methods include the variable level set method (VLSM) used in [12], the alternating direction method of multipliers for the relaxed formation (ADMM) used in [20] and the primal dual method (PDM) [10]. To the segmentation models and algorithms, there include two kinds of parameters as the model-based parameter λ and the algorithm-based parameters. To the former, the chosen rule is based on the trial-and-error method in order to obtain the satisfied segmentation result. To the latter, we set ρ1 = ρ2 = 1.01 and γ1 = γ2 = 3 in Algorithm 1 and the threshold value is 0.5 to the ADMM used in [20]. The initial contour of the segmentation method are randomly chosen. The stopping criterions of all of algorithms depend on the segmentation images. All of the numerical methods are implemented with MATLAB(2020a) in Core2 with 3.5GHz and 64G RAM by rescaling testing images in the range [0,1].

Algorithm 1
figure b

Dual-based ADMM to solve the problem (10).

Full size image

3.1 Synthetic images

To illustrate the ability of the DADMM with the different noise level, it is first tested on two-phase synthetic images as shown in Fig. 1. The Fig. 1(A) includes some simpler geometrical structures, but the Fig. 1(B) includes more complicated geometrical structures. Since Fig. 1(A) and Fig. 1(B) can be regarded as the accurate segmentation image, the Segmentation Error (SE)

$$ \begin{array}{@{}rcl@{}} \text{SE}=\frac{\text{Number of uncorrectly classified pixels}}{\text{Total number of pixels}}\times100\% \end{array} $$
Fig. 1
figure 1

Synthetic images and the original noisy images with three different noisy level. Here σ denotes the noisy variance

Full size image

can be used to evaluate the effectiveness of the segmentation scheme. To the noisy images (A1)-(A3) and (B1)-(B3) in Fig. 1, the Matalb function ”imnoise” is used to add the white Gaussian noise with different variances as 0.1, 0.25 and 0.5. The related parameters and segmentation data are shown in Table 1. It is obvious that the DADMM slightly outperforms other methods in terms of the segmentation accuracy.

Table 1 Related data used in segmenting images shown in Fig. 1
Full size table

In order to more deeply understand these numerical methods, the number of iteration is fixed at 20 and then plot the SE curves as shown in Fig. 2 when segmenting the images (A2) and (B2) to be the examples. It can be easily seen that ADMM-based methods converge much faster than other approaches. In other words, the ADMM-based methods evolve more rapidly to the targeted binary value images. To get a more intuitive visualization, the segmentation results after 3, 10 and 20 iterations are shown in Fig. 3. From this, it can be inferred that the ADMM-based methods produce better segmentation results than other approaches when using fewer iterations.

Fig. 2
figure 2

Convergence curve of the SE to segment images (A2) and (B2) in Fig. 1 when fixing the iteration to be 20

Full size image
Fig. 3
figure 3

Segmentation results by using various methods. The 1st–3rd rows represent the segmentation output by using the different iterations as 3, 10 and 20. The 1st–4th columns and the 5th–8th columns represent the segmentation results by using the VLSM, the PDM, the ADMM and the DADMM

Full size image

To furthermore illustrate the capability of the DADMM, we consider to segmentation three images with a little bias field and the noise with a variance of 0.05 as shown in the first column and the ground truths are shown in the second column of Fig. 4. The related parameters and segmentation data are shown in Table 2. It is obvious that the DADMM still has a slight advantage in segmentation accuracy. From three test images in Fig. 4, it can be seen that the PDM and the ADMM have the incorrect segmentation phenomenon of stained points both inside and outside the segmentation target. In particular, the inner corners of the image (Y4,Y5) pentagram are not accurately segmented. Therefore, it still illustrates that the dual-based ADMM has better segmentation performance than other methods.

Fig. 4
figure 4

The 1st–2nd columns represent the original degraded images and ground truth, the 3rd–6th columns represent the segmentation results by using the VLSM, the PDM, the ADMM and the DADMM

Full size image
Table 2 Related data for segmenting the images in Fig. 4
Full size table

3.2 Gray images

Here some numerical comparisons are arranged on the segmentation evaluation dataset http://www.wisdom.weizmann.ac.il/~vision/Seg_Evaluation_DB/dl.html, where the dataset contains 200 gray level images and the corresponding ground truth of the segmentation results. For convenience, seven representative gray images are selected as the testing images. The segmentation accuracy is measured by three indicators: Precision, Segmentation Accuracy (SA) and F1-Score (F1S) as

$$ \begin{array}{@{}rcl@{}} \text{Precision}=\frac{\text{TP}}{\mathrm{TP+FP}}, \text{SA}=\frac{\mathrm{TP+TN}}{\mathrm{TP+FN+FP+TN}}\text{and} \mathrm{F1S}=\frac{\mathrm{2PR}}{\mathrm{P+R}}, \end{array} $$

where \(\mathrm {P}=\frac {\text {TP}}{\mathrm {TP+FP}}, \mathrm {R}=\frac {\text {TP}}{\mathrm {TP+FN}}\) and True Positive (TP), False Negative (FN), False Positive (FP) and True Negative (TN). From the results listed in the Table 3, the evaluation indicators based on the DADMM obviously outperforms other three methods in most cases. These facts can be also observed via the segmentation results from Fig. 5. To more specific, from the images (D1,E1,H1) in Fig. 5, the DADMM accurately extracts the object contours, whereas the other methods produce over-segmentation or under-segmentation. Especially, the DADMM can avoid unnecessary ”island-like” segmentation from the observation from the images (C1,F1,G1), while the other methods have redundant star segmentation. In addition, the DADMM has a good processing of the segmentation details such as the beaks of birds and geese in the images (G1,I1).

Table 3 Related data used in segmenting the gray images shown in Fig. 5
Full size table
Fig. 5
figure 5

The 1st–2nd columns represent the original gray images and ground truth segmentation separately, the 3rd–6th columns represent the segmentation results by using the VLSM, the PDM, the ADMM and the DADMM

Full size image

3.3 Color images

To evaluate the performance on natural color images, the database [15] are still used to test our proposed method. Several representative natural color images are randomly selected for the experimentation comparisons. The final segmentation results are given in Fig. 6 and detailed experimental results are shown in Table 4. From Fig. 6, the DADMM obtains good segmentation results. Taking the image J1 as an example, it can be seen that the DADMM is better than other three methods due to their incorrect segmentation in the interior of the target object. From the images (K1,M1,O1), it can be observed that the object contours of the DADMM are very suitable for the results of the truth value. In addition, some over-segmentations generated by other methods can be observed compared to the DADMM in the image (L1,P1). As a summarization, the conclusions obtained here are very close to those got from testing on gray images.

Fig. 6
figure 6

The 1st–2nd columns represent the original color images and ground truth segmentation separately, the 3rd–6th columns represent the segmentation results by using the VLSM, the PDM, the ADMM and the DADMM

Full size image
Table 4 Related data used in segmenting the color images shown in Fig. 6
Full size table

4 Conclusion

This paper arranged a new numerical method to solve the CV model. Different to some classic methods such as the PDE-based method depending on the Courant-Friedrichs-Lewy condition and the convex relaxation method depending on the threshold value, our proposed method used the dual scheme to equivalently transform the CV model into a saddle point problem and then the solution can be obtained by using the dual-based ADMM. The numerical results showed the superiority of our proposed method in terms of the segmentation accuracy compared with other classic numerical methods. In the future, we want to extend the proposed method to deal with the multiphase image segmentation problem.