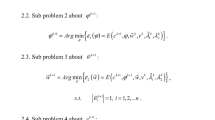Image Segmentation via the Continuous Max-Flow Method Based on Chan-Vese Model

Abstract

The Chan-Vese model using variational level set method (VSLM) has been widely used in image segmentation, but its efficiency is a challenge problem due to high computation costs of curvature as well as the Eiknal equation constraint. In this paper, we propose a continuous Max-Flow (CMF) method based on discrete graph cut approach to solve the VSLM for image segmentation. Firstly, we recast the original Chan-Vese model to a continuous max-flow problem via the primal-dual method and solve it using the alternating direction method of multipliers (ADMM). Then, we use the projection method to recover the continuous level set function for image segmentation expressed as a signed distance function. Finally, some numerical examples are presented to demonstrate the efficiency and accuracy of the proposed method.

1 Introduction

Image segmentation is of great importance in image analysis, which has found a lot of applications in the fields of computer vision, medical imaging processing, remote sensing imaging analysis, etc. Its task is to divide an image into different parts according to image features without vacuum and overlapping. It can be accomplished by variational methods through minimizing a specific energy functional. Among of the existing approaches, the Mumford-Shah model [1] is a fundamental approach, but it is difficult to solve due to different space definitions of variables. The Chan-Vese model [2] can overcome this problem based on a reduced Mumford-Shah model and variational level set method (VLSM) [3, 4] with the concept of total variation (TV) [5].

The Chan-Vese model not only can solve a lot of problems of two-phase image segmentation, but also has become fundamental approach to various variational multi-phase image segmentation models [6]. Moreover, its idea can be extended to solve the related variational multi-phase image segmentation models, thus have received a lot of attentions recently. For the problem of two-phase segmentation $\Omega =\Omega _{1} \, \cup \,\Omega _{2}$, $\Omega _{1} \, \cap \,\Omega _{2} \, = \,\emptyset$, the Chan-Vese model based on the reduced Mumford-Shah model can be described as

$$ \mathop {Min}\limits_{{c_{1} ,c_{2} ,\phi }} \left\{ {\int_{\Omega } {Q_{1} H\left( \phi \right)dx} + \int_{\Omega } {Q_{2} \left( {1 - H\left( \phi \right)} \right)dx + \gamma \int_{\Omega } {\delta \left( \phi \right)\left| {\nabla \phi } \right|dx} } } \right\} $$

(1)

where, $Q_{1} = \alpha_{1} \left( {c_{1} - f} \right)^{2}$, $Q_{2} = \alpha_{2} \left( {c_{2} - f} \right)^{2}$, $c_{1}$ and $c_{2}$ represent piecewise constant approximations of the original image $f$ in regions $\Omega _{1}$ and $\Omega _{2}$ respectively. The function $\phi \left( x \right)$ denotes a level set function. $H\left( \phi \right)$, $\delta \left( \phi \right)$ are Heaviside function and Dirac function of $\phi \left( x \right)$. $H\left( \phi \right)$, $1 - H\left( \phi \right)$ are characteristic functions of $\Omega _{1}$ and $\Omega _{2}$ respectively. If $\phi \left( x \right)$ is defined as a signed distance function, it must fulfill the following Eiknal equation

$$ \left| {\nabla \phi } \right| = 1 $$

(2)

Equations (1) and (2) constitute a constrained optimization problem. After $c_{1}$ and $c_{2}$ are estimated, $\phi \left( x \right)$ can be obtained by solving the following gradient descent equation [2]

$$ \left\{ {\begin{array}{*{20}c} {\frac{\partial \phi }{\partial t} = \left( {\nabla \cdot \left( {\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right) + \left( {Q_{2} - Q_{1} } \right)} \right)\delta \left( \phi \right)} & {x \in\Omega } \\ {\nabla \phi \cdot \vec{n} = 0} & {x \in \partial\Omega } \\ \end{array} } \right., $$

(3)

$$ \left\{ {\begin{array}{*{20}c} {\frac{\partial \psi }{\partial t} + sign\left( \phi \right)\left( {\left| {\nabla \psi } \right| - 1} \right) = 0} \\ {\psi \left( {0,x} \right) = \phi \left( {t,x} \right)} \\ \end{array} } \right.. $$

(4)

In order to avoid the re-initialization process of (4), [7] has augmented the constraint (2) into (1) via the penalty function method as below:

$$ \mathop {Min}\limits_{\phi } \left\{ {\int_{\Omega } {Q_{1} H\left( \phi \right)dx} + \int_{\Omega } {Q_{2} \left( {1 - H\left( \phi \right)} \right)dx + \gamma \int_{\Omega } {\delta \left( \phi \right)\left| {\nabla \phi } \right|dx} } + \frac{\theta }{2}\int_{\Omega } {\left( {\left| {\nabla \phi } \right| - 1} \right)^{2} dx} } \right\}, $$

(5)

Thus, (3), (4) can be replaced with

$$ \left\{ {\begin{array}{*{20}c} {\frac{\partial \phi }{\partial t} = \left( {\nabla \cdot \left( {\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right) + \left( {Q_{2} - Q_{1} } \right)} \right)\delta \left( \phi \right) + \theta \left( {\Delta \phi - \nabla \cdot \left( {\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right)} \right)} & {x \in\Omega } \\ {\nabla \phi \cdot \vec{n} = 0} & {x \in \partial\Omega } \\ \end{array} } \right.. $$

(6)

But the computation of the curvature in (6) using finite difference scheme is highly complex. The Split Bregman projection (SBP) method designed by [8] can circumvent this difficulty by making use of a generalized thresholding formula and projection method in the alternating optimization process. The alternating iterative formulation can be presented as below.

$$ \begin{aligned} & \left( {\phi^{k + 1} ,\vec{w}^{k + 1} } \right) \\ & \quad = Arg\mathop {Min}\limits_{{\phi ,\vec{w}:\left| {\vec{w}} \right| = 1}} \left\{ {\begin{array}{*{20}l} {\int_{\Omega } {Q_{1} H\left( \phi \right)dx} + \int_{\Omega } {Q_{2} \left( {1 - H\left( \phi \right)} \right)dx} } \hfill \\ { + \,\gamma \int_{\Omega } {\delta \left( \phi \right)\left| {\vec{w}} \right|dx} + \frac{\theta }{2}\int_{\Omega } {\left| {\vec{w} - \nabla \phi - \vec{b}^{k + 1} } \right|^{2} dx} } \hfill \\ \end{array} } \right\}, \\ \end{aligned} $$

(7a)

$$ \vec{b}^{k + 1} = \vec{b}^{k} + \nabla \phi^{k} - \vec{w}^{k} , \, \vec{b}^{0} = \vec{w}^{0} = \vec{0} . $$

(7b)

A similar alternating direction method of multipliers projection (ADMMP) method is proposed in [8], which is given by

$$ \begin{aligned} & \left( {\phi^{k + 1} ,\vec{w}^{k + 1} } \right) \\ & \quad = Arg\mathop {Min}\limits_{{\phi ,\vec{w}:\left| {\vec{w}} \right| = 1}} \left\{ {\begin{array}{*{20}l} {\int_{\Omega } {Q_{1} H\left( \phi \right)dx} + \int_{\Omega } {Q_{2} \left( {1 - H\left( \phi \right)} \right)dx} } \hfill \\ { + \,\gamma \int_{\Omega } {\delta \left( \phi \right)\left| {\vec{w}} \right|dx} + \int_{\Omega } {\vec{\tau }^{k} \cdot \left( {\vec{w} - \nabla \phi } \right)dx} + \frac{\theta }{2}\int_{\Omega } {\left| {\vec{w} - \nabla \phi } \right|^{2} dx} } \hfill \\ \end{array} } \right\}. \\ \end{aligned} $$

(8a)

$$ \vec{\tau }^{k + 1} = \vec{\tau }^{k} + \theta \left( {\vec{w}^{k + 1} - \nabla \phi^{k + 1} } \right). $$

(8b)

The SBP method and ADMMP method are motivated by the SB method and ADMM method for the equivalent model of Chan-Vese model [9]

$$ \mathop {Min}\limits_{{c,\lambda (x) \in \left\{ {0,1} \right\}}} \left\{ {\int_{\Omega } {Q_{1} \lambda dx} + \int_{\Omega } {Q_{2} \left( {1 - \lambda } \right)dx + \gamma \int_{\Omega } {\left| {\nabla \lambda } \right|dx} } } \right\}. $$

(9)

After $c$ is estimated, $\lambda$ can be obtained via the fast SB method [10], and ADMM method [11] which were originally proposed to solve TV models for image restoration.

Another fast method to solve (9) is the graph cut approach [12] which recasts it to a Max-Flow/Min-Cut problem on a graph [13]. Also its continuous Max-Flow counterpart was proposed by [14,15,16] to avoid graph construction and complex data structures. In this paper, we will design the Continuous Max-Flow (CMF) method for (1) to provide a new fast implementation of it and lay the foundation for multi-phase image segmentation, 3D image segmentation, etc.

The paper is organized as follows. Section 2 briefly introduces the Continuous Max-Flow method for Chan-Vese model of convex optimization. The CMF method for classic Chan-Vese model under VSLM framework is designed in Sect. 3. In Sect. 4, the numerical experiments are conducted to compare the proposed method with some current fast approaches. Finally, concluding remarks and outlook are given in Sect. 5.

2 The Continuous Max-Flow Method for Equivalent Chan-Vese Model

As one can see that (9) is a minimization problem with two variables, it can be tackled using the alternating optimization strategy. After $c$ is estimated, another sub-problem of minimization on $\lambda$ is as follows.

$$ \mathop {Min}\limits_{{\lambda (x) \in \left\{ {0,1} \right\}}} \left\{ {\int_{\Omega } {Q_{1} \lambda dx} + \int_{\Omega } {Q_{2} \left( {1 - \lambda } \right)dx + \gamma \int_{\Omega } {\left| {\nabla \lambda } \right|dx} } } \right\}. $$

(10)

The procedure of convex optimization to solve it is based on the relaxation of $\lambda \in \left\{ {0,1} \right\}$ to $\lambda \in \left[ {0,1} \right]$, and the thresholding formula for the final results. The relaxified version of (10) can be transformed into the Max-Min problem [14,15,16,17] as below.

$$ \mathop {Max}\limits_{{p_{t} :0 \le p_{t} \le Q_{1} }} \mathop {Max}\limits_{{p_{s} :0 \le p_{s} \le Q_{2} }} \mathop {Max}\limits_{{\vec{P}:\left| {\vec{p}} \right| \le \gamma }} \mathop {Min}\limits_{{\lambda (x) \in \left[ {0,1} \right]}} \left\{ {\begin{array}{*{20}l} {\int_{\Omega } {p_{t} \lambda dx} + \int_{\Omega } {p_{s} \left( {1 - \lambda } \right)dx + \int_{\Omega } {\nabla \cdot \vec{p}\lambda dx} } } \hfill \\ { = \int_{\Omega } {p_{s} dx} + \int_{\Omega } {\left( {p_{t} - p_{s} + \nabla \cdot \vec{p}} \right)\lambda dx} } \hfill \\ \end{array} } \right\}. $$

(11)

Due to the following dual formulas

$$ \int_{\Omega } {Q_{1} \lambda dx} = \mathop {Max}\limits_{{p_{t} :0 \le p_{t} \le Q_{1} }} \int_{\Omega } {p_{t} \lambda dx} , $$

(12a)

$$ \int_{\Omega } {Q_{2} \left( {1 - \lambda } \right)dx} = \mathop {Max}\limits_{{p_{s} :0 \le p_{s} \le Q_{2} }} \int_{\Omega } {p_{s} \left( {1 - \lambda } \right)dx} , $$

(12b)

$$ \gamma \int_{\Omega } {\left| {\nabla \lambda } \right|dx} = \mathop {Max}\limits_{{\vec{P}:\left| {\vec{p}} \right| \le \gamma }} \int_{\Omega } {\nabla \cdot \vec{p}\lambda dx} . $$

(12c)

Then, (11) can become the following Continuous Max-Flow optimization problem

$$ \mathop {Max}\limits_{{p_{s} }} \int_{\Omega } {p_{s} dx} , $$

(13a)

$$ s.t. \, p_{t} - p_{s} + \nabla \cdot \vec{p} = 0,0 \le p_{t} \le Q_{1} ,0 \le p_{s} \le Q_{2} ,\left| {\vec{p}} \right| \le \gamma . $$

(13b)

which can be solved via the ADMM method as given by

$$ \begin{aligned} & \left( {p_{t}^{k + 1} ,p_{s}^{k + 1} ,\vec{p}_{{}}^{k + 1} } \right), \\ & \quad = Arg\mathop {Max}\limits_{\begin{subarray}{l} p_{t} :0 \le p_{t} \le Q_{1} \\ p_{s} :,0 \le p_{s} \le Q_{2} \\ \vec{p}:\left| {\vec{p}} \right| \le \gamma \end{subarray} } \int_{\Omega } {\left( {p_{s} + \lambda^{k} \left( {p_{t} - p_{s} + \nabla \cdot \vec{p}} \right) - \frac{\mu }{2}\left| {p_{t} - p_{s} + \nabla \cdot \vec{p}} \right|^{2} } \right)dx} , \\ \end{aligned} $$

(14a)

$$ \lambda^{k + 1} = \lambda^{k} - \mu \left( {p_{t}^{k + 1} - p_{s}^{k + 1} + \nabla \cdot \vec{p}_{{}}^{k + 1} } \right). $$

(14b)

where $\mu$ is a penalty parameter, $\lambda$ is a Lagrangian multiplier.

3 The Continuous Max-Flow Method for the Chan-Vese Model

For the classic Chan-Vese model (1), (2) under the VLSM, after $c$ has been estimated, it can be transformed into the following constrained optimization problem

$$ \left\{ {\begin{array}{*{20}l} {\mathop {Min}\limits_{\phi } \left\{ {\int_{\Omega } {Q_{1} H\left( \phi \right)dx} + \int_{\Omega } {Q_{2} \left( {1 - H\left( \phi \right)} \right)dx + \gamma \int_{\Omega } {\left| {\nabla H\left( \phi \right)} \right|dx} } } \right\}} \hfill \\ {s.t.\quad \left| {\nabla \phi } \right| = 1} \hfill \\ \end{array} } \right.. $$

(15)

In order to solve it, [2] has introduced the regularized Heaviside function $H_{\varepsilon } \left( \phi \right)$ and the regularized Dirac function $\delta_{\varepsilon } \left( \phi \right)$ as

$$ H_{\varepsilon } \left( \phi \right) = \frac{1}{2} + \frac{1}{\pi }\arctan \left( {\frac{\phi }{\varepsilon }} \right), $$

(16a)

$$ \delta_{\varepsilon } \left( \phi \right) = \frac{1}{\pi }\frac{\varepsilon }{{\phi^{2} + \varepsilon^{2} }}. $$

(16b)

Here $\varepsilon$ is a small positive parameter and $H_{\varepsilon } \left( \phi \right) \in \left[ {0,1} \right]$. Let $\lambda = H_{\varepsilon } \left( \phi \right)$, then (15) becomes

$$ \left\{ {\begin{array}{*{20}l} {\mathop {Min}\limits_{{\lambda \in \left[ {0,1} \right]}} \left\{ {\int_{\Omega } {Q_{1} \lambda dx} + \int_{\Omega } {Q_{2} \left( {1 - \lambda } \right)dx + \gamma \int_{\Omega } {\left| {\nabla \lambda } \right|dx} } } \right\}} \hfill \\ {s.t.\quad \left\{ {\begin{array}{*{20}c} {\lambda = H_{\varepsilon } \left( \phi \right)} \\ {\left| {\nabla \phi } \right| = 1} \\ \end{array} } \right.} \hfill \\ \end{array} } \right.. $$

(17)

The first formulation is just the relaxified version of (10), so its solution can be obtained via the CMF method as (14a), (14b) i.e.

$$ \left( {p_{t}^{k + 1} ,p_{s}^{k + 1} ,\vec{p}_{{}}^{k + 1} } \right) = Arg\mathop {Max}\limits_{\begin{subarray}{l} p_{t} :0 \le p_{t} \le Q_{1} \\ p_{s} :0 \le p_{s} \le Q_{2} \\ \vec{p}:\left| {\vec{p}} \right| \le \gamma \end{subarray} } \int_{\Omega } {\left( {\vec{p}_{s} + \lambda^{k} \left( {p_{t} - p_{s} + \nabla \cdot \vec{p}} \right) - \frac{\mu }{2}\left| {p_{t} - p_{s} + \nabla \cdot \vec{p}} \right|^{2} } \right)dx} $$

(18a)

$$ \lambda^{k + 1} = \lambda^{k} - \mu \left( {p_{t}^{k + 1} - p_{s}^{k + 1} + \nabla \cdot \vec{p}_{{}}^{k + 1} } \right), \, \lambda^{k + 1} \in \left[ {0,1} \right]. $$

(18b)

In fact, (18a) can be divided into the following sub-problems of minimization in terms of alternating optimization respectively,

$$ \left( {p_{t}^{k + 1} } \right) = Arg\mathop {Max}\limits_{{p_{t} :0 \le p_{t} \le Q_{1} }} \int_{\Omega } {\left( {\lambda^{k} \left( {p_{t} - p_{s}^{k} + \nabla \cdot \vec{p}^{k} } \right) - \frac{\mu }{2}\left| {p_{t} - p_{s}^{k} + \nabla \cdot \vec{p}^{k} } \right|^{2} } \right)dx} , $$

(19a)

$$ \left( {p_{s}^{k + 1} } \right) = Arg\mathop {Max}\limits_{{p_{s} :0 \le p_{s} \le Q_{2} }} \int_{\Omega } {\left( {p_{s} + \lambda^{k} \left( {p_{t}^{k + 1} - p_{s} + \nabla \cdot \vec{p}^{k} } \right) - \frac{\mu }{2}\left| {p_{t}^{k + 1} - p_{s} + \nabla \cdot \vec{p}^{k} } \right|^{2} } \right)dx} , $$

(19b)

$$ \left( {\vec{p}_{{}}^{k + 1} } \right) = Arg\mathop {Max}\limits_{{\vec{p}:\left| {\vec{p}} \right| \le \gamma }} \int_{\Omega } {\left( {\lambda^{k} \left( {p_{t}^{k + 1} - p_{s}^{k + 1} + \nabla \cdot \vec{p}} \right) - \frac{\mu }{2}\left| {p_{t}^{k + 1} - p_{s}^{k + 1} + \nabla \cdot \vec{p}} \right|^{2} } \right)dx} . $$

(19c)

And their solutions are given by

$$ \left\{ {\begin{array}{*{20}c} {\tilde{p}_{t}^{k + 1} = p_{s}^{k} - \nabla \cdot \vec{p}^{k} + \frac{{\lambda^{k} }}{\mu }} \\ {p_{t}^{k + 1} = Max\left( {0,Min\left( {\tilde{p}_{t}^{k + 1} ,Q_{1} } \right)} \right)} \\ \end{array} } \right., $$

(20a)

$$ \left\{ {\begin{array}{*{20}l} {\tilde{p}_{s}^{k + 1} = \left( {p_{t}^{k + 1} + \nabla \cdot \vec{p}^{k} } \right) + \frac{{1 - \lambda^{k} }}{\mu }} \hfill \\ {p_{s}^{k + 1} = Max\left( {0,Min\left( {\tilde{p}_{s}^{k + 1} ,Q_{2} } \right)} \right)} \hfill \\ \end{array} } \right., $$

(20b)

$$ \left\{ {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} { - \nabla \lambda^{k} + \mu \nabla \left( {p_{t}^{k + 1} - p_{s}^{k + 1} + \nabla \cdot \tilde{\vec{p}}^{k + 1} } \right) = 0} & {x \in\Omega } \\ {\lambda^{k} - \mu \left( {p_{t}^{k + 1} - p_{s}^{k + 1} + \nabla \cdot \tilde{\vec{p}}^{k + 1} } \right) = 0} & {x \in \partial\Omega } \\ \end{array} } \right.} \\ {\vec{p}^{k + 1} = \frac{{\tilde{\vec{p}}^{k + 1} }}{{Max\left( {1,\left| {\tilde{\vec{p}}^{k + 1} } \right|} \right)}}} \\ \end{array} } \right.. $$

(20c)

Also, the solution of (18b) is given by

$$ \left\{ {\begin{array}{*{20}c} {\tilde{\lambda }^{k + 1} = \lambda^{k} - \mu \left( {p_{t}^{k + 1} - p_{s}^{k + 1} + \nabla \cdot \vec{p}_{{}}^{k + 1} } \right)} \\ {\lambda^{k + 1} = Max\left( {0,Min\left( {\tilde{\lambda }^{k + 1} ,1} \right)} \right)} \\ \end{array} } \right.. $$

(21)

One can see that the constraints in (17) can recast the continuous level set function as a signed distance function. It can be implemented by the ADMMP method as

$$ \left\{ {\begin{array}{*{20}l} {(\phi^{k + 1} ,\vec{w}^{k + 1} )} \hfill \\ {\begin{array}{*{20}c} { = Arg\,\mathop {Min}\limits_{{\phi ,\vec{w}}} \left\{ {\frac{1}{2}\int_{\Omega } {\left( {\lambda - H_{\varepsilon } (\phi )} \right)}^{2} dx + \int_{\Omega } {\vec{\sigma }^{k} \cdot \left( {\vec{w} - \nabla \phi } \right)dx} + \frac{{\mu_{0} }}{2}\int_{\Omega } {\left| {\vec{w} - \nabla \phi } \right|^{2} } dx} \right\},} \\ {s.t. \, \left| {\vec{w}^{k + 1} } \right| = 1} \\ \end{array} } \hfill \\ \end{array} } \right. $$

(22a)

$$ \vec{\sigma }^{k + 1} = \vec{\sigma }^{k} + \mu_{0} \left( {\vec{w}^{k + 1} - \nabla \phi^{k + 1} } \right). $$

(22b)

Now, by applying the alternating optimization strategy to (22a), we can obtain $\phi^{k + 1}$ using the standard variational method while fixing $\vec{w}^{k}$ as

$$ \left\{ {\begin{array}{*{20}l} {\left( {H_{\varepsilon } \left( \phi \right) - \lambda } \right){\kern 1pt} \delta_{\varepsilon } \left( \phi \right) + \nabla \cdot \vec{\sigma }^{k} - \mu_{0} \nabla \cdot \left( {\nabla \phi - \vec{w}^{k} } \right) = 0} \hfill \\ {\left( { - \vec{\sigma }^{k} + \nabla \phi - \vec{w}^{k} } \right) \cdot \vec{n} = 0} \hfill \\ \end{array} } \right.. $$

(23)

Finally, (23) can be solved through Gauss-Seidel scheme approximately. Then, we can get $\vec{w}^{k + 1}$ while fixing $\phi^{k}$ as

$$ \left\{ {\begin{array}{*{20}l} {\vec{\sigma }^{k} + \mu_{0} \cdot \left( {\tilde{\vec{w}}^{k + 1} - \nabla \phi^{k + 1} } \right) = 0} \hfill \\ {\vec{w}^{k + 1} = \frac{{\tilde{\vec{w}}^{k + 1} }}{{Max\left( {\left| {\tilde{\vec{w}}^{k + 1} } \right|,1} \right)}}} \hfill \\ \end{array} } \right.. $$

(24)

Now we summarize the algorithm introduced in this section as follows.

4 Numerical Experiments

In this section, we present some numerical experiments to compare the effectiveness and efficiency of our proposed continuous max-flow method with the current fast algorithms (SBP, ADMMP) through the segmentation of three classic images. The experiments are implemented on PC (Intel (R) Core (TM) i5 Duo CPU @3.30 GHz 3.30 GHz; memory: 4 GB; code running environment: Matlab R2010b). Figure 1 shows the three images for segmentation. The segmentation results using SBP, ADMMP and the CMF method are shown in Figs. 2, 3, and 4. Here, we draw a red outline to represent the segmented contour.

Fig. 1.

Tested images for image segmentation: (a) liver image, (b) cameraman image, (c) irregular graphic picture.

Fig. 2.

Segmentation results of Fig. 1(a) by (a) SBP, (b) ADMMP, (c) CMF, respectively. (Color figure online)

Fig. 3.

Segmentation results of Fig. 1(b) by (a) SBP, (b) ADMMP, (c) CMF, respectively. (Color figure online)

Fig. 4.

Segmentation results of Fig. 1(c) by (a) SBP, (b) ADMMP, (c) CMF, respectively. (Color figure online)

One can observe from Fig. 2 that the blood vessels of liver are more accurately separated by the proposed CMF method than SBP, ADMMP (see the middle blood vessels of liver). Figure 3 demonstrates that the cameraman and the background are separated more clearly by the proposed CMF than the SBP, ADMMP (see the right of the cameraman image). The results in Fig. 4 shows that the CMF method provides better segmentation of irregular picture components than the SBP and ADMMP methods (see the edge of the irregular graphic picture).

To further illustrate the effectiveness of CMF method, the processing result using level set function of the three tested images are compared, as shown in Figs. 5, 6 and 7, respectively. It can be seen that all the three method achieve good performance on liver image, cameraman image and irregular graphic picture.

Fig. 5.

The result of level set function of Fig. 1(a) by (a) SBP, (b) ADMMP, (c) CMF, respectively.

Fig. 6.

The result of level set function of Fig. 1(b) by (a) SBP, (b) ADMMP, (c) CMF, respectively.

Fig. 7.

The result of level set function of Fig. 1(c) by (a) SBP, (b) ADMMP, (c) CMF, respectively.

In order to compare the efficiency of the proposed CMF with the SBP and ADMMP, we list the numbers of iterations and CPU time of them in Table 1. It can be seen that our proposed method CMF needs much fewer iterations and CPU time, which proves that the computational efficiency of CMF method is faster than the current fast SBP method and ADMMP method.

Table 1. Comparison on the number of iterations and CPU times of SBP, ADMMP and CMF methods.

5 Conclusions and Future Topics

Graph cut is a fast algorithm for the min-cut on graphs in computer vision, it is dual to the max-flow method on networks. The continuous max flow method inspired by its discrete counterpart has been proposed to solve some variational model in image processing. In this paper, we design the continuous max flow method for classic Chan-Vese model for image segmentation under the framework of variational level set with constraints of Eiknal equations. Firstly, the Chan-Vese model is transformed into a max-min problem by using dual formulations, based on it, the continuous max flow method is proposed using the alternating direction method of multipliers. Then, the Eiknal equation is solved by introducing an auxiliary variable and ADMM method. Numerical experiments demonstrate that this method is better than the current fast methods in efficiency and accuracy. The investigations in this paper can be extended to the problems of multiphase image segmentation and 3D image segmentation naturally.