1 Introduction

Image segmentation is important for visual information analysis processes, such as object detection and scene understanding [6,7,8, 14, 15, 25,26,27]. Many segmentation algorithms have been proposed over the last few decades [5, 6, 10, 12, 17, 18, 21, 22], among which the active contour model (ACM) [11, 30] is one of the most successful models. ACM is based on the theory of surface evolution under a speed function which is determined by local, global and other independent properties. It divides an image into sub-regions with closed and smooth boundaries. According to the nature of constraints ACM can be generally categorized into two classes: the edge-based models [11, 30] and the region-based models [1, 9, 15, 17, 20, 26, 27]. The edge-based models stop evolving contours on the object boundaries through the image gradient information. One advantage of the models is that they are generally not affected by intensity inhomogeneity because it is mainly the edge property that is utilized for segmentation. However, the edge-based models have some limitations such as being sensitive to noise, weak edges and initial location of the curve, difficulty in handling topological changes, and its dependency of parameterization. These limitations have negative impacts on their applications in practice.

Instead of the edge properties, the region-based active contour models use the region properties of image by defining a region descriptor to guide the motion of the level set function. Without relying on image gradients, these models perform better on images with weak object boundaries and are less sensitive to the location of initial contours. They can also naturally represent the contours of complex topology and deal with topological changes (such as contour splitting and merging). Based on the functional, Chan and Vese developed the Chan-Vese (CV) model [27], which is able to handle images with weak boundaries and detect an object’s inner contour. The most remarkable feature of the CV model is its fast and low-costing computation. However, since CV assumes that the intensity of each region of image is statistically uniform, it may fail to segment images with inhomogeneous intensity.

To deal with images with inhomogeneous intensity, a number of approaches have been proposed. Assuming that the intensities in a relatively small local region are separable, Tsai et al. [26] proposed a piecewise smooth (PS) model. Despite of exhibiting certain capability of handling the inhomogeneity of intensity, the PS model is extremely computation intensive due to re-initialization of the level set function [16]. Lankton et al. [13] proposed a region-based model to handle images with inhomogeneity and the performance of the model depends on the local fitting radius setting. Li et al. [15] proposed a Local Binary Fitting(LBF) model to overcome the difficulty caused by intensity inhomogeneity. The method defines a weighted K-means clustering objective function for image intensities in a neighborhood around each point, and the function is integrated over the entire domain and incorporated into a variational level set formulation. A model driven by local-Gaussian-distribution-fitting (LGDF) energy model was proposed by Wang et al. [28] to use more complete statistical characteristics of local intensities for more accurate segmentation. Later Chai et al. [4] proposed a local Chan-Vese (LCV) model which can utilize both local and global image information for image segmentation.

However, all existing models utilize the L2 − norm to measure the global information, instead of the Bregman divergence which can be considered as a data-dependent weighted L2 − norm. Compared with the L2 − norm, the Bregman divergence applies multi-region information to express the global information, especially, the data-dependent weighted term can be considered as the prior information. This term takes advantage of multi-level information of image to assist boosting stability of the image segmentation model, particularly, the robustness to initial placement. Inspired by these advantages, in this paper we propose a ACM based on Bregman divergence and multi-scale Local Binary Fitting(MLBF) [17], which we call Bregman-MLBF. Applying the Taylor expansion, the Bregman divergence can be approximated by a data-dependent weighted L2 − norm, thus boosting stability and accelerating the curve evolution.

In comparison with the MLBF model [17], ours Bregman-MLBF model enjoys the following three advantages: (1) it is more efficient to update the level set functions ; (2) it improves the possibility of gaining the global optimal solution; (3) it strengthens the robustness to the initial placement. In addition, compared with CV, Bregman-MLBF has the capability of handling the problem caused by the intensity inhomogeneity due to the use of local information.

The rest of the paper is organized as follows. The related work is reviewed in Section 2. We present our model and illustrate its advantages in Section 3. And in Section 4 we conduct the experiments on synthetic images, medical images and natural images, and compare the results with existing approaches(LCV incorporated with B-spline [4], MLBF model [17] and LGIF model [1]) in terms of effectiveness and efficiency, followed by conclusion in Section 5.

2 Related work

Amongst the region-based active contour models, define Ω as a bounded open subset R2 and I : Ω→R as an image to be segmented. Given a level set function ϕ, the curve C is represented implicitly as C = {(x,y)|ϕ(x,y) = 0}. The evolution of the curve is given by the zero-level curve during the minimization of the variational functional.

2.1 Local binary fitting model (LBF)

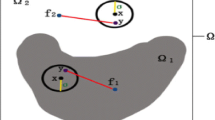
Local Binary Fitting Model(LBF) model was proposed by Li et al. [15]. Assume x is a point in a given gray image defined on Ω, x ∈Ω, and I : Ω ⊂ R2 → R. Let C be a closed contour in Ω which separates Ω into two regions fitting as f1(x) and f2(x). The fitting energy of LBF model is defined as

$$ E^{Fit}=\sum\limits^{2}_{i = 1}\lambda_{i}{\int}_{\Omega}{\int}_{{\Omega}_{i}}K_{\sigma}(\textbf{x}-\textbf{y})|I(\textbf{y})-f_{i}(\textbf{x})|^{2}d\textbf{y}d\textbf{x} $$
(1)

where λ1, λ2 are weighted parameters and Kσ(x −y) is a kernel function with a scale parameter σ > 0. The physical meaning of the fitting energy in the LBF model is demonstrated in Fig. 1. In sub-region Ωi, y is the points in a circular neighborhood with radius σ centered at each point x in the sub-region domain. The fitting energy is the summation of distances between fi(x) and the intensity of y represented as red lines. The minimization of EFit can guide the contour C to find the object boundary and the fitting values fi(x) to optimally approximate the local image intensities on the two sides of the contour C.

Fig. 1
figure 1

The schematic representing of the fitting energy in the LBF model

Full size image

To smooth the contour C, a penalizing term of contour length |C| is added to the energy function, which is redefined as

$$ E^{LBF} =E^{Fit}+\nu |C| $$
(2)

The LBF model is one of the most successful models to cope with inhomogeneous intensity. However, the drawbacks of the LBF model are also obvious. First, each iteration needs to calculate four time-consuming convolutions. Second, the LBF model is sensitive to the initial placement because it does not utilize global information to guide the contours evolution. Moreover, compared with the CV model, the characteristic of the LBF model is that the force of the LBF model is edged, meaning that the force is small at the flat area and large at the edge of image. The force of the CV model that makes the level set evolution is regional and distributed over the whole image domain. This characteristic is partially the reason for the sensitivity of the LBF model to the initial placement and is inefficient when the contour is far away from object boundaries. As show in Fig. 2a–b, the LBF model assumes that the intensities in a relatively small local region are separable, while the CV model requests that the intensities be globally separable. Further discussion will be presented in Section 3.2.

Fig. 2
figure 2

Two case of CV model and LBF model can deal with,respectively. a The case of CV model, b The case of LBF model

Full size image

2.2 Local Chan-Vese model (LCV)

Chaiet al. [4] proposed a local Chan-Vese (LCV) model which can utilize both local and global image information in order to handle the problem caused by the intensity inhomogeneity. This model is defined by the following minimization problem:

$$ E^{LCV} = E^{G} +E^{L}+E^{R}+E^{P} $$
(3)

where EG, EL, ER and EP are the global term, the local term, the regularization term and the penalization term, respectively. The global term and the local term are defined as:

$$ E^{G} = \lambda_{1}{\int}_{{\Omega}(in)} |I(x)-c_{1}|^{2}dx+ \lambda_{2}{\int}_{{\Omega}(out)} |I(x)-c_{2}|^{2}dx $$
(4)
$$ \begin{array}{@{}rcl@{}} E^{L}(d_{1},d_{2},C) &=& \lambda_{1}{\int}_{{\Omega}(in)} |g_{k}(I(x))-I(x)-d_{1}|^{2}dx+ \\ &&\lambda_{2}{\int}_{{\Omega}(out)} |g_{k}(I(x))-I(x)-d_{2}|^{2}dx \end{array} $$
(5)

where λ1 and λ2 are positive constants, C is the curve, gk is a verging filter with k × k window size and gk(I(x)) is the smoothed image by the verging filter. c1 and c2 are the mean intensity inside C and outside C, respectively. d1 and d2 are the averages of the difference image gk(I(x)) − I(x) inside C and outside C, respectively.

2.3 Local and global intensity fitting model (LGIF)

Wang et al. [28] proposed an active contour model based on local and global intensity fitting (LGIF) for image segmentation. This model is defined by the following minimization problem:

$$ E^{LGIF} = (1-\omega)E^{LIF} + \omega E^{GIF} $$
(6)

where ω is a positive constant (0 < ω < 1). When the images are corrupted by intensity inhomogeneity, the parameter value ω should be chosen small enough. ELIF and EGIF are the local term, the global term, respectively. The global term and the local term are defined as:

$$ \begin{array}{@{}rcl@{}} E^{GIF} &=& \lambda_{1}\int[\int K_{\sigma}(\textbf{x}-\textbf{y})|I(\textbf{y})-f_{1}(\textbf{x})|^{2}H(\phi(y))d\textbf{y}]d\textbf{x} \\ &&\lambda_{2}\int[\int K_{\sigma}(\textbf{x}-\textbf{y})|I(\textbf{y})-f_{2}(\textbf{x})|^{2}(1-H(\phi(y)))d\textbf{y}]d\textbf{x} \end{array} $$
(7)
$$ E^{LIF} = \lambda_{1}{\int}_{{\Omega}(in)} |I(x)-c_{1}|^{2}dx+ \lambda_{2}{\int}_{{\Omega}(out)} |I(x)-c_{2}|^{2}dx $$
(8)

where H(⋅) is the Heaviside function.

3 Bregman divergence incorporated with local binary fitting

To overcome the sensitivity to initial position and enhance the robustness to noise of the level set of existing models, in this section, we present our new region-based model based on Bregman divergence [3, 23] and multi-scale Local Binary Fitting (MLBF) [17], which we call Bregman-MLBF model. This model can be regarded as an extended LBF model and is more robust to the initial position of the level set and Gaussian noise. It can also reduce the number of iterations required for convergence. Moreover, compared with other segmentation models such as LCV incorporated with B-spline(BLCV) [4], MLBF model [17] and LGIF model [1], Bregman-MLBF is more effective to deal with the inhomogeneous image segmentation.

3.1 Bregman divergence for energy measure

To implement the segmentation of inhomogeneous image and solve the sensitivity to initial placement, the multi-region information is utilized to formulate our proposed model and defined as the following minimization problem:

$$ \begin{array}{@{}rcl@{}} &&{E^{Bregman-MLBF}}(\boldsymbol{C},{c_{1}},{c_{2}},{f_{1}},{f_{2}}) \\ &&= \eta{E^{B}(\boldsymbol{C},{c_{1}},{c_{2}})} + (1 - \eta){E^{L}(\boldsymbol{C},{f_{1}},{f_{2}})} + {E^{R}(\boldsymbol{C})} \end{array} $$
(9)
$$ \begin{array}{@{}rcl@{}} &&E^{B}(\boldsymbol{C},{c_{1}},{c_{2}}) = {\lambda_{1}}\int\limits_{in(\boldsymbol{C})} {{B_{\varphi (y) = {{y}^{2\alpha }}}}({c_{1}}||I_{\boldsymbol{y}})} d\boldsymbol{y} \\ &&+ {\lambda_{2}}\int\limits_{out(\boldsymbol{C})} {{B_{\varphi (y) = {{y}^{2\beta }}}}({c_{2}}||I_{\boldsymbol{y}})} d\boldsymbol{y}\\ &&{E^{L}(\boldsymbol{C},{f_{1}},{f_{2}})} = \sum\limits^{n}_{j = 1} w_{j} E_{\textbf{x}}^{\sigma_{j}}(f_{1,j}(\textbf{x}),f_{2,j}(\textbf{x})) \\ &&=\sum\limits^{n}_{j = 1} w_{j} \sum\limits^{2}_{i = 1}\lambda_{i} {\int}_{{\Omega}_{i}}K_{\sigma_{j}}(\textbf{x}-\textbf{y})|I(\textbf{y})-f_{i,j}(\textbf{x})|^{2}d\textbf{y} \\ &&{E^{R}(\boldsymbol{C})}= \mu {Length}(\boldsymbol{C}) \end{array} $$
(10)

where α, β, λ1, λ2 are positive constants, and α ≥ 1 ≥ β ≥ 0, C is the curve, c1, c2 are the mean intensities inside and outside C, respectively. η is the weight factor to balance the global information energy term EB and the local information energy term EL. \({B_{\varphi (y) = {{y}^{2\alpha }}}}({c_{1}}||I_{\boldsymbol {y}})\) and \({B_{\varphi (y) = {{y}^{2\beta }}}}({c_{2}}||I_{\boldsymbol {y}})\) are the Bregman divergence corresponding to the point pair (c1,Iy) and (c2,Iy), respectively. Iy is the intensity at the point y. n is the number of the multi-scale kernel. The definition of other parameters is the same as that in the LBF model. wj(j = 1,2,…,n) is the Gauss kernel weight of local fitting energy \(k_{\sigma _{j}}\). f1j(x) and f2j(x) are the approximate values of the pixel brightness inside and outside the corresponding curves of Cj in the Gauss kernel weight \(k_{\sigma _{j}}\), respectively, with x as the center point. The local information energy term is defined in (1).

The definition of the Bregman divergence Bφ(⋅||⋅) is associated with a continuously differentiable, real-valued and strictly convex function φ : S →R defined on a closed convex set S. Then, for any pair of points (p,q) ∈S2,

$$ B_{\varphi}(p||q) = \varphi(p) - \varphi(q) - \varphi^{\prime}(q)(p - q) $$
(11)

the Bregman divergence can be interpreted as the difference between the function φ evaluated at p and its first-order Taylor approximation around q, evaluated at p. As the function φ is differentiable, according to the Taylor’ expansion, we can obtain the following equation:

$$ \varphi(p) = \varphi(q) + \varphi\prime(q)(p-q) + \frac{\varphi\prime\prime(q)}{2!}(p-q)^{2} + o({| p - q |}^{3}) $$
(12)

Substituting (12) to (11) gives us

$$ B_{\varphi}(p||q) = \frac{\varphi\prime\prime(q)}{2!}(p-q)^{2} + o({| p - q |}^{3}) $$
(13)

Let φ(y) = y2α, p = c1, q = Iy and φ(y) = y2β, p = c2, q = Iy, respectively, according to (13), we can readily obtain the following equation:

$$ \begin{array}{@{}rcl@{}} &&B_{\varphi (y) = {y^{2\alpha }}}({c_{1}}||I_{\boldsymbol{y}}) = \alpha_{1}{I_{\boldsymbol{y}}^{2\alpha - 2}}{(I_{\boldsymbol{y}} - {c_{1}})^{2}} + R_{1}\\ &&B_{\varphi (y) = {{y}^{2\beta }}}({c_{2}}||I_{\boldsymbol{y}})= \beta_{1}{I_{\boldsymbol{y}}^{2\beta - 2}}{(I_{\boldsymbol{y}} - {c_{2}})^{2}} + R_{2} \end{array} $$
(14)

where R1 = o(|Iy − c1|3), R2 = o(|Iy − c2|3) are the third-order of the Taylor expanded remaining terms, and α1 = 2α2 − α, β1 = 2β2 − β are two coefficients.

Only are the zeroth-, the first- and the second- order the Taylor terms considered in this research. Hence, the Bregman divergence can be considered as the data-dependent weighted L2 − norm. Then the energy term EB can be rewritten as follows:

$$ \begin{array}{@{}rcl@{}} E^{B}(\boldsymbol{C},{c_{1}},{c_{2}})&=& {\lambda_{1}}\int\limits_{in(\boldsymbol{C})} {\alpha_{1} {I_{\boldsymbol{y}}^{2\alpha - 2}}{{(I_{\boldsymbol{y}} - {c_{1}})}^{2}}} d\boldsymbol{y} \\&&+ {\lambda_{2}}\int\limits_{out(\boldsymbol{C})} {\beta_{1}{I_{\boldsymbol{y}}^{2\beta - 2}}{{(I_{\boldsymbol{y}} - {c_{2}})}^{2}}} d\boldsymbol{y} \end{array} $$
(15)

Substitute (15) to (9). And the energy EBregman−MLBF in (9) written as level set form. Besides, the penalization term is embedded to avoid the time-consuming re-initialization and preserve the regularity of the level set function. Hence, we can obtain the following equation:

$$ {E^{P}}(\phi) = v\int\limits_{{\Omega}{\frac{1}{2}{{(|\nabla \phi (\boldsymbol{x})| - 1)}^{2}}d \boldsymbol{x}}} $$
(16)

where v is a positive constant, and in most cases, v = 1. Hence, we can obtain the following equation:

$$ \begin{array}{@{}rcl@{}} &&{E^{\text{Bregman-MLBF}}}(\phi ,{c_{1}},{c_{2}},{f_{1}},{f_{2}}) \\ &=& {\lambda_{1}}\int\limits_{\Omega} (e_{1} + e_{3}){H_{\varepsilon}(\phi(\boldsymbol{x}))} d\boldsymbol{x} \\&&+ {\lambda_{2}}\int\limits_{\Omega} (e_{2} + e_{4})({1 - H_{\varepsilon}(\phi(\boldsymbol{x}))})d\boldsymbol{x} \\&&+\mu\int\limits_{\Omega} {{\delta_{\varepsilon} }(\phi(\boldsymbol{x}) )d\boldsymbol{x}} + v\int\limits_{\Omega} {\frac{1}{2}(|\nabla \phi (\boldsymbol{x})| - 1)^{2}d\boldsymbol{x}} \end{array} $$
(17)

where ϕ(x) is the level set function, Hε(ϕ(x)) and δε(ϕ(x)) are Heaviside function and Dirac function, respectively,

$$ \begin{array}{@{}rcl@{}} &&{e_{1}(\boldsymbol{x})} = (1-\eta)\sum\limits_{j = 1}^{n} \int\limits_{\Omega} K_{\sigma_{j}}(\boldsymbol{y} - \boldsymbol{x})|I_{\boldsymbol{x}} - {f_{1}}(\boldsymbol{y}){|^{2}}d\boldsymbol{y} \\ &&{e_{2}(\boldsymbol{x})} = (1-\eta)\sum\limits_{j = 1}^{n} \int\limits_{\Omega} K_{\sigma_{j}}(\boldsymbol{y} - \boldsymbol{x})|I_{\boldsymbol{x}} - {f_{2}}(\boldsymbol{y}){|^{2}}d\boldsymbol{y} \\ &&{e_{3}(\boldsymbol{x})} = \eta \alpha_{1}{I_{\boldsymbol{x}}^{2\alpha - 2}}{{(I_{\boldsymbol{x}} - {c_{1}})}^{2}} \\ &&{e_{4}(\boldsymbol{x})} = \eta \beta_{1}{I_{\boldsymbol{x}}^{2\beta - 2}}{{(I_{\boldsymbol{x}} - {c_{2}})}^{2}}\\ &&{H_{\varepsilon} }(x) = \frac{1}{2}\left[1 + \frac{2}{\pi }\arctan \left( \frac{x}{\epsilon }\right)\right] \\ &&{\delta_{\varepsilon} }(x) = {{H^{\prime}}_{\varepsilon} }(x) = \frac{1}{\pi }\frac{\varepsilon }{{{\varepsilon^{2}} + {x^{2}}}} \end{array} $$
(18)

where ε is a small positive constant. Let 𝜖 → 0, H𝜖(x) and δ𝜖(x) s.t.

$$ \begin{array}{ll} &\lim_{\epsilon \rightarrow 0}{H_{\epsilon}(x)} = H(x)= \left\{\begin{array}{ll} 1, &x \ge 0 \\ 0, &otherwise \end{array}\right. \\ &\lim_{\epsilon \rightarrow 0}{\delta_{\epsilon}(x)} = \left\{\begin{array}{ll} 1, & x = 0 \\ 0, & otherwise \end{array}\right. \end{array} $$
(19)

The value of 𝜖 relates to the speed and accuracy of the contour evolving. To make the level set evolution fast, typically, 𝜖 = 1. α1, β1 are same as that in the (14).

We utilize the two-step iteration method to minimize the function EBregman−MLBF(ϕ(x),c1,c2,f1,f2) in (17). First, we fix the level set function ϕ(x), according to the following (20) update the mean intensity c1, c2 and the local fitting intensity f1(x), f2(x) inside and outside curve C, respectively.

$$ \begin{array}{@{}rcl@{}} &&{c}_{1} = \frac{{\int\limits_{\Omega} {I_{\boldsymbol{x}}^{(2\alpha -1)}{H_{\varepsilon} }(\phi (x))d\boldsymbol{x}} }}{{\int\limits_{\Omega} {I_{\boldsymbol{x}}^{(2\alpha - 2)}{H_{\varepsilon} }(\phi (\boldsymbol{x}))d\boldsymbol{x}} }} \\ &&{c}_{2} = \frac{{\int\limits_{\Omega} {I_{\boldsymbol{x}}^{(2\beta -1)}(1 - {H_{\varepsilon} }(\phi (\boldsymbol{x})))d\boldsymbol{x}} }}{{\int\limits_{\Omega} {I_{\boldsymbol{x}}^{(2\beta -2)}(1 - {H_{\varepsilon} }(\phi (\boldsymbol{x})))d\boldsymbol{x}} }} \\ &&\overline{f_{i,j}}(\textbf{y}) = \frac{{{K_{{\sigma_{j}}}}(\textbf{y} - \textbf{x}) * (M_{_{i}}^{\varepsilon} (\phi (\textbf{x}))I(\textbf{x}))}}{{{K_{{\sigma_{j}}}}(\textbf{y} - \textbf{x})*M_{_{i}}^{\varepsilon} (\phi (\textbf{x}))}} \\ &&{i = 1,2} ; {j = 1,...,n}\\ && M_{1}^{\varepsilon} (\phi (\textbf{x})) = {H_{\varepsilon} }(\phi (\textbf{x})), \\ && M_{2}^{\varepsilon} (\phi (\textbf{x})) = 1 - {H_{\varepsilon} }(\phi (\textbf{x})) \\ &&{f_{1}(y)} = \max{(\overline{f_{i,j}}(y))} \\ &&{f_{2}(y)} = \min{(\overline{f_{i,j}}(y))} \end{array} $$
(20)

Second, fix the mean intensity c1, c2 and the local fitting intensity f1(y), f2(y) inside and outside the curve C. Then, update the Bregman-MLBF model level set function ϕ(x) according to (21). Applying the calculus of variations and gradient descent method, we have the gradient flow equation:

$$ \begin{array}{@{}rcl@{}} \frac{{\partial \phi (\boldsymbol{x},t)}}{{\partial t}} &=& {\delta_{\varepsilon} }(\phi )\left( F + \mu div\left( \frac{{\nabla \phi }}{{|\nabla \phi |}}\right)\right)\\ && + v\left( {\nabla^{2}}\phi + div\left( \frac{{\nabla \phi }}{{|\nabla \phi|}}\right)\right) \end{array} $$
(21)

where

$$ {F} = - {\lambda_{1}}[{e_{1}(\boldsymbol{x}) + e_{3}(\boldsymbol{x})}] + {\lambda_{2}}[{e_{2}(\boldsymbol{x}) + e_{4}}(\boldsymbol{x})] $$
(22)

3.2 Analysis of the Bregman-MLBF model

In this section, we discuss the relationship between the proposed model and the conventional model of level set method. The comparisons are listed in Table 1.

Table 1 The parameter’s relationship between the Bregman-MLBF model and the other model
Full size table

The weight factor of the first term in (15) is an increasing function, whereas the second term is a decreasing function, so either term is biased to the point with small or large intensity. Therefore, this method can accelerate the curve evolution.

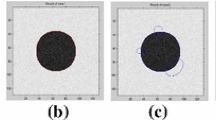
As discussed in Section 2, we declare that the force of the LBF model is edged while the force of the CV model is regional. Similarly, the force corresponding to (15) is regional. We discuss the gradient of level set function at any point in a strict-binary image I(x). According to the gradient flow equation corresponding to (15) and the LBF model, we discard the Dirac function in the gradient flow equation. The gradient of level set function at point P corresponding to different models is as follows:

$$ \begin{array}{@{}rcl@{}} &&{F^{Bregman}} \! = \! - {\lambda_{1}}\alpha_{1}{I_{\boldsymbol{P}}^{2\alpha {- 2}}}{(I_{\boldsymbol{P}} - {c_{1}})^{2}} \!+ \!{\lambda_{2}}\beta_{1}{I_{\boldsymbol{P}}^{2\beta - 2}}{(I_{\boldsymbol{P}} - {c_{2}})^{2}} \\ &&{F^{\text{MLBF}}} = - {\lambda_{1}}{e_{1}} + {\lambda_{2}}{e_{2}} \end{array} $$
(23)

where c1, c2 are the mean intensities inside and outside curve C, respectively. λ1 and λ2 are constants. IP is the intensity at point P, whereas e1 and e2 are defined in (18). FB is the sum of squared difference which is almost impossible to be zero. However, FMLBF is almost zero, if the point P is far away from the edge and more than the size of Gaussian kernel. Otherwise, FMLBF is non-zero. The results are shown in Fig. 3b–c. From Fig. 3b, we can observe that the force is non-zero at the edge, compared with the MLBF model. And in Fig. 3c we can see that the force is non-zero on the area inside curve C.

Fig. 3
figure 3

The force of the Bregman-MLBF model and the global energy term. a Strict binary image with the zero level set (the red circle). bFMLBF in (23). cFBregman in (23)

Full size image

4 Experimental results and performance analysis

We apply the Bregman-MLBF model on various images, and the segmentation results are presented and compared with three existing models: LCV incorporated with B-spline(BLCV) [4], MLBF model [17] and LGIF model [1]. There are parameters λ1, λ2, α, β, μ and v in the Bregman-MLBF model and the time step Δt for the implementation. In our experiments, we fixed them as λ1 = 1, λ2 = 1, α = 1.05, β = 0.95 , v = 1. In this experiment, the proposed MLBF model was compared with the traditional LBF model. When applying the LBF model, because there is no general guideline to choose suitable scale parameters, different scale values ranging from 1 to 16 were tested one by one. The segmentation results of MLBF model are shown in Fig. 4. Among all the segmentation results of MLBF model, the one with n = 3 is best (enclosed by red rectangle in Fig. 4). so the number of multi-scale kernel n is set to 3. The parameter μ of the length constraint term varies with the images to be segmented (the value of the parameter μ gets bigger when the image is larger). The weight factor w is decided by the image’s quality, because the global energy term can effectively segment the piece-wise image, while the local energy term is utilized to cope with the inhomogeneity image segmentation problem. In order to improve the quality of the segmentation results, we should be careful in choosing an appropriate weight factor for images of different quality.

Fig. 4
figure 4

Segmentation results of LBF model with different scale parameter ranging from 1 to 16

Full size image

4.1 Accuracy of contour location

The effectiveness of the Bregman-MLBF model is evaluated by applying it to both synthetic and medical images, as shown in Figs. 5, 6 and 7. The first column in Fig. 5 (synthetic images) illustrates the initial contours and the second to the fifth column are the segmentation results by using MLBF, LGIF, BLCV and our Bregman-MLBF model respectively. Also, we perform some experiments on medical images which are provided by the 4th Affiliated Hospital of Harbin Medical University in China. The columns in Figs. 6 and 7 from left to right are the original images (initial contours), the results with MLBF, LGIF, BLCV and Bregman-MLBF, respectively. The segmentation results have demonstrated clearly that the Bregman-MLBF model has better segmentation ability than the other three models.

Fig. 5
figure 5

Comparison of the segmentation results with synthetic images

Full size image
Fig. 6
figure 6

Comparison of the segmentation results with medical images

Full size image
Fig. 7
figure 7

Comparison of the segmentation results with breast medical images

Full size image

We also apply Bregman-MLBF to the natural images from the Berkeley segmentation dataset BSDS300 [19], which contains more than 300 images. Over 100 images are randomly selected from the dataset. Figure 8 shows the segmentation results of 10 sample images. The columns in Fig. 8 from left to right are the original images, the manual segmentation results, the results obtained with MLBF, LGIF, BLCV and Bregman-MLBF, respectively. It can be clearly seen that Bregman-MLBF has achieved the result which is closer to that of the manual segmentation than the other three models.

Fig. 8
figure 8

Comparison of the segmentation results with breast natural images

Full size image

To evaluate the Bregman-MLBF model objectively, we use two well-known metrics, the Hausdorff distance [24] and the PRA metric [2]. As defined in [24], the Hausdorff distance measures the similarity between two images. The lower it is, the better the segmentation result is. The Hausdorff distance between two images is computed as follows:

$$ HAU(I_{c},I_{ref})=max(h(I_{c},I_{ref}),h(I_{ref},I_{c})) $$
(24)

where \(h(I_{c},I_{ref})=max_{a\in I_{c}}(min_{b\in I_{ref}}\|a-b\|)\) and Ic denotes the detected contours obtained through a segmentation result of an image I. Iref denotes the reference contours corresponding to the ground truth. Pratt et al. [2] proposed an empirical measure for PRA, which is one of the most commonly used measures for two pixel sets comparison. The PRA is computed as

$$ PRA(I_{ref},I_{c}) = \frac{{\sum}^{card(I_{c})}_{k = 1}\frac{1}{1+d^{2}(k)}}{max\{card(I_{ref}),card(I_{c})\}} $$
(25)

where d(k) is the distance between the k th pixel belonging to the segmented contour Ic and the nearest pixel of the reference contour Iref.

Table 2 lists the evaluation results of the MLBF model, the LGIF model, the BLCV model and the Bregman-MLBF model by using the Hausdorff distance and PRA metric in Fig. 8. They are computed by using the manual segmentation as Iref and segmentation results of the models as Ic. It is obvious that the Bregman-MLBF method has the lowest values of the criteria by Hausdorff, except for the image 5. The Hausdorff distance is the maximum among the minimum distances between the points of contours in the image Ic and Iref. Since the contours of the segmentation results of the MLBF and the LGIF model that shown in Fig. 8 are in a relatively local area, and those of the Bregman-MLBF have some points out the object. This leads to the bigger Hausdorff distance of the Bregman-MLBF model than those of the MLBF and the LGIF model. It also causes that the PRA metric results of the Bregman-MLBF model is lower than that of the MLBF model in the image 5. However, the segmentation results shown in Fig. 8 illustrates that the Bregman-MLBF model has better segmentation ability. Therefore, the Bregman-MLBF model has better segmentation performance than those of the comparative three models.

Table 2 Results of the quantitative evaluation in Fig. 7
Full size table

The analysis of experimental results shows the BLCV model is more effective than the LBF model. By utilizing the global image information, the BLCV model improves the robustness to initialization of contour. However, the local term of the BLCV model can be regarded as the energy function that the CV model acts on the difference image gk(I(x)) − I(x). Consequently, it is challenging for LCV to correctly segment the image with intensity inhomogeneity, especially when high noise exists. Compared with MLBF, BLCV and LGIF, the Bregman-MLBF model measured by Bregman divergence which can be approximated by the data-dependent weighted L2 − norm not only accelerates the contour evolution, especially, when the contour is far away from object boundaries but also boosts the robustness to the initial placement. The local information is used to improve the capability of coping with intensity inhomogeneity and to attract the contour to stop at the object boundaries.

4.2 Speed of evolution convergence

The Bregman-MLBF’s efficiency can be reflected by the iteration times required for obtaining the final contour and the total CPU time taken to complete the segmentation. The iteration times and the CPU time required for the segmentation as in Figs. 5, 6 and 8 are shown in Tables 3, 4 and 5. Tables 3 and 4 show that Bregman-MLBF requires fewer iteration times than the other three models in general. From Table 5, it is obvious that only the iteration times of BLCV model for segmenting the image 4 is less than that of Bregman-MLBF. This is because the BLCV model falls into a local optimum, which needs fewer iteration times. But the segmentation result of BLCV is worse than that of Bregman-MLBF, as shown in Fig. 8. Worth to note that, the CPU time spent for LGIF to obtain the final segmentation results is less than that for Bregman-MLBF in the image 4. However the segmentation results of these images are rather poor, as seen in Fig. 8. In contrast, the segmentation results of Bregman-MLBF are more accurate than the other three models, which has been proved objectively in the Section 4.1.

Table 3 Comparison of processing speed for the experiment shown in Fig. 5
Full size table
Table 4 Comparison of processing speed for the experiment shown in Fig. 6
Full size table
Table 5 Comparison of processing speed for the experiment shown in Fig. 8
Full size table

4.3 Robustness against initial position

To demonstrate the robustness of our proposed model to contour initialization, experiments are preformed, respectively, on a synthetic image , a medical images which are typical images with intensity inhomogeneity and a real world image which is almost piece-wise, as shown in Figs. 9, 10 and 11. The different initial contours are shown in column (a) in each figure, the corresponding results of the MLBF model, the BLCV model, the LGIF model and the Bregman-MLBF model are shown in column (b), (c), (d), (e), respectively.

Fig. 9
figure 9

Segmentation results with different initial locations in medical images. Column a is the initial contours. Columns b–e are the segmentation results of the BLCV model, the MLBF model, the LGIF model and the Bregman-MLBF model, respectively

Full size image
Fig. 10
figure 10

Segmentation results with different initial locations in synthetic images. Column a is the initial contours. Columns b–e are the segmentation results of the MLBF model, the BLCV model, the LGIF model and the Bregman-MLBF model, respectively

Full size image
Fig. 11
figure 11

Segmentation results with different initial locations in real images. Column a is the initial contours. Columns b,–e are the segmentation results of the MLBF model, the BLCV model, the LGIF model and the Bregman-MLBF model, respectively

Full size image

From the results shown in Fig. 9, we can conclude that the MLBF model and the BLCV model failed to correctly segment the object in three different initial contours. Compared with the MLBF model and the BLCV model, the results given by the LGIF model shown in column (d) shows better performance in some cases. However, the results shown in the row 2 demonstrate that all compared models (MLBF, BLCV, LGIF) fail to segment the real boundaries satisfactorily, while the Bregman-MLBF model can successfully extract the boundaries for three different initial contours.

4.4 Robustness against noise

In order to demonstrate the robustness of our proposed model to Gaussian noise and intensity inhomogeneity, we generated different images with the same objects in it, whose boundaries are known and used as the ground truth. These images are generated by smoothing an ideal binary image, adding intensity inhomogeneity of different profiles and different levels of Gaussian noise. In Fig. 12, the results of corresponding image with the same initial contour (the blue circle) are the red contours, shown in Fig. 12. It is obvious that the Bregman-MLBF model produces accurate segmentation results. To evaluate the accuracy quantitatively, we compute the error ratio which is plotted in Fig. 13, where the X-axes represent the number of iteration and the Y-axes represent the error ratio. The (a), (b), (c) in Fig. 13 are the error ratio corresponding to row 1, 2 and 3 in Fig. 12, respectively. We can observe that the error ratio is very low, 3% at most. Moreover, clearly the heavier of the intensity inhomogeneity or/and the level of noise is, the more iterations are required. These results demonstrate the robustness of the Bregman-MLBF model to Gaussian noise and intensity inhomogeneity.

Fig. 12
figure 12

Segmentation results of the Bregman-MLBF model in different image conditions, e.g. different noises and intensity inhomogeneities. The red circle is the initial contour while the green contours are the segmentation results. For the row 1-3, each image in the same row has the same intensity inhomogeneity but different noises. Image in the same column have the same level of Gaussian noise but different intensity inhomogeneities (The level of Gaussian noise corresponding to each column are mean μ = 0, variance σ2 = 5,10,18,23, respectively)

Full size image
Fig. 13
figure 13

The error ratios corresponding to the row 1-3 in Fig. 11, and the curve of error ratio of image 1, 2, 3, 4 corresponding to column (a), (b), (c), (d) in each figure, respectively

Full size image

In Fig. 14, the experiments are performed on images contaminated by various degrees of noise. Since the image 2 in Fig. 5 consists of more objects, it is chosen as the test image. The first column in Fig. 14 shows the noisy images with different degrees of Gaussian noise (mean μ = 0, variance σ2 = 10,15,20,25, respectively). The second to the fifth Columns are the segmentation results of MLBF, BLCV, LGIF and Bregman-MLBF, respectively. It is obvious that Bregman-MLBF not only achieves better segmentation results, but also is robust to noise.

Fig. 14
figure 14

Comparison of segmentation results of image with noises. Column a is the various degrees of Gaussian noise image. Columns b–e are the segmentation results of the MLBF model, the BLCV model, the LGIF model and the Bregman-MLBF model, respectively

Full size image

5 Conclusion

In this paper, we proposed a region-based active contour model Bregman-MLBF for image segmentation in a variational level set framework. Bregman-MLBF takes into account both the global and the local information to formulate the energy function in order to control the contour evolution. The global information is utilized in a way that boosts its robustness to the initial position and accelerates the contour evolution, resulting in the improved segmentation results and reduction of overall computational cost. The local information is utilized to improve the ability of handling intensity inhomogeneity. The experiments on synthetic images, medical images and natural images from the Berkeley BSDS300 dataset have demonstrated that Bregman-MLBF can achieve more accurate segmentation results than existing approaches such as MLBF, LGIF, BLCV, etc. In terms of robustness, the experiments have proved that Bregman-MLBF are more robust to noise and initial contour than other models. Moreover, Bregman-MLBF’s also converges faster, thanks to the improved energy function.