1 Introduction

Point set registration is a fundamental and challenging problem which has a wide range of application in pattern recognition, medical image analysis, and computer vision [2, 4, 8, 10, 25, 27, 28]. Many tasks in these fields, including image fusing, shape matching, motion tracking, stereo correspondence, and image mosaic, can be typically formulated as point set registration problem, since point representations is simplest form of salient structure [4]. With a shape contour represented by the edge points, or the point feature in a image represented by the locations of interest points, the registration problem is to find the correct correspondence between two sets of points extracted from the input data and recover the underlying spatial mapping.

In order to match two point set accurately a small target, a variety of approaches have been proposed for point set registration in the past few decades. These methods can be classified into rigid or non-rigid registration, and the choice of them depends on the application and different characteristics of the data. For rigid transformation includes only for scaling, rotation, and translation, rigid registration is relatively easy and has reached some maturity [2, 4, 11]. By contrast, solving the non-rigid registration problem is quite difficult, because the underlying non-rigid spatial mappings, which allow anisotropic skews and scaling, are usually complex, unknown, and hard to model [8]. However, non-rigid registration is an issue of critical importance since it have been used in many real world tasks including:medical image mosaic, shape recognition, hand-written character recognition, and deformable motion tracking.

In this paper, we present a effective algorithm for non-rigid case. To solve this problem, we have to solve two unknown variables: the correspondence and the underlying spatial mapping. Because solving for either variable without information regarding the other tends to be difficult to handle, an iterated optimization method can be used [6, 35]. In this iterative process, the estimated transformation is used to refine the estimated correspondence, and vice versa. Their performance degenerates quickly if there are errors in the correspondence which occurs in many applications particularly if there are a significant number of outliers in the data and/or the transformation is large [6, 20].

Many algorithms have been proposed to tackle the problem. The most popular point registration approach is the iterated closest point (ICP) algorithm [2] proposed by Besl and McKay. They iteratively assign a binary correspondence based on the nearest-neighbor relationships and refine the rigid transformation by using the estimated correspondence. The main drawback of this approach is that the correspondence is binary makes a lot of local minimum. Its performance will degrade badly in the presence of outliers. Chui and Rangarajan [8] proposed a general framework for non-rigid point matching based on the optimal correspondences between two points sets found by with soft-assignment and the non-rigid spatial mapping modeled as thin-plate spline (TPS). The deterministic annealing technique is used to jointly solve the soft-assignment and the non-rigid spatial mapping. This method is quite similar to the EM algorithm and perform better than ICP. In related work, a rich descriptor called shape context (SC) for point set registration was proposed by Belongie et al. [1]. They attach a descriptor, which captures the distribution of the remaining points relative to it, to each point. The correspondence problem is solved as a binary linear assignment problem. But these methods ignore robustness when they recover the transformation from the correspondence.

To address the robust issue, Lian and Zhang [17] proposed to reduce the energy function of the robust point matching (RPM) method [8] to a concave function after eliminating the transformation variables and use concave optimization technique to minimize the resulting energy function. Ma et al. [19, 21] proposed to solve for correspondence by interpolating a vector field between the two point sets. Alternatively, the coherence point drift (CPD) algorithm [29] uses probability density estimation to find the alignment of two point sets, and it was shown to be robust and accurate performance with respect to outliers, noise and missing points. Other related work includes the multi-Layer motion based method [22], Gaussian mixture model based method [15], as well as Locally Linear Transforming based method [23, 24].

The main contribution of our approach is to robustly estimate the transformations from the contaminated correspondences. More precisely, the underlying transformation is recovered by using the global and local geometrical constraint between a set of point correspondences. Our approach jointly estimates the point correspondences and transformation between two point sets. Firstly, we use feature descriptors such as shape context to find correspondence between two point sets. Secondly, we estimate a coherent spatial mapping fitting for the inlier as the transformation. To this end, we preserve the local geometry of inlier point after transformation. Moreover, the spatial transformation is parameterized by the thin-plate spline (TPS) [30].

The rest of the paper is organized as follows. Section 2 describes the proposed GLC method for estimating TPS from point correspondences with global and local geometry constraints. In Section 3, we demonstrates our experimental results on various data. Section 4 concludes this paper.

2 Estimating coherent spatial mapping from correspondence

In this section, we consider the global spatial relationship and local geometrical constraint between a set of point correspondences, and propose an efficient point matching method which is able to establish accurate correspondences without hurting the correct matches.

2.1 Problem formulation

Given a set of point correspondences \(S = \{ (\mathbf {x}_{n}, \mathbf {y}_{n} ) \}^{N}_{n = 1}\) which are typically perturbed by noise and by outliers which undergo different transformations, our goal is to distinguish inliers from the outliers by estimating a coherent spatial mapping f for the underlying inliers, i.e., for an inlier correspondence (xn, yn), yn = f(xn).

Due to the existence of noise and outliers, it is desirable to have a robust estimation of f. To make this problem tractable, we assume that, the noise on inliers is isotropic Gaussian with zero mean and uniform standard deviation σ; the outlier distribution is to be uniform \(\frac {1}{a}\) with being a constant. Suppose there are two data in R, the observed input set X = {xn, n = 1,⋅,N} with point \(\mathbf {x}_{n} = ({\mathbf {x}_{n}^{x}}, {\mathbf {x}_{n}^{y}}, 1)\), and the observed output set y = {yn, n = 1,⋅,N} with point \(\mathbf {y}_{n} = ({\mathbf {y}_{n}^{x}}, {\mathbf {y}_{n}^{y}}, 1)\) Thus, the likelihood is a mixture model given by

$$\begin{array}{@{}rcl@{}} p(\mathbf{Y}|\mathbf{X}&&, \boldsymbol{\theta}) = \prod\limits_{n = 1}^{N} \sum\limits_{z_{n}} p(\mathbf{y}_{n}, z_{n} | \mathbf{x}_{n}, \boldsymbol{\theta}) \\ &&= \prod\limits_{n = 1}^{N} \left( \frac{\gamma}{ (2 \pi {\sigma}^{2})^{D / 2} } e^{- \frac{\| \mathbf{y}_{n} - \mathbf{f}(\mathbf{x}_{n}) \|^{2}}{2 {\sigma}^{2}}} + \frac{1-\gamma}{a} \right), \end{array} $$
(1)

where 𝜃 = {f,σ2, γ} includes a set of unknown parameters, and γ is the mixing coefficient which specifies the marginal distribution over the latent variable, i.e., ∀zn, p(zn = 1) = γ. zn ∈{0,1} is a latent variable of the n-th sample, where zn = 1 indicates a Gaussian distribution and zn = 0 points to a uniform distribution.

It is worthy nothing that true parameter set 𝜃 can be estimated by maximizing likelihood (1). A maximum likelihood estimation of 𝜃, i.e. \(\boldsymbol {\theta }^{*} = \mathop {\arg \max }_{\boldsymbol {\theta }} p(\mathbf {Y}|\mathbf {X}, \boldsymbol {\theta })\), can be obtained by seeking the minimal energy

$$ E(\boldsymbol{\theta}) = - \sum\limits_{n = 1}^{N} \ln \sum\limits_{z_{n}}p(\mathbf{y}_{n}, z_{n} | \mathbf{x}_{n}, \boldsymbol{\theta}). $$
(2)

The coherent spatial mapping f will be directly obtained from the optimal solution 𝜃∗.

In this work, the well known EM algorithm [9] is used to address the problem. It alternates with two steps: an expectation step (E-step) and a maximization step (M-step). The EM algorithm jointly estimates the responsibility indicating to what degree a correspondence belonging to inlier under the given transformation f and updates f based on the current estimate of the responsibility. Following standard notations [3], we omit some terms that are independent of 𝜃. Considering the negative log likelihood function, i.e. (2), the complete-data log likelihood takes the following form:

$$\begin{array}{@{}rcl@{}} \mathcal{Q}(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text{old}}) &=& -\frac{1}{2 \sigma^{2}} \sum\limits_{n = 1}^{N} p_{n} \| \mathbf{y}_{n} - \mathbf{f}(\mathbf{x}_{n}) \|^{2} - \ln \sigma^{2} \sum\limits_{n = 1}^{N} p_{n} \\ &&+ \ln \gamma \sum\limits_{n = 1}^{N} p_{n} + \ln (1 - \gamma) \sum\limits_{n = 1}^{N} (1-p_{n}). \end{array} $$
(3)

where pn = P(zn = 1|xn, yn, 𝜃old) is a soft decision, which indicates to what degree being inlier.

  • E-step: Denote P = diag(p1,…,pN) as a diagonal matrix. pn can be obtained based on Bayes rule, i.e.,

    $$ p_{n} = \frac{ \gamma e^{- \frac{\| \mathbf{y}_{n} - \mathbf{f}(\mathbf{x}_{n}) \|^{2}}{2 {\sigma}^{2}}} } { \gamma e^{- \frac{\| \mathbf{y}_{n} - \mathbf{f}(\mathbf{x}_{n}) \|^{2}}{2 {\sigma}^{2}}} + 2 \pi {\sigma}^{2} (1 - \gamma) / a }. $$
    (4)

  • M-step: Reestimate the parameter set 𝜃new as follows: \(\boldsymbol {\theta }^{\text {new}} = \mathop {\arg \max }_{\boldsymbol {\theta }} \mathcal {Q}(\boldsymbol {\theta }, \boldsymbol {\theta }^{\text {old}})\). The minimum solution σ2 of \(\mathcal {Q}(\boldsymbol {\theta })\) can be obtained by letting \(\frac {\partial \mathcal {Q}(\boldsymbol {\theta })}{\partial \sigma ^{2}}= 0\)

    $$\begin{array}{@{}rcl@{}} \sigma^{2} &=& \frac{ (\mathbf{Y} - \mathbf{V})^{\mathrm{T}} \mathbf{P} (\mathbf{Y} - \mathbf{V}) }{2 \cdot \text{tr} (\mathbf{P}) }, \end{array} $$
    (5)

    Similar to σ2, the minimum solution γ is

    $$ \gamma = \text{tr} (\mathbf{P}) / N, $$
    (6)

    where V = (f(x1);⋯ ;f(xN)), and tr(⋅) is the trace.

After the EM iteration converges, a correspondence (xn, yn) is considered as inlier if pn > τ, otherwise it is a outlier, where τ is a predefined threshold. It is worth nothing that the smaller the threshold τ, the higher the outlier rate and registration error are.

2.2 Global and local regularizations

Next we consider the minimization with respect to f. According to the complete negative log-likelihood (3), the mapping f is estimated by minimizing a weighted empirical error

$$ \mathcal{Q}(\mathbf{f}) = \frac{1}{2 \sigma^{2}} \sum\limits_{n = 1}^{N} p_{n} \parallel \mathbf{y}_{n} - \mathbf{f}(\mathbf{x}_{n}) \parallel^{2}. $$
(7)

This is in general ill-posed since f is not unique. To generate a smooth mapping fitting for the point correspondences, we adopt the TPS for parametrization. The TPS is chosen because it is a general purpose spline tool which can be cleanly decomposed into affine and non-affine subspaces controlled by coefficients A and W respectively [30]:

$$ \mathbf{f}(\mathbf{x}) = \mathbf{x} \cdot \mathbf{A} + \widetilde{K}(\mathbf{x}) \cdot \mathbf{W}, $$
(8)

where \(\widetilde {K}(\mathbf {x})\) is a 1 × N vector defined by the TPS kernel, i.e. K(r) = r2 log r, and each entry \(\widetilde {K}_{n}(\mathbf {x}) = K(|\mathbf {x}-\mathbf {x}_{n}|)\). Define the kernel matrix KN×N = {Kij} where Kij = K(|xi −xj|).

To have a stable solution, a typical strategy is to impose regularization on f to control the complexity of the hypothesis space. Here, we consider the standard TPS regularization which is given by

$$ \phi (\mathbf{W}) = \text{tr} (\mathbf{W}^{\mathrm{T}} \mathbf{K} \mathbf{W}) $$
(9)

which is the bending energy, and is independent on the linear component of the coherent spatial mapping.

The TPS regularization is a global constraint, and it is useful to keep the overall spatial connectivity of the point correspondences during registration. However, for point set registration, the local structures among neighboring points are also very strong and stable. This is particularly beneficial when the motion between the two point sets is nonrigid. In this case, a local geometrical constraint is desired to establish accurate correspondences. We preserve the local neighborhood structure during registration.

In our problem, we hope that the local structures in Y could be preserved after the displacement of X. Each point in X can be reconstructed by a weighted sum of the M nearest neighbors

$$ \mathbf{x}_{i} = \sum\limits_{j = 1}^{N} \alpha_{ij} \mathbf{x}_{j}, with \sum\limits_{j = 1}^{N} \alpha_{ij}= 1, $$
(10)

where the αij are homogeneous barycentric coordinates, and enforce αij = 0 if xj does not belong to the set of neighbors of xi.

The same relation holds after the transformation f and we can also write

$$ \mathbf{f}(\mathbf{x}_{i}) = \sum\limits_{j = 1}^{N} \alpha_{ij} \mathbf{f}(\mathbf{x}_{j}). $$
(11)

We then write the local geometry term as follows:

$$ \mathcal{E}(\alpha)= \sum\limits_{i = 1}^{N} l \lVert \mathbf{f}(\mathbf{x}_{i}) - \sum\limits_{j = 1}^{N} \alpha_{ij} \mathbf{f}(\mathbf{x}_{j}) \rVert^{2} $$
(12)

To preserve the local geometry of each inlier point after the transformation f, we combine TPS regularization term in (9) and the local constraint in (12). This lets us express the mapping f estimation as the following minimizing problem

$$ {\Psi}(\mathbf{f}) = \frac{1}{2 \sigma^{2}} \sum\limits_{n = 1}^{N} p_{n} \parallel \mathbf{y}_{n} - \mathbf{f}(\mathbf{x}_{n}) \parallel^{2} +\frac{\lambda^{L}}{2}\sum\limits_{i = 1}^{N} p_{i} \lVert \mathbf{f}(\mathbf{x}_{i}) - \sum\limits_{j = 1}^{N} \alpha_{ij} \mathbf{f}(\mathbf{x}_{j}) \rVert^{2} +\frac{\lambda^{G}}{2} \text{tr} (\mathbf{W}^{\mathrm{T}} \mathbf{K} \mathbf{W}). $$
(13)

where the positive real numbers λG and λL control the tradeoff between data fitting and global/local geometric preserving.

If we substitute (8) into the expression (13), the error function can be written in the form

$$\begin{array}{@{}rcl@{}} {\Psi}(\mathbf{f})& = &\frac{1}{2 \sigma^{2}} \sum\limits_{n = 1}^{N} p_{n} \lVert \mathbf{y}_{n} - \mathbf{x}_{n} \mathbf{A} - \widetilde{K}(\mathbf{x}_{n}) \mathbf{W} \rVert^{2} \\ &&+\frac{\lambda^{L}}{2}\sum\limits_{i = 1}^{N} p_{i} \lVert (\mathbf{x}_{i}-\sum\limits_{j = 1}^{N} \alpha_{ij} \mathbf{x}_{j})\mathbf{A} + (\widetilde{K}_{i}- \sum\limits_{j = 1}^{N} \alpha_{ij} \widetilde{K}_{j})\mathbf{W} \rVert^{2} \\ &&+\frac{\lambda^{G}}{2} \text{tr} (\mathbf{W}^{\mathrm{T}} \mathbf{K} \mathbf{W}) \\ &= &\frac{1}{2 \sigma^{2}} \sum\limits_{n = 1}^{N} p_{n} \lVert \mathbf{y}_{n} - \mathbf{x}_{n} \mathbf{A} - \widetilde{K}(\mathbf{x}_{n}) \mathbf{W} \rVert^{2} +\frac{\lambda^{L}}{2}\sum\limits_{i = 1}^{N} p_{i} \lVert \mathbf{x}_{i}^{L}\mathbf{A} + {K}_{i}^{L}\mathbf{W} \rVert^{2} \\ &&+\frac{\lambda^{G}}{2} \text{tr} (\mathbf{W}^{\mathrm{T}} \mathbf{K} \mathbf{W}). \end{array} $$
(14)

where \(\mathbf {x}_{i}^{L}=\mathbf {x}_{i}-{\sum }_{j = 1}^{N} \alpha _{ij} \mathbf {x}_{j}\) and \({K}_{i}^{L}=\widetilde {K}_{i}- {\sum }_{j = 1}^{N} \alpha _{ij} \widetilde {K}_{j}\).

It is worthy noting that the (14) can be rewritten as follows

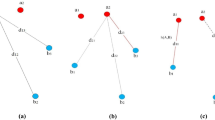
$$\begin{array}{@{}rcl@{}} \mathcal{E}(\mathbf{\mathbf{A}, \mathbf{W}}) &=& \frac{1}{2 \sigma^{2}} \| \widetilde{\mathbf{Y}} - \widetilde{\mathbf{X}} \mathbf{A} - \mathbf{P}^{1/2}\mathbf{K}\mathbf{W}\|^{2} +\frac{\lambda^{L}}{2} \| \widetilde{\mathbf{X}}^{L}\mathbf{A}+{\mathbf{P}^{L}}^{1/2}\mathbf{K}^{L} \mathbf{W}\|^{2} +\frac{\lambda^{G}}{2} \text{tr} (\mathbf{W}^{\mathrm{T}} \mathbf{K} \mathbf{W}). \end{array} $$
(15)

where \(\widetilde {\mathbf {X}} = \mathbf {P}^{1/2} \mathbf {X}\), \(\widetilde {\mathbf {Y}} = \mathbf {P}^{1/2} \mathbf {Y}\), and \(\widetilde {\mathbf {X}}^{L}={\mathbf {P}^{L}}^{1/2} \mathbf {X}^{L}\). The third smoothness term is the standard TPS regularization term. Thus, the local constraint term in (15) has the form \(\frac {\lambda ^{L}}{2} \| \widetilde {\mathbf {X}}^{L}\mathbf {A}+{\mathbf {P}^{L}}^{1/2}\mathbf {K}^{L} \mathbf {W}\|^{2}\). As PL and KL are fixed during transformation estimation, the local constraint term then becomes \(\frac {\lambda ^{L}}{2} \| \widetilde {\mathbf {X}}^{L}\mathbf {A}+\widetilde {\mathbf {K}}^{L} \mathbf {W}\|^{2}\), where \(\widetilde {\mathbf {K}}^{L}={\mathbf {P}^{L}}^{1/2}\mathbf {K}^{L}\) is an N × N constant matrix. In this context, the local constraint term plays a role of regularization on the transformation f, which ensures the well-posedness of the error function minimization, and it is controlled by a locally linear constraint (i.e., \(\frac {\lambda ^{L}}{2} \| \widetilde {\mathbf {X}}^{L}\mathbf {A}+\widetilde {\mathbf {K}}^{L} \mathbf {W}\|^{2}\)). Figure 1 illustrates the schematic of the local geometrical constraint.

Fig. 1
figure 1

Schematic of the local geometrical constraint. a Model point sets X (red circles) and target point sets Y (blue pluses). The goal is to align X onto Y. b Registration result by the proposed method. c Set of putative correspondences. d Assign neighbors to each point xi, e.g., the five solid pluses around xi. e Compute the weights Wij that best linearly reconstruct xi from its neighbors. f Optimize the transformation f under the constraint that each point xi can be reconstructed by its neighbors with weights Wij after the transformation

Full size image

To solve the TPS parameter pair A and W, we use a QR decomposition [8, 30]

$$ \widetilde{ \mathbf{X} } = [\mathbf{Q}_{1} \hspace{0.03in} \mathbf{Q}_{2}] \left[ \begin{array}{c} \mathbf{R} \\ \mathbf{0} \end{array} \right], \widetilde{ \mathbf{X} }^{L} = [\mathbf{Q}_{1}^{L} \hspace{0.03in} \mathbf{Q}_{2}^{L}] \left[ \begin{array}{c} \mathbf{R}^{L} \\ \mathbf{0} \end{array} \right], $$
(16)

where Q1 and \(\mathbf {Q}_{1}^{L}\) are orthonormal matrices of sizes N × 3, Q2 and \(\mathbf {Q}_{2}^{L}\) are orthonormal matrices of sizes N × (N − 3), and R and RL are upper triangular matrices of size 3 × 3. With the QR decomposition in place, equation (15) becomes

$$\begin{array}{@{}rcl@{}} \mathcal{E}(\mathbf{\mathbf{A}, \mathbf{{\Gamma}}}) &=&\frac{1}{2 \sigma^{2}} \left( \| \mathbf{Q}_{2}^{\mathrm{T}}\widetilde{\mathbf{Y}} - \mathbf{Q}_{2}^{\mathrm{T}}\mathbf{P}^{1/2}\mathbf{K}\mathbf{Q}_{2}\mathbf{{\Gamma}}\|^{2} + \| \mathbf{Q}_{1}^{\mathrm{T}}\widetilde{\mathbf{Y}} - \mathbf{R}\mathbf{A} - \mathbf{Q}_{1}^{\mathrm{T}}\mathbf{P}^{1/2}\mathbf{K}\mathbf{Q}_{2}\mathbf{{\Gamma}}\|^{2} \right) \\ && +\frac{\lambda^{L}}{2}\left( \| {\mathbf{Q}_{2}^{L}}^{\mathrm{T}} {\mathbf{P}^{L}}^{1/2} \mathbf{K}^{L}\mathbf{Q}_{2}\mathbf{{\Gamma}}\| + \| {\mathbf{Q}_{1}^{L}}^{\mathrm{T}}{\mathbf{P}^{L}}^{1/2}\mathbf{K}^{L}\mathbf{Q}_{2}\mathbf{{\Gamma}}+\mathbf{R}^{L}\mathbf{A} \| \right) \\ &&+ \frac{\lambda^{G}}{2} \text{tr} (\mathbf{{\Gamma}}^{\mathrm{T}} \mathbf{Q}_{2}^{\mathrm{T}} \mathbf{K} \mathbf{Q}_{2}\mathbf{{\Gamma}}), \end{array} $$
(17)

where W = Q2Γ and Γ is a matrix of size (N − 3) × 3. Setting W = Q2Γ implies that \(\widetilde {\mathbf {X}}^{\mathrm {T}}\mathbf {W} = 0\), which enables us to clearly separate the warping into affine and non-affine subspaces [8].

Minimizing the energy function (17) with respect to Γ and A, we obtain

$$\begin{array}{@{}rcl@{}} \mathbf{W}& = &\mathbf{Q}_{2} \mathbf{{\Gamma}} \\ &= &\mathbf{Q}_{2} (\mathbf{S}^{\mathrm{T}} \mathbf{S} + \lambda^{L}\sigma^{2} {\mathbf{S}^{L}}^{\mathrm{T}} \mathbf{S}^{L}+ \lambda^{G} \sigma^{2} \mathbf{T} + \tilde{\epsilon} \mathbf{I} )^{-1} \mathbf{S}^{\mathrm{T}} \mathbf{Q}_{2}^{\mathrm{T}} \widetilde{\mathbf{Y}}, \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} \mathbf{A} &= &(R^{\mathrm{T}}R+\lambda^{L}\sigma^{2} {R^{L}}^{\mathrm{T}{R^{L}}})^{-1}\left[\mathbf{R}^{\mathrm{T}}\mathbf{Q}_{1}^{\mathrm{T}}(\widetilde{\mathbf{Y}} - \mathbf{P}^{1/2}\mathbf{K}{\mathbf{W}})\right.\\ &&\left.-{R^{L}}^{\mathrm{T}} {\mathbf{Q}_{1}^{L}}^{\mathrm{T}}{{\mathbf{P}^{L}}}^{1/2}\mathbf{K}^{L}\mathbf{W}\right] . \end{array} $$
(19)

where \(\mathbf {S} = \mathbf {Q}_{2}^{\mathrm {T}} \mathbf {P}^{1/2} \mathbf {K} \mathbf {Q}_{2}\), \(\mathbf {S}^{L} = {\mathbf {Q}_{2}^{L}}^{\mathrm {T}} {\mathbf {P}^{L}}^{1/2} \mathbf {K}^{L} \mathbf {Q}_{2}\), \(\mathbf {T} = \mathbf {Q}_{2}^{\mathrm {T}} \mathbf {K} \mathbf {Q}_{2}\), and \(\tilde {\epsilon }\mathbf {I}\) is used for numerical stability. Thus we obtain the coherent spatial mapping f in (8).

2.3 Non-rigid point set registration

Point set registration aims to align two point sets \(\{\mathbf {x}_{m}\}_{m = 1}^{M}\) (the model point set) and \(\{\mathbf {y}_{l}\}_{l = 1}^{L}\) (the target point set). Typically, in the non-rigid case, it requires estimating a non-rigid transformation f which warps the model point set to the target point set. Our approach iteratively recovers the point correspondences and estimates the transformation between two point sets. In the first step of the iteration, feature descriptors are used to establish correspondence. We use the shape context (SC) [1] descriptor proposed by Belongie, which is a 60-dimensional vector, to offer a globally discriminative characterization. The χ2 distance was used to measure the difference of two points, and then the Hungarian method [5] is applied to find the initial correspondences between \(\{\mathbf {x}_{m}\}_{m = 1}^{M}\) and \(\{\mathbf {y}_{l}\}_{l = 1}^{L}\). In the second step, we adopt the proposed method to estimate a coherent spatial mapping fitting for the inlier as the transformation.

The performance of point matching algorithms depends, typically, on the coordinate system in which points are expressed. We use data normalization to control for this. In our evaluation, we compute two similarity transformations Tx and Ty for the point sets {xn} and {yn}, i.e. \(\hat {\mathbf {x}}_{n} = T_{\mathbf {x}}\mathbf {x}_{n}\), which ensure that point sets have zero means and average distance \(\sqrt {2}\) to the origin [14]. The regularization parameters λG and λL control the trade-off between the closeness to the data and the smoothness of the mapping. We set them to 500 in throughout our experiments. Moreover, the uniform distribution parameter a is set to be 5. We summarize the method in Algorithm 1.

figure c

3 Experimental results

In this section we compare our algorithm to other state-of-the-art approaches such as SC [1], TPS-RPM [8], CPD [29], and MR-RPM [26]. The stability and accuracy of registration methods is evaluated using the average Euclidean distance between the transformed model points and their template points.

3.1 Experiments with synthesized data

We first test our method on the synthesized data set by Chui and Rangarajan [8]. The data have two different shape models: a fish and a Chinese character. The fish consists of 96 points. The Chinese character consists of 108 points. For each model, there are three sets of data designed to measure the robustness of registration algorithms under deformation, occlusion, and rotation. In each test, one of the above distortions is applied to a model set to create a target set, and 100 samples are generated for each degradation level. Figure 2 shows examples from the synthetic data used to evaluate our approach. We use the shape context as the feature descriptor to establish initial correspondences. It is easy to make shape context translation and scale invariant, and in some applications, the rotation invariant shape context is used as in [35] if necessary.

Fig. 2
figure 2

Examples of synthetic data used in the experiments. Top row: the shapes of the fish. Bottom row: the shapes of the Chinese character. The left column: the template point sets. From the second to the right column: examples of the target point sets for the deformation, occlusion, and rotation tests, respectively

Full size image

Figure 3 illustrates the registration progress of the proposed method on fish point sets. The columns show the iterative alignment progress, and each row provides a different type of distortion. We align the model point set X (red circles) onto the observed data point set Y (blue pluses). From Fig. 3, we can see that our method is robust and accurate, and it typically converges in several iterations.

Fig. 3
figure 3

Illustration of registration progress of our method on fish point sets. The goal is to align X (red circles) onto Y (blue pluses). From top to bottom: results on deformation, occlusion, and rotation tests, respectively. The columns show the iterative alignment progress

Full size image

Figures 4 and 5 show the registration results of our method with comparison to four state-of-the-art methods: SC [1], TPS-RPM [8], CPD [29], and and MR-RPM [26], which are implemented using publicly available codes. In the tests of rotation, we use the rotation invariant shape context as the feature descriptor in our approach. As shown in the results, we see that SC and CPD can only generate satisfactory alignments for the shapes with deformation and occlusion, however, our method is able to produce an almost perfect alignment in all experiments. Note that the other four algorithms are not robust to large rotation, as shown in the right column of the figures. By contrast, our method is not affected by rotation since we use a rotation invariant feature descriptor.

Fig. 4
figure 4

Registration examples by different methods on the fish shape. The goal is to align the model point set (red circles) onto the target point set (blue pluses). Top row: template and target. From the second row to the bottom row: registration results by SC, TPS-RPM, CPD, MR-RPM, and our method, respectively. From left to right column: the deformation, occlusion, and rotation tests, respectively

Full size image
Fig. 5
figure 5

Registration examples by different methods on the Chinese character shape. The goal is to align the model point set (red circles) onto the target point set (blue pluses). Top row: template and target. From the second row to the bottom row: registration results by SC, TPS-RPM, CPD, MR-RPM, and our method, respectively. From left to right column: the deformation, occlusion, and rotation tests, respectively

Full size image

We further provide a quantitative comparison on the two shape models, and we test on all the three sets. The registration error on a pair of shapes is quantified as the average Euclidean distance between a point in the warped model and the corresponding point in the target. Then the registration performance of each algorithm is compared by the mean and standard deviation of the registration error of all the 100 samples. The performance of the proposed method is compared with four state-of-the-art point matching methods, SC [1], TPS-RPM [8], CPD [29], and MR-RPM [26]. The statistical results for each setting are summarized in Fig. 6. The results for the shapes of fish and Chinese character with deformation are shown in Fig. 6a and b, respectively. For minor deformations, four methods behave similarly. But our method performs best, especially for large deformations. Figure 6c and d show the results for the shapes of fish and Chinese character with occlusion, respectively. The error means of SC, CPD, MR-RPM, and our approach are nearly horizontal, showing good robustness to occlusion. However, our approach performs best, and it consistently outperforms CPD. Figures 6e and f show the results for the shapes of fish and Chinese character with rotation, respectively. The best results are obtained by our method. These plots clearly show the sensitivity of the CPD, and TPS-RPM to the rotation.

Fig. 6
figure 6

Comparison of the registration performance of our method with SC, TPS-RPM, and CPD on the fish and Chinese character shapes [8]. Left column: the shape of fish. Right column: the shape of a Chinese character. The error bars indicate the registration error means and standard deviations over 100 trials

Full size image

3.2 Experiments with MNIST handwritten digit database

In this section, we perform experiments on the MNIST handwritten digit database [16]. The database consists 10 categories corresponding to the 10 digits (from 0 to 9), where each category has 1000 images. The size of each image is 28 × 28. Figure 7 shows the ten templates. For each image, the 48 brightest points were sampled to represent a digit from the Canny edges. The first sample in each category is used as template and the rest images are used as the targets for registration test. The spatial mapping f between these two sets of points is established by the proposed method. Then the estimated f is used to warp the template shape.

Fig. 7
figure 7

The first sample in each category used as template

Full size image

We compare the proposed method with state-of-the-art point methods including SC [1], TPS-RPM [8], CPD [29], and MR-RPM [26]. The registration error of a pair of digits, which is quantified as the average Euclidean distance between a point in the warped template and the corresponding point in the target, is used to quantify the accuracy of the registration methods. Table 1 shows the average error of the evaluated methods. As shown in Table 1, our method outperforms the other three algorithms. The average error of the proposed method is 0.0172 and is less than 0.0595, 0.0511, 0.0833, and 0.0275 respectively, provided by the SC, TPS-RPM, CPD, and MR-RPM methods.

Table 1 Performance comparison on the MNIST database
Full size table

3.3 Shape classification results

In this section we test our method on the articulated shape data set [18], which contains 40 images from 8 different objects with articulation, as shown in Fig. 8. Each object has 5 images articulated to different degrees. The dataset is extremely challenging due to the high similarity between different objects. We compare our method to SC [1], CPD [29], and MR-RPM [26]. In our evaluation, we first sampled two hundred points from the outer contours of every shape, and run each point matching method to find the correspondence between two shapes and use the correspondence to warp one of the shapes. We then use SC distance to measure the similarity between the warped template shape and the target. For both shape representations, the χ2 distance was used to compare the SC histograms and the Hungarian method [13] is applied to compute distances between pairs of shapes.

Fig. 8
figure 8

Articulated shape database. The dataset contains 40 images from 8 articulated objects. Each column has 5 images from the same object

Full size image

For each image, the four most similar matches from other images in the dataset are chosen to evaluate the retrieval results. Table 2 gives the number of 1st, 2nd, 3rd and 4th most similar matches that come from the correct object. From Table 2, we can note that our method outperforms the other methods. For these shapes, the SC does not work well since a large deformation in the histogram is incured by the articulation.

Table 2 Retrieval results on the articulated shapes dataset [18]
Full size table

3.4 Retinal image registration results

In this section, we apply the proposed methods to the tasks of retinal image registration. Given an retinal image, the ridge based vascular tree segmentation [12] is adopted to detect the vascular trees. We use the structure-matching method (SM) [7] to establish the initial correspondence. Then the proposed method is used to estimate the transformation for the inlier. Figure 9a and b are a typical pair of retinal images taken at different times. Figure 9c and d are the mosaic vessel image results by MS and our method,respectively. Figure 9e and f are the mosaic retinal image results by MS and our method, respectively. From the seams marked by the red rectangles in Fig. 9c, we can see that the vessel image pairs are not accurately aligned. By contrast, the matching accuracy of our method is much higher, as shown the seams marked by the red rectangles in Fig. 9c. A quantitative comparison of our method with SM is reported in Table 3. As shown in Table 3, our method outperform SM method. In conclusion, our method is robust for non-rigid registration.

Fig. 9
figure 9

Comparison of the retinal image registration performance of our method with SM. a and b a pair of retinal images taken at different times. c and d mosaic vessel image results by MS and our method, respectively. e and f mosaic retinal image results by MS and our method, respectively

Full size image
Table 3 comparison of the Root Mean Squared Error(RMSE) of our method with SM on the vessel retinal image in Fig. 9c and d
Full size table

4 Conclusion

In this paper, a new approach is proposed for non-rigid point set registration. The two steps of estimating the point correspondences and transformation between two point sets are iterated to obtained a reliable result. To this end, we preserve the local structures by expressing each point as a weighted sum of several nearest neighbors. Experiments on various synthetic and real data demonstrate that the proposed approach yields superior results to those of the state-of-the-art methods. We have also presented a method for using the proposed approach for retinal image registration. Since the matrix inversion and matrix multiplication operations in (18) and (19), the design of a more robust and efficient measure is required. It might then be combined sparse approximation based methods or parallel based methods [31,32,33,34] to reduce the time and space complexities.