Non-rigid Point Set Registration Based on Iterative Linear Optimization

Abstract

This paper presents a novel point set registration algorithm based on iterative linear optimization, which can be used to register both rigid and non-rigid point set. Firstly, a new cost function was constructed to evaluate the summation of squared distance between the two point sets, in which rigid transformation, non-rigid elastic deformation and complex deformation were all included for consideration. Secondly, the proposed cost was linearized using to obtain a linear cost function of registration parameters. Thirdly, the registration parameters were solved by iterative optimization using Tikhonov regularization. Experimental results validated the performances of proposed method.

1 Introduction

With the rapid development of 3d scanning technology, 3d point set could be obtained more and more conveniently. As an important part, registration of rigid and non-rigid point set has become popular for the researchers who proposed many registration algorithms. For example, Fitsgibbon et al. [1] developed a robust iterative closest point algorithm, which optimize the registration energy function via LM algorithm, making registration error minimum. Although the algorithm greatly reduces the possibility of trapping in local minima, it is not consider noise perturbation in the matrix of coefficients, thus leading to poor stability. Hasler et al. [2] obtained the statistical modeling of interference noise before maximum likelihood estimation to register the point set. Bing et al. [3] proposed a novel point cloud registration method based on GMM, obtained sound registered results for rigid point set. In the field of non-rigid point set registration, the most famous algorithm was proposed by Chui et al. [4], in which thin plate splint was taken as the deformation template, and deterministic annealing technique was adopted. Although, this algorithm occluded abnormal shrinkage points, the speed is rather slow. Sofien et al. [5] presented a more efficient algorithm for non-rigid point set registration via the constraint of the energy change generated by the single template during registration process. But it will be accompanied by a large number of abnormal shrinkage points.

Main contents of this paper were organized as follow: Sect. 2 presented the basic principle and the pipeline of the algorithm. Section 3 constructed a new cost function for non-rigid point registration, followed by the linearization of the cost function in Sect. 4. In Sect. 5, the register parameters were solved by iterative linear optimization. And Sect. 6 presented the experimental results. The main achievements of this paper were concluded in Sect. 7.

2 Pipeline of the Algorithm

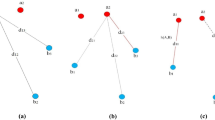
Let S and M be two 3d point sets(S is the Scene point set, M is the Model point set). Due to the registration was performed in an iterative manner, the intermediate point sets M^t and S^t were defined as illustrated in Fig. 1. In order to evaluate the degree of transformation, translation, deformation and distance between the point sets, cost functions ${\text{Cost}}({\text{M}}^{\text{t}} ,{\text{ M}}^{{{\text{t}} + 1}} )$, ${\text{Cost}}({\text{S}}^{\text{t}} ,{\text{ S}}^{{{\text{t}} + 1}} )$ and ${\text{Cost}}({\text{M}}^{\text{t}} ,{\text{ S}}^{{{\text{t}} + 1}} ;{\text{ S}}^{{{\text{t}} + 1}} ,{\text{ M}}^{{{\text{t}} + 1}} )$ were defined, and the total cost function of t th iteration was defined by weighted summation of the three cost functions. Based on the cost function, Tikhonov regularization was used to linearize the cost function. In addition, linear optimization was used to solve the registration parameters in each step. This process was iterated until preset tolerance was achieved. Pipeline of overall algorithm was illustrated in Fig. 2.

Fig. 1.

Basic principle of proposed method

Fig. 2.

Pipeline of the proposed algorithm

3 Cost Function for Non-rigid Point Set Registration

In rigid or non-rigid point set registration, a proper cost function is very important to avoid the iteration trapped in local minima, as well as speed up the convergence progress. In our construction, the cost function was divided into three parts, which were $Cost\,\left( {{\mathbf{M}}^{i} ,\,{\mathbf{M}}^{i + 1} } \right)$, $Cost\,\left( {{\mathbf{S}}^{i} ,\,\,\,{\mathbf{S}}^{i + 1} } \right)\,$ and $Cost\left( {{\mathbf{M}}^{t} ,\,{\mathbf{S}}^{t + 1} ;\,\,{\mathbf{S}}^{t + 1} ,\,\,{\mathbf{M}}^{t + 1} } \right)$, as illustrated in Fig. 1. And the total cost function ${\text{Cost}}\left( {i,i + 1} \right)$ was defined by weighted summation of the three parts as

$$ Cost\left( {i,i + 1} \right) = w_{1} Cost\left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right)\,\, + \,\,w_{2} \,Cost\left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{S}}^{i + 1} ;\,\,{\mathbf{S}}^{i + 1} ,\,\,{\mathbf{M}}^{i + 1} } \right) + w_{3} Cost\,\left( {{\mathbf{S}}^{i} ,\,\,{\mathbf{S}}^{i + 1} } \right) $$

(1)

where $w_{1} ,w_{2}$ and $w_{3}$ are the weights, used to control the relative significance during registration.

For $Cost\left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right)$, this cost function was defined to evaluate the averaged distance between point set M ⁱ and M ⁱ⁺¹. In which, rigid and non-rigid were both involved. Further more, for non-rigid transformation elastic deformation and complex deformation should be involved to perform complex deformation. Thus the cost function $Cost\,\left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right)$ between M ⁱ and M ⁱ⁺¹, was defined by

$$ Cost\,\left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right) = \,\,w_{11} \,Cost_{rigid} \,\left( {{\mathbf{M}}^{i} ,\,{\kern 1pt} {\mathbf{M}}^{i + 1} } \right) + w_{12} Cost_{nonrigid} \,\left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right) $$

(2)

where w ₁₁ and w ₁₂ were the weights, fulfilling $w_{ 1 1} \, + \,w_{ 1 2} \, = \, 1,\,\,Cost_{\text{rigid}} \,\left( {{\mathbf{M}}^{i} ,\,\,\,{\mathbf{M}}^{i + 1} } \right)$ was the cost function describing rigid transformation of the point set, $Cost_{\text{nonrigid}} \left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right)$ was the cost function describing non-rigid transformation of the point set defined below

$$ Cost_{nonrigid} \left( {{\mathbf{M}}^{i} ,{\mathbf{M}}^{i + 1} } \right) = w_{121} Cost_{elastic} \left( {{\mathbf{M}}^{i} ,{\mathbf{M}}^{i + 1} } \right) + w_{122} Cost_{complex} \left( {{\mathbf{M}}^{i} ,{\mathbf{M}}^{i + 1} } \right) $$

(3)

where w ₁₂₁ and w ₁₂₂ were the weights. $Cost_{\text{elastic}} \left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right)$ was the cost function describing elastic deformation of the point set, $Cost_{\text{complex}} \left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right)$ was the cost function describing complex deformation of the point set. $Cost_{\text{elastic}} \left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right)$ and $Cost_{\text{complex}} \left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right)$ were defined in following subsections.

For $Cost\left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{S}}^{i + 1} ;\,\,{\mathbf{M}}^{i + 1} ,\,\,{\mathbf{S}}^{i + 1} } \right)$ , the cost function was defined to evaluate the averaged distance between point set M ⁱ and S ⁱ⁺¹ and between point set M ⁱ⁺¹ and S ⁱ⁺¹, a symmetrical distance was defined based on projection to nearest plane in our work.

For $Cost\left( {{\mathbf{S}}^{i} ,\,\,{\mathbf{S}}^{i + 1} } \right)$, the cost function was defined to evaluate the degree of rigid transformation between point set S ⁱ and S ⁱ⁺¹, because only rigid transformation was involved for scene point set. Thus,

$$ Cost\left( {{\mathbf{S}}^{i} ,{\mathbf{S}}^{i + 1} } \right) = Cost_{rigid} \left( {{\mathbf{S}}^{i} ,{\mathbf{S}}^{i + 1} } \right) $$

(4)

3.1 Cost Function for Rigid Point Set Transformation

In order to evaluate the degree of rigid transformation, $Cost_{\text{rigid}} \left( {{\mathbf{X}}^{i} ,\,\,{\mathbf{X}}^{i + 1} } \right)$ was defined in this subsection. Due to X ⁱ⁺¹ is the transformed point set of X ⁱ, the cost function was defined by summation of squared distance between the points in X ⁱ and their transformed points in X ⁱ⁺¹. The $Cost_{\text{rigid}} \left( {{\mathbf{X}}^{i} ,\,\,{\mathbf{X}}^{i + 1} } \right)$ was defined by

$$ Cost_{rigid} \left( {{\mathbf{X}}^{i} ,{\mathbf{X}}^{i + 1} } \right) = \sum\limits_{k = 1}^{N} {\left\| {{\mathbf{x}}_{k}^{i + 1} - \left( {{\mathbf{Rx}}_{k}^{i} + {\mathbf{t}}} \right)} \right\|_{2}^{2} } $$

(5)

where ${\mathbf{x}}_{k}^{i}$ and ${\mathbf{x}}_{k}^{i + 1}$ are the kth point in ${\mathbf{X}}^{i}$ and ${\mathbf{X}}^{i + 1}$, ${\mathbf{R}}$ is the rotation matrix, ${\mathbf{t}}$ is the translation vector.

Equation (5) could be used in the definition of $Cost\left( {{\mathbf{S}}^{i} ,\,\,{\mathbf{S}}^{i + 1} } \right)$ and rigid part of $Cost\left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{M}}^{i + 1} } \right)$.

On the contrary, in the definition of $Cost\left( {{\mathbf{M}}^{i} ,\,\,{\mathbf{S}}^{i + 1} ;\,\,{\mathbf{M}}^{i + 1} ,\,\,{\mathbf{S}}^{i + 1} } \right)$, symmetrical distance was defined based on projection to nearest plane, the point projection was illustrated in Fig. 3.

Fig. 3.

Illustration of point projection

Let m _j be a point in M ⁱ, s _k , s _k+1 and s _k+2 were three nearest points in S ⁱ⁺¹, Π is the nearest plane defined by point s _k , s _k+1 and s _k+2, p(m _j ) is the point on Π projected by m _j , $d_{ms} \left( j \right) = \left\| {{\mathbf{m}}_{j} - p\left( {{\mathbf{m}}_{j} } \right)} \right\|_{2}^{2}$ is the squared distance between m _j and its projected point. In the same way, the squared distance between point s _j (a point in S ⁱ⁺¹) and its projected point can also be computed by $d_{sm} \left( j \right) = \left\| {{\mathbf{s}}_{j} - p\left( {{\mathbf{s}}_{j} } \right)} \right\|_{2}^{2}$ _. Thus the cost function $Cost\left( {{\mathbf{M}}^{t} ,\,\,{\mathbf{S}}^{t + 1} ;\,\,{\mathbf{S}}^{t + 1} ,\,\,{\mathbf{M}}^{t + 1} } \right)$ was defined symmetrically, by

$$ Cost\left( {{\mathbf{M}}^{i} ,{\mathbf{S}}^{i + 1} ;{\mathbf{S}}^{i + 1} ,{\mathbf{M}}^{i + 1} } \right) = \sum\limits_{j = 1}^{N} {d_{ms} \left( j \right)} + \sum\limits_{j = 1}^{M} {d_{sm} \left( j \right)} $$

(6)

where N and M are the point numbers of M ⁱ and S ⁱ⁺¹.

3.2 Cost Function for Non-rigid Point Set Transformation

During registration, the model point set was deformed non-rigidly, thus the deformation model constraints the deformation performances, a simple model often causes inadequate deformation or abnormal deformation, and a complex model would reduce the efficiency of the algorithm. Thus, in our construction, elastic deformation and complex deformation model were used in our construction.

3.2.1 Cost Function for Elastic Deformation

Let m ₁, m ₂, m ₃ and m ₄ be four points in M ⁱ, q ₁, q ₂, q ₃ and q ₄ be the corresponding deformed points, as illustrated in Fig. 4.

Fig. 4.

Illustration of elastic deformation

In this paper, the elastic deformation cost $Cost_{elastic} \left( {{\mathbf{M}}^{i} ,{\mathbf{M}}^{i + 1} } \right)$ was defined

$$ Cost_{elastic} \left( {{\mathbf{M}}^{i} ,{\mathbf{M}}^{i + 1} } \right) = \sum\limits_{j = 1}^{N} {\sum\limits_{{k \in \eta_{j} }} {\left\| {\left( {{\mathbf{q}}_{j} - {\mathbf{q}}_{k} } \right) - {\tilde{\mathbf{R}}}_{j} \left( {{\mathbf{m}}_{j} - {\mathbf{m}}_{k} } \right)} \right\|_{2}^{2} } } $$

(7)

where N is the point number of M ⁱ, η _j is the neighboring index set of point m _j , ${\tilde{\mathbf{R}}}_{j}$ is the rotation matrix. Equation (7) performed a block rotation to deformable template elastically or approximate elastically, but for every block, one block correspond to one rotation matrix, presenting approximate rigid transformation within the block, maintaining local structure.

3.2.2 Cost Function for Complex Deformation

In complex deformation, former elastic deformation model is not enough to describe the deformation form, thus, a data driven method was adopted to evaluate the complex deformation quantitatively.

Let M be a point set, represented by a N × d matrix, where N is the point number, d is the dimension, P ⁰, P ¹, P ², …, P ^N−1 be the circular shifted point sets of M. Representing M and its ith circular shifted form P ⁱ by

$$ {\mathbf{M}} = {\mathbf{P}}^{0} = \left[ {\begin{array}{*{20}c} {x_{11} } & {x_{12} } & \cdots & {x_{1d} } \\ {x_{21} } & {x_{22} } & \cdots & {x_{2d} } \\ \vdots & \vdots & \vdots & \vdots \\ {x_{N1} } & {x_{N2} } & \cdots & {x_{Nd} } \\ \end{array} } \right] $$

(8)

$$ {\mathbf{P}}^{i} = \left[ {\begin{array}{*{20}c} {x_{{\left( {i + 1} \right)1}} } & {x_{{\left( {i + 1} \right)2}} } & \cdots & {x_{{\left( {i + 1} \right)d}} } \\ {x_{{\left( {i + 2} \right)1}} } & {x_{{\left( {i + 2} \right)2}} } & \cdots & {x_{{\left( {i + 2} \right)d}} } \\ \vdots & \vdots & \vdots & \vdots \\ {x_{N1} } & {x_{N2} } & \cdots & {x_{Nd} } \\ {x_{11} } & {x_{12} } & \cdots & {x_{1d} } \\ \vdots & \vdots & \vdots & \vdots \\ {x_{i1} } & {x_{i2} } & \cdots & {x_{id} } \\ \end{array} } \right],\;i = 1,2, \cdots ,N - 1 $$

(9)

Then, a complex deformed point set M’ was defined by linear combination of P ⁰, P ¹, P ² … P ^N−1, represented by

$$ {\mathbf{M^{\prime}}} = \sum\limits_{i = 0}^{N - 1} {\lambda_{i} {\mathbf{P}}^{i} } $$

(10)

where $\lambda_{i} ,i = 0,1, \cdots ,N - 1$ are the coefficients and $\lambda_{0} = 1$.

Defining the deformation cost performed by Eq. (10) according to the summation of squared distance between the two point sets, by

$$ Cost_{complex} \left( {{\mathbf{M}},{\mathbf{M^{\prime}}}} \right) = \sum\limits_{k = 1}^{N} {\left\| {{\mathbf{m}}_{k} - {\mathbf{m^{\prime}}}_{k} } \right\|_{2}^{2} } $$

(11)

where ${\mathbf{m}}_{k}$ and ${\mathbf{m^{\prime}}}_{k}$ are the kth point in point set ${\mathbf{M}}$ and ${\mathbf{M}}^{'}$ respectively.

In above section, the cost function to register two point sets was defined (see Eq. (1)) rigidly or non-rigidly. The type of registration the algorithm performed depends on the weights w ₁₂ in Eq. (2), if w ₁₂ = 0, rigid registration would be performed, or non-rigid registration would be performed, a larger w ₁₂ often leads to a more flexible deformation during registration.

4 Linearization of the Cost Function

Based on constructed cost function in above section, optimal registration parameters could be solved by minimizing the cost function using linear or non-linear optimization. In this paper, the cost function was firstly linearized, then, the registration parameters were solved by Tikhonov regularization.

For non- rigid registration, the total cost for ith iteration can be written as

$$ \begin{aligned} Cost\left( {i,i + 1} \right)\; = w_{1} \sum\limits_{k = 1}^{N} {\left\| {{\mathbf{m}}_{k}^{i + 1} - \left( {{\mathbf{R}}_{1} {\mathbf{m}}_{k}^{i} + {\mathbf{t}}_{1} } \right)} \right\|_{2}^{2} } + w_{2} \sum\limits_{j = 1}^{N} {\sum\limits_{{k \in \eta_{j} }} {\left\| {\left( {{\mathbf{q}}_{j} - {\mathbf{q}}_{k} } \right) - {\tilde{\mathbf{R}}}_{j} \left( {{\mathbf{m}}_{j} - {\mathbf{m}}_{k} } \right)} \right\|_{2}^{2} } } + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;w_{3} \sum\limits_{k = 1}^{N} {\left\| {{\mathbf{m}}_{k} - {\mathbf{m^{\prime}}}_{k} } \right\|_{2}^{2} } + w_{4} \sum\limits_{j = 1}^{N} {\left\| {{\mathbf{m}}_{j} - p\left( {{\mathbf{m}}_{j} } \right)} \right\|_{2}^{2} } + w_{5} \sum\limits_{j = 1}^{M} {\left\| {{\mathbf{s}}_{j} - p\left( {{\mathbf{s}}_{j} } \right)} \right\|_{2}^{2} } + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;w_{6} \sum\limits_{k = 1}^{M} {\left\| {{\mathbf{s}}_{k}^{i + 1} - \left( {{\mathbf{R}}_{2} {\mathbf{s}}_{k}^{i} + {\mathbf{t}}_{2} } \right)} \right\|_{2}^{2} } \hfill \\ \end{aligned} $$

(12)

Equation (12) is a non-linear function of registration parameters, especially on the aspects of the rotating angles in R ₁ and R _2, in which, sine and cosine computation were involved. Because the point sets were transformed slightly, the rotating angles in R ₁ and R ₂ are all very small, thus R ₁ and R ₂ could be approximated by

$$ {\mathbf{R}}_{1} = \left[ {\begin{array}{*{20}c} 1 & { - \gamma_{1} } & {\beta_{1} } \\ {\gamma_{1} } & 1 & { - \alpha_{1} } \\ { - \beta_{1} } & {\alpha_{1} } & 1 \\ \end{array} } \right]\,,\,\,\,\,{\mathbf{R}}_{2} = \left[ {\begin{array}{*{20}c} 1 & { - \gamma_{2} } & {\beta_{2} } \\ {\gamma_{2} } & 1 & { - \alpha_{2} } \\ { - \beta_{2} } & {\alpha_{2} } & 1 \\ \end{array} } \right] $$

(13)

Substitute Eq. (13) to Eq. (12), besides $p\left( \bullet \right)$ in Eq. (12) is a linear projection operator. Thus, Eq. (12) was transformed into a linear model, rewrite Eq. (12) in the following form

$$ \begin{aligned} Cost\left( {i,i + 1} \right) = w_{1} \left\| {{\mathbf{A}}_{1} {\mathbf{x}} - {\mathbf{b}}_{1} } \right\|_{2}^{2} + w_{2} \left\| {{\mathbf{A}}_{2} {\mathbf{x}} - {\mathbf{b}}_{2} } \right\|_{2}^{2} + w_{3} \left\| {{\mathbf{A}}_{3} {\mathbf{x}} - \mathop b\nolimits_{3} } \right\|_{2}^{2} + w_{4} \left\| {{\mathbf{x}} - \mathop b\nolimits_{4} } \right\|_{2}^{2} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;w_{5} \left\| {{\mathbf{x}} - \mathop b\nolimits_{5} } \right\|_{2}^{2} + w_{6} \left\| {{\mathbf{A}}_{6} {\mathbf{x}} - {\mathbf{b}}_{6} } \right\|_{2}^{2} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| {\mathop D\nolimits^{0.5} ({\mathbf{Ax}} - {\mathbf{b}})} \right\|_{2}^{2} + \left\| {{\mathbf{\varGamma x}}} \right\|_{2}^{2} \hfill \\ \end{aligned} $$

(14)

where ${\mathbf{x}}$ is the state variable induced by rotation angles in ${\mathbf{R}}_{1}$, ${\mathbf{R}}_{2}$, the translating vector ${\mathbf{t}}_{1}$, ${\mathbf{t}}_{2}$ and the new point set ${\mathbf{M}}^{i + 1}$, ${\mathbf{S}}^{i + 1}$. D was a coefficient matrix who encoded $w_{1}$, $w_{2}$, $w_{3}$,$w_{4}$, $w_{5}$ and $w_{6}$. ${\mathbf{A}}$ was encoded ${\mathbf{A}}_{1}$, ${\mathbf{A}}_{2}$, ${\mathbf{A}}_{3}$ and ${\mathbf{A}}_{4}$, in which point sets ${\mathbf{M}}^{i}$ and ${\mathbf{S}}^{i}$ were used. ${\mathbf{b}}$ was the biased vector who encoded ${\mathbf{b}}_{1} ,{\mathbf{b}}_{2}$, ${\mathbf{b}}_{3}$ and ${\mathbf{b}}_{4}$, in which point sets ${\mathbf{M}}^{i}$, ${\mathbf{S}}^{i}$ and the two linear projection operators were used. $\varGamma$ was a coefficient matrix to involve the solution of rotation angles in ${\mathbf{R}}_{1}$, ${\mathbf{R}}_{2}$ and the translating vector ${\mathbf{t}}_{1}$, ${\mathbf{t}}_{2}$. Thus, non-rigid registration was transformed into the problem of linear minimization of Eq. (14).

5 Tikhonov Regularization

Up to now, non-rigid point set registration can be solved by minimizing linear optimization proved by Eq. (14). In this paper, Tikhonov regularization was used to minimize the two formulas. According to Tikhonov regularization method, the extreme of $\left\| { {{\mathbf{Ax}} - {\mathbf{b}}} } \right\|_{2}^{2} + \left\| {{\mathbf{\Gamma x}}} \right\|_{2}^{2}$ expressed by

$$ \mathop {\arg \hbox{min} }\limits_{{\mathbf{x}}} ||{\mathbf{Ax}} - {\mathbf{b}}||^{2} +\left\| {{\mathbf{\Gamma x}}} \right\|^{2} $$

(15)

can be solved by

$$ {\mathbf{x}}^{ * } = \left( {{\mathbf{A}}^{\rm T} {\mathbf{A}} + {\varvec{\Gamma}}^{\text{T}} {\varvec{\Gamma}}} \right)^{ - 1} {\mathbf{A}}^{\text{T}} {\mathbf{b}} $$

(16)

This optimization was performed step by step, until preset tolerances were reached.

6 Experimental Results

In order to validate the performances of proposed method, point sets were registered non-rigidly, using both proposed method and the method in [5]. Non-rigid registration results of 3D wolf point sets were shown in Fig. 5. It can be seen from the registered point sets, in our method, the model point set and the scene point set were registered accurately(corresponding points overlapped accurately), while [5] obtained slightly biased result, which means, our proposed method could reduce the residue error appeared in [5]. Numerical results were listed in Table 1. In Table 1, residue addition, our proposed method maintained more points after registration. It indicates our proposed method is more robust to point contraction than [5]. There will also offer relationship curves of non-rigid registration experiment to illustrate the change of residue error and maintained points with the registration in Figs. 6 and 7. In addition, our proposed method maintained more points after registration. It indicates our proposed method is more robust to point contraction than [5]. There will also offer relationship curves of non-rigid registration experiment to illustrate the change of residue error and maintained points with the registration in Figs. 6 and 7.

Fig. 5.

Non-rigid registration test of method in [5] and proposed method

Table 1. The residual and abnormal contraction points after registration

Fig. 6.

Relationship curve between residue error and iteration number

Fig. 7.

Relationship curve between maintained point and iteration number

7 Conclusions

This paper presented a novel point set registration method based on newly constructed cost function, linearization and Tikhonov regularization based optimization. The proposed method can be used in registration of both rigid and non-rigid point sets, achieving relative smaller residue error and larger maintained points. Experimental results indicate the proposed method is more accurate and robust than traditional method on the aspect of abnormal contraction.