1 Introduction

Image registration is a crucial step in computer vision, pattern recognition and image processing, which is widely used in medical image processing [15, 16, 27], image retrieval and classification [9, 10, 26] and many other applications. Point set registration, as a fundamental technique, aims to assign the correspondence between two point sets, and yields one certain transformation that aligns two point sets. The iterative closest point (ICP) algorithm is one of the most classical methods proposed by Besl and McKay [3, 4, 25], which can solve the rigid point set registration efficiently. Based on their work, many scholars extended the ICP algorithm to the scale and affine case. To tackle with the scale registration problem, Ying et al. [23] proposed the scale ICP algorithm by incorporating a scale factor to the standard ICP algorithm to handle the registration with different scales. To solve the ill-posed problem of the affine registration, Du et al. [7] proposed the affine ICP algorithm based on lie group. As the non-rigid case is a hard problem, many scholars proposed a large number of methods. For instance, Amberg et al. [1] proposed to assign an affine transformation to each vertex by using a locally affine regularization and minimize the difference in the transformation of neighboring vertices. However, the efficiency and precision of the registration methods rely heavily on initial parameters.

To register point sets with the outliers and noise, some scholars studied the variant ICP algorithm for much more robustness. To solve the registration problem with outliers, Chetverikov et al. [5] proposed the trimmed ICP based on the overlapping percent, which enhanced the robustness of the registration. Meanwhile, Phillips et al. [21] introduced the outlier robust ICP algorithm by minimizing fractional root mean squared distance, and the outliers were discarded in a statistically manner. In the noisy case, Jian et al. [14] treated point set registration as the alignment of two mixtures of Gaussians, and developed a robust and efficient registration imposing the distance between two mixtures. Scholars also introduced the Gaussian model into ICP, using the expectation maximization (EM) principles to update the Gaussian model by the distance and variance between two point sets [11]. Unfortunately, the aforementioned approaches based on ICP still work badly with non-rigid deformations, which are quite common in real world.

To solve the non-rigid registration problem, researchers proposed many efficient methods which are not based on ICP algorithm. Chui et al. [6] developed the thin plate spline-robust point matching (TPS-RPM) algorithm to deal with non-rigid registration problem, which employs the TPS as the parameterization of the non-rigid spatial mapping and the softassign as the correspondence. Furthermore, the coherent point drift (CPD) algorithm [19] considered the registration between two point sets as a probability density estimation problem. The method introduced the coherence constraint by regularizing the displacement field and using the variational calculus to calculate the optimal transformation. These methods, however, are still problematic between two point sets with large shape difference. Consequently, many approaches were presented to solve this problem using tree or graph. Jia et al. [13] found that most methods considered the point sets independently, so they introduced the tree-based groupwise registration method and an iterative groupwise segmentation method which used the segmentation information to acquire accurate results. Ying et al. [24] modeled the distribution of all images via a graph, and each image was warped to its nearby images in the graph. Wolz et al. [22] proposed to propagate the initial atlases to all images and the large deformation was modeled as a series smaller deformations. Du et al. [8] accomplished the non-rigid registration with large deformation via the heuristic tree matching, where the linked point sets in the tree are very similar and the large deformation is divided into several small deformations by the heuristic tree. However, the incorrect registration results may propagate along the trees or graphs in the above-mentioned approaches.

Aiming at improving the performance of point set registration, we propose a non-rigid registration method based on dynamic tree with each node in the tree representing a point set, which can bear large shape deformations and eliminate the wrong pairs. First, the similarity of each point set pairs is evaluated using affine ICP algorithm with bidirectional distance. Then, non-rigid registration is conducted on similar model and subject pairs. The links are established between the models and subjects with accurate registration, and the wrong pairs are rejected. The tree extends progressively until all subjects are added to the tree. As a consequence, the method divides large shape difference into several small ones via the intermediate point sets, and non-rigid registration results are evaluated in real-time to avoid the propagation of the wrong results. Experiments on fish shape and Tangut character database employing CPD method show that our method improves the accuracy of registration with large shape difference.

The rest of the paper is organized as follows. Section 2 simply introduces non-rigid registration CPD algorithm. In Section 3, the proposed method is explained in detail. After that, Section 4 presents the experiments of our method integrating CPD algorithm. Finally, the work is concluded in the last section.

2 Coherent point drift methods

As one of the most popular non-rigid registration methods, CPD [19] considers the alignment between two point sets as a probability density estimation problem, by coherently moving the point set. We denote the model and subject point sets as \( X={\left\{{\overrightarrow{x}}_i\right\}}_{i=1}^N \) and \( Y={\left\{{\overrightarrow{y}}_j\right\}}_{j=1}^M \) respectively. CPD fits the Gaussian mixture model (GMM) centroids to the data by maximizing the likelihood. The GMM centroids move coherently as a group by the parameter θ to keep the topological structure of the point set. The objective function of CPD is formulated as follows:

$$ Q\left(\theta, {\sigma}^2\right)=\frac{1}{2{\sigma}^2}{\displaystyle \sum_{m,n=1}^{M,N}{P}^{old}\left(m|{x}_n\right)\left|\right|{x}_n-T\left({y}_m,\theta \right)\left|\right|{}_2^2}+\frac{N_PD}{2} \log {\sigma}^2 $$
(1)

where \( {N}_P={\displaystyle \sum_{n=1}^N{\displaystyle \sum_{m=1}^M{P}^{old}\left(m|{x}_n\right)}} \), σ 2 is the isotropic covariance, and P old represents the posterior probabilities of GMM components.

The EM algorithm can be used to solve the CPD registration problem and obtain the non-rigid registration result. The algorithm iteratively calculates the parameter, which includes E-step and M-step. The E-step computes the probability distributions of two point sets and set up the correspondence, and the M-step updates the transformation parameters by using the known correspondence. The EM algorithm is repeated until the algorithm converges.

3 The proposed method

3.1 The framework of the proposed method

In reality, the number of images in a database is enormous and many images bear large shape difference with the model image. As large shape difference can be decomposed into small deformations with the help of a series of similar point sets in the database, the tree is applied to conduct the non-rigid registration. Moreover, to improve the accuracy of registration results, dynamic tree is presented to prevent the error propagation. The framework of non-rigid registration based on dynamic tree is illustrated in Fig. 1.

Fig. 1
figure 1

The framework of non-rigid registration based on dynamic tree

Full size image

First, we use the affine ICP algorithm with bidirectional distance to calculate the similarity between every two point sets in the database. Point set registration with large shape difference has inaccurate results. Therefore, accurate non-rigid registration is only conducted on the similar point set pairs. The links among similar models and subjects are established, with which the non-rigid registration is conducted between the models and subjects. Only the subjects owning accurate non-rigid registration results will be added to the dynamic tree, and they are added to the model set to register other subjects. Subjects with incorrect results wait for the next time to register. Consequently, the dynamic tree extends progressively by repeating the above steps until the subject set is empty. In this way, all subjects are attached to the tree, and the registration results of the model and each subject in the tree are accurate by the guidance of the intermediate point sets.

3.2 Similarity measurement

Similarity measurement is an important procedure in the proposed method, as it could help to build the dynamic tree efficient and reliable. The affine ICP algorithm is suitable for this measurement for its efficiency and ability of preserving the linear structure of the point sets. Therefore, we use the affine ICP algorithm with bidirectional distance [8] to calculate the similarity of images, which can also avoid local minimum.

In the affine registration problem, A is denoted as a rotation matrix and \( \overrightarrow{t} \) is a translation vector. For the model point set \( X={\left\{{\overrightarrow{x}}_i\right\}}_{i=1}^N \) and the subject point set \( Y={\left\{{\overrightarrow{y}}_j\right\}}_{j=1}^M \), \( {\left\{i,c(i)\right\}}_{i=1}^N \) and \( {\left\{d(j),j\right\}}_{j=1}^M \) represent the correspondence. The affine registration problem based on the least square (LS) criterion with bidirectional distance is formulated as:

$$ \underset{\begin{array}{l}\kern2.5em \det \left(\mathbf{A}\right)\ne 0,\overrightarrow{t},\\ {}d(j)\in \left\{1,2,\cdots, N\right\},c(i)\in \left\{1,2,\cdots, M\right\}\end{array}}{ \min }{\displaystyle \sum_{i=1}^N\left|\right|\left(\mathbf{A}{\overrightarrow{x}}_i+\overrightarrow{t}\right)-{\overrightarrow{y}}_{c(i)}\left|\right|{}_2^2+{\displaystyle \sum_{j=1}^M\left|\right|\left(\mathbf{A}{\overrightarrow{x}}_{d(j)}+\overrightarrow{t}\right)-{\overrightarrow{y}}_j\left|\right|{}_2^2}} $$
(2)

where \( {\displaystyle \sum_{i=1}^N\left|\right|\left(\mathbf{A}{\overrightarrow{x}}_i+\overrightarrow{t}\right)-{\overrightarrow{y}}_{c_k(i)}\left|\right|{}_2^2} \) is the forward square distance while \( {\displaystyle \sum_{j=1}^M\left|\right|\left(\mathbf{A}{\overrightarrow{x}}_{d_k(j)}+\overrightarrow{t}\right)-{\overrightarrow{y}}_j\left|\right|{}_2^2} \) is the backward square distance. To solve this problem, the affine ICP algorithm is given, which includes two steps.

Step 1, we employ the (k − 1)th affine transformation \( \left({\boldsymbol{A}}_{k-1},{\overrightarrow{t}}_{k-1}\right) \) to find the correspondence between two point sets.

$$ \begin{array}{c}\hfill {c}_k(i)=\underset{c(i)\in \left\{1,2,\cdots, M\right\}}{ \arg \min}\left|\right|\left({\mathbf{A}}_{k-1}{\overrightarrow{x}}_i+{\overrightarrow{t}}_{k-1}\right)-{\overrightarrow{y}}_j\left|\right|{}_2^2,i=1,2,\cdots, N\hfill \\ {}\hfill {d}_k(j)=\underset{d(j)\in \left\{1,2,\cdots, N\right\}}{ \arg \min}\left|\right|\left({\mathbf{A}}_{k-1}{\overrightarrow{x}}_i+{\overrightarrow{t}}_{k-1}\right)-{\overrightarrow{y}}_j\left|\right|{}_2^2,j=1,2,\cdots, M\hfill \end{array} $$
(3)

Step 2, we use the bidirectional correspondences \( \left\{{\overrightarrow{x}}_i,{\overrightarrow{y}}_{c_k(i)}\right\} \) and \( \left\{{\overrightarrow{x}}_{d_k(j)},{\overrightarrow{y}}_j\right\} \) built in the last step to obtain the kth affine transformation\( \left({\boldsymbol{A}}_k,{\overrightarrow{t}}_k\right) \).

$$ \left({\mathbf{A}}_k,{\overrightarrow{t}}_k\right)=\underset{ \det \left(\boldsymbol{A}\right)\ne 0,\overrightarrow{t}}{ \min}\left({\displaystyle \sum_{i=1}^N\left|\right|\left(\mathbf{A}{\overrightarrow{x}}_i+\overrightarrow{t}\right)-{\overrightarrow{y}}_{c_k(i)}\left|\right|{}_2^2}+{\displaystyle \sum_{j=1}^M\left|\right|\left(\mathbf{A}{\overrightarrow{x}}_{d_k(j)}+\overrightarrow{t}\right)-{\overrightarrow{y}}_j\left|\right|{}_2^2}\right) $$
(4)

These two steps repeat until the results converge. As it is a local convergent algorithm, the initial value \( \left({\boldsymbol{A}}_0,{\overrightarrow{t}}_0\right) \) is important, which won’t be introduced here.

In Step 1, searching the closest point globally as the correspondence is very slow when there are too many points in the point sets. Thus, Delaunay triangulation [2] or k-d tree [12, 20] could be used to build the correspondence between two point sets efficiently.

In Step 2, to solve A and \( \overrightarrow{t} \), Eq.(4) can be formulated as:

$$ F\left(\mathbf{A},\overrightarrow{t}\right)={\displaystyle \sum_{i=1}^N\left|\right|\left(\mathbf{A}{\overrightarrow{x}}_i+\overrightarrow{t}\right)-{\overrightarrow{y}}_{c_k(i)}\left|\right|{}_2^2}+{\displaystyle \sum_{j=1}^M\left|\right|\left(\mathbf{A}{\overrightarrow{x}}_{d_k(j)}+\overrightarrow{t}\right)-{\overrightarrow{y}}_j\left|\right|{}_2^2} $$
(5)

Suppose K = N + M. Point sets \( R={\left\{{\overrightarrow{r}}_i\right\}}_{i=1}^K \) and \( S={\left\{{\overrightarrow{s}}_i\right\}}_{i=1}^K \) are defined as:

$$ {\overrightarrow{r}}_l=\left\{\begin{array}{cc}\hfill {\overrightarrow{x}}_l\hfill & \hfill 1\le l\le N\hfill \\ {}\hfill {\overrightarrow{x}}_{d_k\left(l-N\right)}\hfill & \hfill N+1\le l\le K\hfill \end{array}\right.,{\overrightarrow{s}}_l=\left\{\begin{array}{cc}\hfill {\overrightarrow{y}}_{c_k(l)}\hfill & \hfill 1\le l\le N\hfill \\ {}\hfill {\overrightarrow{y}}_{l-N}\hfill & \hfill N+1\le l\le K\hfill \end{array}\right. $$

Then, Eq. (5) can be simplified as:

$$ F\left(\mathbf{A},\overrightarrow{t}\right)={\displaystyle \sum_{l=1}^K\left|\right|\left(\mathbf{A}{\overrightarrow{r}}_l+\overrightarrow{t}\right)-{\overrightarrow{s}}_l\left|\right|{}_2^2} $$
(6)

The function (6) gets the minimum when \( \overrightarrow{t}=\frac{1}{K}{\displaystyle \sum_{l=1}^K{\overrightarrow{s}}_l}-\frac{1}{K}{\displaystyle \sum_{l=1}^K\boldsymbol{A}{\overrightarrow{r}}_l} \), so it can be rewritten as:

$$ F\left(\mathbf{A}\right)={\displaystyle \sum_{l=1}^K{\left\Vert \mathbf{A}{\overrightarrow{a}}_l-{\overrightarrow{b}}_l\right\Vert}_2^2} $$
(7)

where \( {\overrightarrow{a}}_l={\overrightarrow{r}}_l-\frac{1}{K}{\displaystyle \sum_{l=1}^K{\overrightarrow{r}}_l} \) and \( {\overrightarrow{b}}_l={\overrightarrow{s}}_l-\frac{1}{K}{\displaystyle \sum_{l=1}^K{\overrightarrow{s}}_l} \).

To minimize the objective function (7), we can recover the differential equation dF(A)/d A = 0 to obtain the affine transformation:

$$ \mathbf{A}=\left({\displaystyle \sum_{l=1}^K{b_l}^T{a}_l}\right){\left({\displaystyle \sum_{l=1}^K{a}_l{a_l}^T}\right)}^{-1} $$
(8)

Thus far, the affine transformation parameters A and \( \overrightarrow{t} \) are derived from the equations above.

When conducting on point set pairs, the affine ICP algorithm with bidirectional distance generates the registration error, which can be given as follows:

$$ \mathrm{D}\left(\mathbf{X},\mathbf{Y}\right)={\displaystyle \sum_{i=1}^N\left|\right|\left({\mathbf{A}}_f{\overrightarrow{x}}_i+{\overrightarrow{t}}_f\right)-{\overrightarrow{y}}_{c_f(i)}\left|\right|{}_2^2}/N+{\displaystyle \sum_{j=1}^M\left|\right|\left({\mathbf{A}}_f{\overrightarrow{x}}_{d_f(j)}+{\overrightarrow{t}}_f\right)-{\overrightarrow{y}}_j\left|\right|{}_2^2}/M $$
(9)

where D(•) is distance of subject and transformed model point set, \( \left\{{\overrightarrow{x}}_i,{\overrightarrow{y}}_{c_f(i)}\right\} \) and \( \left\{{\overrightarrow{x}}_{d_f(j)},{\overrightarrow{y}}_j\right\} \) are the final bidirectional correspondence, and \( \left({\boldsymbol{A}}_f,{\overrightarrow{t}}_f\right) \) is the final transformation parameter.

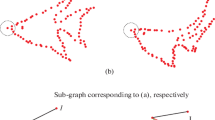
Figure 2 illustrates the registration results of two subjects with the same model. The structure of the subject in Fig. 2b is similar to the model while the subject Fig. 2c bears large shape difference with the model. As shown in Fig. 2d, e, the registration result of the similar point sets is correct in structure while the result of the dissimilar point sets with large shape difference is completely wrong. The results indicate that the affine ICP algorithm with bidirectional distance could measure the similarity between two point sets for the following non-rigid registration.

Fig. 2
figure 2

The registration results of affine ICP algorithm with bidirectional distance. (a) The model point set. (b) Subject point set similar to the model point set. (c) Registration result of (b). (d) Subject point set has large shape difference with the model point set. (e) Registration result of (d)

Full size image

We set a threshold by experience to evaluate the similarity, which are yielded by the affine ICP algorithm with bidirectional distance, so two point sets are similar when their distance is smaller than the threshold.

3.3 Non-rigid registration based on dynamic tree

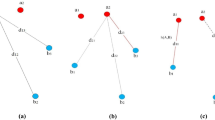
As non-rigid registration completes well between two point sets with similar shapes, but gets worse results for dissimilar point sets, so we build a tree to connect similar point sets for the non-rigid registration. However, the non-rigid registration method may fail for the linked point sets sometime. To deal with this problem, we apply a dynamic tree to complete the non-rigid registration, which can get rid of some wrong results and prevent the wrong results from propagating along the tree. In the following part, we illustrate the proposed approach via a set of examples shown in Fig. 3.

Fig. 3
figure 3

An example of the process of building dynamic tree. (a) The model and subjects. (b) Establish preliminary links between model and subjects, which are shown in dotted line. (c) Conduct non-rigid registration on point set pairs with preliminary links, where black line represents precise results and red line stands for inaccurate results. (d) Build up the second layer of dynamic tree. (e) Establish the third layer. (f) Final tree

Full size image

Suppose that there are 9 point sets numbered from (1) to (9) in Fig. 3a. We take point set (1) as the initial model set as well as the root node of the dynamic tree, and the other point sets are the initial subject sets. Firstly, affine ICP algorithm with bidirectional distance is used to evaluate the similarity of every two point sets. As revealed in Fig. 3b, the shapes of point sets (2), (3), (4), (7) and (8) are similar to the model, and a series of preliminary connections are established between these subjects and the model, which are expressed as dotted line in the Fig. 3b. Then, non-rigid registration method is conducted on the subjects by using the model and yields registration errors. We set a threshold to estimate the accuracy of the non-rigid registration results. Based on this threshold, as shown in Fig. 3c, the registration errors of (2), (4) and (7) are satisfactory, so we move these successfully registered point sets from subjects to the model sets. Meanwhile, red lines represent the incorrect registration results, since the registration errors of the linked point sets are over the threshold. Thus, (3) and (8) look forward to another registration in the next iteration and their connections (the red lines) should be cut off. After the above procedures, a layer of the dynamic tree is built, and in the example, (2), (4), (7) constitute the second layer of the tree. Then, the dynamic tree is extended layer by layer via the above iterations until the entire initial subjects are attached to the tree. The subjects bearing large shape difference such as (3) and (6) are in the deeper layers, and with the guidance of the intermediate point sets, the model can register all subjects accurately.

In a word, we use the affine ICP algorithm with bidirectional distance to calculate the similarity between every two point sets firstly. The model is the root node of the tree and preliminary links are established between the model and subjects via the similarity measurement. Then, non-rigid registration is implemented on the model and subject pairs where preliminary links exist, and we use the non-rigid registration errors to evaluate the registration accuracy. The registration is considered to be precise only if the error is less than the threshold obtained by experiences. We confirm the links between model and subjects which have accurate registration results, and add these subjects to the model set. Meanwhile, subjects with incorrect registration results wait for the following registration. We assign the root node as the first layer of dynamic tree, and build the second layer after the above procedures while the registration results of overall subject point sets are correct. Repeat these steps, the dynamic tree is built layer by layer until all subjects are connected to tree.

In non-rigid registration, the performances of registration with similar point sets are much more satisfactory. In the dynamic tree, the model warps with the guidance of intermediate point sets, and becomes very similar to the subjects with large shape difference. Besides, the connections between the model and subjects with wrong registration results are cut in real time, which prevents incorrect registration results propagating along the paths on the tree and guarantees the accuracy of registration in the meanwhile.

In our approach, we need a distance to get rid of the wrong results and preserve the correct one. Here, we use the bidirectional Euclidian distance as the non-rigid registration error to evaluate the accuracy, which can be formulated as:

$$ e=\left({\displaystyle \sum_{i=1}^N\left|\right|{\overrightarrow{q}}_i-{\overrightarrow{y}}_{r(i)}\left|\right|{}_2^2+{\displaystyle \sum_{j=1}^M\left|\right|{\overrightarrow{q}}_{s(j)}-{\overrightarrow{y}}_j\left|\right|{}_2^2}}\right)/\left(N+M\right) $$
(10)

where e is the bidirectional Euclidian distance which can avoid local convergence. \( \boldsymbol{Q}={\left\{{\overrightarrow{q}}_i\right\}}_{i=1}^N \) is the transformed model point set after non-rigid registration while \( \left\{{\overrightarrow{q}}_i,{\overrightarrow{y}}_{r(i)}\right\} \) and \( \left\{{\overrightarrow{q}}_{s(j)},{\overrightarrow{y}}_j\right\} \) are the correspondences built by the shortest distance.

4 Experimental results

In order to evaluate the performance of our algorithm, we implement the proposed method integrated with the CPD algorithm on two different database: a fish and a Tangut character. In the 2D fish shape database [17, 18], it is the contours of fish images and the number of these points varies from 400 to 1600 for images. The Tangut character database is acquired from the 80th volume of “Avatamsaka Sutra”. We eliminate the noises and extract the edges and skeletons, with which a shape database is established. The database contains several different characters and each character contains hundreds of points. Both the CPD algorithm based on dynamic tree and the traditional CPD algorithm are conducted on the databases mentioned above and the registration results of these two approaches are compared to prove the improvement of our method.

Moreover, 46 different point sets of fish shapes and 134 different point sets of character ‘fo’ are chosen for the experiments. In each experiment, we select one point set as the model, and the others as subjects. To avoid the influence of the image size, we normalize the size of all images firstly. The subjects on the second layer of the dynamic tree are registered directly with the model node via CPD. Therefore, the registration results are the same as the traditional CPD, which are meaningless to compare. Therefore, we only use the results of subjects on the third and deeper layers to analyze the registration accuracy.

4.1 Performance on the shapes

First, we implement the experiment on the fish shapes. No. 3 fish shape is chosen as the model, which marked as the root node of the heuristic tree. The other similar subjects are linked to the root node directly or indirectly, which depends on the similarity measurement.

To demonstrate that the non-rigid registration method based on dynamic tree could eliminate the wrong pairs, which could get better results than the method based on static tree, the trees are shown as Fig. 4. In the figure, we find No. 45 in the third layer of 4-level static tree is moved to the fourth layer in the tree, which could improve the registration accuracy. Moreover, we find No. 168 has changed to connect to No. 18. The reason is that No. 45 gets worse registration result, which leads No. 168 to worse result. Figure 5 exhibits the compared registration results. The CPD registration results based on 4-level static tree are wrong in Fig. 5d leads to the further mistake in Fig. 5e, while our method can eliminate the potential risk and obtain better results in Fig. 5f, g.

Fig. 4
figure 4

The heuristic tree of 46 fish shapes. (a) 4-level static tree. (b) The final dynamic tree

Full size image
Fig. 5
figure 5

Non-rigid registration results of fish shapes. (a) The model point set. (b) The subject point set no. 45. (c) The subject point set no. 168. (d) Registraton result of (b) using CPD based on 4-level static tree. (e) Registration result of (c) using CPD based on 4-level static tree. (f) Registraion results of (b) using CPD based on the dynamic tree. (g) Registration results of (c) using CPD based on the dynamic tree

Full size image

To provide a quantitative comparison, we respectively use Nos. 3 and 22 point sets as the model point set. Table 1 lists the mean values and 95th percentile errors of both CPD algorithm and CPD based on dynamic tree algorithm. Experimental results show that the mean errors are decreased, which proves that our method significantly improves the precision of non-rigid registration compared with CPD algorithm. The reduction of the 95th percentile errors reveals that inaccurate CPD registration results are remedied via our method, since it is generally caused by large shape difference.

Table 1 Non-rigid registration results of the subjects on the third and forth layers
Full size table

Figure 6 gives the examples of registration results with No. 3 as the model point set. In the figure, Fig. 6a has large shape difference with Nos. 45 and 64 as subjects in Fig. 6b, c. The CPD registration results are completely incorrect in Fig. 6d, e. In our method, these two subjects are both in the fourth layer of the dynamic tree, which means that both of the subjects accomplish their registration. In the experiment, our method performs extremely well which can be seen in Fig. 6f, g.

Fig. 6
figure 6

Non-rigid registration results of fish shapes. (a) The model point set. (b) One subject point set. (c) Another subject point set. (d) Registraton result of (b) by CPD directly. (e) Registration result of (c) by CPD directly. (f) Registraion results of (b) using CPD based on the dynamic tree. (g) Registration results of (c) using CPD based on the dynamic tree

Full size image

4.2 Performance on the character skeletons

The second experiment is conducted on the skeleton of character ‘fo’ captured from the “Vimalakirti Sutra”. In general, skeleton represents the shape of a character. The registration errors are listed in Table 2 with two different model point sets. Some typical registration results are displayed in Fig. 7.

Table 2 Non-rigid registration results of the subjects on the third and deeper layers
Full size table
Fig. 7
figure 7

Non-rigid registration results of character fo’s edges. (a) The model point set. (b) One subject point set. (c) Another subject point set. (d) Registraton result of (b) by CPD. (e) Registration result of (c) by CPD. (f) Registraion results of (b) using CPD based on dynamic tree. (g) Registration results of (c) using CPD based on dynamic tree

Full size image

As shown in Table 2, the registration errors of our method are much smaller. In the figure, Fig. 7b, c are located in the third layer of the dynamic tree while Fig. 7a is the root node, and the registration results of these two subjects are much more precise comparing with CPD algorithm which can be seen in Fig. 7f, g. According to Fig. 7, our method is also able to produce a good alignment. Both table and figure demonstrate that our method has great performance of registration with large shape difference.

4.3 Performance on the character edges

The third experiment is executed on the edges of character ‘fo’. The canny operator is employed to extract the edges. The registration errors are listed in Table 3 with two different model point sets, and Fig. 8 shows several registration results of edges with No. 58 as the model point set. Comparing with skeletons, edges contain much more details of characters and thus are more reliable to represent the character.

Table 3 Non-rigid registration results of the subjects on the third and deeper layers
Full size table
Fig. 8
figure 8

Non-rigid registration results of character fo’s skeletons. (a) The model point set. (b) One subject point set. (c) Another subject point set. (d) Resigtration result of (b) by CPD. (e) Registration result of (c) by CPD. (f) Registration result of (b) using CPD based on dynamic tree. (g) Registration result of (c) using CPD based on dynamic tree

Full size image

In Table 3, both the mean values and 95th percentile errors of our method achieve remarkable results. In the experiment, our method performs extremely well which can be seen in Fig. 8f, g. Moreover, our method gains better results compared with CPD algorithm. In brief, the robustness and accuracy of the registration of point sets with large shape difference are highly improved.

In addition, the registration of ancient characters helps us to distinguish whether the characters in the image database come from one mold, and contributes to the study in the history of movable type printing.

5 Conclusion

We propose the non-rigid registration method based on dynamic tree to solve the registration problem with large shape difference. Firstly, we use the affine ICP algorithm with bidirectional distance to measure the similarity of point sets, and then the CPD algorithm is applied for non-rigid registration during the process of building the dynamic tree. Experiments on a public 2D dataset and Tangut characters reveal that our method significantly improves the robustness and accuracy of non-rigid registration in bearing large deformations. The main contributions of our method are: (1) A large shape difference is divided into several small deformations which are much easier to acquire accurate registration results. (2) Inaccurate registration results are excluded in real-time, which can avoid the error propagation. The method performs well in non-rigid registration with large shape difference, and it will be applied to much more applications in the future, such as medical image registration and movable type printing identification.