Investigating the Instability of Parametric Vibrations of Composite Plates under Arbitrary Pulsating Loads Based on High-Order Plate Theories

The instability of composite plates subjected to an arbitrary periodic dynamic loading is investigated based on Lo’s high-order shear-deformation plate theory. The differential equations of motion of Mathieu-type are formed by Hamilton’s principle and employing the Galerkin method. Using Bolotin’s method, the excitation frequencies of composite plates are evaluated to determine their dynamic stability region and dynamic instability index. Omitting the high-order terms of Lo’s displacement field, the system equations can be simplified to governing equations in the first-order plate theory. The dynamic instability determined by the present theory is compared with results of the first-order plate theory. Results show that high order terms have a significant impact on the dynamic instability of composite plates.

Introduction

Since composite plates can provide a higher strength- and stiffness-to-weight ratios than the traditional metal plates, they are widely used in many engineering fields. The dynamic instability of the plates is a phenomenon that requires special attention in the design of structural components. The instability in the form of parametric resonance may occur when a such structure is subjected to a periodic dynamic loading. How to accurately determine the dynamic instability region of the plates is a very important topic in practical applications. A comprehensive study of dynamic stability problems under periodical loadings has been performed by Bolotin [1]. Vijayaraghavan [2] studied the dynamic instability of cylindrical thin shells subjected to in-plane loads under sinusoidal base excitations. The linear bending theory used in this analysis is sufficient to predict the onset of their dynamic instability.

The dynamic resonance is one of the most important subjects in studying the dynamic instability characteristics of structures. Mohamad [3] presented a broad review on the studies of the dynamic behavior of composite shells. Fazilati [4] investigated the dynamic instability of composite laminated structures subjected to axially harmonic loadings using two types of finite-strip method. Results showed that the present model is capable of predicting the parametric resonance of the structures investigated. The parametric instability of composite curved panels under nonuniform axial loadings were also studied by Ovesy [5] based on the finite-strip method. The static and dynamic components of the load varied according to a parabolic function. Bolotin’s method was used to investigate the effects of loading and geometric parameters on the instability regions. Kao [6] applied Bolotin’s method to studying the dynamic instability of foam-filled sandwich plates under a periodic loading. The dynamic instability index was used to investigate the effects of various parameters affecting the dynamic stability behavior of the plate. Chen [7] investigated the dynamic instability of composite plates subjected to periodic loads based on the first-order theory. Bolotin’s method was used to solve Mathieu–Hill differential equations to determine the dynamic instability region. Darabi [8] studied the nonlinear dynamic instability of composite plates under harmonic loadings. The nonlinear Mathieu–Hill equations were obtained based on the Galerkin method. Then, Bolotin’s method was applied to determining the dynamic instability regions and unstable vibration amplitudes. The dynamic instability behavior of laminated composite sandwich plates was investigated by Sahoo [9] based on the zigzag theory, which takes into account the nonlinear distribution of transverse shear stresses. An efficient finite-element method was developed for studying the dynamic instability. The excitation frequency boundaries of principal instability regions were determined using Bolotin’s method. The dynamic instability of composite plates with variable stiffness under periodic loads was studied by Rasool [10]. A set of Mathieu–Hill equations of motion was obtained by the modal transformation technique and was solved by a multiple scales method to determine the dynamic instability regions associated with various types of resonance. Mohanty [11] studied the dynamic instability of delaminated composite plates under periodic loads by the finite-element method based on the first-order shear deformation plate theory. Bolotin’s method was also employed to evaluate the boundaries of instability zones. Results showed that the increasing delamination shifted the instability region lower excitation frequencies.

However, the classical and first-order plate theories cannot adequately model the behavior of composite structures. Therefore, various high-order plate theories have been proposed to improve their accuracy. Lee [12] analyzed the dynamic stability of laminated composite skew plates under periodic loads based on a high-order plate theory. The dynamic instability regimes were determined by Bolotin’s method, and the influence of the pulsating load on the dynamic instability index was discussed. The dynamic instability of sandwich plates with carbon-nanotube-reinforced face sheets under periodic forces was studied by Sankar [13]. The effect of carbon nanotube volume fraction and core-surface layer thickness on the instability region and its excitation frequency was investigated. Based on first-order and high-order theories, Ramachandra [14] studied the dynamic instability of composite plates under uniform, linear, and parabolic dynamic loads. The dynamic instability regions were determined for various periodic loads using Bolotin’s method. The influences of load types, aspect ratio, and restraint conditions were investigated. Noh [15] investigated the dynamic instability of delaminated composite skew plates subjected to periodic loads by using a high-order plate theory. The boundaries of the unstable regions were obtained by Bolotin’s method. The effects of skew angle, fiber angle, delamination lengths, and static and dynamic load factors on the dynamic instability characteristics were discussed. The dynamic stability of composite skew plates under parabolic and linear periodic loads based on higher order plate theory was studied by Kumar [16]. Following Bolotin’s method, the dynamic unstable regions were evaluated based on a high-order approximation method. The effects of various geometric parameters, loading types, and boundary conditions were investigated. Based on a polynomial highorder plate theory, Adhikari [17] examined the dynamic instability of composite plates under periodic loads with various nonuniform distributions. Mathieu-type equations were formulated and then solved using Bolotin’s method to obtain the dynamic instability regions. The influence of various kinds of nonuniform harmonic loading on the parametric instability behavior of the plates was studied.

The dynamic instability of composite plates has been investigated by many researchers, but studies on the dynamic instability of composite plates under arbitrary periodic loads with bending and normal stress by using a high-order plate theory are rare. Therefore, the present work is devoted to the dynamic vibration instability of composite plates subjected to an arbitrary periodic load based on a high-order Lo, Christensen and Wu [18] plate theory. Hamilton’s principle is utilized to establish the governing partial differential equations of motion, which are then reduced to ordinary differential equations by using the Galerkin method. Employing Bolotin’s method, a set of ordinary differential equations of Mathieu–Hill type is established and solved to obtain the excitation frequencies of composite plates. Their dynamic instability region and dynamic instability index are determined through the excitation frequencies to investigate the dynamic instability behavior of composite plates. The difference between the effects of high-order and first-order plate theories on the dynamic instability regions and indices is studied.

Basic Formulation

Let us establish the dynamic governing equation of a composite plate under the general state of time-varying external force using Hamilton’s principle as described by Brunelle [19], to derive the governing equations of motion of the plate, namely,

$$ \delta {\int}_{t_0}^{t_1}\left({U}_S-{K}_t-{W}_i-{W}_e\right) dt=0, $$

(1)

where ${U}_S={\int}_{V_0}{\upsigma}_{ij}{\varepsilon}_{ij} dV,{K}_t=\frac{1}{2}{\int}_{V_0}\rho {\dot{v}}_i{\dot{v}}_i dV,\kern0.5em {W}_i={\int}_{V_0}{X}_i{v}_i dV,{W}_e={\int}_{S_0}{p}_i{v}_i dS.$

Here, δ is the variation of a function; U_S and K_t are potential and kinetic energies; W_i and W_e are internal and external works; σ_ij and ε_ij are the stress and strain fields; ρ and v_i are the mass density and displacements; X_i is the body force per unit initial volume; pi is the surface force per unit area; V₀ and S₀ are the volume and the boundary surface. Inserting the integral forms of U_S, K_t, W_i, and W_e into Eq. (1), performing variational operations, and assuming that δv_i disappears at times t₀ and t₁, Eq. (1) becomes

$$ {\int}_{t_0}^{t_1}\left[{\int}_{V_0}\left({\sigma}_{ij}\delta {\varepsilon}_{ij}-{X}_i\delta {v}_i-\rho \ddot{v}\delta {v}_i\right) dV-\underset{S_0}{\int}\left({p}_i\delta {v}_i\right) dS\right] dt=0. $$

(2)

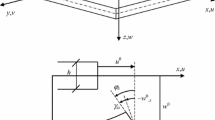
According to the Lo, Christensen and Wu theory, the incremental displacements u,v, and w at any position assume the following forms:

$$ u\left(x,y,z,t\right)={u}_x\left(x,y,t\right)+z{\varphi}_x\left(x,y,t\right)+{z}^2{\xi}_x\left(x,y,t\right)+{z}^2{\phi}_x\left(x,y,t\right), $$

(3)

$$ v\left(x,y,z,t\right)={u}_y\left(x,y,t\right)+z{\varphi}_y\left(x,y,t\right)+{z}^2{\xi}_y\left(x,y,t\right)+{z}^2{\phi}_y\left(x,y,t\right), $$

(4)

$$ w\left(x,y,z,t\right)=w\left(x,y,t\right)+z{\varphi}_z\left(x,y,t\right)+{z}^2{\xi}_z\left(x,y,t\right). $$

(5)

Equations (3)-(5) are obtained by expanding the displacements u,v, and w into Taylor series in terms of the thickness variable z to take into account the parabolic variation of transverse shear strains and the nonlinear change of transverse normal strains across the plate thickness. Therefore, in the Lo, Christensen, and Wu theory, in-plane displacements are expanded into cubic functions of the thickness variable by Taylor series, and the lateral displacement is expanded as a square function. Eleven unknowns, including high-order flexural deformation modes, are considered in the displacement field. Concerning other displacement-based theories in this field, it is worth mentioning that the expansion of different power of the thickness coordinate results in different theories with various unknowns. The simplest is the first-order shear deforma tion theory with five unknowns [20, 21]. A high-order shear deformation theory with seven unknowns was presented by Essenburg [22], and another one with nine unknowns was developed by Pandya [23]. In addition, a third-order shear deformation theory with five unknowns was developed by Levinson [24] and Reddy [25] considering the requirement that the transverse shear stresses have to vanish at the top and bottom surfaces of the plate to reduce the displacement field of nine unknowns to that with five variables. Further, Lo’s high-order transverse shear and normal deformations theory will be designated as NSNT. Ignoring higher order normal strains in Eqs. (3) and (4), and dropping the transverse shear strains in Eq. (5), the displacement field of the simple first-order shear deformation theory (FSDT) is obtained. The stress–strain relationship for a k th layer of a composite plate, made of a monoclinic material ca n be written as

$$ \left[\begin{array}{c}{\sigma}_{xx}\\ {}{\sigma}_{yy}\\ {}\begin{array}{c}{\sigma}_{zz}\\ {}{\sigma}_{yz}\\ {}\begin{array}{c}{\sigma}_{zx}\\ {}{\sigma}_{xy}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{ccc}{C}_{11}& {C}_{12}& {C}_{13}\kern0.5em 0\kern0.5em \begin{array}{cc}0& {C}_{16}\end{array}\\ {}{C}_{12}& {C}_{22}& \begin{array}{ccc}{C}_{23}& 0& \begin{array}{cc}0& {C}_{26}\end{array}\end{array}\\ {}\begin{array}{c}{C}_{13}\\ {}0\\ {}\begin{array}{c}0\\ {}{C}_{16}\end{array}\end{array}& \begin{array}{c}{C}_{23}\\ {}0\\ {}\begin{array}{c}0\\ {}{C}_{26}\end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}{C}_{33}\\ {}0\\ {}\begin{array}{c}0\\ {}{C}_{36}\end{array}\end{array}& \begin{array}{c}0\\ {}{C}_{44}\\ {}\begin{array}{c}{C}_{45}\\ {}0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ {}{C}_{45}\\ {}\begin{array}{c}{C}_{55}\\ {}0\end{array}\end{array}& \begin{array}{c}{C}_{36}\\ {}0\\ {}\begin{array}{c}0\\ {}{C}_{66}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{\varepsilon}_{xx}\\ {}{\varepsilon}_{yy}\\ {}\begin{array}{c}{\varepsilon}_{zz}\\ {}{\varepsilon}_{yz}\\ {}\begin{array}{c}{\varepsilon}_{zx}\\ {}{\varepsilon}_{xy}\end{array}\end{array}\end{array}\right]. $$

(6)

It is assumed that the external forces system applied to the composite plate changes with time in the form

$$ {\sigma}_{ij}={\sigma}_{ij}^n+\frac{2z}{h}{\sigma}_{ij}^m=\left({\sigma}_{ij}^S+{\sigma}_{ij}^D\cos \varpi t\right)+2z\left({\sigma}_{ij}^{Sm}+{\sigma}_{ij}^{Dm}\cos \varpi t\right),\left(i,j=x,y,z\right). $$

(7)

Here, ${\sigma}_{ij}^n$ is the periodic normal or shear stress, and ${\sigma}_{ij}^S$ and ${\sigma}_{ij}^D$ are the corresponding static and dynamic components; ${\sigma}_{ij}^m$ is the periodic pure bending or torsion stress, and ${\sigma}_{ij}^{Sm}$ and ${\sigma}_{ij}^{Dm}$ are the associated static and dynamic components; 𝜛 is the disturbing frequency of the periodic loading. Inserting Eqs. (3)-(7) into Eq. (2), performing partial integrations, removing derivatives from the variation of the displacements, and grouping terms by the displacement variations leads to the following governing equations for the composite plate:

$$ {Q}_{1,x}+{Q}_{2,y}+{\left({R}_1+{R}_5+{R}_{17}\right)}_{,x}+{\left({S}_1+{S}_6+{S}_{17}\right)}_{,y}+{f}_x={I}_1{\ddot{u}}_x+{I}_3{\ddot{\xi}}_x, $$

(8)

$$ {Q}_{2,x}+{Q}_{3,y}+{\left({R}_9+{R}_{13}+{R}_{21}\right)}_{,x}+{\left({S}_9+{S}_{13}+{S}_{21}\right)}_{,y}+{f}_y={I}_1{\ddot{u}}_y+{I}_3{\ddot{\xi}}_y, $$

(9)

$$ {Q}_{4,x}+{Q}_{5,y}+{\left({R}_{30}+{R}_{33}+{R}_{25}\right)}_{,x}+{\left({S}_{30}+{S}_{33}+{S}_{25}\right)}_{,y}+{f}_z={I}_1\ddot{w}+{I}_3{\ddot{\xi}}_z, $$

(10)

$$ {Q}_{6,x}+{Q}_{7,y}+{Q}_4{\left({R}_2+{R}_6+{R}_{18}\right)}_{,x}+{\left({S}_2+{S}_6+{S}_{18}\right)}_{,y}-\left({U}_1+{U}_5+{W}_1\right)+{m}_x={I}_3{\ddot{\varphi}}_x+{I}_5{\ddot{\phi}}_x, $$

(11)

$$ {\displaystyle \begin{array}{c}{Q}_{7,x}+{Q}_{8,y}+{Q}_5{\left({R}_{10}+{R}_{14}+{R}_{22}\right)}_{,x}+{\left({S}_{10}+{S}_{14}+{S}_{22}\right)}_{,y}-\left({U}_9+{U}_{13}+{W}_5\right)\\ {}+{m}_y={I}_3{\ddot{\varphi}}_y+{I}_5{\ddot{\phi}}_y,\end{array}} $$

(12)

$$ {\displaystyle \begin{array}{c}{Q}_{9,x}+{Q}_{10,y}+{Q}_{11}{\left({R}_{31}+{R}_{34}+{R}_{36}\right)}_{,x}\\ {}+{\left({S}_{31}+{S}_{34}+{S}_{36}\right)}_{,y}-\left({V}_1+{V}_4+{W}_9\right)+{m}_z={I}_3{\ddot{\varphi}}_z,\end{array}} $$

(13)

$$ {\displaystyle \begin{array}{c}{Q}_{12,x}+{Q}_{13,y}-2{Q}_9+{\left({R}_3+{R}_7+{R}_{19}\right)}_{,x}\\ {}+{\left({S}_3+{S}_7+{S}_{19}\right)}_{,y}-2\left({U}_2+{U}_6+{W}_2\right)+{n}_x={I}_3{\ddot{u}}_z+{I}_5{\ddot{\xi}}_z,\end{array}} $$

(14)

$$ {Q}_{13,x}+{Q}_{14,y}-2{Q}_{10}+{\left({R}_{11}+{R}_{15}+{R}_{23}\right)}_{,x}+{\left({S}_{11}+{S}_{15}+{S}_{23}\right)}_{,y}+{n}_y={I}_3{\ddot{u}}_y+{I}_5{\ddot{\xi}}_y, $$

(15)

$$ {\displaystyle \begin{array}{c}{Q}_{15,x}+{Q}_{16,y}-2{Q}_{17}+{\left({R}_{32}+{R}_{35}+{R}_{27}\right)}_{,x}\\ {}+{\left({S}_{32}+{S}_{35}+{S}_{27}\right)}_{,y}-2\left({V}_2+{V}_5+{W}_{10}\right)+{n}_z={I}_3\ddot{w}+{I}_5{\ddot{\xi}}_z,\end{array}} $$

(16)

$$ {\displaystyle \begin{array}{c}{Q}_{18,x}+{Q}_{19,y}-3{Q}_{15}+{\left({R}_4+{R}_8+{R}_{20}\right)}_{,x}\\ {}+{\left({S}_4+{S}_8+{S}_{20}\right)}_{,y}-3\left({U}_3+{U}_7+{W}_3\right)+{q}_x={I}_5{\ddot{\varphi}}_x+{I}_7{\ddot{\phi}}_x,\end{array}} $$

(17)

$$ {\displaystyle \begin{array}{c}{Q}_{19,x}+{Q}_{20,y}-3{Q}_{16}+{\left({R}_{12}+{R}_{16}+{R}_{24}\right)}_{,x}\\ {}+{\left({S}_{12}+{S}_{16}+{S}_{24}\right)}_{,y}-3\left({U}_{11}+{U}_{15}+{W}_7\right)+{q}_y={I}_5{\ddot{\varphi}}_y+{I}_7{\ddot{\phi}}_y,\end{array}} $$

(18)

where Q are related to the strain–displacement of the composite plate; the terms R, S,U,V, and W are arbitrary external forces associated with initial stresses; I are the inertia-related terms; f_x, f_y, f_z, m_x, m_y, m_z, n_x, n_y, n_z, q_x, and q_y are body forces and lateral loads. More detailed information about the relevant parameters in Eqs. (8)-(18) is given in the Appendix, which is recalled and rewritten from [26].

Solution Procedure

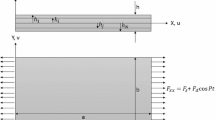
It is difficult to give results for all cases, because the dynamic behavior of the composite plate studied in this paper is affected by too many parameters. Therefore, the case studied is the dynamics of a simply supported cross-ply laminated plate subjected to a spatially uniform periodic in-plane stress system, which is composed of a pulsating uniaxial stress and a pure bending stress. The lateral external load and body force are set to zero. Therefore, the periodic stress system (7) becomes

$$ {\sigma}_{xx}={\sigma}_{xx}^n+\frac{2z{\sigma}_{xx}^m}{h}{\sigma}_n+2z{\sigma}_m/h. $$

(19)

Here, σ_n = σ^S + σ^D cos ϖt and σ_m = σ^Sm + σ^Dm cos ϖt are the normal and bending stresses, respectively, σ^S, σ^Sm, and σ^D, σ^Dm are the corresponding static dynamic components assumed to be constants. The nonzero periodic loads are ${N}_{xx}=h{\sigma}_n,{M}_{xx}=S{h}^2{\sigma}_m/6,{M}_{xx}^{\ast }={h}^3{\sigma}_n/12,{P}_{xx}=S{h}^2{\sigma}_n/40,{P}_{xx}^{\ast }={h}^5{\sigma}_n/80,{R}_{xx}=S{h}^6{\sigma}_n/224$, and ${R}_{xx}^{\ast }={h}^7{\sigma}_n/448$. In the ratio S = σ_m/σ_n, σ_m and σ_n are periodic bending normal stresses.

Regarding the composite plate with simply supported edges, displacement field (20) that satisfying geometric boundary conditions can be expressed as follows.

$$ {\displaystyle \begin{array}{c}{u}_x=\sum \sum h{U}_{mm}\cos \left( m\pi x/a\right)\sin \left( n\pi y/b\right),\\ {}{u}_y=\sum \sum h{V}_{mm}\sin \left( m\pi x/a\right)\cos \left( n\pi y/b\right),\\ {}\begin{array}{c}w=\sum \sum h{W}_{mm}\sin \left( m\pi x/a\right)\sin \left( n\pi y/b\right),\\ {}{\varphi}_x=\sum \sum {\psi}_{xmn}\cos \left( m\pi x/a\right)\sin \left( n\pi y/b\right),\\ {}\begin{array}{c}{\varphi}_y=\sum \sum {\psi}_{ymn}\sin \left( m\pi x/a\right)\cos \left( n\pi y/b\right),\\ {}{\varphi}_z=\sum \sum {\psi}_{zmn}\sin \left( m\pi x/a\right)\sin \left( n\pi y/b\right),\\ {}\begin{array}{c}{\xi}_x=\sum \sum \left({\zeta}_{xmn}/h\right)\cos \left( m\pi x/a\right)\sin \left( n\pi y/b\right),\\ {}{\xi}_y=\sum \sum \left({\zeta}_{ymn}/h\right)\sin \left( m\pi x/a\right)\cos \left( n\pi y/b\right),\\ {}\begin{array}{c}{\xi}_z=\sum \sum \left({\zeta}_{zmn}/h\right)\sin \left( m\pi x/a\right)\sin \left( n\pi y/b\right),\\ {}{\phi}_x=\sum \sum \left({\Phi}_{xmn}/{h}^2\right)\cos \left( m\pi x/a\right)\sin \left( n\pi y/b\right),\\ {}{\phi}_y=\sum \sum \left({\Phi}_{ymn}/{h}^2\right)\sin \left( m\pi x/a\right)\cos \left( n\pi y/b\right).\end{array}\end{array}\end{array}\end{array}\end{array}} $$

(20)

Inserting the displacement field and periodic loads into governing equations (8)-(18), employing the Galerkin method, and grouping coefficients, the governing matrix equation of motion is obtained in the form

$$ {\displaystyle \begin{array}{c}\left[M\right]\left[\ddot{\Delta}\right]+\left\{\left[C\right]+\left[G\right]\right\}\kern0.5em \left[\Delta \right]=0,\\ {}\left\{\Delta \right\}={\left[{U}_{mn},{V}_{mn},{W}_{mn},{\psi}_{xmn},{\psi}_{ymn},{\psi}_{zmn},{\zeta}_{xmn},{\zeta}_{ymn},{\zeta}_{zmn},{\Phi}_{xmn},{\Phi}_{ymn}\right]}^T,\end{array}} $$

(21)

where ∆ is a time-dependent displacement vector of HSNT. The time-dependent displacement vector of FSDT is [U_mn, V_mn, W_mn, ψ_xmn, ψ_ymn]^T. [M], [C], and [G] are the inertia, elastic stiffness, and geometric stiffness matrices, respectively. Matrix equation (21) can be used to analyze the eigenvalue problems of free vibration, static buckling stability, and dynamic instability.

Neglecting the in-plane external loads and the [G] matrix and inserting Δ(t) = Δe^iωt into Eq. (21), Eq. (21) reduces to

$$ \left\{\left[C\right]-{\omega}^2\left[M\right]\right\}\kern0.5em \left[\Delta \right]=0, $$

(22)

which is the eigenvalue equation associated with free vibrations of the composite plate. The condition for the existence of a nonzero solution is that the determinant of the coefficient matrix has to be equal to zero, namely,

$$ \left|\left[C\right]-{\omega}^2\left[M\right]\right|=0 $$

(23)

from which the natural frequency ω can be found,

To analyze the static buckling, the matrix of inertia terms of Eq. (21) is asumed zero. The eigenvalue equation for the static buckling load N_xx is

$$ \left\{\left[C\right]+{N}_{xx}{\left[G\right]}^{\ast}\right\}\kern0.75em \left[\Delta \right]=0. $$

(24)

Likewise, the static buckling load can be obtained by equating the determinant of the coefficient matrix of Eq. (24) to zero. The nonzero periodic load N_xx is obtained by integrating Eq. (19), which gives that

$$ {N}_{xx}=h{\sigma}_n=h\left({\sigma}^S+{\sigma}^D\cos \varpi t\right)={\alpha}_S{P}_{cr}+{\alpha}_D{P}_{cr}\cos \varpi t $$

(25)

where P_c , α_S, and α_D are the buckling load and parameters of static and dynamic loads, respectively. Inserting Eq. (25) into Eq. (21) leads to the relation

$$ \left[\mathrm{M}\right]\left[\ddot{\Delta}\right]+\left\{\left[C\right]+{\alpha}_S{P}_{cr}\left[G\right]+{\alpha}_D{P}_{cr}\left[G\right]\cos \varpi t\right\}\ \left[\Delta \right]=0, $$

(26)

which is a second-order ordinary differential equation of Mathieu–Hill type. Then, Bolotin’s method is used to find the boundaries between the stable and the unstable regions of the parametrically excited structure through the periodic solutions of period T and 2T in Fourier series, where T = 2π / w. The periodic solutions ∆ of Eq. (26) with periods T and 2T can be found by Fourier series as

$$ \Delta =\sum_{k=\mathrm{1.3.5}\dots}^{\infty}\left({a}_k\sin \frac{k\varpi t}{2}+{b}_k\cos \frac{k\varpi t}{2}\right), $$

(27)

$$ \Delta =\sum_{k=\mathrm{0.2.4}\dots}^{\infty}\left({a}_k\sin \frac{k\varpi t}{2}+{b}_k\cos \frac{k\varpi t}{2}\right), $$

(28)

where a_k and b_k are arbitrary time-invariant constants. Inserting expansions (27) and (28) into Eq. (26) and grouping the sin and cosine parts, respectively, two sets of linear algebraic equations in a_k and b_k are obtained. Generally, the primary unstable region defined by the solution with a period 2T is much larger than the secondary unstable region defined by the solution with a period T . Therefore, the primary instability region with the period 2T has the greatest practical significance and gives a sufficiently accurate solution. Since the first-order approximation to a₁ and b₁ of the primary instability region can be solved with a sufficient accuracy, the first-order solution of the primary instability region can be obtained as

$$ \left[C\right]+{\alpha}_S{P}_{cr}\left[G\right]\pm \frac{1}{2}{\alpha}_D{P}_{cr}\left[G\right]-\frac{1}{4}{\varpi}^2\left[M\right]=0. $$

(29)

Analyses and Discussion

Let us investigate the dynamic instability of composite plates based on a high-order plate theory. The material properties of laminates are E_x / E_y = open, E_y = E_z, G_xy = G_xz = 0.6E_y, G_yz = 0.5E_y, and υ_xy = υ_xz = υyz = 0.25. The current HSNT can be simplified to FSDT by neglecting the higher-order terms and introducing a shear correction factor into the resultants of shear stresses. In the following, the results obtained based on the HSNT and FSDT are presented to show the difference between the two theories. The nondimensional parameter $\Omega =\varpi {b}^2/h\sqrt{\rho /{E}_y}$ of excitation frequency and the dynamic instability index Ω_DI = 100ΔΩ/(ω_nf/P_cr) are utilized in the following study. Among them, ${\omega}_{nf}=\omega {b}^2/h\sqrt{\rho /{E}_y}$ and P_cr = 10σ_nb²/E_yh⁴ are the fundamental natural frequency and critical buckling load, respectively; ΔΩ = Ω^U − Ω^L is the width of the instability region bounded by the upper Ω^U and lower Ω_L excitation frequency. The dynamic instability index Ω_{_DI} quantifies the instability measure through the instability area, natural frequency, and buckling load.

To verify the accuracy of the present model, some representative examples were investigated. First, the free vibration of antisymmetric cross-ply laminated plates according to FSDT and HSNT is considered. Table 1 present the natural frequencies of laminated plates with various layer numbers and modulus ratios. The frequencies calculated by the present model agree well with those by Whitney [27] and Kant [28]. It can be seen in Table 1 that the frequency increases with E_x / E_y and layer number. Second, the dynamic stability of a symmetrically four-layer cross-ply laminate plate under various static and dynamic loads was studied. Table 2 show the upper and lower excitation frequencies of the laminate plate by using the HSNT along with the results obtained by Wang [29] and Chen [30] based on the FSDT. The numerical values of HSNT were in a good agreement with those of FSDT. As seen in Table 2, with increasing dynamic load (α_S = 0), the upper excitation frequency increases but the lower one reduces. Additionally, the upper and lower excitation frequencies decrease as both the static and dynamic loads increase. The results obtained by the present method match well with other research results. It verifies the reliability and accuracy of the present computer program.

Table 1. Natural Frequencies of Antisymmetric Cross-Ply Square Laminated Plates with Various Numbers of Layers and Modulus Ratios. (a/b = 1, a/h = 5)

Table 2. Excitation Frequencies for a Symmetrical Four-Layer Cross-Ply Laminated Plates with Various Static and Dynamic Load Parameters

Figure 1 presents the effect of static loading on the ratio Ω /ω_nf excitation frequencies. The plot shows that excitation frequency first appears near 2 at α_S = α_D = 0. It can be observed that, as the compressive static (α_S < 0) load increases, the upper and lower excitation frequency ratios decrease. However, an increasing tensile static load leads to an opposite effect. The width between boundaries of both excitation frequency ratios increases with growing static load parameter. Meanwhile, the static compression load reduces the stiffness of the plate, so it has a more significant influence on the boundary width than the static tension load. The effect of dynamic loads on the excitation frequency ratio of the instability region is shown in Fig. 2. Under a compressive static load, the initial excitation frequency ratio is smaller than 2 (α_D = 0), while under a tensile static load, the initial excitation frequency ratio is greater than 2. An increase in the dynamic load parameter increases the upper excitation frequency ratio, reduces the lower one, and enlarges the width of the unstable region. The dynamic load parameter has a greater influence on the excitation frequency ratio than the static load parameter. As shown in Figs. 1 and 2, the width of the unstable region obtained by FSDT is larger than that given by HSNT, especially under a compressive static load.

Fig. 1.

Effect of static loads on Ω / ω_nf (a/b = 1, a/h = 10, n = 1, α_D /|α_S|= 0.3, S =0, α_S < 0 tensile load, and α_S > 0 compressive load).

Fig. 2.

Effect of dynamic loads on Ω / ω_nf (a/b = 1, a/h = 10, n =1, S = 0, α_D /|α_S|= 0.3.

The effects of layer number and modulus ratio on the excitation frequency, instability region, and dynamic instability index of antisymmetric cross-ply laminated plates under the static load parameter α_S = 0.5 and load parameter ratio α_D /α_S = 0.3 are presented in Table 3. As the modulus ratio increases, the excitation frequencies and instability region grow, but the dynamic instability index diminishes. With increasing number of layers, the excitation frequencies and unstable region grow, but the dynamic instability index first increases and then decreases. For plates with different numbers of layers and modulus ratios, there is no obvious difference between the values obtained based on the HSNT and FSDT for the respective excitation frequency, instability area, and dynamic instability index, except for the instability area of the plate with two layer laminates and higher modulus ratio. The size of the instability region evaluated by FSDT is greater than that of HSNT, and the difference increases with increasing modulus ratio and decreasing layer number.

Table 3. Excitation Frequencies, Instability Regions, and Dynamic Instability Index of Antisymmetric Cross-Ply Laminated Plates with Various Numbers of Layer and Modulus Ratios (a/b = 1, a/h = 5, α_S =0.5, α_D /α_S = 0.3)

Tables 4 and 5 show the effects of static and dynamic loads on the dynamic instability characteristics of laminated plates with various modulus ratio. As can be seen, when the static or dynamic load increases, both the instability region and dynamic instability index increase. Thus, the composite plate is more dynamically unstable when it is subjected to a high static or dynamic load. An increase in the modulus ratio enhances the rigidity of the laminated plate, decreases the dynamic instability index and make the laminated plate dynamically more stable. An increase in the static or dynamic load enhances the difference between calculation results of FSDT and HSNT, which is most obvious at low excitation frequencies and an unstable region. It can be seen in Tables 4 and 5 that the difference between FSDT and HSNT results caused by the compressive static load is significantly greater than by a dynamic load. This is because, when studying the influence of a dynamic load in Table 5, the static load applied was relatively small. In the case of a large static load, an increasing dynamic load also increases the difference between FSDT and HSNT results. Figures 3 and 4 present the effects of modulus ratios on the instability regions of laminated plates under various static and dynamic loads, based on the HSNT. Whether a laminated plate is under a tensile or compressive static load, increasing the modulus ratio always enhances the instability region. The unstable region of a laminated plate under a compressive load is larger than that under a tensile load, and as the magnitude of the applied load increases, the difference between them becomes greater. The effects of modulus ratios on the dynamic instability index are presented in Figs. 5 and 6. As is seen, increasing the modulus ratio decreases the dynamic instability index, which is the opposite of the influence of the modulus ratio on the instability region. The influence of a static load on the dynamic instability index is similar to that on the instability region, as is seen in Figs. 3 and 4.

Table 4. Effect of the Modulus Ratio E_x / E_y on the Excitation Frequencies, Instability Regions, and Dynamic Instability Index of Laminated Plates under Various Static Loads (a/b = 1, a/h = 5, n =1, S =0, α_D /α_S = 0.3)

Table 5. Effect of the Modulus Ratio E_x / E_y on the Excitation Frequencies. Instability Regions. and Dynamic Instability Index of Laminated Plates under Various Dynamic Loads (a/b = 1. a/h = 5. n = 1. S = 0. α_S = 0.1)

Fig. 3.

Effect of modulus ratios on the instability regions at various static load types. (a/b = 1, a/h = 5, n = 1, S =0, α_D /|α_S|= 0.3).

Fig. 4.

Effect of modulus ratios on the instability region at various dynamic loads. (a/b = 1, a/h = 5, n = 1, S = 0).

Fig. 5.

Effect of modulus ratios on the dynamic instability index at various static load types. (a/b = 1, a/h = 5, n = 1, S = 0, α_D/|α_S|= 0.3).

Fig. 6.

Effect of modulus ratios on the dynamic instability index at various dynamic loads (a/b = 1, a/h = 5, n = 1, S = 0).

In addition, a compressive static load increases the dynamic instability index more than a tensile static load, which means that a compressive load increases the instability of the laminated plate more than a tensile one.

The effect of the load parameter ratio α_D /α_S on the excitation frequency, instability region, and dynamic instability index of the laminated plates under different static loads is illustrated in Table 6. As the load parameter ratio increases, the upper excitation frequency, instability region and dynamic instability index increase, but the lower excitation frequency shows a reverse trend. When the magnitude of the static load in compression or tension increases, the instability region and the dynamic instability index increase. As can be seen in Table 6, the difference between results of FSDT and HSNT increases with the increasing magnitude of the static load. When a laminated plate with a high load parameter ratio is subjected to a high compressive static load, the discrepancy between the two theories becomes more pronounced. Variation trends of the instability region and dynamic instability index against the static loads for the laminated plates with different load parameter ratios and modulus ratios based on HSNT are presented in Figs. 7 and 8, respectively. At various load parameter ratios, the influence of the compressive load on the instability area and dynamic instability index is greater than that of the tensile load. Regardless the value of the load parameter ratio, an increase in the modulus ratio increases the instability region, but decreases the dynamic ins tability index.

Table 6. Effect of the Load Parameter Ratio on the Excitation Frequencies. Instability Regions. and Dynamic Instability Index of Laminated Plates under Various Dynamic Loads (a/b = 1. a/h = 5. n = 1. S = 0. E_x / E_y = 40)

Fig. 7.

Effect of the load parameter ratio on the instability region at various static loads (a/b = 1, a/h = 5, n = 1, S = 0).

Fig. 8.

Effect of the load parameter ratio on the dynamic instability index at various static loads (a/b = 1, a/h = 5, n = 1, S = 0).

Tables 7 and 8 show the effect of bending stress on the dynamic instability of laminated plates subjected to various static and dynamic loads. With increasing bending stress ratio, the excitation frequency decreases, but the instability region and dynamic instability index increase. However, the effect of the bending stress ratio is small. As the bending stress ratio increases, the difference between the calculates results based on FSDT and HSNT decreases for the excitation frequency and the unstable region and increases for the dynamic instability index. Meanwhile, the greater the bending stress ratio, the more obvious the difference between the results of FSDT and HSNT for the dynamic instability index. For example, for laminated plates with a bending stress S = 10 and load parameters α_D /α_S = 0.3 and α_S ≥ 0.3, or α_S = 0.3 and α_D ≥ 0.2, the difference between the dynamic instability indices obtained by FSDT and HSNT exceeds 10%. The plots of the bending stress ratio versus the dynamic instability index for the laminated plates under different static and dynamic loads based on the HSNT are shown in Figs. 9 and 10. The results reveal that, when a laminated plate is under a higher bending stress ratio, the compressive static load has a greater hardening effect on the dynamic instability index , but the tensile static load has a reverse effect. In addition, it can be found that the difference between the calculated results under the respective tensile and compressive static load with the same magnitude becomes greater when the bending stress increases. Hence, the laminated plate is more dynamically stable, because it is under a tensile load and a higher bending stress.

Table 7. Effect of the Bending Stress Parameter on the Excitation Frequencies, Instability Regions and Dynamic Instability Index of Laminated Plates under Various Compressive Loads (a/b = 1, a/h = 5, n = 1, E_x / E_y = 40, α_D /α_S = 0.3)

Table 8 Effect of the Bending Stress Parameter on the Excitation Frequencies, Instability Regions and Dynamic Instability Index of Laminated Plates under Various Dynamic Loads (a/b = 1, a/h = 5, n = 1, E_x / E_y = 40, α_S = 0.3)

Fig. 9.

Effect of the bending stress parameter on the dynamic instability index at various static loads (a/b = 1, a/h = 5, E_x / E_y = 40, n = 1, α_D /|α_S|= 0.3).

Fig. 10.

Effect of the bending stress parameter on the dynamic instability index at various dynamic loads (a/b = 1, a/h = 5, E_x / E_y = 40, n = 1, α_S = 0.1).

Conclusions

The dynamic behavior of laminate plates under a periodic load based on the higher order plate theory has been described and examined. From the results obtained, the following conclusions can be drawn.

1. The static and, dynamic loads and the modulus ratio have a significant effect on the excitation frequency, instability region, and dynamic instability index. The bending stress has only a slight influence.

2. As the modulus ratio decreases under a static load in tension or compression, the instability region increases and the dynamic instability index decreases. Under a static compressive load, the bending stress enhances the instability region and the dynamic instability index. However, under a static tensile load, the bending stress has an opposi te effect.

3. As the static load, dynamic load or the modulus ratio increases, the difference between the results by FSDT and HSNT becomes more pronounced. This is especially significant for laminated plates under a compressing static load. The HSNT theory has an important influence on the instability region and dynamic instability, especially for laminated plates with a high modulus ratio, bending stress, and static and dynamic loads.

Appendix

Expressions of Q.

$$ {\displaystyle \begin{array}{c}\left[\begin{array}{c}\left[{X}_1\right]\\ {}\left[{X}_2\right]\\ {}\begin{array}{c}{Q}_{11}\\ {}\left[{X}_3\right]\\ {}\begin{array}{c}{Q}_{17}\\ {}\left[{X}_4\right]\end{array}\end{array}\end{array}\right]=\left[\begin{array}{ccc}\left[{A}_1\right]& \left[{B}_1\right]& \begin{array}{ccc}\left[{A}_2\right]& \left[{D}_1\right]& \begin{array}{cc}2\left[{B}_1\right]& \left[{E}_1\right]\end{array}\end{array}\\ {}\left[{B}_1\right]& \left[{D}_1\right]& \begin{array}{ccc}\left[{B}_2\right]& \left[{E}_1\right]& \begin{array}{cc}2\left[{D}_2\right]& \left[{F}_1\right]\end{array}\end{array}\\ {}\begin{array}{c}\left[{A}_3\right]\\ {}\left[{D}_1\right]\\ {}\begin{array}{c}\left[{B}_3\right]\\ {}\left[{E}_1\right]\end{array}\end{array}& \begin{array}{c}\left[{B}_3\right]\\ {}\left[{E}_1\right]\\ {}\begin{array}{c}\left[{D}_3\right]\\ {}\left[{F}_1\right]\end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}{A}_{33}\\ {}\left[{D}_2\right]\\ {}\begin{array}{c}{B}_{33}\\ {}\left[{E}_2\right]\end{array}\end{array}& \begin{array}{c}\left[{D}_3\right]\\ {}\left[{F}_1\right]\\ {}\begin{array}{c}\left[{E}_3\right]\\ {}\left[{G}_1\right]\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}2{B}_{33}\\ {}2\left[{E}_2\right]\\ {}\begin{array}{c}2{D}_{33}\\ {}2\left[{F}_2\right]\end{array}\end{array}& \begin{array}{c}\left[{E}_3\right]\\ {}\left[{G}_1\right]\\ {}\begin{array}{c}\left[{F}_3\right]\\ {}\left[{H}_1\right]\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}\left[{T}_1\right]\\ {}\left[{T}_2\right]\\ {}\begin{array}{c}\left[{\varphi}_z\right]\\ {}\left[{T}_3\right]\\ {}\begin{array}{c}\left[{\xi}_z\right]\\ {}\left[{T}_4\right]\end{array}\end{array}\end{array}\right]\\ {}\left[\left[\begin{array}{c}{X}_5\\ {}{X}_6\\ {}{X}_7\end{array}\right]\right]=\left[\begin{array}{ccc}\left[{A}_4\right]& \left[{A}_4\right]& \begin{array}{ccc}\left[{B}_4\right]& 2\left[{B}_4\right]& \begin{array}{cc}\left[{D}_4\right]& 3\left[{D}_4\right]\end{array}\end{array}\\ {}\left[{B}_4\right]& \left[{B}_4\right]& \begin{array}{ccc}\left[{D}_4\right]& 2\left[{D}_4\right]& \begin{array}{cc}\left[{E}_4\right]& 3\left[{E}_4\right]\end{array}\end{array}\\ {}\left[{D}_4\right]& \left[{D}_4\right]& \begin{array}{ccc}\left[{E}_4\right]& 2\left[{E}_4\right]& \begin{array}{cc}\left[{F}_4\right]& 3\left[{F}_4\right]\end{array}\end{array}\end{array}\right]\left[\left[{X}_8\right]\right],\end{array}}, $$

where

$$ {\displaystyle \begin{array}{c}\left[{X}_1\right]={\left[{Q}_1{Q}_2{Q}_3\right]}^T,\left[{X}_2\right]={\left[{Q}_6{Q}_7{Q}_8\right]}^T,\left[{X}_3\right]={\left[{Q}_{12}{Q}_{13}{Q}_{14}\right]}^T,\\ {}\left[{X}_4\right]={\left[{Q}_{18}{Q}_{19}{Q}_{20}\right]}^T,\left[{X}_5\right]={\left[{Q}_4{Q}_5\right]}^T,\left[{X}_6\right]={\left[{Q}_9{Q}_{10}\right]}^T,\left[{X}_7\right]={\left[{Q}_{15}{Q}_{16}\right]}^T,\\ {}\begin{array}{c}\left[\left[{X}_8\right]\right]={\left[\left[{T}_5\right]\left[{T}_6\right]\left[{T}_7\right]\left[{T}_8\right]\left[{T}_9\right]\left[{T}_{10}\right]\right]}^T,\\ {}\left[{T}_1\right]={\left[{u}_{x,x}{u}_{x,y}{u}_{y,x}{u}_{y,y}\right]}^T,\left[{T}_2\right]={\left[{\varphi}_{x,x}{\varphi}_{x,y}{\varphi}_{y,x}{\varphi}_{y,y}\right]}^T,\left[{T}_3\right]={\left[{\xi}_{x,x}{\xi}_{x,y}{\xi}_{y,x}{\xi}_{y,y}\right]}^T,\\ {}\begin{array}{c}\left[{T}_4\right]={\left[{\phi}_{x,x}{\phi}_{x,y}{\phi}_{y,x}{\phi}_{y,y}\right]}^T,\left[{T}_5\right]={\left[{w}_{z,x}{w}_{z,y}\right]}^T,\left[{T}_6\right]={\left[{\varphi}_x{\varphi}_y\right]}^T,\left[{T}_7\right]={\left[{\varphi}_{z,x}{\varphi}_{z,y}\right]}^T,\\ {}\left[{T}_8\right]={\left[{\xi}_x{\xi}_y\right]}^T,\left[{T}_9\right]={\left[{\xi}_{z,x}{\xi}_{z,y}\right]}^T,\left[{T}_6\right]={\left[{\phi}_x{\phi}_y\right]}^T,\end{array}\end{array}\end{array}} $$

Matrices [A_i], [B_i], [D_i], [E_i], [F_i], [G_i], and [H_i] can be obtained by the following expressions.

$$ {\displaystyle \begin{array}{c}\left[{\Gamma}_1\right]=\left[\begin{array}{ccc}{\Gamma}_{11}& {\Gamma}_{16}& \begin{array}{cc}{\Gamma}_{16}& {\Gamma}_{12}\end{array}\\ {}{\Gamma}_{16}& {\Gamma}_{66}& \begin{array}{cc}{\Gamma}_{66}& {\Gamma}_{26}\end{array}\\ {}{\Gamma}_{12}& {\Gamma}_{26}& \begin{array}{cc}{\Gamma}_{26}& {\Gamma}_{22}\end{array}\end{array}\right],\Gamma =A,B,D,E,F,{G}^{\ast },H,\\ {}\left[{\Gamma}_2\right]={\left[{\Gamma}_{13}{\Gamma}_{36}{\Gamma}_{23}\right]}^T,\Gamma =A,B,D,E,F,\\ {}\begin{array}{c}\left[{\Gamma}_3\right]={\left[{\Gamma}_{13}{\Gamma}_{36}{\Gamma}_{36}{\Gamma}_{23}\right]}^T,\Gamma =A,B,D,E,F,\\ {}\left[{\Gamma}_4\right]=\left[\begin{array}{cc}{\Gamma}_{55}& {\Gamma}_{45}\\ {}{\Gamma}_{45}& {\Gamma}_{55}\end{array}\right],\Gamma =A,B,D,E,F,\end{array}\end{array}} $$

where

$$ \left({A}_{ij},{B}_{ij},{D}_{ij},{E}_{ij},{G}_{ij},{H}_{ij}\right)=\int {C}_{ij}\left(1,z,{z}^2,{z}^3,{z}^4,{z}^5,{z}^6\right) dz\left(i,j=1,2,3,4,5,6\right). $$

Here, C_ij is the stiffness matrix of elastic constants. A_ij, B_ij, D_ij, E_ij, F_ij,G_ij, and H_ij are the matrices of laminate stiffness coefficients. The expressions of terms R, S,U,V, and W are

$$ {\displaystyle \begin{array}{c}\left\{{O}_1\right\}=\left[{\Sigma}_{xx}\right]\left\{{\Delta}_{xx}\right\},\left\{{O}_2\right\}=\left[{\Sigma}_{xy}\right]\left\{{\Delta}_{xy}\right\},\left\{{O}_3\right\}=\left[{\Sigma}_{xx}\right]\left\{{\Delta}_{yx}\right\},\\ {}\left\{{O}_4\right\}=\left[{\Sigma}_{xy}\right]\left\{{\Delta}_{yy}\right\},\left\{{O}_5\right\}=\left[{\Sigma}_{yy}\right]\left\{{\Delta}_{xy}\right\},\left\{{O}_6\right\}=\left[{\Sigma}_{xy}\right]\left\{{\Delta}_{xx}\right\},\\ {}\begin{array}{c}\left\{{O}_7\right\}=\left[{\Sigma}_{yy}\right]\left\{{\Delta}_{yy}\right\},\left\{{O}_8\right\}=\left[{\Sigma}_{xy}\right]\left\{{\Delta}_{yx}\right\},\left\{{O}_9\right\}=\left[{\Sigma}_{xz}\right]\left\{{\Delta}_{zx}\right\},\\ {}\left\{{O}_{10}\right\}=\left[{\Sigma}_{yz}\right]\left\{{\Delta}_{zx}\right\},\left\{{O}_{11}\right\}=\left[{\Sigma}_{xz}\right]\left\{{\Delta}_{zy}\right\},\left\{{O}_{12}\right\}=\left[{\Sigma}_{yz}\right]\left\{{\Delta}_{zy}\right\},\\ {}\begin{array}{c}\left\{{O}_{13}\right\}=\left[{\upgamma}_{xx}\right]\left\{{\Delta}_x\right\},\left\{{O}_{14}\right\}=\left[{\upgamma}_{xy}\right]\left\{{\Delta}_y\right\},\left\{{O}_{15}\right\}=\left[{\upgamma}_{xy}\right]\left\{{\Delta}_x\right\},\\ {}\left\{{O}_{16}\right\}=\left[{\upgamma}_{yy}\right]\left\{{\Delta}_y\right\},\left\{{O}_{17}\right\}=\left[{\Omega}_{xz}\right]\left\{{\pi}_x\right\},\left\{{O}_{18}\right\}=\left[{\Omega}_{yz}\right]\left\{{\pi}_z\right\},\\ {}\begin{array}{c}\left\{{O}_{19}\right\}=\left[{\Sigma}_{zx}\right]\left\{{\Delta}_{xx}\right\},\left\{{O}_{20}\right\}=\left[{\Sigma}_{zy}\right]\left\{{\Delta}_{xy}\right\},\left\{{O}_{21}\right\}=\left[{\Sigma}_{zz}\right]\left\{{\Delta}_{zx}\right\},\\ {}\left\{{O}_{22}\right\}=\left[{\Sigma}_{zx}\right]\left\{{\Delta}_{yx}\right\},\left\{{O}_{23}\right\}=\left[{\Sigma}_{zy}\right]\left\{{\Delta}_{yy}\right\},\left\{{O}_{24}\right\}=\left[{\Sigma}_{zz}\right]\left\{{\Delta}_{zy}\right\},\\ {}\left\{{O}_{25}\right\}=\left[{\upgamma}_{zx}\right]\left\{{\Delta}_x\right\},\left\{{O}_{26}\right\}=\left[{\upgamma}_{zy}\right]\left\{{\Delta}_y\right\},\left\{{O}_{27}\right\}=\left[{\Omega}_{zz}\right]\left\{{\pi}_z\right\},\end{array}\end{array}\end{array}\end{array}} $$

where

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\begin{array}{c}\left\{{O}_1\right\}=\left\{{R}_1,{R}_2,{R}_3,{R}_4\right\},\left\{{O}_2\right\}=\left\{{R}_5,{R}_6,{R}_7,{R}_8\right\},\left\{{O}_3\right\}=\left\{{R}_9,{R}_{10},{R}_{11},{R}_{12}\right\},\\ {}\left\{{O}_4\right\}=\left\{{R}_{13},{R}_{14},{R}_{15},{R}_{16}\right\},\left\{{O}_5\right\}=\left\{{S}_1,{S}_2,{S}_3,{S}_4\right\},\left\{{O}_6\right\}=\left\{{S}_5,{S}_6,{S}_7,{S}_8\right\},\\ {}\begin{array}{c}\left\{{O}_7\right\}=\left\{{S}_9,{S}_{10},{S}_{11},{S}_{12}\right\},\left\{{O}_8\right\}=\left\{{S}_{13},{S}_{14},{S}_{15},{S}_{16}\right\},\left\{{O}_9\right\}=\left\{{R}_{17},{R}_{18},{R}_{19},{R}_{20}\right\},\\ {}\left\{{O}_{10}\right\}=\left\{{S}_{17},{S}_{18},{S}_{19},{S}_{20}\right\},\left\{{O}_{11}\right\}=\left\{{R}_{21},{R}_{22},{R}_{23},{R}_{24}\right\},\left\{{O}_{12}\right\}=\left\{{S}_{21},{S}_{22},{S}_{23},{S}_{24}\right\},\\ {}\begin{array}{c}\left\{{O}_{13}\right\}=\left\{{R}_{30},{R}_{31},{R}_{32}\right\},\left\{{O}_{14}\right\}=\left\{{R}_{33},{R}_{34},{R}_{35}\right\},\left\{{O}_{15}\right\}=\left\{{S}_{30},{S}_{31},{S}_{32}\right\},\\ {}\left\{{O}_{16}\right\}=\left\{{S}_{33},{S}_{34},{S}_{35}\right\},\left\{{O}_{17}\right\}=\left\{{R}_{25},{R}_{26},{R}_{27}\right\},\left\{{O}_{18}\right\}=\left\{{S}_{25},{S}_{26},{S}_{27}\right\},\\ {}\begin{array}{c}\left\{{O}_{19}\right\}=\left\{{U}_1,{U}_2,{U}_3,{U}_4\right\},\left\{{O}_{20}\right\}=\left\{{U}_5,{U}_6,{U}_7,{U}_8\right\},\left\{{O}_{21}\right\}=\left\{{W}_1,{W}_2,{W}_3,{W}_4\right\},\\ {}\left\{{O}_{22}\right\}=\left\{{U}_9,{U}_{10},{U}_{11},{U}_{12}\right\},\left\{{O}_{23}\right\}=\left\{{U}_{13},{U}_{14},{U}_{15},{U}_{16}\right\},\left\{{O}_{24}\right\}=\left\{{W}_5,{W}_6,{W}_7,{W}_8\right\},\\ {}\begin{array}{c}\left\{{O}_{25}\right\}=\left\{{V}_1,{V}_2,{V}_3\right\},\left\{{O}_{26}\right\}=\left\{{V}_4,{V}_5,{V}_6\right\},\left\{{O}_{26}\right\}=\left\{{W}_9,{W}_{10},{W}_{11}\right\},\\ {}\left\{{\Delta}_{ij}\right\}={\left\{{u}_{i,j}{\varphi}_{i,j}{\xi}_{i,j}{\phi}_{i,j}\right\}}^T,\left(i,j=x,y\right)\left\{{\Delta}_{zi}\right\}={\left\{{\varphi}_i2{\xi}_i3{\phi}_i\right\}}^T,\left(i=x,y\right),\\ {}\left\{{\pi}_i\right\}={\left\{{\varphi}_i2{\xi}_i\right\}}^T,\left(i=x,y\right),\left\{{\Delta}_i\right\}={\left\{{w}_{,i}{\varphi}_{z,i}{\xi}_{z,i}\right\}}^T\left(i=x,y\right),\end{array}\end{array}\end{array}\end{array}\end{array}\\ {}\left[{\Sigma}_{ij}\right]=\left[\begin{array}{ccc}{N}_{ij}& {M}_{ij}& \begin{array}{cc}{M}_{ij}^{\ast }& {P}_{ij}\end{array}\\ {}{M}_{ij}& {M}_{ij}^{\ast }& \begin{array}{cc}{P}_{ij}& {P}_{ij}^{\ast}\end{array}\\ {}\begin{array}{c}{M}_{ij}^{\ast}\\ {}{P}_{ij}\end{array}& \begin{array}{c}{P}_{ij}\\ {}{P}_{ij}^{\ast}\end{array}& \begin{array}{cc}\begin{array}{c}{P}_{ij}^{\ast}\\ {}{R}_{ij}\end{array}& \begin{array}{c}{R}_{ij}\\ {}{R}_{ij}^{\ast}\end{array}\end{array}\end{array}\right],\left(i=x,y,z;j=x,y\right),\\ {}\begin{array}{c}\left[{\Sigma}_{iz}\right]=\left[\begin{array}{ccc}{N}_{iz}& {M}_{iz}& {M}_{iz}^{\ast}\\ {}{M}_{iz}& {M}_{iz}^{\ast }& {P}_{iz}\\ {}\begin{array}{c}{M}_{iz}^{\ast}\\ {}{P}_{iz}\end{array}& \begin{array}{c}{P}_{iz}\\ {}{P}_{iz}^{\ast}\end{array}& \begin{array}{c}{P}_{iz}^{\ast}\\ {}{R}_{iz}\end{array}\end{array}\right],\left(i=x,y,z\right),\\ {}\left[{\gamma}_{ij}\right]=\left[\begin{array}{ccc}{N}_{ij}& {M}_{ij}& {M}_{ij}^{\ast}\\ {}{M}_{ij}& {M}_{ij}^{\ast }& {P}_{ij}\\ {}{M}_{ij}^{\ast }& {P}_{ij}& {P}_{ij}^{\ast}\end{array}\right],\left(i=x,y,z;j=x,y\right)\end{array}\end{array}\\ {}\left[{\Omega}_{iz}\right]=\left[\begin{array}{cc}{N}_{iz}& {M}_{iz}\\ {}{M}_{iz}& {M}_{iz}^{\ast}\\ {}{M}_{iz}^{\ast }& {P}_{iz}\end{array}\right],\left(i=x,y,z\right).\end{array}} $$

Here, N_ij, M_ij and ${M}_{ij}^{\ast }$, P_ij, ${P}_{ij}^{\ast }$ R_ij and ${R}_{ij}^{\ast }$ are the stress resultants associated with arbitrary periodic stresses and are defined as follows:

$$ \left({N}_{ij},{M}_{ij},{M}_{ij}^{\ast },{P}_{ij},{P}_{ij}^{\ast },{R}_{ij},{R}_{ij}^{\ast}\right)=\int {\sigma}_{ij}\left(1,z,{z}^2,{z}^3,{z}^4,{z}^5,{z}^6\right) dz,\left(i,j=x,y,z\right), $$

where the higher-order resultants mean high-order moments and shear forces. It should be noted that the high-order resultants are purely mathematical terms and cannot be prescribed on the physical boundaries. The quantities f_x, f_y, f_z, m_x, m_y, m_z, n_x, n_y, n_z, q_x , and q_y are the loads consisting of lateral loads at the top and bottom face of the plate and the body force, and they are given below. The superscripts + and – mean that the stresses are calculated at the top and bottom faces of plate.

$$ {\displaystyle \begin{array}{c}{f}_x=\int_{-h/2}^{h/2}\left(\overline{X_x}+\Delta {X}_x\right) dz+{\sigma}_{zx}^{+}-{\sigma}_{zx}^{-},\\ {}{f}_y=\int_{-h/2}^{h/2}\left(\overline{X_y}+\Delta {X}_y\right) dz+{\sigma}_{zy}^{+}-{\sigma}_{zy}^{-},\\ {}\begin{array}{c}{f}_z=\int_{-h/2}^{h/2}\left(\overline{X_z}+\Delta {X}_z\right) dz+\left({\sigma}_{zy}^{+}-{\sigma}_{zy}^{-}\right)+{\sigma}_{zz}^{+}-{\sigma}_{zz}^{-},\\ {}+\left({w}_{,y}+z{\varphi}_{z,y}+{z}^2{\xi}_{z,y}\right)\left({\sigma}_{zy}^{+}-{\sigma}_{zy}^{-}\right)+{\sigma}_{zz}^{+}-{\sigma}_{zz}^{-},\\ {}\begin{array}{c}{m}_x=\int_{-h/2}^{h/2}\left({\overline{X}}_x+\Delta {X}_x\right) zdz+h\left({\sigma}_{zx}^{+}-{\sigma}_{zx}^{-}\right)/2,\\ {}{m}_y\int_{-h/2}^{h/2}\left({\overline{X}}_y+\Delta {X}_y\right) zdz+h\left({\sigma}_{zy}^{+}-{\sigma}_{zy}^{-}\right)/2,\\ {}\begin{array}{c}{m}_z\int_{-h/2}^{h/2}\left({\overline{X}}_Z+\Delta {X}_Z\right) zdz+\left({\sigma}_{zx}^{+}-{\sigma}_{zx}^{-}\right)\left({hw}_{,x}+{z}^3{\xi}_{z,x}/8\right)+\left({h}^2/4\right){\varphi}_{z,x}\left({\sigma}_{zx}^{+}-{\sigma}_{zx}^{-}\right)\\ {}+\left({hw}_{,y}+{z}^3{\xi}_{z,y}/8\right)\left({\sigma}_{zy}^{+}-{\sigma}_{zy}^{-}\right)+\left({h}^2/4\right){\varphi}_{z,y}\left({\sigma}_{zy}^{+}-{\sigma}_{zy}^{-}\right)+z\left({\sigma}_{zz}^{+}-{\sigma}_{zz}^{-}\right)/2,\\ {}\begin{array}{c}{n}_x=\int_{-h/2}^{h/2}\left({\overline{X}}_x+\Delta {X}_x\right){z}^2 dz+{h}^2\left({\sigma}_{zx}^{+}-{\sigma}_{zx}^{-}\right)/4,\\ {}{n}_y=\int_{-h/2}^{h/2}\left({\overline{X}}_y+\Delta {X}_y\right){z}^2 dz+{h}^2\left({\sigma}_{zy}^{+}-{\sigma}_{zy}^{-}\right)/4,\\ {}\begin{array}{c}{n}_z\int_{-h/2}^{h/2}\left({\overline{X}}_Z+\Delta {X}_Z\right){z}^2 dz+\left({\sigma}_{zx}^{+}-{\sigma}_{zx}^{-}\right)\left({hw}_{,x}/4+{z}^4{\xi}_{z,x}/16\right)+\left({h}^3/8\right){\varphi}_{z,x}\left({\sigma}_{zx}^{+}-{\sigma}_{zx}^{-}\right)+\\ {}\left({h}^2{w}_{,y}/4+{z}^4{\xi}_{z,y}/16\right)\left({\sigma}_{zy}^{+}-{\sigma}_{zy}^{-}\right)+\left({h}^3/8\right){\varphi}_{z,y}\left({\sigma}_{zy}^{+}-{\sigma}_{zy}^{-}\right)+{z}^2\left({\sigma}_{zz}^{+}-{\sigma}_{zz}^{-}\right)/4,\\ {}\begin{array}{c}{q}_x=\int_{-h/2}^{h/2}\left({\overline{X}}_x+\Delta {X}_x\right){z}^3 dz+{h}^3\left({\sigma}_{zx}^{+}-{\sigma}_{zx}^{-}\right)/8,\\ {}{q}_y=\int_{-h/2}^{h/2}\left({\overline{X}}_y+\Delta {X}_y\right){z}^3 dz+{h}^3\left({\sigma}_{zy}^{+}-{\sigma}_{zy}^{-}\right)/8.\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}} $$

The inertia related terms are defined as

$$ \left({I}_1,{I}_3,{I}_5,{I}_7\right)=\int \rho \left(1,{z}^2,{z}^4,{z}^6\right) dz. $$