Nonlinear dynamic instability analysis of laminated composite thin plates subjected to periodic in-plane loads

Abstract

In this paper, the dynamic instability of thin laminated composite plates subjected to harmonic in-plane loading is studied based on nonlinear analysis. The equations of motion of the plate are developed using von Karman-type of plate equation including geometric nonlinearity. The nonlinear large deflection plate equations of motion are solved by using Galerkin’s technique that leads to a system of nonlinear Mathieu-Hill equations. Dynamically unstable regions, and both stable- and unstable-solution amplitudes of the steady-state vibrations are obtained by applying the Bolotin’s method. The nonlinear dynamic stability characteristics of both antisymmetric and symmetric cross-ply laminates with different lamination schemes are examined. A detailed parametric study is conducted to examine and compare the effects of the orthotropy, magnitude of both tensile and compressive longitudinal loads, aspect ratios of the plate including length-to-width and length-to-thickness ratios, and in-plane transverse wave number on the parametric resonance particularly the steady-state vibrations amplitude. The present results show good agreement with that available in the literature.

1 Introduction

Laminated composite plates are being increasingly used in aerospace, automotive, and civil engineering as well as in many other applications of modern engineering structures. Tailoring ability of fiber-reinforced polymer composite (FRPC) materials for the stiffness and strength properties with regard to reduction of structural weight made them superior compared with metals in such structures. To use them efficiently as a structural component it is required to have a good knowledge and understanding of their mechanical behavior such as deformations, stress distributions, natural frequencies, and static and dynamic instabilities under various loading and boundary conditions. Many scholars and researchers from different disciplines have been conducting their research works to study and investigate those mentioned structural behavior of composite structures. One of the most interesting fields of study of laminated composite plates is the dynamic instability under periodic in-plane loads.

When the lightweight structural components are subjected to dynamic loading particularly periodic in-plane loads, when the frequency of in-plane dynamic load and the frequency of vibration satisfy certain specific conditions, parametric resonance will occur in the structure, which makes the plate enter into a state of dynamic instability [1]. This instability is of concern because it can occur at load magnitudes that are much less than the static buckling load, so a component designed to withstand static buckling may fail in a periodic loading environment. Further, the dynamic instability occurs over a range of forcing frequencies rather than at a single value [1, 2].

The interest to study the dynamic stability behavior of engineering structures dates back to the text by Bolotin [3] which addresses numerous problems on the stability of structures under pulsating loads. According to the general theory of dynamic stability of elastic systems by using Bolotin’s method a set of differential equations of the Mathieu-Hill type are derived, and by seeking periodic solutions using Fourier series expansion the boundaries of unstable regions are determined. An extensive bibliography of the earlier works on parametric response of structures was presented by Evan-Iwanowsky [4].

A detailed research survey on the dynamic stability behavior of plates and shells in which the literature from 1987 to 2005 has been reviewed can be found in the review paper by Sahu and Datta [5].

Srinivasan and Chellapandi [6] studied the dynamic instability of rectangular laminated composite plates under longitudinal periodic loads. They used finite strip method and using Bolotin’s procedure to obtain the parametric instability regions. Although the numerical results have been limited only for the clamped plates but their method is applicable for any boundary conditions. They investigated three different configurations including symmetric, antisymmetric and asymmetric plates and the effects of aspect ratios of the plate on unstable regions.

Influence of out-of-plane transverse shear deformation on dynamic instability also has been addressed in the literature [7, 8]. Moorthy and Reddy et al. [9] used first order shear deformation plate theory to study the effects of damping, length-thickness ratio, boundary conditions, number of layers and lamination angles on instability regions.

Dynamic instability of laminated composite plates supported on elastic foundation, subjected to periodic in-plane loads was investigated by Patel et al. [10]. They used $C^{1}$ eight-nodded shear-flexible plate element which allows both displacement and stress continuity at the interfaces between the layers. The influences of various parameters such as ply-angle, static load factor, thickness and aspect ratios, and elastic foundation stiffness on dynamic instability regions were examined.

Ramachandra and Panda [11] investigated the dynamic instability problem of composite plates subjected to periodic nonuniform in-plane loads. Both the static and dynamic components of the applied load were assumed to vary according to either parabolic or linear distributions. They used Ritz method to estimate the in-plane stress distribution within the pre-buckling range due to the applied nonuniform load. Galerkin’s method was implemented to derive the Mathieu type of equations. The effects of span-thickness and aspect ratios, boundary conditions and static load factor on dynamic instability regions were investigated.

All these mentioned works are based on linear analysis and so lead to the determination of dynamic instability regions. Stability analysis based on classical linear theories provided only an outline of the parameter regimes where nonlinear effects are of importance. According to Popov [12] without adequate nonlinear analysis the results in some cases can be inaccurate. According to linear theory, one expects the vibration amplitudes in the regions of dynamic instability to increase unboundedly with time indeed very rapidly so as to increase exponentially. However, this conclusion contradicts experimental results which reveal that vibrations with steady-state amplitudes exist in the instability regions. As the amplitude increases, the character of the vibrations changes; the speed of the growth gradually decreases until vibrations of constant (or almost constant) amplitude are finally established [3].

Some nonlinear vibrations of composite panels have been addressed by Alijani and Amabili [13] from 2003 to 2013. But a few works have been conducted considering the nonlinear plate theories for dynamic stability problems. A higher-order geometrically nonlinear theory was used by Librescu and Thangjitham [14] to investigate the parametric instability of symmetrically laminated plates. The geometrically nonlinear parametric instability characteristics of composite plates based on finite element formulation using $C^{1}$ eight-noded shear-flexible plate element have been studied by Ganapathi et al. [15]. They used Newmark integration scheme coupled with a modified Newton–Raphson iteration procedure to solve the nonlinear governing equations.

To the best of authors’ knowledge, there is no comprehensive work on nonlinear dynamic instability of thin laminated composite plates which considers the effects of stacking sequence, aspect ratios, lamination symmetry and so on. In the present paper, von Karman-type of plate equation is used to develop the equation of motion of plate including geometric nonlinearity for thin laminated composite flat plate subjected to harmonic in-plane loading. Galerkin’s technique is then employed to solve the nonlinear large deflection plate equations of motion and a system of nonlinear Mathieu-Hill equations are derived. The dynamically unstable regions, and both stable- and unstable-solution amplitudes of steady-state vibrations are determined by applying the Bolotin’s method. The parametric studies are performed to investigate and compare the effects of lamination schemes including stacking sequence and number of plies of symmetric and antisymmetric cross-ply laminated plates, the magnitude of in-plane loads both tensile and compressive loads, aspect ratios of the plate including length-to-width and length-to-thickness ratios, and in-plane transverse wave number on the parametric resonance particularly of the steady-state vibrations. The present results show good agreement when compared with that available in the literature and hence can be used as bench mark results for future studies.

2 Formulation

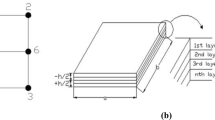
A thin simply supported laminated composite rectangular plate, having length a and width b with respect to the Cartesian coordinates (X, Y, Z) which are assigned in the mid-plane of the plate is considered as shown in Fig. 1.

Here, u, v and w are the displacement components of the plate with reference to this coordinate system in the $X, Y, {\text {and }} Z$ directions, respectively.

The plate as shown in Fig. 1 is subjected to a periodically pulsating load in the length direction with the longitudinal loading per unit length as follow:

$$\begin{aligned} F_{xx}\left( t \right) =F_{s}+F_{d}\mathrm{cos}Pt \end{aligned}$$

(1)

where $F_{s}$ is a time-invariant component, $F_{d}\mathrm{cos}Pt$ is the harmonically pulsating component, and P denotes the frequency of excitation in radians per unit time.

Fig. 1

The geometry and loading condition of a laminated composite rectangular plate

Since $u_{0}\ll w_{0}$ and $v_{0}\ll w_{0}$ we can consider that $\rho _{t}\,\partial ^{2}u_{0}\big /{\partial t}^{2}\rightarrow 0$ and $\rho _{t}\,\partial ^{2}v_{0}\big /{\partial t}^{2}\rightarrow 0$ . Therefore by neglecting the in-plane inertia forces the equations of motion in the form of that originally presented by von Karman [16] and used in further development in Lagrangian coordinates by Fung [16, 17], under the longitudinal pulsating load are given by

$$\begin{aligned}&\frac{{\partial N}_{xx}}{\partial x}+\frac{{\partial N}_{xy}}{\partial y}=0 \end{aligned}$$

(2)

$$\begin{aligned}&\frac{{\partial N}_{xy}}{\partial x}+\frac{{\partial N}_{yy}}{\partial y}=0 \end{aligned}$$

(3)

$$\begin{aligned}&\frac{{\partial ^{2}M}_{xx}}{{\partial x}^{2}}+2\frac{{\partial ^{2}M}_{xy}}{\partial x\partial y}+\frac{{\partial ^{2}M}_{yy}}{{\partial y}^{2}}+N_{xx}\frac{\partial ^{2}w_{0}}{{\partial x}^{2}}\nonumber \\&\quad +\,2N_{xy}\frac{\partial ^{2}w_{0}}{\partial x\partial y}+N_{yy}\frac{\partial ^{2}w_{0}}{{\partial y}^{2}}=\rho _{t}\frac{\partial ^{2}w_{0}}{{\partial t}^{2}} \end{aligned}$$

(4)

where

$$\begin{aligned} \rho _{t}=\int _{-\frac{h}{2}}^\frac{h}{2} {\rho \mathrm{d}z} \end{aligned}$$

(5)

and ($N_{xx}$ , $N_{yy}$, $N_{xy})$ are the total in-plane force resultants and ($M_{xx}$ , $M_{yy}$, $M_{xy})$ are the total moment resultants that are defined by

$$\begin{aligned}&\left\{ {\begin{array}{l} N_{xx}\\ N_{yy}\\ N_{xy}\\ \end{array} } \right\} =\int _\frac{-h}{{2}}^\frac{h}{{2}} {\left\{ {\begin{array}{l} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{xy}\\ \end{array} } \right\} \mathrm{d}z} \end{aligned}$$

(6)

$$\begin{aligned}&\left\{ {\begin{array}{l} M_{xx}\\ M_{yy}\\ M_{xy}\\ \end{array} } \right\} =\int _\frac{-h}{{2}}^\frac{h}{{2}} {\left\{ {\begin{array}{l} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{xy}\\ \end{array} } \right\} Z\mathrm{d}z} \end{aligned}$$

(7)

The nonzero von Karman strains associated with nonlinear large deflections and curvatures are given by

$$\begin{aligned}&\left\{ {\begin{array}{l} \epsilon _{xx}\\ \epsilon _{yy}\\ \gamma _{xy}\\ \end{array} } \right\} =\left\{ {\begin{array}{l} \epsilon _{xx}^{{(0)}}\\ \epsilon _{yy}^{{(0)}}\\ \gamma _{xy}^{{(0)}}\\ \end{array} } \right\} +z\left\{ {\begin{array}{l} \epsilon _{xx}^{(1)}\\ \epsilon _{yy}^{(1)}\\ \gamma _{xy}^{(1)}\\ \end{array} } \right\} \end{aligned}$$

(8)

$$\begin{aligned}&\left\{ \epsilon ^{0} \right\} =\left\{ {\begin{array}{l} \epsilon _{xx}^{{(0)}}\\ \epsilon _{yy}^{{(0)}}\\ \gamma _{xy}^{{(0)}}\\ \end{array} } \right\} = \left\{ {\begin{array}{l} \frac{\partial u_{0}}{\partial x}+\frac{\mathrm {1}}{\mathrm {2}}{\left( \frac{\partial w_{0}}{\partial x}\right) }^{\mathrm {2}}\\ \frac{\partial v_{0}}{\partial y}+\frac{\mathrm {1}}{\mathrm {2}}{\left( \frac{\partial w_{0}}{\partial y}\right) }^{\mathrm {2}}\\ \frac{\partial u_{0}}{\partial y}+\frac{\partial v_{0}}{\partial x}+\frac{\partial w_{0}}{\partial x}\frac{\partial w_{0}}{\partial y}\\ \end{array} } \right\} \end{aligned}$$

(9)

$$\begin{aligned}&\left\{ \epsilon ^{\mathrm {1}} \right\} =\left\{ {\begin{array}{l} \epsilon _{xx}^{\mathrm {(1)}}\\ \epsilon _{yy}^{\mathrm {(1)}}\\ \gamma _{xy}^{\mathrm {(1)}}\\ \end{array} } \right\} = \quad \left\{ {\begin{array}{l} -\frac{\partial ^{\mathrm {2}}w_{0}}{{\partial x}^{\mathrm {2}}}\\ -\frac{\partial ^{\mathrm {2}}w_{0}}{{\partial y}^{\mathrm {2}}}\\ \mathrm {-2}\frac{\partial ^{\mathrm {2}}w_{0}}{\partial x\partial y}\\ \end{array} } \right\} \end{aligned}$$

(10)

where $(\epsilon _{xx}^{(0)}, \epsilon _{yy}^{(0)}, \gamma _{xy}^{(0)})$ are the membrane strains, $(\epsilon _{xx}^{(1)}, \epsilon _{yy}^{(1)}, \gamma _{xy}^{1)})$ are the flexural (bending) strains and ${(u}_{0}, v_{0}, w_{0})$ are mid-plane displacements.

The thin rectangular plate is constructed by a cross-ply laminated composite material having density $\rho$. Hence, the state of stress is governed by the generalized Hooke’s law. The linear constitutive relations for the kth orthotropic lamina in the principal material coordinates of a lamina are

$$\begin{aligned} \left\{ {\begin{array}{l} \sigma _{\mathrm {1}}\\ \sigma _{\mathrm {2}}\\ \sigma _{\mathrm {6}}\\ \end{array} } \right\} ^{(k)}=\left[ {\begin{array}{lll} Q_{\mathrm {11}} &{} Q_{\mathrm {12}} &{} 0\\ Q_{\mathrm {12}} &{} Q_{\mathrm {22}} &{} 0\\ 0 &{} 0 &{} Q_{\mathrm {66}}\\ \end{array} } \right] ^{(k)}\left\{ {\begin{array}{l} \epsilon _{\mathrm {1}}\\ \epsilon _{\mathrm {2}}\\ \epsilon _{\mathrm {6}}\\ \end{array} } \right\} \end{aligned}$$

(11)

where $\left[ Q \right] ^{(k)}$ is the reduced stiffness matrix of the kth lamina and its components $Q_{ij}^{(k)}$ are known in terms of the engineering constants of the kth layer, as

$$\begin{aligned} Q_{11}= & {} \frac{E_{11}}{1-\upsilon _{12}\upsilon _{21}} \end{aligned}$$

(12a)

$$\begin{aligned} Q_{12}= & {} \frac{\upsilon _{12}E_{22}}{1-\upsilon _{12}\upsilon _{21}} \end{aligned}$$

(12b)

$$\begin{aligned} Q_{22}= & {} \frac{E_{22}}{1-\upsilon _{12}\upsilon _{21}} \end{aligned}$$

(12c)

$$\begin{aligned} Q_{66}= & {} G_{12} \end{aligned}$$

(12d)

where $E_{11}$ and $E_{22}$ are the elastic moduli in the principal material coordinates, $G_{12}$ is the shear modulus and $\upsilon _{12}$ and $\upsilon _{21}$ are the Poisson’s ratios.

The constitutive equation of the laminate which is made of several orthotropic layers, with the arbitrarily oriented material axes to the laminate coordinate, can be obtained by transformation of the stress-strain relations in the laminate coordinates as follow:

$$\begin{aligned} \left\{ {\begin{array}{l} \epsilon _{xx}\\ \epsilon _{yy}\\ \gamma _{xy}\\ \end{array} } \right\} ^{(k)}=\left[ {\begin{array}{lll} \bar{Q}_{\mathrm {11}} &{} \bar{Q}_{\mathrm {12}} &{} \bar{Q}_{\mathrm {16}}\\ \bar{Q}_{\mathrm {12}} &{} \bar{Q}_{\mathrm {22}} &{} \bar{Q}_{\mathrm {26}}\\ \bar{Q}_{\mathrm {16}} &{} \bar{Q}_{\mathrm {26}} &{} \bar{Q}_{\mathrm {66}}\\ \end{array} } \right] ^{(k)}\left\{ {\begin{array}{l} \epsilon _{xx}\\ \epsilon _{yy}\\ \gamma _{xy}\\ \end{array} } \right\} \end{aligned}$$

(13)

where $\left[ \bar{Q} \right] ^{(k)}$ is the transformed reduced stiffness matrix defined as follow:

$$\begin{aligned} \left[ \bar{Q} \right] =\left[ T \right] ^{-1}\left[ Q \right] \left[ T \right] ^{-T} \end{aligned}$$

(14)

where $\left[ T \right]$ is the transformation matrix between the principal material coordinates and the plate’s coordinates given by

$$\begin{aligned} \left[ T \right] =\left[ {\begin{array}{ccc} \cos ^{2}\vartheta &{} \sin ^{2}\vartheta &{} \mathrm {2}\cos \vartheta \sin \vartheta \\ \sin ^{2}\vartheta &{} \cos ^{2}\vartheta &{} \mathrm {-2}\cos \vartheta \sin \vartheta \\ -\cos \vartheta \sin \vartheta &{} \mathrm {2}\cos \vartheta \sin \vartheta &{} \cos ^{2}{\vartheta -\sin ^{2}\vartheta }\\ \end{array} } \right] \end{aligned}$$

(15)

and $\vartheta$ is the angular orientation of the fibers. By following Eqs. (6–15) the force and moment resultants are defined as

$$\begin{aligned} \left\{ {\begin{array}{l} N_{xx}\\ N_{yy}\\ N_{xy}\\ M_{xx}\\ M_{yy}\\ M_{xy}\\ \end{array} } \right\} =\left[ {\begin{array}{llllll} A_{\mathrm {11}} &{} A_{\mathrm {12}} &{} A_{\mathrm {16}} &{} B_{\mathrm {11}} &{} B_{\mathrm {12}} &{} B_{\mathrm {16}}\\ A_{\mathrm {12}} &{} A_{\mathrm {22}} &{} A_{\mathrm {26}} &{} B_{\mathrm {12}} &{} B_{\mathrm {22}} &{} B_{\mathrm {26}}\\ A_{\mathrm {16}} &{} A_{\mathrm {26}} &{} A_{\mathrm {66}} &{} B_{\mathrm {16}} &{} B_{\mathrm {26}} &{} B_{\mathrm {66}}\\ B_{\mathrm {11}} &{} B_{\mathrm {12}} &{} B_{\mathrm {16}}&{} D_{\mathrm {11}} &{} D_{\mathrm {12}} &{} D_{\mathrm {16}}\\ B_{\mathrm {12}} &{} B_{\mathrm {22}} &{} B_{\mathrm {26}}&{} D_{\mathrm {12}} &{} D_{\mathrm {22}} &{} D_{\mathrm {26}}\\ B_{\mathrm {16}} &{} B_{\mathrm {26}} &{} B_{\mathrm {66}}&{} D_{\mathrm {16}} &{} D_{\mathrm {26}} &{} D_{\mathrm {66}}\\ \end{array} } \right] \left\{ {\begin{array}{l} \epsilon _{xx}^{\mathrm {(0)}}\\ \epsilon _{yy}^{\mathrm {(0)}}\\ \gamma _{xy}^{\mathrm {(0)}}\\ \epsilon _{xx}^{(1)}\\ \epsilon _{yy}^{(1)}\\ \gamma _{xy}^{(1)}\\ \end{array} } \right\} \end{aligned}$$

(16)

where $A_{ij}$ denote the extensional stiffnesses, $D_{ij}$ the bending stiffnesses, and $B_{ij}$ the bending-extensional coupling stiffnesses

$$\begin{aligned} A_{ij}= & {} \sum \nolimits _{k{=1}}^N {\bar{Q}_{ij}^{\left( k \right) }\left( h_{k}-h_{k\mathrm {+1}} \right) }, \quad (i, j=1, 2, 6) \end{aligned}$$

(17a)

$$\begin{aligned} B_{ij}= & {} \frac{\mathrm {1}}{\mathrm {2}}\,\sum \nolimits _{k{=1}}^N {\bar{Q}_{ij}^{\left( k \right) }(h_{k}^{\mathrm {2}}-h_{k\mathrm {+1}}^{\mathrm {2}})} \end{aligned}$$

(17b)

$$\begin{aligned} D_{ij}= & {} \frac{\mathrm {1}}{\mathrm {3}}\sum \nolimits _{k{=1}}^N {\bar{Q}_{ij}^{\left( k \right) }(h_{k}^{\mathrm {3}}-h_{k\mathrm {+1}}^{\mathrm {3}})} \end{aligned}$$

(17c)

where $h_{k}$ and $h_{k+1}$ are measured from the plate reference surface to the outer and inner surfaces of the kth layer, respectively, as shown in Fig. 1. From Eq. (16), the strains can be written as

$$\begin{aligned}&\left\{ {\begin{array}{c} \epsilon _{xx}^{\left( 0 \right) }\\ \epsilon _{yy}^{\left( 0 \right) }\\ \gamma _{xy}^{\left( 0 \right) }\\ \end{array} } \right\} \nonumber \\&\quad =\left[ A_{ij} \right] ^{-1}\left\{ {\begin{array}{l} N_{xx}\\ N_{yy}\\ N_{xy}\\ \end{array} } \right\} -\left[ A_{ij} \right] ^{{-1}}\left[ B_{ij} \right] \left\{ {\begin{array}{l} \epsilon _{xx}^{\left( \mathrm {1} \right) }\\ \epsilon _{yy}^{\left( \mathrm {1} \right) }\\ \gamma _{xy}^{\left( \mathrm {1} \right) }\\ \end{array} } \right\} \nonumber \\&\quad =\left\{ {\begin{array}{l} a_{\mathrm {11}}N_{xx}+a_{\mathrm {12}}N_{yy}-b_{\mathrm {11}}\epsilon _{xx}^{\left( \mathrm {1} \right) }-b_{\mathrm {12}}\epsilon _{yy}^{\left( \mathrm {1} \right) }\\ a_{\mathrm {12}}N_{xx}+a_{\mathrm {22}}N_{yy}-b_{\mathrm {21}}\epsilon _{xx}^{\left( \mathrm {1} \right) }-b_{\mathrm {22}}\epsilon _{yy}^{\left( \mathrm {1} \right) }\\ a_{\mathrm {66}}N_{xy}-b_{\mathrm {66}}\gamma _{xy}^{\left( \mathrm {1} \right) }\\ \end{array} } \right\} \end{aligned}$$

(18)

where

$$\begin{aligned} a_{\mathrm {11}}= & {} \Delta A_{\mathrm {22}} , a_{\mathrm {12}}=-\Delta A_{\mathrm {12}} , a_{\mathrm {22}}=\Delta A_{\mathrm {11}}, a_{\mathrm {66}}\nonumber \\&=\frac{\mathrm {1}}{A_{\mathrm {66}}} , \nonumber \\ b_{\mathrm {11}}= & {} \Delta (A_{\mathrm {22}}B_{\mathrm {11}}-A_{\mathrm {12}}B_{\mathrm {12}}),\nonumber \\ b_{\mathrm {12}}= & {} \Delta (A_{\mathrm {22}}B_{\mathrm {12}}-A_{\mathrm {12}}B_{\mathrm {22}}),\nonumber \\ b_{\mathrm {21}}= & {} \Delta (A_{\mathrm {11}}B_{\mathrm {12}}-A_{\mathrm {12}}B_{\mathrm {11}}), b_{\mathrm {22}}\nonumber \\= & {} \Delta (A_{\mathrm {11}}B_{\mathrm {22}}-A_{\mathrm {12}}B_{\mathrm {12}}),\nonumber \\ b_{\mathrm {66}}= & {} \frac{B_{\mathrm {66}}}{A_{\mathrm {66}}} , \Delta =\frac{\mathrm {1}}{(A_{\mathrm {11}}A_{\mathrm {22}}-A_{\mathrm {12}}^{\mathrm {2}})} \end{aligned}$$

(19)

The moment resultants also can be written from Eq. (16) as

$$\begin{aligned}&\left\{ {\begin{array}{l} M_{xx}\\ M_{yy}\\ M_{xy}\\ \end{array} } \right\} \nonumber \\&\quad =\left[ b_{ij} \right] ^{T}\left\{ {\begin{array}{l} N_{xx}\\ N_{yy}\\ N_{xy}\\ \end{array} } \right\} +\left[ d_{ij} \right] \left\{ {\begin{array}{l} \epsilon _{xx}^{\left( \mathrm {1} \right) }\\ \epsilon _{yy}^{\left( \mathrm {1} \right) }\\ \gamma _{xy}^{\left( \mathrm {1} \right) }\\ \end{array} } \right\} \nonumber \\&\quad =\left\{ {\begin{array}{l} b_{\mathrm {11}}N_{xx}+b_{\mathrm {21}}N_{yy}+d_{\mathrm {11}}\epsilon _{xx}^{\left( \mathrm {1} \right) }+d_{\mathrm {12}}\epsilon _{yy}^{\left( \mathrm {1} \right) }\\ b_{\mathrm {12}}N_{xx}+b_{\mathrm {22}}N_{yy}+d_{\mathrm {12}}\epsilon _{xx}^{\left( \mathrm {1} \right) }+d_{\mathrm {22}}\epsilon _{yy}^{\left( \mathrm {1} \right) }\\ b_{\mathrm {66}}N_{xy}+d_{\mathrm {66}}\gamma _{xy}^{\left( \mathrm {1} \right) }\\ \end{array} } \right\} \end{aligned}$$

(20)

where

$$\begin{aligned}&\left[ b_{ij} \right] =\left[ A_{ij} \right] ^{-1}\left[ B_{ij} \right] \end{aligned}$$

(21a)

$$\begin{aligned}&\left[ d_{ij} \right] =-\left[ B_{ij} \right] \left[ b_{ij} \right] +\left[ D_{ij} \right] \end{aligned}$$

(21b)

$$\begin{aligned}&d_{11}=\Delta (A_{11}A_{22}D_{11}-A_{11}B_{12}^{2}-A_{12}^{2}D_{11}\nonumber \\&\qquad \, +\,2A_{12}B_{11}B_{12}-A_{22}B_{11}^{2}) \nonumber \\&d_{12}=\Delta (A_{11}A_{22}D_{12}-{A_{11}B}_{12}B_{22}-A_{12}^{2}D_{12}\nonumber \\&\qquad \, +\,A_{12}B_{11}B_{22}+A_{12}B_{12}^{2}-{A_{22}B}_{11}B_{12})\nonumber \\&d_{21}=\Delta (A_{11}A_{22}D_{12}-{A_{11}B}_{12}B_{22}-A_{12}^{2}D_{12}\nonumber \\&\qquad \, +\,A_{12}B_{11}B_{22}+A_{12}B_{12}^{2}-{A_{22}B}_{11}B_{12})\nonumber \\&d_{22}=\Delta (A_{11}A_{22}D_{22}-A_{11}B_{22}^{2}-A_{12}^{2}D_{22}\nonumber \\&\qquad \, +\,2A_{12}B_{12}B_{22}-A_{22}B_{12}^{2})\nonumber \\&d_{66}=\frac{{A_{66}D}_{66-}B_{66}^{2}}{A_{66}} \end{aligned}$$

(21c)

Here, we define the membrane forces in terms of Airy’s stress function $\varphi$ as

$$\begin{aligned} N_{xx}= & {} \frac{\partial ^{2}{\upphi }}{{\partial y}^{2}} \end{aligned}$$

(22a)

$$\begin{aligned} N_{yy}= & {} \frac{\partial ^{2}\phi }{{\partial x}^{2}} \end{aligned}$$

(22b)

$$\begin{aligned} N_{xy}= & {} -\frac{\partial ^{2}\phi }{\partial x\partial y} \end{aligned}$$

(22c)

Substituting Eqs. (10) and (22 a–c) into Eqs. (18) and (20) the strains and moment resultants are given in terms of the Airy’s stress function $\upphi$ and $w_{0}$. By combining the mid-plane strains, the compatibility equation can be expressed as

$$\begin{aligned} \frac{\partial ^{\mathrm {2}}\epsilon _{yy}^{\mathrm {(0)}}}{{\partial x}^{\mathrm {2}}}+\frac{\partial ^{\mathrm {2}}\epsilon _{xx}^{\mathrm {(0)}}}{{\partial y}^{\mathrm {2}}}-\frac{\partial ^{\mathrm {2}}\gamma _{xy}^{\left( 0 \right) }}{\partial x\partial y}={\left( \frac{\partial ^{\mathrm {2}}w_{0}}{\partial x\partial y}\right) }^{\mathrm {2}}-\frac{\partial ^{\mathrm {2}}w_{0}}{{\partial x}^{\mathrm {2}}}\frac{\partial ^{\mathrm {2}}w_{0}}{{\partial y}^{\mathrm {2}}} \end{aligned}$$

(23)

Replacing the strains in terms of the Airy’s stress function ${\upphi }$ from Eq. (18) and $w_{0}$ into Eq. (23) the nonlinear equation of compatibility can be derived as:

$$\begin{aligned}&a_{{22}}\frac{\partial ^{\mathrm {4}}{\upphi }}{{\partial x}^{{4}}}+a_{\mathrm {11}}\frac{\partial ^{{4}}{\upphi }}{{\partial y}^{\mathrm {4}}}+\left( \mathrm {2}a_{\mathrm {12}}+a_{\mathrm {66}} \right) \frac{\partial ^{\mathrm {4}}{\upphi }}{{\partial x}^{\mathrm {2}}{\partial y}^{\mathrm {2}}}\nonumber \\&\quad +b_{\mathrm {21}}\frac{\partial ^{\mathrm {4}}w_{0}}{{\partial x}^{\mathrm {4}}}+b_{\mathrm {12}}\frac{\partial ^{\mathrm {4}}w_{0}}{{\partial y}^{\mathrm {4}}}+\left( b_{\mathrm {11}}{+b}_{\mathrm {22}}\mathrm {-2}b_{\mathrm {66}} \right) \frac{\partial ^{\mathrm {4}}w_{0}}{{\partial x}^{\mathrm {2}}{\partial y}^{\mathrm {2}}}\nonumber \\&={\left( \frac{\partial ^{\mathrm {2}}w_{0}}{\partial x\partial y}\right) }^{{2}} -\frac{\partial ^{\mathrm {2}}w_{0}}{{\partial x}^{\mathrm {2}}}\frac{\partial ^{\mathrm {2}}w_{0}}{{\partial y}^{\mathrm {2}}} \end{aligned}$$

(24)

3 Solution for laminated orthotropic plates

Considering the simply supported boundary condition for the laminated orthotropic plate, the Navier’s double Fourier series with the time-dependent coefficient $q_{mn}(t)$ is chosen to describe the out-of-plane displacement function $w_{0}(x,y, t)$ :

$$\begin{aligned} w_{0}=\sum \nolimits _{m=1}^\infty \sum \nolimits _{n=1}^\infty {q_{mn}\left( t \right) \sin {\frac{m\pi }{a}x\cos {\frac{n\pi }{b}y}}} \end{aligned}$$

(25)

where m and n represent the number of longitudinal and transverse half waves in corresponding standing wave pattern, respectively.

$F_{xx}$ is the average longitudinal force at the edge, thus the stress function has to satisfy the following condition

$$\begin{aligned} \frac{1}{b}\int _0^b \frac{\partial ^{2}\phi }{{\partial y}^{2}} dy=F_{xx}\,\mathrm{at}\,x=0\, , a \end{aligned}$$

(26)

Airy’s stress function can be governed by substituting Eq. (25) into (24) and applying different trigonometric relations, as:

$$\begin{aligned} \phi= & {} \frac{\mathrm {1}}{\mathrm {2}}F_{xx}y^{\mathrm {2}}+\sum \nolimits _{m{=1}}^{\infty } \sum \nolimits _{n{=1}}^{\infty }\nonumber \\&\times \left\{ -\frac{\mathrm {1}}{\mathrm {2}}{A_{mn}q}_{mn}\left( t \right) \xi _{\mathrm {1}}\left[ \sin {\left( \lambda _{m}x-\lambda _{n}y \right) }\right. \right. \nonumber \\&\left. {+\sin \left( \lambda _{m}x+\lambda _{n}y \right) } \right] \nonumber \\&+\frac{\mathrm {1}}{\mathrm {32}}B_{mn}q_{mn}^{\mathrm {2}}\left( t \right) \left[ \xi _{\mathrm {2}}\cos {\left( \mathrm {2}\lambda _{m}x \right) }\right. \nonumber \\&\left. \left. {-\,\xi _{\mathrm {3}}\cos \left( \mathrm {2}\lambda _{n}y \right) } \right] \right\} \end{aligned}$$

(27)

where $\lambda _{m}={m\pi } \big / a$, $\lambda _{n}={n\pi } \big / b$ and

$$\begin{aligned}&A_{mn}=b_{\mathrm {21}}\lambda _{m}^{\mathrm {4}}+b_{\mathrm {12}}\lambda _{n}^{\mathrm {4}}+\left( b_{\mathrm {11}}{+b}_{\mathrm {22}}\mathrm {-2}b_{\mathrm {66}} \right) \lambda _{m}^{\mathrm {2}}\lambda _{n}^{\mathrm {2}} \end{aligned}$$

(28a)

$$\begin{aligned}&B_{mn}=\lambda _{m}^{\mathrm {2}}\lambda _{n}^{\mathrm {2}} \end{aligned}$$

(28b)

$$\begin{aligned}&\xi _{\mathrm {1}}=\mathrm {1}\bigg /\left( a_{\mathrm {22}}\lambda _{m}^{\mathrm {4}}+a_{\mathrm {11}}\lambda _{n}^{\mathrm {4}}\mathrm {+(2}a_{\mathrm {12}}+a_{\mathrm {66}})\lambda _{m}^{\mathrm {2}}\lambda _{n}^{\mathrm {2}} \right) \end{aligned}$$

(28c)

$$\begin{aligned}&\xi _{\mathrm {2}}=1 \bigg /{(a_{\mathrm {22}}\lambda _{m}^{\mathrm {4}})}\end{aligned}$$

(28d)

$$\begin{aligned}&\xi _{\mathrm {3}}=1 \bigg /{(a_{\mathrm {11}}\lambda _{n}^{\mathrm {4}})} \end{aligned}$$

(28e)

Substituting the relations (22a–c) in Eqs. (2) and (3), these equations are satisfied automatically. With the definitions (22a-c), the membrane forces $N_{xx}, N_{yy}$ and $N_{xy}$ are computable by this solution and the boundary condition (26) is satisfied. As mentioned before by substituting Eqs. (10) and (22a–c) into equations (20) the moments are given in terms of the Airy’s stress function $\upphi$ and $w_{0}$ so by inserting these functions the moment resultants $M_{xx}, M_{yy}$ and $M_{xy}$ are also computable. By substituting these stress and moment resultants and the out-of-plane displacement as defined in Eq. (25) into the third equation of motion, Eq. (4) and after multiplying the governing equation by $\sin {\lambda _{m}x\cos {\lambda _{n}y}}$ and integrating over the plate area, a system of $m\times n$ second-order ordinary differential equations is obtained:

$$\begin{aligned}&M_{mn}\ddot{q}_{mn}\left( t \right) +K_{mn}q_{mn}\left( t \right) \nonumber \\&\quad -\,(F_{s}+F_{d}\cos pt)Q_{mn}q_{mn}\left( t \right) \nonumber \\&\quad +\,\eta _{mn}q_{mn}^{\mathrm {3}}(t)=0 \end{aligned}$$

(29)

where $M_{mn}$, $K_{mn}$ ,$Q_{mn}$ and $\eta _{mn}$ are matrices that are defined in appendix and $\ddot{q}_{mn}\left( t \right) ,q_{mn}\left( t \right)$ and $q_{mn}^{\mathrm {3}}(t)$ are column vectors consisting of the $\ddot{q}_{mn}\left( t \right)$’s,$q_{mn}\left( t \right)$’s and $q_{mn}^{\mathrm {3}}(t)$’s, respectively. The subscripts m and n have the following ranges:

$$\begin{aligned} m,n=1,2,3,4,..,\,N. \end{aligned}$$

(30)

Introducing following notation:

$$\begin{aligned}&\omega _{mn}=\sqrt{\frac{K_{mn}}{M_{mn}}} \end{aligned}$$

(31a)

$$\begin{aligned}&\gamma _{mn}=\frac{\eta _{mn}}{M_{mn}} \end{aligned}$$

(31b)

$$\begin{aligned}&N_{*}=\frac{K_{mn}}{Q_{mn}} \end{aligned}$$

(31c)

Equation (29) can be written in the form of the nonlinear Mathieu equation as follow:

$$\begin{aligned}&\ddot{q}_{mn}\left( t \right) +{\Omega }_{mn}^{2} (1-2\mu _{mn}\cos pt)q_{mn}\left( t \right) \nonumber \\&\quad +\,\gamma _{mn}q_{mn}^{3}\left( t \right) =0 \end{aligned}$$

(32)

where ${\Omega }_{mn}$ is the frequency of the free vibration of the plate loaded by a constant longitudinal force $F_{s}$,

$$\begin{aligned} {\Omega }_{mn}=\omega _{mn}\sqrt{1-\frac{F_{s}}{N_{*}}} \end{aligned}$$

(33)

and $\mu _{mn}$ is a quantity that is called the excitation parameter,

$$\begin{aligned} {\mu }_{mn}=\frac{F_{d}}{2(N_{*}-F_{s})} \end{aligned}$$

(34)

4 Amplitude of vibrations at the principal parametric resonance

As mentioned above Eq. (32) is a nonlinear Mathieu equation where the nonlinear term $\gamma q_{mn}^{3}(t)$ represents the effect of large deflection. According to Liapunov Principle, dynamically unstable region is determined by the linear parts of the Eq. (32) [3] which will be discussed in the next section. Here the focus is set on the parametric resonance of the system. The basic solutions of Mathieu equation include two periodic solutions: i.e., periodic solutions of periods T and 2T with $T={2\pi }/P$. The solutions with period 2T are of greater practical importance as the widths of these unstable regions are usually larger than those associated with solutions having period T. Using Bolotin’s [3] method for parametric vibration, the solution of period 2T is given by the following equation:

$$\begin{aligned} q\left( t \right) =\sum \nolimits _{k=1,3,5,\ldots }^\infty {f_{k}\sin {\frac{kPt}{2}+g_{k}\cos \frac{kPt}{2}}} \end{aligned}$$

(35)

where $f_{k}$ and $g_{k}$ are arbitrary vectors. If we investigate the vibration at the principal resonance at frequency ${\approx 2\Omega }$ , we can neglect the influence of higher harmonics in the expansion of above equation and can assume

$$\begin{aligned} q\left( t \right) =f\sin {\frac{Pt}{2}+g\cos \frac{Pt}{2}} \end{aligned}$$

(36)

as an approximation. By substituting this function into Eq. (32) and equating the coefficients of $\sin {({Pt}/2}$ and $\cos {({Pt}2)}$ terms and neglecting terms containing higher harmonics, the following system of equations for the coefficients a and b remains:

$$\begin{aligned} \left[ {\Omega }_{mn}^{2}\left( 1+\mu _{mn} \right) -\frac{P^{2}}{4} \right] f+{\Gamma }\left( f,g \right)= & {} 0, \end{aligned}$$

(37a)

$$\begin{aligned} \left[ {\Omega }_{mn}^{2}\left( 1-\mu _{mn} \right) -\frac{P^{2}}{4} \right] g+{\Psi }\left( f,g \right)= & {} 0, \end{aligned}$$

(37b)

where ${\Gamma }\left( f,g \right)$ and $\Psi \left( f,g \right)$ are defined as coefficients of the terms including $\sin {({Pt} / 2)}$ and $\cos {({Pt} /2)}$ which were obtained from the first approximation of expansion in a Fourier series as:

$$\begin{aligned} {\Gamma }\left( f,g \right)= & {} \frac{3\gamma _{mn}}{4}A^{2}f \end{aligned}$$

(38a)

$$\begin{aligned} {\Psi }\left( f,g \right)= & {} \frac{3\gamma _{mn}}{4}A^{2}g \end{aligned}$$

(38b)

where A is the amplitude of steady-state vibrations and is given by:

$$\begin{aligned} A=\sqrt{f^{2}+g^{2}} \end{aligned}$$

(39)

By substitution of Eqs. (38a, b) into (37a, b) a system of two homogeneous linear equations with respect to f and g can be obtained. This system has solutions that differ from zero only in the case where the determinant composed of the coefficients disappears:

$$\begin{aligned} \left| {\begin{array}{cc} \mathrm {1+}\mu _{mn}-n_{mn}^{\mathrm {2}}+\frac{\mathrm {3}\gamma _{mn}}{\mathrm {4}{\Omega }_{mn}^{\mathrm {2}}}A^{\mathrm {2}} &{} 0\\ 0 &{} \mathrm {1-}\mu _{mn}-n_{mn}^{\mathrm {2}}+\frac{\mathrm {3}\gamma _{mn}}{\mathrm {4}{\Omega }_{mn}^{\mathrm {2}}}A^{\mathrm {2}}\\ \end{array} } \right| {=0} \end{aligned}$$

(40)

where

$$\begin{aligned} n_{mn}= \quad \frac{P}{2{\Omega }_{mn}} \end{aligned}$$

(41)

Expanding the determinant and solving the resulting equation with respect to the amplitude, A, of the steady-state vibrations the following equation is obtained:

$$\begin{aligned} A=\frac{2{\Omega }_{mn}}{\sqrt{3\gamma _{mn}} }\sqrt{n_{mn}^{2}-1\pm \mu _{mn}} \end{aligned}$$

(42)

It can be proved that in the $\pm \mu _{mn}$ term of the above equation, only $+\mu _{mn}$term yields the stable solution, and all the other terms yield unstable solutions.

5 Dynamic instability regions

The resonance curve is not influenced by nonlinearity of Eq. (29) and as mentioned in the previous section the dynamic instability regions are determined by linear part of Mathieu-Hill equation, and so Eq. (29) can be rewritten as follow:

$$\begin{aligned}&M_{mn}\ddot{q}_{mn}\left( t \right) \mathrm {+(}K_{mn}^{{*}}-Q_{mn}^{{*}}\cos {Pt)q_{mn}\left( t \right) }\nonumber \\&\quad +\,\eta _{mn}q_{mn}^{\mathrm {3}}(t)=0 \end{aligned}$$

(43)

where

$$\begin{aligned} K_{mn}^{*}=K_{mn}-F_{s}Q_{mn} \end{aligned}$$

(44)

and

$$\begin{aligned} Q_{mn}^{*}=F_{d}Q_{mn} \end{aligned}$$

(45)

The principal region of dynamic instability which corresponds to solution of period 2T is determined by substituting Eq. (37) into (43) and equating the determinant of the coefficient matrix of linear part of the governing equation to zero as follow:

$$\begin{aligned} \left| {\begin{array}{cc} K_{mn}^{{*}}-\frac{Q_{mn}^{{*}}}{\mathrm {2}}-\frac{M_{mn}}{\mathrm {4}}P^{\mathrm {2}} &{} 0\\ 0 &{} K_{mn}^{{*}}+\frac{Q_{mn}^{{*}}}{\mathrm {2}}-\frac{M_{mn}}{\mathrm {4}}P^{\mathrm {2}}\\ \end{array} } \right| {=0} \end{aligned}$$

(46)

Comparing Eqs. (46) and (40) by replacing $\upmu _{mn}$, $\text {n}_{mn}$ , $\gamma _{mn}$ and ${\Omega }_{mn}$ in terms of $K_{mn}^{*}$, $Q_{mn}^{*}$ and $M_{mn}$ reveals that the dynamic instability regions are determined by setting $A=0$ in Eq. (40).

Equation (46) can be rearranged to the more simplified form of an eigenvalue problem as follow:

$$\begin{aligned} \left| {\begin{array}{cc} K_{mn}^{{*}}-\frac{Q_{mn}^{{*}}}{\mathrm {2}} &{} 0\\ 0 &{} K_{mn}^{{*}}+\frac{Q_{mn}^{{*}}}{\mathrm {2}}\\ \end{array} } \right| -P^{\mathrm {2}}\left| {\begin{array}{cc} \frac{M_{mn}}{\mathrm {4}} &{} 0\\ 0 &{} \frac{M_{mn}}{\mathrm {4}}\\ \end{array} } \right| {=0} \end{aligned}$$

(47)

Fig. 2

The first unstable region of a four-layered symmetric $[(0^{\circ }, {90}^{\circ })_{1}]_{S}$ cross-ply laminated square plate with thickness ratio of $a/h=25$ subjected to periodic longitudinal load having static load factor of $\alpha =0$

6 Numerical results and discussions

Nonlinear dynamic stability characteristics of cross-ply laminated composite rectangular plates subjected to combined static and periodic longitudinal loads are studied here. The material properties used in the present analysis are chosen in accordance with Ramachandra et al. [11] as $E_{1}/ {E_{2}=40}$ , $G_{12}/ E_{2}=0.5$ and $\upsilon _{12}=0.25.$

As mentioned before the main objective of this paper is to study the influence of geometric nonlinearity on the dynamic instability of laminated composite rectangular plates which are characterized by the nonlinear Mathieu-Hill equation as given by Eqs. (29) and (32). In Sect. 5 it was observed that the dynamic instability regions based on the large deflection formulation are achieved by either linear part of the nonlinear Mathieu-Hill equation or by setting $A=0$ in Eq. (40).

6.1 Validation

In order to validate the present formulation which is based on the nonlinear analysis we also obtain the numerical results that correspond to the dynamically unstable regions to compare them with those available in the literature [9, 11], for cross-ply laminated composite plates.

Figure 2 displays the boundaries of the first (from left to the right of the frequency axis) dynamically unstable region of a four-layered symmetric $[(0^{\circ },{{90}}^{{\circ }})_{1}]_{S}$ cross-ply laminated square plate having thickness ratio of $a/h=25$. Here to compare the results with Moorthy et al. [9] and Ramachandra et al. [11] the static and periodic components of the longitudinal load are considered as $F_{s}=\alpha N_{\mathrm{cr}}$ and $F_{d}=\beta N_{\mathrm{cr}}$ where $\alpha$ and $\upbeta$ are static and periodic load factors, respectively. In this figure $\alpha$ is zero and the critical buckling load $N_{\mathrm{cr}}$ of the studied plate has been calculated as follow:

$$\begin{aligned} \left| K_{mn}-N_{\mathrm{cr}}Q_{mn} \right| =0 \end{aligned}$$

(48)

Fig. 3

Effect of orthotropy on the first unstable region, $\left( m,n \right) =(1,1)$, of a four-layered symmetric $[(0^{\circ }, {90}^{\circ })_{1}]_{S}$ cross-ply laminated square plate with thickness ratio of $a/h=25$ subjected to periodic longitudinal load having static load factor of $\alpha =0$

The free vibration frequencies of the studied plate are also calculated as follow:

$$\begin{aligned} \left| K_{mn}-\omega ^{2}M_{mn} \right| =0 \end{aligned}$$

(49)

As it can be observed from this figure each unstable region is separated by two lines with a common point of origin. Actually these two lines are not completely straight and they curved slightly outward. In this figure the “$1{\mathrm{st}}$ approximation” predicate to the smallest possible truncation which corresponds to $k=1$ in Eq. (35) and the next smallest truncation, called the “$2{\mathrm{nd}}$ approximation” corresponds to $k=3$ in Eq. (35). As it has been mentioned in Sect. 4, in the present work the influence of higher harmonics in the expansion of Eq. (35) has been neglected and led to Eq. (36) which is the “$1{\mathrm{st}}$ approximation”. It is observed from this figure that there is an excellent agreement between the present results with those obtained by Moorthy et al. [9] and Ramachandra et al. [11] and as one can see all the corresponding three plots almost completely coincide with each other.

As an another comparison of the present results with Moorthy et al. [9] and also to investigate the effects of orthotropy on the first unstable region, $\left( m,n \right) =(1,1)$, the results are plotted in Fig. 3. The figure represents the plots for four-layered symmetric $[(0^{\circ }, 90^{\circ })_{1}]_{S}$ cross-ply laminated square plate with thickness ratio of $a/ h=25$ subjected to periodic longitudinal load having again static load factor of $\alpha =0$ . For a better comparison of the results here the plots are depicted based on the critical buckling load and fundamental frequency of the plate having orthotropic ratio of $\frac{E_{1}}{E_{2}}=40$ for all the three cases, i.e., for $\frac{E_{1}}{E_{2}}=40$, $\frac{E_{1}}{E_{2}}=30$ and $\frac{E_{1}}{E_{2}}=20$. As it can be observed from this figure for the case $\frac{E_{1}}{E_{2}}=40$ the present plot and the corresponding one by Moorthy et al. [9] almost completely coincide with each other and there is a very small difference between present plots and that of Moorthy et al. [9] for the orthotropic ratios of 30 and 20. This figure illustrates that at any certain value of load factor $\beta$, that is, at any certain longitudinal periodic load, once the ratio of $\frac{E_{1}}{E_{2}}$ is decreased, the values of excitation frequency for instability tend to decrease and the range of values (or in other words the width of instability region) increases. Here again there is an excellent agreement between these two studies.

Fig. 4

Effect of orthotropy on both the stable- and unstable-solution amplitudes of steady-state vibrations of the first mode, $\left( m,n \right) =\left( 1,1 \right) ,$ for the four-layered symmetric $[(0^{\circ },{90}^{\circ })_{1}]_{S}$ cross-ply laminated square plate having thickness ratio of $a/h=25$ subjected to periodic longitudinal load having static load factor of $\alpha =0$ and dynamic load factor of $\beta =0.3$

In the analysis of dynamic stability of plates and shells, there exists simultaneously the stable- and unstable solutions. Figure 4 presents the effect of orthotropy on both the stable- and unstable-solution amplitudes of steady-state vibrations of the first mode, $\left( m,n \right) =\left( 1,1 \right) ,$ for the four-layered symmetric ${[{(0^{\mathrm {^{\circ }}},90^{\mathrm {^{\circ }}})}_{1}]}_{S}$ cross-ply laminated square plate. The plates have thickness ratio of $a/h=25$ and subjected to periodic longitudinal load with static load factor of $\alpha =0$ and dynamic load factor of $\beta =0.3$. The critical buckling load and fundamental frequency of the plate for all these three cases of $\frac{E_{1}}{E_{2}}$ are the same as the case which is explained in Fig. 3. It is a characteristic of the nonlinear response that the resonance curves are bent toward the axis of increasing frequencies [3]. The difference between these two solutions refers to the required magnitudes of frequency and amplitude to stimulate a parametric resonance. If this difference between them is small, then there might be the possibility of occurring parametric resonance. If the difference is large, it means high values of vibration frequency and amplitude are needed to stimulate a possible parametric resonance. The dynamic stability of such a plate or shell system is said to be good [1, 18]. As it is observed from this figure both the stable and unstable amplitudes of steady-state vibrations shift to the right having lower frequencies of excitation; or in other words, at any certain excitation frequency both stable and unstable amplitudes of steady-state vibrations increase as the ratio of $\frac{E_{1}}{E_{2}}$ is decreased. Also it is evident from this figure that once the amplitude is zero the corresponding excitation frequency coincides with the boundaries of dynamically unstable regions, having dynamic load factor of $\beta =0.3$. The zero stable- and unstable-solution amplitudes of this figure exactly coincide with the left and right curves of corresponding unstable regions, respectively, shown in Fig. 3 and the range of frequencies between these two solutions at $A=0$ predicate the dynamically unstable regions at this certain value of dynamic load factor $\beta$. So this figure shows graphically that unstable regions could be obtained by setting $A=0$ in Eq. (40) and it could be considered as a validation of this nonlinear part of dynamic instability analysis.

Fig. 5

Comparison of both the stable- and unstable-solution amplitudes of steady-state vibrations of the present study with those of Ostiguy et al. [19] for isotropic homogeneous rectangular plate having aspect ratios of $a/h=400$ and $a/b=2.45$ subjected to periodic longitudinal load having static component of $F_{s}=-0.5\,N_{\mathrm{cr}}^{*}$ and dynamic component of $F_{d}=-0.2\,N_{\mathrm{cr}}^{*}$

Fig. 6

Comparison of both the stable- and unstable-solution amplitudes of steady-state vibrations of the present study with those of Ostiguy et al. [19] for isotropic homogeneous rectangular plate having aspect ratios of $a/h=400$ and $a/b=2.45$ subjected to periodic longitudinal load having static component of $F_{s}=-0.8\,N_{\mathrm{cr}}^{*}$ and dynamic component of $F_{d}=-0.2\,N_{\mathrm{cr}}^{*}$

As another validation of the nonlinear part of dynamic instability analysis, i.e., both the stable- and unstable-solution amplitudes of steady-state vibrations, the present results are compared with those given by Ostiguy et al. [19] for isotropic homogeneous rectangular plate in Figs. 5 and 6. To compare the results we set in our formulation the material property as $E_{1}=E_{2}=E=4.83$ GPa, $\upsilon _{12}=\upsilon =0.38$ and $\rho =1190$ kg/m$^{3}$ and the geometry of the plate as $a=50$ cm, $b=20.4$ cm and $h=0.125$ cm. The static component of the periodic longitudinal load in these two figures is considered as $F_{s}=-0.5\,N_{\mathrm{cr}}^{*}$ and $F_{s}=-0.8\,N_{\mathrm{cr}}^{*}$ , respectively, and the dynamic component is considered as $F_{d}=-0.2\,N_{\mathrm{cr}}^{*}$ for both figures where $N_{\mathrm{cr}}^{*}$ is the buckling load according to Ostiguy et al. [19] as follow:

$$\begin{aligned} N_{\mathrm{cr}}=\frac{\pi ^{2}D}{b^{2}}{\left( m_{c}\frac{b}{a}+\frac{1}{m_{c}}\frac{a}{b}\right) }^{2} \end{aligned}$$

(50a)

where

$$\begin{aligned} D=\frac{Eh^{3}}{12(1-\upsilon _{12}^{2})} \end{aligned}$$

(50b)

and $m_{c}$ is the “number of half waves of prevalent buckling mode” which “depends strongly on the aspect ratio of the plate” [19]. It is observed from these figures that there is an excellent agreement between the present results with those obtained by Ostiguy et al. [19] and as one can see all the corresponding plots of $\left( m,n \right) =\left( 3,1 \right) ,\,\left( 4,1 \right) {\text { and }}\left( 5,1 \right)$ completely coincide with each other and there is small and acceptable difference for lower mode of $\left( m,n \right) =\left( 2,1 \right)$ between the present results and those by Ostiguy et al. [19]. This difference could be due to considering the Navier’s double Fourier series for displacement function $w_{0}(x,y,t)$ of simply supported boundary condition in the present work which is more accurate even for lower value of $m=2$ of upper limits of summation in Eq. (25) than the solution for the stress function which has been represented by a truncated double series consisting of Beam Functions in the later study that leads to “determination of the elasticity parameter, whose value is dependent on the number of terms taken in the double series” [19]. The authors of the later article also mentioned in their work that the convergence characteristic of that elasticity parameter indicates that more terms were needed for convergence as the order of (m) of the spatial mode is increased [19]. Hence their solution for lower values of m doesn’t have sufficient accuracy so one can see from these two figures (Figs. 5, 6) that once the upper limits of summation of m increase to $m=3,4,5,\ldots$ excellent agreement is achieved between these two studies.

6.2 Effect of variation of lamination schemes

For isotropic plate the buckling load in terms of engineering constants is given by Timoshenko and Gere as [20]

$$\begin{aligned} N_{\mathrm{cr}}=\frac{\pi ^{2}D}{b^{2}}{\left( \frac{b}{a}+\frac{a}{b}\right) }^{2} \end{aligned}$$

(51a)

where

$$\begin{aligned} D=\frac{Eh^{3}}{12(1-\nu ^{2})} \end{aligned}$$

(51b)

The mechanism of dynamic buckling is similar to static buckling and the only difference is the additional considerations of the inertia force so that it leads to the dynamic buckling load to be lower than the static buckling load for the same structure. But the mechanism of dynamic instability is much more complex since in both static and dynamic buckling the main factor is only the critical static or dynamic load amplitude while in dynamic instability, not only the vibration amplitude of dynamic load, but also the vibration frequency together with the simulating frequency will play important roles. So the dynamic instability of the plate or shell structure will be occurred at much lower loads.

For laminated rectangular plates, the critical buckling load is approximated as

$$\begin{aligned} {{(N}_{\mathrm{cr}})}_\text {Composite}=\frac{\pi ^{2}D^{*}}{b^{2}}{\left( \frac{b}{a}+\frac{a}{b}\right) }^{2} \end{aligned}$$

(52a)

where

$$\begin{aligned} D^{*}=\frac{E_{2}h^{3}}{12(1-\nu _{12}\nu _{21})} \end{aligned}$$

(52b)

This approximates the static buckling load for laminated rectangular plate and hence for the dynamic instability analysis both the static part of the load $F_{s}$ and the periodic part $F_{d}$ in Eq. (1) should be a percentage of this buckling load. This is why we have considered conservatively in the next tables and figures that $F_{s}=(0.1, 0.3, 0.5)N_{\mathrm{cr}}$ and corresponding periodic part as $F_{d}=0.3F_{s}$.

The dimensionless excitation frequency parameter p which is mentioned in the next figures and tables is introduced as follow:

$$\begin{aligned} p=2\pi bP\sqrt{\frac{\rho _{t}}{A_{11}}} \end{aligned}$$

(53)

To compare the results in the following tables we specified each unstable region by the nondimensional frequency parameter p of the point of origin and the half angle of the unstable region as $\theta$.

Here and in following figures, tables and discussions the first two primary steady-state vibrations (from left to right) refer to the first two modes.

Fig. 7

The first mode unstable region corresponding to various lamination schemes for the antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.1N_{\mathrm{cr}}$

Fig. 8

The stable-solution amplitude of steady-state vibrations of the first mode corresponding to various lamination schemes for the antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.1N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$

Table 1 The first two unstable regions of an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.1N_{\mathrm{cr}}$

Table 2 The stable- and unstable-solution amplitudes corresponding to first mode, $\left( m,n \right) =(1,1)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.1N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=1$

Table 3 The stable- and unstable-solution amplitudes corresponding to second mode, $\left( m,n \right) =(1,2)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.1N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=3.5$

Table 4 The stable- and unstable-solution amplitudes corresponding to first mode, $\left( m,n \right) =(1,1)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.3N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=1$

The effects of variation of the lamination scheme on the first two modes, dynamically unstable regions and both stable- and unstable-solution amplitude of steady-state vibrations of antisymmetric cross-ply laminated rectangular plates are presented in Figs. 7, 8, and Tables 1, 2 and 13. Figure 7 and 8 show the influence of the lamination scheme on the fundamental mode of dynamically unstable regions and corresponding stable-solution amplitude-frequency curve of steady-state vibrations for antisymmetric cross-ply laminated plates, respectively. The plates are subjected to tensile loading of $F_{s}=0.1N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$. It is observed that the first mode unstable regions and amplitude of steady-state vibrations shift to the right along the frequency axis having higher frequencies of excitation as the number of layers are increased. This is probably due to the bending-extension coupling of lamination which is reduced by increasing the number of the plies in antisymmetric cross-ply laminates. This shifting to the right of frequency axis of both unstable regions and the steady-state amplitude (reducing the amplitude at a certain excitation frequency) is reduced once the number of layers is doubled and appears to converge at a certain value as can be observed from these figures that the unstable regions of eight- and ten-layered laminates are too close to each other and the amplitudes of eight- and ten-layered laminates almost coincide with each other.

Table 5 The stable- and unstable-solution amplitudes corresponding to second mode, $\left( m,n \right) =(1,2)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.3N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=3.5$

Table 6 The stable- and unstable-solution amplitudes corresponding to first mode, $\left( m,n \right) =(1,1)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.5N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=1$

Table 7 The stable- and unstable-solution amplitudes corresponding to second mode, $\left( m,n \right) =(1,2)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.5N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=3.5$

Table 8 The stable- and unstable-solution amplitudes corresponding to first mode, $\left( m,n \right) =(1,1)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to compressive loading of $F_{s}=-0.1N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=1$

Table 9 The stable- and unstable-solution amplitudes corresponding to second mode, $\left( m,n \right) =(1,2)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to compressive loading of $F_{s}=-0.1N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=3.5$

Table 10 The stable- and unstable-solution amplitudes corresponding to first mode, $\left( m,n \right) =(1,1)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to compressive loading of $F_{s}=-0.3N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=1$

Table 11 The stable- and unstable-solution amplitudes corresponding to second mode, $\left( m,n \right) =(1,2)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to compressive loading of $F_{s}=-0.3N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=3.5$

Table 12 The stable- and unstable-solution amplitudes corresponding to first mode, $\left( m,n \right) =(1,1)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to compressive loading of $F_{s}=-0.5N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=1$

Table 13 The stable- and unstable-solution amplitudes corresponding to second mode, $\left( m,n \right) =(1,2)$, of steady-state vibrations for an antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to compressive loading of $F_{s}=-0.5N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=3.5$

Table 14 The first two unstable regions of a ten-layered antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to various tensile loading

Table 15 The first two unstable regions of a ten-layered antisymmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to various compressive loading

Table 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 also present a detailed study considering again the effects of variation of the lamination scheme on the first two modes of unstable regions and both stable and unstable-solution amplitude of steady-state vibrations of antisymmetric cross-ply laminated plate, respectively. In Table 1 the results have been listed for unstable regions which are specified by the points of origin and the half angle of the unstable region $\theta$ as mentioned before for the tensile load, $F_{s}=0.1N_{\mathrm{cr}}$. Tables 2, 3, 4, 5, 6, 7 present the result for both stable- and unstable-solution amplitude of steady-state vibrations for three different tensile loads, $F_{s}=0.1N_{\mathrm{cr}}$, $F_{s}=0.3N_{\mathrm{cr}}$ and $F_{s}=0.5N_{\mathrm{cr}}$ and the corresponding results for compressive loads, $F_{s}=-0.1N_{\mathrm{cr}}$, $F_{s}=-0.3N_{\mathrm{cr}}$ and $F_{s}=-0.5N_{\mathrm{cr}}$ are tabulated in Tables 8, 9, 10, 11, 12 and 13. For the comparison studies the results in Tables 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13 are normalized using the same nondimensional excitation frequency $p{=1}$. All the discussions and corresponding observations that were mentioned in the previous paragraph about Figs. 5 and 6 for unstable regions and amplitude of stead-state vibrations are also observed from Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13, respectively, and hence are valid. In addition it is also observed from Tables 1 and 2 and 3 which are for the first two modes’ unstable regions and amplitude of steady-state vibrations, respectively, of the plate with stacking sequence of ${(0}^{\circ }\,/{90}^{\circ }\,/0^{\circ } \ldots )$ have exactly the same unstable regions and amplitude of steady-state vibrations both in stable- and unstable-solutions in comparison with the laminations with the stacking sequence of ${(90}^{\circ }\,/0^{\circ }\,/{90}^{\circ } \ldots )$. It means that these two different stacking sequences for the plate show equal rigidity although in the study of Ng et al. [21] for dynamic unstable regions of laminated cylindrical shells it is revealed that ${(0}^{\circ }/{90}^{\circ }\, /0^{\circ } \ldots )$ laminate shows more rigidity. Hence in the following Tables 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13 only the results are listed for one of these lamination stacking sequences, i.e., the stacking sequence of ${(0}^{\circ }/{90}^{\circ }\,/0^{\circ } \ldots )$.

6.3 Effect of magnitude and direction of the longitudinal loads

Comparing the results in Tables 2, 3, 4, 5, 6, and  7 indicate that by increasing the magnitude of tensile longitudinal loading from $F_{s}{=0.1}N_{\mathrm{cr}}$ to $F_{s}{=0.5}N_{\mathrm{cr}}$ both the stable and unstable solutions of amplitudes decrease which means that the corresponding excitation frequency that causes instability shifts to the right along frequency axis having higher frequencies. Hence it can be expected that by increasing the tensile longitudinal load the plate stiffness is also increased. The inverse trend can be seen in the case of compressive loading. For the compressive loading the results for amplitudes have been listed in Tables 8, 9, 10, 11, 12 and 13. The plates have higher stable and unstable amplitudes as the magnitude of longitudinal compressive loading is increased from $F_{s}{=-0.1}N_{\mathrm{cr}}$ to $F_{s}{=-0.5}N_{\mathrm{cr}}$ meaning that the corresponding excitation frequency that causes instability shifts to the left along frequency axis having lower frequencies. This was expected since by increasing the magnitude of longitudinal compressive loading the plate stiffness reduces. To study these effects for first two modes of unstable regions the results for points of origin and the corresponding angle of unstable region which predicate as a factor for magnitude of the areas of these regions, are listed in Tables 14 and 15 for a ten-layered antisymmetric laminated rectangular plate subjected to various magnitudes of tensile and compressive loads, respectively. The results illustrate that instability regions shift to the right along frequency axis having higher excitation frequencies once the magnitude of longitudinal tensile load is increased from $F_{s}{=0.1}N_{\mathrm{cr}}$ to $F_{s}{=0.5}N_{\mathrm{cr}}$. This also can be expected as was mentioned above that increasing the tensile longitudinal loads causes the plate’s stiffness to increase. Although the results in Table 15 indicate that the inverse trend can be seen in the case of compressive loading, in compressive loading conditions increasing the absolute magnitude of compressive loads from $Fs= -0.1Ncr$ to $Fs=-0.3Ncr$ causes the instability region to shift to the left along frequency axis having lower excitation frequencies. This can be expected and noted in the above that by increasing the magnitude of longitudinal compressive loads plate’s stiffness is reduced. It can be observed from these two tables that the widths of instability regions are increased once the absolute values of magnitude of longitudinal loads are increased for both tensile and compressive loading conditions. Comparing the results for symmetric laminates in Tables 16, 17, 18 and 19 with corresponding results for antisymmetric laminate in Tables 5, 6, 11 and 12 also reveal that at the same nondimensional frequency parameter (p) for both the tensile and compressive load conditions, symmetric laminates having stacking sequence of ${[{(0^{\circ },90^{\circ })}_{n}]}_{S}$ have higher amplitudes (having lower excitation frequencies) than antisymmetric $(0^{\circ }{/9}0^{\circ }{/\ldots )}$ laminates even though this trend is inverse for the case of lamination schemes of symmetric ${[{(90^{\circ },0^{\circ })}_{n}]}_{S}$ and antisymmetric $(90^{\circ }{/}0^{\circ }{/\ldots )}$ laminates. This outcome is in good agreement with that reported by Najafov et. al [22] for nonlinear free vibration of truncated orthotropic thin laminated conical shells.

Table 16 The stable- and unstable-solution amplitudes corresponding to first mode, $\left( m,n \right) =(1,1)$, of steady-state vibrations for a symmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.5N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=1$

Table 17 The stable- and unstable-solution amplitudes corresponding to second mode, $\left( m,n \right) {=(1,2)}$, of steady-state vibrations for a symmetric cross-ply laminated rectangular plate having aspect ratios of $a/b{=2}$ and $a/h{=100}$ subjected to tensile loading of $F_{s}{=0.5}N_{\mathrm{cr}}$ and $F_{d}{=0.3}F_{s}$ under the excitation with nondimensional frequency parameter $p=3.5$

Table 18 The stable- and unstable-solution amplitudes corresponding to first mode, $\left( m,n \right) =(1,1)$, of steady-state vibrations for a symmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to compressive loading of $F_{s}=-0.5N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=1$

6.4 Effect of symmetry in variation of lamination schemes

To examine the effect of symmetry in lamination schemes of the studied laminated plate on both stable- and unstable-solution amplitudes of the steady-state vibrations, the results are listed in Tables 16, 17, 18 and 19 for the tensile and compressive axial loads, respectively. A graphical presentation of Table 16 also is provided in Fig. 9. The first and second modes in these tables refer to the modes (1,1) and (1,2), respectively, which shows no change in terms of wave numbers in comparison with antisymmetric laminates which are listed in Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15. All the above discussions about Tables 6, 7, 12, and 13 and Fig. 8 are valid about Tables 16, 17, 18 and 19 and Fig. 9, respectively. It can also be observed from these tables and Fig. 9 again that by increasing the number of plies in symmetric laminate the amplitude of steady-state vibrations converges at a certain value where the nondimensional amplitude vs nondimensional frequency curves of twenty, twenty-four and twenty-eight plies almost coincide with each other. It is also observed that in symmetric laminated plates both stable- and unstable-solutions amplitude of steady-state vibration do not have the same values for stacking sequence of ${[{(0^{\circ },90^{\circ })}_{n}]}_{S}$ and ${[{(90^{\circ },0^{\circ })}_{n}]}_{S}$ although as it was mentioned before these results have the same values in the case of antisymmetric laminated plates. However by increasing the number of plies in symmetric laminate the difference is decreased.

Fig. 9

The stable-solution amplitude of steady-state vibrations of the first mode corresponding to various lamination schemes for the symmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to tensile loading of $F_{s}=0.5N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$

Comparing the results of symmetric laminates in Tables 16, 17, 18 and 19 with corresponding results for antisymmetric laminate in Tables 5, 6, 11 and 12 also reveal that at the same nondimensional frequency parameter (p) for the both tensile and compressive load conditions, symmetric laminates having stacking sequence of ${[{(0^{\circ },90^{\circ })}_{n}]}_{S}$ have higher amplitudes (having lower excitation frequencies) than antisymmetric $(0^{\circ }{/9}0^{\circ }{/\ldots )}$ laminates even though this trend is inverse for the case of lamination schemes of symmetric ${[{(90^{\circ },0^{\circ })}_{n}]}_{S}$ and antisymmetric $(90^{\circ }{/}0^{\circ }{/\ldots )}$. This outcome is in good agreement with that reported by Najafov et. al [22] for nonlinear free vibration of truncated orthotropic thin laminted conical shells.

Table 19 The stable- and unstable-solution amplitudes corresponding to second mode, $\left( m,n \right) =(1,2)$, of steady-state vibrations for a symmetric cross-ply laminated rectangular plate having aspect ratios of $a/b=2$ and $a/h=100$ subjected to compressive loading of $F_{s}=-0.5N_{\mathrm{cr}}$ and $F_{d}=0.3F_{s}$ under the excitation with nondimensional frequency parameter $p=3.5$

Fig. 10

Variation of the first mode unstable region with plate’s length of a ten-layered ${(0^{^{\circ }}/90^{^{\circ }})}_{5}$ antisymmetric cross-ply laminated rectangular plate having thickness ratio $a/h=100$ subjected to tensile loading of $F_{s}=0.5N_{\mathrm{cr}}^{*}$; $N_{\mathrm{cr}}^{*}$ corresponds to buckling load of the case $a/b=2$

Table 20 Variation of the first two unstable regions with plate’s aspect ratio of a ten-layered ${(0^{^{\circ }}/{90}^{^{\circ }})}_{5}$ antisymmetric cross-ply laminated plate having thickness ratio of $a/h=100$ subjected to tensile loading of $F_{s}=0.5N_{\mathrm{cr}}^{*}$; $N_{\mathrm{cr}}^{*}$ corresponds to buckling load of the case $a/b=2$

Fig. 11

Variation of the first two stable-solution amplitudes of steady-state vibrations with plate’s length of a ten-layered ${(0^{^{\circ }}/{90}^{^{\circ }})}_{5}$ antisymmetric cross-ply laminated rectangular plate having thickness ratio $a/h=100$ subjected to tensile loading of $F_{s}=0.5N_{\mathrm{cr}}^{*}$; $N_{\mathrm{cr}}^{*}$ corresponds to buckling load of the case $a/b=2$ and $F_{d}=0.3F_{s}$

Fig. 12

Variation of the first mode unstable region with plate’s thickness of a ten-layered ${(0^{^{\circ }}/90^{^{\circ }})}_{5}$ antisymmetric cross-ply laminated square plate subjected to compressive loading of $F_{s}=-0.3N_{\mathrm{cr}}^{*}$; $N_{\mathrm{cr}}^{*}$ corresponds to buckling load of the case $a/h=120$

6.5 Effect of the length-to-width ratio

The effect of variation of the aspect ratio of the laminated plates, i.e., length-to-width ratio a / b on the instability regions and stable-solution amplitudes of the steady-state vibrations for the ten-layered ${(0^{^{\circ }},{90}^{^{\circ }})}_{5}$ cross-ply laminated plate having thickness ratio $a/h=100$ subjected to longitudinal tensile loading of $F_{s}=0.5N_{\mathrm{cr}}$ are shown in Fig. 10, Table 20 and Fig. 11, respectively. The plots of amplitudes are depicted in Fig. 11 based on the dynamic term of the longitudinal load as $F_{d}=0.3F_{s}$. Since here the length a of the plates is kept constant and to study the variation of aspect ratio the width of the plates b is varied the nondimensional frequency parameter $p^{*}$ is defined as follow:

$$\begin{aligned} p^{*}=2\pi aP\sqrt{\frac{\rho _{t}}{A_{11}}} \end{aligned}$$

(54)

The results show that with a decrease in width of the plate, i.e., overall increase in aspect ratio of a / b , the plate’s stiffness is increased as well, hence the dynamically unstable regions shift to the right along frequency axis having higher frequencies of excitation of point of origins, the widths of instability regions are increased and also the amplitudes of steady-state vibrations at any specific frequency are decreased. This is in full agreement with the corresponding study of Ramachandra et al. [11] for dynamically unstable regions.

6.6 Effect of the length-to-thickness ratio

Figure 12, Table 21 and Fig. 13 present the effect of variation of the thickness ratio a / h on the instability regions and stable-solution amplitudes of the steady-state vibrations for the ten-layered ${(0^{\circ },90^{\circ })}_{\mathrm {5}}$ cross-ply laminated square plate subjected to longitudinal compressive loading of $F_{s}{=-0.3}N_{\mathrm{cr}}$. The plots of amplitudes are depicted in Fig. 13 based on the dynamic term of the longitudinal load as $F_{d}{=0.3}F_{s}$. It is observed that with a decrease in thickness of the plate, i.e., overall increasing the length-to-thickness ratio a / h , the dynamically unstable regions shift to the left along the frequency axis having lower frequencies of point of origin, the widths of instability regions are decreased and also the amplitudes of steady-state vibrations at any specific frequency are increased. This is due to the fact that decreasing the thickness of plate makes the plate to be less stiff. This is also in full agreement with the corresponding study of Moorthy and Reddy [9]. This is also in full agreement with the corresponding study of Lam and Ng [21] for dynamically unstable regions of laminated composite cylindrical shells.

Table 21 Variation of the first two dynamically unstable regions with plate’s thickness of a ten-layered ${(0^{^{\circ }}/{90}^{^{\circ }})}_{5}$ antisymmetric cross-ply laminated square plate subjected to compressive loading of $F_{s}=-0.3N_{\mathrm{cr}}^{*}$; $N_{\mathrm{cr}}^{*}$ corresponds to buckling load of the case $a/h=120$

Fig. 13

Variation of the first two stable-solution amplitudes of steady-state vibrations with plate’s thickness of a ten-layered ${(0^{^{\circ }}/90^{^{\circ }})}_{5}$ antisymmetric cross-ply laminated square plate subjected to compressive loading of $F_{s}=-0.3N_{\mathrm{cr}}^{*}$; $N_{\mathrm{cr}}^{*}$ corresponds to buckling load of the case $a/h=120$ and $F_{d}=0.3F_{s}$

7 Conclusions

The nonlinear dynamic stability of both antisymmetric and symmetric cross-ply laminated composite plates under combined static and periodic longitudinal loading has been studied. Equations of motion with von Karman-type of nonlinearity were solved by employing Galerkin’s technique. By applying Bolotin’s method to the governing system of nonlinear Mathieu-Hill equations the amplitudes of both stable and unstable solutions were obtained for steady-state vibrations. It is confirmed that instability regions and both stable and unstable-solution amplitudes of steady-state vibrations are significantly influenced by the lamination schemes including symmetric and antisymmetric lamination, the number and sequence of the plies, magnitude and direction of the longitudinal periodic loads, aspect ratios of the plate including length-to-width and length-to-thickness ratios, and in-plane transverse wave number. Hence in any particular application specific configurations of laminate should be considered in design of composite plates. A comparative study of the present work with those available in literature shows a very good agreement. However, as the results of the present study reveal, the linear analysis carried out in available literature can only provide the information about the instability region and unable to predict the vibration amplitudes in these regions. The nonlinear analysis developed in the present work can determine such vibration amplitudes. The present work has shown that there is vibration with steady-state amplitude in the instability region which approaches almost constant amplitude when the excitation frequencies are increased. Hence, for more perfect and complete studies of dynamic instability of laminated plates, the nonlinear analysis is required to determine both the stable and unstable amplitudes of steady-state vibrations in addition to instability regions. Where the occurrence of dynamic instability is inevitable, in order to have a control on vibration amplitudes in the unstable regions the nonlinear analysis is required. By adjusting the corresponding effective parameters as explained in the present work, steady-state vibrations with allowable amplitudes based on the design criteria can be achieved in the dynamically unstable regions.

The major outcomes of the present study are summarized as follow:

• For both symmetric and antisymmetric laminated plates, amplitudes of steady-state vibrations are decreased, corresponding dynamically unstable regions shift to the right along the frequency axis having higher frequencies of excitation, and the widths of the instability regions are decreased when the number of plies are increased. Convergence is also achieved at a specific number of the plies in each case.

• Increasing the magnitude of compressive longitudinal load causes increasing amplitude of steady-state vibrations, shifting dynamically unstable regions to the left along the frequency axis, and increasing albeit the widths of instability regions.

• Increasing the magnitude of tensile longitudinal loads results in decreasing the amplitude of steady-state vibrations, shifting dynamically unstable regions to the right along the frequency axis, and increasing albeit the widths of instability regions.

• With an increase in aspect ratio a / b of the plate, the dynamically unstable regions shift to the right along frequency axis having higher frequencies of excitation of point of origin, the widths of instability regions are increased and also the amplitudes of steady-state vibrations are decreased.

• Increasing the thickness ratio a / h causes the dynamically unstable regions shift to the left along frequency axis having lower frequencies of excitation of point of origin. Moreover the widths of instability regions are decreased and also the amplitudes of steady-state vibrations are increased.

The present work can be used as a bench mark study in future studies on dynamic instability of laminated composite plates.

Appendix A

$$\begin{aligned} M_{mn}= & {} -16 {\uppi } a^{4} \,A22\,{\uprho }_{t}A11(A22\,A66\,a^{4}\,n^{4}+n^{2}(A11 A22\\&-\,A12(A12+2A66)) m^{2}b^{2}a^{2}+A11 \,A66 \,b^4 m^{4})mb^{4}\\ Q_{mn}= & {} 16 \,A11 \,A33 \,a^{2} m^{3} (A22 \,A66 \,a^{4}n^{4}+ n^{2}(A11\,A22\\&-\,A12 (A12+2 A66))m^{2}\,b^{2}\,a^{2} +A11 \,A66 \,b^{4}m^{4}){\uppi }^{3}b^{4} \\ {\upeta }_{mn}= & {} (A11 b^{4} \,m^{4}+ A22\, a^{4}n^{4}) {\uppi }^{5}m (A11 \,A22\\&-\,A12^2)(A22 \,A66 \,a^{4}\,n^{4}+n^2(A11 \,A22-A12 (A12\\&+\,2 A66)) m^2 b^2a^2+A11 \,A66 b^{4} m^{4}) \\ K_{mn}= & {} 16m \,A22 \,A11{\uppi }^{5}(b^{8}\,A66 (-A11 \,D11 +B11^{2})m^{8}\\&+\,(D11\, A12^{2}+ (2 D11 \,A66-2B11 (B12\\&+\,2B66))A12+(-D11 \,A22 + (-2 D12-4 D66)A66\\&+\,(B12+2B66)^2)A11+B11^{1}\, A22) a^{2}\,n^{2}\,b^{6}\,m^{6}\\&+\,2\,a^{4} n^{4}\,b^{4}((D12+2D66)A12^{2}\\&+\,((2D12+4D66)A66-B22 \,B11-B12^{2}\\&-\,4B66\,B12-4B66^2)A12+ \left( (-2D66-D12)A22 \right. \\&\left. -\,\frac{1}{2}D22\,A66+B22(B12+2 B66)\right) A11 \\&+\left( \frac{1}{2}D11 A66+ B11 (B12+2B66)\right) A22\\&-\,B11\,B22\,A66) m^4+(D22 \,A12^{2} \\&+\,(2 D22 \,A66 -2 B22(B12+2B66))A12\\&+\,(-A22\,D22+B22^2)A11+A22((-2D12\\&-\,4D66)A66+(B12+2B66)^2))a^{6}\,n^{6}b^{2}m^{2}\\&+\,a^{8}n^{8}A66(-A22 \,D22 +B22^{2})) \end{aligned}$$