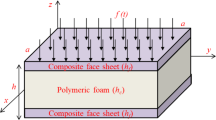
In this paper, the dynamic stability of foam-filled sandwich plates with stiff composite laminated faces subjected to an arbitrary periodic load is studied. The load is taken to be a combination of periodic bending and normal stresses. The governing equations are established by using the Galerkin method with a reduced eigenfunctions transformation. The equations of motion of Mathieu type are derived and used to determine the regions of dynamic instability based on Bolotin’s method. A numerical approach is developed to determine the dynamic stability of foam-filled sandwich plates. The effects of load parameters and core layer thickness on the excitation frequency, dynamic stability region and dynamic instability index are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1. Introduction
Sandwich structures have been increasingly used in many engineering applications. Sandwich plates confront the problem of dynamic stability when they are subjected to a periodic load. The plate under a periodic in-plane load generally experience in-plane vibrations, but out-of plane vibrations also arise at certain frequencies. A periodic load can also induce a violent vibration that is called the dynamic instability phenomenon of parametric resonance. A comprehensive study on the dynamic stability is given in the book by Bolotin [1].
The problems of dynamic stability of sandwich plates have been studied by many researchers with the use various approximate methods. To estimate the dynamic behavior of a sandwich plate with a viscoelastic core, Chen employed an integral finite-element method [2]. Sorokin [3] performed an analysis of resonant vibrations of a sandwich plate with a honeycomb core by using the parametric stiffness modulation. Mackerle [4] presented special finite elements developed for the analysis of sandwich plates in various fields of engineering. A bibliographical review of sandwich structures, including their properties, vibration, dynamic response, heat transfer, contact problems, fracture mechanics, and so on, was presented. The dynamic stability of circular sandwich plates subjected to a periodic uniform radial loading was studied by Wang [5]. A modified complex eigensolution method was employed to solve eigenvalue problems. The numerical results obtained revealed that a constrained damping layer attached to circular plates tended to stabilize the systems of circular plates. The parametric resonance of sandwich plates with a viscoelastic core layer subjected to a periodic uniform radial stress was studied by Chen [6]. The tensile and shear moduli of the core were described by complex quantities. The regions of dynamic instability were determined by Bolotin’s method. The effects of various parameters on the regions were investigated. The dynamic stability of a sandwich plate with an electrorheological fluid core was investigated by Yeh [7]. Smart composite plates with periodically arranged embedded actuators were investigated by Kalamkarov [8]. Matsunaga [9] presented an analyzis of free vibrations and stability of sandwich plates subjected to a thermal loading. Several approximate theories were employed to solve the corresponding governing equations. The natural frequencies and critical temperatures of sandwich plates under thermal loadings were studied. The dynamic instability of sandwich plates with interfacial slips was investigated by Chakrabatri [10]. A linear spring-layer model was used to model interfacial slips and to understand the behavior of laminated materials.
Pomazi [11] presented a review report on the stability of sandwich plates with hard orthotropic and soft isotropic layers. The vibration frequencies and buckling stresses of sandwich plates were studied by Yuan [12]. The plate were reinforced with a number of longitudinal stiffeners attached to faceplates. A stability analysis of simply supported sandwich plates with stiff face sheets bonded to a soft core layer was carried out by Kant [13]. Their equilibrium equations were obtained using the principle of minimum potential energy. A stability analysis of sandwich plates resting on elastic media was used by Jayachandran [14] to compute the elastic buckling coefficient of the plates. A finite element for stability analyses of sandwich plates was proposed by Linke [15]. Shiau [16] developed a linear flutter analysis of thermally buckled composite sandwich plates. Free vibrations of sandwich plates with honeycomb and PVC foam cores were considered by Burlayenko [17]. The natural frequencies and the corresponding vibration modes of the plates were calculated by the finite-element method. The dynamic response of square honeycomb sandwich plates was investigated by Wang [18]. The vibration behavior of composite plates with arbitrary initially stresses were analyzed in [19–21]. The Galerkin method was used to reduce the corresponding partial differential equations to ordinary differential ones.
In the present paper, dynamic vibrations of foam-filled sandwich plates are investigated. Foam-filled sandwich plates with stiff face sheets bonded to the soft core material exhibit a higher bending stiffness and offer lightweight high-strength laminated structures. The effects of transverse shear strains and rotary inertia are included in the partial differential governing equations. In the analysis, the Galerkin method is applied to the governing partial differential equations to get ordinary differential equations. The Mathieu equations obtained are solved by employing Bolotin’s method to obtain the regions of dynamic instability. The effects of various parameters on the excitation frequency, the region of dynamic stability, and the dynamic instability index are investigated.
2. Theoretical Formulation
Following the technique described by Brunelle [22] and Chen [21], the governing equations are derived using the perturbation technique. For a nonuniform initially stressed body which is in equilibrium and is subjected to time-varying incremental deformations, the governing equations can be expressed as
where σ ij , \( {\bar{\sigma}_{is}} \), \( {\bar{u}_s} \), \( {\bar{F}_s} \), and ∆F s are the initial stress, the perturbing stress, displacement, the perturbing body force, and the body force, respectively.
In this paper, the Reissner–Mindlin plate theory is used to study the dynamic behavior of sandwich plates. The incremental displacements are assumed in the form
where u x , u y , and w are midplane displacements in the x, y, and z directions, respectively; φ x and φ y are rotation angles about the y and x axes, respectively. The x and y axes of the coordinate system used are set to coincide with two edges of the rectangular laminate. The constitutive relationships of the laminate can be written in the following form:
where C ij are stiffnesses of the material.
The general time-dependent initial stress system applied to the rectangular sandwich plate is assumed to be
which consists of spatially uniform longitudinal, transverse, shear, bending, and twisting stresses. Here, σ ij S and σD ij are the static and dynamic components of the periodic normal or shear stress σ ij n; σ ij Sm and σ ij Dm are the static and dynamic components of the periodic pure bending or torsion stress σ ij m; ω is the disturbing frequency of dynamic loads.
The governing equations can be obtained by using the method of average stresses. Inserting Eqs. (2)-(4) into Eq. (1) and performing integration yields the dynamic equations for the rectangular sandwich plate
where
Here, C ij are the elastic constants and ρ is density; A ij , B ij , and D ij are the stiffness coefficients; κ is a shear correction factor; N ij , M ij , and M * ij are stress resultants; f x , f y , f z , m x , and m y are the lateral loads at the top and bottom faces of the plate and the body forces. The superscripts ‘+’ and ‘–’ denote the stresses at the top and bottom face of the plate, respectively.
3. Analysis of Dynamic Instability
It would be difficult to present results for the dynamic behavior of arbitrary sandwich plates under periodic loads. Therefore, only a simply supported rectangular sandwich plate of uniform thickness h subjected to a periodic load is considered. The lateral loads and body forces are taken to be zero, namely f x , f y , f z , m x , m y = 0. The periodic load in Eq. (4) is assumed to be a combination of a pulsating uniform tensile stress σ n and a pure bending stress σ m :
where σ n = σS xx + σD xx cos ωt = σS + σD cos ωt and σ m = σSm xx + σDm xx cos ωt = σSm +σDm cos ωt. The static and dynamic stresses σS, σD, σSm, and σDm are taken to be constant. The only nonzero initial loads are N xx = hσ n , M xx = βh 2σ m /6, and M xx * = h 3σ n /12, where β = σ m /σ n .
For a sandwich plate simply supported along the sides x = 0, a, and y = 0, b, the vibration modes satisfying the geometric boundary conditions are
All the sums are taken from m, n = 1 to ∞. Insertion of Eqs. (10) into Eqs. (5)-(9) leads to the matrix equation
Here, [M], [K], and [G] are the mass, elastic stiffness, and geometric stiffness matrices, respectively, of the sandwich plate; Δ denotes the time-dependent generalized displacement parameters.
In the absence of an in-plane load and with ∆(t) = ∆e iωt, Eq. (11) is reduced to the form
which is associated with the eigenvalue problem of free vibrations of the sandwich plate. For existence of a nontrivial solution to the equation system, its determinant must be equal to zero. Hence, the natural frequency can be obtained by solving the equation
When the inertia term in Eq. (11) is set to zero, the eigenvalue problem related to buckling of the plate is obtained. The static buckling loads N xx are found from the equation
An analysis of the dynamic stability of the sandwich plate under a periodic normal load is presented next. The periodic load N xx is expressed in the form
where P cr is the critical static buckling load and ϖ is the frequency of the dynamic in-plane load; α S = hσS/P cr and α D = hσD/P cr are parameters of the static and dynamic loads, respectively. Inserting Eq. (12) into Eq. (11), the equation of motion can be rewritten as
Since (13) is a Mathieu-type equation, the procedures proposed by Bolotin [1] can be used to obtain the instability regions. The solution Δ with period 2T can be sought in the form
and the solution with a period T in the form
where a k and b k are arbitrary time-invariant constants. Inserting series expansions (14) and (15) into Eq. (13) and separating the sine and cosine parts, two sets of linear algebraic equations in a k and b k are obtained for each solution. Then, the boundaries between stable and unstable regions are obtained from the condition that the set of equations has a nontrivial solution. The eigenvalue system for the dynamic stability boundaries with a period 2T is given as
For the period T, the equations are
and
Equations (16)-(18) are infinite, but the results required can be obtained by considering only the first few terms. The primary instability region with the period 2T are usually much larger than the secondary instability region defined by solutions with the period T and are therefore of greater practical importance. As the first-order approximation (a 1 and b 1) of the primary instability region is good enough for obtaining solutions with a sufficient accuracy [23], the eigenvalue problem for determining the first-order approximation of the primary instability region of sandwich plate under a periodic load is given as
4. Results and Discussion
In the present analysis, the foam-filled sandwich plate consists of two materials — graphite/epoxy and an isotropic material. The densities of graphite expoxy (face sheets) and isotropic material (core layer) are 1627 and 97 kg/m3, respectively. The other material properties of the foam-filled sandwich plates for the stiff face sheets and soft core are as follows [24].
The thicknesses of face sheets and of the core layer are t f and t c , respectively. The layers are assumed to be perfectly bonded together. To verify the algorithm and calculations used in this paper, the nondimensional natural frequencies of sandwich plates without an external load were predicted. They are shown in Tables 1 and 2. As seen, our coincide well with those obtained by Whitney [25]. The data in Tables 1 and 2 also show that the natural frequencies increase with decreasing thickness ratio t c /t f .
Now let us consider the nondimensional coefficients of the excitation frequency Ω. To evaluate the dynamic stability of the laminated plate, the dynamic instability index Ω DI = 100 ΔΩ/(ω nf K cr), which is related to its fundamental natural frequency and critical buckling load, is introduced and used. Here, ΔΩ = ΩU – ΩL is the dynamic stability region, and ΩU and ΩL are the upper and lower boundary excitation frequencies, respectively. The instability region presents the range of parametric excitation frequency at a particular load level; ω nf is the nondimensional fundamental natural frequency, which is given by \( {\omega_{nf}} = {{{\omega {b^2}}} \left/ {{h\sqrt {{{\rho^f \left/ {E_2^f } \right.}}} }} \right.} \); the nondimensional excitation frequency is defined as \( \varOmega = {{{\varpi {b^2}}} \left/ {{h\sqrt {{{\rho^f \left/ {E_2^f } \right.}}} }} \right.} \), and the dimensionless critical buckling load is given by K cr = 10 σ n b 2/E 2 f h 4. The higher the dynamic instability index, the more dynamically unstable is the laminated plate. The calculated values of the upper and lower excitation frequencies which define the boundaries of the primary instability region for a symmetrically four-layer cross-ply laminate plate are listed in Table 3. As seen, the results given by the present model are in close agreement with those obtained by Wang [26].
Parametric studies were also performed to investigate the dynamic stability of foam-filled sandwich plates. Figure 1 shows the effects of the parameter of static load α S on the principal unstability regions of foam-filled sandwich plates. As expected, the primary instability region occurs in the vicinity of Ω/ω nf = 2(α S = α D = 0). An increasing compressive static load (α S > 0) decreases both the upper and lower excitation frequencies of the sandwich plates, but an increase in the tensile static load has a reverse effect. The unstable region always becomes larger as the magnitude of the static load increases. However, the impact of a compressive static load is more significant. Figure 2 shows the influence of dynamic load on the unstability region of foam-filled sandwich plates. With increasing parameter of dynamic load, the upper excitation frequency increases, but the lower one decreases. The dynamic instability region ΔΩ increases with the parameter of dynamic load. The results in Figs.1 and 2 reveal that the dynamic instability region is mainly controlled by the dynamic load rather than by the static one.
Tables 4-6 illustrate the influence of core thickness ratio on the excitation frequency Ω, the unstability region ΔΩ, and the dynamic instability index Ω DI of foam-filled sandwich plates under various conditions. An increase in the thickness ratio t c /t f always decreases the upper and lower excitation frequencies and the instability region. However, the dynamic instability index increases with core thickness. As can be seen, the dynamic instability index of a sandwich plate subjected to a tensile load is smaller than that of the plate under a compressive load of the same magnitude. Thus, a foam-filled sandwich plate under an edge tensile force is dynamically more stable. Figure 3 depicts the effects of thickness ratio and of the parameter static load on the dynamic instability index for foam-filled sandwich plates with various parameters of dynamic load. The dynamic instability index increases with increasing thickness ratio and parameters of static and dynamic loads. Therefore, the higher the core thickness of a foam-filled sandwich plate, the more dynamically unstable is the plate.
Tables 7-9 show the effect of the coefficient of bending stress b on the dynamic instability of foam-filled sandwich plates under different static and dynamic loads. An increase in the coefficient of bending stress decreases the excitation frequencies for the sandwich plates under a static or dynamic load. The coefficient of bending stress increases the unstable region and the dynamic instability index for the sandwich plates under compressive loads, but reduces those for the plates subjected to tensile loads. However, the effect of bending stress on the dynamic instability is minor.
5. Conclusions
The dynamic behavior of foam-filled sandwich plates under a periodic load have been examined and discussed. The preliminary results can be summarized as follows.
-
1. The parameter of static and dynamic loads and the core layer thickness have a significant impact on the excitation frequency, the instability region, and the dynamic instability index of foam-filled sandwich plates. However, the influence of bending stress on the dynamic instability is minor.
-
2. The parameters of static and dynamic loads both have a destabilizing effect on the dynamic stability of foam-filled sandwich plates, because they increase the dynamic instability index.
-
3. With decrease in core layer thickness, the excitation frequency and the unstability region increases, but the dynamic instability index decreases. Hence, a decreasing core thickness will stabilize foam-filled sandwich plates.
References
V. V. Bolotin, The Dynamic Stability of Elastic Systems, San Francisco, Holden-Day (1964).
Q. Chen and Y. W.Chan, “Integral finite element method for dynamical analysis of elastic-viscoelastic composite structures,” Comp. Struct., 74, 51–64 (2000).
S. V. Sorokin, S. V. Grishina, and O. A. Ershova, “Analysis and control of vibrations of honeycomb plates by parametric stiffness modulations,” Smart Mat. Struct., 10, 1031–1045 (2001).
J. Mackerle, “Finite element analyses of sandwich structures: A bibliography 1980-2001,” Engng. Comput., 19, 206–245 (2002).
H. J. Wang and L. W. Chen, “Axisymmetric dynamic stability of sandwich circular plates,” Comp. Struct., 59, 99–107 (2003).
Y. R. Chen and L. W. Chen, “Axisymmetric parametric resonance of polar orthotropic sandwich annular plates,” Comp. Struct., 65, 269–277 (2004).
J. Y. Yeh and L. W. Chen, “Dynamic stability of a sandwich plate with a constraining layer and electrorheological fluid core,” J. Sound Vibr., 285, 637–652 (2005).
A. L. Kalamkarov, A. V. Georgiades, K. Challagulla and G. C. Saha, “Micromechanics of smart composite plates with periodically embedded actuators and rapidly varying thickness,” J. Therm. Comp. Mat., 19, 251–276 (2006).
H. Matsunaga, “Free vibration and stability of angle-ply laminated composite and sandwich plates under thermal loading,” Comp. Struct., 77, 249–262 (2007).
A. Chakrabatri and A. H. Sheikh, “Dynamic instability of composite and sandwich laminates with interfacial slips,” Int. J. Struct. Stab. Dyn. 10, 205–224 (2010).
L. Pomazi and J. Uj, “Stability of asymmetrically built and loaded multi-layered rectangular sandwich-type plates,” Mech. Engng., 44, 127–138 (2000).
T. Kant and K. Swaminathan, ”Analytical solutions using a higher order refined theory for the stability analysis of laminated composite and sandwich plates,” Struct. Engng. Mech., 10, 337–357 (2000).
W. X. Yuan and D. J. Dawe, “Free vibration and stability analysis of stiffened sandwich plates,” Comp. Struct., 63, 123–137 (2004).
S. A. Jayachandran, A. Soundararajan, S. Seetharaman, and G. M. S.Knight, “Modulus of core reaction approach to buckling of sandwich plate,” Int. J. Struct. Stab. Dyn., 4, 579–588 (2004).
M. Linke, W. Wohlers, and H. G. Reimerdes, “Finite element for the static and stability analysis of sandwich plates,” J. Sand. Struct. Mat., 9, 123–142 (2007).
L. C. Shiau and S. Y. Kuo, “Flutter of thermally buckled composite sandwich plates,” Comput. Mat. Cont., 5, 213–221 (2007).
V. N. Burlayenko and T. Sadowski, “Dynamic behaviour of sandwich plates containing single/multiple debonding” Comput. Mat. Sci., 50, 1263–1268 (2011).
T. Wang, Q. Qin, and T. J. Wang, “Dynamic response of metallic square honeycomb sandwich plate subjected to blast loading,” Key Engng. Mat., 462, 720–725 (2011).
C. S. Chen, “Analysis of nonlinear vibration of composite laminated plate,” Comp. Part B: Engng., 38, 437–447 (2007).
C. S. Chen, C. P. Fung, and R.D. Chien, “Nonlinear vibration of an initially stressed laminated plate according a higher order theory,” Comp. Struct. 77, 521–532 (2007).
C. S. Chen, C. P. Fung, and J. G. Yang, “Assessment of plate theories for initially stressed hybrid laminated plates,” Comp. Struct., 88, 195–201 (2009).
E. J. Brunell and S. R. Robertson, “Initially stressed Mindlin plates,” AIAA J. 12, 1036–1045 (1974).
L. W. Chen and J. Y. Yang, “Dynamic stability of laminated composite plates by the finite element method,” Comput. Struct., 36, 845–851 (1990).
T. Kant and K. Swaminathan, “Analytical solutions for free vibration of laminated composite and sandwich plates based on a higher-order refined theory,” Comp. Struct., 53, 73–85 (2001).
J. M. Whitney and N. J. Pagano, “Shear deformation in heterogeneous anisotropic plates,” ASME J. Appl. Mech., 37, 1031–1036 (1970).
S. Wang and D. J. Dawe, “Dynamic instability of composite laminated rectangular plates and prismatic plate structures,” Comput. Meth. Appl. Mech. Engng., 191, 1791–1826 (2002).
Author information
Authors and Affiliations
Corresponding author
Additional information
Russian translation published in Mekhanika Kompozitnykh Materialov, Vol. 48, No. 5, pp. 765-782 , September-October, 2012.
Rights and permissions
About this article
Cite this article
Kao, JY., Chen, CS. & Chen, WR. Parametric vibration response of foam-filled sandwich plates under periodic loads. Mech Compos Mater 48, 525–538 (2012). https://doi.org/10.1007/s11029-012-9297-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11029-012-9297-z