Introduction

Recently, the number of studies regarding piezoelectric structures have shown an upward trend owing to their wide engineering applications. Unlike pure elastic solids, piezoelectric ones can detect changes in the external environment and then react in accordance with these changes. With this amazing property, many issues can be addressed, e.g., vibration and noise control, smart devices, transducers, and acoustic filters. Studies on these materials and the corresponding mechanical problems are increasing constantly. As examples, two interesting studies [1, 2] can be mentioned. Many theoretical and experimental investigations of systems including piezoelectric materials have been performed. The fundamental monographs by Yang [3] and Tiersten [4] contain comprehensive information related to the background of mechanical structures from such materials.

Problems related to the electroelastic wave propagation in isotropic and piezoelectric media have also been investigated. However, various factors cause nonlinear effects during solving related problems; e.g., a static initial stress state in the body or configuration of the system, which have to be taken into consideration. At the beginning of the XXth century, the first attempts to construct 3D linearized equations (TDLEs) began. Southwell [5], Biezeno and Henky [6], many scientists have contributed to the development of this theory. Here, we should mention the fundamental studies by Biot [7], Neuber [8], Trefftz [9], and Green [10]. This theory has been updated by Guz [11], Zubov [12], Tiersten [13], Ogden [14], Akbarov and Guz [15], and Reddy [16]. In particular, the 3D linearized elasticity theory for solids under initial stress (TLTESIS) laid down by Guz [17] and investigated extensively by Akbarov [18] is very modern today. There are many papers regarding this mentioned theory and its variants. Akbarov et al. presented their analysis considering the dynamical stress in forced vibration of a bilayered plate-strip with initial stresses based on a rigid foundation [19]. Gupta et al. investigated the dispersion relationships corresponding to the velocity of torsional surface waves in a homogeneous layer of finite thickness on a prestressed non-homogenous half-space [20]. Hu and Chan analyzed the effect of a uniform applied initial stress to the radial surfaces of a hollow compound cylinder [21]. Guo and Wei studied the influence of the initial stress state on the dispersion relations of elastic waves in a piezoelectric phononic crystal [22]. Yesil solved both natural and forced vibration problems for a prestressed slab with two parallel cylindrical cavities [23]. Daşdemir considered the dynamical response of a prestressed system with a piezoelectric core and elastic faces [24] and then extended the study to the case with imperfect contact interactions at layers of the system [25]. The detailed information on the problem under consideration can be also found in the works of Guz [26] and Akbarov [27, 28].

In our work, a modal analysis of the problem of forced vibration of a two-axially prestressed piezoelectric plate with finite lengths is performed using a piecewise homogeneous body model. The plate is exposed to a time-harmonic force and can be polled in various directions. Considering the current literature, to our knowledge, this problem has yet to be analyzed, because a mathematical model explaining the influence of various poling directions on the effective properties of the system is still missing. To fill this gap, we will develop a modal mathematical model for the current problem in terms of the TLTESIS and will solve this problem approximately by employing the 3D finite element method (3D-FEM). In particular, we will compare and discuss the influence of various poling directions on the dynamical behavior of the plate.

Statement of the Forced Vibration Problem

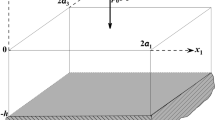
Let us consider a prestressed transversely isotropic piezoelectric plate resting on a rigid foundation in a Cartesian coordinate system Ox1x2x3. The side lengths of the plate are 21 a and 23 a along the Ox1 and Ox3 axes, and its thickness is h in the direction of Ox2 axis. The geometry of the plate is described as

$$ V=\left\{\left({x}_1{x}_2{x}_3\right):0\le {x}_1\le 2{a}_1,-h\le {x}_2\le 0,0\le {x}_3\le 2{a}_3\right\}. $$
(1)

Let Γ = Γ1± ∪ Γ2± ∪ Γ3± be the boundary of the volume V, where Γi± indicates the outer surface parts in the positive and negative directions of respectively Oxi axis.

The plate is uniaxially loaded in the directions of Ox1 and Ox3 axes, creating a two-axial initial stress state in it. As a result, initial electrical displacements arise in the piezoelectric plate. Note that the initial stresses and electrical displacements are interrelated. We will explain these relationships later. The plate is placed on a rigid foundation, and a time-harmonic mechanical load is applied to the system. All the fields in the problem are then time-harmonic. Hence, we can assume the dynamic force, displacements, and the electric potential in the forms p0(t) = poδ∗eiωt, uj(x1x2x3, t) = uj(x1x2x3, t)eiωt, and φ(x1x2x3, t) = φ(x1x2x3, t)eiωt, respectively, and discretize the time multiplier from the governing equations and the related boundary-contact conditions. Here, i is the complex unit and δ* is the Dirac delta function of two variables defined as δ(x1 − a1)δ(x3 − a3). Let us use the coordinate transformation rule \( {\hat{x}}_j={x}_j/h \) to investigate the problem in a simpler geometry. For simplicity, we omit the circumflex over the space components. Instead of the general expressions, we can investigate our problem in a simpler case. Let us consider the boundary-value problem

$$ {T}_{ji,j}+\rho {\omega}^2{h}^2{u}_i=0, $$
(2)
$$ {S}_{i,i}=0, $$
(3)
$$ {\left.{\upsigma}_{2\ell}\right|}_{{\Gamma_2}^{+}}=0,\kern1em {\left.{\upsigma}_{22}\right|}_{{\Gamma_2}^{+}}=-{p}_o{\delta}^{\ast }, $$
(4)
$$ {\left.{T}_{ij}\right|}_{{\Gamma_{\ell}}^{\pm }}=0,\kern1.5em {\left.{S}_i\right|}_{{\Gamma_{\ell}}^{\pm }}=0, $$
(5)
$$ {\left.{u}_i\right|}_{{\Gamma_2}^{-}}=0,\kern1.5em {\left.\varphi \right|}_{{\Gamma_2}^{\pm }}=0, $$
(6)

where Tij is the first Piola–Kirchhoff stress tensor, Si is the electrical density tensor, σij is the stress tensor, ρ is the density of the plate, and the subscripts after a comma mean partial differentiation. Summation over subscripts repeated twice is carried out. Here and below, ℓ = 1,3 . These boundary conditions can be explained as follows: Eq. (4) presents mechanical traction-free conditions at the free surface of the plate, Eq. (5) gives mechanically and electrically open conditions at the lateral surfaces, the first equation in (6) is a mechanically short condition at the bottom surface of the plate, and the second one is an electrically short condition at the free and bottom surface of the plate.

In the above relations, we use the designations

$$ {T}_{ji}={\upsigma}_{ij}+{\upsigma_{jk}}^0{u}_{i,k} $$
(7)

and

$$ {S}_i={D}_i+{D_i}^0{u}_{j,i}, $$
(8)

where Di is the tensor of electric displacements and the superscript “0” indicates the quantities related to the initial stresses. The strain–displacement and electric field–electric potential relationships are related as

$$ {\varepsilon}_{ij}=\frac{1}{2}\left({u}_{i,j}+{u}_{j,i}\right)\ \mathrm{and}\ {E}_i=-{\varphi}_{,i}. $$
(9)

The constitutive relations are

$$ {\upsigma}_{ij}={\overset{\sim }{C}}_{ij kl}{\varepsilon}_{kl}-\tilde{e}_{k}ij {E}_k $$
(10)

and

$$ {D}_i=\tilde{e}_{i}k l{\varepsilon}_{kl}+{\gamma}_{ik}{E}_k, $$
(11)

where \( {\overset{\sim }{C}}_{ijkl} \) is the tensor of elastic constants, \( \tilde{e}_{k}ij \) is the tensor of piezoelectric constants, and γij is the tensor of dielectric constants. Note that Eqs. (10) and (11) are described by fourth- and third-order tensors of the material constants. The tensors \( {\overset{\sim }{C}}_{ijkl} \) and \( \tilde{e}_{k}ij \) can be written as Cpq and ekp, by employing the Voight notation

$$ ij\to p\ \mathrm{and}\ kl\to q\equiv 11\to 1,\kern0.5em 22\to 2,23\to 4,13\to 5,12\to 6. $$
(12)

Then, relations (10) and (11) can be presented in the matrix form

$$ \left\{\begin{array}{c}\mathbf{S}\\ {}\mathbf{D}\end{array}\right\}=\overset{\sim }{\mathbf{M}}\left\{\begin{array}{c}\boldsymbol{\upvarepsilon} \\ {}\mathbf{E}\end{array}\right\}\ \mathrm{and}\ \overset{\sim }{\mathbf{M}}=\left[\begin{array}{cc}\overset{\sim }{\mathbf{C}}& -\overset{\sim }{\boldsymbol{e}}\\ {}{\overset{\sim }{\boldsymbol{e}}}^T& \overset{\sim }{\gamma}\end{array}\right], $$
(13)

where the superscript T means transposition, \( \overset{\sim }{\mathbf{C}}=\left[\tilde{c}_{p}q\right] \) is a 6 6 × matrix of mechanical constants, \( \overset{\sim }{\mathbf{e}}=\left[\tilde{e}_{i}p\right] \) is a 3× 6 matrix of piezoelectric constants, and \( \overset{\sim }{\upgamma}=\left[{\overset{\sim }{\upgamma}}_{ij}\right] \) is a 3× 3 matrix of dielectric constants γij. Depending on the poling direction of the piezoelectric material, the entries of the matrices \( \overset{\sim }{\mathbf{C}} \), \( \overset{\sim }{\mathbf{e}} \), and \( \overset{\sim }{\upgamma} \) can change. It should be mentioned that \( \overset{\sim }{\mathbf{M}}=\left[\tilde{m}_{f}h\right] \) is a symmetric 9× 9 matrix, where f,h = 1,2,…,9. Other notations used here are

$$ \mathbf{S}={\left\{{\upsigma}_{11}\ {\upsigma}_{22}\ {\upsigma}_{33}\ {\upsigma}_{23}\ {\upsigma}_{13}\ {\upsigma}_{12}\right\}}^T, $$
(14)
$$ \mathbf{S}={\left\{{D}_1\ {D}_2{D}_3\right\}}^T, $$
(15)
$$ \boldsymbol{\upvarepsilon} ={\left\{{\varepsilon}_{11}\ {\varepsilon}_{22}\ {\varepsilon}_{33}\ 2{\varepsilon}_{23}\ 2{\varepsilon}_{13}\ 2{\varepsilon}_{12}\right\}}^T, $$
(16)

and

$$ \mathbf{E}={\left\{{E}_1\ {E}_2{E}_3\right\}}^T. $$
(17)

Solution Methodology

Let us use the finite-element method (FEM) to solve the problem described by Eqs. (2)-(6). For this purpose, a weak form of the problem is constructed. To do this, we introduce test functions wi and φ that satisfy the boundary-contact conditions in Eqs. (4)-(6). Integrating the resultant equation obtained multiplying Eqs. (2) and (3) by respectively wi and φ and summation over the volume V yields

$$ {\displaystyle \begin{array}{c}0=\underset{V}{\int}\left({T}_{ij,j}{w}_i+\rho {\omega}^2{h}^2{u}_i{w}_i+{S}_{i,i}\phi \right) dV\\ {}\underset{V}{\int}\left[{\left({T}_{ij}{w}_i\right)}_{,j}-{T}_{ij}{w}_{i,j}+{\left({S}_i\phi \right)}_{,i}-{S}_i{\phi}_{,i}\right] dV+\rho {\omega}^2{h}^2\underset{V}{\int }{u}_i{w}_i dV\end{array}} $$
(18)

Using the well-known Gauss theorem, Eq. (18) is written in the form

$$ \underset{V}{\int}\left({T}_{ij}{w}_{i,j}+{S}_i{\phi}_{,i}\right) dV=\underset{\Gamma}{\int}\left[{T}_{ij}{w}_i\left(n,{x}_j\right)+{S}_i\phi\ \cos \left(n,{x}_i\right)\right]d\Gamma +\rho {\upomega}^2{h}^2\underset{V}{\int }{u}_i{w}_i dV, $$
(19)

where cos(n, xi) is the direction cosine. Now, the boundary integral in the right-hand side of Eq. (19) can be computed. For the boundary Γ = Γ1± ∪ Γ2± ∪ Γ3± and the boundary-contact conditions in Eqs. (4)-(6), the integral mentioned takes the form

$$ {\displaystyle \begin{array}{c}\underset{\Gamma}{\int}\left[{T}_{ij}{w}_i\cos \left(n,{x}_j\right)+{S}_i\phi\ \cos \left(n,{x}_i\right)\right]d\Gamma =\underset{{\Gamma_k}^{\pm }}{\int }{T}_{ij}{w}_i\cos \left(n,{x}_j\right)d{\Gamma}_k\\ {}\underset{{\Gamma_k}^{\pm }}{\int }{S}_i\phi\ \cos \left(n,{x}_i\right)d{\Gamma}_k=-\underset{{\Gamma_2}^{+}}{\int }{p}_o{\delta}^{\ast }{w}_2d{\Gamma_2}^{+}.\end{array}} $$
(20)

As a result, we obtain that

$$ \underset{V}{\int}\left({T}_{ij}{w}_{i,j}+{S}_i{\phi}_{,i}\right) dV=-\underset{{\Gamma_2}^{+}}{\int }{p}_o{\delta}^{\ast }{w}_2d{\Gamma_2}^{+}+p{\omega}^2{h}^2\underset{V}{\int }{u}_i{w}_i dV. $$
(21)

In the explicit form, Eq. (21) can be written as

$$ \underset{V}{\int}\left({\upsigma}_{ij}{\varepsilon_{ij}}^w+{\theta_{ij}}^{\sigma }{w}_{i,j}+{D}_i{\phi}_{,i}+{\theta_{ij}}^D{\phi}_{,j}\right) dV=-\underset{{\Gamma_2}^{+}}{\int }{p}_o{\delta}^{\ast }{w}_2d{\Gamma_2}^{+}+p{\omega}^2{h}^2\underset{V}{\int }{u}_i{w}_i dV, $$
(22)

where \( {\theta_{ij}}^{\sigma }={\upsigma_{kj}}^0{u}_{i,k},{\theta_{ij}}^D={D}_i^0{u}_{j,i} \) and εijw = (wi, j + wj, i)/2 is the strain relation for the test function wi. This completes the construction of the weak form of the problem.

Next, based on the Hamilton variational principle, the variational formulation of the 3D piezoelectric plate with the utilization of one of the above weak forms is constructed. Considering the test functions wi and φ with the respective displacement functions δui and electric potential δφ that satisfy the boundary-contact terms in (4)-(6), we can write Eq. (22) as

$$ \underset{V}{\int}\left({\upsigma}_{ij}\delta {\varepsilon}_{ij}+{\theta_{ij}}^{\sigma}\delta {u}_{i,j}+{D}_i\delta {\varphi}_{,i}+{\theta_{ij}}^D\delta {\varphi}_{,i}\right) dV=-\underset{{\Gamma_2}^{+}}{\int }{p}_o{\delta}^{\ast }{u}_2d{\Gamma_2}^{+}+p{\omega}^2{h}^2\underset{V}{\int }{u}_i\delta {u}_i dV. $$
(23)

Let us take the integral in the left-hand side of Eq. (23) into account. Note that we employ a circumflex to distinguish the mechanical parts of a quantity, respectively, e.g. \( {\hat{\sigma}}_{ij}={C}_{ij kl}{u}_{k,l} \). Now, we write that:

$$ {\displaystyle \begin{array}{c}{\upsigma}_{ij}\delta {\varepsilon}_{ij}+{\theta_{ij}}^{\sigma}\delta {u}_{i,j}+{D}_i\delta {\varphi}_{,i}+{\theta_{ij}}^D\delta {\varphi}_{,i}\\ {}=\left({\hat{\sigma}}_{ij}+{r}_{kij}\right)\delta {\varepsilon}_{ij}+{\upsigma_{kj}}^0{u}_{i,k}\delta {u}_{i,j}+\left({r}_{kij}{u}_{i,j}-{s}_{kn}{\varphi}_{,n}\right)\delta {\varphi}_{,k}\\ {}\begin{array}{c}=\left({\hat{\sigma}}_{ij}+{\upsigma_{kj}}^0{u}_{i,k}\right)\delta {u}_{i,j}+{r}_{kij}\left({\varphi}_{,k}\delta {u}_{i,j}+{u}_{i,j}\delta {\varphi}_{,k}\right)-{s}_{kn}{\varphi}_{,n}\delta {\varphi}_{,k}\\ {}={p}_{mjkl}{u}_{k,l}\delta {u}_{i,j}+{r}_{kij}\left({\varphi}_{,k}\delta {u}_{i,j}+{u}_{i,j}\delta {\varphi}_{,k}\right)-{s}_{kn}{\varphi}_{,n}\delta {\varphi}_{,k}\\ {}\begin{array}{c}=\frac{1}{2}\delta \left({p}_{mjkl}{u}_{k,l}{u}_{i,j}\right)+\delta \left({r}_{kij}{\varphi}_{,k}{u}_{i,j}\right)-\frac{1}{2}\delta \left({s}_{kn}{\varphi}_{,n}{\varphi}_{,k}\right)\\ {}=\frac{1}{2}\delta \left({p}_{mjkl}{u}_{k,l}{u}_{i,j}+2{r}_{kij}{\varphi}_{,k}{u}_{i,j}-{s}_{kn}{\varphi}_{,n}{\varphi}_{,k}\right),\end{array}\end{array}\end{array}} $$
(24)

where

$$ {p}_{ijk n}={C}_{ijk n}+{\upsigma_{in}}^0,{r}_{ijk}={e}_{ijk}+\frac{1}{2}{D_k}^0,\mathrm{and}\ {s}_{kn}={\gamma}_{kn}. $$
(25)

Eq. (23) can be put in the form

$$ \delta \left[\frac{1}{2}\rho {\omega}^2{h}^2\underset{V}{\int }{u_i}^2 dV-\frac{1}{2}\underset{V}{\int}\left({p}_{ijkl}{u}_{k,l}{u}_{i,j}+2{r}_{kij}{\varphi}_{,k}{u}_{i,j}-{s}_{kn}{\varphi}_{,n}{\varphi}_{,k}\right) dV-\underset{{\Gamma_2}^{+}}{\int }{p}_o{\delta}^{\ast }{u}_2d{\Gamma_2}^{+}\right]=0. $$
(26)

Introducing the expressions

$$ {\displaystyle \begin{array}{c}\mathrm{P}=\frac{1}{2}\underset{V}{\int}\left({p}_{ijkl}{u}_{k,l}{u}_{i,j}+2{r}_{kij}{\varphi}_{,k}{u}_{i,j}-{s}_{kn}{\varphi}_{,n}{\varphi}_{,k}\right) dV,\\ {}K=\frac{1}{2}\rho {h}^2\underset{V}{\int }{u}_i^2 dV,\mathrm{and}\kern0.5em \mathrm{M}=\underset{{\Gamma_2}^{+}}{\int }{p}_o{\delta}^{\ast }{u}_2d{\Gamma_2}^{+},\end{array}} $$

the initial problem can be written as

$$ \delta \left({\omega}^2\mathrm{K}-\mathrm{P}-\mathrm{M}\right)=0, $$
(27)

where Ρ , Κ , and Μ are the potential and kinetic energies, and the virtual work done by the external force, respectively. Note that Eq. (27) can also be expressed as

$$ \delta \left({\omega}^2\mathrm{K}-{\mathrm{P}}_{\upsigma}-{\mathrm{P}}_m+{\mathrm{P}}_e\right)=0, $$
(28)

with

$$ {\displaystyle \begin{array}{c}\mathrm{K}=\frac{1}{2}\rho {h}^2\underset{V}{\int }{u}_i^2 dV,{\mathrm{P}}_{\upsigma}=\frac{1}{2}\underset{V}{\int }{p}_{ijkl}{u}_{k,l}{u}_{i,j} dV-\underset{{\Gamma_2}^{+}}{\int }{p}_o{\delta}^{\ast }{u}_2d{\Gamma_2}^{+},\\ {}{\mathrm{P}}_m=\underset{V}{\int }{r}_{kij}{\varphi}_{,k}{u}_{i,j} dV,\mathrm{and}\ {\mathrm{P}}_e=\frac{1}{2}{s}_{kn}{\varphi}_{,n}{\varphi}_{,k} dV,\end{array}} $$

where Pσ, Ρm, and Ρe are the mechanical, mixed, and electrical energies, respectively. It is noted that Eq. (28) can occasionally be a more suitable than Eq. (27). For instance, when \( {\overset{\sim }{c}}_{11}={\overset{\sim }{c}}_{22}={\overset{\sim }{c}}_{33}=\lambda +2\mu, {\overset{\sim }{c}}_{12}={\overset{\sim }{c}}_{21}={\overset{\sim }{c}}_{13}={\overset{\sim }{c}}_{31}={\overset{\sim }{c}}_{23}={\overset{\sim }{c}}_{32}=\lambda, {\overset{\sim }{c}}_{44}={\overset{\sim }{c}}_{55}={\overset{\sim }{c}}_{66}=\mu, \) and \( \tilde{e}_{i}j={\overset{\sim }{\gamma}}_{ij}=0 \) in the matrices \( \overset{\sim }{\mathbf{C}} \), \( \overset{\sim }{\mathbf{e}} \), and \( \overset{\sim }{\upgamma} \), our original problem is reduced to the case of forced vibration in the 3D prestressed elastic plate. However, in this case, the related rows and columns in the matrix-vector statements should be deleted. Otherwise, there can sometimes lead indefinite cases in the solution procedure. Here, λ and μ are the Lamé constants.

To solve the problem numerically, we will employ the finite-element technique. For this purpose, let Vh be the domain of a finite element mesh, namely, Vh ⊂V and Vh = ⋃mVem. According to the usual procedure, we will search for the weak solution for the displacements uh = ⌊u1h u2h u3h⌋ϵ Vuh, electrical fields Eh = ⌊E1h E2h E3h⌋ϵ Vuh, and their virtual

structures δuh and δEh in the form

$$ {\mathbf{u}}_h\cong {\mathbf{N}}_{uh}\overset{\sim }{\mathbf{U}},{\mathbf{E}}_h\cong {\mathbf{N}}_h\overset{\sim }{\mathbf{E}},\delta {\mathbf{u}}_h\cong {\mathbf{N}}_{uh}\delta \overset{\sim }{\mathbf{U}},\mathrm{and}\ \delta {\mathbf{E}}_h\cong {\mathbf{N}}_{Eh}\delta \overset{\sim }{\mathbf{E}}, $$
(29)

where \( \overset{\sim }{\mathbf{U}} \) and \( \overset{\sim }{\mathbf{E}} \) are the global vectors of nodal displacements and nodal electrical fields, Nuh is the matrix of shape functions for the displacements, and NEh is the row vector of shape functions for the electrical fields. In this paper, we used eight-node quadrilateral elements, but, depending on the convergence desired, this choice was changed. The nodal degrees of freedom are collected in the form of a single vector as

$$ {\displaystyle \begin{array}{c}{\mathbf{u}}_h^e={\left[{\mathbf{u}}_1^e\kern0.5em {\mathbf{u}}_2^e\kern0.5em {\mathbf{u}}_3^e\right]}^T\\ {}={\left[\left.{u}_{11}^e\kern0.5em {u}_{12}^e\kern0.5em \cdots {u}_{18}^e\right|\left.\kern0.5em {u}_{21}^e\kern0.5em {u}_{22}^e\kern0.5em \cdots {u}_{28}^e\right|\kern1.25em {u}_{31}^e\kern0.5em {u}_{32}^e\kern0.5em \cdots {u}_{38}^e\right]}^T\end{array}} $$

and

$$ {\displaystyle \begin{array}{c}{\mathbf{E}}_h^e={\left[{\mathbf{E}}_1^e\kern0.5em {\mathbf{E}}_2^e\kern0.5em {\mathbf{E}}_3^e\right]}^T\\ {}={\left[\left.{E}_{11}^e\kern0.5em {E}_{12}^e\kern0.5em \cdots {E}_{18}^e\right|\kern0.5em \left.{E}_{21}^e\kern0.5em {E}_{22}^e\kern0.75em \cdots {E}_{28}^e\right|\kern0.5em {E}_{31}^e\kern0.5em {E}_{32}^e\kern0.75em \cdots {E}_{38}^e\right]}^T.\end{array}} $$

Substituting Eq. (29) for Vh and Γh in Eq. (27) (or Eq. (28)), we obtain

$$ \left\{{\mathbf{K}}_{uu}-{\omega}^2{\mathbf{M}}_{uu}\right\}\overset{\sim }{\mathbf{U}}+{\mathbf{K}}_{uE}\overset{\sim }{\mathbf{E}}={\mathbf{F}}_u, $$
(30)
$$ {\mathbf{K}}_{uE}\overset{\sim }{\mathbf{U}}+{\mathbf{K}}_{EE}\overset{\sim }{\mathbf{E}}={\mathbf{F}}_E, $$
(31)

where \( {\mathbf{K}}_{uu}=\sum {\mathbf{K}}_{uu}^{em},{\mathbf{K}}_{uE}=\sum {\mathbf{K}}_{uE}^{em},{\mathbf{K}}_{EE}=\sum {\mathbf{K}}_{EE}^{em}, \) and \( {\mathbf{M}}_{uu}=\sum {\mathbf{M}}_{uu}^{em} \) are the global stiffness and global mass matrices, obtained from the corresponding ensemble “Σ•” of local stiffness matrices. Fu and FE are the nodal force vectors. From Eq. (27), the explicit forms of the element matrices above are found, namely,

$$ {\mathbf{M}}_{uu}^{em}=\underset{V^{em}}{\int }{\mathbf{N}}_{uh}^e\bullet {{\mathbf{N}}_{uh}^e}^Td{V}^{em},{\mathbf{K}}_{uu}^{em}=\underset{V^{em}}{\int }{{\mathbf{S}}_{uh}^e}^T\bullet \mathbf{C}\bullet {\mathbf{S}}_{uh}^ed{V}^{em} $$
(32)
$$ {\mathbf{K}}_{uE}^{em}=\underset{V^{em}}{\int }{{\mathbf{N}}_{uh}^e}^{\boldsymbol{T}}\bullet {e}^T\bullet {\mathbf{N}}_{Eh}^ed{V}^{em},{\mathbf{K}}_{EE}^{em}=\underset{V^{em}}{\int }{{\mathbf{S}}_{Eh}^e}^T{\bullet}^{\mathbf{3}}\bullet {\mathbf{S}}_{Eh}^ed{V}^{em} $$
(33)
$$ {\mathbf{S}}_{Eh}^e=\mathbf{L}\left(\nabla \right)\bullet {{\mathbf{N}}_{uh}^e}^T,{\mathbf{S}}_{Eh}^e=\nabla {{\mathbf{N}}_{Eh}^e}^T, $$
(34)
$$ \mathbf{L}\left(\nabla \right)={\left[\begin{array}{ccc}{\partial}_1& 0& 0\kern0.5em 0\kern0.5em \begin{array}{cc}{\partial}_3& {\partial}_2\end{array}\\ {}0& {\partial}_2& \begin{array}{ccc}0& {\partial}_3& \begin{array}{cc}0& {\partial}_1\end{array}\end{array}\\ {}0& 0& \begin{array}{ccc}{\partial}_3& {\partial}_2& \begin{array}{cc}{\partial}_1& 0\end{array}\end{array}\end{array}\right]}^T. $$
(35)

Equation system (30) and (31) can be written in the reduced form

$$ \left(\mathbf{K}-{\omega}^2\mathbf{M}\right)\mathbf{U}=\mathbf{F}, $$
(36)

where

$$ \mathbf{K}=\left[\begin{array}{cc}{\mathbf{K}}_{uu}& {\mathbf{K}}_{uE}\\ {}{\mathbf{K}}_{uE}& {\mathbf{K}}_{EE}\end{array}\right],\mathbf{M}=\left[\begin{array}{cc}{\mathbf{M}}_{uu}& 0\\ {}0& 0\end{array}\right],\mathbf{U}=\left\{\begin{array}{c}\overset{\sim }{\mathbf{U}}\\ {}\overset{\sim }{\mathbf{E}}\end{array}\right\},\mathrm{and}\ \mathbf{F}=\left\{\begin{array}{c}{\mathbf{F}}_u\\ {}{\mathbf{F}}_E\end{array}\right\}. $$
(37)

Note that the global stiffness matrices K and M in Eq. (37) are symmetric and positive definite, because the weak form in Eq. (21) is positive definite. Hence, matrix equation (36) has a solution for the finite-element algorithm in the elasticity theory. When evaluating the matrix equation mentioned, we obtain the displacements related to the dynamic response of the piezoelectric plate, and can then express the relative stresses and electrical displacements using the generalized Hooke’s law. Finally, our solution procedure can be used to solve some variants of the problem under consideration or an analogous problem for elastic media.

Numerical Applications and Examples

It was stated in Sect. 2 that the constitutive relations (10), (11), and (13) can differ according to the choice of the polarization direction. In Sect. 3, the solution process for the most general case was presented. Utilizing of our results, numerical solutions can be found for any case. We will present numerical solutions based on the assumption that the piezoelectric plate is polled only in the directions of Ox1, Ox2, and Ox3 axes, the matrices in Eq. (13) for the cases considered are given in Appendix A. The letters a , b , and c in the parts of figures indicate that the graphs were plotted for polarizations in the directions of Ox1, Ox2, and Ox3 axes. To be able to notice the related numerical results, we use the designation “[●]” as a superscript; for instance, σ22[1]h/p0 is the value of σ22h/p0 for polarization in the direction of the Ox1 axis. We also assume that the numbers of finite elements in the directions of the Ox1, Ox2, and Ox3 axes are equal to fifty, twelve, and fifty, respectively. Thus, the number of total nodal degrees of freedom is 135,252.

Let us, introduce the designations

$$ \Omega =\omega h\sqrt{\frac{\rho }{{\overset{\sim }{c}}_{33}}},{\eta}_{\ell }=\frac{\upsigma_{\mathcal{ll}}^0}{{\overset{\sim }{c}}_{33}},{\kappa}_{\ell }=\frac{{D_{\ell}}^0}{2{\overset{\sim }{c}}_{33}},{a}_{\ast }=\frac{a_1}{a_3},\mathrm{and}\ {h}_{\ast }=\frac{h}{2{a}_{\ast }}, $$
(38)

where Ω_ is the dimensionless frequency parameter, ηℓ is the parameter of initial stress, κℓ is the parameter of initial electric displacement, a* is the aspect ratio, and h* is the thickness ratio. As already mentioned previously, there exist relations between the mechanical initial stresses and the electrical initial displacements. When considering the constitutive equations for polarizations in the directions of the Ox1 and Ox3 axes with the boundary-contact conditions in Eq. (5), we can easily obtain relations as

$$ {D_1}^0=\frac{e_{33}\left({c}_{11}+{c}_{12}\right)-2{c}_{13}{e}_{31}}{c_{33}\left({c}_{11}+{c}_{12}\right)-2{c_{13}}^2}{\upsigma_{11}}^0\ \mathrm{and}\ {D_3}^0=\frac{\left({c}_{11}+2{c}_{12}+{c}_{22}\right){c}_{13}{e}_{31}+\left({c_{12}}^2+{c}_{11}{c}_{22}\right){e}_{33}}{\left({c}_{11}+2{c}_{12}+{c}_{22}\right){c_{12}}^2+\left({c_{12}}^2+{c}_{11}{c}_{22}\right){c}_{33}}{\upsigma_{33}}^0. $$
(39)

It should be noted that the equations in (39) are linear. This agrees with the well-known electromechanical considerations. For examples, barium titanate (BaTiO3), with c44 = 44 GPa , e15 = 11.4 C/m2, and γ11 = 1.115 nF/m was chosen as the material of the plate, as also considered by the author of [25]. Throughout the paper, the bottom surface of the plate under at Ω = 0, η = η1 = η3, η = 0, a∗ = 1, and h* = 0.2 is considered unless specified otherwise.

First, the PC programs and algorithms used were validated. The author of [29] investigated the dynamic behavior of a prestressed piezoelectric plate-strip subjected to a time-harmonic force. The problem considered here takes a similar form when a* → ∞ for fixed values of other relevant parameters. Therefore, the numerical results in graphs found at x3 / h = a3 / h and a* → ∞ must approach the corresponding ones given in [29] for the same assumptions. Figure 1 complies with this estimation, confirming the validity of our PC algorithm. Note that the dashed graph in Fig. 1 was taken from Fig. 4d in [29].

Fig. 1.
figure 1

Distributions of the stress σ22h / p0 along the line x1 / h for polarization in the direction of Ox2 axis at x3 / h = a3 / h.

Full size image

Figure 2 shows the projection of the 3D graphs of the normal stress σ22 h / p0 on the Ox1x3 plane. It is seen from the graphs that the smallest value of the stress σ22 h / p0 occur for the polarization in the direction of Ox2 axis, σ22[2]h/p0 < σ22[1]h/p0 = σ22[3]h/p0. This means that, in terms of stress insulation, the ideal polarization direction is along the Ox2 axis. The stress distributions in each graph can be categorized as follows. There is a region where the stress is higher than in other regions. This region is colored blue in the graphs and can be called the essential effect zone. The region where the stress is relatively low is colored green in the graph and can be called the medium effect zone. The region where the stress almost zero is colored orange in the graph and can be called the faint zone. It is seen that the shapes of the essential and medium effect zones are composed of circular structures in Fig. 2b, but of ellipses with center at the point (2.5, 2.5) in Figs. 2a and 2c. According to the distributions of the graphs, the principal axis of the ellipses in Fig. 2a lies on the line x3 / h = 2.5 while that in Fig. 2c is on the line x1 / h = 2.5. We have a very curious situation here. The focal points of the boundary ellipse of the medium effect zone coincide with vertices of one of the essential effect zone. For example, in Fig. 2c, the foci of the corresponding ellipse are F1 ≈ (2.5, 2.15) and F2 ≈ (2.5, 2.85), which are approximately the vertices of the other related ellipse. Although the 3D graphs for the polarization in the direction of Ox2 axis take the shape a right circular cone, those for the polarization in the directions of Ox1 and Ox3 axes form a right elliptic cone. According to the foregoing discussions, the Ox2 axis as the polarization direction can be the best choice to ensure lower stresses in the body with a rather homogeneous distribution.

Fig. 2.
figure 2

Distributions of the stress σ22 h / p0 on the Ox1x3 plane for polarizations in the directions of Ox1 (a), Ox2 (b), and Ox3 (c) axes.

Full size image

Let us focus now on the frequency response of the plate to a time-harmonic force. In Fig. 3, relations between σ22 h / p0 and Ω_ for the polarizations in the directions of the Ox1 , Ox2 , and Ox3 axes are displayed. Apparently, we obtain the same graphs of the stresses under consideration for the polarizations in the directions of the Ox1 and Ox3 axes. It can be said from the graphs that although the stress in the plate increases with Ω, these relations are non-monotonous. The absolute values of σ22 h / p0 increase as the thickness ratio decreases. The distributions of the graph curves shows that the stress has an extremal value for certain values of Ω_ and then start to oscillate frequently. These values of Ω , designated as Ω* are called the “resonant value.” We can observe that, for polarization, instead of Ox1 or Ox3 axes, the choice of the Ox2 axis increases the values of Ω*. This means that, in this case, the system is more stable than in other cases. Note that the greatest number of oscillations in distributions of the graphs arises for the polarization in the direction of Ox2 axis; namely, in the case where the polarization is in the same direction than the operating time-harmonic force.

Fig. 3.
figure 3

Relations between σ22 h / p0 and Ω_ for polarizations in the directions of Ox1 (a), Ox2 (b), and Ox3 (c) axes.

Full size image

Figure 4 displays the relation between σ22 h / p0 and η for certain values of the aspect ratio a*. The graphs presented here are drawn on the assumption that the length a3 changes at a fixed value of a1. Note that the positive (negative) sign of the initial stress parameter η indicates that a tensile (compression) force is applied to the plate. It is seen that the stress σ22 h / p0 in the plate decrease with increasing values of aspect ratio a*. Although the stress in the plate increases in

Fig. 4.
figure 4

Relations between σ22 h / p0 and η for polarizations in the directions of Ox1 (a), Ox2 (b), and Ox3 (c) axes.

Full size image

accord with the initial compression, the initial tension decreases its value. These are natural result and coincide well with the well-known mechanical considerations. However, there are some interesting cases in the graphs. As is seen from slopes of the graphs, the influence of the initial stress parameter η increases with aspect ratio a*. Further, the crosscheck of the graphs in Figs. 4a and 4b proves that, instead of Ox3 axis, the choice of the Ox1 axis for the polarization of plate decreases the values of σ22 h / p0 for a* < 1; i.e., σ22[2]/p0 < σ22[1]/p0 < σ22[3]/p0. For a∗ > 1, σ22[2]/p0 < σ22[3]/p0 < σ22[1]/p0 This means that lower stresses arise in the plate polarized along the longest edge, because the polarization of the plate along the longest edge has a larger effective area.

Conclusions

In this paper, the forced vibration behavior of a prestressed piezoelectric plate resting on a rigid foundation is described. This is a challenging task because, unlike elastic media, there is no analytical expression for estimating the dynamic response of such a mechanical system within the scope of TLTESIS. Further, piezoelectric materials may have various constitutive relationships depending on poling directions. A modal investigation was presented herein for evaluating such and similar problems.

Certain results for three special cases were given. The numerical data found prove that the best stress insulation occurs for the polarization paralleled to the dynamic force applied. All these results show that the system becomes more steady for the case mentioned. Unlike the other cases examined, the vertical polarization in the plate increases the resonant values of the system. It was also observed that there are close relationships both quantitative and qualitative between the aspect ratio and the poling direction. In addition, the effect of the initial stress parameter on the stress distribution diminishes as the aspect ratio decreases. It should be mentioned that the numerical results presented here are valid generally, even though they are presented for barium titanate ( BaTiO3) as a material.