1 Introduction

In recent years, axially deploying cantilevered composite structures have been used [1, 2] for novel variable-span wings of e.g. long-range missiles, extension of robot arms, and other similar applications. Because these types of structure are often used in high-speed operating environments, external disturbance or even their own axial motion can induce large-amplitude vibrations and cause geometrically nonlinear problems that affect both the stability and accurate operation of the structure. The nonlinear dynamic characteristics of the extension process of such cantilever structures remain unknown and would be interesting to analyze.

To conduct theoretical dynamic analysis, such structures are usually modeled as axially extendable cantilever laminated composite beams or plates. The nonlinear dynamic equation that describes their extension is usually a time-varying partial differential equation or an ordinary differential equation. Unfortunately, in contrast to steady nonlinear dynamic systems, no systematic solutions of such time-varying nonlinear dynamic equations are available at present. Therefore, investigations of this problem usually focus on time-varying dynamic modeling and numerical simulation. An equation for the motion of axially deploying cantilever beams was found by Tabarrok et al. [3] based on Newton’s second law, and the group studied the problem of linear vibration of a cantilever beam during its extension for constant speeds. The small-deformation transverse vibrations of cantilever beams of equal annular cross-section during extension at constant speed in an incompressible fluid were investigated by Taleb and Misra [4]. They also analyzed the effects of relevant variables on the dynamic stability of the deploying beam. A flexible robot arm was modeled by Wang and Wei [5] as a removable slender cantilever beam, using Newton’s second law, to investigate its dynamic behavior during extension. An equation of motion for extendable flexible beams was deduced by Behdinan et al. [6] using Hamilton’s principle, and the time-varying dynamical behavior of the axially moving system investigated numerically. The dynamic properties of a deploying cantilever beam were investigated by Deng et al. [7] under various deploying laws using a precision integration method. The exact forced response of a translating string of arbitrarily varying length under constant tension with general initial conditions and external excitation was analyzed by Zhu and Zheng [8]. The stability of an axially deploying beam in dense liquids was studied by Gosselin et al. [9], who also deduced the equation of motion for flexible slender cantilever beams with equal annular cross-section during axial extension at constant speed in a dense incompressible fluid. Furthermore, they analyzed the effects of extension speed on the structural stability. The vibration and stability of an axially moving cantilever beam in dense liquids were studied by Wang and Ni [10]. The nonlinear dynamic response of axially deploying cantilever beams in supersonic flow was studied by Zhang et al. [11]. Variable-span wings were modeled by Huang and Qiu [12] as extendable cantilever beams, and their transient aerodynamic response and fluttering characteristics during a morphing process under aerodynamic force investigated numerically. The linear vibration of an extendable cantilever plate model was studied by Wang et al. [13], who deduced the partial differential equation for its motion and analyzed the variations in frequency and dynamic stability during motion. A nonlinear dynamic equation for axially deploying cantilevered laminated composite plates under combined third-order nonlinear aerodynamic load and in-plane excitation was found by Zhang et al. [14]. The group used Reddy’s high-order shear theory, and studied the nonlinear dynamical behavior of the time-varying structure using a numerical approach. The equation governing an axially moving viscoelastic plate was derived by Yang et al. [15] based on Newton’s second law, who also studied the complex natural frequencies for linear free vibrations as well as bifurcation and chaos for forced nonlinear vibrations of the plate using the finite difference method. The natural frequencies of nonlinear planar vibration of axially moving beams were investigated numerically by Ding and Chen [16] using Galerkin methods. Various scholars have studied the dynamical behavior of axially movable cantilever beam structures under external loads using experimental techniques [17,18,19]. The results of the above-mentioned studies show that such axially deploying cantilever structures show complex dynamical behavior under external loads, and that nonlinear dynamic phenomena such as vibration amplitude jumps and divergences can readily occur in the vibration process. Therefore, control of large-amplitude vibration of cantilever structures during their extension remains a great challenge, and it would be highly desirable to improve the design and development of such structures.

Fig. 1
figure 1

Model of axially deploying piezoelectric cantilever plate

Full size image

Piezoelectric materials are widely used to study vibration suppression for plate–shell structures [20]. A piezoelectric laminated composite plate made of piezoelectric material and fiber-reinforced composite benefits from the advantages of the latter, including high specific strength and stiffness and excellent fatigue resistance. Such structures also exhibit improved controllability because the fiber-reinforced composite and piezoelectric materials can be stacked in many ways in the laminated composite plate structure. Studies of the nonlinear dynamics of such piezoelectric laminated composite plates have been carried out for many years. The stretching and bending motions of piezoelectric laminated composite plates were studied by Reddy and Mitchell [21] using two different models. They developed a geometrically nonlinear theory for laminated composite plates with piezoelectric laminates. The nonlinear free and forced vibrations of piezoelectric functionally graded shells under electrothermal and third-order aerodynamic loads were studied by Rafiee et al. [22]. The nonlinear dynamic response of a damaged piezoelectric laminated composite plate was investigated by Fu et al. [23] using a finite difference method. A dynamic equation based on high-order shear deformation theory and the von Karman equation was found by Huang and Shen [24]. They investigated the nonlinear free and forced vibrations of a laminated composite plate with embedded piezoelectric actuators under electrothermomechanical loads using an improved perturbation method. A nonlinear vibration equation for a laminated composite plate with an embedded piezoelectric laminate was deduced by Dash and Singh [25] by applying high-order shear deformation theory. A control equation for piezoelectric functionally graded shells in a thermomagnetic environment was found by Wang et al. [26]. The group used Reddy’s high-order shear plate theory and Hamilton’s principle. The one-to-two internal resonance problem of a piezoelectric laminated composite plate under external load was studied by Zhang et al. [27]. The dynamic behavior of axial and transverse vibrations of a piezoelectric laminated composite plate was studied numerically by Zhang and Shen [28]. Smart control of the vibration of a piezoelectric laminated composite plate was investigated by Wang et al. [29] using first-order shear deformation theory. Active control of the vibration of laminated composite shells containing piezoelectric fiber-reinforced composites was studied by Ray and Reddy [30]. Some experimental and theoretical studies on vibration control of piezoelectric laminated composite plate structures were conducted by Qiu et al. [31] and Dong et al. [32] using several methods. In the present work, piezoelectric materials were used in an axially extendable cantilever laminated composite plate structure, and the nonlinear dynamic behavior of the deploying cantilever piezoelectric laminated composite plate, under the combined action of aerodynamic load and piezoelectric excitation, was studied. Using Reddy’s high-order shear deformation theory for laminates and Hamilton’s principle, a partial differential nonlinear model for the dynamics of the deploying cantilever was obtained. Considering the displacement boundary conditions of the structure, a time-dependent modal function for structural vibration was found. The ordinary differential form of the time-varying nonlinear dynamic equation for the extendable cantilevered laminated composite plate was obtained by truncating the partial differential form of the nonlinear dynamic equation using the Galerkin method. Then, the effects of variables such as piezoelectric excitation and extension speed on the time-varying nonlinear dynamic stability of the cantilevered piezoelectric laminated composite plate during the extension process were analyzed, considering the characteristic of the piezoelectric material.

2 Equation of motion for deploying piezoelectric laminated composite plate

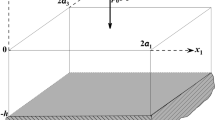
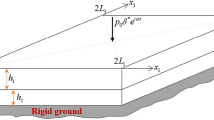
We consider a model of an axially deploying rectangular cantilevered piezoelectric laminated composite plate formed by bonding a polyvinylidene fluoride (PVDF) piezoelectric membrane with fiber-reinforced composites (Fig. 1). The initial length of the plate is \(l_0 \), the width is b, the thickness is h, and the Cartesian coordinate center \(O_{xy}\) is located at the center of the plate. The rectangular cantilever piezoelectric laminated composite plate extends along the x-axis at a time-varying speed with the form \(V=V_0 +V_{d} \cos \left( {\varOmega _{1} t} \right) \). The external piezoelectric excitation can be described as \(V_{e} =V_{z} \cos \left( {\varOmega _{2} t} \right) \). The structure is also subjected to a transverse aerodynamic load \(\Delta p\); first-order linear piston theory was employed to study the effect of the aerodynamic load on the nonlinear dynamical behavior of the deploying cantilever piezoelectric laminated composite plate.

Based on Reddy’s [33] third-order shear theory for laminates, the displacement field of the laminated composite plate can be described as

$$\begin{aligned}&u(x,y,t)=u_0 \left( {x\left( t \right) ,y,t} \right) +z\mathop \phi \nolimits _{x} \left( {x\left( t \right) ,y,t} \right) \nonumber \\&\quad -z^{3}\frac{4}{3h^{2}}\left( {\mathop \phi \nolimits _{x} +\frac{\partial w_0 }{\partial x}} \right) , \end{aligned}$$
(1a)
$$\begin{aligned}&v(x,y,t)=v_0 \left( {x\left( t \right) ,y,t} \right) +z\phi _y \left( {x\left( t \right) ,y,t} \right) \nonumber \\&\quad -z^{3}\frac{4}{3h^{2}}\left( {\phi _y +\frac{\partial w_0 }{\partial y}} \right) , \end{aligned}$$
(1b)
$$\begin{aligned}&w(x,y,t)=w_0 \left( {x\left( t \right) ,y,t} \right) , \end{aligned}$$
(1c)

where \(u_0 \), \(v_0 \), and \(w_0 \) are the displacements of an arbitrary point on the middle surface in x, y, and z directions, and \(\phi _x \) and \(\phi _y \) are angles along the y- and x-axis, respectively.

Using von Karman’s geometry theory for the large deformation of a plate, the relationship between the strain displacement \(\varepsilon _i\) (\(i=xx , yy\)) and curvature displacement \(\gamma _i\) (\(i=xy , yz, zx\)) can be expressed as

$$\begin{aligned} \varepsilon _{xx}= & {} \frac{\partial u_0 }{\partial x}+\frac{1}{2}\left( {\frac{\partial w_0 }{\partial x}} \right) ^{2}, \quad \varepsilon _{yy} =\frac{\partial v_0 }{\partial y}+\frac{1}{2}\left( {\frac{\partial w_0 }{\partial y}} \right) ^{2},\nonumber \\ \gamma _{xy}= & {} \frac{1}{2}\left( {\frac{\partial u_0 }{\partial y}+\frac{\partial v_0 }{\partial x}+\frac{\partial w_0 }{\partial x}\frac{\partial w_0 }{\partial y}} \right) ,\nonumber \\ \gamma _{yz}= & {} \frac{1}{2}\left( {\frac{\partial v_0 }{\partial z}+\frac{\partial w_0 }{\partial y}} \right) , \quad \gamma _{zx} =\frac{1}{2}\left( {\frac{\partial u_0 }{\partial z}+\frac{\partial w_0 }{\partial x}} \right) . \end{aligned}$$
(2)

When introducing a piezoelectric laminate into the laminated composite plate, the relationships between the strain displacement \(\varepsilon _i\) (\(i=xx , yy\)) and curvature displacement \(\gamma _i\) (\(i=xy , yz , zx\)) become

$$\begin{aligned}&\left\{ {{\begin{array}{c} {\sigma _{xx} } \\ {\sigma _{yy} } \\ {\sigma _{yz} } \\ {\sigma _{zx} } \\ {\sigma _{xy} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{ccccc} {Q_{11} }&{} {Q_{12} }&{} 0&{} 0&{} 0 \\ {Q_{21} }&{} {Q_{22} }&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {Q_{44} }&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {Q_{55} }&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {Q_{66} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{c} {\varepsilon _{xx} } \\ {\varepsilon _{yy} } \\ {\gamma _{yz} } \\ {\gamma _{zx} } \\ {\gamma _{xy} } \\ \end{array} }} \right\} \nonumber \\&\quad -\left\{ {{\begin{array}{l} {e_{31} } \\ {e_{32} } \\ 0 \\ 0 \\ {e_{36} } \\ \end{array} }} \right\} \;E_{k} , \end{aligned}$$
(3)

where \(e_{ij} \) is the piezoelectric constant and \(E_{k} \) is the electric field strength. The stiffness coefficient \(Q_{ij} \) can be expressed as

$$\begin{aligned} Q_{11}= & {} \frac{E_1 }{1-v_{12} v_{21} }, \quad Q_{12} =\frac{v_{12} E_2 }{1-v_{12} v_{21} },\nonumber \\ Q_{22}= & {} \frac{E_2 }{1-v_{12} v_{21} },\nonumber \\ Q_{66}= & {} G_{12} , \quad Q_{44} =G_{23} , \quad Q_{55} =G_{13} . \end{aligned}$$
(4)

According to Hamilton’s principle, the nonlinear dynamic equation for the deploying cantilevered piezoelectric laminated composite plate can be expressed as

$$\begin{aligned} \delta \int _{t_1 }^{t_2 } {\;L\hbox {d}t} +\int _{t_1 }^{t_2 } {\;\delta W\hbox {d}t} =0, \end{aligned}$$
(5)

where

$$\begin{aligned} L=\int _V {\frac{1}{2}} \rho \dot{u}_i \dot{u}_i \hbox {d}V-\int _V {\frac{1}{2}} H\left( {\varepsilon _{ij} ,E_{ij} } \right) \hbox {d}V. \end{aligned}$$
(6)

In Eq. (6), the variation of the kinetic energy can be written as

$$\begin{aligned}&\int _{t_1 }^{t_2 } \delta \int _V {\frac{1}{2}} \rho \dot{u}_i \dot{u}_i \hbox {d}V\hbox {d}t=\int _{t_1 }^{t_2 } {\int _V {\frac{1}{2}} \rho \dot{u}_i \delta \dot{u}_i \hbox {d}V} \hbox {d}t\nonumber \\&\quad =\int _V {\rho \dot{u}_i \delta \dot{u}_i } \hbox {d}V\left| {_{t_1 }^{t_2 } } \right. -\int _{t_1 }^{t_2 } {\int _V {\rho \ddot{u}_i \delta u_i \hbox {d}V} } \hbox {d}t. \end{aligned}$$
(7)

The potential energy of the piezoelectric laminate is

$$\begin{aligned} H(\varepsilon _{ij} ,E_i )=\frac{1}{2}Q_{ijkl} \varepsilon _{ij} \varepsilon _{kl} -e_{ijk} E_i \varepsilon _{jk} -\frac{1}{2}\zeta _{ij} E_i E_j , \end{aligned}$$
(8)

where \(Q_{ijkl} \), \(e_{ijk} \), \(\zeta _{ij} \), and \(E_i \) are the Young’s modulus, piezoelectric constant, permittivity, and electric field strength, respectively.

The relationship between the electric field strength, electric potential energy, stress, and electric displacement can be described by the following formulas [21]

$$\begin{aligned} E_i =-\frac{\partial \phi }{\partial x_i }, \quad \sigma _{ij} =\frac{\partial H}{\partial \varepsilon _{ij} }, \quad D_i =-\frac{\partial H}{\partial E_i }. \end{aligned}$$
(9)

Thus, the variation of the potential energy for a piezoelectric laminated composite plate is

$$\begin{aligned}&\delta \int _V \left( \frac{1}{2}Q_{ijkl} \varepsilon _{ij} \varepsilon _{kl} -e_{ijk} E_i \varepsilon _{jk} -\frac{1}{2}\zeta _{ij} E_i E_j \right) \hbox {d}V\nonumber \\&\quad =\delta \int _V \left( \frac{1}{2}Q_{ijkl} \varepsilon _{ij} \varepsilon _{kl}-e_{ijk} E_i \varepsilon _{jk} \right) \hbox {d}V\nonumber \\&\qquad -\int _V \zeta _{ij} E_i \delta E_j \hbox {d}V. \end{aligned}$$
(10)

The virtual work of the external force on the system is

$$\begin{aligned}&\int _{t_1 }^{t_2 } {{\delta }W} \hbox {d}t=\int _{t_1 }^{t_2 } \left( {\delta }\int \int {\Delta p\;{\delta }w_0 } \hbox {d}x\hbox {d}y\right. \nonumber \\&\quad \left. -\int \int {\gamma \dot{w}_0 {\delta }w_0 \hbox {d}x\hbox {d}y} \right) \hbox {d}t, \end{aligned}$$
(11)

where \(\gamma \) is the structural damping coefficient.

By substituting Eqs. (7), (10), and (11) into Eq. (5) and considering Hamilton’s principle, the nonlinear dynamic equation for the deploying cantilevered piezoelectric laminated composite plate can be obtained as

$$\begin{aligned}&N_{xx,x} +N_{xy,y} =I_0 \frac{\hbox {d}^{2}x}{\hbox {d}t^{2}}+I_0 \ddot{u}_0 +\left( {I_1 -c_1 I_3 } \right) \ddot{\phi }_x\nonumber \\&\qquad -c_1 I_3 \frac{\partial \ddot{w}_0 }{\partial x}, \end{aligned}$$
(12a)
$$\begin{aligned}&N_{yy,y} +N_{xy,x} =I_0 \ddot{v}_0 +\left( {I_1 -c_1 I_3 } \right) \ddot{\phi }_y -c_1 I_3 \frac{\partial \ddot{w}_0 }{\partial y}, \end{aligned}$$
(12b)
$$\begin{aligned}&\frac{\partial w_0 }{\partial x}\left( {N_{xx,x} +N_{xy,y} } \right) +\frac{\partial w_0 }{\partial y}\left( {N_{yy,y} +N_{xy,x} } \right) \nonumber \\&\qquad +N_{xx} \frac{\partial ^{2}w_0 }{\partial x^{2}}+N_{yy} \frac{\partial ^{2}w_0 }{\partial y^{2}}+2N_{xy} \frac{\partial ^{2}w_0 }{\partial y\partial x}\nonumber \\&\qquad +Q_{x,x} +Q_{y,y} +c_1 \left( {P_{xx,xx} +2P_{xy,xy} +P_{yy,yy} } \right) \nonumber \\&\qquad -c_2 \left( {R_{x,x} +R_{y,y} } \right) +\varDelta p-\gamma \dot{w}_0\nonumber \\&\quad =I_0 \ddot{w}_0 +c_1 I_3 \left( {\frac{\partial \ddot{u}_0 }{\partial x}+\frac{\partial \ddot{v}_0 }{\partial x}} \right) \nonumber \\&\qquad +c_1 \left( {I_4 -c_1 I_6 } \right) \left( {\frac{\partial \ddot{\phi }_x }{\partial x}+\frac{\partial \ddot{\phi }_y }{\partial y}} \right) \nonumber \\&\qquad -c_1^2 I_6 \left( {\frac{\partial ^{2}\ddot{w}_0 }{\partial x^{2}}+\frac{\partial ^{2}\ddot{w}_0 }{\partial y^{2}}} \right) , \end{aligned}$$
(12c)
$$\begin{aligned}&M_{xx,x} +M_{xy,y} -c_1 \left( {P_{xx,x} +P_{xy,y} } \right) -\left( {Q_x -c_2 R_x } \right) \nonumber \\&\quad =\left( {I_1 -c_1 I_3 } \right) \ddot{u}_0 +\left( {I_2 -2c_1 I_4 +c_1^2 I_6 } \right) \ddot{\phi }_x\nonumber \\&\qquad -c_1 \left( {I_4 -c_1 I_6 } \right) \frac{\partial \ddot{w}_0 }{\partial x},\end{aligned}$$
(12d)
$$\begin{aligned}&M_{yy,y} +M_{xy,x} -c_1 \left( {P_{yy,y} +P_{xy,x} } \right) -\left( {Q_y -c_2 R_y } \right) \nonumber \\&\quad =\left( {I_1 -c_1 I_3 } \right) \ddot{v}_0 +\left( {I_2 -2c_1 I_4 +c_1^2 I_6 } \right) \ddot{\phi }_y\nonumber \\&\qquad -c_1 \left( {I_4 -c_1 I_6 } \right) \frac{\partial \ddot{w}_0 }{\partial y}, \end{aligned}$$
(12e)

where \(\Delta p\) in Eq. (12c) denotes the transverse aerodynamic load obtained by first-order piston theory [34]. Since the length of the plate varies with time, the expression for the first-order aerodynamic force applied on the deploying cantilevered plate can be formulated as

$$\begin{aligned} \Delta p=-\frac{4q_d \lambda }{M_\infty }\left( {\frac{1}{v}\frac{\partial w_0 }{\partial x}\frac{\hbox {d}x}{\hbox {d}t}+\frac{\partial w_0 }{\partial y}+\frac{1}{v}\frac{\partial w_0 }{\partial t}} \right) . \end{aligned}$$
(13)

The moment of inertia can be calculated using the following equation

$$\begin{aligned} I_i =\int _{{\;-h}/2}^{{\;h}/2} {z^{i}\rho (z)} \hbox {d}z, \quad {i=0 , 1 , 2 , 3 , 4 , 6}. \end{aligned}$$
(14)

For an orthotropic piezoelectric laminated composite plate, the internal forces can be expressed as

$$\begin{aligned}&\left\{ {{\begin{array}{c} {N_x } \\ {N_y } \\ {N_{xy} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{ccc} {A_{11} }&{} {A_{12} }&{} 0 \\ {A_{21} }&{} {A_{22} }&{} 0 \\ 0&{} 0&{} {A_{66} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{l} {\varepsilon _x^{\left( 0 \right) } } \\ {\varepsilon _y^{\left( 0 \right) } } \\ {\gamma _{xy}^{\left( 0 \right) } } \\ \end{array} }} \right\} -\left\{ {{\begin{array}{l} {N_{xx}^\mathrm{pz} } \\ {N_{yy}^\mathrm{pz} } \\ {N_{xy}^\mathrm{pz} } \\ \end{array} }} \right\} , \end{aligned}$$
(15a)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {M_x } \\ {M_y } \\ {M_{xy} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{ccc} {D_{11} }&{} {D_{12} }&{} 0 \\ {D_{21} }&{} {D_{22} }&{} 0 \\ 0&{} 0&{} {D_{66} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{l} {\varepsilon _x^{\left( 1 \right) } } \\ {\varepsilon _y^{\left( 1 \right) } } \\ {\gamma _{xy}^{\left( 1 \right) } } \\ \end{array} }} \right\} \nonumber \\&\quad -c_{1} \left\{ {{\begin{array}{ccc} {F_{11} }&{} {F_{12} }&{} 0 \\ {F_{21} }&{} {F_{22} }&{} 0 \\ 0&{} 0&{} {F_{66} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{l} {\varepsilon _x^{\left( 2 \right) } } \\ {\varepsilon _y^{\left( 2 \right) } } \\ {\gamma _{xy}^{\left( 2 \right) } } \\ \end{array} }} \right\} -\left\{ {{\begin{array}{l} {M_{xx}^\mathrm{pz} } \\ {M_{yy}^\mathrm{pz} } \\ {M_{xy}^\mathrm{pz} } \\ \end{array} }} \right\} , \end{aligned}$$
(15b)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {P_x } \\ {P_y } \\ {P_{xy} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{ccc} {F_{11} }&{} {F_{12} }&{} 0 \\ {F_{21} }&{} {F_{22} }&{} 0 \\ 0&{} 0&{} {F_{66} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{l} {\varepsilon _x^{\left( 1 \right) } } \\ {\varepsilon _y^{\left( 1 \right) } } \\ {\gamma _{xy}^{\left( 1 \right) } } \\ \end{array} }} \right\} \nonumber \\&\quad -c_1 \left\{ {{\begin{array}{lll} {H_{11} }&{} {H_{12} }&{} 0 \\ {H_{21} }&{} {H_{22} }&{} 0 \\ 0&{} 0&{} {H_{66} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{l} {\varepsilon _x^{\left( 2 \right) } } \\ {\varepsilon _y^{\left( 2 \right) } } \\ {\gamma _{xy}^{\left( 2 \right) } } \\ \end{array} }} \right\} -\left\{ {{\begin{array}{l} {P_{xx}^\mathrm{pz} } \\ {P_{yy}^\mathrm{pz} } \\ {P_{xy}^\mathrm{pz} } \\ \end{array} }} \right\} , \end{aligned}$$
(15c)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {Q_y } \\ {Q_x } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{cc} {A_{{44}} }&{} 0 \\ \hbox {0}&{} {A_{{55}} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{l} {\gamma _{yz}^{\left( 0 \right) } } \\ {\gamma _{xz}^{\left( 0 \right) } } \\ \end{array} }} \right\} \nonumber \\&\quad -c_2 \left\{ {{\begin{array}{cc} {D_{{44}} }&{} \hbox {0} \\ \hbox {0}&{} {D_{{55}} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{l} {\gamma _{yz}^{\left( {2} \right) } } \\ {\gamma _{xz}^{\left( {2} \right) } } \\ \end{array} }} \right\} , \end{aligned}$$
(15d)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {R_y } \\ {R_x } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{cc} {D_{{44}} }&{} \hbox {0} \\ \hbox {0}&{} {D_{{55}} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{l} {\gamma _{yz}^{\left( {0} \right) } } \\ {\gamma _{xz}^{\left( 0 \right) } } \\ \end{array} }} \right\} \nonumber \\&\quad -c_2 \left\{ {{\begin{array}{ll} {F_{{44}} }&{} \hbox {0} \\ \hbox {0}&{} {F_{{55}} } \\ \end{array} }} \right\} \left\{ {{\begin{array}{l} {\gamma _{yz}^{\left( 2 \right) } } \\ {\gamma _{xz}^{\left( 2 \right) } } \\ \end{array} }} \right\} , \end{aligned}$$
(15e)

where \(N_{ij}^\mathrm{pz} \), \(M_{ij}^\mathrm{pz} \), and \(P_{ij}^\mathrm{pz}\) (\(i, j = x , y \)) denote the internal forces induced by the piezoelectric material. If only the change of the electric field in the thickness direction is considered, these variables can be defined as

$$\begin{aligned} N_{xx}^\mathrm{pz}= & {} \sum _{k=1}^N {\int _z^{z+1} {e_{31} E_z \hbox {d}z} } ,\nonumber \\ N_{yy}^\mathrm{pz}= & {} \sum _{k=1}^N {\int _z^{z+1} {e_{32} E_z \hbox {d}z} } , \quad N_{xy}^\mathrm{pz} =N_{xz}^\mathrm{pz} =N_{yz}^\mathrm{pz} =0, \end{aligned}$$
(16a)
$$\begin{aligned} M_{xx}^\mathrm{pz}= & {} \sum _{k=1}^N {\int _z^{z+1} {z e_{31} E_z \hbox {d}z} } ,\nonumber \\ M_{yy}^\mathrm{pz}= & {} \sum _{k=1}^N {\int _z^{z+1} {z e_{32} E_z \hbox {d}z} } , \quad M_{xy}^\mathrm{pz} =M_{xz}^\mathrm{pz} =M_{yz}^\mathrm{pz} =0,\nonumber \\ \end{aligned}$$
(16b)
$$\begin{aligned} P_{xx}^\mathrm{pz}= & {} \sum _{k=1}^N {\int _z^{z+1} {z^{3} e_{31} E_z \hbox {d}z} } ,\nonumber \\ P_{yy}^\mathrm{pz}= & {} \sum _{k=1}^N {\int _z^{z+1} {z^{3} e_{32} E_z \hbox {d}z} } , \quad P_{xy}^\mathrm{pz} =P_{xz}^\mathrm{pz} =P_{yz}^\mathrm{pz} =0,\nonumber \\ \end{aligned}$$
(16c)

where \(e_{ij} \) is the piezoelectric constant, k is the number of the piezoelectric laminate, and \(E_{z} \) is the electric field strength. The relationship between the electric field strength and applied voltage \(V_{e} \) is \(E_{z} =V_{e} /h_{z} \), where \(h_z \) is the thickness of the piezoelectric laminate.

Inserting Eqs. (15) and (16) into Eq. (12), the nonlinear dynamic equation for the deploying cantilever piezoelectric laminated composite plate, expressed in terms of generalized displacement variables, can be obtained as

$$\begin{aligned}&A_{11} \frac{\partial ^{2}u_0 }{\partial x^{2}}+A_{66} \frac{\partial ^{2}u_0 }{\partial y^{2}}+\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}v_0 }{\partial x\partial y}\nonumber \\&\quad +\left( {A_{12} +A_{66} } \right) \frac{\partial w_0 }{\partial y}\frac{\partial ^{2}w_0 }{\partial x\partial y}+A_{11} \frac{\partial w_0 }{\partial x}\frac{\partial ^{2}w_0 }{\partial x^{2}}\nonumber \\&\quad +A_{66} \frac{\partial w_0 }{\partial x}\frac{\partial ^{2}w_0 }{\partial y^{2}}\nonumber \\&\quad =I_0 \frac{\hbox {d}^{2}x}{\hbox {d}t^{2}}+I_0 \ddot{u}_0 +\left( {I_1 -c_1 I_3 } \right) \ddot{\phi }_x -c_1 I_3 \frac{\partial \ddot{w}_0 }{\partial x}, \end{aligned}$$
(17a)
$$\begin{aligned}&A_{22} \frac{\partial ^{2}v_0 }{\partial y^{2}}+A_{66} \frac{\partial ^{2}v_0 }{\partial x^{2}}+\left( {A_{21} +A_{66} } \right) \frac{\partial ^{2}u_0 }{\partial x\partial y}\nonumber \\&\quad +\left( {A_{21} +A_{66} } \right) \frac{\partial w_0 }{\partial x}\frac{\partial ^{2}w_0 }{\partial x\partial y}+A_{22} \frac{\partial w_0 }{\partial y}\frac{\partial ^{2}w_0 }{\partial y^{2}}\nonumber \\&\quad +A_{66} \frac{\partial w_0 }{\partial y}\frac{\partial ^{2}w_0 }{\partial x^{2}}\nonumber \\&\quad =I_0 \ddot{v}_0 +\left( {I_1 -c_1 I_3 } \right) \ddot{\phi }_y -c_1 I_3 \frac{\partial \ddot{w}_0 }{\partial y}, \end{aligned}$$
(17b)
$$\begin{aligned}&\left( {A_{55} +c_2^2 F_{55} -2c_2 D_{55} -N_{xx}^\mathrm{pz} } \right) \frac{\partial ^{2}w_0 }{\partial x^{2}}\nonumber \\&\quad +\left( {A_{44} +c_2^2 F_{44} -2c_2 D_{44} -N_{yy}^\mathrm{pz} } \right) \frac{\partial ^{2}w_0 }{\partial y^{2}}\nonumber \\&\quad +A_{11} \frac{\partial u_0 }{\partial x}\frac{\partial ^{2}w_0 }{\partial x^{2}}+A_{21} \frac{\partial u_0 }{\partial x}\frac{\partial ^{2}w_0 }{\partial y^{2}}+2A_{66} \frac{\partial u_0 }{\partial y}\frac{\partial ^{2}w_0 }{\partial x\partial y}\nonumber \\&\quad +A_{11} \frac{\partial ^{2}u_0 }{\partial x^{2}}\frac{\partial w_0 }{\partial x}+A_{66} \frac{\partial ^{2}u_0 }{\partial y^{2}}\frac{\partial w_0 }{\partial x}\nonumber \\&\quad +\left( {A_{21} +A_{66} } \right) \frac{\partial ^{2}u_0 }{\partial x\partial y}\frac{\partial w_0 }{\partial y}+\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}v_0 }{\partial x\partial y}\frac{\partial w_0 }{\partial x}\nonumber \\&\quad +A_{22} \frac{\partial ^{2}v_0 }{\partial y^{2}}\frac{\partial w_0 }{\partial y}+A_{12} \frac{\partial v_0 }{\partial y}\frac{\partial ^{2}w_0 }{\partial x^{2}}\nonumber \\&\quad +A_{66} \frac{\partial ^{2}v_0 }{\partial x^{2}}\frac{\partial w_0 }{\partial y}+\frac{3}{2}A_{11} \left( {\frac{\partial w_0 }{\partial x}} \right) ^{2}\frac{\partial ^{2}w_0 }{\partial x^{2}}\nonumber \\&\quad +A_{22} \frac{\partial v_0 }{\partial y}\frac{\partial ^{2}w_0 }{\partial y^{2}} +2A_{66} \frac{\partial v_0 }{\partial x}\frac{\partial ^{2}w_0 }{\partial x\partial y}\nonumber \\&\quad +\frac{3}{2}A_{22} \left( {\frac{\partial w_0 }{\partial y}} \right) ^{2}\frac{\partial ^{2}w_0 }{\partial y^{2}}\nonumber \\&\quad +\left( {\frac{1}{2}A_{21} +A_{66} } \right) \left( {\frac{\partial w_0 }{\partial x}} \right) ^{2}\frac{\partial ^{2}w_0 }{\partial y^{2}} -c_1^2 H_{11} \frac{\partial ^{4}w_0 }{\partial x^{4}}\nonumber \\&\quad +\left( {A_{66} +\frac{1}{2}A{ }_{21}} \right) \left( {\frac{\partial w_0 }{\partial y}} \right) ^{2}\frac{\partial ^{2}w_0 }{\partial x^{2}}+( A_{12} +A_{21}\nonumber \\&\quad +4A_{66} )\frac{\partial w_0 }{\partial x}\frac{\partial w_0 }{\partial y}\frac{\partial ^{2}w_0 }{\partial x\partial y}-c_1^2 H_{22} \frac{\partial ^{4}w_0 }{\partial y^{4}}\nonumber \\&\quad +\left( {A_{55} -2c_2 D_{55} +c_2^2 F_{55} } \right) \frac{\partial \phi _x }{\partial x}\nonumber \\&\quad +\left( {c_1 F_{22} -c_1^2 H_{22} } \right) \frac{\partial ^{3}\phi _y }{\partial y^{3}} +\left( {c_1 F_{11} -c_1^2 H_{11} } \right) \frac{\partial ^{3}\phi _x }{\partial x^{3}}\nonumber \\&\quad +\left( {A_{44} -2c_2 D_{44} +c_2^2 F_{44} } \right) \frac{\partial \phi _y }{\partial y}+c_1 \left( F_{21} +2F_{66}\right. \nonumber \\&\quad \left. -c_1 H_{21} -2c_1 H_{66} \right) \frac{\partial ^{3}\phi _x }{\partial x\partial y^{2}}\nonumber \\&\quad -2c_1^2 \left( {H_{21} -2H_{66} } \right) \frac{\partial ^{4}w_0 }{\partial x^{2}\partial y^{2}}+c_1 \left( F_{12} +2F_{66} -c_1 H_{12}\right. \nonumber \\&\quad \left. -2c_1 H_{66} \right) \frac{\partial ^{3}\phi _y }{\partial x^{2}\partial y}+\varDelta p-\gamma \frac{\partial w_0 }{\partial t}\nonumber \\&\quad =I_0 \ddot{w}_0 -c_1^2 I_6 \left( {\frac{\partial ^{2}\ddot{w}_0 }{\partial x^{2}}+\frac{\partial ^{2}\ddot{w}_0 }{\partial y^{2}}} \right) \nonumber \\&\quad +c_1 I_3 \left( {\frac{\partial \ddot{u}_0 }{\partial x}+\frac{\partial \ddot{v}_0 }{\partial y}} \right) \nonumber \\&\quad +c_1 \left( {I_4 -c_1 I_6 } \right) \left( {\frac{\partial \ddot{\phi }_x }{\partial x}+\frac{\partial \ddot{\phi }_y }{\partial y}} \right) , \end{aligned}$$
(17c)
$$\begin{aligned}&\left( {D_{11} -2c_1 F_{11} +c_1^2 H_{11} } \right) \frac{\partial ^{2}\phi _x }{\partial x^{2}}\nonumber \\&\quad +\left( {D_{66} -2c_1 F_{66} +c_1^2 H_{66} } \right) \frac{\partial ^{2}\phi _x }{\partial y^{2}}\nonumber \\&\quad -\left( c_1 F_{11}-c_1^2 H_{11} \right) \frac{\partial ^{3}w_0 }{\partial x^{3}}\nonumber \\&\quad +c_1 \left( {-F_{12} -2F_{66} +c_1 H_{12} +2c_1 H_{66} } \right) \frac{\partial ^{3}w_0 }{\partial x\partial y^{2}}\nonumber \\&\quad -\left( {A_{55} -2c_2 D_{55} +c_2^2 F_{55} } \right) \frac{\partial w_0 }{\partial x}\nonumber \\&\quad +\left( D_{12} -2c{ }_1F_{12} -2c_1 F_{66} +D_{66} +c_1^2 H_{12}\right. \nonumber \\&\quad \left. +c_1^2 H_{66} \right) \frac{\partial ^{2}\phi _y }{\partial x\partial y} -\left( {A_{55} -2c_2 D_{55} +c_2^2 F_{55} } \right) \phi _x\nonumber \\&\quad =\left( {I_1 -c_1 I_3 } \right) \ddot{u}_0 +\left( {I_2 -2c_1 I_4 +c_1^2 I_6 } \right) \ddot{\phi }_x\nonumber \\&\quad -c_1 \left( {I_4 -c_1 I_6 } \right) \frac{\partial \ddot{w}_0 }{\partial x}, \end{aligned}$$
(17d)
$$\begin{aligned}&\left( {D_{22} -2c_1 F_{22} +c_1^2 H_{22} } \right) \frac{\partial ^{2}\phi _y }{\partial y^{2}}+\left( D_{66} -2c_1 F_{66}\right. \nonumber \\&\quad \left. +c_1^2 H_{66} \right) \frac{\partial ^{2}\phi _y }{\partial x^{2}} -\left( c_1 F_{22}-c_1^2 H_{22} \right) \frac{\partial ^{3}w_0 }{\partial y^{3}}\nonumber \\&\quad +c_1 \left( {-F_{21} -2F_{66} +c_1 H_{21} +2c_1 H_{66} } \right) \frac{\partial ^{3}w_0 }{\partial x^{2}\partial y}\nonumber \\&\quad -\left( {A_{44} -2c_2 D_{44} +c_2^2 F_{44} } \right) \frac{\partial w_0 }{\partial y}\nonumber \\&\quad +\left( D_{21} -2c{ }_1F_{21} -2c_1 F_{66} +D_{66} +c_1^2 H_{21}\right. \nonumber \\&\quad \left. +c_1^2 H_{66} \right) \frac{\partial ^{2}\phi _x }{\partial x\partial y} -\left( {A_{44} -2c_2 D_{44} +c_2^2 F_{44} } \right) \phi _y\nonumber \\&\quad =\left( {I_1 -c_1 I_3 } \right) \ddot{v}_0 +\left( {I_2 -2c_1 I_4 +c_1^2 I_6 } \right) \ddot{\phi }_y\nonumber \\&\quad -c_1 \left( {I_4 -c_1 I_6 } \right) \frac{\partial \ddot{w}_0 }{\partial y}. \end{aligned}$$
(17e)

3 Galerkin discretization

Due to the difficulty in finding an analytical solution to these partial differential equations describing the vibration of the system, they are usually discretized into equations of ordinary differential form for analysis. Moreover, as lower-frequency vibrations are dominant in nonlinear vibration systems, truncation at the first two modes is accurate enough in this case. In this work, the Galerkin method was employed to perform second-order truncation of the nonlinear dynamics in Eq. (17) in partial differential form, selecting the following time-dependent modal function satisfying the displacement boundary conditions

$$\begin{aligned}&u(x, y, t)=u_1 (t)\sin \frac{\uppi x}{2l}\cos \frac{\uppi y}{b}\nonumber \\&\quad +u_2 (t)\sin \frac{3\uppi x}{2l}\cos \frac{2\uppi y}{b}, \end{aligned}$$
(18a)
$$\begin{aligned}&v(x, y, t)=v_1 (t)\sin \frac{\uppi x}{2l}\sin \frac{\uppi y}{b}\nonumber \\&\quad +v_2 (t)\sin \frac{3\uppi x}{2l}\sin \frac{2\uppi y}{b}, \end{aligned}$$
(18b)
$$\begin{aligned}&w(x,y,t)=w_1 (t)X_1 (x)Y_1 (y)+w_2 (t)X_2 (x)Y_2 (y), \end{aligned}$$
(18c)
$$\begin{aligned}&\phi _x (x,y,t)=\phi _{x1} (t)\sin \frac{{\uppi }x}{2l}\cos \frac{{\uppi }y}{b}\nonumber \\&\quad +\phi _{x2} (t)\sin \frac{{\uppi }x}{l}\cos \frac{2{\uppi }y}{b}, \end{aligned}$$
(18d)
$$\begin{aligned}&\phi _y (x,y,t)=\phi _{y1} (t)\left( {1-\cos \frac{{\uppi }x}{2l}} \right) \sin \frac{{\uppi }y}{b}\nonumber \\&\quad +\phi _{y2} (t)\left( {1-\cos \frac{{\uppi }x}{l}} \right) \sin \frac{2{\uppi }y}{b}. \end{aligned}$$
(18e)

The general solution for the fourth-order ordinary differential equations, \(X_i (x)\) and \(Y_j (y)\), in Eq. (18c) is

$$\begin{aligned}&X_i (x)=\sin \frac{k_i x}{l}-\sinh \frac{k_i x}{l}\nonumber \\&\quad +\alpha _i \left( \cosh \frac{k_i x}{l}-\cos \frac{k_i x}{l}\right) , \end{aligned}$$
(19a)
$$\begin{aligned}&Y_i (y)=\sin \frac{k_j y}{b}+\sinh \frac{k_j y}{b}\nonumber \\&\quad -\alpha _i \left( \cosh \frac{k_j y}{b}+\cos \frac{k_j y}{b}\right) , \end{aligned}$$
(19b)

where \(X_i (x)\) is the clamped–free beam function along the x-axis, \(Y_j (y)\) is the free–free beam function along the y-axis, and \(k_i \) and \(k_j \) are roots of the characteristic equation with the following relationship

$$\begin{aligned} \cos k_i l_0 \cdot \cosh k_i l_0 +1=0, \quad \cos k_j b\cdot \cosh k_j b-1=0,\nonumber \\ \end{aligned}$$
(20a)

and

$$\begin{aligned} \alpha _i =\frac{\sinh k_i l_0 +\sin k_i l_0 }{\cosh k_i l_0 +\cos k_i l_0 }, \quad \beta _i =\frac{\sinh k_j b-\sin k_j b}{\cosh k_j b-\cos k_j b},\nonumber \\ \end{aligned}$$
(20b)

where l is an abbreviation for l(t).

Considering the effect of the change in the length of the plate along the x-axis as time varies, in the process of substituting the vibration mode function into the relevant equations to perform the Galerkin discretization, the accompanying compound derivative argument should be considered. Therefore, the following relational expressions are used for the derivation

$$\begin{aligned}&\frac{\hbox {D}}{\hbox {D}t}=\frac{\partial }{\partial t}+\frac{\partial }{\partial x}\frac{\hbox {d}x}{\hbox {d}t}, \end{aligned}$$
(21a)
$$\begin{aligned}&\frac{\hbox {D}^{2}}{\hbox {D}t^{2}}=\frac{\partial ^{2}}{\partial t^{2}}+2\frac{\partial ^{2}}{\partial x\partial t}\frac{\hbox {d}x}{\hbox {d}t}+\frac{\partial ^{2}}{\partial x^{2}}\left( {\frac{\hbox {d}x}{\hbox {d}t}} \right) ^{2}+\frac{\partial }{\partial x}\frac{\hbox {d}^{2}x}{\hbox {d}t^{2}}. \end{aligned}$$
(21b)

To normalize Eq. (17), the following dimensionless parameters and variables are introduced

$$\begin{aligned}&\bar{{u}}_0 =\frac{u_0 }{l_0 }, \quad \bar{{v}}_0 =\frac{v_0 }{b}, \quad \bar{{w}}_0 =\frac{w_0 }{h}, \quad \bar{{\phi }}_x =\phi _x , \quad \bar{{\phi }}_y =\phi _y ,\nonumber \\&\bar{{x}}=\frac{x}{l_0 }, \quad \bar{{y}}=\frac{y}{b}, \quad \bar{{f}}=\frac{b^{2}}{Eh^{3}}f,\nonumber \\&\overline{\gamma }=\frac{1}{l_0 b}\sqrt{\frac{1}{\rho E}}\;\gamma , \quad \bar{{\varOmega }}=\frac{1}{{\uppi }^{2}}\left( {\frac{l_0 b\rho }{E}} \right) ^{1/2}\varOmega ,\nonumber \\&\bar{{t}}=\mathop \uppi \nolimits ^{2}\left( {\frac{E}{l_0 b\rho }} \right) ^{1/2}t, \quad \bar{{A}}_{ij} =\frac{\left( {l_0 b} \right) ^{1/2}}{Eh^{2}}A_{ij} ,\nonumber \\&\bar{{D}}_{ij} =\frac{\left( {l_0 b} \right) ^{1/2}}{Eh^{4}}D_{ij} , \quad \bar{{F}}_{ij} =\frac{\left( {l_0 b} \right) ^{1/2}}{Eh^{6}}F_{ij} ,\nonumber \\&\bar{{H}}_{ij} =\frac{\left( {l_0 b} \right) ^{1/2}}{Eh^{8}}H_{ij} , \quad \bar{{I}}_i =\frac{1}{\left( {l_0 b} \right) ^{({i+1})/2}\rho }I_i . \end{aligned}$$
(22)

Substituting the modal function Eq. (18) into Eq. (17), the Galerkin method is employed to perform the second-order discretization to obtain normalized ordinary differential equations. Because the main structural vibration is out of plane, \(u_0 \), \(v_0 \), \(\phi _x \), and \(\phi _y \) are expressed using the transverse variables \(w_1 \) and \(w_2 \). The dimensionless two-degree of freedom (DOF) nonlinear dynamic equations describing the transverse vibration of the deploying cantilever piezoelectric laminated composite plate can then be formulated as

$$\begin{aligned}&\alpha _1 \ddot{w}_1 +\alpha _2 \dot{w}_1 +\alpha _3 \dot{w}_2 +\alpha _4 w_1\nonumber \\&\quad +\alpha _5 \left( {f_0 +f_1 \cos \left( {\varOmega _2 t} \right) } \right) w_1 +\alpha _6 w_2\nonumber \\&\quad +\alpha _7 w_1 ^{3}+\alpha _8 w_1 ^{2}w_2 +\alpha _9 w_1 w_2 ^{2}+\alpha _{10} w_2 ^{3}=0, \end{aligned}$$
(23a)
$$\begin{aligned}&\beta _1 \ddot{w}_2 +\beta _2 \dot{w}_2 +\beta _3 \dot{w}_1 +\beta _4 w_2\nonumber \\&\quad +\beta _5 \left( {f_0 +f_1 \cos \left( {\varOmega _2 t} \right) } \right) w_2 +\beta _6 w_1\nonumber \\&\quad +\beta _7 w_1 ^{3}+\beta _8 w_1 ^{2}w_2 +\beta _9 w_1 w_2 ^{2}+\beta _{10} w_2 ^{3}=0, \end{aligned}$$
(23b)

where the coefficients \(\alpha _i \) and \( \beta _i\) (\(i=1, 2,\ldots , 10\)) consider time t explicitly.

Fig. 2
figure 2

Time history curves for \({V}_{{z}}=0\,\hbox {V}\)

Full size image
Fig. 3
figure 3

Time history curves for \(V_{{z}} =130\,\hbox {V}\)

Full size image

4 Numerical simulations

We selected as a model a deploying symmetric cross-ply piezoelectric laminated composite cantilever plate with the following parameters, constructed from PVDF membrane and fiber-reinforced laminates: \(l_0 =2.0\,\hbox {m}\), \(b=1.5\,\hbox {m}\), \(h=0.004\,\hbox {m}\), \(f_0 =2000\,\hbox {N/m}^{{2}}\), \(V_{d} =0.005\,\hbox {m/s}\), \(\varOmega _{1} =15\), \(M_{a} =3.0\) in hypersonic flow, \(V_\mathrm{a} =900\,\hbox {m/s}\), \(\kappa =1.4\), and air density \(\rho _{a} =0.65\,\hbox {kg/m}^{{3}}\) at height of 10, 000 m. The material properties of the fiber-reinforced composite composed of graphite–epoxy HT3/QY8911 include: \(E_1 =125.0\,\,\hbox {GPa}\), \(E_2 =7.2\,\,\hbox {GPa}\), \(G_{12} =G_{13} =4.1\,\hbox {GPa}\), \(G_{23} =1.43\,\,\hbox {GPa}\), \(\nu _{12} =0.33\), \(\nu _{21} =\nu _{12} \,E_2 /E_1 \), \(\rho =1570\,\hbox {kg/m}^{{3}}\), \(\gamma =350\,\hbox {N}\cdot \hbox {s/m}\), with thickness of the piezoelectric layer \(h_{z} =0.00015\,\,\hbox {m}\). Based on the time-varying two-DOF nonlinear dynamic Eq. (23), the nonlinear dynamical behavior of the cantilever piezoelectric laminated composite plate, extending from 2 to 4 m at various extending speeds under first-order aerodynamic force, was investigated numerically.

4.1 Nonlinear dynamical behavior of plate for extension speed \(V_0 =0.05\)

Figures 2–7 show the time history curves for the transverse first- and second-order modal vibration of the cantilever piezoelectric laminated composite plate during the extension process for different piezoelectric excitations. For better observation of the second-order vibration of the structure, the seemingly stable parts in subfigure b are magnified and shown in subfigure c. The effects of the applied voltage on the stability of the time-varying nonlinear dynamics can be observed in the time-domain plots.

The obtained time history curves well reflect the effects of changing the applied voltage on the stability of the time-varying nonlinear dynamics. For applied voltage of 0 (Fig. 2), the structural nonlinear dynamic behavior is consistent with that of the fiber-reinforced laminated composite plate without piezoelectric laminates, consistent with Ref. [14]. More specifically, during the extension process to 2 m length, three different phases present either the first- or second-order vibration of the structure, including two jumps of vibration amplitude and a stable motion phase between them. Throughout the process, the vibration amplitude of the structure changes greatly, and the structure easily becomes unstable and divergent. For excitation voltage of \(V_{{z}} =130\,\hbox {V}\) (Fig. 3), the period of the two jumps in vibration amplitude increases, while the period of stable motion between them decreases. As the excitation voltage increases (Fig. 4), the stable motion phase in both the first- and second-order vibrations of the structure gradually decreases and eventually vanishes. Hence, the nonlinear dynamical behavior is very unstable, as the structure experiences a second jump in vibration amplitude immediately after the first one.

Fig. 4
figure 4

Time history curves for \(V_{{z}} =150\,\hbox {V}\)

Full size image
Fig. 5
figure 5

Time history curves for \(V_{{z}} =-40\,\hbox {V}\)

Full size image
Fig. 6
figure 6

Time history curves for \(V_{{z}} =-45\,\hbox {V}\)

Full size image
Fig. 7
figure 7

Time history curves for \(V_{{z}} =-50\,\hbox {V}\)

Full size image
Fig. 8
figure 8

Time history curves for \(V_{{z}} =0\,\hbox {V}\)

Full size image
Fig. 9
figure 9

Time history curves for \(V_{{z}} =100\,\hbox {V}\)

Full size image

On changing the polarity of the excitation voltage, we observe a change in the structural dynamical behavior. When the excitation voltage is \(V_{{z}} =-40\,\hbox {V}\) (Fig. 5), it is found that the increasing trend in amplitude is slowed in both the first- and second-order vibration. When the excitation voltage is increased to \(V_{{z}} =-45\,\hbox {V}\) (Fig. 6) and the dimensionless time is around \(t=250\), the first- and second-order jumps of the vibration amplitude are suppressed. On further increasing the excitation voltage to \(V_{{z}} =-50\,\hbox {V}\) (Fig. 7), the cantilevered piezoelectric laminated composite plate accomplishes the extension from 2 to 4 m without a second vibration amplitude jump in the first- or second-order vibration.

Overall, the piezoelectric excitation has a significant impact on the stability of the structural nonlinear vibration. During the extension of the cantilever piezoelectric laminated composite plate from 2 to 4 m, when the excitation voltage is positive, the structural stability of the first- and second-order vibrations gradually decreases. The stable motion phase of the system gradually shrinks in time, and the structure is liable to exhibit a second jump immediately after the first jump of the vibration amplitude. When the voltage is increased further, the vibration of the structure gradually deviates from the equilibrium position until the structure eventually diverges. On changing the polarity of the voltage, as the voltage increases in the negative direction, even though the first jump of the first two vibration amplitudes is not suppressed, the second jump in the first- and second-order vibrations is avoided. As a result, the scale of the vibration amplitude in the stable motion phase is reduced. By calculating the coefficients of the in-plane stiffness terms in Eq. (23), we note that the in-plane stiffness of the plate was improved with increase of the applied negative voltage. This increase of the in-plane stiffness leads to a corresponding increase of the structural vibration frequency, which explains why the nonlinear vibration amplitude was suppressed.

Fig. 10
figure 10

Time history curves for \(V_{{z}} =150\,\hbox {V}\)

Full size image
Fig. 11
figure 11

Time history curves for \(V_{{z}}=-150\,\hbox {V}\)

Full size image

4.2 Nonlinear dynamic behavior of plate for extension speed of \(V_0 =0.10\)

To study the effects of changing the extension speed on the structural stability of the nonlinear dynamics, the time history response curves of the deploying cantilever piezoelectric laminate, extending from 2 to 4 m at extension speed of \(V_0 =0.10\,\hbox {m/s}\), are shown in Figs. 8–11. When the amplitude of the excitation voltage is increased from 0 to 150 V, the time-varying first- and second-order nonlinear vibrations gradually lose their stability, and the instability of the extension process is exacerbated. On gradually adjusting the negative excitation voltage, it was found that, when the excitation voltage was \(V_{{z}} =-150\,\hbox {V}\), the second jump of the structural vibration amplitude in the first- and second-order vibrations was avoided. However, the first jump was not suppressed, although the scale of the vibration amplitude in the stable motion phase was suppressed. At the same time, the vibration amplitude during the stable motion phase was suppressed. In other words, choice of an appropriate excitation voltage can effectively suppress the nonlinear vibration of the system during the extension process. In addition, on comparison with Sect. 4.1, it is found that the stability of the system gradually decreased during the extension process as the extension speed was increased. When the structure extended at higher speed, the negative applied voltage necessary to avoid the second jump of the amplitude of the first- and second-order structural vibrations also increased correspondingly.

5 Conclusions

Considering the piezoelectric material characteristics, the time-varying nonlinear dynamic behavior of a deploying laminated composite plate, under the combined action of first-order aerodynamic load and piezoelectric excitation, was investigated. The effect of the introduction of the piezoelectric material on the stability of the nonlinear dynamics of the composite piezoelectric laminate during the extension process was investigated numerically. The following conclusions can be drawn:

(1) Using Reddy’s third-order shear theory for laminates and von Karman’s geometric relation for large deformation, and applying Hamilton’s principle, a nonlinear dynamic model in partial differential form for the deploying laminated composite plate, considering the combined action of aerodynamic load and piezoelectric excitation, was developed. Based on a selected time-dependent modal function, we performed second-order discretization using the Galerkin method, resulting in the derivation of a time-varying nonlinear dynamic model describing the transverse vibration of the deploying cantilever piezoelectric laminated composite plate.

(2) Using the obtained ordinary differential equation, the time-varying nonlinear dynamic behavior of the deploying cantilever piezoelectric laminated composite plate was simulated numerically, and the effect of the piezoelectric effect on the time-varying nonlinear dynamical behavior discussed. The results reveal that, when the applied voltage is positive, the extension process becomes more unstable, and the time-varying structural divergence is exacerbated. As a result, the piezoelectric laminated composite plate is more liable to failure and destruction. When the applied voltage was set to a negative value, the polarity of the voltage changed, and it was found that not only was the increasing trend of the vibration amplitude of the time-varying structure suppressed, but also the vibration amplitude was suppressed. Thus, the piezoelectric material has a significant impact on the nonlinear dynamic stability of the fiber-reinforced laminated composite plate, and choice of a suitable voltage and polarity can effectively suppress the nonlinear vibration of the deploying cantilever laminate. The applied negative voltage enhances the in-plane stiffness of the time-varying structure, which leads to a corresponding increase of the structural vibration frequency and suppression of the nonlinear vibration amplitude. It is also found that increasing the extension speed can decrease the nonlinear dynamic stability of the structure during the extension process. Therefore, the applied excitation voltage required to suppress the divergence of the nonlinear vibration amplitude should be increased correspondingly when the structure extends at higher speed.