Keywords

1 Introduction

The heat and mass transfer and convective motion in a porous media (Nield and Bejan [1] and the references therein) with primarily concerned with Soret convection in porous matrix have been a subject of significant interest in the past as it is now, due to the various applications in astrophysics, geophysics, industrial processes, crustal structures, Earth's crust, and since the gravity field's inhibitory effect on the initiation of convection is used, for example, in binary alloy directional solidification. There is a wide range of the literature on various aspects of porous convection. In particular, Bidin and Rees [2] considered convective motion in a horizontal porous matrix of an unstable thermal boundary layer; Barletta and Celli [3] were performed in a double-diffusive flow with open upper boundary linear stability of a uniform parallel flow; Braga et al. [4] analyzed thermal instability on the boundary walls with two different boundary conditions. Chamkha [5] initiated penetrative double-diffusive convective motion with absorption effects. Capone and De Luca [6] carried out convective motion in a horizontal porous matrix with a magnetic field effect, in which the effect of the inertia term in the Darcy equation was included by Capone and De Luca [7]. Recently, Storesletten and Rees [8] analyzed thermal convection with heat source strength in an inclined anisotropic porous matrix.

It is known that the gravity field of the earth varies in a significant amount of the wide-ranging convection situation in the atmosphere with elevation from its surfaces, the earth's mantle or the sea (Pradhan and Samal [9] and Rionero and Straughan [10]). As the gravity field varies with the measurement, the fluid layer will undergo distinctive buoyancy forces at various points. In this way, it becomes imperative to investigate convective motion with gravity variance with height. The effect of gravity field on a porous matrix was investigated by Pradhan and Samal [9]. Alex and Patil [11, 12] made an extension to the anisotropic porous matrix with heat source and inclined temperature gradient. Rionero and Straughan [10] investigated the penetrative convection with gravity field effects on convective motion in a porous matrix. Three separate types of depth variations in the gravity field were considered: linear, parabolic and exponential. Harfash [13] has researched the impact of gravity fluctuations and magnetic field on the porous matrix flow.

However, the study of variable gravity double-diffusive convection is very limited. Alex and Patil [14] and Harfash and Alshara [15] used the Galerkin method to analyze effect of Soret parameter and gravity variance on the onset of convective motion in a porous matrix. Shi et al. [16] made an extension to nonlinear variation of the gravity field. In this paper, in the presence of the four cases of linear and nonlinear gravity fields, we wish to study a model of double-diffusive convective movement in a porous matrix.

2 Conceptual Model

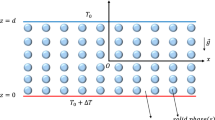
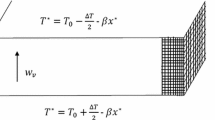
Figure 1 illustrates the physical configuration of the present study. The physical model under consideration is a horizontal porous bed bounded between planes at \(z = 0\,\) and \(z = d\) with constant upward through flow of vertical velocity \(W_{0}\) and changeable gravity \(g\left( z \right).\) We assume that the gravity vector \(\overrightarrow {g\,}\) is,

$$ \overrightarrow {g\,} = - g_{0} \left( {1 + \lambda \,H\left( z \right)} \right)\,\hat{k} $$
Fig.1
figure 1

Physical configuration

Full size image

where \(\lambda\)is the variable gravity coefficient.

3 Mathematical Formulation

The porous layer governing equations are:

$$ \nabla \, \cdot \overrightarrow {V} = 0\,\,\,\, $$
(1)
$$ \frac{{\rho_{0} }}{\phi }\frac{{\partial \vec{V}}}{\partial t} = - \nabla p - \frac{\mu }{K}\vec{V} + \rho_{0} \left[ {1 - \beta \left( {T - T_{0} } \right)} \right]\,\vec{g}\left( z \right) $$
(2)
$$ \frac{\partial T}{{\partial t}} + \left( {\overrightarrow {V} \cdot \nabla } \right)T = \nabla^{2} T $$
(3)
$$ \frac{\partial S}{{\partial t}} + \left( {\overrightarrow {V} \cdot \nabla } \right)S = \tau \,\nabla^{2} S + \,\tilde{D}\,\nabla^{2} T $$
(4)

In these equations, \(\vec{V}\) denotes the velocity vector, \(\kappa\) is the thermal diffusivity, \(A\) is the ratio of heat capacities,\(\rho_{0}\) is the reference fluid density, and \(T\) is the temperature.

The basic steady-state solution is of the form

$$ \left( {u,v,\,w,p,T} \right) = \,\left( {0,0,0,p_{b} (z),T_{b} (z),\,\,S_{b} (z)} \right) $$
(5)

Basic state is slightly perturbed using the relation given by

$$ \vec{V} = \vec{V}^{\prime},\,p = p_{b} (z) + p^{\prime}\,,\,\,\,T = T_{b} \left( z \right) + \theta $$
(6)

Small disturbance analysis.

We assume that the solution is of the form.

$$ \left( {w,T} \right) = \left[ {W\left( z \right),\Theta \left( z \right)} \right]\,\,\,{\text{e}}^{{i\left( {lx + my} \right)}} $$
(7)

The linearized equations governing the perturbation are [17, 18]

$$ \left( {D^{2} - a^{2} } \right)W - a^{2} \left( { - R_{{\text{T}}} \theta + R_{{\text{S}}} S} \right)\left( {1 + \eta \,H\left( z \right)} \right) = 0 $$
(8)
$$ \left( {D^{2} - a^{2} + i\,\sigma } \right)\theta \, + \,W = 0 $$
(9)
$$ \left( {D^{2} - a^{2} + i\frac{\sigma }{\tau }} \right)S\, + \left( {\frac{{S_{r} R_{T} }}{{R_{S} }}} \right)\,\left( {D^{2} - a^{2} } \right)\theta \, + \,\frac{W}{\tau } = 0 $$
(10)

The boundary conditions take the form

$$ W\left( z \right) = \theta \left( z \right) = S\left( z \right) = 0\,\quad {\text{at}}\quad \,z = 0,\,1.\,\, $$
(11)

where \(R_{{\text{T}}}\) is the thermal Rayleigh number, \(W\) is the vertical velocity, \(S_{{\text{r}}}\) is the Soret parameter, and \(R_{{\text{S}}}\) solute Rayleigh number.

4 Technique of Solution

Equations (8) and (10) along with the boundary conditions given by Eq. (11) constitute an eigenvalue problem with \(R\) as the eigenvalue. Accordingly,\(\,W,\,\,\Theta \,\,{\text{and}}\,S\) are written as

$$ \,W = \,\,\sum\limits_{i = 1}^{n} {A_{i} } \,W_{i} \,,\,\Theta = \,\,\sum\limits_{i = 1}^{n} {B_{i} } \,\Theta_{i} \,\,S = \sum\limits_{i = 1}^{n} {C_{i} } \,S_{i} $$
(12)

Let the trial functions be

$$ W = W_{0} \,\sin \left( {\pi z} \right)\,,\,\,S = S_{0} \,\sin \left( {\pi z} \right)\,\,\,\& \,\Theta = \,\,\Theta_{0} \,\sin \left( {\pi z} \right) $$
(13)

Substituting solution (12) into Eqs. (8)–(10), integrating each equation from 0 and 1, we get the following matrix equations,

$$ \left[ \begin{gathered} \, - \frac{1}{2}\left( {a^{2} + \pi^{2} } \right)\,\,\,\,\,\,\,\frac{1}{4}a^{2} R_{{\text{T}}} \left( {2 - \eta } \right)\,\,\,\,\,\,\,\frac{1}{4}a^{2} R_{{\text{S}}} \left( {2 - \eta } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{2}\left( {a^{2} + \pi^{2} + \sigma } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\frac{1}{2\tau }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{S_{r} \left( {a^{2} + \pi^{2} } \right)R_{{\text{T}}} }}{{2R_{{\text{S}}} }}\,\,\,\,\,\,\,\,\,\,\,\,\frac{{\sigma + \left( {a^{2} + \pi^{2} } \right)\tau }}{2\tau } \hfill \\ \end{gathered} \right]\,\,\,\left[ \begin{gathered} W_{0} \hfill \\ \hfill \\ \Theta_{0} \hfill \\ \hfill \\ S_{0} \hfill \\ \hfill \\ \end{gathered} \right]\,\,\, = \,\,\,\left[ \begin{gathered} 0 \hfill \\ \hfill \\ 0 \hfill \\ \hfill \\ \hfill \\ 0 \hfill \\ \end{gathered} \right] $$

On solving the above matrix, we get a non-trivial solution

$$ R_{{\text{T}}} = - \frac{{\left( {a^{2} + \pi^{2} + \sigma } \right)\left( {2a^{2} R_{s} - a^{2} R_{s} \eta + 2a^{2} \sigma + 2a^{2} \pi + 2\left( {a^{2} + \pi^{2} } \right)^{2} \tau } \right)}}{{a^{2} \left( { - 2 + \eta } \right)\left( {\sigma + \left( {1 + S_{{\text{r}}} } \right)\left( {a^{2} + \pi^{2} } \right)\tau } \right)}}\, $$
(14)

where the growth parameter is a complex number such that \(\sigma = \sigma_{{\text{r}}} + i\,\sigma_{i}\) the system is stable for \({\text{Re}} \left( \sigma \right) < 0\) , unstable for \({\text{Re}} \left( \sigma \right) > 0\) and neutrally stable for \({\text{Re}} \left( \sigma \right) = 0.\)

4.1 Marginal Stationary State

For stationary convection \(\sigma = 0,\) Eq. (14) reduces

$$ R_{{{\text{ST}}}} = - \frac{{2a^{2} R_{s} - a^{2} R_{s} \eta + 2\left( {a^{2} + \pi^{2} } \right)^{2} \tau }}{{a^{2} \left( {1 + S_{{\text{r}}} } \right)\left( { - 2 + \eta } \right)\tau }}\, $$
(15)

which has the critical value \(R_{{{\text{ST}}}} = 4\pi^{2}\). The minimum Rayleigh number \(R_{{{\text{ST}}}}\) occurs, at the critical wave number \(a_{{\text{c}}} = \pi^{2}\) when \(R_{{\text{s}}} = 0\) obtained by Horton and Rogers [19] and Lapwood [20].

4.2 Oscillatory Convection

For oscillatory convection, we have \(\sigma \ne 0,\) thus obtained critical Rayleigh number is

$$ R_{{{\text{osc}}}} = \frac{{\delta^{4} \tau \left( {a^{2} S_{{\text{r}}} R_{{\text{s}}} \left( { - 2 + \eta } \right) + S_{{\text{r}}} \left( {\delta^{2} } \right) + 4a^{2} \pi^{2} \tau^{2} } \right)}}{{\left( {a^{2} \left( { - 2 + \eta } \right)S_{{\text{r}}}^{2} \delta^{2} \tau^{2} + + a^{2} Rs\eta \delta^{2} } \right)}} $$
(16)

5 Outcomes and Discussion

The binary fluid flow in a porous matrix in the presence of Soret effect with different gravity field variations: (1) \(H\left( z \right) = - z\), (2) \(H\left( z \right) = - z^{2}\), (3) \(H\left( z \right) = - z^{3}\) and (4) \(H\left( z \right) = - \left( {e^{z} - 1} \right)\) are studied analytically using linear analyses. The neutral stability curves in the \(R^{{\text{c}}} - a\) plane for steady convection (Eq. (15)) and oscillatory convection (Eq. (16)) have been presented graphically in Figs. 2, 3, 4, 5, 6, 7, 8 and 9.

Fig. 2
figure 2

\( R_{{{\text{ST}}}}^{{\text{c}}} \) versus \(a_{{\text{c}}}\) with \(\tau = 0.01,\,\,R_{{\text{S}}} = 0.1\) for different values of \(\eta\) with linear gravity field \(H\left( z \right) = - z\) a \(S_{{\text{r}}} = 200\), b \(S_{{\text{r}}} = 0\)

Full size image
Fig. 3
figure 3

\( R_{{{\text{ST}}}}^{{\text{c}}} \) versus \(a_{{\text{c}}}\) with \(\tau = 0.01,\,\,R_{{\text{S}}} = 0.1\) for different values of \(\eta\) with linear gravity field \(H\left( z \right) = - z^{2}\) a \(S_{{\text{r}}} = 200\), b \(S_{{\text{r}}} = 0\)

Full size image
Fig. 4
figure 4

\( R_{{{\text{ST}}}}^{{\text{c}}} \) versus \(a_{{\text{c}}}\) with \(\tau = 0.01,\,\,R_{{\text{S}}} = 0.1\) for different values of \(\eta\) with linear gravity field \(H\left( z \right) = - z^{3}\) a \(S_{{\text{r}}} = 200\), b \(S_{{\text{r}}} = 0\)

Full size image
Fig. 5
figure 5

\( R_{{{\text{ST}}}}^{{\text{c}}} \) versus \(a_{{\text{c}}}\) with \(\tau = 0.01,\,\,R_{{\text{S}}} = 0.1\) for different values of \(\eta\) with linear gravity field \(H\left( z \right) = - \left( {e^{z} - 1} \right)\) a \(S_{{\text{r}}} = 200\), b \(S_{{\text{r}}} = 0\)

Full size image
Fig. 6
figure 6

\(R^{{\text{c}}}\) versus \(a_{{\text{c}}}\) with \(\tau = 0.01,\,\,R_{{\text{S}}} = 0.1\) for different values of \(\eta\) with linear gravity field \(H\left( z \right) = - z\) for \(S_{{\text{r}}} = 10\)

Full size image
Fig. 7
figure 7

\(R^{{\text{c}}}\) versus \(a_{{\text{c}}}\) with \(\tau = 0.01,\,\,R_{{\text{S}}} = 0.1\) for different values of \(\eta\) with linear gravity field \(H\left( z \right) = - z^{2}\) for \(S_{{\text{r}}} = 10\)

Full size image
Fig. 8
figure 8

\(R^{{\text{c}}}\) versus \(a_{{\text{c}}}\) with \(\tau = 0.01,\,\,R_{{\text{S}}} = 0.1\) for different values of \(\eta\) with linear gravity field \(H\left( z \right) = - z^{3}\) for \(S_{{\text{r}}} = 10\)

Full size image
Fig. 9
figure 9

\(R^{{\text{c}}}\) versus \(a_{{\text{c}}}\) with \(\tau = 0.01,\,\,R_{{\text{S}}} = 0.1\) for different values of \(\eta\) with linear gravity field \(H\left( z \right) = - \left( {e^{z} - 1} \right)\) for \(S_{{\text{r}}} = 10\)

Full size image

The effect of variable gravity parameters on the neutral stability curves is depicted in Figs. 2, 3, 4 and 5. From these figure, we find that the effect of rising the variable gravity parameter \(\lambda\) for all four cases of gravity field is to increase the value of the \(R^{c}\) with and without Soret parameter for stationary modes and the corresponding wave number. Thus, the variable gravity parameter \(\lambda\) in a porous matrix bed has a stabilizing effect on the binary convection. Further, it noted that for gravity field case (4) \(H\left( z \right) = - \left( {e^{z} - 1} \right)\) changes the system to become more stable, while for gravity field case (3) \(F\left( z \right) = - z^{3}\) causes the system become more unstable.

Figures 6, 7, 8 and 9 give a visual representation of \(R^{c} - a_{c}\) for various values \(\lambda\). These figures demonstrate that the minimum value of the \(R^{{\text{c}}}\) corresponding to \(- a_{{\text{c}}}\) for both oscillatory and stationary modes increases with improvement in the value of the variable gravity parameter \(\lambda\) for all four cases of gravity field, and clearly, it demonstrate that the effect of the gravity field parameter is to stabilize the system. We also found that for case (4) gravity field \(\left( {{\text{i.e.}}\,\,H\left( z \right) = - \left( {e^{z} - 1} \right)} \right)\), the system is more stable, while for case (3) \({\text{gravity field }}\left( {{\text{i.e. H}}\left( z \right) = - z^{3} } \right)\), the system is more unstable.

6 Conclusions

The binary fluid flow in a porous matrix, the impact of Soret effect with the presence of different gravity field variations: (1) \(H\left( z \right) = - z\) (2) \(H\left( z \right) = - z^{2}\) (3) \(H\left( z \right) = - z^{3}\) and (4) \(H\left( z \right) = - \left( {e^{z} - 1} \right)\) is studied analytically using linear analyses. For both case convective motion (oscillatory and stationary modes), it is noted that increasing the values of variable gravity parameter \(\lambda\) is to stabilize the system. The increases in the values of \(Sr\) decrease the marginal curves for the stationary mode, and there is a marginal effect of \(Sr\) on the oscillatory mode. We also found that for case (4) gravity field \(\left( {{\text{i.e.}}\,H\left( z \right) = - \left( {e^{z} - 1} \right)} \right)\), the system is more stable, while for case (3) \({\text{gravity field }}\left( {{\text{i.e.}}\,H\left( z \right) = - z^{3} } \right)\), the system is more unstable.