1 Introduction

It is now well understood that a classical local continuum modeling, although certainly accurate in a wide spectrum of engineering applications, may fail to capture those phenomena where microstructure and long-range intermolecular forces play a crucial role. Such inadequacy, due to the intrinsic free scale formulation of the classical local continuum theory, has been revealed theoretically based on molecular simulations, and experimentally by static and dynamic tests on several materials.

Molecular simulations may seem a most appropriate way to account for microstructural effects, but they involve as a major drawback a considerable computational effort. For this reason, and in recognition of the fact that even to build a molecular model some theoretical assumptions are still needed, scientists and engineers have turned their attention to the formulation of “enriched” continua, i.e. classical continuum models where microstructural effects are accounted for in an average sense, by introducing appropriate non-local terms. Since the pioneering work by Eringen [1, 2], these formulations have been awarded a considerable attention, especially due to the fact that a continuum formulation, although endowed with the additional non-local terms, generally allows established numerical solution methods to be applied, with considerable advantages for design purposes. In this context the following approaches can be cast: the well-known Eringen’s integral theory [1, 2], involving a stress–strain relation between the stress at a given point and the strain in the whole volume of the continuum; the gradient elasticity theories [3, 4], with constitutive equations depending on the gradients of stresses or strains; the peridynamic theory [5], involving long-range elementary forces depending on relative displacements between non-adjacent points; the well-known micropolar “Cosserat” theory [6] and the couple-stress theory [7], according to which any material point is endowed with translational and rotational degrees of freedom, with resulting work-conjugate curvatures and couple stresses. Regarding micropolar or couple-stress theories, many interesting studies have been devoted to explain, on a physical basis, the relation with microstructural effects, see for instance those by Kröner [8] and Lakes [9].

Within the context of non-local enriched continua formulations, several non-local beam theories have been derived. The interest in non-local beam models is certainly motivated by the increasing importance of small-size beam-like devices, used for instance as sensors or actuators in micro- and nano-technologies (see the comprehensive review by Qian et al. [10]), where a significant deviation from the theoretical predictions of the classical Euler–Bernoulli (EB) or Timoshenko (TM) beam theory has been revealed by atomistic simulations [11] and experimental evidence on several materials, such as epoxy [12], polypropylene [13], graphite [14] and copper [15]. Existing non-local beam models have generally involved linearly-elastic non-local terms, used in conjunction with the classical continuum of the EB or TM beam theories. Dynamic and static responses have been investigated.

Most of the early non-local beam models have been built on Eringen’s integral theory [1, 2]. In this context, based on the assumption that non-local terms affect the normal stress only, the motion equation of a EB beam has been formulated by Zhang et al. [16], Xu [17], Wang and Varadan [18]. Wang and Varadan [18] have also formulated the motion equations of a TM beam. Lu and et al. have later clarified some inconsistencies in these first studies, due to an incorrect use of Eringen’s non-local stress law [19]. Following these clarifications, Reddy [20] and Aydogdu [21] have formulated alternative higher-order non-local beam theories based on certain assumptions on the displacement field.

There exist also many non-local beam models derived from non-local theories alternative to Eringen’s integral theory. For instance, non-local EB beam models have been built by Kong et al. [22] based on a modified couple stress theory, by Zhang et al. [23] based on a so-called hybrid approach, which involves a strain energy functional depending on local and non-local curvatures. A non-local TM beam model has been built by Wang et al. [24] in conjunction with the gradient elasticity theory presented by Lam et al. [12], and by Ma et al. [25] based on a modified couple stress theory. In all these studies, the motion equations have been derived by Hamilton’s principle. More recently, non-local EB and TM beam models have been proposed by Pradhan [26] and Yang and Lim [27] based on a stress gradient elasticity theory, the former with a weak formulation of the motion equations in conjunction with finite element analysis [26], and the latter using Hamilton’s principle [27]. Specifically, Yang and Lim [27] have used a strain energy density built on a non-local normal stress expressed in terms of higher-order derivatives of the normal strain and, as a result, the corresponding motion equations and boundary conditions (B.C.) involve higher-order derivatives of the non-local bending moment (in this respect, see also Ref. [28, 29]). Yang and Lim [27] have shown that if the motion equations and the pertinent B.C. are not derived by a consistent variational framework and in particular by Hamilton’s principle, but instead by a direct replacement of the non-local stress resultants (non-local bending moment and non-local shear) into the classical beam motion equations, some inconsistencies do arise in terms of equilibrium and B.C. For this reason, the softening effects that those theories predict in the bending stiffness or the natural frequencies cannot be considered, according to Yang and Lim [27], as reliable results. These conclusions have been drawn for both EB and TM beam models.

Along with the studies above, where in general static and dynamic responses of non-local beam models have been investigated, some studies focusing on the static response only are worth mentioning. For instance, Eringen’s integral theory has been used by Peddieson et al. [30], Wang and Shindo [31], Civalek and Demir [32] to derive non-local EB beam models, by Wang and Liew [33], Wang and et al. [34] to derive non-local TM beam models, the latter in conjunction with the principle of virtual work. A non-local EB beam model has been presented by Challamel and Wang [35] based on a gradient elastic model and a non-local integral elastic model, where the constitutive relation is expressed by combining local and non-local curvatures. A non-local EB model has been also presented by McFarland and Colton [13] based on a micropolar elasticity constitutive law. Lam et al. [12] have investigated a non-local EB model as derived from a general strain gradient elasticity theory, while Park and Gao [36] have studied a non-local EB model based on a modified couple stress theory. The static response of EB beam models based on strain gradient and couple stress theories has been investigated by Chen and Feng [37], Akgöz and Civalek [38].

The purpose of this paper is to illustrate a new non-local TM beam model, derived within the framework of a mechanically-based non-local elasticity theory recently proposed by the authors [39–46], where non-local effects are modelled as long-range interactions resulting from the relative displacement between volume elements. Consistently with typical engineering beam theories, where the equilibrium of a beam segment is set in an average (weak) sense based on the stress resultants acting on the cross section, in the proposed non-local beam model the long-range interactions are modelled as volume forces and moments, mutually exerted by non-adjacent beam segments, that contribute to the equilibrium of any beam segment along with the local stress resultants. The long-range volume forces/moments are built as linearly depending, through pertinent attenuation functions governing the spatial decay of the non-local effects, on the product of the volumes of the interacting beam segments and on generalized measures of their relative motion. These generalized measures are based on the pure beam deformation modes derived by Fuchs [47, 48], i.e. a “pure axial” symmetric mode, a “pure bending” symmetric mode and a “pure shear” asymmetric mode.

These are the key issues addressed in the paper: (i) the non-local beam model will be cast within a consistent variational framework (on the importance of a consistent variational formulation see, e.g., Ref. [27–29]); in particular, the equilibrium equations will be derived based on a pertinent total elastic potential energy, where local and non-local contributions reflect the mechanical interpretation given to the long-range interactions; (ii) the behavior of the non-local beam model will be investigated for a variety of non-local and geometrical parameters; in this context, a comparison with some alternative models in the literature will be presented; (iii) it will be shown that the non-local beam model captures very well experimental data on the static response of cantilever micro-beams [12].

The paper is organized as follows. Upon recalling the basic equations of the local TM beam theory in Sect. 2, the long-range volume forces/moments are introduced in Sect. 3. The equilibrium equations of the non-local TM beam model along with the mechanical B.C. are derived in Sect. 4 by a variational formulation. Numerical results including comparisons with experimental data are presented in Sect. 5.

2 Local Timoshenko beam theory: basic equations

In this Section, for the sake of clarity as well as to introduce some basic notations, the classical TM beam theory is briefly summarized.

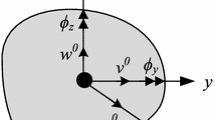
Consider the initially straight beam of length L and uniform cross section shown in Fig. 1. The material is assumed to be isotropic and linearly elastic. The beam is referred to a Cartesian (orthogonal) coordinate system Oxyz, where the x-axis coincides with the centroidal axis, the y-and z-axes are principal axes of the cross section, and xz is the bending plane.

Fig. 1
figure 1

Shear deformable beam of arbitrary cross section. Positive sign conventions are reported

Full size image

Based on the classical TM beam theory, the displacement field is described as follows:

$$ u_{x} ({\mathbf{x}}) = u(x) - z\varphi (x); \, u_{y} ({\mathbf{x}}) = 0; \, u_{z} ({\mathbf{x}}) = v(x), $$
(1a-c)

where \( {\mathbf{x}} = \left[ {\begin{array}{*{20}c} x & y & z \\ \end{array} } \right]^{\rm T} \) is the position vector; u(x) and v(x) denote the x- and z- components of the displacement of a point at x on the centroidal axis and φ(x) is the rotation about the y-axis. The latter is taken as positive if clockwise. The axial, transverse shear and bending strains ensuing from the above kinematic model are given, respectively, by:

$$ \varepsilon (x) = \frac{{{\text{d}}u(x)}}{{{\text{d}}x}} ;\quad \gamma (x) = \frac{{{\text{d}}v(x)}}{{{\text{d}}x}} - \varphi (x) ;\quad \chi (x) = - \frac{{{\text{d}}\varphi (x)}}{{{\text{d}}x}}. $$
(2a-c)

The associated stress resultants are the classical local normal stress, shear stress and bending moment, given by:

$$ N^{\left( l \right)} (x) = \int_{A} {\sigma_{x}^{\left( l \right)} ({\mathbf{x}}){\text{d}}A} { ;}\quad T^{\left( l \right)} (x) = \int_{A} {\tau_{xz}^{\left( l \right)} ({\mathbf{x}}){\text{d}}A \, ;} \quad M^{\left( l \right)} (x) = \int_{A} {\sigma_{x}^{\left( l \right)} ({\mathbf{x}})z{\text{d}}A} $$
(3a-c)

where the superscript in parentheses means local, while σ (l) x (x) and τ (l) xz (x) are two of the six components of the Cauchy stress tensor gathered into the vector \( {\varvec{\upsigma}}^{\left( l \right)} ({\mathbf{x}}) = \left[ {\begin{array}{*{20}c} {\sigma_{x}^{\left( l \right)} } & {\sigma_{y}^{\left( l \right)} } & {\sigma_{z}^{\left( l \right)} } & {\tau_{yz}^{\left( l \right)} } & {\tau_{xz}^{\left( l \right)} } & {\tau_{xy}^{\left( l \right)} } \\ \end{array} } \right]^{\rm T} . \)

Collecting the stress resultants (3a–c) and generalized strain components (2a–c) into the vectors \( {\mathbf{s}}^{(l)} (x) = \left[ {\begin{array}{*{20}c} {N^{\left( l \right)} (x)} & {T^{\left( l \right)} (x)} & {M^{\left( l \right)} (x)} \\ \end{array} } \right]^{\text{T}} \) and \( {\mathbf{d}}^{(l)} (x) = \left[ {\begin{array}{*{20}c} {\varepsilon (x)} & {\gamma (x)} & {\,\chi (x)} \\ \end{array} } \right]^{\text{T}} \), the linear-elastic constitutive laws can be written in compact form as:

$$ {\mathbf{s}}^{(l)} (x) = {\mathbf{D}}^{*} {\mathbf{d}}^{(l)} (x) $$
(4)

where \( {\mathbf{D}}^{*} = Diag\left[ {\begin{array}{*{20}c} {E^{*} A} & {K_{s} G^{*} A\,} & {E^{*} I} \\ \end{array} } \right] \), with E * = β 1 E and G * = β 1 G, E and G being Young’s modulus and shear modulus respectively, whereas 0 ≤ β 1 ≤ 1 is a dimensionless real coefficient weighting the amount of local effects when the beam model includes also long-range interactions [42–44], as will be outlined in the next Section; A and I are the area and moment of inertia of the cross section; K s is the shear correction factor. Obviously, the classical local TM beam parameters correspond to β 1 = 1, so that E * = E and G * = G.

Denoting by F x (x) and F z (x) the external forces per unit length in the x- and z- directions, the equilibrium of the TM beam is governed by the following equations:

$$ \begin{aligned} \frac{{{\text{d}}N^{\left( l \right)} (x)}}{{{\text{d}}x}} + F_{x} (x) = 0; \hfill \\ \, \frac{{{\text{d}}T^{\left( l \right)} (x)}}{{{\text{d}}x}} + F_{z} (x) = 0; \hfill \\ \frac{{{\text{d}}M^{\left( l \right)} (x)}}{{{\text{d}}x}} - T^{\left( l \right)} (x) = 0. \hfill \\ \end{aligned} $$
(5a-c)

The pertinent kinematic B.C. read:

$$ u(x_{i} ) = u_{i} ;\quad v(x_{i} ) = v_{i} ;\quad \varphi (x_{i} ) = \varphi_{i} ;\quad i = 0 ,L $$
(6a-c)

being u i , v i and φ i the displacements and rotations at the beam ends, i.e. at x 0 = 0 and x L  = L. Finally, if N i , M i and T i denote the external forces/moments acting at the ends of the beam (i = 0, L), the mechanical B.C. are given by:

$$ N^{(l)} (x_{i} ) = \mp N_{i} ;\quad T^{(l)} (x_{i} ) = \mp T_{i} ;\quad M^{(l)} (x_{i} ) = \pm M_{i} . $$
(7a-c)

3 Non-local Timoshenko beam model with long-range interactions

This Section presents the main features of the proposed non-local beam model. It is derived within the framework of a mechanically-based approach to non-local elasticity theory [39–46], where non-local effects are represented as long-range interactions exchanged by non-adjacent volume elements as a result of their relative motion. Herein, such a general idea is applied within the context of typical engineering beam theories, where the equilibrium of a beam segment is set in an average (weak) sense based on the stress resultants acting on the cross section. In particular, the long-range interactions are modeled as volume forces and moments, exchanged by non-adjacent beam segments as a result of their relative motion measured by the pure deformation modes of the beam [47, 48]. As will be outlined next, this modeling of long-range interactions can be interpreted on a meaningful mechanical basis, as corresponds to assuming a spring-like connection between couples of non-adjacent beam segments where pure axial, pure bending and pure shear long-range springs (with distance-decaying stiffness) can be separately accounted for. In the following, the analytical expressions and mechanical interpretation of the long-range volume forces/moments are given. Hence, the equilibrium equations are built by direct introduction of the long-range volume forces/moments in the standard equilibrium equations of a beam segment. A similar approach allows to derive the mechanical B.C.

3.1 Long-range resultants

By means of an eigenvalue analysis, Fuchs [47, 48] decomposed a TM beam element into three unimodal components acting in parallel: a “pure axial”, a “pure bending” and a “pure shear” element. Such decomposition yields uncoupled constitutive laws between generalized stress and strain measures associated with each deformation mode. Fuchs [47, 48] provided a clear geometrical interpretation of the deformation modes: the “pure axial” mode is a symmetric mode defined by the relative axial displacements between the ends; the “pure bending” mode is a symmetric mode defined by the relative rotation between the ends; the “pure shear” mode is an asymmetric mode defined by the relative rotation between the ends, with respect to the line given by the relative transverse displacements. Furthermore, Fuchs [47, 48] derived the self-equilibrated forces/moments at the ends of the TM beam element resulting from the pure deformation modes.

In order to define the long-range interactions based on Fuchs’ unimodal components, a discrete model of the beam is built by dividing the beam domain in N segments of length Δx, so that x i  = iΔx with i = 0, 1, …, N − 1 (x N  = x L ), defines the position of the segment ΔV(x i ) = AΔx along the axis (see Fig. 2).

Fig. 2
figure 2

Equilibrium of an elementary beam segment: a axial; b transverse; c bending

Full size image

It is assumed that the equilibrium of each beam segment is attained due to: (i) the local stress resultants in Eq. (3) exerted by the adjacent beam segments; (ii) the resultants of the volume forces/moments, R x , R z and R φ exerted by all the non-adjacent beam segments. Such resultants are shown in Fig. 2 where the equilibrium of an elementary beam segment located at x = x i is displayed.

The key assumption of the proposed non-local beam model is that the long-range volume forces/moments mutually exerted by two non-adjacent beam segments ΔV(x i ) and ΔV(ξ k ) located, respectively, at x = x i and x = ξ k , arise due to their relative motion described by Fuchs’ generalized measures of relative displacement/rotations (see Fig. 3) i.e., the relative axial displacement:

$$ \eta \left( {x_{i} ,\xi_{k} } \right) = u\left( {\xi_{k} } \right) - u\left( {x_{i} } \right){ ;} $$
(8)

the relative rotation:

$$ \theta \left( {x_{i} ,\xi_{k} } \right) = \varphi \left( {\xi_{k} } \right) - \varphi \left( {x_{i} } \right); $$
(9)

and the rotation with respect to the line given by the relative transverse displacement:

Fig. 3
figure 3

Pure deformation modes of the Timoshenko beam and associated long-range springs: a axial; b pure bending; c pure shear

Full size image
$$ \psi \left( {x_{i} ,\xi_{k} } \right) = \left[ {\frac{{v\left( {\xi_{k} } \right) - v\left( {x_{i} } \right)}}{{\xi_{k} - x_{i} }} - \varphi \left( {\xi_{k} } \right)} \right] + \left[ {\frac{{v\left( {\xi_{k} } \right) - v\left( {x_{i} } \right)}}{{\xi_{k} - x_{i} }} - \varphi \left( {x_{i} } \right)} \right]. $$
(10)

Based on the analytical expressions of the generalized stress measures derived by Fuchs [47, 48] for each unimodal component, the long-range volume forces/moments are taken as proportional to the pure deformation modes. By analogy to the mechanically-based model of non-local bar proposed by Di Paola et al. [42, 45, 46], a linear dependence on the product of the volumes of the interacting beam segments through appropriate attenuation functions governing the spatial decay of non-local effects is also included.

The pure axial deformation mode (see Fig. 3a) gives rise to long-range volume axial forces r x (x i , ξ k ) mutually exerted by two non-adjacent beam segments ΔV(x i ) and ΔV(ξ k ), as a result of their relative axial displacement η(x i , ξ k ), i.e.:

$$ r_{x} \left( {x_{i} ,\xi_{k} } \right) = q_{x} \left( {x_{i} ,\xi_{k} } \right)\Delta V\left( {x_{i} } \right)\Delta V\left( {\xi_{k} } \right) \, ;\quad q_{x} \left( {x_{i} ,\xi_{k} } \right) = g_{x} \left( {x_{i} ,\xi_{k} } \right)\eta \left( {x_{i} ,\xi_{k} } \right) $$
(11a,b)

where q x (x i , ξ k ) given by Eq. (11b) is the specific long-range axial force depending on the relative axial displacement (8), through an appropriate symmetric real-valued attenuation function g x (x, ξ) governing the spatial decay of non-local axial effects.

The pure bending mode (see Fig. 3b) gives rise to long-range volume moments r φφ (x i , ξ k ) mutually exerted by two non-adjacent beam segments ΔV(x i ) and ΔV(ξ k ) as a result of their relative rotation θ(x i , ξ k ), i.e.:

$$ r_{\varphi \varphi } \left( {x_{i} ,\xi_{k} } \right) = q_{\varphi \varphi } \left( {x_{i} ,\xi_{k} } \right)\Delta V\left( {x_{i} } \right)\Delta V\left( {\xi_{k} } \right){ ; }\quad q_{\varphi \varphi } \left( {x_{i} ,\xi_{k} } \right) = g_{\varphi } \left( {x_{i} ,\xi_{k} } \right)\theta \left( {x_{i} ,\xi_{k} } \right) $$
(12a,b)

where q φφ (x i , ξ k ) given by Eq. (12b) is the specific long-range moment proportional to the relative rotation (9) through an appropriate symmetric real-valued distance-decaying attenuation function g φ (x i , ξ k ).

Finally, the pure shear mode (see Fig. 3c) gives rise to long-range volume transverse forces and moments, r z (x i , ξ k ) and r φz (x i , ξ k ), mutually exerted by two non-adjacent beam segments ΔV(x i ) and ΔV(ξ k ) as a result of their rotations with respect to the line given by the relative transverse displacement, ψ(x i , ξ k ), i.e.:

$$ r_{z} \left( {x_{i} ,\xi_{k} } \right) = q_{z} \left( {x_{i} ,\xi_{k} } \right)\Delta V\left( {x_{i} } \right)\Delta V\left( {\xi_{k} } \right) \, ;\quad q_{z} \left( {x_{i} ,\xi_{k} } \right) = 2\frac{{\text{sgn}} \left( {\xi_{k} - x_{i} } \right)}{\left| {\xi_{k} - x_{i} } \right|} g_{z} \left( {x_{i} ,\xi_{k} } \right)\psi \left( {x_{i} ,\xi_{k} } \right) $$
(13a,b)
$$ r_{\varphi z} \left( {x_{i} ,\xi_{k} } \right) = q_{\varphi z} \left( {x_{i} ,\xi_{k} } \right)\Delta V\left( {x_{i} } \right)\Delta V\left( {\xi_{k} } \right) \, ;\quad q_{\varphi z} \left( {x_{i} ,\xi_{k} } \right) = g_{z} \left( {x_{i} ,\xi_{k} } \right)\psi \left( {x_{i} ,\xi_{k} } \right) $$
(14a,b)

In the previous equations, q z (x i , ξ k ) in Eq. (13b) and q φz (x i , ξ k ) in Eq. (14b) are the specific long-range volume transverse forces and moments, depending on ψ(x i , ξ k ) through a symmetric real-valued distance-decaying attenuation function g z (x i , ξ k ). In Eq. (13b), \( \text{sgn} \left( {\xi - x} \right) = + 1 \) if (ξ − x) > 0 and \( \text{sgn} \left( {\xi - x} \right) = - 1 \) if (ξ − x) < 0 is introduced to ensure consistency of r z (x, ξ) with the sign convention of the long-range resultants in Fig. 2. Hence, the total long-range volume moments due to bending and shear deformation modes can be expressed as:

$$ r_{\varphi } \left( {x_{i} ,\xi_{k} } \right) = q_{\varphi } \left( {x_{i} ,\xi_{k} } \right)\Delta V\left( {x_{i} } \right)\Delta V\left( {\xi_{k} } \right);\quad q_{\varphi } \left( {x_{i} ,\xi_{k} } \right) = q_{\varphi \varphi } \left( {x_{i} ,\xi_{k} } \right) + q_{\varphi z} \left( {x_{i} ,\xi_{k} } \right). $$
(15a,b)

Based on the above definitions, the resultants of the long-range volume forces/moments exerted on the beam segment ΔV(x i ) at x = x i by all the non-adjacent beam segments ΔV(ξ k ) at x = ξ k , ξ k  ≠ x i ,  can be obtained as follows:

$$ \begin{aligned} R_{x} \left( {x_{i} } \right) &=& \sum\limits_{k = 0, \, k \ne i}^{N - 1} {r_{x} \left( {x_{i} ,\xi_{k} } \right)} { ;} \hfill \\ R_{z} \left( {x_{i} } \right) &=& \sum\limits_{k = 0, \, k \ne i}^{N - 1} {r_{z} \left( {x_{i} ,\xi_{k} } \right)} { ;} \hfill \\ R_{\varphi } \left( {x_{i} } \right) &=& \sum\limits_{k = 0, \, k \ne i}^{N - 1} {r_{\varphi } \left( {x_{i} ,\xi_{k} } \right)} \, .\hfill \\ \end{aligned} $$
(16a-c)

For brevity, R x (x i ), R z (x i ) and R φ (x i ) hereinafter will be referred to as long-range resultants.

A close inspection of the above equations suggests that the long-range volume forces/moments can be interpreted as the result of three spring-like connections between non-adjacent beam segments which separately account for pure axial, pure bending and pure shear modes (see Fig. 3). Thus, from a mechanical point of view, the proposed non-local beam model is conceptually equivalent to the non-local bar built by Di Paola et al. [42, 45, 46], where the long-range volume axial forces are represented, within the context of a discrete model, as linearly-elastic springs of distance-decaying stiffness connecting non-adjacent volume elements. In this regard it worth remarking that, if the long-range volume transverse forces/moments were taken as depending on the relative transverse displacement and not on the pure shear deformation (10), long-range volume transverse forces/moments would erroneously arise from a relative transverse displacement induced, for instance, by a rigid rotation of the beam. In this sense, it can be stated that the proposed non-local beam model is invariant with respect to rigid body motion and that the axial, bending and shear non-local behaviors are mechanically consistent.

Finally, some remarks are in order on the choice of the attenuation functions g s (x, ξ), with s = x, z, φ, governing the spatial decay of non-local effects. To ensure that the long-range resultants have a restoring nature, for any couple of interacting beam segments, the attenuation functions must be strictly positive. Furthermore, these functions are taken as symmetric functions with respect to the arguments x and ξ, to ensure that the long-range resultants exchanged by the interacting beam segments are mutual, according to Newton’s third law.

To make the beam model as general and versatile as possible, three different functions g s (x, ξ), with s = x, z, φ, have been introduced in the definition of the long-range forces/moments. Indeed, non-local axial, bending or shear effects may exhibit a different spatial decay depending on the material microstructure. In general, both the mathematical form of the attenuation functions [39–46, 49, 51] and the pertinent parameters depend on the material and should be determined based on experimental evidence.

3.2 Equilibrium equations

Within the context of the proposed non-local beam model, each beam segment is in equilibrium under: (i) the local stress resultants (3a–c) exerted by the adjacent beam segments; (ii) the resultants of the volume forces/moments exerted by all non-adjacent beam segments [see Eqs. (16a–c)]; and the external forces represented here by the unit length forces F x (x) and F z (x). Then, the equilibrium equations of the beam segment ΔV(x i ) = AΔx at x = x i , for i = 0, 1, …, N − 1, read (see Fig. 2):

$$ \begin{aligned} N^{(l)} \left( {x_{i} + \Delta x} \right) - N^{(l)} \left( {x_{i} } \right) + R_{x} \left( {x_{i} } \right) + F_{x} \left( {x_{i} } \right)\Delta x = 0; \hfill \\ T^{(l)} \left( {x_{i} + \Delta x} \right) - T^{(l)} \left( {x_{i} } \right) + R_{z} \left( {x_{i} } \right) + F_{z} \left( {x_{i} } \right)\Delta x = 0; \hfill \\ M^{(l)} \left( {x_{i} + \Delta x} \right) - M^{(l)} \left( {x_{i} } \right) - T^{(l)} \left( {x_{i} } \right)\Delta x - R_{\varphi } \left( {x_{i} } \right) = 0. \hfill \\ \end{aligned} $$
(17a-c)

Substituting Eqs. (16a–c) for the long-range resultants R x (x i ), R z (x i ) and R φ (x i ) into Eqs. (17a–c), dividing both sides by Δx and taking the limit as Δx → 0, the following integro-differential equilibrium equations are obtained:

$$ \begin{aligned} \frac{{{\text{d}}N^{(l)} (x)}}{{{\text{d}}x}} + A^{2} \int_{0}^{L} {q_{x} \left( {x,\xi } \right){\text{d}}\xi } + F_{x} \left( x \right) = 0; \hfill \\ \frac{{{\text{d}}T^{(l)} (x)}}{{{\text{d}}x}} + A^{2} \int_{0}^{L} {q_{z} \left( {x,\xi } \right){\text{d}}\xi } + F_{z} \left( x \right) = 0 { }; \hfill \\ \frac{{{\text{d}}M^{(l)} (x)}}{{{\text{d}}x}} - T^{(l)} (x) - A^{2} \int_{0}^{L} {q_{\varphi } \left( {x,\xi } \right){\text{d}}\xi } = 0. \hfill \\ \end{aligned} $$
(18a-c)

Notice that Eqs. (18a–c) differ from the differential equilibrium equations of the local TM beam (5a–c) just for the integral terms representing the long-range resultants per unit length.

The B.C. associated with Eqs. (18a–c) coincide with the ones pertaining to the local beam, given in Eqs. (6) and (7). Indeed, at the beam ends the long-range resultants can be considered as infinitesimal of higher order with respect to the local stress resultants (see Ref. [42–44]).

4 Variational formulation

In this Section, the equilibrium equations of the non-local TM beam along with the pertinent B.C. are derived within a variational framework by applying the minimum potential energy principle.

A variational formulation of the equations governing the proposed non-local beam model can be pursued starting from the work identity [42–44]:

$$ \int_{0}^{L} {{\mathbf{s}}^{{(l){\text{T}}}} \left( x \right){\mathbf{d}}^{(l)} \left( x \right){\text{d}}x = } \int_{0}^{L} {{\mathbf{F}}^{\text{T}} \left( x \right)} {\mathbf{u}}\left( x \right){\text{d}}x + {\mathbf{s}}_{0}^{\rm T} {\mathbf{u}}_{0} + {\mathbf{s}}_{L}^{\rm T} {\mathbf{u}}_{L} + A^{2} \int_{0}^{L} {\int_{0}^{L} {{\tilde{\mathbf{q}}}^{\rm T} \left( {x,\xi } \right){\mathbf{u}}\left( x \right){\text{d}}x{\text{d}}\xi } } $$
(19)

where \( {\mathbf{s}}^{(l)} \left( x \right) \) and \( {\mathbf{d}}^{(l)} \left( x \right) \) are the vectors collecting the local stress resultants (3a–c) and generalized strain components (2a–c), respectively, defined in Sect. 2; while the vectors \( {\mathbf{u}}\left( x \right) \), \( {\mathbf{F}}\left( x \right) \) and \( {\tilde{\mathbf{q}}}\left( {x,\xi } \right) \) are given by:

$$ \begin{aligned} {\mathbf{u}}\left( x \right) = \left[ {\begin{array}{*{20}c} {u\left( x \right)} & {v\left( x \right)} & {\varphi \left( x \right)} \\ \end{array} } \right]^{\text{T}} ; \hfill \\ {\mathbf{F}}\left( x \right) = \left[ {\begin{array}{*{20}c} {F_{x} \left( x \right)} & {F_{z} \left( x \right)} & 0 \\ \end{array} } \right]^{\text{T}} ; \hfill \\ {\tilde{\mathbf{q}}}\left( {x,\xi } \right) = \left[ {\begin{array}{*{20}c} {q_{x} \left( {x,\xi } \right)} & {q_{z} \left( {x,\xi } \right)} & {q_{\varphi } \left( {x,\xi } \right)} \\ \end{array} } \right]^{\text{T}} . \hfill \\ \end{aligned} $$
(20a-c)

Furthermore, in Eq. (19), \( {\mathbf{s}}_{i} \) (i = 0, L) is the vector listing the axial force, transverse force and moment at the beam ends, N i , T i and M i , (i = 0, L); the corresponding displacements and rotations are gathered into vector \( {\mathbf{u}}_{i} \) (i = 0, L).

The double integral on the r.h.s of Eq. (19) is obtained as the continuous counterpart of the work done by the long-range resultants (16a–c) exchanged between non-adjacent beam segments of the discrete model built in the previous Section (see Fig. 2), i.e.:

$$ \begin{aligned} \mathop {\lim }\limits_{\Delta x,\Delta \xi \to 0} \, \sum\limits_{i = 0}^{N - 1} {{\mathbf{R}}^{\text{T}} \left( {x_{i} } \right){\mathbf{u}}\left( {x_{i} } \right)} \, = \mathop {\lim }\limits_{\Delta x,\Delta \xi \to 0} \, A^{2} \sum\limits_{i = 0}^{N - 1} {\sum\limits_{k = 0,k \ne i}^{N - 1} {{\tilde{\mathbf{q}}}^{\text{T}} \left( {x_{i} ,\xi_{k} } \right){\mathbf{u}}\left( {x_{i} } \right)\Delta x\Delta \xi } } \hfill \\ \, = A^{2} \int_{0}^{L} {\int_{0}^{L} {{\tilde{\mathbf{q}}}^{\text{T}} \left( {x,\xi } \right){\mathbf{u}}\left( x \right){\text{d}}x{\text{d}}\xi } } \hfill \\ \end{aligned} $$
(21)

where \( {\mathbf{R}}\left( {x_{i} } \right) = \left[ {\begin{array}{*{20}c} {R_{x} \left( {x_{i} } \right)} & {R_{z} \left( {x_{i} } \right)} & {R_{\varphi } \left( {x_{i} } \right)} \\ \end{array} } \right]^{\text{T}} \).

Due to the symmetry of the attenuation functions g s (x, ξ), s = x, z, φ, with respect to the arguments x and ξ, the following identity holds (see Appendix 1):

$$ \int_{0}^{L} {\int_{0}^{L} {{\tilde{\mathbf{q}}}^{\text{T}} ({x,\xi}){\mathbf{u}}(x){\text{d}}x{\text{d}}\xi }} = - \frac{1}{2}\int_{0}^{L} {\int_{0}^{L} {{\mathbf{q}}^{\text{T}} ({x,\xi}){\mathbf{e}}({x,\xi}){\text{d}}x{\text{d}}\xi } } $$
(22)

where

$$ \begin{aligned} {\mathbf{e}}\left( {x,\xi } \right) = \left[ {\begin{array}{*{20}c} {\eta \left( {x,\xi } \right)} & {\theta \left( {x,\xi } \right)} & {\psi \left( {x,\xi } \right)} \\ \end{array} } \right]^{\text{T}} ; \hfill \\ {\mathbf{q}}\left( {x,\xi } \right) = \left[ {\begin{array}{*{20}c} {q_{x} \left( x \right)} & {q_{\varphi \varphi } \left( {x,\xi } \right)} & {q_{\varphi z} \left( {x,\xi } \right)} \\ \end{array} } \right]^{\text{T}} \hfill \\ \end{aligned} $$
(23a,b)

are the vectors collecting the generalized measures of relative motion and the associated specific-long-range forces/moments, respectively. Vectors \( {\mathbf{q}}\left( {x,\xi } \right) \) and \( {\mathbf{e}}\left( {x,\xi } \right) \) are related by Eq. (11b), Eq. (12b), and Eq. (14b), which can be rewritten in compact form as:

$$ {\mathbf{q}}\left( {x,\xi } \right) = {\mathbf{G}}\left( {x,\xi } \right){\mathbf{e}}\left( {x,\xi } \right) $$
(24)

where

$$ {\mathbf{G}}\left( {x,\xi } \right) = Diag\left[ {\begin{array}{*{20}c} {g_{x} \left( {x,\xi } \right)} & {g_{\varphi } \left( {x,\xi } \right)} & {g_{z} \left( {x,\xi } \right)} \\ \end{array} } \right] $$
(25)

is a diagonal matrix listing the attenuation functions. Equation (24) may be viewed as the constitutive law between the specific long-range forces and the associated generalized measures of relative motion.

Taking into account Eq. (22), the work identity can be rewritten as follows:

$$ \int_{0}^{L} {{\mathbf{s}}^{{(l){\text{T}}}} } \left( x \right){\mathbf{d}}^{(l)} \left( x \right){\text{d}}x + \frac{A^{2}}{2}\int_{0}^{L} {\int_{0}^{L} {{\mathbf{q}}^{\text{T}} \left( {x,\xi } \right){\mathbf{e}}\left( {x,\xi } \right){\text{d}}x{\text{d}}\xi } } = \int_{0}^{L} {{\mathbf{F}}^{\text{T}} } \left( x \right){\mathbf{u}}\left( x \right){\text{d}}x + {\mathbf{s}}_{ 0}^{\text{T}} {\mathbf{u}}_{0} + {\mathbf{s}}_{L}^{\text{T}} {\mathbf{u}}_{L} . $$
(26)

Based on Eq. (26), the elastic potential energy stored in the TM beam with long-range interactions can be defined as sum of local and non-local contributions:

$$ \begin{aligned} \varPhi \left( {{\mathbf{d}}^{(l)} \left( x \right),{\mathbf{e}}\left( {x,\xi } \right)} \right) & = \varPhi^{(l)} \left( {{\mathbf{d}}^{(l)} \left( x \right)} \right) + \varPhi^{(nl)} \left( {{\mathbf{e}}\left( {x,\xi } \right)} \right) \\ & = \int_{0}^{L} {\phi^{(l)} \left( {{\mathbf{d}}^{(l)} \left( x \right)} \right){\text{d}}x} + \frac{A^{2}}{2}\int_{0}^{L} {\int_{0}^{L} {\phi^{(nl)} \left( {{\mathbf{e}}\left( {x,\xi } \right)} \right){\text{d}}x} } {\text{d}}\xi \\ & = \frac{1}{2}\int_{0}^{L} {{\mathbf{d}}^{{(l){\text{T}}}} \left( x \right){\mathbf{D}}^{*} {\mathbf{d}}^{(l)} \left( x \right){\text{d}}x} + \frac{A^{2}}{4}\int_{0}^{L} {\int_{0}^{L} {{\mathbf{e}}^{\text{T}} \left( {x,\xi } \right){\mathbf{G}}\left( {x,\xi } \right){\mathbf{e}}\left( {x,\xi } \right){\text{d}}x} } {\text{d}}\xi \\ \end{aligned} $$
(27)

where the linear-elastic constitutive laws (4) and Eq. (24) have been introduced. In the previous equation, \( \phi^{(l)} \left( {{\mathbf{d}}^{(l)} \left( x \right)} \right) \) and \( \phi^{(nl)} \left( {{\mathbf{e}}\left( {x,\xi } \right)} \right) \) denote the local and non-local elastic potential energy per unit length, respectively. The consistency of the elastic potential energy (27) may be assessed by deriving \( \phi^{(l)} \left( {{\mathbf{d}}^{(l)} \left( x \right)} \right) \) and \( \phi^{(nl)} \left( {{\mathbf{e}}\left( {x,\xi } \right)} \right) \) with respect to the pertinent state variables, i.e.:

$$ {\mathbf{s}}^{(l)} \left( x \right) = \frac{{\partial \phi^{(l)} }}{{\partial {\mathbf{d}}^{(l)} }} = {\mathbf{D}}^{*} {\mathbf{d}}^{(l)} \left( x \right); \, {\mathbf{q}}\left( {x,\xi } \right) = \frac{{\partial \phi^{(nl)} }}{{\partial {\mathbf{e}}}}{\mathbf{ = G}}\left( {x,\xi } \right){\mathbf{e}}\left( {x,\xi } \right). $$
(28a,b)

These relationships are coincident with the constitutive equations for the local stress resultants (4) and the specific long-range forces/moments (24).

Taking into account Eq. (22), the first variation of the elastic potential energy (27) can be written as:

$$ \delta \varPhi \left( {{\mathbf{d}}^{(l)} \left( x \right),{\mathbf{u}}\left( x \right)} \right) = \int_{0}^{L} {{\mathbf{d}}^{{(l){\text{T}}}} \left( x \right){\mathbf{D}}^{*} \delta {\mathbf{d}}^{(l)} \left( x \right){\text{d}}x} - A^{2}\int_{0}^{L} {\int_{0}^{L} {{\tilde{\mathbf{q}}}\left( {x,\xi } \right)\delta {\mathbf{u}}\left( x \right){\text{d}}x{\text{d}}\xi } } . $$
(29)

The equilibrium equations and the associated natural B.C. of the non-local TM beam can be derived by enforcing that the first variation of the total potential energy functional Π = Φ − W ext vanishes in correspondence of the solution, i.e.:

$$ \delta \varPi \left( {{\mathbf{d}}^{(l)} \left( x \right),{\mathbf{u}}\left( x \right)} \right) = \delta \varPhi \left( {{\mathbf{d}}^{(l)} \left( x \right),{\mathbf{u}}\left( x \right)} \right) - \delta W_{ext}^{{}} \left( {{\mathbf{u}}\left( x \right)} \right) = 0 $$
(30)

where

$$ \delta W_{ext}^{{}} \left( {{\mathbf{u}}\left( x \right)} \right) = \int_{0}^{L} {{\mathbf{F}}^{\text{T}} } \left( x \right)\delta {\mathbf{u}}\left( x \right){\text{d}}x + {\mathbf{s}}_{0}^{\text{T}} \delta {\mathbf{u}}_{0} + {\mathbf{s}}_{L}^{\text{T}} \delta {\mathbf{u}}_{L} $$
(31)

is the first variation of the work done by the external forces.

Taking into account the local strain–displacement relationships (2a–c), and applying the standard rules of variational calculus along with integration by parts, the stationarity condition (30) yields the following Euler–Lagrange equations:

$$ \begin{aligned} E^{*} A\frac{{{\text{d}}^{2} u\left( x \right)}}{{{\text{d}}x^{2} }} + A^{2}\int_{0}^{L} {q_{x} \left( {x,\xi } \right){\text{d}}\xi + F_{x} \left( x \right)} = 0; \hfill \\ K_{s} G^{*} A\left( {\frac{{{\text{d}}^{2} v\left( x \right)}}{{{\text{d}}x^{2} }} - \frac{{{\text{d}}\varphi \left( x \right)}}{{{\text{d}}x}}} \right) + A^{2}\int_{0}^{L} {q_{z} \left( {x,\xi } \right){\text{d}}\xi + F_{z} \left( x \right)} = 0; \hfill \\ E^{*} I\frac{{{\text{d}}^{2} \varphi \left( x \right)}}{{{\text{d}}x^{2} }} + K_{s} G^{*} A\left( {\frac{{{\text{d}}v\left( x \right)}}{{{\text{d}}x}} - \varphi \left( x \right)} \right) + A^{2}\int_{0}^{L} {q_{\varphi } \left( {x,\xi } \right){\text{d}}\xi } = 0. \hfill \\ \end{aligned} $$
(32a-c)

The associated static and kinematic B.C. read:

$$ \begin{aligned} N^{(l)} \left( {x_{i} } \right) = E^{*} A\left. {\frac{{{\text{d}} u\left( x \right)}}{{{\text{d}}x }}} \right|_{{x = x_{i} }} = \mp N_{i} ;{\text{ or }}u\left( {x_{i} } \right) = u_{i} ; \hfill \\ T^{(l)} \left( {x_{i} } \right) = K_{s} G^{*} A\left. {\left( {\frac{{{\text{d}}v\left( x \right)}}{{{\text{d}}x}} - \varphi \left( x \right)} \right)} \right|_{{x = x_{i} }} = \mp T_{i} ;{\text{ or }}v\left( {x_{i} } \right) = v_{i} ; \hfill \\ M^{(l)} \left( {x_{i} } \right) = - E^{*} I\left. {\frac{{{\text{d}}\varphi \left( x \right)}}{{{\text{d}}x}}} \right|_{{x = x_{i} }} = \pm M_{0} ;{\text{ or }}\varphi \left( {x_{i} } \right) = \varphi_{i} ,{ (}i = 0,L). \hfill \\ \end{aligned} $$
(33a-c)

Notice that Eqs. (32) and (33) coincide with the equilibrium equations and B.C. derived in Sect. 3.2 on a mechanical basis, once the local stress resultants N (l)(x), T (l)(x), M (l)(x) are expressed in terms of the kinematic variables u(x), v(x) and φ(x) by using the strain–displacement and constitutive relationships (2) and (4). This result demonstrates the variational consistency of the proposed non-local beam model. In this regard, it worth remarking that the fully local nature of the B.C. has been derived also on a variational basis.

An important remark concerns the B.C. (33): the fact that they hold the same form of classical local theory is a remarkable advantage, which allows standard solution methods, such as the finite difference method or the finite element method, to be applied for solving the equilibrium Eqs. (32) in a straightforward manner. In particular, notice that the variational formulation above can be used for deriving a finite element formulation of the equilibrium equations, as customary in the mechanics of elastic solids. On further advantages involved by the fact that the B.C. hold the same form of classical local theory, in particular with respect to lattice mechanics models, comments can be found in a previous paper by the authors [42], and are not repeated here for brevity.

5 Numerical applications

The applications focus on the flexural response of the proposed non-local beam model. Firstly, theoretical results are presented for epoxy micro-beams of rectangular cross section of width b and thickness h. Simply-supported and cantilever beams will be considered as study cases. Secondly, it will be shown that the proposed non-local beam model can capture the experimental static response of a cantilever epoxy micro-beam subjected to a tip load, as reported by Lam et al. [12].

In all cases, it will be assumed that pure bending and shear behaviors are governed by the same attenuation functions, i.e. g s (x, ξ) = g(x, ξ), s = φ, z, which are given here an exponential form:

$$ g\left( {x,\xi } \right) = \frac{C}{{h^{2} }}\exp \left( { - \frac{{\left| {x - \xi } \right|}}{l}} \right) $$
(34)

where C is a constant; h denotes the thickness of the cross section; l is an internal length. The larger is the internal length l, the wider is the so-called influence distance, i.e. the maximum distance beyond which the attenuation functions and thus the non-local effects become negligible. Further, in the local constitutive Eq. (4) β 1 = 1 is selected. As a result of this choice for β 1, the non-local solution will tend to the solution obtained by the classical local TM theory, as l → 0 in the attenuation function g(x, ξ) given by Eq. (34).

The numerical solution of the equilibrium Eqs. (32b, c) is found using a finite difference method. The numerical results reported are obtained for N = 800 intervals in the beam domain. No significant differences are encountered for N > 800. The finite difference method is applied using a standard discrete approximation of the differential operators and a standard trapezoidal approximation of the integrals in Eqs. (32b, c), and no difficulties are encountered in enforcing the B.C., as coincide with those of classical local theory; it can be implemented by any user, also by those not familiar with more involved and specific numerical methods as, for instance, the finite element method. The proposed finite difference solution involves separate local and non-local stiffness matrices, which correspond to the discretized differential operator and scalar integral, respectively. This means that, when implementing sensitivity analyses for varying local or non-local parameters, the local matrix or the non-local matrix only shall be updated.

5.1 Numerical results

Epoxy micro-beams with the following material properties are considered: Young’s modulus \( E = 1.40 \, {\text{GPa}} \), Poisson’s coefficient ν = 0.35. The non-local parameters C and l in Eq. (34) are set on a theoretical basis, in order to enhance non-local effects and assess how they affect the static response. Specifically, C = 1011 Nm−6 and different values of the internal length l are considered.

5.1.1 Simply-supported beam

A simply-supported epoxy micro-beam with the following geometrical properties is considered: L = 300 μm, h = L/20 = 15 μm, b = 30 μm. A uniformly distributed load p = 1 Nm−1 is assumed.

Figures 4 and 5 illustrate the dimensionless deflection v(x)/L and rotation φ(x) versus the non-dimensional location x/L, for different values of the internal length l. For comparison, the dimensionless classical local TM beam response is also reported. It is apparent that the non-local response is generally smaller than the classical local TM beam response. This behavior can be explained considering that the elastic long-range interactions provide additional stiffness with respect to the local terms in Eqs. (32b, c) and, since such terms coincide with the classical local TM beam terms [β 1 = 1 has been set in Eq. (4)], the additional stiffness yields a non-local response that is stiffer than the classical local TM response. It can be also noted that the larger is the internal length l, the smaller is the non-local response: a larger internal length l corresponds indeed to a larger amount of mutually interacting non-adjacent beam segments, with a consequent stiffening of the solution.

Fig. 4
figure 4

Simply-supported beam: non-local and local dimensionless deflection for different l (internal length)

Full size image
Fig. 5
figure 5

Simply-supported beam: non-local and local rotation for different internal lengths l

Full size image

To have a better insight into the response of the proposed non-local beam model, the ratio of the mid-span maximum non-local deflection to the mid-span maximum local deflection, v (nl)max /v (l)max , versus h/L (thickness-to-length ratio) is reported in Fig. 6, for fixed values of L and b, i.e. L = 300 μm, b = 30 μm, different values of thickness h and internal length l (from 5 to 40 μm). It is seen that, for a given value of l, the smaller is h, the smaller is the non-local deflection, i.e. more significant are the non-local effects and, consequently, the deviation from the corresponding classical local TM response. To explain this behavior it is noticed that, if one considers the classical local TM beam without long-range interactions, for L = cost and b = cost the deformability increases with decreasing thickness h. As the beam undergoes deformation, the relative motion between non-adjacent beam segments activates the elastic long-range interactions, and their magnitude, for a given distance between two beam segments, depends on the magnitude of the relative motion [see Eqs. (11), (12), (13) and (14)]. For this reason, it is evident that the “weight” of the non-local terms shall increase as the deformability of beam increases, with the consequent stiffening effect with respect to the classical local TM beam response observed in Fig. 6, for decreasing thickness h. It can be also noted that larger deviations from the classical local response are encountered, as expected, for increasing values of the internal length l. It is quite interesting to point out that the stiffening effects shown in Fig. 6, for L = cost and b = cost and decreasing h are predicted by other non-local theories [27] and are considered in agreement with experimental evidence on small-size effects in many materials [12, 13].

Fig. 6
figure 6

Simply-supported beam: non-local to local maximum deflection ratio for L = cost (length), b = cost (width), variable h (thickness) and different values of the internal length l (from 5 to 40 μm)

Full size image

Further insight into the behavior of the proposed non-local beam model is provided by Fig. 7, that shows the ratio of the mid-span maximum non-local deflection to the mid-span maximum local deflection, v (nl)max /v (l)max , versus thickness h, for fixed values of the ratios L/h = 10, b/h = 2, and different values of the internal length l (from 5 to 40 μm). As in the previous case, it is seen that the smaller is h (i.e. the smaller are the overall dimensions of the beam being L/h = cost), the smaller is the non-local deflection, i.e. more significant are the non-local effects. Such a behavior, for a given value of the internal length l, can be expected in consideration of the fact that L decreases with h (L/h = cost). As the beam becomes shorter while the internal length l is fixed, each beam segment interacts with a relatively increasing number of beam segments (i.e., relatively to the total number of interacting beam segments) and, as a consequence, the “weight” of the non-local terms does increase with respect to that of the local ones. It can be also noted that larger deviations from the classical local response are encountered, as in Fig. 6, for increasing values of the internal length l. It is quite interesting to point out that the stiffening effects shown in Fig. 7, for L/h = cost, b/h = cost, and decreasing h are predicted by other non-local theories [25] and are generally considered in agreement with experimental evidence on small-size stiffening effects in several materials [12, 13].

Fig. 7
figure 7

Simply-supported beam: non-local to local maximum deflection ratio for L/h = cost (length to thickness ratio), b/h = cost (width to thickness ratio), variable h (thickness) and different values of the internal length l (from 5 to 40 μm)

Full size image

5.1.2 Cantilever beam

A cantilever epoxy micro-beam with the following parameters is considered: L = 300 μm, h = L/20 = 15 μm, b = 30 μm. A tip load P = 100 μN is assumed. Figure 8 through Fig. 11 show: (i) the dimensionless deflection v(x)/L (Fig. 8) and rotation φ(x) (Fig. 9) versus the non-dimensional location x/L, for different values of the internal length l; (ii) the ratio of the tip maximum non-local deflection to the tip maximum local deflection, v (nl)max /v (l)max , versus h/L (Fig. 10), for fixed values of L and b, i.e. L = 300 μm, b = 30 μm, and different values of the internal length l (from 5 to 40 μm); (iii) the ratio of the tip maximum non-local deflection to the tip maximum local deflection, v (nl)max /v (l)max , versus h (Fig. 11), for fixed values of the ratio L/h = 10, b/h = 2, and different values of the internal length l (from 5 to 40 μm). All the results appear in agreement with those obtained for a simply-supported beam. They can be explained based upon the same reasoning and, for this, further comments are omitted for brevity. It is only worth remarking that similar behaviors are predicted by alternative non-local theories [25, 27] and are generally considered in agreement with small-size stiffening effects in many materials [12, 13].

Fig. 8
figure 8

Cantilever beam: non-local and local dimensionless deflection for different l (internal length)

Full size image
Fig. 9
figure 9

Cantilever beam: non-local and local rotation for different l (internal length)

Full size image
Fig. 10
figure 10

Cantilever beam: non-local to local maximum deflection ratio for L = cost (length), b = cost (width), variable h (thickness) and different values of the internal length l (from 5 to 40 μm)

Full size image
Fig. 11
figure 11

Cantilever beam: non-local to local maximum deflection ratio for L/h = cost (length to thickness ratio), b/h = cost (width to thickness ratio), variable h (thickness) and different values of the internal length l (from 5 to 40 μm)

Full size image

5.2 Comparison with experimental results

Lam et al. [12] have reported the experimental response of a cantilever epoxy micro-beam with a rectangular cross section, subjected to a tip static load P. They have considered the following parameters [12, 36]: b = 0.235 mm, E = 1.44 GPa, ν = 0.38 (Poisson’s coefficient), P = 300 μN. The response has been measured for a fixed ratio h/L = 0.1 and four different thickness values h: 20, 38, 75 and 115 μm. The results reported by Lam et al. [12] show that the experimental bending rigidity of the beam increases as the thickness decreases. This stiffening effect is not predicted by the classical EB beam theory, where the bending rigidity is constant when the ratio h/L is held constant. It is now of interest to assess if, instead, it can be captured by the proposed non-local beam model.

For this purpose, the parameters/functions defining the proposed non-local beam model are selected as specified above, say: (i) β 1 = 1 in Eq. (4) for the local terms in Eqs. (32b, c), i.e. the local stiffness coincides with the stiffness of the classical TM theory; in this manner, the sought non-local solution will be stiffer than the local solution, consistently with the experimental behavior reported by Lam et al. [12]; (ii) the attenuation functions g φ (x, ξ) and g z (x, ξ) governing pure bending and pure shear non-local effects are given the exponential form (34). Being β 1 = 1 and due to the exponential form (34) of the attenuation functions, the sought non-local solution will revert to the classical local TM beam solution as l → 0, as already pointed out in Sect. 5.

Under these assumptions, the unknown parameters left are C and l in Eq. (34). To determine these parameters an error minimization procedure is pursued, based on the experimental data reported in Fig. 12 of the paper by Lam et al. [12]. They describe the ratio of the experimental bending rigidity to the classical bending rigidity of the EB beam theory, computed by Lam and coworkers as the ratio of the tip deflection of the classical EB beam theory v (l)(L) to the experimental tip deflection v ex (L) (see pag. 1503 of the paper by Lam et al. [12]), i.e. as

$$ R_{ex} = \frac{{v^{\left( l \right)} \left( L \right)}}{{v_{ex} \left( L \right)}} . $$
(35)
Fig. 12
figure 12

Cantilever beam: bending stiffness ratio predicted by the proposed model for a varying thickness versus experimental data by Lam et al. [12]

Full size image

Therefore, in the error minimization procedure the sought values of C and l are computed as those that minimize, for the different thicknesses (20, 38, 75 and 115 μm) in Fig. 12 of the paper by Lam et al. [12], the squared difference between R ex , Eq. (35), and

$$ R_{th} = \frac{{v^{\left( l \right)} \left( L \right)}}{v\left( L \right)} , $$
(36)

where v(L) is the tip deflection predicted by the proposed non-local beam model. As in Sect. 5, the latter is computed by a finite difference approximation, with N = 800 intervals in the beam domain. For completeness it shall be also noted that, in Fig. 12 of the paper by Lam et al. [12], a few experimental data are reported for each thickness (20, 38, 75 and 115 μm). However since they appear very close, for each thickness their average value will be assumed as reference value in the error minimization procedure.

The results obtained in this manner are reported in Fig. 12. It can be seen that a very good agreement between the experimental bending rigidity ratios and those predicted by the proposed non-local beam model is attained for \( C = 3.17 \cdot 10^{11} {\text{ Nm}}^{ - 6} \) and l = 30 μm in Eq. (34). Figure 12 reports the results obtained also for two alternative sets of C, l (Set II: \( C = 1.8 \cdot 10^{11} {\text{ Nm}}^{ - 6} \), l = 30 μm; Set III: \( C = 1.8 \cdot 10^{11} {\text{ Nm}}^{ - 6} \), l = 40 μm), in order to show that even for different sets of parameters, the qualitative behavior of the proposed non-local beam model still reflects the experimental data trend.

6 Conclusions

A displacement-based non-local TM beam model has been illustrated. The key idea involves modeling non-local effects as elastic long-range volume forces/moments exchanged by non-adjacent beam segments, that contribute to the equilibrium of any beam segment along with the classical stress resultants. The long-range volume forces/moments have been built as linearly-elastic terms that depend, through appropriate attenuation functions, on the product of the volumes of the interacting beam segments and on generalized measures of their relative motion based on the pure deformation modes of the beam, to ensure invariance with respect to rigid body motion. This modeling has allowed a meaningful mechanical interpretation of the long-range interactions as resulting from three spring-like connections acting in parallel, which account separately for pure axial, pure bending and pure shear modes.

The variational consistency of the model has been proved by deriving the beam equilibrium equations along with the pertinent B.C. based on a total elastic potential energy involving local and non-local contributions. The mechanical B.C. have been derived in the same form of the classical local theory. These aspects allow a straightforward implementation of classical solution methods, such as the finite difference method or the finite element method.

A certain number of parameters/functions shall be set in the proposed non-local beam model, concerning the local terms, [see β 1 in Eq. (4)] as well as non-local terms, namely the attenuation functions [g x (x, ξ), g φ (x, ξ), g z (x, ξ)] with the related parameters. In practical applications, they shall be generally determined via an optimization procedure, where a fitting to experimental data is sought. It is worth remarking that a similar procedure is not necessary in the proposed non-local beam model only, but is necessary in all classical non-local theories involving an enriched continuum with additional non-local terms. Depending on the formulation, the non-local terms always involve a number of unknown parameters/functions that only experimental evidence may allow to select. For instance, examples of enriched continua with five additional parameters for non-local terms exist in the literature [12, 50], or non-local beam models with different potential choices of the attenuation functions [49, 51]. Obviously, any optimization procedure to fit experimental evidence shall be generally preceded by numerical simulations, that may serve to determine the expected order of magnitude of the non-local terms, with respect to the local ones.

Numerical results, presented in Sect. 5 for a variety of geometrical parameters, have shown stiffening effects with respect to the classical local TM beam solution in agreement with the behavior predicted by alternative non-local theories [12, 25, 27, 36]. It has been also seen that the proposed non-local beam model captures very satisfactorily the experimental small-size stiffening effects reported by Lam et al. [12], for a cantilever epoxy micro-beam subjected to a tip static load. In all these applications, β 1 = 1 has been set in Eq. (4) for the local terms in Eqs. (32b, c) and exponential attenuation functions have been selected, depending on an internal length l governing the spatial decay of non-local effects.

In the authors’ opinion, the proposed non-local TM beam model involves some advantages, summarized as follows.

Due to the fact that non-local effects are modeled on a mechanical basis, specifically as elastic long-range force/moments counteracting the relative motion between couples of non-adjacent beam segments, the results provided by the proposed model are readily predictable. In general it can be stated that, because of the elastic long-range forces/moments counteracting the relative motion between beam segments, the non-local solution is generally stiffer than the local solution, i.e. the solution that would be obtained if only the local terms were considered in the equilibrium Eqs. (32). In particular:

  1. (i)

    if β 1 = 1 is set in Eq. (4) for the local terms, as in the numerical applications of Sect. 5, the non-local solution will always be stiffer than the classical TM beam solution, because for β 1 = 1, the local terms in Eq. (4) coincide with the classical terms of the TM beam theory;

  2. (ii)

    if β 1 < 1 is set in Eq. (4) for the local terms, the non-local solution will be either stiffer or softer than the classical TM beam solution. Because of the additional stiffness provided by the long-range interactions, the non-local solution will be stiffer than the local solution corresponding to the selected value β 1 < 1; however, because the latter is softer than the classical TM beam solution (that corresponds to β 1 = 1), the non-local solution will be either stiffer or softer than the classical TM beam solution depending on the amount of additional stiffness provided by the non-local terms, i.e. depending on the parameters of the attenuation functions g x (x,ξ), g φ (x,ξ) and g z (x,ξ) (for the exponential functions considered in the paper such parameters are constant C and internal length l). A pertinent example of this behavior is provided in Appendix 2. As a concluding comment in this respect, it is pointed out that the possibility of obtaining either stiffer or softer solutions with respect to the classical TM beam solution can be considered, in the authors’ opinion, a quite useful feature of the proposed model, especially in view of the fact that experimental evidence on non-local effects is not yet fully available for all existing materials, and considering that most likely more complex materials will be produced in the future.

It is finally important to remark that the proposed mechanical description of non-local effects allows predicting how results may vary with beam geometry (e.g., for varying thickness with constant length and cross-section width, or for varying thickness with constant length-to-thickness and width-to-thickness ratios of the cross section), as discussed thoroughly in the comments on the numerical results reported in Sect. 5.