1 Introduction

The study of shock waves in a mixture of a gas and small solid particles is of great importance due to its applications to nozzle flow, lunar ash flow, bomb blast, coal-mine blast, under-ground, volcanic and cosmic explosions, metallized propellant rocket, supersonic flight in polluted air, collision of coma with a planet and many other engineering problems (see [1–11]). Shock waves often arise in nature because of a balance between wave breaking non-linear and wave damping dissipative forces [12]. Collisional and collisionless shock waves can appear because of friction between the particles and wave–particle interaction [13, 14], respectively. Miura and Glass [15] obtained an analytical solution of a planar dusty gas flow with constant velocities of the shock and the piston moving behind it. As they neglected the volume occupied by the solid particles mixed into the perfect gas, the dust virtually has a mass fraction but no volume fraction. Their results reflect the influence of the additional inertia of the dust upon the shock propagation. Pai et al. [1] generalized the well known solution of a strong explosion due to an instantaneous release of energy in gas [16, 17]) to the case of two-phase flow of a mixture of perfect gas and small solid particles, and brought out the essential effects due to presence of dusty particles on such a strong shock wave. As they considered non-zero volume fraction of solid particles in the mixture, their results reflect the influence of both the decrease of mixture compressibility and the increase of mixture’s inertia on the shock propagation [18, 19].

In extreme conditions that prevail in most of the problems associated with shock waves, the assumption that the gas is ideal is no longer valid. Anisimov and Spiner [20] have taken an equation of state for non-ideal gases in a simplified form, and investigated the effect of the parameter of non-idealness on the problem of a strong point explosion. Recently, Vishwakarma and Nath [6] obtained the similarity solution for the propagation of a strong shock wave in a mixture of a non-ideal gas and small solid particle driven out by a piston moving according to power law, in both the cases when the flow was isothermal or adiabatic.

The influence of radiation on a strong shock wave and on the flow-field behind the shock front has always been of great interest, for instance, in the field of nuclear power and space research. Consequently, similarity models for classical blast wave problems have been extended, taking radiation into account [21–27]. Elliot [21] considered the explosion problem by introducing the radiation flux in its diffusion approximation. Wang [22] has discussed the piston problem with radiative heat transfer in the thin and thick limits and also in the general case with the idealized two direction approximation. Ashraf and Sachdev [24] have not explicitly used the radiation transfer equations, but have evaluated the radiation flux from conservation equations. Their solutions, therefore, hold without any restriction on the optical properties of the medium. Vishwakarma and Vishwakarma [28] have extended the problem considered by Ashraf and Sachdev [24] by taking the medium a mixture of perfect gas and small solid particles in place of perfect gas.

In the present work, we generalize the work of Vishwakarma and Vishwakarma [28] by taking the medium a mixture of a non-ideal gas and small solid particles in place of a mixture of a perfect gas and small solid particles. We, therefore, derive an exact similarity solution for the adiabatic flow behind a strong cylindrical or spherical shock propagating in a mixture of a non-ideal gas and small solid particles in which density remains constant and radiation flux is important.

In order to get some essential features of the shock propagation, small solid particles are considered as a pseudo-fluid, and the mixture at a velocity and temperature equilibrium with a constant ratio of specific heats [29]. For this gas-particle mixture to be treated as a so-called idealized equilibrium gas [30], it is necessary to consider the particle diameter much smaller than a characteristic length of the flow-field and their number density is small in relation to that of the gas particles. The Brownian motion of the solid particles in negligible small. No deformation and no phase changes of the solid particles occur. Gas and solid particles are chemically inert. In this case, we may assume that the viscous stress and heat conduction of the medium are negligible [1, 2, 6, 18]. Effects of a change in the value of the parameter of non-idealness of the gas in the mixture \(\overline{b}\), the mass concentration of solid particles in the mixture \({k_p}\), the ratio of the density of solid particles to the initial density of gas \({G_1}\) on the strength of the shock and on the flow-field behind it are obtained.

2 Fundamental equations and boundary conditions

The basic conservation equations of mass, momentum and energy for one-dimensional unsteady flow of a mixture of non-ideal gas and small solid particles in which the effect of radiation heat-flux may be significant, can be written (c.f. [1, 24]) as

$$\begin{aligned}&\frac{{\partial {\rho } }}{{\partial t}} + u\frac{{\partial {\rho } }}{{\partial r}} + \frac{\rho }{{{r^j}}}\frac{\partial }{{\partial r}}\left( {u{r^j}} \right) = 0, \end{aligned}$$
(2.1)
$$\begin{aligned}&\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial r}} + \frac{1}{\rho }\frac{{\partial p }}{{\partial r}} = 0, \end{aligned}$$
(2.2)
$$\begin{aligned}&\frac{{\partial {U_m}}}{{\partial t}} + u\frac{{\partial {U_m}}}{{\partial r}} - \frac{p}{{{\rho ^2}}}\left( {\frac{{\partial {\rho } }}{{\partial t}} + u\frac{{\partial {\rho } }}{{\partial r}}} \right) + \frac{1}{{{\rho } {r^j}}}\frac{\partial }{{\partial r}}\left( {F{r^j}} \right) = 0, \end{aligned}$$
(2.3)

where, \({\rho }\), u, p, \({U_m}\), F, r, t are the density of mixture, flow velocity, pressure, internal energy per unit mass of the mixture,radiation heat-flux per unit mass, radial distance and time, and j = 1, 2 correspond to the cylindrical and spherical symmetries, respectively.

We consider the medium to be a dusty gas (a mixture of small solid particles and non-ideal gas). The equation of state of the non-ideal gas in the mixture is taken to be [6, 20, 31]

$$\begin{aligned} {p_g} = {R^*}{\overline{\rho } _g}\left( {1 + b{{\overline{\rho }}_g}} \right) T, \end{aligned}$$
(2.4)

where \(R^*\) is the gas constant, \({p_g}\) and \(\overline{\rho }_g\) are the partial pressure and density of the gas in the mixture, T is the temperature of the gas (and of the solid particles as the equilibrium flow condition is maintained), and b the internal volume of the molecules of the gas. In this equation the deviations of an actual gas from the ideal state are taken into account which result from the interaction between its component molecules. It is assumed that the gas is still so rarefied that triple, quadruple, etc. collisions between molecules are negligible, and their interaction is assumed to occur only through binary collisions. The specific volume of solid particles is assumed to remain unchanged by variations in temperature and pressure. Therefore, the equation of state of the solid particle in the mixture is simply

$$\begin{aligned} {\rho _{sp}}={\hbox {constant}}, \end{aligned}$$
(2.5)

where \({\rho _{sp}}\) is the species density of the solid particles. Proceeding on the same lines as Pai [29], we obtain the equation of state of the mixture as

$$\begin{aligned} p = \frac{{\left( {1 - {k_p}} \right) }}{{\left( {1 - z} \right) }}\left[ {1 + b{\rho } \left( {1 - {k_p}} \right) } \right] {\rho } {R^*}T, \end{aligned}$$
(2.6)

where z is the volume fraction of solid particles in the mixture and \({k_p}\) the mass concentration of solid particles.

The relation between \({k_p}\) and z is given by [29]

$$\begin{aligned} {k_p} = \frac{{z{\rho _{sp}}}}{\rho }. \end{aligned}$$
(2.7)

In equilibrium flow, \(k_p\) is constant in whole flow-field. Therefore from (2.7)

$$\begin{aligned} \frac{z}{\rho } =\,{\mathrm{constant}}\,=\,\frac{z_1}{\rho _1}, \end{aligned}$$
(2.7a)

where \({z_1}\) and \({\rho _1}\) are the initial values of z and \({\rho }\), respectively.

The internal energy per unit mass of the mixture may be written as

$$\begin{aligned} {U_m} = \left[ {{k_p}{C_{sp}} + \left( {1 - {k_p}} \right) {C_v}} \right] T = {C_{vm}}T, \end{aligned}$$
(2.8)

where \(C_{sp}\) is the specific heat of the solid particles, \({C_v}\) specific heat of the gas at constant volume and \({C_{vm}}\) the specific heat of the mixture at constant volume.

The specific heat of the mixture at constant pressure is

$$\begin{aligned} {C_{pm}} = {k_p}{C_{sp}} + \left( {1 - {k_p}} \right) {C_p}, \end{aligned}$$
(2.9)

where \({C_p}\) is the specific heat of the gas at constant pressure.

The ratio of the specific heats of the mixture is given by [1, 29]

$$\begin{aligned} \Gamma = \frac{{{C_{pm}}}}{{{C_{vm}}}} = \gamma \frac{{\left( {1 + \frac{{\delta \beta '}}{\gamma }} \right) }}{{\left( {1 + \delta \beta '} \right) }}, \end{aligned}$$
(2.10)

where

$$\begin{aligned} \gamma = \frac{{{C_p}}}{{{C_v}}}, \qquad \delta = \frac{{{k_p}}}{{1 - {k_p}}}\qquad {\mathrm{and}} \qquad \beta ^\prime = \frac{{{C_{sp}}}}{{{C_v}}}. \end{aligned}$$

Now

$$\begin{aligned} {C_{pm}} - {C_{vm}} = \left( {1 - {k_p}} \right) \left( {{C_p} - {C_v}} \right) = \left( {1 - {k_p}} \right) {R^*}, \end{aligned}$$
(2.11)

neglecting the term containing \({b^2}{\rho ^2}\) [20].

The internal energy per unit mass of the mixture is, therefore, given by

$$\begin{aligned} {U_m} = \frac{{p\left( {1 - z} \right) }}{{\rho \left( {\Gamma - 1} \right) \left[ {1 + b{\rho } \left( {1 - {k_p}} \right) } \right] }}. \end{aligned}$$
(2.12)

We consider that a strong shock wave is propagated into the mixture of the non-ideal gas and small solid particles of constant density \(\rho _1\), which is at rest (\({u_1} = 0\)) and with negligibly small counter pressure (\({p_1} \simeq 0\)). We assume the shock surface to be transparent, therefore the radiative heat-flux is continuous across it.

The boundary conditions at the strong shock are as follows [6]

$$\begin{aligned}&{u_2} = \left( {1 - \beta } \right) \dot{R} \end{aligned}$$
(2.13)
$$\begin{aligned}&{\rho _2} = \frac{{{\rho _1}}}{\beta }, \end{aligned}$$
(2.14)
$$\begin{aligned}&{z_2} = \frac{{{z_1}}}{\beta }, \end{aligned}$$
(2.15)
$$\begin{aligned}&{p_2} = \left( {1 - \beta } \right) {\rho _1}\dot{{R^2}} \end{aligned}$$
(2.16)

where \(\beta \) is given by

$$\begin{aligned} \left( {\Gamma + 1} \right) {\beta ^2} + \left[ {\left\{ {\left( {1 - {k_p}} \right) \overline{b} - 1} \right\} \left( {\Gamma - 1} \right) - 2{z_1}} \right] \beta - \overline{b} \left( {\Gamma - 1} \right) \left( {1 - {k_p}} \right) = 0. \end{aligned}$$
(2.17)

Here, R is shock radius, \(\overline{b} = b \rho _1\) is the parameter of non-idealness of the gas in the mixture and dot denotes the differentiation with respect to time t. A quantity with suffix ‘2’ denotes the value of that quantity just behind the shock front.

The relation between \({k_p}\) and \({z_1}\) is given by [32]

$$\begin{aligned} {z_1} = \frac{{{k_p}}}{{{G_1}\left( {1 - {k_p}} \right) + {k_p}}}, \end{aligned}$$
(2.18)

where \({G_1}\) is the ratio of the density of solid particles to the initial density of gas. This shows that \(z_1\) is a constant. Hence, from relation (2.7a), \(\rho _1\) should also be a constant. This is the reason why \(\rho _1\) has already been assumed constant.

The shock radius is assumed to be given by [24]

$$\begin{aligned} \dot{{R^2}} = {A^2}{R^{ - \alpha }}, \end{aligned}$$
(2.19)

where A and \(\alpha \) are constants.

3 Similarity solutions

Let the solution of the problem exist in the following similarity form

$$\begin{aligned}&u = \dot{R} \,\overline{u} \left( x \right) ,\quad \rho = {\rho _1} \overline{\rho } \left( x \right) ,\quad p = {\rho _1}\dot{{R^2}}\, \overline{p} \left( x \right) ,\quad {U_m} = \dot{{R^2}} \, {\overline{U} _m}\left( x \right) ,\nonumber \\&F = {\rho _1}\dot{{R^3}} \overline{F} \left( x \right) ,\quad z = {z_1}\,\overline{\rho } \left( x \right) , \end{aligned}$$
(3.1)

where \(x = \frac{r}{R}\) is a dimensionless quantity.

Using (3.1), the equations of motion (2.1), (2.2) and (2.3) transform into the following form

$$\begin{aligned}&\left( {\overline{u} - x} \right) \frac{{\overline{\rho }^\prime }}{{\overline{\rho }}} = - \left( {\overline{u}^\prime + j\frac{{\overline{u} }}{x}} \right) , \end{aligned}$$
(3.2)
$$\begin{aligned}&\left( {\overline{u} - x} \right) \overline{u}^\prime - \frac{\alpha }{2}\overline{u} = \frac{{\overline{p}^\prime }}{{\overline{\rho }}}, \end{aligned}$$
(3.3)
$$\begin{aligned}&\left( {\overline{u} - x} \right) \overline{U} _m^\prime - \alpha {\overline{U} _m} + \overline{\frac{p}{{\overline{\rho }}}} \left( {\overline{u}^\prime + j\frac{{\overline{u} }}{x}} \right) + \frac{1}{{\overline{\rho } {x^j}}}\frac{d}{{dx}}\left( {{x^j}\overline{F} } \right) =0. \end{aligned}$$
(3.4)

Also, the strong shock conditions (2.11), (2.12) and (2.14) change into the form

$$\begin{aligned} \overline{u} \left( 1 \right)&= \left( {1 - \beta } \right) , \end{aligned}$$
(3.5)
$$\begin{aligned} \overline{z} \left( 1 \right)&= \overline{\rho } \left( 1 \right) = \frac{1}{\beta }, \end{aligned}$$
(3.6)
$$\begin{aligned} \overline{p} \left( 1 \right)&= \left( {1 - \beta } \right) . \end{aligned}$$
(3.7)

We assume the ‘Product Solution’ of the progressive wave given by Mc Vittie [33] in the form

$$\begin{aligned} u&= \frac{{a\left( t \right) }}{t} r, \end{aligned}$$
(3.8)
$$\begin{aligned} \rho&= \left( {\lambda + 1} \right) f\left( t \right) {t^{ - 2\alpha ^\prime }}{\eta ^{\lambda - 2}}, \end{aligned}$$
(3.9)
$$\begin{aligned} p&= \alpha {'^2}f\left( t \right) {t^{ - 2}}b_0 \left( t \right) {\eta ^\lambda }, \end{aligned}$$
(3.10)

where \(\eta = r{t^{ - \alpha }}\) and \(\lambda \) and \(\alpha ^\prime \) are some constants. Also ‘a’ and ‘\(b_0\)’ are some functions of t and are given by

$$\begin{aligned} a\left( t \right)&= \frac{\lambda \alpha ^\prime - t{{f^\prime }} \big / t}{\lambda }, \end{aligned}$$
(3.11)
$$\begin{aligned} b_0\left( t \right)&= \frac{{\lambda + 1}}{{\lambda \alpha ^{\prime 2}}}\left( { - {a^2} + a - ta^\prime } \right) . \end{aligned}$$
(3.12)

It can be easily seen that these equations satisfy the Eqs. (2.1) and (2.2) identically.

After changing this solution to similarity form which requires ‘a’ to be a constant (equal to \(\dfrac{{2\left( {1 - \beta } \right) }}{{\alpha + 2}}\) ), we apply boundary conditions (3.5), (3.6) and (3.7) and finally obtain

$$\begin{aligned} \overline{u} \left( x \right)&= \left( {1 - \beta } \right) x, \end{aligned}$$
(3.13)
$$\begin{aligned} \overline{z} \left( x \right)&= \overline{\rho } \left( x \right) = \frac{1}{\beta }{x^{\lambda - 2}}, \end{aligned}$$
(3.14)
$$\begin{aligned} \overline{p} \left( x \right)&= \left( {1 - \beta } \right) {x^\lambda }. \end{aligned}$$
(3.15)

Using Eq. (2.10) in Eq. (3.4), we get

$$\begin{aligned}&\left( {\overline{u} - x} \right) \left[ {\frac{{\overline{p}^\prime }}{{\overline{p} }} - \frac{{\overline{\rho }^\prime }}{{\overline{\rho } \left( {1 - z} \right) }} - \frac{{\overline{\rho }^\prime \overline{b} \left( {1 - {k_p}} \right) }}{{1 + \overline{b} \overline{\rho } \left( {1 - {k_p}} \right) }}} \right] - \alpha + \left[ {1 + \overline{b} \overline{\rho } \left( {1 - {k_p}} \right) } \right] \times \nonumber \\&\frac{{\left( {\Gamma - 1} \right) }}{{\left( {1 - z} \right) }}\left( {j\frac{{\overline{u} }}{x} + \overline{u}^\prime } \right) + \left[ {1 + \overline{b} \overline{\rho } (1 - {k_p})} \right] \Big ( {\frac{{\Gamma - 1}}{{1 - z}}} \Big )\frac{1}{{\overline{p} {x^j}}}\frac{d}{{dx}}({\overline{F} {x^j}}) = 0. \end{aligned}$$
(3.16)

Using Eqs. (3.13) and (3.15) in (3.2), we obtain

$$\begin{aligned} \lambda = \frac{{\left( {1 + \beta } \right) + \left( {1 - \beta } \right) j}}{\beta }. \end{aligned}$$
(3.17)

Using Eqs. (3.13), (3.14) and (3.15) in equation (3.3), we obtain

$$\begin{aligned} \alpha = 2\left[ {\left( {1 - \beta } \right) j + 1} \right] . \end{aligned}$$
(3.18)

Relations (3.17) and (3.18) are the same as derived in [28].

From Eqs. (3.13), (3.14), (3.15) and (3.16), we obtain

$$\begin{aligned}&\frac{d}{{dx}}\left( {{x^j}\overline{F}} \right) = \frac{{\left( {1 - \beta } \right) \left( {\beta - {z_1}{x^{\lambda - 2}}} \right) }}{{\beta \left( {\Gamma - 1} \right) }}\left[ \left\{ \lambda - \frac{\beta (\lambda - 2)}{\beta - z_1 x^{\lambda - 2}} - \frac{\overline{b} (\lambda - 2)(1 - {k_p} )}{\beta x^{2 - \lambda } + \overline{b} (1 - {k_p})}\right\} \right. \nonumber \\&\qquad \frac{\beta ^2}{\beta + \overline{b} (1 - {k_p})\,x^{\lambda - 2}} + \frac{{\alpha \beta }}{{\beta + \overline{b} \left( {1 - {k_p}} \right) {x^{\lambda - 2}}}} \nonumber \\&\qquad - \left. {\frac{{\beta \left( {1 - \beta } \right) \left( {\Gamma - 1} \right) \left( {j + 1} \right) }}{{\beta - {z_1}{x^{\lambda - 2}}}}} \right] {x^{\lambda + j}}. \end{aligned}$$
(3.19)

We also have the relations

$$\begin{aligned} \frac{u}{{{u_2}}} = \frac{{\overline{u} \left( x \right) }}{{\overline{u} \left( 1 \right) }},\,\,\,\,\,\,\,\,\frac{\rho }{{{{\rho } _2}}} = \frac{{\overline{\rho } \left( x \right) }}{{\overline{\rho } \left( 1 \right) }},\,\,\,\,\,\,\frac{p}{{{p_2}}} = \frac{{\overline{p} \left( x \right) }}{{\overline{p} \left( 1 \right) }},\,\,\,\,\,\,\,\,\frac{F}{{{F_2}}} = \frac{{\overline{F} \left( x \right) }}{{\overline{F} \left( 1 \right) }},\,\,\,\,\,\,\,\,\,\,\frac{z}{{{z_2}}} = \frac{\rho }{{{{\rho } _2}}} \end{aligned}$$

and

$$\begin{aligned} \frac{T}{{{T_2}}} = \left( {\frac{p}{{{p_2}}}} \right) {{\left( {1 - \frac{{{z_1}}}{\beta }\frac{\rho }{{{\rho _2}}}} \right) } \Big /{\left( {1 - \frac{{{z_1}}}{\beta }} \right) }}{{\left[ {\frac{{\beta + \overline{b} \left( {1 - {k_p}} \right) }}{{\beta + \overline{b} \left( {1 - {k_p}} \right) {x^{\lambda - 2}}}}} \right] } \Big / {\left( {\frac{\rho }{{{\rho _2}}}} \right) }}. \end{aligned}$$
(3.20)

Equations (3.13), (3.14), (3.15) and (3.19) give the solution of our problem.

This solution is an example of exact solutions for the flows of mixture of a non-ideal gas and small solid particles corresponding to exact solution in ordinary gas dynamics by Mc Vittie [33] and Sedov [16], in radiation gas dynamics by Ashraf and Sachdev [24], and in the mixture of a perfect gas and small solid particles by Vishwakarma and Vishwakarma [28].

4 Results and discussion

For the density to remain finite at the centre and for the radiation flux not be negative anywhere, we have from Eqs. (3.14) and (3.19),

$$\begin{aligned} \beta < 1, \end{aligned}$$
(4.1)

and

$$\begin{aligned}&\left[ {\left\{ {\lambda - \frac{{\beta \left( {\lambda - 2} \right) }}{{\beta - {z_1}{x^{\lambda - 2}}}} - \frac{{\overline{b} \left( {\lambda - 2} \right) \left( {1 - {k_p}} \right) }}{{\beta {x^{2 - \lambda }} + \overline{b} \left( {1 - {k_p}} \right) }}} \right\} \frac{{{\beta ^2}}}{{\beta + \overline{b} \left( {1 - {k_p}} \right) {x^{\lambda - 2}}}}} \right. \nonumber \\&\qquad \qquad + \frac{{\alpha \beta }}{{\beta + \overline{b} \left( {1 - {k_p}} \right) {x^{\lambda - 2}}}} - \left. {\frac{{\beta \left( {1 - \beta } \right) \left( {\Gamma - 1} \right) \left( {j + 1} \right) }}{{\beta - {z_1}{x^{\lambda - 2}}}}} \right] > 0. \end{aligned}$$
(4.2)

Inequality (4.1) is not only a necessary condition for density to remain finite at the centre, but it must also be satisfied for existence of the shock wave.

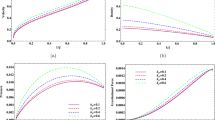
In Figs. 1, 2, 3 and 4, we have plotted the values of \(\dfrac{\rho }{{{\rho _2}}}\left( { = \dfrac{z}{{{z_2}}}}\right) \), \(\dfrac{p}{{{p_2}}},\,\,\dfrac{T}{{{T_2}}}\,\,and\,\,\dfrac{F}{{{F_2}}}\) for [6, 31, 32] \(\gamma = 1.4;\,\overline{b} = 0,\,0.05,\,0.1;\,{k_p} = 0,\,0.2,\,0.4;\,{G_1} = 1,\,100;\,\beta ^\prime = 1\) and \(j = 2\) as \(x = \dfrac{r}{R}\) varies from 0 to 1. Here \(\overline{b} = 0\) corresponds to the case of mixture of a perfect gas and small solid particles [28]; \({k_p} = 0\) to the dust-free case, and j = 2 to the spherical shock.

Fig. 1
figure 1

Variation of density with distance in a region behind the shock front

Full size image
Fig. 2
figure 2

Variation of pressure with distance in a region behind the shock front

Full size image
Fig. 3
figure 3

Variation of temperature with distance in a region behind the shock front

Full size image
Fig. 4
figure 4

Variation of radiation flux with distance in a region behind the shock front

Full size image

Values of \(\dfrac{\rho }{{{\rho _2}}},\,\dfrac{p}{{{p_2}}},\,\dfrac{T}{{{T_2}}}\) are calculated from Eqs. (3.14), (3.15) and (3.20). Values of \(\dfrac{F}{{{F_2}}}\) are obtained by numerical integration of the differential equation (3.19). If \(\overline{b} = 0\) (the case mixture of perfect gas and small solid particles), we can obtain the exact integral of the Eq. (3.19) which gives \(\overline{F} = 0\) at x = 0. Therefore, for the purpose of numerical integration of Eq. (3.19), we start from \(\overline{F} = 0\) at x = 0 and move forward up to x = 1. Actually, since the shock is transparent and the radiative heat transfer equations are not used explicitly, we do not have the value of \(\overline{F}\) at the shock (x = 1) to use as the boundary conditions for the purpose of numerical integration of the differential equation (3.19).

This solution predicts the velocity, the density, the pressure, the temperature and the radiation flux to tend to zero as the centre of symmetry is approached. The values of velocity, density and pressure decrease from highest at the shock to zero at the centre of symmetry. The radiation flux also decreases from highest at the shock to zero at the centre in the cases when the gas is dust-free or when the value of \({G_1}\) (the ratio of density of solid particles to the initial density of gas) is much higher (\({G_1} = 100\)). In the cases where \({G_1} = 1\), the radiation flux at first increases from the shock front, and after attaining a maximum stats to decrease to zero towards the centre. The temperature decreases from highest at the shock to zero at the centre in the cases when the medium is a perfect gas or when it is mixture of a perfect gas and small solid particles with much higher values of \({G_1}\)(=100). In almost all other cases, the temperature at first increases behind the shock and after attaining a maximum decreases to zero at the centre.

Since \(\dfrac{u}{{{u_2}}} = x\), it does not vary with any variation in \({k_p},\,{G_1}\) and \(\overline{b}\).

Effects of an increase in the value of \({k_p}\) are

  1. 1.

    to increase the value of \(\beta \left( ={\rho }_1/{{\rho }_2}\right) \) significantly when \({G_1} = 1\), and to decrease it when \({G_1} = 100\) (Table 1), i.e. to decrease the shock strength significantly when \({G_1} = 1\) and to increase it when \({G_1} = 100\);

  2. 2.

    to increase the density \({\rho /{{{\rho }_2}}}\), the pressure \({p / {{p_2}}}\), and the radiation flux \({F /{{F_2}}}\) at any point in the flow-field behind the shock when \({G_1} = 1\) and to decrease these flow variables when \({G_1} = 100\); and

  3. 3.

    to increase the temperature \({T /{{T_2}}}\) at any point in the flow-field behind the shock.

Thus, the effects of an increase in \({k_p}\) are significant when \({G_1} = 1\). Actually, when \({G_1} = 1\), the volume fraction of solid particle in the initial medium \({z_1}\) is equal to \({k_p}\) and when \({k_p}\) is increased from 0.2 to 0.4, \({z_1}\) also increases from 0.2 to 0.4, on the other hand when \({G_1} = 100\), the corresponding increase in \({z_1}\) is very small. This fact causes the above significant effects on the shock strength and on the flow variables, when \({G_1} = 1\).

Table 1 Variation of the density ratio \(\beta \) across the shock-front for different values of \({k_p}\) and \(\overline{b}\) with \(\beta ^\prime = 1\) and \(\gamma = 1.4\) (cases of \(\overline{b} = 0\) are the results of [28])
Full size table

Effects of an increase in the value of \({G_1}\) from 1 to 100 are

  1. 1.

    to increase the shock strength (to decrease the value of \(\beta \) (Table 1);

  2. 2.

    to decrease the flow variables \({{\rho } /{{{\rho }_2}} },\,{p /{{p_2}}},\,{T /{{T_2}}}\) and \({F /{{F_2}}}\) at any point in the flow-field behind the shock. When \({G_1} = 100\) and \({k_p}\) is higher (=0.4), the profiles of these flow-variables become closer to the corresponding profiles in the dust-free case;

  3. 3.

    to decrease the tendency of maxima formation in the profiles of temperature \({T /{{T_2}}}\) and radiation flux \({F /{{F_2}}}\). This shows that when \({G_1} = 100\) the transport of energy by radiation is faster in comparison to that when \({G_1} = 1\), causing the removal of maxima formation in the profiles of temperature and radiation. Actually, when \({G_1} = 1\) the volume occupied by solid particles in the mixture is much higher which prevents the faster transport of energy.

Effects of an increase in the value of \(\overline{b}\) are

  1. 1.

    to decrease the shock strength (to increase the value of \(\beta \));

  2. 2.

    to increase the flow variables \({{\rho } /{{{\rho }_2}}}\) and \({p /{{p_2}}}\) at any point in the flow-field behind the shock front (see Figs. 1, 2);

  3. 3.

    to increase the flow variables \({T /{{T_2}}}\) and \({F /{{F_2}}}\) at any point in the flow-field behind the shock front except for near the shock front in the case of \({G_1} = 1\).

These effects are significant when \({G_1}\) is much larger (\({G_1} = 100\)) in the dusty gas or when the gas is dust-free. This show that the effects of non-idealness of the gas on the shock propagation is reduced due to presence of dust particles.

5 Conclusion

The present work investigates the self-similar solution for the flow behind a strong shock wave propagating in a mixture of a non-ideal gas and small solid particles with radiation heat-flux. On the basis of this work, one may draw the following conclusions:

  1. 1.

    An increase in mass concentration of solid particle in the mixture \({k_p}\), increases the volume fraction of solid particles significantly when \({G_1} = 1\). This increase in volume fraction of solid particle results in significant decrease of the shock strength and significant change in profiles of flow variables in the flow-field behind the shock.

  2. 2.

    When \({G_1} = 100\) and \({k_p}\) is higher, the profiles of the flow-variables in the flow-field behind the shock become closer to the corresponding profiles in the dust-free case.

  3. 3.

    An increase in the value of \({G_1}\) reduces the tendency of maxima formation in the profiles of temperature and radiation flux. In fact, for higher values of \({G_1}\) (i.e. for lower volume fraction of solid particles) the transport of energy by radiation is faster which causes the above behavior of temperature and radiation flux profiles.

  4. 4.

    The effects of the non-idealness of the gas on the shock strength and on the flow-profiles in the flow-field behind the shock are reduced by the presence of solid particles in the gas.