1 Introduction

Shock phenomena, such as a global shock resulting from a stellar pulsation or supernova explosion passing outward through a stellar envelope or perhaps a shock emanating from a point source such as a man-made explosion in the Earth’s atmosphere or an impulsive flare in the Sun’s atmosphere, have tremendous importance in astrophysics and space science. Shocks are ubiquitous throughout the observed universe and are thought to play a crucial role in the transportation of energy into the interstellar medium, setting in motion processes observed in nebulae that eventually could lead to the creation of new stars. Shock waves produced by solar flares represent, in a very real sense, the most extreme (one might even say the most pathological) manifestation of solar activity which occurs in the study of solar-terrestrial physics. It is now generally accepted that more than half of the energy released in small or large flares is distributed by shock waves. A shock driven by any amount of flare ejecta would be classified as a piston driven shock with a radially dependent shock velocity (\(W_{s} = (n + 1)\frac{r_{s}}{t}\)) quite unlike that of blast produced shock (see Dryer 1958). Radiation is key to this since it plays a significant role in energy transport over the vast distances encountered between stellar objects, and can significantly modify the dynamics of a shock or blast wave. Consequently the study of radiative shocks has been an active area of numerical, theoretical and experimental research over many years. The influence of radiation on the shock wave and on the flow-field behind it have been studied by similarity method by Marshak (1958), Elliott (1960), Wang (1964), Helliwell (1969), Nicastro (1970), Ghoniem et al. (1982), Gretler and Regenfelder (2005), Vishwakarma and Nath (2010, 2012a), Vishwakarma and Singh (2009), Nath (2012a), Nath and Vishwakarma (2014) and many others.

Marshak (1958) studied the effect of radiation on the shock propagation by introducing the radiation diffusion approximation. Using the same mode of radiation Elliott (1960) discussed the conditions leading to self-similarity with a specified functional form of the mean free-path of radiation and obtained a solution for self-similar spherical explosions. Wang (1964), Helliwell (1969) and Nicastro (1970) treated the problems of radiating walls, either stationary or moving, generating shocks at the head of self-similar flow-fields. The non-similar problem of a blast wave associated with diffusive radiation was analyzed by Kim et al. (1975), using matched expansions upon the assumption that the radiation and conduction effects are significant only in a boundary-layer around the centre of explosion. A similar approach was also used by Kamel et al. (1977) to find self-similar solutions for blast waves in a detonating medium. Gretler and Wehle (1993) studied the propagation of blast waves with exponential heat release by taking internal heat conduction and thermal radiation in a detonating medium. Ghoneim et al. (1982) obtained a self-similar solution for spherical explosions taking into account the effects of both conduction and radiation in the two limits of Rosseland radiative diffusion and Plank radiative emission. Abdel-Raouf and Gretler (1991) obtained a non-similar solution for blast waves with internal heat transfer effects. Also, Vishwakarma and Nath (2011) studied the cylindrical shock wave generated by a piston moving in a non-uniform self-gravitating rotational axisymmetric gas in the presence of conduction and radiation heat flux.

The study of shock waves in a mixture of a gas and small solid particles is of great importance due to its applications to nozzle flow, lunar ash flow, bomb blast, coal-mine blast, under-ground, volcanic and cosmic explosions, metallized propellant rocket, supersonic flight in polluted air, collision of coma with a planet, description of star formation, particle acceleration in shocks, formation of dusty crystals and many other engineering problems (see Pai et al. 1980; Higashino and Suzuki 1980; Miura and Glass 1983; Gretler and Regenfelder 2005; Popel and Gisko 2006; Vishwakarma and Nath 2006, 2009, 2010, 2012a; Igra et al. 2004; Sommerfeld 1985; Conforto 2000; Elperine et al. 1987; Miura 1990; Vishwakarma et al. 2008; Nath 2010, 2012b, 2013, 2014). The flow field, that develops when a moving shock wave hits a two-phase medium of gas and particles, has a close practical relation to industrial applications (solid rocket engine in which aluminum particles are used to reduce the vibration due to instability) as well as industrial accidents such as explosions in coalmines and grain elevators (Park and Baek 2003). Shock waves often arise in nature because of a balance between non-linear wave breaking and wave damping dissipative forces (Zel’dovich and Raizer 1967). Collisional and collisionless shock waves can appear because of friction between the particles and wave-particle interaction respectively (Sagdeev 1966; Chen 1974). Miura and Glass (1985) obtained an analytical solution of a planar dusty gas flow with constant velocities of the shock and the piston moving behind it. As they considered that the dust virtually has a mass fraction but no volume fraction. Their results reflect the influence of both the decrease of mixture compressibility and the increase of mixture’s inertia on the shock propagation (Steiner and Hirschler 2002; Vishwakarma et al. 2008; Gretler and Regenfelder 2002, 2008). Vishwakarma and Nath (2006, 2009, 2010, 2012a), Gretler and Regenfelder (2005) obtained the similarity solution for strong shock waves in radiating and non-radiating dusty gas (a mixture of small solid particles and non-ideal or perfect gas).

In extreme conditions that prevail in most of the problems associated with shock waves, the assumption that the gas is ideal is no longer valid. In recent years, several studied have been performed concerning the problem of shock waves in non-ideal gases, in particular, by Anisimov and Spiner (1972), Ranga Rao and Purohit (1976), Wu and Roberts (1993), Madhumita and Sharma (2004), Arora and Sharma (2006), Vishwakarma and Nath (2007, 2009, 2010, 2012a), Nath (2012a, 2012b, 2012c, 2013), Nath and Vishwakarma (2014), Singh et al. (2010a, 2010b), Ojha and Tiwari (2002) and Roberts and Wu (1996) among others. Anisimov and Spiner (1972) have taken the equation of state for non-ideal gases in a simplified form, and investigated the effect of the parameter for non-idealness on the problem of a strong point explosion, which describe the behavior of the medium satisfactorily at low densities. Vishwakarma and Nath (2009) obtained the similarity solution for the propagation of a strong shock wave in a mixture of a non-ideal gas and small solid particles driven out by a piston moving according to power law, in both the cases when the flow behind the shock was isothermal or adiabatic. Ranga Rao and Purohit (1976) have analyzed the self-similar flows of a non-ideal gas driven by an expanding gas.

In all of the works mentioned above, the influence of gravitational field on the medium is not considered. The gravitational force has considerable effect on many astrophysical problems. Carrus et al. (1951) have studied the propagation of shock waves in a gas under the gravitational attraction of a central body of fixed mass (Roche model) and obtained the similarity solutions by numerical method. Rogers (1957) discussed a method for obtaining analytical solution of the same problem. Ojha et al. (1998) have discussed the dynamical behavior of an unsteady magnetic star by employing the concepts of the Roche model in an electrically conducting atmosphere. Singh (1988) studied the self-similar flow of a non-conducting perfect gas, moving under the gravitational attraction of a central body of fixed mass, behind spherical shock waves driven out by a propelling contact surface into quite solar wind region. Vishwakarma and Nath (2012b) obtained the similarity solutions by taking the shock Mach number not infinite, but finite and the medium under the gravitational attraction towards the heavy nucleus at the centre, and obtained the solutions in both the isothermal and adiabatic cases, we presented the solutions for the flow taken to be adiabatic.

In the present work, we have obtained the self-similar solutions for the flow behind the spherical shock wave propagating in a dusty gas (a mixture of non-ideal gas and small solid particles) with conductive and radiative heat fluxes. The medium is assumed to be under the influence of a gravitational field due to central mass (\(\bar{m}\)) at the origin (Roche model). The gravitational effect of the mixture itself is assumed to be negligible in comparison with the attraction of the central mass. In order to get some essential features of the shock propagation, small solid particles are considered as a pseudo-fluid, and the mixture at a velocity and temperature equilibrium with a constant ratio of specific heats (Pai 1977). For this gas particle mixture to be treated as a so-called idealized equilibrium gas (Geng and Groenig 1980), it is necessary to consider the particle diameter much smaller than a characteristic length of the flow-field. In this case, we may assume that the viscous stress of the mixture is negligible (but not the heat conduction of the medium). In spite of the fact that the viscosity and heat conduction have the same physical mechanism, the viscosity term are negligible and may be dropped from the momentum and energy equations based on order of magnitude analysis applied to the conservation equations (Kamel et al. 1977 have shown that the inclusion of viscosity changes the flow-field parameters only by order of 0.001 %). The heat transfer fluxes are expressed in terms of Fourier’s law for heat conduction and a diffusion radiation model for an optically thick grey dusty gas, which is typical of large-scale explosions. The thermal conductivity and absorption coefficient of the gas are assumed to be proportional to appropriate powers of temperature and density (Ghoneim et al. 1982; Vishwakarma et al. 2008). Also, it is assumed that the dusty gas is grey and opaque, and the shock is isothermal. The assumption that the shock is isothermal is a result of some physical process in which the heat flux is taken to be proportional to the temperature gradient; this excludes the possibility of temperature jumps (Zel’dovich and Raizer 1967; Rosenau and Frankenthal 1976, 1978; Vishwakarma et al. 2008; Vishwakarma and Nath 2010, 2012a; Nath and Vishwakarma 2014; Nath 2012a).

In our model radiative losses are not considered though radiative transfer is taken into account because the radiative losses from the shock surface are small in comparison to the variation of the total energy of the disturbance (see (67)). Due to increase in total energy of the disturbance a radiative-precursor shock may occur when the flux of ionizing photons being radiated forward from the shock front exceeds the flux of atoms approaching the shock front. This requires that the shock velocity should exceed the threshold velocity required to produce the necessary photon flux. The radiative-precursor heats the medium ahead of the density discontinuity to a temperature approximately equal to the temperature at the forward shock front (Keiter et al. 2002). Radiative-precursor shocks are relevant to astrophysics, for example in supernova, supernova remnants and jets (Ensman et al. 1992; Sutherland et al. 1993; Feinstein et al. 1999; Raga et al. 1999; Ghavamian et al. 2000; Reipurth and Bally 2001). The consideration of the effects of conductive and radiative heat fluxes provided that there holds a simple relationship between certain exponents in the expressions for the piston speed, the thermal conductivity and the absorption coefficient, all of which supposed to be non-uniform. The particular forms chosen for these are stated explicitly as (39) and (20), respectively. The counter pressure (the pressure ahead of the shock) is taken into account. The radiation pressure and radiation energy are neglected (Elliott 1960; Wang 1964; Ghoneim et al. 1982; Vishwakarma and Nath 2010, 2012a; Nath and Vishwakarma 2014; Nath 2012a). The assumption of an optically thick grey gas is physically consistent with the neglected radiation pressure and radiation energy (Nicastro 1970). In order to obtain the similarity solutions of the problem the density of the undisturbed medium is taken to be constant. The effects of a change in the value of the parameter of non-idealness of the gas in the mixture \(\bar{b}\), the mass concentration of solid particles in the mixture \(K_{p}\), the ratio of the density of solid particles to the initial density of the gas \(G_{1}\) and the gravitational parameter \(G_{0}\) are obtained.

2 Fundamental equations and boundary conditions

We consider the medium to be a dusty gas (a mixture of small solid particles and non-ideal gas), which is under the gravitational attraction of central mass (\(\bar{m}\)) at the center. The equation of state of the non-ideal gas in the mixture is taken to be (Anisimov and Spiner 1972; Vishwakarma and Nath 2007; Nath 2012b)

$$ p_{g} = R^{*} \rho_{g} ( 1+b \rho_{g} ) T, $$
(1)

where \(p_{g}\) and \(\rho_{g}\) are the pressure and density of the gas occupying the volume \(V_{g}\), \(T\) is the temperature of the gas (and of the solid particles as the equilibrium flow condition is maintained), \(R^{*}\) is the specific gas constant and ‘\(b\)’ is the internal volume of the molecule of the gas. In this equation the deviation of an actual gas from the ideal state is taken into account, which results from the interaction between its component molecules. It is assumed that the gas is still so rarefied that triple, quadruple, etc., collisions between molecules are negligible, and their interaction is assumed to occur only through binary collisions.

The specific volume of solid particles is assumed to remain unchanged by variations in temperature and pressure. Therefore the equation of state of the solid particles in the mixture is, simply,

$$ \rho_{sp} = \mbox{constant}, $$
(2)

where \(\rho_{sp}\) is the specific density of the solid particles. As for any field in a mixture the gas take the \((1-Z)\)th a part of the area, and the \(Z\)th part is occupied with the particles not brining the contribution to the pressure \(p\). Therefore \(p=(1-Z) p_{g}\), we obtain the equation of state of mixture as (Nath 2012b)

$$ p= \frac{ ( 1- K_{p} )}{ ( 1-Z )} \bigl[ ( 1-Z ) +b\rho ( 1- K_{p} ) \bigr] \rho R^{*} T, $$
(3)

where \(p\) and \(\rho\) are the pressure and density of the mixture, \(Z= \frac{V_{sp}}{V}\) is the volume fraction and \(K_{p} = ( \frac{m_{sp}}{ m} )\) is the mass fraction (concentration) of the solid particles in the mixture, where \(m_{sp}\) and \(V_{sp}\) are total mass and the volumetric extensions of the solid particles and \(V\) and \(m\) are the total volume and total mass of the mixture.

The relation between \(K_{p}\) and \(Z\) is given by Pai (1977)

$$ K_{p} = \frac{Z \rho_{sp}}{\rho}. $$
(4)

In the equilibrium flow, \(K_{p}\) is a constant in the whole flow-field. Therefore from (4)

$$ \frac{Z}{\rho} = \mbox{constant}. $$
(5)

Also, we have the relation (Pai 1977)

$$ Z= \frac{K_{p}}{ ( 1- K_{p} ) G+ K_{p}}, $$
(6)

where \(G = \frac{\rho_{sp}}{\rho_{g}}\) is the ratio of the density of the solid particles to the species density of the gas.

The internal energy per unit mass of the mixture may be written as

$$ e_{m} = \bigl( K_{p} C_{sp} + ( 1- K_{p} ) C_{v} \bigr) T= C_{v_{m}} T, $$
(7)

where \(C_{sp}\) is the specific heat of the solid particles, \(C_{v}\) is the specific heat of the gas at constant volume and \(C_{vm}\) is the specific heat of the mixture at the constant volume.

The specific heat of the mixture at constant pressure is

$$ C_{pm} = K_{p} C_{sp} + ( 1- K_{p} ) C_{p}, $$
(8)

where \(C_{p}\) is the specific heat of the gas at constant pressure.

The enthalpy of the mixture per unit mass is

$$ H_{m} = e_{m} + \frac{p}{\rho}. $$
(9)

The ratio of the specific heat of the mixture is given by Pai (1977), Marble (1970)

$$ \varGamma = \frac{C_{pm}}{C_{vm}} = \gamma \frac{1+ \delta {\alpha} / {\gamma}}{1+ \delta \alpha}, $$
(10)

where \(\gamma = \frac{C_{p}}{C_{v}}\), \(\delta = \frac{K_{p}}{ ( 1 - K_{p} )}\) and \(\alpha = \frac{C_{sp}}{C_{v}}\).

Now,

$$ C_{pm} - C_{vm} = ( 1 - K_{p} ) ( C_{p} - C_{v} ) = ( 1 - K_{p} ) R^{*}, $$
(11)

after neglecting the term containing \(b^{2} \rho^{2}\) (Anisimov and Spiner 1972; Vishwakarma and Nath 2007; Nath 2012b). The internal energy and enthalpy per unit mass of the mixture are, therefore, given by

$$ e_{m} = \frac{p (1 - Z )}{ ( \varGamma - 1 ) \rho [ ( 1 - Z ) + b\rho ( 1 - K_{p} ) ]}, $$
(12)

and

$$\begin{aligned} H_{m} &= \biggl[ C_{pm} + \frac{b\rho ( 1 - K_{p} )^{2}}{ ( 1 - Z )} R^{*} \biggr] T \\ & = \frac{p [ ( 1 - Z ) \varGamma + ( \varGamma - 1 ) b\rho ( 1 - K_{p} ) ]}{ ( \varGamma - 1 ) \rho [ ( 1 - Z ) + b\rho ( 1 - K_{p} ) ]}. \end{aligned}$$
(13)

For \(b=0\), the state equation(3), the internal energy equation (12) and enthalpy equation (13) are identical to the state equation, the internal energy equation and the enthalpy equation of the perfect gas with a gas constant \(( 1 - K_{p} ) R^{*}\) and with the ratio of heat capacities (the adiabatic exponent) \(\varGamma\). This fact is for one velocity and one temperature mixture of the perfect gas with heterogeneous particles.

The fundamental equations governing the unsteady, adiabatic spherically symmetric flow of the mixture of a non-ideal gas and small particles in presence of a gravitational field with heat conduction and radiation heat flux taken into account may be expressed in Eulerian coordinates as (cf. Ghoneim et al. 1982; Vishwakarma et al. 2008; Vishwakarma and Nath 2010, 2012a; Rogers 1957; Carrus et al. 1951; Gretler and Wehle 1993; Steiner et al. 1998; Gretler and Regenfelder 2008)

$$\begin{aligned} &\frac{\partial\rho}{\partial t} + u \frac{\partial\rho}{\partial r} + \rho \frac{\partial u}{\partial r} + \frac{2 \rho u}{r} =0, \end{aligned}$$
(14)
$$\begin{aligned} & \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial r} + \frac{1}{\rho} \frac{\partial p}{\partial r} + \frac{\bar{m} \bar{G}}{r^{2}} =0, \end{aligned}$$
(15)
$$\begin{aligned} &\frac{\partial e_{m}}{\partial t} + u \frac{\partial e_{m}}{\partial r} - \frac{p}{\rho^{2}} \biggl( \frac{\partial\rho}{\partial t} + u \frac{\partial\rho}{\partial r} \biggr) + \frac{1}{r^{2} \rho} \frac{\partial}{\partial r} \bigl( r^{2} q \bigr) =0, \end{aligned}$$
(16)

where \(r\) is the radial distance and \(t\) is the time, \(u\) is the fluid velocity, \(\bar{m}\) is the mass of the heavy nucleus at the center, \(\bar{G}\) is the gravitational constant and \(q\) is the total heat flux.

The total heat flux \(q\), which appear in the energy equation may be decomposed as

$$ q = q_{c} + q_{R}, $$
(17)

where \(q_{c} = \mbox{conductive}\) heat flux and \(q_{R}= \mbox{radiative}\) heat flux.

According to Fourier’s law of heat conduction

$$ q_{c} = - K \frac{\partial T}{\partial r}, $$
(18)

where \(K\) is the coefficient of thermal conductivity of the gas and \(T\) is the absolute temperature of the medium. It is important to remember that this expression for the conduction heat flux can only be considered valid for a plasma state near local thermodynamic equilibrium. Variations over space and time must be greater than local mean-free-paths and mean-free-times (Moses and Duderstadt 1977).

Assuming local thermodynamic equilibrium and using the radiative diffusion model for an optically thick grey gas (Pomraning 1973), which is typical for large-scale explosion, the radiative heat flux \(q_{R}\) may be obtained from the differential approximation of the radiation transport equation in the diffusion limit as

$$ q_{R} = - \frac{4}{3} \biggl( \frac{\sigma}{\alpha_{R}} \biggr) \frac{\partial T^{4}}{\partial r}, $$
(19)

where \(\sigma\) is the Stefan-Boltzman constant and \(\alpha_{R}\) is the Rosseland mean absorption coefficient.

The thermal conductivity \(K\) and absorption coefficient \(\alpha_{R}\) of the medium are assumed to vary with temperature and density. These can be written in the form of power law, namely (Ghoneim et al. 1982; Vishwakarma et al. 2008; Vishwakarma and Nath 2010, 2012a)

$$ K = K_{0} \biggl( \frac{T}{T_{0}} \biggr)^{\beta_{c}} \biggl( \frac{\rho}{ \rho_{0}} \biggr)^{\delta_{c}},\qquad \alpha_{R} = \alpha_{R 0} \biggl( \frac{T}{T_{0}} \biggr)^{\beta_{R}} \biggl( \frac{\rho}{\rho_{0}} \biggr)^{\delta_{R}}, $$
(20)

where the subscript 0 denotes a reference state. In the above equations the exponents and the constants \(K_{0}\), \(\alpha_{R_{0}}\) are to be determined from gas-property data within the appropriate temperature range; if a self-similar solution is sought they must also satisfy the similarity requirements. The above equation (20) is a consequence of data concerning optical properties.

We assume that a spherical shock wave is propagating outwards from the centre of symmetry in the undisturbed medium (mixture of non-ideal gas and small solid particles) with constant density, under the gravitational force. The flow variables immediately ahead of the shock front are

$$\begin{aligned} &u =0, \end{aligned}$$
(21)
$$\begin{aligned} &\rho = \rho_{1} = \mbox{constant}, \end{aligned}$$
(22)
$$\begin{aligned} &p = p_{1} = \frac{\rho_{1} \bar{m} \bar{G}}{ r_{s}}, \end{aligned}$$
(23)
$$\begin{aligned} &q = q_{1} =0 \quad \mbox{(Laumbach and Probstein 1970)}, \end{aligned}$$
(24)

where \(r_{s}\) is the shock radius, and the subscript ‘1’ denotes the conditions immediately ahead of the shock.

The expression for the initial volume fraction of the solid particles \(Z_{1}\) is given by, from (6),

$$ Z_{1} = \frac{V_{sp}}{V_{1}} = \frac{K_{p}}{ ( 1 - K_{p} ) G_{1} + K_{p}}, $$
(25)

where \(G_{1} = \frac{\rho_{sp}}{\rho_{g_{1}}}\) is the ratio of the species density of the solid particles to the initial species density of the gas \(\rho_{g_{1}}\) in the mixture.

The shock is assumed to be isothermal (the formation of an isothermal shock is a result of some physical process in which the flux is taken to be proportional to the temperature gradient. This exclude the possibility of a temperature jump, see for example Zel’dovich and Raizer (1967), Rosenau and Frankenthal (1976, 1978), Vishwakarma et al. (2008); Vishwakarma and Nath (2010, 2012a)) and hence, the boundary conditions across it are

$$\begin{aligned} &\rho_{2} ( W_{s} - u_{2} ) = \rho_{1} W_{s} = m_{s} (\mathrm{say}), \end{aligned}$$
(26)
$$\begin{aligned} &p_{2} + \rho_{2} ( W_{s} - u_{2} )^{2} = p_{1} + \rho_{1} W_{s}^{2}, \end{aligned}$$
(27)
$$\begin{aligned} &e_{m_{2}} + \frac{p_{2}}{\rho_{2}} + \frac{1}{2} ( W_{s} - u_{2} )^{2} - \frac{q_{2}}{\rho_{1} W_{S}} = e_{m_{1}} + \frac{p_{1}}{ \rho_{1}} + \frac{1}{2} W_{s}^{2}, \end{aligned}$$
(28)
$$\begin{aligned} &\frac{Z_{2}}{\rho_{2}} = \frac{Z_{1}}{\rho_{1}}, \end{aligned}$$
(29)
$$\begin{aligned} &T_{2} = T_{1}, \end{aligned}$$
(30)

where the subscript ‘2’ denotes the condition immediately behind the shock front and \(W_{S} = \frac{d r_{s}}{dt}\) denotes the velocity of the shock front. From (26)–(30), we obtain

$$\begin{aligned} &u_{2} = ( 1 - \beta ) W_{s}, \end{aligned}$$
(31)
$$\begin{aligned} & \rho_{2} = \frac{\rho_{1}}{\beta}, \end{aligned}$$
(32)
$$\begin{aligned} &p_{2} = \biggl[ ( 1 - \beta ) + \frac{1}{\gamma M^{2}} \biggr] \rho_{1} W_{s}^{2}, \end{aligned}$$
(33)
$$\begin{aligned} & \begin{aligned}[b] q_{2} &= ( 1 - \beta ) \biggl[ \frac{\bar{b} ( 1 - K_{p} )}{\gamma M^{2} [ ( 1 - Z_{1} ) + \bar{b} ( 1 - K_{p} ) ]}\\ &\quad {} - \frac{1}{2} ( 1+ \beta ) \biggr] \rho_{1} W_{s}^{3}, \end{aligned} \end{aligned}$$
(34)
$$\begin{aligned} &Z_{2} = \frac{Z_{1}}{\beta}, \end{aligned}$$
(35)

where \(M = ( \frac{\rho_{1} W_{s}^{2}}{\gamma p_{1}} )^{\frac{1}{2}}\) is the shock-Mach number referred to the frozen speed of sound \(( \frac{\gamma p_{1}}{\rho_{1}} )^{\frac{1}{2}}\) in the dust free perfect gas. Also, the relation between shock Mach number \(M\) and the effective shock-Mach number \(M_{e}\) referred to the speed of sound

$$\begin{aligned} a_{1} = \biggl( \frac{ [ \varGamma ( 1 - Z_{1} )^{2} + b \rho_{1} ( 1 - K_{p} ) \{ 2 \varGamma ( 1 - Z_{1} ) + Z_{1} \} ] p_{1}}{\rho_{1} ( 1 - Z_{1} ) [ ( 1 - Z_{1} ) + b \rho_{1} ( 1 - K_{p} ) ]} \biggr)^{\frac{1}{2}} , \end{aligned}$$

in the mixture is

$$ M_{e}^{2} = \frac{ ( 1 - Z_{1} ) [ ( 1 - Z_{1} ) + b \rho_{1} ( 1 - K_{p} ) ] \gamma M^{2}}{ [ \varGamma ( 1 - Z_{1} )^{2} + b \rho_{1} ( 1 - K_{p} ) \{ 2 \varGamma ( 1 - Z_{1} ) + Z_{1} \} ]}, $$
(36)

where \(M_{e}^{2}\) is defined as

$$\begin{aligned} M_{e}^{2} &= \frac{W_{s}^{2}}{a_{1}^{2}} \\ &= \frac{ ( 1 - Z_{1} ) \rho_{1} W_{S}^{2} [ ( 1 - Z_{1} ) + b \rho_{1} ( 1 - K_{p} ) ]}{ [ \varGamma ( 1 - Z_{1} )^{2} + b \rho_{1} ( 1 - K_{p} ) \{ 2 \varGamma ( 1 - Z_{1} ) + Z_{1} \} ] p_{1}}, \end{aligned}$$
(37)

and, the density ratio \(\beta (0< \beta <1)\) across the shock is obtained by the cubic equation

$$\begin{aligned} &\beta^{3} - \beta^{2} \biggl( \frac{1}{\gamma M^{2}} +1+ Z_{1} \biggr) \\ &\quad {}+ \beta \biggl[ Z_{1} \biggl( \frac{1}{\gamma M^{2}} +1 \biggr) + \frac{ ( 1 - Z_{1} )}{\gamma M^{2} [ ( 1 - Z_{1} ) + \bar{b} ( 1 - K_{p} ) ]} \biggr] \\ &\quad {}+ \frac{ ( 1 - Z_{1} ) [ - Z_{1} + \bar{b} ( 1 - K_{p} ) ]}{\gamma M^{2} [ ( 1 - Z_{1} ) + \bar{b} ( 1 - K_{p} ) ]} =0, \end{aligned}$$
(38)

where \(\bar{b} = b \rho_{1}\). For all values of the parameters \(\gamma\), \(\bar{b}\), \(K_{p}\), \(M^{2}\), \(G_{1}\), \(\alpha\) within physical limit, (38) gives three different values of \(\beta\) out of which only one lies in the required range \(0< \beta <1\) satisfying the physical condition of the problem.

3 Self-similarity transformations

The inner boundary of the flow-field behind the shock is assumed to be an expanding piston. In frame work of self-similarity (Sedov 1982) the velocity \(W_{p} = \frac{d r_{p}}{dt}\) of the piston is assumed to obey a power law which results in Nath (2012b)

$$ W_{p} = \frac{d r_{p}}{dt} = V_{0} t^{n}, $$
(39)

where \(r_{p}\) is the radius of the piston, \(V_{0}\) is the dimensional constant and \(n\) is a constant. The consideration of ambient pressure \(p_{1}\) sets a value of \(n\) as \(n = - \frac{1}{3}\) (see (43)). Thus the piston velocity jumps, almost instantaneously, from zero to infinity leading to the formation of shock of high strength in the initial phase. The piston is then decelerated. To justify the introduction of the form (39) for piston speed it may be observed that, in non-radiative hypersonic flow theory with slender bodies possessing power law profiles, the flow in the shocked layer is given by the solution of analogous unsteady piston problems with the stated piston speed. It is thus natural to take the same form for the corresponding radiative piston problems (following Wang 1964 and Helliwell 1969). Concerning the shock boundary conditions, self-similarity require that the velocity of the shock \(W_{s}\) is proportional to the velocity of the piston, that is

$$ W_{s} = \frac{d r_{s}}{dt} = C V_{0} t^{n}, $$
(40)

where ‘\(C \)’ is a dimensionless constant. Using (40), the time and space coordinates can be change into a dimensionless self-similarity variable \(\eta\) as follows

$$ \eta = \frac{r}{r_{s}} = \frac{ ( n +1 ) r}{C V_{0} t^{n +1}}. $$
(41)

Evidently, \(\eta = \eta_{p} = \frac{r_{p}}{r_{s}}\) at the piston and \(\eta =1\) at the shock. To obtain the similarity solutions, we write the unknown variables in the following form (Vishwakarma and Nath 2010, 2012a; Zel’dovich and Raizer 1967)

$$ \begin{aligned}[c] &u = W_{s} U ( \eta ),\qquad \rho = \rho_{1} D ( \eta ), \qquad p = \rho_{1} W_{s}^{2} P ( \eta ), \\ &Z = Z_{1} D ( \eta ), \qquad q = \rho_{1} W_{s}^{3} Q ( \eta ), \end{aligned} $$
(42)

where \(U\), \(D\), \(P\) and \(Q\) are functions of \(\eta\) only.

For the existence of similarity solution, \(M_{e}\) should be a constant, therefore

$$ n = - \frac{1}{3}. $$
(43)

Thus

$$\begin{aligned} M_{e}^{2} &= ( 1 - Z_{1} ) \bigl[ ( 1 - Z_{1} ) + b \rho_{1} ( 1 - K_{p} ) \bigr] \\ &\quad{}\times \bigl\{ G_{0} \bigl[ \varGamma ( 1 - Z_{1} )^{2} + b \rho_{1} ( 1 - K_{p} ) \\ &\quad{}\times \bigl\{ 2 \varGamma ( 1 - Z_{1} ) + Z_{1} \bigr\} \bigr] ( n +1)\bigr\} ^{-1} \\ &= \mbox{constant}, \end{aligned}$$
(44)

where \(G_{0} = ( \frac{\bar{m} \bar{G}}{C^{3} V_{0}^{3}} )\) is the gravitational parameter. Equation (44) shows that the solutions of the present problem cannot be reduced to the non-gravitational case (i.e. the case in which \(G_{0} =0\)).

The conservation equations (14)–(16) can be transformed into a system of ordinary differential equations with respect to \(\eta\)

$$\begin{aligned} &( U - \eta ) \frac{dD}{d\eta} + D \frac{dU}{d\eta} + \frac{2 DU}{\eta} =0, \end{aligned}$$
(45)
$$\begin{aligned} &( U - \eta ) \frac{dU}{d\eta} + \frac{1}{D} \frac{dP}{d\eta} + \biggl( \frac{n}{n +1} \biggr) U + \frac{ ( n +1 ) G_{0}}{ \eta^{2}} =0, \end{aligned}$$
(46)
$$\begin{aligned} &\frac{dP}{d\eta} + J \frac{dD}{d\eta} + S \frac{dQ}{d\eta} + \frac{P}{ ( U - \eta )} + \frac{2 QS}{\eta} =0, \end{aligned}$$
(47)

where

$$\begin{aligned} J &= J ( \eta )\\ & = \bigl\{ \bar{b}^{2} D^{2} ( 1 - K_{p} ) \bigl[ - Z_{1} + \bar{b} ( 1 - K_{p} ) \bigr] \\ &\quad {}- \varGamma \bigl[ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) \bigr]^{2} \bigr\} P\\ &\quad {}\times \bigl\{ D ( 1 - Z_{1} D ) \bigl[ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) \bigr]\bigr\} ^{-1} \end{aligned}$$

and

$$S = S ( \eta ) = \frac{ ( \varGamma - 1 ) [ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) ]}{ ( 1 - Z_{1} D ) ( U - \eta )}. $$

By using (18)–(20) in (17), we obtain

$$\begin{aligned} q = - \frac{K_{0}}{T_{0}^{\beta_{c}} \rho_{0}^{\delta_{c}}} T^{\beta_{c}} \rho^{\delta_{c}} \frac{\partial T}{\partial r} - \frac{16 \sigma T_{0}^{\beta_{R}} \rho_{0}^{\delta_{R}}}{3 \alpha_{R_{0}}} T^{3 - \beta_{R}} \rho^{- \delta_{R}} \frac{\partial T}{\partial r}. \end{aligned}$$
(48)

Using (3) and (42) in (48), we obtain

$$\begin{aligned} Q &= - \biggl[ \frac{K_{0} ( C V_{0} )^{{1} / {n}}}{ T_{0}^{\beta_{c}} \rho_{0}^{\delta_{c}} R^{* ( \beta_{c} +1 )}} \rho_{1}^{ ( \delta_{c} - 1 )} ( 1 - K_{p} )^{- ( \beta_{c} +1)} \\ &\quad {}\times W_{s}^{ ( 2 \beta_{c} - 2 - {1} / {n} )} \biggl\{ \frac{P ( 1 - Z_{1} D )}{ [ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) ]} \biggr\} ^{\beta_{c}} \\ &\quad {}\times D^{\delta_{c} - \beta_{c}} + \frac{16 \sigma T_{0}^{\beta_{R}} \rho_{0}^{\delta_{R}} ( C V_{0} )^{{1} / {n}}}{3 \alpha_{R_{0}} R^{* ( 4 - \beta_{R} )}} \\ &\quad {}\times \rho_{1}^{- 1 - \delta_{R}} ( 1 - K_{p} )^{\beta_{R} - 4} W_{s}^{ ( 4 - 2 \beta_{R} - {1} / {n} )} \\ &\quad {}\times \biggl\{ \frac{P ( 1 - Z_{1} D )}{ [ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) ]} \biggr\} ^{3 - \beta_{R}} D^{- \delta_{R} - 3+ \beta_{R}} \biggr] \\ &\quad {}\times ( n +1 ) \frac{d}{d\eta} \biggl[ \frac{P ( 1 - Z_{1} D )}{D [ (1 - Z_{1} D) + \bar{b} D ( 1 - K_{p} ) ]} \biggr]. \end{aligned}$$
(49)

Equation (49) shows that the similarity solution of the present problem exists only when

$$ \beta_{c} =1+ \frac{1}{2 n}\quad \mbox{and}\quad \beta_{R} =2 - \frac{1}{2 n}. $$
(50)

Similar expressions of \(\beta_{R}\) were obtained earlier by Sedov (1982), Elliott (1960), Helliwell (1969) and Nicastro (1970) by the use of dimensional analysis. Also, Ghoniem et al. (1982) obtained the similar type of expression for \(\beta_{c}\) and \(\beta_{R}\). The expressions given above show the effect of the process of energy exchange, reflected by the dependence of \(\beta_{c}\) and \(\beta_{R}\) on the piston velocity index \(n\).

Therefore (49) becomes

$$\begin{aligned} Q &= - X \biggl[ \frac{ ( 1 - Z_{1} D )}{D [ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) ]} \frac{dP}{d\eta} \\ &\quad {} - \frac{P [ (1 - Z_{1} D )+ \bar{b} D ( 1 - K_{p} ) ] + P}{D^{2} [ (1 - Z_{1} D )+ \bar{b} D ( 1 - K_{p} ) ]^{2}} ( 1 - Z_{1} D ) \\ &\quad {}\times D \bigl[ - Z_{1} + \bar{b} ( 1 - K_{p} ) \bigr] \frac{dD}{d\eta} \biggr], \end{aligned}$$
(51)

where

$$\begin{aligned} X &= ( n +1 ) \bigl[ \varGamma_{c} D^{\delta_{c} - 1 - ( \frac{1}{2 n} )} + \varGamma_{R} D^{\delta_{R} - 1 - ( \frac{1}{2 n} )} \bigr] \\ &\quad {}\times ( 1 - K_{p} )^{- 2 - ( \frac{1}{2 n} )}\\ &\quad {}\times \biggl[ \frac{P ( 1 - Z_{1} D )}{ [ (1 - Z_{1} D )+ \bar{b} D ( 1 - K_{p} ) ]} \biggr]^{ ( 1+ \frac{1}{2 n} )}, \end{aligned}$$

and \(\varGamma_{c}\) and \(\varGamma_{R}\) are the conductive and radiative non-dimension heat transfer parameters, respectively. The parameter \(\varGamma_{c}\) and \(\varGamma_{R}\) depend on the thermal conductivity \(K\) and the mean free path of radiation \(\frac{1}{\alpha_{R}}\) respectively, and also on the exponent \(n\), and they are given by

$$\varGamma_{c} = \frac{K_{0} \rho_{1}^{ ( \delta_{c} - 1 )}}{T_{0} \rho_{0}^{\delta_{c}} R^{*^{2}}} \biggl( \frac{C V_{0}}{\sqrt{T_{0} R^{*}}} \biggr)^{{1} / {n}}$$

and

$$\varGamma_{R} = \frac{16 \sigma T_{0}^{2} \rho_{0}^{\delta_{R}}}{3 \alpha_{R_{0}} R^{*^{2}} \rho_{1}^{ ( \delta_{R} +1 )}} \biggl( \frac{C V_{0}}{\sqrt{T_{0} R^{*}}} \biggr)^{{1} / {n}}. $$

Using the self-similarity transformation (42), (31)–(35) can be written as

$$\begin{aligned} &U ( 1 ) = ( 1 - \beta ), \end{aligned}$$
(52)
$$\begin{aligned} &D ( 1 ) = \frac{1}{\beta}, \end{aligned}$$
(53)
$$\begin{aligned} &P ( 1 ) = \biggl[ ( 1 - \beta ) + \frac{1}{\gamma M^{2}} \biggr], \end{aligned}$$
(54)
$$\begin{aligned} & \begin{aligned}[b] Q ( 1 ) &= ( 1 - \beta ) \biggl[ \frac{\bar{b} ( 1 - K_{p} )}{\gamma M^{2} [ ( 1 - Z_{1} ) + \bar{b} ( 1 - K_{p} ) ]}\\ &\quad {} - \frac{1}{2} ( 1+ \beta ) \biggr]. \end{aligned} \end{aligned}$$
(55)

By solving (45)–(47) and (51) for \(\frac{dU}{d\eta}\), \(\frac{dP}{ d\eta}\), \(\frac{dQ}{d\eta}\) and \(\frac{dD}{d\eta}\), we have

$$\begin{aligned} &\frac{dU}{d\eta} = - \frac{ ( U - \eta )}{D} \frac{dD}{d\eta} - \frac{2 U}{\eta}, \end{aligned}$$
(56)
$$\begin{aligned} & \begin{aligned}[b] \frac{dP}{d\eta} &= ( U - \eta )^{2} \frac{dD}{d\eta} + UD \biggl[ \frac{2 ( U - \eta )}{\eta} - \biggl( \frac{n}{n +1} \biggr) \biggr]\\ &\quad {} - \frac{ ( n +1 ) D G_{0}}{ \eta^{2}}, \end{aligned} \end{aligned}$$
(57)
$$\begin{aligned} & \begin{aligned}[b] \frac{dQ}{d\eta} &= - \frac{1}{S} \bigl[ ( U - \eta )^{2} + J \bigr] \frac{dD}{d\eta} + \frac{UD}{S} \biggl[ \biggl( \frac{n}{n +1} \biggr) \\ &\quad {}- \frac{2 ( U - \eta )}{\eta} \biggr] + \biggl[ \frac{ ( n +1 ) D G_{0}}{\eta^{2}} - \frac{P}{ ( U - \eta )} \biggr] \frac{1}{S}\\ &\quad {} - \frac{2 Q}{\eta}, \end{aligned} \end{aligned}$$
(58)
$$\begin{aligned} & \begin{aligned}[b] \frac{dD}{d\eta} &= D \bigl[ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) \bigr] \\ &\quad \times{}\biggl[ ( 1 - Z_{1} D ) \biggl\{ \frac{ ( n +1 ) D G_{0}}{\eta^{2}} - \frac{2 UD ( U - \eta )}{\eta}\\ &\quad {} + \biggl( \frac{n}{n +1} \biggr) UD \biggr\} \\ &\quad {} - \frac{QD [ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) ]}{X} \biggr]\\ &\quad {}\times \bigl\{ \bigl[ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) \bigr]\\ &\quad {}\times \bigl\{ ( 1 - Z_{1} D ) D ( U - \eta )^{2} - P \bigr\} \\ &\quad {}- PD ( 1 - Z_{1} D ) \bigl\{ - Z_{1} + \bar{b} ( 1 - K_{p} ) \bigr\} \bigr\} ^{-1}. \end{aligned} \end{aligned}$$
(59)

For an isentropic change of state of the mixture of the non-ideal gas and small solid particles, under the thermodynamic equilibrium condition, we may calculate the equilibrium sound speed of the mixture, as follows

$$\begin{aligned} a_{m} &= \biggl( \frac{\partial p}{\partial\rho} \biggr)_{S}^{{1} / {2}} \\ & = \biggl[ \frac{ \{ \varGamma ( 1 - Z )^{2} + [ 2 \varGamma ( 1 - Z ) + Z ] b\rho ( 1 - K_{p} ) \} p}{ ( 1 - Z ) \rho [ ( 1 - Z ) + b\rho ( 1 - K_{p} ) ]} \biggr]^{{1} / {2}}, \end{aligned}$$
(60)

neglecting \(b^{2} \rho^{2}\), where ‘\(S\)’ refers to the process of constant entropy. In addition, the isothermal speed of sound may also play a role, where thermal radiation is taken into account. The isothermal sound speed in the mixture is

$$\begin{aligned} a_{iso} &= \biggl( \frac{\partial p}{\partial\rho} \biggr)_{T}^{{1} / {2}} \\ &= \biggl[ \frac{p \{ ( 1 - Z )^{2} + b\rho ( 1 - K_{p} ) ( 2 - Z ) \}}{ ( 1 - Z ) \rho [ ( 1 - Z ) + b\rho ( 1 - K_{p} ) ]} \biggr]^{{1} / {2}}, \end{aligned}$$
(61)

where the subscript ‘\(T\)’ refers to the process of constant temperature.

By using (42) in (61), we get the expression for reduced isothermal speed of sound as

$$ \frac{a_{iso}}{W_{s}} = \biggl[ \frac{P \{ ( 1 - Z_{1} D )^{2} + \bar{b} D ( 1 - K_{p} ) ( 2 - Z_{1} D ) \}}{D ( 1 - Z_{1} D ) \{ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) \}} \biggr]^{{1} / {2}}. $$
(62)

The adiabatic compressibility of the mixture of non-ideal gas and small solid particles may be calculated as (cf. Moelwyn-Hughes 1961)

$$\begin{aligned} C_{adi} &= - \rho \biggl( \frac{\partial}{\partial p} \biggl( \frac{1}{\rho} \biggr) \biggr)_{S} = \frac{1}{\rho a_{m}^{2}} \\ &= \frac{ ( 1 - Z ) [ ( 1 - Z ) + b\rho ( 1 - K_{p} ) ]}{ [ \varGamma ( 1 - Z )^{2} + \{ 2 \varGamma ( 1 - Z ) + Z \} b\rho ( 1 - K_{p} ) ] p}. \end{aligned}$$
(63)

Using (42) in (63), we get the expression for the adiabatic compressibility as,

$$\begin{aligned} &( C_{adi} ) p_{1} \\ &\quad = ( 1 - Z_{1} D ) \bigl[ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) \bigr] \\ &\qquad{}\times \bigl\{ \bigl[ \varGamma ( 1 - Z_{1} D )^{2} + \bar{b} D ( 1 - K_{p} ) \\ &\qquad{}\times \{ 2 \varGamma ( 1 - Z_{1} D ) + Z_{1} D \} \bigr] \gamma M^{2} P\bigr\} ^{-1} . \end{aligned}$$
(64)

The principle of global conservation of energy can be expressed in terms of the following integral relation

$$\begin{aligned} E &= 4 \pi \int_{r_{p}}^{r_{s}} \rho \biggl[ e_{m} + \frac{1}{2}u^{2} - \frac{\bar{G} \bar{m}}{r}\biggr] r^{2} dr \\ &= 4\pi \int_{0}^{r_{s}} \rho_{1} \biggl[ e_{m_{i}} - \frac{\bar{G} \bar{m}}{r}\biggr] r^{2} dr + E_{0}t^{s}, \end{aligned}$$
(65)

where \(E\) is the total energy of the flow between the piston and the shock front, \(e_{m_{i}}\)is the initial internal energy per unit mass, ‘\(s\)’ is so-called energy-input parameter, \(E_{0}\) is a proportionality constant and

$$ E_{0}t^{s} = 4\pi \int_{0}^{r_{p}} r_{p}^{2} p_{p} dr, $$
(66)

is the work done by the piston.

Using (42) and (12), in (65) the total energy of the disturbance

$$E = 4 \pi \int_{r_{p}}^{r_{s}} \rho \biggl[ e_{m} + \frac{1}{2}u^{2} - \frac{\bar{G} \bar{m}}{r}\biggr] r^{2} dr$$

is transformed into

$$ E =4 \pi \rho_{1} ( C V_{0} )^{ ( \frac{2}{n+1} )} ( n +1 )^{ ( \frac{2n}{n+1} )} r_{s}^{3+ \frac{2 n}{n +1}} \lambda, $$
(67)

where

$$\begin{aligned} \lambda &= \int_{\eta_{p}}^{1} \biggl[ \frac{1}{2} D U^{2} + \frac{P ( 1 - Z_{1} D )}{ ( \varGamma - 1 ) [ ( 1 - Z_{1} D ) + \bar{b} D ( 1 - K_{p} ) ]} \\ &\quad {}- \frac{G_{0} ( n +1 ) D}{\eta} \biggr] \eta^{2} d\eta. \end{aligned}$$

Hence, the total energy of the shock wave is non-constant and varies as \(r_{s}^{3+ \frac{2n}{n +1}}\). This increase of total energy may be achieved by the pressure exerted on the fluid by inner expanding surface (a contact surface or piston). This surface may be physically, the surface of the stellar corona or the condensed explosives or the diaphragm containing a very high-pressure driver gas. By sudden expansion of the stellar corona or the detonation products or the driver gas into the ambient gas, a shock wave is produced in the ambient gas. The shocked gas is separated from this expanding surface which is a contact discontinuity. This contact surface acts as a ‘piston’ for the shock wave. Thus the flow is headed by a shock front and has an expanding surface as an inner boundary (piston).

The piston path coincides at \(\eta_{p} = \frac{r_{p}}{r_{S}}\) with a particle path. Using (39) to (42) the relation

$$ U ( \eta_{p} ) = \eta_{p} = \frac{1}{C} = \biggl( \frac{W_{p}}{ W_{s}} \biggr), $$
(68)

can be derived. In addition to the shock conditions (52) to (55), the kinematic condition (68) at the piston surface must be satisfied.

For exhibiting the numerical solutions, it is convenient to write the field variables in non-dimensional form as

$$ \begin{aligned}[c] &\frac{u}{u_{2}} = \frac{U ( \eta )}{U (1)}, \qquad \frac{\rho}{\rho_{2}} = \frac{D ( \eta )}{D (1)},\\ & \frac{p}{p_{2}} = \frac{P ( \eta )}{P (1)},\qquad \frac{q}{q_{2}} = \frac{Q ( \eta )}{Q (1)}. \end{aligned} $$
(69)

4 Results and discussion

The distribution of the flow variables between the shock front (\(\eta = 1\)) and the piston (\(\eta = \eta_{p}\)) is obtained by numerical integration of (56) to (59) with the boundary conditions (52) to (55) by the Runge-Kutta method of fourth order. Parameters of the inert mixture (alumina \(\mathrm{Al}_{2}\mathrm{O}_{3}\) or glass) were within the following range: dust particle size is in the order of 10 μm (Higashino and Suzuki 1980; Fedorov and Kratova 2012), the material density of solid particles \(\rho_{sp} = 2.5\ \mbox{g/cm}^{3}\) and the mass fraction (concentration) of solid particles in the mixture is varied from \(K_{p} = 0\) to \(K_{p} = 0.3\). This case may be realized in an air flow with a suspension of alumina or glass particles. The diameter of small solid particles used in the present study \(d = 10\ \upmu \mbox{m}\) is two orders of magnitude larger than the shock wave thickness which is of the order of 0.066 μm, it can be assumed that the small solid particles are unaffected when they pass through the shock fronts. In addition to the above parameters, the following values may be taken as initial conditions: \(P = 1\ \mbox{atm}\), \(T_{ \mathit{initial}} = 300\ \mbox{K}\), \(C_{ sp} = 800\ \mbox{J}/(\mbox{kg}\,\mbox{K})\), specific gas constant \(R^{*} = 8314\ \mbox{J}/(\mbox{kg}\,\mbox{mol}\,\mbox{K})\), \(C_{ p}\) is calculated from \(C_{ p} = \frac{\gamma R^{*}}{(\gamma - 1)M_{a}}\), where \(M_{a}( = 29)\) is the effective molecular weight of air (Elperin et al. 1988). Also, the particle size 1 μm to 10 μm corresponds to interplanetary dust (Popel and Gisko 2006). The typical values of the physical quantities involved in the computation are taken as (Pai et al. 1980; Miura and Glass 1983; Vishwakarma and Nath 2006, 2007, 2009, 2010, 2012b) \(\gamma = 1.4\); \(K_{p} = 0, 0.1, 0.3\); \(G_{1} = 1,10, 100\); \(\alpha = 1\); \(\delta_{C} = 1\), \(\delta_{R} = 2\); \(\varGamma_{R} = 10\); \(\varGamma_{c} = 1\); \(M^{2} = 25\); \(\bar{b} = 0, 0.05, 0.1\); \(G_{0} = 0.1, 1, 5, 10, 20, 50\) and \(n = - \frac{1}{3}\). The values \(\gamma = 1.4\); \(\alpha = 1\) may correspond to the mixture of air and glass particles (Miura and Glass 1985). The value \(K_{p} = 0\), \(\bar{b} = 0\) corresponds to the perfect gas case and \(K_{p} = 0\) to the dust-free case. The value \(n = - \frac{1}{3}\) corresponds to a decelerated piston (shock produced by solar flares). The value \(M = 5\) of the shock Mach-number is appropriate, because we have treated the flow of a non-ideal gas and a pseudo-fluid (small solid particles) at a velocity and temperature equilibrium. The assumption of velocity and temperature equilibrium may be a good approximation for strong shock waves, because the thickness of the relaxation zone behind the shock front becomes very small for higher Mach-numbers (Vishwakarma and Nath 2010, 2012a). The exponent \(\delta_{C}\) and \(\delta_{R}\) are arbitrary within appropriate temperature range, unlike \(\beta_{C}\) and \(\beta_{R}\). The set of values \(\delta_{C} = 1,\delta_{R} = 2\) is the representative of the case of high-temperature, low-density medium (Ghoneim et al. 1982). Also, the set of values \(\varGamma_{c} = 1\), \(\varGamma_{R} = 10\) is the representative of the case in which there is heat transfer by both the radiative diffusion and conduction.

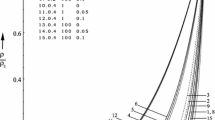
Table 1 shows the variation of density ratio \(\beta = ( \frac{\rho_{1}}{\rho_{2}} )\) across the shock front and the position of the piston (\(\eta_{p}\)) for different values of \(K_{p}\), \(G_{1}\) and \(\bar{b}\) with \(\gamma = 1.4\); \(\alpha = 1\); \(\delta_{C} = 1\), \(\delta_{R} = 2\); \(\varGamma_{R} = 10\); \(\varGamma_{c} = 1\); \(M^{2} = 25\); \(n = - \frac{1}{3}\) and \(G_{0} =1\). Figures 1(a)–(f) show the variation of the flow variables \(\frac{u}{ u_{2}}\), \(\frac{\rho}{\rho_{2}}\), \(\frac{p}{p_{2}}\), \(\frac{q}{q_{2}}\), \(\frac{a_{iso}}{W_{s}}\) and the adiabatic compressibility \(( C_{adi} ) P_{1}\) with \(\eta\) at various values of the parameters \(K_{p}\), \(G_{1}\) and \(\bar{b}\) with \(\gamma = 1.4\); \(\alpha = 1\); \(\delta_{C} = 1\), \(\delta_{R} = 2\); \(\varGamma_{R} = 10\); \(\varGamma_{c} = 1\); \(M^{2} = 25\); \(n=- \frac{1}{3}\) and \(G_{0} =1\). Also, Figs. 2(a)–(f) show the variation of the flow variables \(\frac{u}{u_{2}}\), \(\frac{\rho}{\rho_{2}}\), \(\frac{p}{p_{2}}\), \(\frac{q}{ q_{2}}\), \(\frac{a_{iso}}{W_{s}}\) and the adiabatic compressibility \(( C_{adi} ) P_{1}\) for different value of gravitational parameter \(G_{0}\) with \(\gamma = 1.4\); \(K_{p} =0.1\); \(G_{1} =10\); \(\bar{b} = 0.05\); \(\alpha = 1\); \(\delta_{C} = 1\), \(\delta_{R} = 2\); \(\varGamma_{R} = 10\); \(\varGamma_{c} = 1\); \(M^{2} = 25\) and \(n=- \frac{1}{3}\). These figures show that the flow variables \(\frac{u}{u_{2}}\), \(\frac{\rho}{\rho_{2}}\), \(\frac{p}{p_{2}}\), \(\frac{a_{iso}}{W_{s}}\) increase and the adiabatic compressibility \(( C_{adi} ) P_{1}\), the total heat flux \(\frac{q}{q_{2}}\) decrease as we move from the shock front to the piston, whereas the density \(\frac{\rho}{ \rho_{2}}\) decreases for \(G_{0} =0.5\) and the heat flux \(\frac{q}{q_{2}}\) decreases after attaining the maximum near the shock for higher values of \(G_{0} (> 5)\). The heat flux profiles behavior is similar to those obtained by Elliott (1960), Ghoniem et al. (1982), and Vishwakarma and Nath (2010, 2012a).

Fig. 1
figure 1

Distribution of the flow variables in the region behind the shock front with \(\alpha = 1\), \(\delta_{C} = 1\), \(\delta_{R} = 2\); \(\varGamma_{R} = 10\); \(\varGamma_{c} = 1\); \(M^{2} = 25\); \(n = - \frac{1}{3}\); \(G_{0} = 1\) and \(\gamma = 1.4\). (a) The fluid velocity \(\frac{u}{u_{2}}\), (b) the density \(\frac{\rho}{ \rho_{2}}\), (c) the pressure \(\frac{p}{p_{2}}\), (d) the total heat flux \(\frac{q}{q_{2}}\), (e) the isothermal speed of sound \(\frac{a_{iso}}{W_{s}}\), (f) the adiabatic compressibility \(( C_{adi} ) P_{1}\). 1. \(K_{p} = 0\), \(\bar{b} = 0\) (perfect gas); 2. \(K_{p} = 0\), \(\bar{b} = 0.05\); 3. \(K_{p} = 0\), \(\bar{b} = 0.1\); 4. \(K_{p} = 0.1\), \(G_{1} = 10\), \(\bar{b} = 0\); 5. \(K_{p} = 0.1\), \(G_{1} = 10\), \(\bar{b} = 0.05\); 6. \(K_{p} = 0.1\), \(G_{1} = 10\), \(\bar{b} = 0.1\); 7. \(K_{p} = 0.1\), \(G_{1} = 100\), \(\bar{b} = 0\); 8. \(K_{p} = 0.1\), \(G_{1} = 100\), \(\bar{b} = 0.05\); 9. \(K_{p} = 0.1\), \(G_{1} = 100\), \(\bar{b} = 0.1\); 10. \(K_{p} = 0.3\), \(G_{1} = 10\), \(\bar{b} = 0\); 11. \(K_{p} = 0.3\), \(G_{1} = 10\), \(\bar{b} = 0.05\); 12. \(K_{p} = 0.3\), \(G_{1} = 10\), \(\bar{b} = 0.1\); 13. \(K_{p} = 0.3\), \(G_{1} = 100\), \(\bar{b} = 0\); 14. \(K_{p} = 0.3\), \(G_{1} = 100\), \(\bar{b} = 0.05\); 15. \(K_{p} = 0.3\), \(G_{1} = 100\), \(\bar{b} = 0.1\)

Full size image
Fig. 2
figure 2

Distribution of the flow variables in the region behind the shock front with \(K_{p} = 0.1\), \(G_{1} = 10\), \(\bar{b} = 0.05\), \(\alpha = 1\), \(\delta_{C} = 1\), \(\delta_{R} = 2\); \(\varGamma_{R} = 10\); \(\varGamma_{c} = 1\); \(M^{2} = 25\); \(n = - \frac{1}{3}\) and \(\gamma = 1.4\). (a) The fluid velocity \(\frac{u}{u_{2}}\), (b) the density \(\frac{\rho}{ \rho_{2}}\), (c) the pressure \(\frac{p}{p_{2}}\), (d) the total heat flux \(\frac{q}{q_{2}}\), (e) the isothermal speed of sound \(\frac{a_{iso}}{W_{s}}\), (f) the adiabatic compressibility \(( C_{adi} ) P_{1}\). 1. \(G_{0} = 0.1\); 2. \(G_{0} = 1\); 3. \(G_{0} = 5\); 4. \(G_{0} = 10\); 5. \(G_{0} = 20\); 6. \(G_{0} = 50\)

Full size image
Table 1 Variation of the density ratio \(\beta ( = \frac{\rho_{1}}{\rho_{2}} )\) across the shock front and the position of the piston surface \(\eta_{p}\) for different values of \(K_{p}\), \(G_{1}\) and \(\bar{b}\) with \(\alpha = 1\); \(\delta_{C} = 1\), \(\delta_{R} = 2\); \(\varGamma_{R} = 10\); \(\varGamma_{c} = 1\); \(M^{2} = 25\); \(n = - \frac{1}{3}\); \(G_{0} = 1\) and \(\gamma = 1.4\)
Full size table

4.1 Distribution of flow variables with the parameter of non-idealness of the gas

The fluid velocity \(\frac{u}{u_{2}}\), the pressure \(\frac{p}{p_{2}}\) and the density \(\frac{\rho}{\rho_{2}}\) in the disturbed region decrease, in general as we move inward from the shock front, whereas the total heat flux \(\frac{q}{q_{2}}\) increases with an increases in the parameter of non-idealness \(\bar{b}\) of the gas (see Figs. 1(a), (b), (c), (d)). The isothermal speed of sound \(\frac{a_{iso}}{W_{s}}\) increases near shock and decreases near piston, whereas the adiabatic compressibility \(( C_{adi} ) P_{1}\) shows reverse behavior with an increase in \(\bar{b}\) in general (see Figs. 1(e), (f)). Also, the density ratio \(\beta\) across the shock front and the distance of the piston from the shock front increase with an increase in the parameter of non-idealness \(\bar{b}\) of the gas in the mixture i.e. there is a decrease in the shock strength and the flow-field behind the shock become somewhat rarefied (see Table 1).

4.2 The effect of mass concentration of solid particles on the distribution of flow variables

The fluid velocity \(\frac{u}{u_{2}}\), the pressure \(\frac{p}{p_{2}}\), the total heat flux \(\frac{q}{q_{2}}\) and the adiabatic compressibility \(( C_{adi} ) P_{1}\) decrease for \(G_{1} =10, \bar{b} \neq0\) with an increase in the mass concentration \(K_{p}\) of solid particles in the mixture as we move inward from the shock front in the disturbed region, whereas these flow variables increases for \(G_{1} =100, \bar{b} \neq0\) (see Figs. 1(a), (c), (d), (f)). With an increase in \(K_{p}\) in the case of non-ideal gas (\(\bar{b} \neq0\)), the density \(\frac{\rho}{\rho_{2}}\) decreases and the isothermal speed of sound \(\frac{a_{iso}}{W_{s}}\) increases in general (see Figs. 1(b), (e)). The flow variables velocity \(\frac{u}{u_{2}}\), density \(\frac{\rho}{\rho_{2}}\), pressure \(\frac{p}{ p_{2}}\) and the shock strength remain unaffected by an increase in \(K_{p}\) in the case of perfect gas (\(\bar{b} =0\)) but the heat flux \(\frac{q}{ q_{2}}\) and adiabatic compressibility \(( C_{adi} ) P_{1}\) increases (see Figs. 1(a), (b), (c), (d), (f)) and Table 1). Also, the density ratio \(\beta\) and the distance of the piston from the shock front increase with an increase in \(K_{p}\) for \(G_{1} =10, \bar{b} \neq0\) i.e. there is a decrease in the shock strength, whereas the reverse behavior is observed for \(G_{1} =100\), \(\bar{b} \neq0\) (see Table 1).

4.3 Effect of the ratio of density of solid particles to the initial density of the gas on the flow variables

Figures 1(a)–(f) and Table 1 show that in the case of perfect gas (\(\bar{b} =0\)) the flow variables and the shock strength are remain unchanged with an increase in the ratio of density of solid particles to the initial density of the gas in the mixture \(G_{1}\). In the case of non-ideal gas (\(\bar{b} \neq0\)) with an increase in \(G_{1}\) the flow variables \(\frac{u}{u_{2}}\), \(\frac{\rho}{\rho_{2}}\), \(\frac{p}{p_{2}}\), \(( C_{adi} ) P_{1}\) increase, in general as we move inward from the shock front, whereas the total heat flux \(\frac{q}{q_{2}}\) and the isothermal speed of sound \(\frac{a_{iso}}{W_{s}}\) decrease (see Figs. 1(a)–(f)). The density ratio \(\beta\) and the distance of the piston from the shock front decrease with an increase in the parameter \(G_{1}\) i.e. there is an increase in the shock strength (see Table 1).

The above effects are more impressive at higher value of \(K_{p}\) these effects may be physically interpreted as follows:

By an increase in \(G_{1}\) (at constant \(K_{p}\)), there is highly decrease in \(Z_{1}\), i.e. the volume fraction of solid particles in the undisturbed medium becomes, comparatively very small. This causes comparatively more compression of the mixture in the region between shock and the piston, which display the above effects.

4.4 Effect of gravitational parameter on the flow variables

Figures 2(a)–(f) and Table 2 show that the flow variables \(\frac{u}{u_{2}}\), \(\frac{\rho}{\rho_{2}}\), \(\frac{p}{p_{2}}\), \(\frac{a_{iso}}{W_{s}}\) and shock strength increase with an increase in the gravitational parameter \(G_{0}\) as we move inward from shock front, whereas the total heat flux \(\frac{q}{q_{2}}\) and the adiabatic compressibility \(( C_{adi} ) P_{1}\) decrease in general, which is an excellent agreement from our earlier work (Vishwakarma and Nath 2012b).

Table 2 Position of the piston surface \(\eta_{p}\) for different values of gravitational parameter \(G_{0}\) with \(K_{p} = 0.1\); \(G_{1} = 10\); \(\bar{b} = 0.05\); \(\alpha = 1\); \(\delta_{C} = 1\), \(\delta_{R} = 2\); \(\varGamma_{R} = 10\); \(\varGamma_{c} = 1\); \(M^{2} = 25\); \(n = - \frac{1}{3}\); and \(\gamma = 1.4\)
Full size table

The above behavior of the flow variables may be interpreted as follows:

As \(G_{0}\) is proportional to \(\frac{1}{C^{3}}\), an increase in \(G_{0}\) decreases \(C\), and a decrease in \(C\) increases the speed of the piston in comparison with that of the shock. Thus, the distance between the piston and shock is decreased and the flow variables between them are increased. Also, then the strength of the shock is increased and the adiabatic compressibility is decreased.

5 Conclusion

The present study investigates the self-similar flow behind a spherical shock wave, propagating in a mixture of non-ideal gas and small solid particles with heat conduction and radiation heat flux, under the influence of a gravitational field due to central mass at the origin (Roche model). The effect of non-idealness parameter \(\bar{b}\) of the gas, the mass concentration of solid particles in the mixture \(K_{p}\), the density ratio of solid particles to the initial density of the gas \(G_{1}\) and the gravitational parameter \(G_{0}\) are studied. The constructed diagram of variations in the flow variables and the tables give a clear representation of global variations in the flow-field and the shock strength. It is shown that in the non-ideal dusty gas under gravitational field, the propagating shock wave is found to be most influenced by the gravitational parameter. As the gravitational parameter is increased the shock wave strength is increased. On the basis of this study, one may draw the following conclusions:

  1. 1.

    The consideration of the medium under the influence of gravitational field due to central mass at the origin, the adiabatic compressibility \(( C_{adi} ) P_{1}\) and total heat flux \(\frac{q}{q_{2}}\) decrease, whereas the other flow variables and the shock strength increases.

  2. 2.

    The consideration of ambient pressure \(p_{1}\) imposes a restriction on the piston velocity index \(n\) as \(n = - \frac{1}{3}\); whereas in the case when \(p_{1}\) is neglected \(n\) can take any value such that \(n > - 1\) (see Steiner and Hirschler 2002).

  3. 3.

    In the case of non-ideal gas an increase in the gravitational parameter \(G_{0}\) and in the ratio of the density of solid particles to the initial density of the gas \(G_{1}\) has significant effect on the flow variables in the flow-field behind the shock front. Also, an increase in these parameters exhibit similar effect on shock strength and on the distance between the piston and shock.

  4. 4.

    An increase in the parameter of non-idealness \(\bar{b}\) of the gas has significant effects on the flow variables between the piston and the shock. The non-idealness of the gas causes a decrease in the shock strength and widens the disturbed region between the piston and the shock.

  5. 5.

    In the case of non-ideal gas an increase in the mass concentration of solid particles in the mixture \(K_{p}\) has significant effects on the flow-variables between the shock and the piston. When \(G_{1} = 1\), \(\bar{b} \ne 0\) the effects of an increase in the value of \(K_{p}\), on the shock strength and on the distance between piston and shock front are similar to those of an increase in the value of \(\bar{b}\).

We give examples to make clear the nature of shock waves in dusty medium. However, they serve mainly as illustrations of how the shock waves in dusty medium can be described. In reality, many other processes may be important and a more comprehensive analysis of the shock may be needed for its applications in astrophysics or elsewhere. The presence of self-gravitational field increases the compressibility of the medium, due to which it is compressed and therefore the distance between the inner contact surface and the shock surface is reduced. The shock waves in self-gravitating dusty gas can be important for description of shocks in supernova explosions, in the study of central part of star burst galaxies, nuclear explosion, rupture of a pressurized vessel and explosion in the ionosphere. Other potential applications of this study include analysis of data from the measurements carried out by spacecraft in the solar wind and in neighborhood of the Earth’s surface (Korolev and Pushkar 2014). The present study is related to and our results may be helpful to some questions being investigated in astrophysical plasmas (Popel et al. 1998; Popel and Gisko 2006):

Star formation in shocked molecular clouds

One believes that most of new stars are formed in dust-molecular clouds and shock waves initiate this process. They create the increase in density, sufficient for the gravitational self-compression (Jeans instability). The observations show that the presence of dust is well correlated with star formation in dusty clouds. The problem is to determine which process is more important: condensation due to the dust attraction or the gravitational self-compression in the shock wave.

Shocks from supernova explosions

The layer of dust behind the supernova shock is observed usually. The problem is to verify whether the layer of dust is related to the process of dust condensation behind the shock wave front.