Inhomogeneous temperature fields caused by the friction heating of the working elements (pads and disks) of the brakes induce temperature stresses in these elements. If the intensity of these stresses exceeds a certain value critical for a given material, then the cracks may appear in the material, which would lead to the deterioration of the friction thermal resistance of the couple, i.e., its ability to preserve a constant value of the friction coefficient in the process of braking [1]. The analytic models used for the evaluation of the temperature conditions of disk brakes are based on the solutions of one-dimensional thermal friction problems for bodies bounded by the coordinate surfaces [2]; in particular, for a half space or a ball [3]. The stresses caused by one-dimensional nonstationary temperature fields can be found by using the model of the temperature bending of a beam with free ends [4].

In the formulation of thermal problems with friction, it is customary to use the condition of equality of the sum of the intensities of heat flows directed from the contact surface into a pad and into a disk to the specific friction power [5]. Therefore, the variations of temperature in the process of braking are determined, to a significant extent, by the time profile of the friction power. This profile is most often described with the help of a function linearly decreasing from the nominal value at the onset of braking to zero at the end of braking (braking with constant deceleration). Note that the distributions of temperature and temperature stresses in a "layer–half space" [6] and "half space–half space with protective coating" tribosystems were studied in [7] just for the indicated evolution of the specific friction power in braking. The process of braking accompanied by a decrease in the friction power to zero in approaching the time of stop is regarded as rational [8]. The exact solutions of some thermal friction problems for the "half space–half space" tribosystem with three nonlinear rational time profiles of the specific friction power were obtained in [9]. The aim of the present work is to find the temperature stresses and to study the influence of specific friction power varying as a function of time in the course of braking on the thermal stressed states of the pad and the disk.

Temperature Fields

Consider a schematic diagram of friction contact of two half spaces (Fig. 1). In what follows, we denote all quantities and parameters corresponding to the upper (z ≥ 0) and lower (z ≤ 0) half spaces by the subscripts k = 1 and k = 2, respectively. On the surface z = 0, the following conditions of perfect thermal friction contact are satisfied:

$$ {T}_1^{(i)}\left({0}^{+},t\right)={T}_2^{(i)}\left({0}^{-},t\right),\kern0.5em {q}_1^{(i)}(t)+{q}_2^{(i)}(t)={q}^{(i)}(t),\kern0.5em {\displaystyle \begin{array}{cc}0<t\le {t}_s,& i=1,\kern0.5em 2,\kern0.5em 3\end{array}}, $$
(1)
Fig. 1.
figure 1

Schematic diagram of friction heating of the tribosystem.

Full size image

where

\( {T}_k^{(i)}\left(z,t\right) \) are temperature fields;

\( {q}_k^{(i)}(t)\kern1em ,k=1,2 \),are the intensities of heat fluxes directed along the normal to the contact surface into each element;

t is time, and ts is the duration of braking.

The time profiles of the specific friction power in the second condition in (1) are chosen in the form [8]

$$ {\displaystyle \begin{array}{ccc}{q}^{(i)}(t)=q0{q}^{(i)\ast }(t),& 0\le t\le {t}_s,& i=1,\kern0.5em 2,\kern0.5em 3\end{array}}, $$
(2)
$$ {\displaystyle \begin{array}{ccc}{q}^{(1)\ast }(t)=3{\left(1-\frac{t}{t_s}\right)}^2,& {q}^{(2)\ast }(t)=6\left(\frac{t}{t_s}\right)\left(1-\frac{t}{t_s}\right),& {q}^{(3)\ast }(t)=6\sqrt{\frac{t}{t_s}}\left(1-\sqrt{\frac{t}{t_s}}\right),\end{array}} $$
(3)

where q0 is the a priori known nominal value of the specific friction power.

The solution of the one-dimensional parabolic boundary-value problem of heat conduction for two half spaces with the boundary conditions (1)–(3) and a constant initial temperature T0 takes the form [9]

$$ {\displaystyle \begin{array}{cccc}{T}_k^{(i)}\left(z,t\right)={T}_0+{T}_a{T}_k^{(i)}\left(\upzeta, \uptau \right)& 0\le t\le {t}_s,& i=1,\kern0.5em 2,\kern0.5em 3,& k=1,2,\end{array}} $$
(4)
$$ {\displaystyle \begin{array}{c}{T}_k^{(1)\ast}\left(\upzeta, \uptau \right)=2\upgamma \sqrt{\uptau}\left\langle \left\{0.2{\uptau}^{\ast 2}\left[8+18{Z}_k^2\left(\upzeta, \uptau \right)+4{Z}_k^4\left(\upzeta, \uptau \right)\right]\right\}{F}_k\left(\upzeta, \uptau \right)-4\right.{\uptau}^{\ast}\left[+{Z}_k^2\left(\upzeta, \uptau \right)\right]\\ {}\left.+{\uptau}^{\ast}\left\{2{Z}_k\left(\upzeta, \uptau \right)-0.2{\uptau}^{\ast 2}{Z}_k\left(\upzeta, \uptau \right)\left[7+\left(\upzeta, \uptau \right)\right]\right\}{E}_k\left(\upzeta, \uptau \right)+3\right\rangle, \end{array}} $$
(5)
$$ {\displaystyle \begin{array}{c}{T}_k^{(1)\ast}\left(\upzeta, \uptau \right)=4{\upgamma \uptau}^{\ast}\sqrt{\uptau}\left\langle \left\{2\left[1+{Z}_k^2\left(\upzeta, \uptau \right)\right]-0.2{\uptau}^{\ast}\left[8+18{Z}_k^2\left(\upzeta, \uptau \right)+4{Z}_k^4\left(\upzeta, \uptau \right)\right]\right\}{F}_k\left(\upzeta, \uptau \right)\right.\\ {}\left.-\left\{{Z}_k\left(\upzeta, \uptau \right)-0.2{\uptau}^{\ast 2}{Z}_k\left(\upzeta, \uptau \right)\left[7+2{Z}_k^2\left(\upzeta, \uptau \right)\right]\right\}{E}_k\left(\upzeta, \uptau \right)\right\rangle, \end{array}} $$
(6)
$$ {\displaystyle \begin{array}{l}{T}_k^{(3)\ast}\left(\upzeta, \uptau \right)={\upgamma \uptau}^{\ast}\left\langle \left[3\sqrt{{\uppi \uptau}_s}+4\sqrt{\tau }{Z}_k\left(\upzeta, \uptau \right)\right]{E}_k\left(\upzeta, \uptau \right)\right.\\ {}\left.\kern6em -2\left\{3\sqrt{{\uppi \uptau}_s}{Z}_k\left(\upzeta, \uptau \right)+4\sqrt{\tau}\left[1+{Z}_k^2\left(\upzeta, \uptau \right)\right]\right\}{F}_k\left(\upzeta, \uptau \right)\right\rangle, \end{array}} $$
(7)
$$ {\displaystyle \begin{array}{cc}{F}_k\left(\upzeta, \uptau \right)=\mathrm{ierfc}\ {\mathrm{Z}}_k\left(\upzeta, \uptau \right),& {E}_k\left(\upzeta, \uptau \right)=\mathrm{ierfc}\ {\mathrm{Z}}_k\left(\upzeta, \uptau \right),\end{array}} $$
(8)
$$ {\displaystyle \begin{array}{cccc}{Z}_1\left(\upzeta, \uptau \right)=\frac{0.5\upzeta}{\sqrt{\uptau}},& \upzeta \ge 0,& {Z}_2\left(\upzeta, \uptau \right)=-\frac{0.5\upzeta}{\sqrt{k^{\ast}\uptau}},& \upzeta \le 0,\end{array}} $$
(9)
$$ {\displaystyle \begin{array}{c}\begin{array}{cccc}\upzeta =\frac{z}{a_1}& \tau =\frac{k_1t}{a_1^2},& {\tau}_s=\frac{k_1{t}_s}{a_1^2},& \tau \end{array}\ast =\frac{\tau }{\tau_s},\\ {}\begin{array}{cccc}{K}^{\ast }=\frac{K_2}{K_1},& {k}^{\ast }=\frac{k_2}{k_1},& \upgamma =\frac{\sqrt{k^{\ast }}}{\sqrt{k^{\ast }}+{K}^{\ast }},& {T}_a\end{array}=\frac{q_0{a}_1}{K_1},\end{array}} $$
(10)

where K1,2 and k1,2 are the heat-conduction coefficients and thermal diffusivity, respectively,

$$ {\displaystyle \begin{array}{cc}\mathrm{ierfc}\;x=\frac{e^{-{x}^2}}{\sqrt{\pi }}-x\kern0.5em \operatorname{erfc}\kern0.5em x,& \operatorname{erfc}\kern0.5em x=1-\operatorname{erfc}\;x\end{array}}, $$

erf x is the Gaussian error function [10], and \( {a}_k=\sqrt{3{k}_k{t}_s},k=1,2 \), are the effective depths of heat penetration into the elements of the friction couple [1].

Stressed State

We find the temperature stresses \( {\sigma}_k^{(i)}\left(z,t\right) \) corresponding to the temperature fields \( {T}_k^{(i)}\left(z,t\right) \) (4)–(10) by using the relations of the theory of temperature bending of a layer with free edges [4]. Thus, we get [11]

$$ {\displaystyle \begin{array}{cccc}{\sigma}_k^{(i)}\left(z,t\right)\equiv {\sigma}_{x,k}^{(i)}\left(z,t\right)={\sigma}_{y,k}^{(i)}\left(z,t\right),& {\sigma}_{Z,k}^{(i)}\left(z,t\right)=0,& -{a}_2\le z\le {a}_1,& 0\le t\le {t}_s\end{array}}, $$
(11)
$$ {\displaystyle \begin{array}{ccc}{\sigma}_k^{(i)}\left(z,t\right)={\sigma}_{0,k}{\sigma}_k^{(i)}\left(\upzeta, \uptau \right),& {\sigma}_{0,k}=\frac{\alpha_k{E}_k{T}_0}{1-{v}_k},& i=1,\kern0.5em 2,\kern0.5em 3,\end{array}} $$
(12)
$$ {\displaystyle \begin{array}{ccc}{\sigma}_k^{(i)\ast}\left(\zeta, \tau \right)={\upvarepsilon}_k^{(i)\ast}\left(\zeta, \tau \right)-{T}_k^{(i)\ast}\left(\zeta, \tau \right),& {a}_2^{\ast}\le \upzeta \le {a}_1^{\ast },& 0\le \uptau \le \end{array}}{\uptau}_s, $$
(13)
$$ {\upvarepsilon}_k^{(i)\ast}\left(\upzeta, \uptau \right)=\left[{\left(-1\right)}^{k+1}4-6\upzeta \right]{N}_k^{(i)}\left(\uptau \right)+\left[{\left(-1\right)}^{k+1}12\upzeta -6\right]{M}_k^{(i)}\left(\uptau \right), $$
(14)
$$ {\displaystyle \begin{array}{c}\begin{array}{cc}{N}_k^{(i)}\left(\tau \right)=\underset{0}{\overset{a_k^{\ast }}{\int }}{T}_k^{(i)\ast}\left(\upzeta, \uptau \right)d\upzeta, & {M}_k^{(i)}\left(\tau \right)=\underset{0}{\overset{a_k^{\ast }}{\int }}\upzeta {T}_k^{(i)\ast}\left(\upzeta, \uptau \right)d\upzeta, \end{array}\\ {}\begin{array}{cc}{a}_k^{\ast }=\frac{{\left(-1\right)}^{k+1} ak}{a_1},& k=1,2,\end{array}\end{array}} $$
(15)

where E is Young's modulus and ν is Poisson’s ratio, and α is the coefficient of linear thermal expansion. Substituting the dimensionless temperatures \( {T}_k^{(i)\ast}\left(\zeta, \tau \right) \) (5)–(10) in relations (15), we obtain

$$ {\displaystyle \begin{array}{l}{N}_k^{(1)}\left(\uptau \right)=2\upgamma \sqrt{\uptau}{X}_k\left(\tau \right)\left\{3{I}_{0,k}\left(\uptau \right)-2{\uptau}^{\ast}\left[2{I}_{0.k}\left(\uptau \right)+2,{I}_{2,k}\left(\uptau \right)-{J}_{1,k}\left(\uptau \right)\right]\right.\\ {}\kern5em \left.+0.2{\uptau}^{\ast 2}\left[8{I}_{0,k}\left(\uptau \right)+18{I}_{2,k}\left(\uptau \right)+4{I}_{4,k}\left(\uptau \right)-7{J}_{1,k}\left(\uptau \right)-2{J}_{3,k}\left(\uptau \right)\right]\right\},\end{array}} $$
(16)
$$ {\displaystyle \begin{array}{l}{M}_k^{(1)}\left(\uptau \right)=2\upgamma \sqrt{\uptau}{X}_k^2\left(\tau \right)\left\{3{I}_{1,k}\left(\uptau \right)-2{\uptau}^{\ast}\left[2{I}_{0.k}\left(\uptau \right)+2,{I}_{3,k}\left(\uptau \right)-{J}_{2,k}\left(\uptau \right)\right]\right.\\ {}\kern5em \left.+0.2{\uptau}^{\ast 2}\left[8{I}_{1,k}\left(\uptau \right)+18{I}_{3,k}\left(\uptau \right)+4{I}_{5,k}\left(\uptau \right)-7{J}_{2,k}\left(\uptau \right)-2{J}_{4,k}\left(\uptau \right)\right]\right\},\end{array}} $$
(17)
$$ {\displaystyle \begin{array}{l}{N}_k^{(2)}\left(\uptau \right)=4{\upgamma \uptau}^{\ast}\sqrt{\uptau}{X}_k\left(\uptau \right)\left\{2{I}_{0,k}\left(\uptau \right)\left\{\left[2{I}_{0.k}\left(\uptau \right)+2,{I}_{2,k}\left(\uptau \right)-{J}_{1,k}\left(\uptau \right)\right]\right.\right.\\ {}\kern5em \left.-0.2{\uptau}^{\ast}\left[8{I}_{0,k}\left(\uptau \right)+18{I}_{2,k}\left(\uptau \right)+4{I}_{4,k}\left(\uptau \right)-7{J}_{1,k}\left(\uptau \right)-2{J}_{3,k}\left(\uptau \right)\right]\right\},\end{array}} $$
(18)
$$ {\displaystyle \begin{array}{l}{M}_k^{(2)}\left(\uptau \right)=4{\upgamma \uptau}^{\ast}\sqrt{\uptau}{X}_k^2\left(\uptau \right)\left\{\left[2{I}_{1.k}\left(\uptau \right)+2{I}_{3,k}\left(\uptau \right)-{J}_{2,k}\left(\uptau \right)\right]\right.\\ {}\kern5em \left.-0.2{\uptau}^{\ast}\left[8{I}_{1,k}\left(\uptau \right)+18{I}_{3,k}\left(\uptau \right)+4{I}_{5,k}\left(\uptau \right)-7{J}_{2,k}\left(\uptau \right)-2{J}_{4,k}\left(\uptau \right)\right]\right\},\end{array}} $$
(19)
$$ {N}_k^{(3)}\left(\uptau \right)={\upgamma \uptau}^{\ast }{X}_k\left(\uptau \right)\left\{3\sqrt{\pi {\uptau}_s}\ \left[{\mathrm{J}}_{0,k}\left(\uptau \right)-2{I}_{1,\mathrm{k}}\left(\uptau \right)\right]-4\ \sqrt{\uptau}\left[2{I}_{0,k}\left(\uptau \right)+{2}_{I2,k}\left(\uptau \right)-{J}_{1,k}\left(\uptau \right)\right]\right\}, $$
(20)
$$ {M}_k^{(3)}\left(\uptau \right)={\upgamma \uptau}^{\ast }{X}_k\left(\uptau \right)\left\{3\sqrt{\pi {\uptau}_s}\ \left[{J}_{1,k}\left(\uptau \right)-2{I}_{2,\mathrm{k}}\left(\uptau \right)\right]-4\ \sqrt{\uptau}\left[2{I}_{1,k}\left(\uptau \right)+2{I}_{3,k}\left(\uptau \right)-{J}_{2,k}\left(\uptau \right)\right]\right\}, $$
(21)
$$ {I}_{n,k}\left(\uptau \right)=\underset{0}{\overset{Y_k\left(\uptau \right)}{\int }}{Z}_k^n\left(\upzeta, \uptau \right){F}_k\left(\upzeta, \uptau \right){dZ}_k=\frac{L_{n,k}\left(\uptau \right)}{\sqrt{\uppi}}-{J}_{n+1,k}\left(\uptau \right), $$
(22)
$$ {\displaystyle \begin{array}{c}{L}_{n,k}\left(\uptau \right)=\underset{0}{\overset{Y_k\left(\uptau \right)}{\int }}{Z}_k^n\left(\upzeta, \uptau \right){e}^{-{Z}_k^2\left(\upzeta, \uptau \right)}{dZ}_k,\\ {}\begin{array}{cc}{J}_{n,k}\left(\uptau \right)=\underset{0}{\overset{Y_k\left(\uptau \right)}{\int }}{Z}_k^n\left(\upzeta, \uptau \right){E}_k\left(\upzeta, \uptau \right){dZ}_k,& n=0,1,\dots, \end{array}\end{array}} $$
(23)
$$ {\displaystyle \begin{array}{cccc}{X}_1\left(\uptau \right)=2\sqrt{\uptau},& {X}_2\left(\uptau \right)=2\sqrt{k^{\ast}\uptau},& {Y}_k\left(\uptau \right)=\frac{a_k^{\ast }}{X_k\left(\tau \right)},& k=1,2.\end{array}} $$
(24)

By using the recurrence relations [12, 13]

$$ {\displaystyle \begin{array}{c}\begin{array}{cc}{L}_{n,k}\left(\uptau \right)=0.5\left[\left(n-1\right){L}_{n-2,k}\left(\uptau \right)-{Y}_{n-1,k}\left(\uptau \right){e}^{-{Y}_k^2\left(\uptau \right)}\right],& n=2,3,\dots, \end{array}\\ {}{J}_{n,k}\left(\uptau \right)=\frac{0.5n\left(n-1\right){J}_{n-2,k}\left(\uptau \right)+\left[{Y}_k^2\left(\uptau \right)-0.5n\right]{Y}_k^{n-1}\left(\uptau \right)\operatorname{erfc}\kern0.5em {Y}_k\left(\uptau \right)-{Y}_k^n\left(\uptau \right){e}^{-{Y}_k^2\left(\uptau \right)}/\sqrt{\uppi}}{n+1},\\ {}\begin{array}{cc}{L}_{0,k}\left(\uptau \right)=0.5\sqrt{\uppi}\left[1-{\mathrm{erfcY}}_k\left(\uptau \right)\right],& {L}_{1,k}\left(\uptau \right)=0.5\left[1-{e}^{-{Y}_k^2\left(\uptau \right)}\right],\end{array}\end{array}} $$
(25)
$$ {\displaystyle \begin{array}{cc}{J}_{0,k\left(\tau \right)}=\frac{1}{\sqrt{\uppi}}-\mathrm{ierfc},& {J}_{1,k}\left(\uptau \right)\end{array}}=0.25\mathrm{er}{Y}_k\left(\uptau \right)-0.5{Y}_k\left(\uptau \right)\mathrm{ierfc}{Y}_k\left(\uptau \right), $$
(26)

we can take integrals (23) for n = 2, 3,..., 6 :

$$ {\displaystyle \begin{array}{cc}{L}_{2,k}\left(\uptau \right)=0.25\sqrt{\uppi}\kern0.5em \operatorname{erf}\kern0.5em {Y}_k\left(\uptau \right)-0.5{Y}_k\left(\uptau \right){e}^{-{Y}_k^2\left(\uptau \right)},& {L}_{3,k}\left(\uptau \right)=0.5\left\{1-\left[1+{Y}_k^2\left(\uptau \right)\right]{e}^{-{Y}_k^2\left(\uptau \right)}\right\},\end{array}} $$
(27)
$$ {L}_{4,k}\left(\tau \right)=0.375\ \sqrt{\pi } \operatorname {erf}\ {Y}_k\left(\uptau \right)-0.5{Y}_k\left(\uptau \right)\left[{Y}_k^2\left(\uptau \right)+1.5\right]e-{Y}_k^2\left(\uptau \right), $$
(28)
$$ {L}_{5,k}\left(\uptau \right)=1-\left[0.5{Y}_k^4\left(\uptau \right)+{Y}_k^2\left(\uptau \right)+1\right]{e}^{-{Y}_k^2\left(\tau \right)}, $$
(29)
$$ {J}_{2,k}\left(\uptau \right)=\frac{\left\langle {Y}_k^3\left(\uptau \right)\operatorname{erfc}{Y}_k\left(\uptau \right)+\left\{1-\left[{Y}_k^2\left(\uptau \right)+1\right]{e}^{-{Y}_k^2\left(\tau \right)}\right\}/\sqrt{\uppi}\right\rangle }{3}, $$
(30)
$$ {J}_{3,k}\left(\tau \right)=\frac{\left\{{Y}_k^4\left(\uptau \right)\kern0.5em \operatorname{erfc}\kern0.5em {Y}_k\left(\uptau \right)+0.75\kern0.5em \operatorname{erf}\kern0.5em {Y}_k\left(\uptau \right)-\kern0.5em {Y}_k\left(\uptau \right)\left[{Y}_k^2\left(\uptau \right)+1.5\right]{e}^{-{Y}_k^2\left(\uptau \right)}/\sqrt{\uppi}\right\}}{4}, $$
(31)
$$ {J}_{4,k}\left(\tau \right)=\frac{\left\langle {Y}_k^5\left(\uptau \right)\kern0.5em \operatorname{erfc}\kern0.5em {Y}_k\left(\uptau \right)+\left\{2-\left[{Y}_k^4\left(\uptau \right)+2{Y}_k^2\left(\uptau \right)+2\right]{e}^{-{Y}_k^2\left(\uptau \right)}\right\}/\sqrt{\uppi}\right\rangle }{5}, $$
(32)
$$ {J}_{5,k}\left(\tau \right)=\frac{\left\{{Y}_k^6\left(\uptau \right)\kern0.5em \operatorname{erfc}\kern0.5em {Y}_k\left(\uptau \right)+1.875\kern0.5em \operatorname{erf}\kern0.5em {Y}_k\left(\uptau \right)-{Y}_k\left(\uptau \right)\left[{Y}_k^4\left(\uptau \right)+2.5{Y}_k^2\left(\uptau \right)+3.75\right]{e}^{-{Y}_k^4\left(\uptau \right)}/\sqrt{\uppi}\right\}}{6}, $$
(33)
$$ {J}_{6,k}\left(\tau \right)=\frac{\left\langle {Y}_k^7\left(\uptau \right)\kern0.5em \operatorname{erfc}\kern0.5em {Y}_k\left(\uptau \right)+\left\{6-\left[{Y}_k^4\left(\uptau \right)+3{Y}_k^4\left(\uptau \right)+6{Y}_k^2+6\right]{e}^{-{Y}_k^2\left(\uptau \right)}\right\}/\sqrt{\uppi}\right\rangle }{5}, $$
(34)

Substituting the functions Ln,k (τ) and Jn,k (τ) (25)–(34) in relations (22), we get

$$ {I}_{0,k}\left(\uptau \right)=\frac{0.5{Y}_k\left(\uptau \right){e}^{-{Y}_k^2\left(\uptau \right)}}{\sqrt{\uppi}}+0.25\operatorname{erf}\kern0.5em {Y}_k\left(\uptau \right)-0.5{Y}_k^2\left(\uptau \right)\kern0.5em \operatorname{erf}\kern0.5em {Y}_k\left(\uptau \right), $$
(35)
$$ {I}_{1,k}\left(\uptau \right)=\frac{\left\langle \left\{1+\left[2{Y}_k^2\left(\uptau \right)-1\right]{e}^{-{Y}_k^2}\right\}/\sqrt{\uppi}-2{Y}_k^2\left(\uptau \right)\kern0.5em \operatorname{erfc}{Y}_k\left(\uptau \right)\right\rangle }{6}, $$
(36)
$$ {I}_{2,k}\left(\uptau \right)=\frac{\left\{{Y}_k\left(\uptau \right)\left[2{Y}_k^2\left(\uptau \right)-1\right]{e}^{-{Y}_k^2\left(\uptau \right)}/\sqrt{\uppi}+0.5\kern0.5em \operatorname{erf}\kern0.5em {Y}_k\left(\uptau \right)-2{Y}_k^4\left(\uptau \right)\kern0.5em \operatorname{erf}\kern0.5em {Y}_k\left(\uptau \right)\right\}}{8}, $$
(37)
$$ {I}_{3,k}\left(\uptau \right)=\frac{\left\langle 0.5\left\{1+\left[2{Y}_k^4\left(\uptau \right)-{Y}_k^2\left(\uptau \right)-1\right]{e}^{-{Y}_k^2\left(\uptau \right)}\right\}/\sqrt{\uppi}-{Y}_k^2\left(\uptau \right) \operatorname {erfc}\ {Y}_k\left(\uptau \right)\right\rangle }{5}, $$
(38)
$$ {I}_{4,k}\left(\uptau \right)=\frac{\left\{0.25{Y}_k\left(\uptau \right)\left[4{Y}_k^4\left(\uptau \right)-2{Y}_k^2\left(\uptau \right)-3\right]{e}^{-{Y}_k^2\left(\uptau \right)}/\sqrt{\uppi}+0.375\kern0.5em \operatorname{erf}\kern0.5em {Y}_k\left(\uptau \right)-{Y}_k^6\left(\uptau \right)\kern0.5em \operatorname{erf}\kern0.5em {Y}_k\left(\uptau \right)\right\}}{6} $$
(39)
$$ {I}_{5,k}\left(\uptau \right)=\frac{\left\langle \left\{1+\left[{Y}_k^6\left(\uptau \right)-0.5{Y}_k^4\left(\uptau \right){-}_k^2\left(\uptau \right)-1\right]{e}^{-{Y}_k^2\left(\uptau \right)}\right\}/\sqrt{\uppi}-{Y}_k^7\left(\uptau \right) \operatorname {erfc}\ {Y}_k\left(\uptau \right)\right\rangle }{7}, $$
(40)

where the functions Yk (τ) have the form (24). If we know the functions Jn,k (τ) (26), (30)–(34) and In,k (τ) (35)–(40), then we can find the dimensionless temperatures \( {N}_k^{(i)}\left(\tau \right) \) averaged over the thicknesses of the layers and the temperature moments \( {M}_k^{(i)}\left(\tau \right) \) by using relations (16)–(21). Substituting these quantities in relations (11)–(14), we determine the stresses \( {\sigma}_k^{(i)}\left(z,t\right) \) , i = 1, 2, 3, k = 1, 2.

Numerical Results

The influence of the time profiles of specific friction power q(i)(t), i = 1, 2, 3, (2), (3) on the temperature fields \( {T}_k^{(i)}\left(z,t\right) \) (4)–(10) in a tribosystem formed by a disk of cast iron (K1 = 51Wm−1K−1 and k1 = 14 · 10−6m2sec−1) and pads made of FM-16L retinax (K2 = 0.65Wm−1K−1, k2 = 4 · 10−7 m2sec−1) was studied in [9]. For the same friction couple, we now study the distributions of dimensionless temperature stresses \( {\sigma}_k^{(i)\ast } \) (ζ, τ), 0 ≤ τ ≤ τs = 1 (13)–(15) in the disk for \( 0\le \zeta \le {a}_1^{\ast }=1 \) and in the pad for \( -0.17={a}_2^{\ast}\le \zeta \le 0 \).

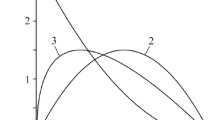
For the rational modes of braking, the evolution of temperature on the contact surface of a pad with a disk occurs in the following specific form: at the beginning of braking, the temperature rapidly increases, then attains its the maximum value, and finally, monotonically decreases up to the complete stop [9]. The maximum value of temperature, the time of its attainment, and the rate of subsequent cooling of the contact surface depend on the time profile of the specific friction power. In view of the indicated time of behavior of temperature in the course of braking, the corresponding normal temperature stresses on the contact surface between the pad and the disk (ζ = 0) are compressive. Moreover, their absolute values increase from zero at the initial time to the maximum values different for the pad and the disk. After this, the compressive stresses begin to decrease (Fig. 2). For three chosen time profiles of the specific friction power q(i)(t), i = 1, 2, 3 [see (2) and (3)], the maximum values of the dimensional compressive stresses on the contact surface between the disk (k = 1) and the pad (k = 2) and of the time of their attainment \( {\tau}_{\mathrm{max}}^{(i)} \) , are equal to 0.26 and 0.08 (k = 1) and 0.56 and 0.25 (k = 2) (Fig. 2a), 0.14 and 0. 47 (k = 1) and 0.51 and 0.7 (k = 2) (Fig. 2b), and 0.15 and 0.24 (k = 1) and 0.48 and 0.53 (k = 2) (Fig. 2c), respectively. In view of the lower heat conduction of retinax, as compared with cast iron, the maximum temperatures and temperature stresses on the working surface of the pad are higher than for the disk. Unlike the stresses acting on the surface of the pad, which are compressive for the entire braking process, the compressive temperature stresses on the surface of the disk become tensile at the times τ* = 0.67, 0.96, and 0.9, and their values at the time of stop are 0.034, 0.026, and 0.03 for i = 1; 2; 3, respectively.

Fig. 2.
figure 2

Time dependences of the dimensionless thermal stresses \( {\sigma}_k^{(i)\ast}\left(\upzeta, \uptau \right) \) : (a) i = 1, (b) i = 2, (c) i = 3, in the disk (solid curves; k = 1) and in the pad (dashed curves; k = 2) at different distances |ζ| from the contact surface.

Full size image

As the distance from the contact surface increases, the compressive stresses in the disk and in the pad decrease and become tensile at a certain depth depending on the braking time τ. The highest values of tensile stresses inside the disk are attained at a depth ζ = 0.5 at the same times for which the compressive stresses on the working surface of the disk are maximum. On approaching the surface \( \zeta ={a}_1^{\ast } \), we see that the temperature stresses in the disk again become compressive. The tensile stresses in the pad increase with depth and attain their maximum values 0.1, 0.08, and 0.08 at the times equal to 0.37, 0.72, and 0.55 for i = 1; 2; 3, respectively, at the distance \( \zeta ={a}_2^{\ast } \).

Conclusions

The results of our investigations demonstrate that the evolution of normal stresses on the working surface of the disk runs in three stages. In the first stage, as the onset of braking, the temperature stresses are compressive. Their absolute values rapidly increase and attain the maximum values. Then, in the second stage, we observe a slow decrease in compressive stresses down to zero. In the last stage, not long before the final stop, the temperature stresses become tensile and attain their highest values when the disk stops. The temperature stresses on the working surface of the pad are compressive for the entire process of braking. Their variations as a function of time repeat the first two stages of the evolution of stresses on the disk surface. The maximum values of compressive stresses on the friction surfaces of the pad and the disk and the times of their attainment strongly depend on the behavior of the specific friction power as a function of time in the course of braking.

At fixed time, we select three sections in the distribution of temperature stresses over the thickness of the disk. In the first section located under the working surface and in the third section \( \left(\zeta ={a}_1^{\ast}\right) \) located near the free surface of the disk, the temperature stresses are compressive. In the second section, placed between the first and third sections, the temperature stresses are tensile. The tensile temperature stresses in the pad monotonically increase with the distance from the working surface.

Upon attainment of a certain ultimate value, the tensile temperature stresses acting on the working surface of the disk at the end of the process of braking may initiate the appearance and development of radial cracks on this surface [14, 15].