Optimal location of piezoelectric actuators for active vibration control of thin axially functionally graded beams

Abstract

Up to now, optimal location for active control studies concern principally multilayers or homogeneous structures. In the case of functionally graded materials, very few papers exist and they only concern cross section variations. In this way, this paper deals with the optimization of piezoelectric actuators locations on axially functionally graded beams for active vibration control. For this kind of structures, the free vibration problem is more complicated as the governing equations have variable coefficients. Here, the eigenproblem is solved using Fredholm integral equations. The optimal locations of actuators are determined using an optimization criterion, ensuring good controllability of each eigenmode of the structure. The linear quadratic regulator, including a state observer, is used for active control simulations. Two numerical examples are presented for two kinds of boundary conditions.

1 Introduction

In recent years, a great number of research results has been produced in optimal location of piezoelectric actuators, for active vibration control of flexible structures. It is obvious that misplaced actuators lead to problems such as the lack of controllability which decreases strongly the performance of the control system.

Many papers dealing with the optimization of actuators location can be found in the literature. An exhaustive review until 2001 is presented in Frecker (2003). Two approaches can be distinguished. The first one consists of combining optimization of actuators locations and controller parameters. For example Bruant et al. (2001), Dhingra and Lee (1995), Kondoh et al. (1990), Nam et al. (1996), Ramesh Kumar and Narayanan (2008), Schulz et al. (2013) and Yang and Lee (1993) propose a quadratic cost function taking into account the measurement error and the control energy. The spatial H2 norm of the closed-loop transfer matrix from the disturbance to the distributed controlled output is used as the optimization index (Liu et al. 2006). The energy dissipation method has been adopted as the criterion for the optimization of the control system (Yang et al. 2005). This method is based on the maximization of dissipation energy due to the control action. Gney and Eskinat (2007) and Hiramoto et al. (2000) suggest the simultaneous design of a computationally simple $H_{\infty }$ controller and optimization of the location of actuators. In this first approach, the optimization criteria are dependent on the choice of controllers. Therefore, the optimal locations obtained using one controller may not be a suitable choice for another one. In the second approach, the optimal locations are obtained independently of the controller definition. Several cost functions are used. Arbel (1981), Biglar et al. (2014), Bruant and Proslier (2005), Devasia et al. (1993), Hac and Liu (1993), Jha and Inman (2003) and Peng et al. (2005) propose the maximization of a controllability criterion using the gramian matrix. Wang and Wang (2001) suggests the maximization of the control forces transmitted by the actuators to the structure. Dhuri and Seshu (2006) proposes a modal controllability index based on the same singular value analysis of the control vector. An optimal placement method using H2 norm is presented (Gawronski 1999; Halim and Reza Moheimani 2003; Qiu et al. 2007).

Additionally, new class of composite materials known as “functionally graded materials” (FGMs), first developed by Japanese Scientists in the late 1980s, has attracted much attention these last years. For example, FGMs made of ceramic and metal are capable of both suffering from high-temperature environment because of better thermal resistance of the ceramic phase and exhibiting stronger mechanical performance of metal phase to guarantee the structural integrity of FGMs. They also can be used to increase the mechanical strength of structures. Due to these superior properties, FGMs find extensive applications in various industries, such as reactor vessels, fusion energy devices, biomedical sectors, aircrafts, space vehicles, defense industries and other engineering structures (Mahamood and Akinlabi 2012).

In the case of functionally graded beams or plates, gradient variation may be oriented in the cross-section or/and in the axial/in-plane direction. Researches have been published about dynamic response and active vibration control of FGMs structures, with functionally graded in the thickness direction.

For examples, Bruant and Proslier (2014) and Gharib et al. (2008) focused on active vibration control of FGM beams, Fakhari and Ohadi (2010), Fu et al. (2013), He et al. (2001), Kargarnovin et al. (2007), Liew et al. (2003), Mirzaeifar et al. (2008), Yiqi and Yiming (2010) considered active control of FGM plates, and Kiani et al. (2013), Narayanan and Balamurugan (2010), Sheng and Wang (2009) and Zheng et al. (2009) the shells’ one.

For graded structures in the axial/in plane directions, the free vibration problems become more complicated because of the governing equation with variable coefficients. Less researchers have treated this kind of structures. Sarkar and Ganguli (2014), Shahba and Rajasekaran (2012) and Wu et al. (2005) found the natural frequencies of axially FGM beams which stiffness and material density are polynomials functions. Li et al. (2013) proposed exact frequency equations of free vibration of exponentially axially FG beams. Finite elements of FGM beam have been developed to study free vibration (Alshorbagy et al. 2011; Shahba et al. 2011). The free and forced vibration of a laminated FGM beam under heat conduction is considered in Xiang and Yang (2008). Caddemi and Calio (2009, 2013) focused on the first frequency on beams structures with a decrease of the rigidity. Huang and Li (2010) has studied free vibration of axially functionally graded beams with non uniform cross section. In their work, natural frequencies are determined by Fredholm integral equations. The Mathematica solver was used as the tools for programming of derived new equations of the FGM beam finite element with spatially varying material properties including several features as the effects of the large axial forces, shear forces and elastic foundation (Aminbgahai et al. 2012; Murin et al. 2010, 2013). Huang et al. (2013) presented a new approach to calculate the frequencies of axially functionally graded Timoshenko beams with non uniform cross section. Simsek et al. (2012) studied the dynamic behavior of an axially FGM beam under action of a moving harmonic load. Liu et al. (2010) and Uymaz et al. (2012) have considered the case of FGMs plates frequencies. Liu et al. (2010) used a semi analytic Levy-integration, while the vibrations solutions are obtained using the Ritz method and the Chebyshev polynomials in Uymaz et al. (2012).

The main focus of these previous papers is the determination of the first eigenfrequencies. The variation of mechanical coefficients induces a variation of their values and also of the eigenmodes shapes. Consequently, the active vibration control efficiency should be hit. To the best of author’s knowledge, no previous papers deal with active vibration control and optimal location of actuators for axially FGMs. In this present work, the influence of the variation of the Young modulus and mass density on the optimal positions and on the active control efficiency is considered. The main difference in the FGM active control and optimization study becomes from the determination of eigenfrequencies and eigenmodes, as they depend on the Young modulus and mass density.

The use of finite elements (FE) method induces restriction for location of actuators: usually, the actuators must located on some entire FE and not on a part of some of them. Consequently, to be able to locate actuators everywhere on the beam, we decide to use here a semi-analytical approach. The original method developed by Huang and Li (2010) is evolved here to study FGM beams equipped with piezoelectric actuators and sensors. In this way, the beam is divided in subdivisions where Hermite interpolation is considered, ensuring regular properties of the eigenmodes approximations.

To implement active control, two important parameters have to be considered: the location of actuators and the control law. First, As seen before, several optimization criteria exist to define the actuators locations. In this work, an optimization criterion using the gramian controllability matrix components is considered. The great advantages of this criterion are its computational simplicity, its non-dependance with the external disturbances and with the applied control law. Moreover, this criteria uses homogeneous components from the controllability matrix, allowing the study of all eigenmodes with the same range. Concerning the choice of the control law, previous work for homogeneous or multilayers structures showed the robustness of the linear quadratic regulator (LQR). Especially, Balamurugan and Narayanan (2001) has compared different usual control laws for active control of plates: the LQR optimal control schemes are more effective than classical controls. Therefore, this algorithm will be used here.

In Sect. 2, the active transversal vibration analytical equations of thin FGM beams, equipped with piezoelectric patches located on the top and bottom faces is presented. The semi-analytical method, developed in Huang and Li (2010), to solve free vibration of axially graded beams is evolved to active control problems. Section 3 deals with the optimization problem for actuators locations. The LQR method including a state observer is computed to simulate the active vibration control. In Sect. 4, three numerical tests are presented.

2 Theoretical formulations

2.1 Axially functionally graded beam equipped with piezoelectric patches

2.1.1 FGM constitutive equations

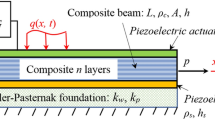
An axially functionally graded beam of length L, width b, thickness h, with co-ordinate system $(O, x, y, z)$ having the origin O is shown Fig. 1.

Fig. 1

A FGM beam equipped with piezoelectric devices

In this work, the Young modulus and the mass density are varying continuously in the axial direction (x-axis). For example, the cross section $x=0$ of the FGM can be a metallic section and the cross section $x=L$ a ceramic one. In this case, according to the power law form, we have:

$$E(x,p)= \left( E_{1}-E_{2}\right) \left( \frac{x}{L}\right) ^{p}\,+\,E_{2}$$

(1)

$$\rho (x,p)= \left( \rho _{1}-\rho _{2}\right) \left( \frac{x}{L}\right) ^{p}\,+\,\rho _{2}$$

(2)

where $E_{1},\,\rho _{1},\,E_{2}$ and $\rho _{2}$ denote respectively values of elasticity modulus and mass density of the right and left ends of the beam and p is the volume fraction index. It represents the material variation profile through the beam length $(0 \le k \le \infty )$. The Poisson’s ratio is considered constant. This power law distribution is one of the most appropriate and also simplest models for a two phase mixture, which is established by Voight-Type estimate (Liu et al. 2010; Markworth et al. 2012).

The constitutive equation of the FGM beam is given by the Hooke’s law:

$${\varvec{\varepsilon }} = \frac{1+\nu }{E} {\varvec{\sigma }} - \frac{\nu }{E} tr({\varvec{\sigma }})$$

(3)

where ${\varvec{\sigma }},\,{\varvec{\varepsilon }}$ and C are respectively the stress vector, the strain vector and the usual constitutive matrix for isotropic structure. Its coefficients are functions of x, from $E(x,p)$.

2.1.2 Piezoelectric constitutive equation

The beam is equipped with $N_{a}$ actuators and $N_{s}$ sensors. In order to consider only pure bending, each actuator and sensor is made up of a pair of piezoelectric materials attached symmetrically. They are assumed to be perfectly bonded to the surface of the structure, and their thickness is assumed to be small compared to the structure thickness. In order to simplify, we consider that the length and thickness of all patches are fixed to $L_{p}$ and $h_{p}$, and the width of piezoelectric is the same as the beam’s one.

The constitutive relationships describing the electrical and mechanical interactions for piezoelectric materials are given as:

$${\varvec{\sigma }}= {\mathbf {c}} {\varvec{\varepsilon }} -{\mathbf {e}}^{\mathbf{T}} \mathbf{E}$$

(4)

$${\mathbf {D}}= \mathbf{e} {\varvec{\varepsilon }} +{\varvec{\epsilon }} \mathbf{E}$$

(5)

Here ${\mathbf {D}}$ is the electric displacement vector, ${\mathbf {E}}=\mathbf{-grad} (\phi )$ is the electric field vector, $\phi$ is the electric potential, ${\mathbf {c}}$ is the elasticity matrix, e is the piezoelectric constants matrix and ${\varvec{\epsilon }}$ is the dielectrical permittivity coefficient matrix. Equation (4) is usually used to model piezoelectric actuators effects on the dynamic of the beam, while Eq. (5) yields to the output equation of sensors (Preumont 1999).

In order to apply and sense electric potential on piezoelectric actuators and sensors, each patch is covered by electrodes at its top and bottom faces. Given their small thickness, we can assume that the electric field is constant and only the component $E_{z}$ is nonzero. It induces that:

$${\mathrm{E}}_{{\mathrm{z}}}=-\frac{{\varDelta \phi }}{{h_{p}}}$$

(6)

where $\varDelta \phi$ is the potential difference across the piezoelectric. Finally, the electric displacement satisfies the electrostatic equilibrium equation:

$${\mathrm{div}}{\mathbf {D}}=0$$

(7)

which reduces to:

$$\frac{\mathrm{{d D}}_{z}}{{\mathrm{d}}z}=0$$

(8)

2.1.3 Governing differential equation

The active vibration control with piezoelectric actuators are mostly used for thin structures. Thereby, thin beams are considered in this work. For this kind of beams, the Euler–Bernoulli theory yields accurate frequency results (Giunta et al. 2011). Then, according to the Euler–Bernoulli theory, the governing bending differential equation of an axially FGM beam equipped with piezoelectric actuators is similar to the one of an homogeneous beam (Bruant et al. 1997; Preumont 1999):

$$ \frac{\partial ^{2} }{\partial x^{2}} \left[ E(x,p)I\frac{\partial ^{2} w }{{\partial x^{2}}}\right] + \rho (x,p) S \frac{\partial ^{2} w}{ \partial t^{2}} =q(x,t)-e_{31}b\left( h_{p}+2h\right) \sum _{i=1}^{N_{a}} \left( \frac{\partial \delta _{a_{i}+{L_{p}/2}}}{\partial x}-\frac{\partial \delta _{a_{i}-{L_{p}/ 2}}}{\partial x}\right) \phi _{ai}(t)$$

(9)

where w is the deflection, q is the distributed transverse loading, I is the inertial moment of cross sectional area, S is the cross sectional area, $\rho (x,p) S$ is the mass distribution, ${a_{i}}$ defines the location of the center of the ith actuator, $\phi _{ai}$ is the applied voltage of the ith actuator and $\delta$ is the Dirac function. In this equation, as usually, the mass inertia moment distribution $\rho (x,p) I$ is neglected.

The application of the active control methods in a dynamic structural problem requires the use of a state space model. To obtain this kind of equation, the solution w is usually decomposed into a normalized orthogonal structural modal basis:

$$w(x,t)=\sum _{n=1}^{\infty } \alpha _{n}(t) W_{n}(x)$$

(10)

where $W_{n}$ is the nth eigenmode. using the orthogonality properties of eigenmodes, the equation of motion becomes the following modal equation:

$$\ddot{\alpha }_{n}(t) +\omega _{n}^{2} \alpha _{n}(t)=\sum _{i=1}^{N_{a}} b_{ni}\phi _{ai}(t)+f_{n} (t)\qquad n=1\ldots \infty$$

(11)

$\alpha _{n},\,\dot{\alpha }_{n}$ and $\ddot{\alpha }_{n}$ represent modal displacement, velocity and acceleration, $\omega _{n}$ and $\zeta _{n}$ are the natural frequency and damping ratio of the nth mode, $f_{n}$ is the modal external disturbance. $b_{ni}$ represents the nth modal actuator force due to the applied voltage of the ith actuator and equals to:

$$b_{ni}=L_{p} \left( 2h+h_{p}\right) e_{31}\left( W_{n}'\left( a_{i}+\frac{L_{p}}{2}\right) -W_{n}'\left( a_{i}-\frac{L_{p}}{2}\right) \right)$$

(12)

2.1.4 Output sensors equations

In the same way, considering an open-circuit configuration in which the total surface charge is assumed to be zero, the voltage of the ith sensor is obtained by integrating the electric field over the sensor (Jha and Inman 2003). From Eq. (8) (Kargarnovin et al. 2007), we get for the ith sensor:

$$ \frac{1}{2} \int _{S_{e}} D_{z}\left( z=-h/2\right) +D_{z}\left( z=-h/2-h_{p}\right) {\mathrm{d}}x{\mathrm{d}}y=0 $$

(13)

where $S_{e}$ is the effective electrode surface, assumed equals to $S_{e}=L_{p}\times l$. By substituting the electric displacement by the relations Eqs. (5) and (8), the electric voltage of the ith sensor, located at $s_{i}$, is given by:

$$ \phi _{si} = {\frac{h_{p}e_{31}}{ L_{p}\epsilon _{33}}\left( h+\frac{h_{p}}{2}\right) \left[ \frac{\partial w }{\partial x}\left( s_{i}+L_{p}/2\right) - \frac{\partial w}{ \partial x} \left( s_{i}-L_{p}/2\right) \right] } $$

(14)

Using the decomposition of the transverse displacement on the modal basis, the output equation of the ith sensor becomes:

$$ {y_{i}(t)=\phi _{si}(t)=\sum _{n=1}^{\infty } C_{in} \alpha _{n}(t) } $$

(15)

$C_{in}$ is the sensing constant of the ith sensor due to the motion of the nth mode. It equals to:

$$ C_{in}=\frac{e_{31}h_{p} }{\epsilon _{33} L_{p}}\left( h+\frac{h_{p} }{ 2}\right) \left( W_{n}'\left( s_{i}+\frac{L_{p} }{2}\right) -W_{n}'\left( s_{i}-\frac{L_{p}}{2}\right) \right. $$

(16)

In order to use these equations for active control applications, the frequencies and eigenmodes have to be calculated. We briefly remind the method in the next section.

2.2 Calculation of the eigenmodes and eigenfrequencies

2.2.1 Introduction to the Fredholm integral equations

Eigenmodes and eigenfrequencies are introduced from the free vibration problem coupling to Eq. (9), where the unknown function w is decomposed as:

$$ w(x,t)=W(x)e^{j\omega t} $$

(17)

Here, the function W and the angular frequency $\omega$ must be solutions of:

$$ \frac{\partial ^{2}}{\partial x^{2}} \left[ E(x,p)I\frac{\partial ^{2} W }{{\partial x^{2}}}\right] - \rho (x,p) S \omega ^{2} W =0 \qquad \forall x \in [0, L] $$

(18)

Introducing the following variables: ${\xi =\frac{x }{L}}$ and $k=\omega ^{2} L^{4}$, Eq. (18) can be rewritten as:

$$ \frac{\partial ^{2}}{\partial \xi ^{2}} \left[ E(\xi ,p)I\frac{\partial ^{2} W}{{\partial \xi ^{2}}}\right] - \rho (\xi ,p) S \omega ^{2} =0 \qquad \forall \xi \in [0, 1] $$

(19)

This equation is more complicated than for homogeneous beams because of variable coefficients.

A novel semi-analytical method is introduced by Huang and Li (2010) using Fredholm integral equations. The main steps are given here. For more details, the reader can referred to Huang and Li (2010). First, the Eq. (18) is converted to an integral one. To this end, we integrate both sides 4th times with respect to $\xi$ from 0 to $\xi$, in order to avoid any derivatives of W. It yields:

$$\begin{aligned} &{E(\xi ,p)I W(\xi )+\int _{0}^{\xi }\left[ E''(s,p)I(\xi -s)-2E'(s,p)I-\frac{1}{6} k \rho (s,p)S(\xi -s)^{3}\right] W(s)ds}\\ &\quad =\,\frac{C_{1}}{6} \xi ^{3}+\frac{C_{2}}{2} \xi ^{2}+C_{3} \xi +C_{4} \end{aligned}$$

(20)

The prime is the derivative with respect to $\xi$. $C_{1},\,C_{2},\,C_{3}$ and $C_{4}$ are integration constants. They are determined in Huang and Li (2010) through considered boundary conditions of both ends of the beam. The study of several boundary conditions yields, for each case, to a Fredholm integral equation as follows:

$$ E(\xi , p)I W(\xi )+\int _{0}^{1}K_{1}(\xi ,s,p)W(s)ds+k\int _{0}^{1} K_{2}(\xi ,s,p)W(s)ds=0 $$

(21)

$K_{1}(\xi ,s,p)$ and $K_{2}(\xi ,s,p)$ depend on the boundary conditions and are respectively functions of E and $\rho$. Their expressions are given in “Appendix” for simply supported beam and clamped–pinned beam.

2.2.2 Approximation of W

For the resulting Fredholm integral equations, several techniques may be employed to determine the numerical solution. The unknown W is approximately expanded as ${W(\xi )=\sum _{n=0}^{N}c_{n}\xi ^{n}}$, where $c_{n}$ are unknown coefficients (Huang and Li 2010). The choice of N is difficult as it must be large enough but a high value can induce instabilities because of bad conditioning. This development is simplest, but the study of active control vibration needs to well known the eigenmodes. Moreover, the use of piezoelectric actuators and sensors introduce derivatives of eigenmodes in dynamic and output equations Eqs. (12), (16), which induce the use of functions of approximation with regular properties (continuity, continuity of the derivatives).

Then, two improvements are considered in this work:

• the beam is discretized in $N_{d}$ subdivisions, and the approximation of W is conducted on each subdivision:

  $$ W(\xi )=W_{i}(\xi ) \qquad \xi \in \left[ \xi _{i}, \xi _{i+1}\right] $$

  (22)

• on the subdivision $[\xi _{i}, \xi _{i+1}]$, W is expanded using an Hermite interpolation:

  $$ W_{i}(\xi )= W_{i}(\xi _{i})P_{0}(\xi )+W_{i}(\xi _{i+1})P_{1}(\xi ) +W_{i}'(\xi _{i})P_{2}(\xi )+W_{i}'(\xi _{i+1})P_{3}(\xi ) $$

  (23)
  $$ W_{i}(\xi )= \sum _{j=0}^{3} c_{ij}P_{j}(\xi ) \qquad \xi \in \left[ \xi _{i}, \xi _{i+1}\right] $$

  (24)

where the Hermite polynomials are:

$$\begin{aligned} &P_{0}(\xi )= {\left( 1+2\frac{\left( \xi -\xi _{i}\right) }{\left( \xi _{i+1}-\xi _{i}\right) }\right) \left( \frac{{\xi -\xi _{i+1}}}{ \left( \xi _{i+1}-\xi _{i}\right) }\right) ^{2}}\\ &P_{1}(\xi )= {\left( 1-2\frac{\left( \xi -\xi _{i+1}\right) }{\left( \xi _{i+1}-\xi _{i}\right) }\right) \left( \frac{{\xi -\xi _{i}}}{ \left( \xi _{i+1}-\xi _{i}\right) }\right) ^{2}} \\ &P_{2}(\xi )= {\left( \xi - \xi _{i}\right) \left( \frac{{\xi -\xi _{i+1}}}{\left( \xi _{i+1}-\xi _{i} \right) }\right) ^{2}} \\ &P_{3}(\xi )= {\left( \xi - \xi _{i+1}\right) \left( \frac{{\xi -\xi _{i+1}}}{\left( \xi _{i+1}-\xi _{i}\right) }\right) ^{2}} \end{aligned}$$

(25)

Inserting Eq. (24) into the Fredholm integral equation Eq. (21) leads to, $\forall \xi \in [\xi _{i}, \xi _{i+1}]$:

$$\begin{aligned} &{\sum _{j=0}^{3} c_{ij}P_{j}(\xi ) E(\xi , p)I +\sum _{j=0}^{3} \sum _{n=1}^{N_{d}}c_{nj}\int _{\xi _{n}}^{\xi _{n+1}} K_{1}(\xi ,s,p)P_{j}(s)ds} \\ &\quad +\,k\sum _{j=0}^{3} \sum _{n=1}^{N_{d}}c_{nj}\int _{\xi _{n}}^{\xi _{n+1}} K_{2}\left( \xi ,s,p\right) P_{j}(s)ds=0 \end{aligned} $$

(26)

The continuity of $W_{i}$ and its derivative $W_{i}'$ induce:

$$\begin{aligned} W_{i}\left( \xi _{i+1}\right)&= c_{i1}=c_{i+1,0} \\ W_{i}'\left( \xi _{i+1}\right)&= c_{i3}=c_{i+1,2} \end{aligned} $$

(27)

Then, the number of unknown coefficients becomes $2(N_{d}+1)$. They are calculated using the same process than in Huang and Li (2010). We multiply both sides of Eq. (26) by $P_{0}(\xi )$ or $P_{1}(\xi )$, and then integrate with respect to $\xi$ between $\xi _{i}$ and $\xi _{i+1}$.

It yields, for $l =0$ or 1:

$$ \begin{aligned} & \sum _{j=0}^{3} c_{ij}\int _{\xi _{i}}^{\xi _{i+1}}P_{l}(\xi )P_{j}(\xi ) E(\xi , p)I d \xi +\,\sum _{j=0}^{3} \sum _{n=1}^{N_{d}}c_{nj} \int _{\xi _{i}}^{\xi _{i+1}}P_{l}(\xi )\int _{\xi _{n}}^{\xi _{n+1}} K_{1}(\xi ,s,p)P_{j}(s)ds d \xi \\&\quad +\,k \sum _{j=0}^{3} \sum _{n=1}^{N_{d}}c_{nj} \int _{\xi _{i}}^{\xi _{i+1}}P_{l}(\xi )\int _{\xi _{n}}^{\xi _{n+1}} K_{2}(\xi ,s,p)P_{j}(s)ds d \xi=0 \end{aligned} $$

(28)

and we obtain $2N_{d}$ equations:

$$ {\sum _{j=0}^{3}\left[ c_{ij}d_{ilj}+ \sum _{n=1}^{N_{d}}c_{nj} K_{1ilj}+k\sum _{n=1}^{N_{d}}c_{nj} K_{2ilj}\right] =0} $$

(29)

where

$$ \begin{aligned} {d_{ilj}}&= {\int _{\xi _{i}}^{\xi _{i+1}} P_{l}(\xi )P_{j}(\xi ) E(\xi , p)I d \xi } \\ {K_{1ilj}}&= {\int _{\xi _{i}}^{\xi _{i+1}} P_{l}(\xi )\int _{\xi _{n}}^{\xi _{n+1}}K_{1}(\xi ,s,p)P_{j}(s)ds d \xi } \\ {K_{2ilj}}&= {\int _{\xi _{i}}^{\xi _{i+1}} P_{l}(\xi )\int _{\xi _{n}}^{\xi _{n+1}}K_{2}(\xi ,s,p)P_{j}(s)ds d \xi } \end{aligned} $$

(30)

These equations can be written in matrix form:

find $(k, {\mathbf {U}})$ solution of:

$$ \left( {\mathbf {d}}+{\mathbf {K}}_{\mathbf{1}}\right) {\mathbf {U}} = -k {\mathbf {K}}_{\mathbf{2}} \mathbf{U} $$

(31)

where ${\mathbf {U}}^{\mathbf{T}}=(c_{10}, c_{11}, c_{20},\ldots c_{N_{d}N_{d}})$, size $2N_{d}+2$, is the unknown vector. In order to obtain a $2N_{d} \times 2N_{d}$ eigenvalue problem, the boundary conditions are used to reduce the number of unknowns. The components of matrix ${\mathbf {d}},\,{\mathbf {K}}_{\mathbf{1}}$ and ${\mathbf {K}}_{\mathbf{2}}$ are respectively in terms of $d_{ilj},\,K_{1ilj},\,K_{2ilj}$.

The solution of problem Eq. (31) gives the eigenfrequencies and eigenmodes of the axially FGM beam. Therefore, the optimization of actuators locations for active vibration control can be considered.

3 The optimization of actuators locations

To set up active control of beams, two main steps have to be considered: the determination of piezoelectric actuators locations and the implementation of the control law. In this section, we briefly present the optimization criterion for actuators locations.

3.1 The state equation

To use the automatic tools, Eqs. (11) and (15) are written in an usual state-space form, considering the N first eigenmodes and using the state vector ${\mathbf {x}}$ (size 2N):

$$ {\mathbf {x}}= \left\{ \omega _{n} \alpha _{n} \qquad \dot{\alpha }_{n}\right\} ^{T} $$

(32)

$$ \frac{d }{dt} {\mathbf {x}}= {\mathbf {Ax}} + {\mathbf {B}}{\varvec{\Phi }} +\mathbf{g} $$

(33)

$$ {\mathbf {y}}= {\mathbf {Cx}} $$

(34)

where ${\mathbf {A}}_{(2N,2N)},\,{\mathbf {B}}_{(2N,N_{a})}$ and ${\mathbf {C}}_{(N_{s},2N)}$ are the state, control and output matrices given by:

$$ {\mathbf {A}}= \left[ \begin{array}{ll} [0] &{} [\omega _{n}] \\ -[\omega _{n}] &{} -[2 \zeta _{n} \omega _{n}] \\ \end{array} \right] $$

(35)

$$ {\mathbf {B}}^{T}= \left[ \begin{array}{ll} [0]&[b_{ni}] \end{array} \right] $$

(36)

$$ {\mathbf {C}}= \left[ \begin{array}{ll} [C_{in}]&{}[0]\\ \end{array} \right] $$

(37)

${\varvec{\Phi }}$ and y are respectively the input and output vectors which their nth components are ${\varPhi }_{n}=\phi _{an}(t)$ and ${y}_{n}=\phi _{sn}(t)$. The components $-2 \zeta _{n} \omega _{n}$ are added in the matrix A in order to take into account the natural damping of each mode.

3.2 The optimization criterion for piezoelectric actuators locations

The optimization criterion used in this paper is instigated from the optimization function developed for homogeneous structures in Bruant and Proslier (2005). It ensures good controllability of each mode considering them with homogeneity and not globally as it is usually done.

The objective here is to find actuators locations that minimize the control energy required to bring the modal system (considering the N first eigenmodes) to a desired state $\{ x_{T}\}$ after some time T:

$$ { J=\min _{{\varvec{\Phi }}}\int _{0}^{T} {\varvec{\Phi }}^{T}{\varvec{\Phi }}dt} $$

(38)

The optimal solution gives the following optimal control energy:

$$ J=\left[ {\mathbf {e}}^{\mathbf{AT}} \mathbf{x}_{\mathbf{0}}-\mathbf{x}_{\mathbf{T}}\right] ^{\mathbf{T}} \mathbf{W}^{\mathbf{-1}}\mathbf{(T)}\left[ \mathbf{e}^{\mathbf{AT}} \mathbf{x}_{\mathbf{0}}-\mathbf{x}_{\mathbf{T}}\right] $$

(39)

where ${\mathbf {W(T)}}$ is the controllability gramian matrix defined by:

$$ {\mathbf {W(T)}}=\int _{0}^{T} {\mathbf {e}}^{\mathbf{At}}\mathbf{BB}^{\mathbf{T}}\mathbf{e}^{\mathbf{A}^{\mathbf{T}}\mathbf{t}}dt $$

(40)

Minimizing J with respect to the actuators locations consists in minimizing ${\mathbf {W}}^{\mathbf{-1}}\mathbf{(T)}$ or maximizing a measure of the controllability gramian matrix (Hac and Liu 1993).

Hac and Liu (1993) has shown that instead of using ${\mathbf {W(T)}}$, a steady state ${\mathbf {W}}_{\mathbf{c}}$ can be considered to eliminate the dependency of the solution T. $W_{c}$ tends to a diagonal form with the nth diagonal term equals to

$$ (W_{c})_{nn}=(W_{c})_{n+N,n+N}= =\sum _{j=1}^{N_{a}} \frac{b_{nj}^{2} }{{ 4 \zeta _{n}\omega _{n}}} =\frac{1}{{4 \zeta _{n} \omega _{n}}} \sum _{j=1}^{N_{a}} b_{nj}^{2} $$

(41)

$(W_{c})_{nn}$ equals to the energy transmitted from the actuators to the structure for the nth eigenmode.

Hence, if the eigenvalue $(W_{c})_{nn}$ is small, the nth eigenmode is difficult to control: there is no controllability for the system.

The usual criteria take into account globally the eigenmode. Instead of maximizing a global norm of ${\mathbf {W}}_{\mathbf{c}}$ which means minimizing the electrical energy, a first optimization criterion could be: to find the actuators location which maximize

$$ {\mathop {\mathrm{min}}\limits _{n=1,\ldots N}} \left( W_{c}( a_{1},\ldots a_{N_{a}}) \right) _{nn} $$

(42)

But as the components of ${\mathbf {W}}_{\mathbf{c}}$ have not the same range, solving this problem can induce the study of particular modes instead of each of them, and then the obtained locations will not be optimal.

Consequently, each term $(W_{c})_{nn}$ is divided by its maximal value obtained when the nth mode is the specific mode to be controlled. This maximal value is the maximal energy which can be transmitted from the actuators for the nth eigenmode.

Hence, using the homogeneous components, the optimization problem becomes: to find the actuators location which maximize

$$ { J_{A}= \min _{n=1,N}\frac{\left( W_{c}\left( a_{1},\ldots a_{N_{a}}\right) \right) _{nn}}{{ \max _{ a_{1},\ldots a_{N_{a}}}\left( W_{c}\left( a_{1},\ldots a_{N_{a}}\right) \right) _{nn}}} =\min _{n=1,N} \frac{{\sum _{j=1}^{N_{a}} b_{nj}^{2}}}{{\max _{ a_{1},\ldots a_{N_{a}}} \sum _{j=1}^{N_{a}} b_{nj}^{2}}}} $$

(43)

and, ${ \forall n=1,\ldots N \quad 0\le \frac{(W_{c}( a_{1},\ldots a_{N_{a}}) )_{nn}}{{ \max _{ a_{1},\ldots a_{N_{a}}}(W_{c}( a_{1},\ldots a_{N_{a}}))_{nn}}} \le 1}$

The greatest advantage of this criterion is that all modes are studied with the same range. Furthermore, the expression inside Eq. (43) has a physical meaning: it is the mechanical energy transmitted for the nth mode divided by the maximal mechanical energy that could be received.

4 Numerical examples

In this section, a first test is carried out to show the effectiveness of the suggested approximation of the eigenmodes. Then, two applications are presented. The first one deals with the optimal location of one actuator on a simply supported beam. In the second one, the optimization of one and two actuators is considered in the case of a clamped–pinned beam. For theses two applications, the FGM beams are equipped with actuators made of PZT5A piezoelectric patch. One PVDF piezoelectric sensor is used, located in $x=0.2\,\hbox {m}$. Piezoelectric rigidity and mass are neglected in the mechanical equation. The active control of the four first eigenmodes is computed and simulations show the influence of the parameter p in results.

For each application, the number and length of actuators are fixed. The criterion (43) is used to find the optimal location of actuators. As the studied structures are beams, there is one variable optimization for each actuator. In this way, there is not need to use specific numerical optimization method. For more complex structures, the use of biologically-inspired optimization techniques (like genetic algorithm, ant colony optimization, particle swarm optimization...) should well suited.

4.1 Free vibration analysis of two axially FGM beams

In this subsection, a numerical example presented in Huang and Li (2010) is studied. It considers the case of Young modulus and mass density of trigonometric functions:

$$ E(x) =E_{0}\left[ 1+ \alpha cos(\pi x)\right] , \qquad \rho (x)=\rho _{0}\left[ 1+ 4 \alpha cos(\pi x)\right] $$

(44)

The geometrical and mechanical properties of the beam are detailed in Table 1.

Table 1 Geometrical and mechanical characteristics of the beam, example 1

For several values of $\alpha$, the first three non-dimensional natural frequencies, given by Huang and Li (2010) $\varOmega _{n}= \omega _{n} L^{2} \sqrt{\rho _{0} S/E_{0}I}$ are calculated from our suggested approximation (with the Hermite interpolation on 11 subdivisions). Results are compared with those of Huang and Li (2010), the results obtained using the FGM finite element developed in Alshorbagy et al. (2011) (with 300 elements) and the analytical solution (when $\alpha$ equals 0). They are shown, for a simply supported beam and a clamped–pinned beam, respectively, in Tables 2 and 3. The results given by the different methods are very similar. The suggested improvements induce frequencies close to analytical solution and finite element results. Values are much precise than with the polynomial approximation, especially for the clamped–pined beam.

Table 2 Non-dimensional natural frequencies for the simply supported beam with the Young modulus and mass density given by (44)

Table 3 Non-dimensional natural frequencies for the clamped–pinned beam with the Young modulus and mass density given by (44)

4.2 Optimal location of one actuator on a simply supported beam

4.2.1 Description of the test

In this test, a simply supported FGM beam is considered. The Young’s modulus and the mass density are given by Eqs. (1) and (2). The geometrical and mechanical properties of the beam and piezoelectrics are detailed in Tables 4, 5 and 6. The material 1 is ceramic and material 2 is metallic. Frequencies are given Table 7 for different values of p. $p=0$ means that the beam is homogeneous made of ceramic material, instead of $p=50$ is the case of a quasi-homogeneous metallic beam. It induces that frequencies decrease according to p as the beam becomes more flexible. The influence of the parameter p on the eigenmodes can also be shown. For several values of p, the beam becomes not materially symmetric and consequently, the shapes of the eigenmodes are modified. Figures 2, 3, 4 and 5 shows the normalized eigenmodes in the case of $p=0$ and the much different case, obtained with $p=1.5$. There is a small shift between the two curves. Especially, the maximal values of each eigenmode are obtained for different values of x. Even if the difference of the two curves seems to be light, these variations can affect the optimization and active vibration results.

Table 4 Geometrical characteristics of the simply supported beam and the piezoelectric patch

Table 5 Characteristics of piezoelectric patch PVDF and PZT5A

Table 6 Mechanical characteristics of the FGM beam

Table 7 Frequencies of the simply supported beam

Fig. 3

Second eigenmode of simply supported FGM beam for $p=0$ (blue cross) and $p=1.5$ (red line). (Color figure online)

Fig. 4

Third eigenmode of simply supported FGM beam for $p=0$ (blue cross) and $p=1.5$ (red line). (Color figure online)

Fig. 5

Fourth eigenmode of simply supported FGM beam for $p=0$ (blue cross) and $p=1.5$ (red line). (Color figure online)

The optimal location of the piezoelectric actuator is determined by Eq. (43) for several values of coefficient p. Results are given Table 8. For $p=0$, the beam is homogeneous and the material properties are constant. The beam being symmetric, it is obvious to obtain two symmetric optimal locations since more than one mode is considered. For the other values of p, the material symmetry of the beam disappeares and it induces only one optimal location. The maximal difference between optimal location for homogeneous beam and FGM beam is obtained with $p=[1;1.5]$. In this case, the length between the two optimal locations equals $0.1123\,\hbox {m}$. For this kind of application, the use of the optimal location of actuator obtained for homogeneous beam, for an FGM axially beam, can induce not efficient active control. To evaluate the sensitivity of the FGM properties on the efficiency of the active control, we suggest the use of a degree of controllability in the next subsection.

Table 8 Optimal location of actuator (m) for the simply supported beam

4.2.2 A comparison parameter: a degree of controllability

To compare the efficiency of the obtained locations, we use the following degree of controllability, and defined, in the general case, for the mode n by:

$$ { DEGCn=\frac{{\sum _{j=1}^{N_{a}} b_{nj}^{2} }}{{\max _{one\,actuator} b^{2}_{n1}}} \times 100 } $$

(45)

It equals to the energy transmitted from the actuators to the structure for the nth mode divided by the maximal value energy obtained if the ith mode is optimally controlled by one actuator (if one actuator is located in order to optimally control this mode). When the 4 first degrees are over 100 % it means that each mode $(n=1,\ldots 4)$ is better controlled than when it is specifically controlled by one actuator.

In Table 9, for each value of parameter p, the degree of controllability of each mode is given, for:

• case 1: the actuator is located at the optimal location obtained for the FGM beam, with parameter p,

• case 2: the actuator is located at one of the optimal locations obtained for the homogeneous beam.

Results show that the use of the optimal location obtained for the homogeneous beam, in the case of an FGM beam, can strongly change the quality of the active control of one or several eigenmodes. The most important aim is to optimize the controllability degree of all modes: they should be over a minimal value, to insure a “good level of controllability”. For example, for $p=1.5$, case 1 induces a worst degree of controllability equals to 44 % (for modes 1 and 4) instead of, in case 2, the worst degree of controllability is 10 % (for mode 3). It means that this eigenmode will be very badly controlled. This variation can be shown Figs. 6, 7, 8 and 9, where each degree of controllability is plotted in relation with the actuator location. For $p=1.5$, the controllability degrees decrease over the beam length as the beam is stiffener at the right end $(x=L)$.

Table 9 Degree of controllability for each optimal actuator location on the simply supported beam

Fig. 6

Variation of the controllability degree for mode 1 of the simply supported FGM beam for $p=0$ (red line) and $p=1.5$ (blue cross). (Color figure online)

Fig. 7

Variation of the controllability degree for mode 2 of the simply supported FGM beam for $p=0$ (red line) and $p=1.5$ (blue cross). (Color figure online)

Fig. 8

Variation of the controllability degree for mode 3 of the simply supported FGM beam for $p=0$ (red line) and $p=1.5$ (blue cross). (Color figure online)

Fig. 9

Variation of the controllability degree for mode 4 of the simply supported FGM beam for $p=0$ (red line) and $p=1.5$ (blue cross). (Color figure online)

In order to show the possible impact of the choice of actuator location to the efficiency of active control, the LQR method (Bruant and Proslier 2014; Kailath 1980), including a state observer, is developed from the state equations Eq. (33) considering the 4 first eigenmodes. In these applications, the matrix ${\mathbf {Q}}$ used in the LQR method is chosen so that ${\mathbf {x}}^{\mathbf{T}}\mathbf{Qx}$ represents the mechanical energy. The matrix ${\mathbf {R}}$ is considered diagonal such that the maximal values of ${\varvec{\Phi }}$ are less than the maximal admissible values for the piezoelectric materials under consideration.

4.2.3 Some results of active control

According to the applied load and if several eigenmodes are considered, the efficiency of the active control will decrease when the optimal location obtained for the homogeneous beam is used in the case of FGM beam. We present two examples.

• (a) Release test

A first example is the case of a release test where the third mode is excited:

$$ \omega _{3} \alpha _{3}(t=0)= 2, \quad \omega _{n}\alpha _{n}(t=0)=0 \quad n=1,2,4 $$

(46)

To show this sensitivity, we consider the FGM beam with $p=1.5$ and we use three possible locations for the actuator:

• the optimal location for $p=1.5$: $a_{1}=0.0886\,\hbox {m}$

• the first optimal location for $p=0$: $a_{1}=0.2\,\hbox {m}$

• the second optimal location for $p=0$: $a_{1}=0.3\,\hbox {m}$.

Test 1 compares the two first locations. The sensor output and the required input actuator voltage are plotted in Figs. 10 and 11. The second test compares the first and last locations. Results are given in Figs. 12 and 13.

In test 1, the results are quite similar. The time response of the output sensor is lightly more reduced using the optimal location of $p=1.5$. On the other hand, in the second test, the plots are very different. The efficiency of the active control decreases strongly when the actuator is located in $a_{1}=0.3\,\hbox {m}$. This is due to the 3th mode of the FGM beam which degree of controllability is <10 %.

• (b) A sinusoidal load

Here, a sinusoidal load is applied along the FGM beam, which load frequency value is near to the second frequency of the FGM beam:

$$ F(t)=5.10^{4} sin (1340t) $$

We consider again the FGM beam with $p=1.5$ and two possible locations for the actuator are used:

• the optimal location for $p=1.5$: $a_{1}=0.0886\,\hbox {m}$

• the second optimal location for $p=0$: $a_{1}=0.3\,\hbox {m}$.

The sensor output and the required input actuator voltage are plotted in Figs. 14 and 15. The vibrations are actively controlled in <0.6 s in the two cases. But, the second case needs twice more electric energy than the first case.

Fig. 10

Test 1: the output of sensor for $a_{1}=0.0886\,\hbox {m}$ and $a_{1}=0.2\,\hbox {m}$

Fig. 11

Test 1: the input actuator for $a_{1}=0.0886\,\hbox {m}$ and $a_{1}=0.2\,\hbox {m}$

Fig. 12

Test 2: the output of sensor for $a_{1}=0.0886\,\hbox {m}$ and $a_{1}=0.3\,\hbox {m}$

Fig. 13

Test 2: the input actuator for $a_{1}=0.0886\,\hbox {m}$ and $a_{1}=0.3\,\hbox {m}$

Fig. 14

A sinusoidal load: the output of sensor for $a_{1}=0.0886\,\hbox {m}$ and $a_{1}=0.3\,\hbox {m}$

Fig. 15

A sinusoidal load: the input actuator for $a_{1}=0.0886\,\hbox {m}$ and $a_{1}=0.3\,\hbox {m}$

4.3 Optimal location of one and two actuators on a clamped–pinned beam

In this last example, we consider a clamped–pinned FGM beam equipped with one or two actuators. Here, material 1 is metallic and material 2 is ceramic. The geometrical properties are given in Table 10. Material properties are the same than in the previous example. Frequencies and eigenmodes are given Table 11 and Figs. 16, 17, 18 and 19. Here, the beam is more flexible for $p=0$. There is again a shift between curves for each eigenmode which can involve variation of optimal location in respect with the parameter p.

Table 10 Geometrical characteristics of the clamped–pinned beam and the piezoelectric patch

Table 11 Frequencies of the clamped–pinned FGM beam

Fig. 16

First eigenmode of clamped–pinned FGM beam for $p=0$ (blue cross) and $p=1.5$ (red line). (Color figure online)

Fig. 17

Second eigenmode of clamped–pinned FGM beam for $p=0$ (blue cross) and $p=1.5$ (red line). (Color figure online)

Fig. 18

Third eigenmode of clamped–pinned FGM beam for $p=0$ (blue cross) and $p=1.5$ (red line). (Color figure online)

Fig. 19

Fourth eigenmode of clamped–pinned FGM beam for $p=0$ (blue cross) and $p=1.5$ (red line). (Color figure online)

The optimization of actuators location was studied for different values of p. Here we present results for the two values of p which induce maximal differences: $p=0$ and $p=1.5$.

4.3.1 Optimal location of one actuator

First, in the case of one actuator, we get:

• for $p=0$: $a_{1}=0.02\,\hbox {m}$

• for $p=1.5$: two optimal locations are obtained: $a_{1}=0.02\,\hbox {m}$ or $a_{1}=0.5875\,\hbox {m}$

In this two cases, the location $a_{1}=0.02\,\hbox {m}$ is optimal or almost optimal. This is due to the clamped edge of the beam. Consequently, in the case of one actuator, the use of the optimal location of homogeneous beam, for FGM beam will give good results.

4.3.2 Optimal location of two actuators

In this subsection, the beam is equipped with two actuators. We get:

• for $p=0$: $a_{1}=0.02\,\hbox {m}$ and $a_{2}=0.317\,\hbox {m}$

• for $p=1.5$: $a_{1}=0.02\,\hbox {m}$ and $a_{2}=0.614\,\hbox {m}$

The location of the second actuator is very different for the two considered cases. In Table 12, the degree of controllability of each mode is given, for:

• case 1: the actuators are located at the optimal locations obtained for the FGM beam, with parameter $p=1.5$,

• case 2: the actuators are located at the optimal locations of the homogeneous beam.

Table 12 Degree of controllability for the FGM clamped–pinned beam with $p=1.5$

If the optimal locations obtained for $p=0$ are used for the FGM beam, the minimal degree of controllability becomes 71 %, due to the third frequency. In this case, as in the previous example, vibrations induced by initial conditions or external loads exciting especially the third eigenmode, won’t be efficiently controlled. Results for the release test with $\alpha _{3}(t=0)=1$ and $\alpha _{1}(t=0)=\alpha _{2}(t=0)=\alpha _{4}(t=0)=0$ are plotted Figs. 20, 21 and 22. Vibrations vanish in <1 s in the first case, instead of in the second case it needs 2 s.

Fig. 20

Output actuators for clamped–pinned FGM beam, locations of case 1

Fig. 21

Output actuators for clamped–pinned FGM beam, locations of case 2

Fig. 22

Output sensor (located in $s_{1}=0.2\,{{\rm m}}$, for clamped–pinned FGM beam, cases 1 and 2

5 Conclusion

In this paper, the optimization of actuators location is considered for active vibration control of thin axially FGM beams. The optimization approach consists in maximizing a measure of the homogeneous components of the gramian controllability matrix. The variation of mechanical properties along the beam induces a more complex vibration equations than for homogeneous beams. Eigenmodes and eigenfrequencies are obtained from Fredholm integral equations, considering an Hermite interpolation of eigenmodes, on each subdivision of the FGM beam.

The simulations point out, for simple structures like beams, that the optimal actuators locations for FGM structures can be very different with the ones obtained for homogenous structures. Therefore, the use of homogeneous beam locations in the case of FGM beams can decrease the efficiency of the active control as some eigenmodes are less controllable. Vibrations can be controlled slowly and/or the vibration control need higher electric input. The use of others optimization criteria would give same comments.

This work shows that the optimization of actuators location must be solved taking into account the FGM properties of the considered structure. Conclusions can be extended to sensors location, as the optimization approaches are similar. In future works, this study could be applied to more complex structures like FGM in plane-plates and shells equipped with several piezoelectric actuators and sensors. Some others investigations could be to use this work for cracked structures.

Appendix: Expressions of \(K_{1}(\xi,s,p)\) and \(K_{2}(\xi,s,p)\)

The following expressions are given in Huang and Li (2010).

1.1 For simply supported beam

$$ \begin{aligned} K_{1}(\xi,s,p)&= (\xi -1)I\left[ E''(s,p)s+2E'(s,p)\right] , \qquad 0 \le s \le \xi \\&= \xi I\left[ (s-1)E''(s,p)+2E'(s,p)\right] , \qquad \xi \le s \le 1 \end{aligned} $$

(47)

$$ \begin{aligned} K_{2}(\xi , s,p)&= {\frac{S}{6} \rho (s,p)s(1-\xi )\left( \xi ^{2}+s^{2}-2\xi \right) , \qquad 0 \le s \le \xi } \\&= {\frac{S}{6} \rho (s,p)\xi (1-s)\left( \xi ^{2}+s^{2}-2s\right) , \qquad \xi \le s \le 1} \end{aligned} $$

(48)

1.2 For clamped–pinned beam

$$ \begin{aligned} K_{1}(\xi , s,p)&= {\frac{1}{ 2} \xi ^{2}(\xi -3)I\left[ E''(s,p)(1-s)-2E'(s,p)\right] +\,IE''(s,p) \left( \xi -s\right) -2IE'(s,p)}, \\ &\qquad 0\le s \le \xi \\&= {\frac{1}{2}\xi ^{2}\left( \xi -3\right) I\left[ E''(s,p)(1-s)-\,2E'(s,p) \right] }, \qquad \xi \le s \le 1 \end{aligned} $$

(49)

$$ \begin{aligned} K_{2}(\xi , s,p)&= {\frac{S}{ 12} \rho (s,p)s^{2}(\xi -1)\left[s(\xi ^{2}-2\xi -2)-3(\xi ^{2}-2\xi )\right], \qquad 0 \le s \le \xi } \\&= {\frac{S}{12} \rho (s,p)\xi ^{2}(s-1)\left[ \xi (s^{2}-2s-2)-3(s^{2}-2s)\right] , \qquad \xi \le s \le 1} \end{aligned} $$

(50)