1 Introduction

The plate model is widely used in various fields, and the earliest modeling methods cannot satisfy the requirements of accuracy and efficiency, which prompts people to conduct in-depth research on plate model. A system of equations is developed for the theory of bending of thin elastic plates which takes into account the transverse shear deformability of the plate by Reissner [1]. The results show that this theory can be applied to other problems with deviations from the classical plate theory. A two-dimensional theory of flexural motions of isotropic, elastic plates is deduced from the three-dimensional equations of elasticity by Mindlin [2]. A general three-dimensional solution for the statics and dynamics of laminated plates of orthotropic materials is presented by Srinivas and Rao, and the solution is in the series form [3]. Özakça analyzed the plate structure, studied the characteristics of tetrahedral three-dimensional solid elements of various nodes, and compared and tested them at the same time [4]. Classical lamination theory and first-order and Reddy's higher-order shear deformation theory are considered by Carvelli, and the deformation and plate thickness stress distribution are compared with equivalent three-dimensional elastic solutions. Sufficiently accurate equilibrium equations of stress distribution are obtained from CLT, FSDT, and HSDT [5]. However, the classical plate theories have inherent disadvantages. The transverse shear deformation is ignored in CPT, and a constant shear stress is assumed in FSDT.

More precise plate models are required to solve the problems of structures with complicated boundary conditions and geometries. The equivalent single-layer model (ESL) and the layer-wise model (LW) were considered by Ballhause. A unified formulation for the electro-mechanical analysis of multilayer plates embedding piezo-layers was proposed [6]. The characteristics of functionally graded material (FGM) plates under lateral mechanical loads were studied by Brischetto, and the unified formulation (UF) and Reissner's mixed variational theorem (RMVT) are extended to FGMs [7]. The Kirchhoff and Reissner–Mindlin theories were improved by Carrera by adding generalized displacement variables to the Taylor-like series expansion of the thickness plate direction [8]. Carrera and Cinefra adopted the tensor component mixed interpolation technique to reduce the influence of shear locking on the results [9,10,11]. Mixed plate elements for accurate evaluation of transverse mechanical stresses and electrical displacement are developed and compared by Carrera and Büttner [12]. Meanwhile, classical formulation based on the principle of virtual displacements is implemented for comparison purposes. Classical (Kirchhoff and Reissner–Mindlin), refined (Reddy and Kant), and other higher-order displacement fields are implemented up to fourth-order expansion by Carrera and Miglioretti [13]. A number of classical and refined two-dimensional theories for the analysis of metallic and composite layered plates are evaluated by Carrera. And thin plate, shear deformation, and higher-order plate theories are compared [14].

With further study of plates, it is found that Carrera unified formulation is more accurate than traditional methods in describing the displacement field of plate models. The free vibration of composite plates with Carrera unified formulation under the finite element framework is analyzed by Pagani, Zappino, Carrera, and Daraei. The solution under mechanical response is given [15,16,17,18]. Carrera and Zappino have compared the results obtained by using an improved one-dimensional model based on CUF theory with classical finite element analysis [19]. Piezoelectric laminated plate is studied by Jiang [20] and Rouzegar [21] based on refined plate theory. Yarasca adopted Carrera unified formulation and proposed an effective objective optimization method. An improved equivalent single-layer plate theory with multiple displacements and multiple stresses as output parameters is developed [22, 23]. The free vibration behavior of functionally graded plates with in-plane material inhomogeneity is studied by Xue [24] by combining isometric analysis and refined plate theory. Cinefra [25] applied Carrera unified formulation to describe the fluid cavity with a standard pressure-based finite element formulation of the acoustic field. Meanwhile, the numerical results of the case of the plate back to a fluid filled cavity are given. Foroutan [26] adopted a total Lagrange approach and established the unified formulation of the full geometrically nonlinear refined plate theory. Van Do establishes thermal buckling response based on higher-order shear deformation plate theory and proposes an enhanced mesh-free radial point interpolation method (RPIM) [27]. According to the Carrera unified formulation (CUF), all equations for shells of revolution of higher order are presented by Carrera [28]. Meanwhile, Carrera and Zozulya research a Navier closed-form solution method for elastic shells of revolution developed using the CUF approach [29]. A layer-wise beam model based on the CUF theory was established by Hui to solve the geometrically nonlinear problem of sandwich beams [30]. CUF higher-order theory is used by Nagaraj [31] and Ferreira [32] to analyze the damage of composite plates. Carrera established a higher-order model of orthotropic plates [33, 34]. CUF theory and multi-objective particle swarm optimization algorithm are adopted by Rahmani to study the multi-objective optimal material distribution of porous functionally graded plates under free vibration [35, 36].

In this paper, the mechanics properties of composite plate are analyzed based on the Carrera unified formulation. And the results are compared with the commercial finite element method (FEM) code analyses. Finally, the geometric parameters of the higher-order model are optimized according to the analysis results, and some meaningful conclusions are found.

2 Geometric and constitutive relations of composite plates

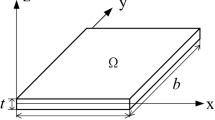
The geometric structure and coordinate system of the composite plate are shown in Fig. 1. It is made of three different metal plates, and the thickness is t1, t2, and t3, respectively, in which Ω represents the cross section of the composite plate and a and b represent the length and width of the composite plate, respectively. For the convenience of research, the upper surface is the xoy plane of coordinates and the thickness direction is the z-axis. The Cartesian coordinate system is established.

Fig. 1
figure 1

Composite plate geometric structure and coordinate system

Full size image

The stress vector σ and strain vector ε are divided into six components, expressed as follows:

$$\begin{gathered} {\varvec{\sigma}} = \left[ {\begin{array}{*{20}l} {\sigma_{xx} } &\quad {\sigma_{yy} } &\quad {\sigma_{xy} } &\quad {\sigma_{xy} } &\quad {\sigma_{xz} } &\quad {\sigma_{zz} } \\ \end{array} } \right]^{T} \hfill \\ {\varvec{\varepsilon}} = \left[ {\begin{array}{*{20}l} {\varepsilon_{xx} } &\quad {\varepsilon_{yy} } &\quad {\varepsilon_{xy} } &\quad {\varepsilon_{xy} } &\quad {\varepsilon_{xz} } &\quad {\varepsilon_{zz} } \\ \end{array} } \right]^{T} \hfill \\ \end{gathered}$$
(1)

where the same subscripts stand for the normal stress (strain) and the different subscripts stand for the shear stress (strain).

Based on the hypothesis of small deformation, the relationship between strain and displacement can be expressed as:

$${\varvec{\varepsilon}} = {\varvec{Bu}}$$
(2)

where linear differential operator matrix B can be expressed as:

$$\varvec{B} = \left[ {\begin{array}{*{20}l} {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \hfill &\qquad 0 \hfill &\qquad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \hfill &\qquad {{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}}} \hfill &\qquad 0 \hfill &\qquad 0 \hfill \\ 0 \hfill &\qquad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \hfill &\qquad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \hfill &\qquad 0 \hfill &\qquad {{{\partial z} \mathord{\left/ {\vphantom {{\partial z} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \hfill &\qquad 0 \hfill \\ 0 \hfill &\qquad 0 \hfill &\qquad 0 \hfill &\qquad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \hfill &\qquad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \hfill &\qquad {{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}}} \hfill \\ \end{array} } \right]$$
(3)

According to Hooke's law, the stress–strain relationship can be expressed as:

$${\varvec{\sigma}} = \user2{C\varepsilon }$$
(4)

where C is the material coefficient matrix. It can be expressed by elastic modulus E and Poisson's ratio v, given as follows:

$${\varvec{C}} = \left[ {\begin{array}{*{20}l} {2\mu + \lambda } & \quad\lambda &\quad \lambda &\quad {} &\quad {} & {} \\ \lambda &\quad {2\mu + \lambda } &\quad \lambda &\quad {} &\quad {} &\quad {} \\ \lambda &\quad \lambda &\quad {2\mu + \lambda } &\quad {} &\quad {} &\quad {} \\ {} &\quad {} &\quad {} &\quad \mu &\quad {} &\quad {} \\ {} &\quad {} &\quad {} &\quad {} &\quad \mu &\quad {} \\ {} &\quad {} &\quad {} &\quad {} &\quad {} &\quad \mu \\ \end{array} } \right]$$
(5)

where μ and λ are, respectively:

$$\mu = \frac{E}{{2\left( {1 + v} \right)}}{ , }\lambda { = }\frac{vE}{{\left( {1 + v} \right)\left( {1 - 2v} \right)}}$$
(6)

In order to obtain the following fundamental nuclei, material coefficient matrix C is divided into Cpp, Cnn, Cpn, and Cnp, expressed as:

$${\varvec{C}}_{pp} = \left[ {\begin{array}{*{20}l} {C_{11} } &\quad {C_{12} } & \quad 0 \\ {C_{12} } &\quad {C_{22} } &\quad 0 \\ 0 &\quad 0 &\quad {C_{66} } \\ \end{array} } \right],{\varvec{C}}_{nn} = \left[ {\begin{array}{*{20}l} {C_{55} } &\quad 0 &\quad 0 \\ 0 &\quad {C_{44} } &\quad 0 \\ 0 &\quad 0 &\quad {C_{33} } \\ \end{array} } \right],{\varvec{C}}_{pn} = {\varvec{C}}_{np}^{T} = \left[ {\begin{array}{*{20}l} 0 &\quad 0 &\quad {C_{13} } \\ 0 &\quad 0 &\quad {C_{23} } \\ 0 &\quad 0 &\quad 0 \\ \end{array} } \right]$$
(7)

For isotropic materials, each element can be expressed as:

$$\begin{gathered} C_{11} = C_{22} = C_{33} = 2\mu + \lambda \hfill \\ C_{12} = C_{13} = C_{23} = \lambda \hfill \\ C_{44} = C_{55} = C_{66} = \mu \hfill \\ \end{gathered}$$
(8)

3 Refined plate model based on CUF theory

According to Carrera unified formulation, the extended function Fτ is introduced to describe the cross-sectional displacement field of composite plate:

$${\varvec{u}}\left( {x,y,z} \right) = {\varvec{F}}_{\tau } \left( z \right){\varvec{u}}_{\tau } \left( {x,y} \right){, }\tau = 0,1, \cdots N$$
(9)

where u(x,y,z) represents the displacement field in three directions of the composite plate model in Cartesian coordinate system, Fτ is a function of thickness coordinate z, uτ is a generalized displacement vector about cross-sectional coordinates x and y, N represents the expansion order of the model, repeated subscript τ represents the dummy index, and the paired subscript τ represents summation according to Einstein summation convention.

The higher-order model of composite plate is established based on CUF frame and the thickness direction of the plate adopts Taylor-like series expansion:

$${\varvec{F}}_{\tau } = z^{\tau } \left( {\tau = 0,1, \cdots N} \right)$$
(10)

The displacement field of composite plate cross section can be expressed as:

$$\begin{gathered} u = u_{0} + zu_{1} + z^{2} u_{2} + z^{3} u_{3} + \cdots + z^{N} u_{N} \hfill \\ v = v_{0} + zv_{1} + z^{2} v_{2} + z^{3} v_{3} + \cdots + z^{N} v_{N} \hfill \\ w = w_{0} + zw_{1} + z^{2} w_{2} + z^{3} w_{3} + \cdots + z^{N} w_{N} \hfill \\ \end{gathered}$$
(11)

where CPT and FSDT are special cases of expansion order N = 1. The displacement field is expressed in the following form:

$$u = u_{0} + zu_{1} {, }v = v_{0} + zv_{1} {, }w = w_{0} + zw_{1}$$
(12)

4 Finite element formulation

The cross section was divided by four-node plate element, and the displacement vector was obtained by Lagrange function Ni(x,y) interpolation:

$${\varvec{u}}\left( {x,y,z} \right) = {\varvec{F}}_{\tau } {\varvec{N}}_{i} \left( {x,y} \right){\varvec{u}}_{\tau i} {, }\quad i = 1,2,3,4$$
(13)

where uτi is the generalized displacement vector of the node. The expression form of Ni(x,y) is as follows:

$$\begin{gathered} N_{1} = 0.25\left( {1 - \xi } \right)\left( {1 - \eta } \right){, }N_{2} = 0.25\left( {1 + \xi } \right)\left( {1 - \eta } \right) \hfill \\ N_{3} = 0.25\left( {1 + \xi } \right)\left( {1 + \eta } \right){, }N_{4} = 0.25\left( {1 - \xi } \right)\left( {1 + \eta } \right) \hfill \\ \end{gathered}$$
(14)

where the value interval of non-dimensional natural coordinate ξ and η is [−1,1]. The four-node plate element and natural coordinate system are shown in Fig. 2. The expression of natural coordinate is as follows:

$$\xi = \frac{2x}{{aa}} - 1, \, \eta = \frac{2y}{{bb}} - 1$$
(15)

where aa and bb stand for the length and width of the four-node plate element.

Fig. 2
figure 2

Four-node plate element and natural coordinate system: a actual element; b basic element

Full size image

5 Differential equation of motion

The governing differential equation of plate element is derived by Hamilton principle, and the formulation is as follows:

$$\begin{gathered} \delta H = \delta \int\limits_{{t_{1} }}^{{t_{2} }} {Ldt = 0} \hfill \\ L = T - U - U_{p} \hfill \\ \delta {\varvec{u}}\left| {_{{t = t_{1} }} } \right. = \delta {\varvec{u}}\left| {_{{t = t_{2} }} } \right. = 0 \hfill \\ \end{gathered}$$
(16)

where δ is the imaginary strain, U is the strain energy, Up is the potential energy, and T is the kinetic energy. Their expressions are written as follows:

$$\begin{gathered} U = \frac{1}{2}\int\limits_{V} {{\varvec{\varepsilon}}^{T} {\varvec{\sigma}}dV} \hfill \\ U_{p} = - \int\limits_{A} {{\varvec{u}}^{T} {\varvec{p}}dA} - \int\limits_{l} {{\varvec{u}}^{T} {\varvec{q}}dy} - {\varvec{u}}^{T} {\varvec{r}} \hfill \\ T = \frac{1}{2}\int\limits_{V} {\rho \frac{{\partial {\varvec{u}}^{T} }}{\partial t}\frac{{\partial {\varvec{u}}}}{\partial t}} dV \hfill \\ \end{gathered}$$
(17)

where ρ represents the density, V represents the volume of the composite plate, A represents the area of surface force p, l represents the length of line load q, and r represents the concentrated load. Substituting Eq. 17 into Eq. 16 gives the unified formulation:

$$\int\limits_{V} {{\varvec{N}}^{T} } {\varvec{F}}_{\tau }^{T} \rho {\varvec{F}}_{\tau } {\varvec{N}}\frac{{\partial^{2} {\varvec{u}}_{\tau } }}{{\partial t^{2} }}dV + \int\limits_{V} {{\varvec{N}}^{T} } {\varvec{F}}_{\tau }^{T} {\varvec{B}}^{T} {\varvec{CBF}}_{\tau } {\varvec{Nu}}_{\tau } dV = \int\limits_{A} {{\varvec{N}}^{T} {\varvec{F}}_{\tau }^{T} {\varvec{p}}dA} + \int\limits_{l} {{\varvec{N}}^{T} {\varvec{F}}_{\tau }^{T} {\varvec{q}}dy} + {\varvec{N}}^{T} {\varvec{F}}_{\tau }^{T} {\varvec{r}}$$
(18)

The following formulation can be obtained by changing the form:

$${\varvec{m}}\frac{{\partial^{2} {\varvec{u}}_{\tau } }}{{\partial t^{2} }} + {\varvec{ku}}_{\tau } = {\varvec{f}}$$
(19)

where m stands for the element mass matrix, k stands for the element stiffness matrix, and f stands for the boundary conditions. Their expressions are as follows:

$$\begin{gathered} {\varvec{m}} = \int\limits_{V} {{\varvec{N}}^{T} {\varvec{F}}_{\tau }^{T} } \rho {\varvec{F}}_{\tau } {\varvec{N}}dV \hfill \\ {\varvec{k}} = \int\limits_{V} {{\varvec{N}}^{T} {\varvec{F}}_{\tau }^{T} {\varvec{B}}^{T} } {\varvec{CBF}}_{\tau } {\varvec{N}}dV \hfill \\ {\varvec{f}} = \int\limits_{A} {{\varvec{N}}^{T} {\varvec{F}}_{\tau }^{T} {\varvec{p}}dA} + \int\limits_{l} {{\varvec{N}}^{T} {\varvec{F}}_{\tau }^{T} {\varvec{q}}dy} + {\varvec{N}}^{T} {\varvec{F}}_{\tau }^{T} {\varvec{r}} \hfill \\ \end{gathered}$$
(20)

kτsij is described in the form of the fundamental nuclei and does not depend on the expansion order. Its expression is written as follows:

$$k^{\tau sij} = \left[ {\begin{array}{*{20}l} {k_{xx}^{\tau sij} } &\quad {k_{xy}^{\tau sij} } &\quad {k_{xz}^{\tau sij} } \\ {k_{yx}^{\tau sij} } &\quad {k_{yy}^{\tau sij} } &\quad {k_{yz}^{\tau sij} } \\ {k_{zx}^{\tau sij} } &\quad {k_{zy}^{\tau sij} } &\quad {k_{zz}^{\tau sij} } \\ \end{array} } \right]$$
(21)

The nine components are listed as follows:

$$\begin{gathered} k_{xx}^{\tau sij} = Z_{pp11}^{\tau s} \int_{\Omega } {N_{i,x} } N_{j,x} d\Omega + Z_{pp66}^{\tau s} \int_{\Omega } {N_{i,y} } N_{j,y} d\Omega + Z_{nn55}^{{\tau_{,z} s_{,z} }} \int_{\Omega } {N_{i} } N_{j} d\Omega \hfill \\ k_{xy}^{\tau sij} = Z_{pp12}^{\tau s} \int_{\Omega } {N_{i,y} } N_{j,x} d\Omega + Z_{pp66}^{\tau s} \int_{\Omega } {N_{i,x} } N_{j,y} d\Omega \hfill \\ k_{xz}^{\tau sij} = Z_{pp13}^{{\tau_{,z} s}} \int_{\Omega } {N_{i} } N_{j,x} d\Omega + Z_{nn55}^{{\tau s_{,z} }} \int_{\Omega } {N_{i,x} } N_{j} d\Omega \hfill \\ k_{yx}^{\tau sij} = Z_{pp12}^{\tau s} \int_{\Omega } {N_{i,x} } N_{j,y} d\Omega + Z_{pp66}^{\tau s} \int_{\Omega } {N_{i,y} } N_{j,x} d\Omega \hfill \\ k_{yy}^{\tau sij} = Z_{pp22}^{\tau s} \int_{\Omega } {N_{i,y} } N_{j,y} d\Omega + Z_{pp66}^{\tau s} \int_{\Omega } {N_{i,x} } N_{j,x} d\Omega + Z_{nn44}^{{\tau_{,z} s_{,z} }} \int_{\Omega } {N_{i} } N_{j} d\Omega \hfill \\ k_{yz}^{\tau sij} = Z_{pn23}^{{\tau_{,z} s}} \int_{\Omega } {N_{i} } N_{j,y} d\Omega + Z_{nn44}^{{\tau s_{,z} }} \int_{\Omega } {N_{i,y} } N_{j} d\Omega \hfill \\ k_{zx}^{\tau sij} = Z_{nn55}^{{\tau_{,z} s}} \int_{\Omega } {N_{i} } N_{j,x} d\Omega + Z_{np13}^{{\tau s_{,z} }} \int_{\Omega } {N_{i,x} } N_{j} d\Omega \hfill \\ k_{zy}^{\tau sij} = Z_{nn44}^{{\tau_{,z} s}} \int_{\Omega } {N_{i} } N_{j,y} d\Omega + Z_{np23}^{{\tau s_{,z} }} \int_{\Omega } {N_{i,y} } N_{j} d\Omega \hfill \\ k_{zz}^{\tau sij} = Z_{nn55}^{\tau s} \int_{\Omega } {N_{i,x} } N_{j,x} d\Omega + Z_{nn44}^{\tau s} \int_{\Omega } {N_{i,y} } N_{j,y} d\Omega + Z_{nn33}^{{\tau_{,z} s_{,z} }} \int_{\Omega } {N_{i} } N_{j} d\Omega \hfill \\ \end{gathered}$$
(22)

where the following notation is introduced to indicate the line integrals along the thickness direction:

$$\begin{gathered} \left( {Z_{pp}^{\tau s} ,Z_{pn}^{\tau s} ,Z_{np}^{\tau s} ,Z_{nn}^{\tau s} } \right) = \left( {{\varvec{C}}_{pp} ,{\varvec{C}}_{pp} ,{\varvec{C}}_{pp} ,{\varvec{C}}_{pp} } \right)E_{\tau s} \hfill \\ \left( {Z_{pn}^{{\tau s_{,z} }} ,Z_{nn}^{{\tau s_{,z} }} ,Z_{np}^{{\tau_{,z} s}} ,Z_{nn}^{{\tau_{,z} s}} ,Z_{nn}^{{\tau_{,z} s_{,z} }} } \right) = \left( {{\varvec{C}}_{pn} E_{{\tau s_{,z} }} ,{\varvec{C}}_{nn} E_{{\tau s_{,z} }} ,{\varvec{C}}_{np} E_{{\tau_{,z} s}} ,{\varvec{C}}_{nn} E_{{\tau_{,z} s}} ,{\varvec{C}}_{nn} E_{{\tau_{,z} s_{,z} }} } \right) \hfill \\ \left( {E_{\tau s} ,E_{{\tau s_{,z} }} ,E_{{\tau_{,z} s}} ,E_{{\tau_{,z} s_{,z} }} } \right) = \int_{A} {\left( {F_{\tau } F_{s} ,F_{\tau } F_{s,z} ,F_{\tau ,z} F_{s} ,F_{\tau ,z} F_{s,z} } \right)} dz \hfill \\ \end{gathered}$$
(23)

where mτsij is the mass matrix in the form of the finite element. Its components are

$$\begin{gathered} m_{xx}^{\tau sij} = m_{yy}^{\tau sij} = m_{zz}^{\tau sij} = \rho \int_{A} {F_{\tau } } F_{s} dz\int_{\Omega } {N_{i} } N_{j} d\Omega \hfill \\ m_{xy}^{\tau sij} = m_{xz}^{\tau sij} = m_{yx}^{\tau sij} = m_{yz}^{\tau sij} = m_{zx}^{\tau sij} = m_{zy}^{\tau sij} = 0 \hfill \\ \end{gathered}$$
(24)

Global integration of the stiffness matrices of the composite plate model is based on the four indices i, j, τ, and s which are associated with the expansion functions and the shape functions.

The contact surfaces of different materials are equivalent to two different four-node plate elements superimposed on each other in the thickness direction, and each element node corresponds to each other. Therefore, the formulation of the element mass matrix mc and element stiffness matrix kc of the composite plate is as follows:

$$\begin{gathered} {\varvec{m}}_{c} = \sum\limits_{j = 1}^{n} {{\varvec{m}}_{j} } = \sum\limits_{j = 1}^{n} {\int\limits_{V} {{\varvec{N}}^{T} } {\varvec{F}}_{\tau }^{T} \rho_{j} {\varvec{F}}_{\tau } {\varvec{N}}} dV,\,\quad j = 1,2, \cdots ,n \hfill \\ {\varvec{k}}_{c} = \sum\limits_{j = 1}^{n} {{\varvec{k}}_{j} } = \sum\limits_{j = 1}^{n} {\int\limits_{V} {{\varvec{N}}^{T} } {\varvec{F}}_{\tau }^{T} {\varvec{B}}^{T} {\varvec{C}}_{i} {\varvec{BF}}_{\tau } {\varvec{N}}} dV,\,\quad j = 1,2, \cdots ,n \hfill \\ \end{gathered}$$
(25)

where mj and kj represent the element mass matrix and stiffness matrix of single-layer plate, respectively, and n represents the number of layers of composite plate.

For the composite plate structure, the global stiffness matrix, mass matrix, and load vector can be obtained in the finite element frame through the assembly program.

6 Shear locking phenomenon and MITC4 element

Shear locking is a numerical problem in finite element analysis. In the analysis of thin plate, when the plate thickness becomes very small, the shear strain energy becomes very larger. This results in shear locking phenomenon. Therefore, the tensor component mixed interpolation (MITC) method is adopted to revise the four-node plate element characteristic matrix.

The shear strains γxz and γyz were interpolated into the sample points (M, N, P, Q) as shown in Fig. 3.

Fig. 3
figure 3

Shear strain interpolations and sample points (M, N, P, Q) of the MITC4 plate element

Full size image

The revised transverse strain vector εm is written as follows:

$${\varvec{\varepsilon}}_{m} = \left[ {\begin{array}{*{20}c} {{\varvec{N}}_{a}^{T} } & {} & {} \\ {} & {{\varvec{N}}_{b}^{T} } & {} \\ {} & {} & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{xz} } \\ {\varepsilon_{zz} } \\ \end{array} } \right]$$
(26)

where interpolation vector and strain vector are written as follows:

$$\begin{gathered} {\varvec{N}}_{a} = \left[ {\begin{array}{*{20}l} {N_{a1} } &\quad {N_{a2} } \\ \end{array} } \right]^{T} {, }{\varvec{N}}_{b} = \left[ {\begin{array}{*{20}l} {N_{b1} } &\quad {N_{b2} } \\ \end{array} } \right]^{T} \\ {\varvec{\gamma}}_{xz} = \left[ {\begin{array}{*{20}l} {\gamma_{xz}^{P} } &\quad {\gamma_{xz}^{Q} } \\ \end{array} } \right]^{T} {, }{\varvec{\gamma}}_{yz} = \left[ {\begin{array}{*{20}l} {\gamma_{yz}^{N} } &\quad {\gamma_{yz}^{M} } \\ \end{array} } \right]^{T} \\ \end{gathered}$$
(27)

where the component of the strain vector is the value of the corresponding strain at the sample point. The interpolation function of the sample point is constructed by using the method of element interpolation function. The expression is as follows:

$$N_{a1} = \frac{1}{2}\left( {1 + \xi } \right){, }N_{a2} = \frac{1}{2}\left( {1 - \xi } \right){, }N_{b1} = \frac{1}{2}\left( {1 + \eta } \right){, }N_{b1} = \frac{1}{2}\left( {1 - \eta } \right)$$
(28)

For the convenience of mathematical formulation derivation, stress vector and strain vector are divided into two groups according to their physical meanings:

$$\begin{gathered} {\varvec{\sigma}}_{p} = \left[ {\begin{array}{*{20}l} {\sigma_{xx} } &\quad {\sigma_{yy} } &\quad {\sigma_{xy} } \\ \end{array} } \right]^{T} , \;{\varvec{\sigma}}_{n} = \left[ {\begin{array}{*{20}l} {\tau_{xz} } &\quad {\tau_{yz} } &\quad {\tau_{zz} } \\ \end{array} } \right]^{T} \\ {\varvec{\varepsilon}}_{p} = \left[ {\begin{array}{*{20}l} {\varepsilon_{xx} } &\quad {\varepsilon_{yy} } &\quad {\varepsilon_{xy} } \\ \end{array} } \right]^{T} ,\;{\varvec{\varepsilon}}_{n} = \left[ {\begin{array}{*{20}l} {\gamma_{xz} } & {\gamma_{yz} } &\quad {\gamma_{zz} } \\ \end{array} } \right]^{T} \\ \end{gathered}$$
(29)

where subscript p stands for the stress–strain term of the vertical cross section and subscript n stands for the stress–strain term within the cross section.

The linear differential operator matrix is divided into two groups:

$${\varvec{B}}_{p} = \left[ {\begin{array}{*{20}l} {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} &\quad 0 &\quad 0 \\ 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} &\quad 0 \\ {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} &\quad 0 \\ \end{array} } \right],\user2{ B}_{n} = \left[ {\begin{array}{*{20}l} {{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0pt} {\partial z}}} &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} \\ 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0pt} {\partial z}}} &\quad 0 \\ 0 &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0pt} {\partial z}}} \\ \end{array} } \right]$$
(30)

According to the formulation of the stiffness matrix, the revised matrix BFτN:

$$\begin{gathered} {\varvec{A}}_{n} = \left[ {\begin{array}{*{20}c} {\left( {{\varvec{B}}_{n} {\varvec{F}}_{\tau } {\varvec{N}}} \right)_{i = 1}^{x = P} } &\quad {\left( {{\varvec{B}}_{n} {\varvec{F}}_{\tau } {\varvec{N}}} \right)_{i = 1}^{x = Q} } &\quad {\left( {{\varvec{B}}_{n} {\varvec{F}}_{\tau } {\varvec{N}}} \right)_{i = 2}^{y = N} } &\quad {\left( {{\varvec{B}}_{n} {\varvec{F}}_{\tau } {\varvec{N}}} \right)_{i = 2}^{y = M} } &\quad {\left( {{\varvec{B}}_{n} {\varvec{F}}_{\tau } {\varvec{N}}} \right)_{i = 3} } \\ \end{array} } \right]^{T} \\ {\varvec{A}}_{p} = {\varvec{B}}_{p} {\varvec{F}}_{\tau } {\varvec{N}} \\ \end{gathered}$$
(31)

where the subscript i represents the number of rows in the matrix. The superscript x = P represents the value of point P on the x-axis. The following similar superscripts will not be explained repeatedly.

$${\varvec{A}}_{m} = {\varvec{N}}_{m} {\varvec{A}}_{n}$$
(32)

where Nm is expressed as follows:

$${\varvec{N}}_{m} = \left[ {\begin{array}{*{20}c} {\frac{1}{2}\left( {1 + \xi } \right)} & {\frac{1}{2}\left( {1 - \xi } \right)} & {} & {} & {} \\ {} & {} & \quad{\frac{1}{2}\left( {1 + \eta } \right)} & {\frac{1}{2}\left( {1 - \eta } \right)} & {} \\ {} & {} & {} & {} & \quad1 \\ \end{array} } \right]$$
(33)

The revised matrix is as follows:

$${\varvec{A}} = \left[ {\begin{array}{*{20}c} {{\varvec{A}}_{p} } & {{\varvec{A}}_{m} } \\ \end{array} } \right]^{T}$$
(34)

The stiffness matrix of MITC4 element is written in the following form:

$${\varvec{k}}_{m} = \int\limits_{V} {{\varvec{A}}^{T} } {\varvec{CA}}dV$$
(35)

The revised element stiffness matrix of composite plate can be expressed as:

$${\varvec{k}}_{cm} = \sum\limits_{j = 1}^{n} {{\varvec{k}}_{jm} } = \sum\limits_{j = 1}^{n} {{\varvec{A}}^{T} {\varvec{C}}_{i} {\varvec{A}}} dV,\;j = 1,2, \cdots ,n$$
(36)

Because the stress–strain does not participate in the derivation of the element mass matrix and load vector, the expressions of the element mass matrix and load vector do not change.

7 Numerical results

Firstly, the convergence of the higher-order model is verified by mechanical analysis of the composite plate. Secondly, the accuracy of the model in this paper is determined by comparing the displacement of the higher-order model and ANSYS model at the verification points (the midpoint of the cross section). Considering the shear locking phenomenon of thin plate, the higher-order model is revised by tensor component mixed interpolation (MITC). Finally, in order to reduce the material loss, the geometric parameters of the composite plate were optimized based on the established higher-order model.

A square plate structure is used for numerical results in this section. The material and geometric parameters of composite plates are given in Table 1. The length and width are fixed, and the ratio of the thickness of each layer to the total thickness is 3:4:3, respectively.

Table 1 Material and geometric parameters
Full size table

7.1 Convergence study

The convergence of the present higher-order theory is demonstrated by implementing the dynamics analysis of the composite plate model. A 10 × 10 mesh was used to divide the cross section, the thickness t = 0.1 m, and one side was completely fixed. The first ten natural frequencies of the TEN (N-order Taylor-like series expansion) model were obtained, and the results are given in Table 2.

Table 2 The first ten natural frequencies of the TEN model
Full size table

According to the data of the first ten modes in the table, when the expansion order N = 2, the modes of the higher-order model tend to be stable.

To obtain the convergence of mesh of the higher-order model, the static analysis of the TE2 model is carried out, and different meshes are used to divide the cross section. The midpoint of cross section is set as the verification point. Meanwhile, the y-displacement (uy) and the z-strain (εz) at the verification points of the composite plate cross section were obtained, and the displacement-mesh and strain-mesh variation curves were drawn, as shown in Fig. 5. The mechanical model is shown in Fig. 4. It should be noted that S stands for the fixed constraint.

Fig. 4
figure 4

Mechanical model

Full size image

As can be illustrated from the curve in Fig. 5, with the increase in the number of meshes, the z-displacement at the verification points of composite plate cross section presents an upward trend and the z-strain presents a downward trend. When the mesh reaches 20 × 20, both curves tend to be stable. Therefore, it can be concluded that stable displacement and strain of the higher-order model can be obtained by employing 20 × 20 finite elements and the expansion order N = 2.

Fig. 5
figure 5

Research on mesh convergence

Full size image

7.2 Accuracy study

The accuracy of the higher-order model is verified by carrying out the statics study of the composite plate model. The expansion order N = 2, the mesh was 20 × 20, and the thickness of the composite plate was a variable. The y-displacement of CPT, FSDT, TE2, and ANSYS models at the verification points is given in Table 3, where eight-node solid element (solid185) is selected for ANSYS model, and 20 × 20 mesh is used to divide the cross section. The mechanical model is shown in Fig. 4.

Table 3 Y-displacement at the verification points under different thicknesses
Full size table

According to the data in the table, as the composite plate thickness decreases, the y-displacement at the verification points of cross section increases, and the error with the ANSYS solid model decreases. When the plate thickness decreases to 0.2 m, the error of displacement reaches an acceptable range. The y-displacement of the TE2 model is closer to ANSYS model than CPT and FSDT models under different thicknesses. That is to say, the CPT and FSDT models cannot achieve reasonable results compared to the ANSYS solid model. It can be concluded that the higher-order model has accuracy and is suitable for thin plate analysis. Meanwhile, the degree of freedom (DOF) of the TE2 model is much smaller than that of the ANSYS model, which indicates that the model in this paper has a high computational efficiency.

In order to verify the accuracy of other nodes of higher-order model, a force of 50,000N is applied to the middle area of the cross section, and the upper and lower sides are completely fixed. The mechanical model is shown in Fig. 6, where S stands for the fixed constraint and aa stands for the length of the four-node plate element. The displacements of nodes on the middle line of the cross section are shown in Fig. 7. Meanwhile, the geometric parameter width-to-thickness ratio St = a/t is introduced. It should be noted that a stands for the width of the composite plate and t stands for the thickness of the composite plate.

Fig. 6
figure 6

Mechanical model of composite plate

Full size image
Fig. 7
figure 7

Displacement of nodes on the middle line

Full size image

Figure 7a represents the y-displacement of TEN higher-order model, and Fig. 7b represents the y-displacement of ANSYS solid model. The mesh of the two figures is 20 × 20 and the width-to-thickness ratio St = 1/0.08. Figure 7c represents the z-displacement of the TE2 higher-order model under different thicknesses, and Fig. 7d represents the z-displacement of ANSYS solid model. The two figures both adopt 20 × 20 mesh dividing cross section.

As can be seen from Fig. 7a and c, when the expansion order N = 2, the higher-order model converges. The variation trend of higher order is consistent with the ANSYS model, and the y-displacement is also very close to the ANSYS model. Meanwhile, it can be shown from Fig. 7b and d that the curve variation trend under different width-to-thickness ratios is the same as the ANSYS model, and the z-displacement is also consistent with the ANSYS model, which proves the accuracy of the higher-order model.

To master the accuracy of the higher-order model under different width-to-thickness ratios and constraints, the y-displacement nephogram of cross section with width-to-thickness ratios St = 1/1, 1/0.5, and 1/0.08 was drawn, respectively, as shown in Fig. 9 (mechanical model: Fig. 8b). Meanwhile, the z-displacement nephogram of cross section under different constraints and loads conditions was drawn, as shown in Fig. 10 (mechanical model: Fig. 8a–c), where the width-to-thickness ratio St = 1/0.08. The mechanical model of the two figures is shown in Fig. 8. It should be noted that S stands for the fixed constraints and aa and bb stand for the length and width of the four-node plate element, respectively. The higher-order model of Figs. 9 and 10 adopts a 20 × 20 mesh dividing cross section, and the expansion order N = 2 (Tables 4 and 5).

Fig. 8
figure 8

Mechanical model

Full size image
Table 4 The meaning of the letters in Fig. 9
Full size table
Table 5 The meaning of the letters in Fig. 10
Full size table

As shown in Fig. 9, with the decrease in the composite plate width-to-thickness ratio, the y-displacement nephogram of the higher-order model approaches the ANSYS model gradually. When the width-to-thickness ratio St = 1/0.08, the displacement nephogram and chromatogram of the two models are consistent, indicating that the model has accuracy for the analysis of thin plates. As can be seen from Fig. 10, with the change in constraints and loads, the z-displacement nephogram and chromatogram of the higher-order model are always consistent with the ANSYS model, which proves that the model has accuracy for different constraints and loads. That is to say, the modeling method presented in this paper can be used for the analysis of composite plates under complex working conditions.

Fig. 9
figure 9

Y-displacement nephogram of cross section under different width-to-thickness ratios

Full size image
Fig. 10
figure 10

Z-displacement nephogram of cross section under different constraints and loads

Full size image

For mastering the deformation of the three-dimensional model, a deformation figure of the higher-order model with a width-to-thickness ratio St = 1/0.08 was drawn. In order to improve the accuracy, draw a more accurate deformation figure. Therefore, a mesh of 41 × 41 was adopted to divide the cross section, and the expansion order N = 3, as shown in Fig. 11.

Fig. 11
figure 11

Three-dimensional deformation figure of composite plate

Full size image

As can be shown from Fig. 11, the three-dimensional deformation figure of composite plates conforms to the corresponding mechanical model under different constraints and loads. That is to say, the three-dimensional modeling of the higher-order model has accuracy.

7.3 Shear locking

Considering the shear locking phenomenon in the thin plate model, MITC4 element is used to revise the higher-order model and verify the availability of the constructed model in this paper. A 20 × 20 mesh is used to divide the cross section, and the expansion order N = 2. The z-displacement uz at the verification points of the cross section under different width-to-thickness ratios is obtained, as shown in Table 6. The width of the width-to-thickness ratio remains unchanged and the thickness changes. The mechanical model is shown in Fig. 4.

Table 6 Z-displacement at the verification points of cross section
Full size table

According to the z-displacement data in the table, with the increase in the width-to-thickness ratio St, the z-displacement at the verification points of the cross section also increases. When St < 12, the displacement of MITC4 revised model is less than that of Q4 model, and the displacement of Q4 model is closer to that of ANSYS model. When St > 12, the opposite conclusion was obtained, which proved that MITC4 model played a role in revising the thin plate.

In order to directly represent the critical value of MITC4 model correction effect, Q4-ANSYS error curve and MITC4-ANSYS error curve were drawn, as shown in Fig. 12.

Fig. 12
figure 12

Error curve figure

Full size image

It can be seen from Fig. 12 that St = 12 is the critical value of MITC4 revised model. Because composite plate causes the shear locking phenomenon, the error reduction margin of Q4 model and ANSYS model keeps decreasing with the increase in the width-to-thickness ratio. However, the correction effect of MITC4 model is enhanced gradually, which proves that the MITC4 model has a certain correction effect on thin plate.

7.4 Optimization of composite plate geometric parameters

To allocate material of plate reasonably and reduce material loss, the geometric parameters of the composite plate are optimized based on the constructed higher-order model. The length (a) and thickness (t) of the plate are set as symbolic variables. The z-displacement and z-strain at the verification points of the cross section are solved by MATLAB software. In order to express the change relation of the objective function, the function expression was used to draw the z-displacement nephogram and z-strain nephogram, as shown in Fig. 14A and B. The horizontal coordinate represents the length of the plate, and the vertical coordinate represents the thickness of the plate. Meanwhile, to make the nephogram clearer, the result of 14-A is represented by log10u, and the result of 14-B is represented by 1/u.

According to the change relation of the objective function, the multi-objective genetic algorithm is used to optimize the objective function. The genetic algorithm is chosen in the MATLAB software optimization tool. The mechanical model is shown in Fig. 13, where S stands for the fixed constraint. Meanwhile, the cross-sectional mesh is 20 × 20, and the expansion order N = 2. The mathematical model of optimization is shown in formulations 37, 38, and 39.

$${\text{Function}}:{\text{Min}} = \left\{ \begin{gathered} {\varvec{u}}_{z} \left( {a,t} \right) = \left( {{\varvec{F}}_{\tau } {\varvec{Nu}}_{\tau 0} } \right)_{{\left( {x,y,z} \right) = \left( {0,0,0} \right)}} \hfill \\ {\varvec{\varepsilon}}_{z} \left( {a,t} \right) = \left( {{\varvec{BF}}_{\tau } {\varvec{Nu}}_{\tau 0} } \right)_{{\left( {x,y,z} \right) = \left( {0,0,0} \right)}} \hfill \\ \end{gathered} \right.$$
(37)
$${\text{Constrains}}:S = {a \mathord{\left/ {\vphantom {a t}} \right. \kern-0pt} t} \ge 12$$
(38)
$${\text{Search domain}}:\left\{ \begin{gathered} 0 \le a \le 2 \hfill \\ 0 \le t \le 0.3 \hfill \\ \end{gathered} \right.$$
(39)
Fig. 13
figure 13

Mechanical model

Full size image

It should be noted that uτ0 represents the generalized node displacement vector containing the verification points of cross section, and it is obtained by extracting a global generalized displacement vector uτ corresponding node, where uτ = k\f, k represents the global stiffness matrix, f represents global load vector, and (x,y,z) = (0,0,0) represents the coordinate value at the verification points of the cross section in the rectangular coordinate system. The results optimized by MATLAB software are shown in Fig. 14C and D, where the objective function 1 of 14-C stands for the z-displacement and the objective function 2 stands for the z-strain.

Fig. 14
figure 14

Function variation nephogram and optimization results figure

Full size image

As can be seen from Fig. 14A and B, with the increase in the length and thickness of the higher-order model, the z-displacement at the verification points of the cross section decreases and the strain increases. Therefore, it is more appropriate for the model in this paper to adopt the multi-objective genetic algorithm.

It can be shown from Fig. 14D that the distribution of individuals decreases gradually. The distribution is the most in region 1 and the least in region 9, and the middle is relatively uniform. That is to say, Fig. 14C contains most of the optimal cases and has strong applicability. As can be seen from Fig. 14C, multi-objective optimization function forms a plane curve. Under the condition of Pareto optimality, it is impossible to make the other party's objective better without damaging an optimization objective. According to the actual working conditions, the z-displacement should be as small as possible. Therefore, it can be seen from the iterative table that when a = 1.3352, t = 0.0919, the objective function reaches the optimal value, where uz = 2.542 × 10−7 m and εz = -3.986 × 10–6.

8 Conclusion

  1. (1)

    The higher-order model in this paper is based on the Carrera unified formulation and adopts the Taylor-like series expansion along the plate thickness direction. This modeling method can select the appropriate expansion series according to the actual model so that the model will be more accurate and the application occasions will be more abundant.

  2. (2)

    The higher-order model established is suitable for thin plate analysis. Compared with the ANSYS solid model, the composite plate model has higher computational efficiency while ensuring accuracy, which means that the constructed model is more suitable for engineering application under complex working conditions.

  3. (3)

    For the shear locking phenomenon that occurs in thin plate models, MITC4 element is used to revise the higher-order model. When the width-to-thickness ratio St < 12, higher-order models are more accurate. When St > 12, MITC4 model is more accurate. Therefore, St = 12 can be considered as the critical value of the revised model, as well as the critical value of thick plate and thin plate.

  4. (4)

    According to the actual working conditions, the multi-objective genetic algorithm is used to optimize the geometric parameters of the higher-order model. When a = 1.3352, t = 0.0919, the z-displacement and z-strain at the verification points of cross section reach optimal.