Stability analysis and implication of Darcy magnetic-radiative hybrid reactive nanofluid heat transfer over a shrinkable surface with Ohmic heating

Abstract

This study focused on Al$_2$O$_3$–Cu/water-based hybrid nanofluid to address the issue related to heat-mass transfer over a Darcy shrinkable surface with the magnetic field with thermal radiation effects. Variable thermal conductivity, Joule dissipation, chemical reaction with velocity, and thermal slip condition for hybrid nanofluid are also considered here. The governing equations of this study are reduced by utilizing similarity transformations before being solved numerically by the bvp4c function in MATLAB. The results also indicate the existence of multiple solutions in the shrinking sheet region for a certain amount of mass suction parameter, where the solution of the upper branch was stable while unstable for the lower branch. The influences of the chosen parameters on the velocity, temperature, skin friction coefficient, local Nusselt number, and Sherwood number are addressed and graphically illustrated. Further, it is found that due to an increase in Al$_2$O$_3$ nanoparticle volume fraction, the coefficient of skin friction with heat transfer rate boosts up, whereas the Sherwood number decays. The results also reveal that increasing values of shrinking parameter decline the local Nusselt number but upsurges skin friction coefficient. Moreover, the hybrid nanofluid velocity decreases (increases) in the first (second) solution for the enhancement of the permeability parameter. The initial solution’s positive minimum eigenvalue was revealed by stability analysis, which distinctly defined a stable and feasible flow. Boundary layer hybrid nanofluid flow in industrial applications such as extrusion processes is attributable to impulsive movement of an extensible moving surface. These results are crucial in the long term because they allow us to optimize heat transmission for cooling and heating applications, to enhance industrial growth, especially in the manufacturing and processing sectors.

Introduction

Because the efficiency of most equipment with heat exchangers is greatly increased with the introduction of nanosized particles into the base fluids, the use of nanofluid in the field of engineering and industrial applications has attained major appeal in recent years. The researchers are considering numerous combinations of nanoparticles, including carbon nanotubes (CNT), metal oxides (Fe$_3$ O$_4$, Al$_2$O$_3$, CuO), semiconductors (SiO$_2$, TiO$_2$), metals (Al, Cu, Ni, Mg, Fe), and metal oxides (Fe$_3$O$_4$, Al$_2$O$_3$, CuO). Choi and Eastman [12] were the first to discuss this process, referring to the resulting combination as “nanofluid” and exposing the rapidly expanding use of nanotechnology and industry research. A hybrid nanofluid mixes several composite materials with a base fluid, such as metal matrix nanocomposites (Al$_2$O$_3$/Cu, Al$_2$O$_3$/Ni, Mg/CNT), ceramic matrix nanocomposites (Al$_2$O$_3$/SiO$_2$, Al$_2$O$_3$/TiO$_2$, CNT/Fe$_3$O$_4$), and polymer matrix nanocomposites (polymer/CNT, polyester/Al$_2$O$_3$–Cu hybrid nanoparticle experiments) were carried out by [56] to investigate improving fluid thermal conductivity. The requirement for heat transfer improvement that could be used in a few industries, including thermal power plants, solar energy, the chemical industry, manufacturing, and the processes industry, was the cause that impacted this growth in demand for a more efficient source. Hybrid nanofluid is utilized in radiators as an example used in the car sector to replace traditional coolant. To transport heat from the engine or cylinder to the surrounding region, radiators often employ common fluids like water, oil, and kerosene. Due to recent advancements in technology, hybrid nanofluids are in great demand for application in heat exchange procedures. Due to the inherent properties of nanoparticles, hybrid nanofluid has better heat conductivity than traditional fluid, which explains why there is such strong demand. Krishna and Chamkha [28] and Krishna et al. [34] focused on the MHD boundary layer flow of nanofluid over an infinite vertical plate embedded in a porous medium. Singh and Sarkar [53] and Farhana et al. [15] both reported on the importance of the combination of Al$_2$O$_3$ and other nanoparticles (2019). Khan et al. [19] have investigated the analysis of heat and mass transfer for the Darcy–Forchheimer Casson hybrid nanofluid flow across an extended curved surface. In addition, Xia et al. [67] concentrated on the analysis of heat and mass transfer for nonlinear mixed convective hybrid nanofluid flow in the presence of numerous slip boundary conditions. Ahmad et al. [2] tested and attempted to increase the thermal efficiency of Maxwell hybrid nanofluid made up of graphene oxide in addition to silver/kerosene oil. Elangovan [38] analyzed entropy minimization for variable viscous couple stress fluid flow and heat transfer in a channel with thermal radiation, heat source/sink, and non-uniform wall temperature. They found that temperature is reduced with an increase in the thermal radiation factor, whereas it is accelerated due to a higher Brinkman number. Nadeem et al. [47] and McCash et al. [44] considered and discussed the peristaltic flow of hybrid nanofluid on different boundary conditions. Lund et al. [41] experimented with the flow of a Cu–Fe$_3$O$_4$/H$_2$O hybrid nanofluid in the presence of a magnetic field and viscous dissipation. Ghazwani et al. [39] considered a mathematical model to disclose the peristaltic flow of carbon nanotubes in an elliptic duct with ciliated walls.

Convection flow via porous media is used in a variety of industrial and environmental systems, including geothermal energy systems, fiber insulation, heat exchanger design, geophysics, and catalytic reactors. The non-Darcian porous medium model is an expansion of the traditional Darcian model that takes into account combinations of these effects as well as vorticity diffusion and tortuosity inertial drag effects. On the other hand, a very effective method to improve the convection heat transfer properties for industrial processes is the employment of a hybrid nanofluid in a Darcy media. Convection flow via porous media is used in a variety of industrial and environmental systems, including geothermal energy systems, fiber insulation, heat exchanger design, geophysics, and catalytic reactors. The non-Darcian porous medium model is an expansion of the traditional Darcian model that takes into account combinations of these effects as well as vorticity diffusion and tortuosity inertial drag effects. In other words, Darcy surfaces have void empty spaces or pores through which fluid particles penetrate the object, such as tissue papers, sands, wooden materials, limestone, human lungs, biological tissue foams, sponges, and many more. Darcy media contain tiny holes in their surfaces that allow the passage of fluids through these holes. This medium has received a lot of attention in the engineering and applied sciences, including geosciences, thermal insulation, oil flow filtration, biology and biophysics, and material sciences, among others. The existence of the dual solutions occurs to the opposing flow, according to Merkin [45], who pioneered the research of mixed convection viscous flow down a vertical surface in a porous media. Chamkha [3, 4] experimented on non-Darcy and hydrodynamic effects in a porous medium with heat generation/absorption. MHD mixed convective-radiative Soret and Dufour’s effects along a permeable surface in a porous medium were discussed by [11]. Chamkha et al. [10] showed the effect of heat generation/absorption on boundary layer flow over a vertical flat plate embedded in a porous medium. The Marangoni model of hybrid nanofluid flow across an endless but permeable disc embedded in a porous medium was investigated by [57]. Hybrid nanofluid flow over a permeable stretching/shrinking surface in the presence of an external magnetic field and thermal radiation was examined by [69, 70]. Abu Bakar et al. [1] identified hybrid nanofluid flow across a permeable shrinking sheet with thermal radiation and slip influences in a porous medium. The effect of a Darcy-Forchheimer porous medium on the flow of a magnetic-radiative hybrid nanofluid through a contracting surface was demonstrated by [13]. A porous vertical cylinder causing mixed convective radiative hybrid nanofluid flow via a porous medium with an uneven heat sink/source was the subject of discussion by [20] in their study. Khashi’ie et al. [23] looked at non-Darcy mixed convective hybrid nanofluid flow with thermal dispersion over a porous media. In a porous media, Lund et al. [40] evaluated a magnetized flow including Cu + Al$_2$O$_3$ + H$_2$O nanoparticles as a hybrid nanofluid and examined the duality of the solutions. Shahzad et al. [51] focused on the entropy with stability analysis through a stenosed artery having permeable walls on the blood flow of nanoparticles.

The problem of heat and mass transfer for hydromagnetic flow with magnetic effect hybrid nanofluids passing through a shrinking sheet has been studied. Porous rocks, foams and foamed solids, alloys, aerogels, polymer blends, and microemulsions are just a few examples of the many applications for this problem. Continuous casting, the manufacture of glass fiber, metal extrusion, hot rolling, wire drawing, the production of paper, the drawing of plastic films, metal and polymer extrusion, and metal spinning are a few examples. Chamkha [5] explored hydromagnetic natural convection flow over an isothermal inclined surface. Chamkha [6] investigated solar radiation-assisted natural convection in a uniform porous medium supported by a vertical flat plate. Three-dimensional hydromagnetic flow on a vertical stretching surface in presence of heat generation/absorption was analyzed by [8]. Takhar et al. [59] experimented with an aligned magnetic field on unsteady flow and heat transfer over a semi-infinite flat plate. Chamkha [9] combined thermal radiation and buoyancy effects on hydromagnetic flow over an accelerating permeable surface with a heat source or sink. Takhar et al. [60] considered magnetic field and Hall currents effects over a moving plate. Modather et al. [46] studied MHD heat and mass transfer flow of a micropolar fluid over a vertical permeable plate in a porous medium. Magyari and Chamkha [42] focused on the combined effect of heat generation/absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface. Sreedevi et al. [55] analyzed the heat and mass transfer of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. Kumar et al. [37] experimented on transverse magnetic field effects on Cattaneo–Christov heat diffusion.

According to theory, Joule heating is the generation of heat as a result of resistive losses during the conversion of electric to thermal state energy. The organization of electrical and electronic devices frequently uses this method. The temperature of the examined nanofluid is increased using this control parameter from the perspective of boundary layer flow. Because it greatly affects the MHD fluid flow, Joule heating has also been one of the fascinating effects to be applied. Joule or Ohmic heating is a method of converting electrical energy into thermal energy that creates heat by causing resistive losses in the medium. Most electronic and electric equipment also extensively and practically employ the Joule heating effect. The stability analysis of a magnetized hybrid nanofluid with Joule heating and different slip circumstances was the main topic of [68]’s study. Krishna [24,25,26,27] and Krishna et al. [35] experimented with the external MHD effects on chemically reactive fluid, Jeffery fluid, and Casson hybrid nanofluid through a porous medium under different boundary conditions. The effects of Joule heating on the magnetohydrodynamics flow and heat transfer of a hybrid nanofluid via a permeable stretching or contracting sheet were computed by [21]. The effects of combined convection and Joule heating on the flow of a hybrid nanofluid via an exponentially stretching/shrinking sheet were demonstrated by [69, 70]. Khashi’ie et al. [22] also investigated the flow of a hybrid nanofluid across a porous cylinder that was contracting under the influence of Joule heating. Waini et al. [63] first described a micropolar hybrid nanofluid that flows past a contracting sheet while experiencing viscous dissipation and Joule heating effects. Wahid et al. [61] discovered the three-dimensional hybrid nanofluid flow with slips and Joule heating across a stretching/shrinking sheet.

When an ionized gas serves as the conducting fluid and a strong magnetic field is applied, the conductivity normal to the magnetic field is reduced as a result of the free spiraling of electrons and ions around the magnetic lines of force before colliding, and a current is induced in a direction normal to both the electric field and the magnetic field. It is known as the Hall effect. When the medium is rarefied or there is a high magnetic field, the fluid’s anisotropic conductivity makes it impossible to ignore the impact of Hall current. Application areas for the study of MHD viscous flows with Hall current include aircraft magnetohydrodynamics and issues with Hall accelerators. The present trend in magnetohydrodynamics application is toward a strong magnetic field (so that the effect of the electromagnetic force is perceptible) and toward a low gas density (such as in space flight and nuclear fusion research). The Hall current is significant in this scenario. [31,32,33, 36] studied Hall and ion slip effects on unsteady MHD rotating flow through a saturated porous medium over an exponentially accelerated plate. Hall effects on the magnetohydrodynamic rotating flow of elastico-viscous fluid through porous medium were also investigated by [29, 30]. Chamkha [7] also studied the Hall effects on MHD-free convective vertical plate embedded in a porous medium.

A thorough review of the literature reveals that the heat and mass transfer of an Al$_2$O$_3$–Cu/H$_2$O hybrid nanofluid flow toward a permeable shrinking surface while taking changing thermal conductivity, chemical reaction, and slip boundary conditions into account has not yet been investigated. Therefore, we have uniquely devised the continuous two-dimensional heat and mass transfer of magnetohydrodynamic flow over an exponentially shrinking surface within the boundary layer porous domain with thermal radiation and Joule heating effects. A hybrid nanofluid contains both copper and alumina nanoparticles in the base fluid water (Pr = 6.2). The novelty of this work is also to consider variable thermal conductivity and chemical reactions in this model. Velocity, and thermal slip at the surface as boundary conditions are also taken into practice. The main objective of the current problem is to find dual solutions with their stability analysis, which may benefit other researchers or academicians from the outcomes. The similarity transformation is used to create closed-form dual-nature solutions. The experiment is crucial for numerous metallurgical medical techniques, including magma flows, blood flow, electronics, nanoscience, food processing, and polymer.

Fig. 1

Schematic flow diagram

Mathematical formulation

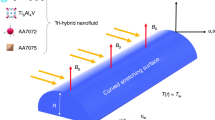
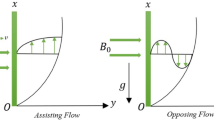
In the presence of velocity and thermal slip boundary conditions, we investigate the steady magnetohydrodynamic boundary layer flow, heat, and mass transfer of a hybrid nanofluid including Al$_2$O$_3$–Cu/water toward an exponentially permeable decreasing sheet. Additionally taken into account are the effects of thermal radiation, fluctuating thermal conductivity, Joule heating, and chemical reaction. The hybrid nanofluid is considered to flow with velocity u in the x-direction along the sheet’s surface, while velocity v in the y-direction measures the surface normal, which is assumed to be positive in the surface’s direction (see Fig. 1). The velocity of the deformable (shrinking) surface is $u_\textrm{w}(x)=ce^{\rm{x/L}}$ Using the formula $v_\textrm{w}(x)=v_0e^{\rm {x/2L}}$ ($v_0<0$ denotes mass suction/removal, while $v_0>0$ denotes mass injection). The constant $\lambda >0,<0,=0$ represents stretching, shrinking, and motionless surfaces, respectively. Further, an applied variable magnetic field $\hat{B}=B_0e^{\rm {x/2L}}$ with constant magnetic strength $B_0$ is directed normally to the flow zone plane $y=0$. An assumption of variable wall temperature is made such that $T_\textrm{w} = T_\infty + T_0 e^{\rm {x/2L}}$ with constant $T_0 > 0$ $(T_\textrm{w} > T_\infty )$ represents a heated sheet for assisting flow, whereas $T_0 < 0$ ($T_\textrm{w} < T_\infty$) signifies a cooled sheet for opposing flow. The nanoparticles of alumina are initially added to the base fluid to produce nanofluid Al$_2$O$_3$/water. The copper nanoparticles are then mixed with the Al$_2$O$_3$/water nanofluid to create the necessary Al$_2$O$_3$–Cu/water hybrid nanofluid. Al$_2$O$_3$–Cu/water hybrid nanofluid, Al$_2$O$_3$/water nanofluid, and water are all believed to have Prandtl numbers of 6.2. Table 1 also lists some of the thermophysical characteristics of water, copper, and aluminum. The present analysis is carried out by taking the assumptions as

• (a) steady, two-dimensional incompressible flow,

• (b) temperature-dependent thermal conductivity, temperature-independent specific heat, viscosity, and thermal diffusivity,

• (c) gravitational effect is negligible,

• (d) porous media inertia effect is negligible,

• (e) variable magnetic field $\hat{B}=B_0e^{x/2L}$ is introduced in the flow,

• (f) the induced magnetic field and so electric field are neglected and

• (g) the base fluid and the suspended nanoparticles maintain thermal equilibrium, and no-slip takes place between them.

The linked boundary layer continuity, momentum, and energy equations, along with the boundary conditions, are written as follows under the aforementioned conditions [18, 57]:

$$\begin{aligned}{} & {} \frac{\partial {u}}{\partial {x}}+\frac{\partial {v}}{\partial {y}} = 0, \end{aligned}$$

(1)

$$\begin{aligned}{} & {} {u}\frac{\partial {u}}{\partial {x}} +{v}\frac{\partial {v}}{\partial {y}} = \frac{\mu _{\text{hnf}}}{\rho _{\text{hnf}}}{\frac{\partial ^2 u}{\partial {y}^2}}-\frac{\mu _{\text{hnf}}}{\rho _{\text{hnf}}}\frac{u}{k^*} \\{} & {} \quad -\frac{\sigma _{\text{hnf}} {\hat{B}}^2}{\rho _{\text{hnf}}}u, \end{aligned}$$

(2)

$$\begin{aligned}{} & {} {u}\frac{\partial {T}}{\partial {x}}+{v}\frac{\partial {T}}{\partial {y}} \\{} & {} \quad =\frac{1}{{(\rho {C_{\text{p}}})_{\text{hnf}}}}\frac{\partial {}}{\partial {y}} \left({\kappa ^{*}_{\text{hnf}}}(T) \frac{\partial {T}}{\partial {y}} \right) -\frac{1}{{(\rho {C_{\text{p}}})_{\text{hnf}}}}\frac{\partial {}}{\partial {y}}(q_{\text{r}}) \\{} & {} \quad +\frac{\sigma _{\text{hnf}}{B_0}^2}{(\rho C_{\text{p}})_{\text{hnf}}}u^2, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} {u}\frac{\partial {C}}{\partial {x}}+{v}\frac{\partial {C}}{\partial {y}} = {D}_{\text{hnf}} \frac{\partial ^2{C}}{\partial {y^2}}-K_{\text{c}}(C-C_\infty ) \end{aligned}$$

(4)

subject to appropriate boundary conditions [54, 58]:

$$\begin{aligned}{} & {} u=u_{\text{w}}(x)\lambda +A_1\frac{\mu _{\text{hnf}}}{\rho _{\text{hnf}}}\frac{\partial {u}}{\partial {y}},v \\{} & {} \quad = v_{\text{w}}, \,T=T_{\text{w}}(x)+B_1\frac{\partial {T}}{\partial {y}},\,\, C=C_{\text{w}},\,\,\,\text{at}\, y = 0, \end{aligned}$$

(5)

$$\begin{aligned}{} & {} u \rightarrow 0, \,T \rightarrow T_\infty , \,C \rightarrow C_\infty , \,\,\,\text{as}\, y \rightarrow \infty .\, \end{aligned}$$

(6)

where $A_1$, $B_1$ represent slip factors for velocity, and thermal, respectively. The correlation with physical properties of hybrid nanofluid’s density $\rho _{\text{hnf}}$, heat capacitance $(\rho {C_{\text{p}}})_{\text{hnf}}$, dynamic viscosity $\mu _{\text{hnf}}$, electrical conductivity ${\sigma _{\text{hnf}}}$, variable thermal conductivity ${{\kappa ^*}_{\text{hnf}}}$, hybrid mass diffusivity $D_{\text{hnf}}$, chemical reaction rate $K_{\text{c}}$ employed in Eqs. (1)–(4)are characterized in Table 2. Utilizing the Rosseland approximation and the net radiation heat flux $q_{\text{r}}[\text{Wm}^{-2}]$ for gray/optically thick media [43] The expression can be used to approximate an isotropic diffusion process:

$$\begin{aligned} {q_{\text{r}}}=-\frac{4\sigma ^*}{3K^*}\frac{\partial T^4}{\partial r}, \end{aligned}$$

(7)

Without considering the higher-order terms, $T_\infty$ can be expanded here as a Taylor series, and we have

$$\begin{aligned} T^4 \approx 4T_\infty ^3T-3T_\infty ^4. \end{aligned}$$

(8)

To nondimensionalize the aforementioned the governing Eqs. (1)–(4), the following similarity variables are introduced [14, 62]:

$$\begin{aligned}{} & {} \psi =e^{\rm {x/2L}}\sqrt{2 \nu _{\text{f}}Lc} f(\eta ), v=-\frac{\partial {\psi }}{\partial {x}},\,u \\{} & {} \quad =\frac{\partial {\psi }}{\partial {y}},\,\theta (\eta )=\frac{T-T_\infty }{T_{\text{w}}-T_\infty },\,\Phi (\eta ) \\{} & {} \quad =\frac{C-C_\infty }{C_{\text{w}}-C_\infty }, \,\eta = y e^{\rm{x/2L}}\sqrt{\frac{c}{2 \nu _{\text{f}}L}}, \end{aligned}$$

(9)

which transform Eqs. (2)–(4) into the nondimensional subsequent equations, before gratifying Eq.(1)

$$\begin{aligned}{} & {} \bigg (\frac{{\mu _{\text{hnf}}}/{\mu _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg )f'''+ff''-2{f'}^2-\bigg (\frac{{\mu _{\text{hnf}}}/{\mu _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg )Pf' \\{} & {} \quad -\bigg (\frac{{\sigma _{\text{hnf}}}/{\sigma _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg )M f'=0, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \frac{1}{\text{Pr}}\bigg [\bigg \{\frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}(1+\epsilon \theta )+Nr\bigg \}\theta '' \\{} & {} \quad +\frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}\epsilon {\theta '}^2\bigg ]+\frac{(\rho C_{\text{p}})_{\text{hnf}}}{(\rho C_{\text{p}})_{\text{f}}}(f\theta '-f'\theta ) \\{} & {} \quad +\bigg (\frac{\sigma _{\text{hnf}}}{\sigma _{\text{f}}}\bigg )\text{Pr} Ec M {f'}^2 =0 \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \frac{D_{\text{hnf}}}{D_{\text{f}}}\frac{1}{\text{Sc}}{{\Phi }}''+(f{{\Phi }}'-f'\Phi - R_{\text{c}} {\Phi }) =0, \end{aligned}$$

(12)

with subjected boundary conditions :

$$\begin{aligned}{} & {} f=s,\,\, f'=\lambda +Af'', \, \theta =1+B\theta ', \\{} & {} \quad \,\Phi =1\,\text{at}\,\eta =0 \,, \end{aligned}$$

(13)

$$\begin{aligned}{} & {} f'\rightarrow 0,\,\,\theta \rightarrow 0,\,\,\,\,\Phi \rightarrow 0,\,\,\text{as}\,\,\eta \rightarrow \infty .\,\, \end{aligned}$$

(14)

the emerging physical parameters as magnetic field parameter M, permeability parameter P, Prandtl number Pr, thermal radiation parameter Nr, velocity slip parameter A, thermal slip parameter B, wall mass flux transfer parameter S, Schmidt number Sc, chemical reaction parameter $R_{\text{c}}$, are defined by $M = \frac{ \sigma {B_0}^2L}{c\rho _{\text{f}}}$, $P=\frac{2L\nu _{\text{f}}}{c\kappa ^*}$, $Pr=(\mu C_{\text{p}})/\kappa _{\text{f}}$, $Nr = \frac{16 \sigma ^{*}{T_\infty }^{3}}{3 \kappa _{\text{f}} \chi }$, $A=A_1\frac{\mu _{\text{hnf}}}{\rho _{\text{hnf}}}e^{x/2L}\sqrt{\frac{c}{2\nu _{\text{f}}L}}$, $B=B_1e^{x/2L}\sqrt{\frac{c}{2\nu _{\text{f}}L}}$, $S=-v_0/\sqrt{\nu _{\text{f}} c/2L}$ (S is the mass flux parameter with $S > 0$ for suction and $s < 0$ for injection), $Sc=\frac{\nu _{\text{f}}}{D_{\text{f}}}$, $R_{\text{c}}=\frac{2LK_{\text{c}}}{c}$.

Additionally, the theoretical models for the thermophysical characteristics of the nanofluid and hybrid nanofluid are shown in Tables 1 and 2, respectively. $\text{Al}_2\text{O}_3$ nanoparticle is represented by the nanoparticle volume fraction $\phi _1$ in the table, while Cu nanoparticle is represented by the nanoparticle volume fraction $\phi _2$. Additionally, for this study, we also assume that there is no thermal slip between the nanoparticles and that they are in thermal equilibrium.

Table 1 Thermophysical properties [49]

Table 2 Nanofluid and hybrid nanofluid’s thermophysical properties [2, 48]

Table 3 Comparison of $f''(0)$ and  $-\theta '(0)$ for viscous fluid ($\phi _2= \phi _1= 0$) when $\text{Pr} = 0.7$, $S = 3$, and $M=Nr=P=A = B = Rc=Ec= \epsilon =0$ for the shrinking sheet ($\lambda =-1$)

Table 4 The comparison table for least eigenvalues with [57]

Table 5 Table for least eigenvalues with $\lambda$ for preferred vales as $S = 2.5$, $\phi _1$ =$\phi _2$= 0.01, $A=0.2$, $B = 0.2$, $M=0.1$,$Nr=0.1$, $P = 0.1$, $Ec=0.01$, $Sc=1.0$, $Rc=0.1$ and $Pr=6.2$,

Physical quantities

From the science and engineering perspective, the physical quantities of curiosity like shear stress coefficient or drag force, heat, and mass flux, have plentiful applications. The mathematical expressions for the physical significant amounts in flow, heat, and mass transfer of nanofluid flow are skin friction $C_{\text{f}}$, Nusselt Number $Nu_{\text{x}}$, and local Sherwood number $Sh_{\text{x}}$, which are defined as [50]:

$$\begin{aligned}{} & {} C_{\text{f}} = \frac{ \mu _{\text{nf}}}{\rho _{\text{f}} u_{\text{w}}^{2}}{\left({\frac{\partial u}{\partial y}}\right)}_{\text{y}=0} , \\{} & {} \text{Nu}_{\text{x}} = \frac{\{{ \kappa _{\text{hnf}}\left(-\frac{\partial T}{\partial y}\right)-\frac{4\sigma ^{*}}{3K^*}\left(-\frac{\partial T^4}{\partial y}\right)}\}_{\text{y}=0}}{\kappa _{\text{f}}(T_{\text{f}}-T_\infty )}, \\{} & {} \,\text{Sh}_{\text{x}}=-\frac{D_{\text{hnf}}}{D_{\text{f}} (C_{\text{w}}-C_\infty )}x \left(\frac{\partial C}{\partial y}\right)_{\text{y}=0}. \end{aligned}$$

(15)

Skin-friction coefficient, local Nusselt number, and local Sherwood number can be expressed using (9) in (15) as

$$\begin{aligned}{} & {} \text{Re}_{\text{x}}^{1/2}C_{\text{f}} = \frac{\mu _{\text{hnf}}}{\mu _{\text{f}}}f''(0), \\{} & {} \quad \text{Re}_{\text{x}}^{-1/2}\text{Nu}_{\text{x}} = -\left( \frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}+Nr\right) \theta '(0), \\{} & {} \quad \text{Re}_{\text{x}}^{1/2}\text{Sh}_{\text{x}}= -\frac{D_{\text{hnf}}}{D_{\text{f}}} {\Phi }'(0). \end{aligned}$$

(16)

where $Re_{\text{x}} = u_{\text{w}}(x)x/\nu _{\text{f}}$ is the local Reynolds number.

Flow stability

Since the boundary value problem (Eqs. (10)–(14)) may have several (dual) solutions, we conduct a stability analysis to determine whether or not these dual solutions are stable or unstable (physically realizable in practice). The unsteady model [45, 66, 68] is used because the disturbance within a solution may exponentially grow (unstable) or decay with time, and it is executed by introducing an unsteady form of Eqs. (2)–(4) in Eqs. (10)–(12), respectively.

$$\begin{aligned}{} & {} {u}\frac{\partial {u}}{\partial {x}}+{v}\frac{\partial {v}}{\partial {y}} \\{} & {} \quad +\frac{\partial {u}}{\partial {t}}= \frac{\mu _{\text{hnf}}}{\rho _{\text{hnf}}}{\frac{\partial ^2 u}{\partial {y}^2}} \\{} & {} \quad -\frac{\mu _{\text{hnf}}}{\rho _{\text{hnf}}}\frac{u}{k^*}-\frac{\sigma _{\text{hnf}} {B_0}^2}{\rho _{\text{hnf}}}u, \end{aligned}$$

(17)

$$\begin{aligned}{} & {} {u}\frac{\partial {T}}{\partial {x}}+{v}\frac{\partial {T}}{\partial {y}} \\{} & {} \quad +\frac{\partial {T}}{\partial {t}} =\frac{1}{{(\rho {C_{\text{p}}})_{\text{hnf}}}}\frac{\partial {}}{\partial {y}} \left({\kappa ^{*}_{\text{hnf}}}(T) \frac{\partial {T}}{\partial {y}} \right) \\{} & {} \quad -\frac{1}{{(\rho {C_{\text{p}}})_{\text{hnf}}}}\frac{\partial {}}{\partial {y}}(q_{\text{r}})+\frac{\sigma _{\text{hnf}}{B_0}^2}{(\rho C_{\text{p}})_{\text{hnf}}}u^2, \end{aligned}$$

(18)

$$\begin{aligned}{} & {} {u}\frac{\partial {C}}{\partial {x}}+{v}\frac{\partial {C}}{\partial {y}} \\{} & {} \quad +\frac{\partial {C}}{\partial {t}}= {D}_{\text{nf}} \frac{\partial ^2{C}}{\partial {y^2}}-K_{\text{c}}(C-C_\infty ) \end{aligned}$$

(19)

The new similarity transformation $\,\tau =\frac{c}{2L}te^{\rm {x/L}}$ is a time variable with time t adopted such that

$$\begin{aligned}{} & {} \,\eta = y e^{\rm{x/2L} }\sqrt{\frac{c}{2 \nu _{\text{f}}L}},\,\psi =e^{\rm{x/2L}}\sqrt{2 \nu _{\text{f}}Lc} f(\eta , \tau ),\,\theta (\eta ,\tau ) \\{} & {} \quad =\frac{T-T_\infty }{T_{\text{w}}-T_\infty }, \,\,\Phi (\eta ,\tau )=\frac{C-C_\infty }{C_{\text{w}}-C_\infty }, \end{aligned}$$

(20)

With the utilization of the above, subsequently transformed equations are procured

$$\begin{aligned}{} & {} \bigg (\frac{{\mu _{\text{hnf}}}/{\mu _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg ) \frac{\partial ^3{f}}{\partial {\eta ^3}} +f\frac{\partial ^2{f}}{\partial {\eta ^2}}-2\bigg ({\frac{\partial {f}}{\partial {\eta }}}\bigg )^2 \\{} & {} \quad -\frac{\partial ^2{f}}{\partial {\eta }\partial {\tau }}\frac{\partial {f}}{\partial {\eta }}-\bigg (\frac{{\mu _{\text{hnf}}}/{\mu _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg )P\frac{\partial {f}}{\partial {\eta }} \\{} & {} \quad -\bigg (\frac{{\sigma _{\text{hnf}}}/{\sigma _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg )M \frac{\partial {f}}{\partial {\eta }}=0, \end{aligned}$$

(21)

$$\begin{aligned}{} & {} \frac{1}{\text{Pr}}\bigg [\bigg \{\frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}(1+\epsilon \theta )+Nr\bigg \}\frac{\partial ^2{\theta }}{\partial {\eta ^2}}+\frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}\epsilon \bigg ({\frac{\partial {\theta }}{\partial {\eta }}}\bigg )^2\bigg ] \\{} & {} \quad +\frac{(\rho C_{\text{p}})_{\text{hnf}}}{(\rho C_{\text{p}})_{\text{f}}}\bigg (f\frac{\partial {\theta }}{\partial {\eta }}-\frac{\partial {f}}{\partial {\eta }}\theta -\frac{\partial {\theta }}{\partial {\tau }}\bigg ) \\{} & {} \quad +\bigg (\frac{\sigma _{\text{hnf}}}{\sigma _{\text{f}}}\bigg )\text{Pr} Ec M \bigg (\frac{\partial {f}}{\partial {\eta }}\bigg )^2 =0, \end{aligned}$$

(22)

$$\begin{aligned}{} & {} \frac{D_{\text{hnf}}}{D_{\text{f}}}\frac{1}{\text{Sc}} \frac{\partial ^2{\Phi }}{\partial {\eta ^2}} \\{} & {} \quad +\bigg (f\frac{\partial {\Phi }}{\partial {\eta }}-\frac{\partial {f}}{\partial {\eta }}\Phi -\frac{\partial {\Phi }}{\partial {\tau }}- R_{\text{c}} {\Phi }\bigg ) =0, \end{aligned}$$

(23)

subject to the boundary conditions

$$\begin{aligned}{} & {} f(0,\tau )=S,\,\, \frac{\partial {f}}{\partial {\eta }}(0,\tau ) \\{} & {} \quad =\lambda +A\frac{\partial ^2{f}}{\partial {\eta ^2}}(0,\tau ), \, \theta (0, \tau ) \\{} & {} \quad =1+B\frac{\partial {\theta }}{\partial {\eta }}(0,\tau )\,\,,\Phi (0, \tau )=1\,, \end{aligned}$$

(24)

$$\begin{aligned}{} & {} \frac{\partial {f}}{\partial {\eta }}(\eta , \tau )\rightarrow 0, \\{} & {} \quad \theta (\eta ,\tau )\rightarrow 0,\,\,\Phi (\eta ,\tau )\rightarrow 0\,\,as\,\,\eta \rightarrow \infty .\,\, \end{aligned}$$

(25)

The perturbation equations must be applied toward Eqs. (20)– (25) to apply the stability solutions. The perturbation equations are [45, 65]

$$\begin{aligned}{} & {} f(\eta ,\tau )=f_0(\eta )+e^{-\gamma \tau }F(\eta ), \theta (\eta ,\tau ) \\{} & {} \quad =\theta _0(\eta )+e^{-\gamma \tau }G(\eta ), \\{} & {} \quad \Phi (\eta ,\tau )=\Phi _0(\eta )+e^{-\gamma \tau }H(\eta ), \end{aligned}$$

(26)

where $\gamma$ is an unidentified eigenvalue parameter that needs to be listed and $F(\eta )$, $G(\eta )$ and $H(\eta )$ are the extremely small eigenvalue parameters in relation to $f_0(\eta )$, $\theta _0(\eta )$, and $\Phi _0(\eta )$, respectively. According to this theory of stability, $f_0(\eta )=f(\eta ), \theta _0(\eta )=\theta (\eta )$, and $\gamma$ is a collection of eigenvalues where $\gamma_1 <\gamma_2<...<\gamma_{\text{n-1}}<\gamma_{\text{n}}$. It is possible to determine the initial decay or increase in the disturbance by incorporating Eq. (26) into Eqs. (20)–(25) and setting $\tau$ to zero. The positive or negative sign of the smallest eigenvalue $\gamma _1$ will determine whether the solution is stable or not. The subsequent attained linearized eigenvalue problem can be expressed as

$$\begin{aligned}{} & {} \bigg (\frac{{\mu _{\text{hnf}}}/{\mu _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg ) F''' +Ff_0''+F''f_0-4f_0'F'+\gamma F' \\{} & {} \quad -\bigg (\frac{{\mu _{\text{hnf}}}/{\mu _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg )PF' \\{} & {} \quad -\bigg (\frac{{\sigma _{\text{hnf}}}/{\sigma _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg )M F'=0, \end{aligned}$$

(27)

$$\begin{aligned}{} & {} \frac{1}{\text{Pr}}\bigg [\bigg \{\frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}(1+\epsilon \theta _0)+Nr\bigg \}G''+\bigg \{\frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}(1+\epsilon G)\bigg \}\theta _0'' \\{} & {} \quad +2\frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}\epsilon \theta _0'(G')\bigg ] \\{} & {} \quad +\frac{(\rho C_{\text{p}})_{\text{hnf}}}{(\rho C_{\text{p}})_{\text{f}}}\bigg (F\theta _0'+G'f_0-\theta _0F'-Gf_0'+\gamma G \bigg ) \\{} & {} \quad +\bigg (\frac{\sigma _{\text{hnf}}}{\sigma _{\text{f}}}\bigg )\text{Pr} Ec M {F'}^2=0, \end{aligned}$$

(28)

$$\begin{aligned}{} & {} \frac{D_{\text{hnf}}}{D_{\text{f}}}\frac{1}{\text{Sc}}{{H}}'' \\{} & {} \quad +\bigg (f_0H'+F{\Phi _0}'-{f_0}'H-F'\Phi _0+\gamma H- R_{\text{c}} {H}\bigg ) =0, \end{aligned}$$

(29)

these are conditioned to linearized conditions

$$\begin{aligned}{} & {} F(0)=0,\,F'(0)=AF''(0), \\{} & {} \quad G(0)=BG'(0)\,\,,\,H(0)=0\,\,, \end{aligned}$$

(30)

$$\begin{aligned}{} & {} F'(\infty )\rightarrow 0,\,\,G(\infty )\rightarrow 0,\,\,\,H(\infty )\rightarrow 0\,.. \end{aligned}$$

(31)

Accordingly, if $\gamma$ is positive, the unstable solution $f(\eta , \tau )$ converges to the steady-state solution $F(\eta )$ as time passes $\tau \rightarrow \infty$. [17] recovered a far-field boundary condition with a new condition F₀″(0)=1 to provide an adequate range of eigenvalues $\gamma$ so that a nontrivial solution (eigenvalue) could be obtained. Thus, the bvp4c solver is employed to discover the unknown eigenvalues $\gamma$ and to determine the stability of the flow. A positive value of the resulting smallest eigenvalue $\gamma _1$ such that $\gamma_1 > 0$ denotes a solution that is physically feasible and stable, while a negative value of $\gamma_1<0$ indicates an impractical solution.

Numerical method and validation

The bvp4c solver in Matlab software is mostly suggested to compute the nonlinear ordinary differential equations for boundary layer flow problems to show the presence of multiple solutions. The bvp4c solver through a calling syntax $sol = bvp4c (@OdeBVP, @OdeBC, solinit, options)$ is entrenched. The bvp4c function eases the computation process of the boundary value problems involving unknown parameters and is efficient in solving the boundary value problems even with poor guesses [52]. In addition, the current problem is numerically solved for the two different solution branches (solutions of the upper and lower branches). Therefore, it is required two different guesses for finding distinct branch outcomes. The upper branch outcome can be easily found due to an early obvious guess, while the guess needed for the lower branch is quite complicated. Hence, the guess selection for the lower branch requires more effort, to get the solutions that satisfy the boundary convergence asymptotically. In order to provide the guesses, a trial-and-error approach is necessary until the dual solutions are discovered. Typically, the term “first solution” refers to the initial solution that asymptotically satisfies Eqs. (5)–(6) and converges within a small boundary layer. The next solution, which has a thicker momentum and temperature boundary layer, is referred to as the second solution in equations. This problem requires two sets of guesses which are coupled with $\eta _\infty = 15$. Every high-accuracy numerical solution to this problem was developed after we fixed the relative tolerance to $10^{-6}$. The residual of the continuous solution serves as the foundation for both mesh selection and error control. Finding the lower branch solution is difficult, even though it can be done even with a subpar initial guess for the upper branch. We begin with a set of parameter values for which the problem can be solved with ease in order to get around this challenge. With a slight adjustment in the parameters, the resulting findings were then used as the first guess for the problem’s solution. Up until the desired parameter values are attained, this phase is repeated. According to [52], this method is known as a continuation. To begin the numerical computation, Eqs. (10)–(12) are first built into the bvp4c algorithm in such a way that

$$\begin{aligned}{} & {} y(1)=f, y(2)=f', y(3)=f'', y(4)=\theta , \\{} & {} \quad y(5)=\theta ', y(6)=\Phi , y(7)=\Phi ' \end{aligned}$$

(32)

The bvp4c code for Eqs. (10)–(12) are as follows

$$\begin{aligned}{} & {} f'''=-\bigg (\frac{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}{{\mu _{\text{hnf}}}/{\mu _{\text{f}}}}\bigg ) \bigg \{y(1)y(3)-2{y(2)}^2 \\{} & {} \quad -\bigg (\frac{{\mu _{\text{hnf}}}/{\mu _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg )Py(2) -\bigg (\frac{{\sigma _{\text{hnf}}}/{\sigma _{\text{f}}}}{{\rho _{\text{hnf}}}/{\rho _{\text{f}}}}\bigg )M y(2)\bigg \}, \\{} & {} \quad \theta ''= -\frac{\text{Pr}}{\bigg (\frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}(1+\epsilon y(4))+Nr\bigg )} \bigg \{ \frac{1}{\text{Pr}}\bigg (\frac{\kappa _{\text{hnf}}}{\kappa _{\text{f}}}\epsilon {y(5)}^2\bigg ) \end{aligned}$$

(33)

$$\begin{aligned}{} & {} +\frac{(\rho C_{\text{p}})_{\text{hnf}}}{(\rho C_{\text{p}})_{\text{f}}}\left(y(1)y(5)-y(2)y(4)\right) \\{} & {} \quad +\bigg (\frac{\sigma _{\text{hnf}}}{\sigma _{\text{f}}}\bigg )\text{Pr} Ec M {y(2)}^2\bigg \} \end{aligned}$$

(34)

$$\begin{aligned}{} & {} {{\Phi }}''= -\frac{D_{\text{f}}}{D_{\text{hnf}}}\frac{\text{Sc}}{1}\bigg \{y(1)y(7)-y(2)y(6)- R_{\text{c}} y(6)\bigg \}, \end{aligned}$$

(35)

Accompanied with the boundary conditions Eqs. (13)–(14), which are written as

$$\begin{aligned}{} & {} ya(1)-S=0, ya(2)-\lambda -ya(3)A =0, \\{} & {} \quad ya(4) -1-ya(5) B =0,ya(6)-1=0. \end{aligned}$$

(36)

$$\begin{aligned}{} & {} yb(2)=0, yb(4)=0, yb(6)=0, \end{aligned}$$

(37)

where ya and yb describe the position at the surface of the shrinking sheet and the free surface, respectively. The relative tolerance has been fixed to $1\times {10}^{-6}$ throughout the computation process. Eqs. (10)–(12) are coded into @OdeBVP to apply the fundamental syntax, and @OdeBC is used to code the conditions. The starting mesh point and educated assumptions are implied by the syntax’s solinit function. If there are two starting guesses in the solinit function, dual solutions are possible. The non-unique solutions exist in a boundary value problem because of the nonlinearity of the mathematical model in (17)–(19), and the variation of the respective governing parameters may lead to bifurcations in solutions that encourage the presence of multiple solutions. The stability analysis process to validate the readily used workable solutions.

Fig. 2

The smallest eigenvalues $\gamma _1$ with $\lambda$

Results and discussion

This study chooses the behavior of hybrid nanoparticles (mixing of alumina and copper nanoparticles) over shrinking ($\lambda < 0$) surfaces with water as the base fluid by maintaining the value of Prandtl number $Pr (=6.2)$ throughout the study. The other parameters are varied to investigate the impacts on the boundary layer flow, heat, and mass transfer in the hybrid nanofluid. Also, the dual solutions and their stability for heat and mass transfer of the hybrid nanofluid flow are discussed in this section. The accessible bvp4c application in the Matlab software is used to solve Eqs. (10)–(12), first converting the equations into bvp4c code. This yields many similarity answers (as discussed in the previous section).

To validate and authenticate the results generated from our used method, we have made a comparison for $f''(0)$ and $-\theta '(0)$ with [16] and [64] for some selected values of parameters, $\phi _1$ = $\phi _2$ =M=Nr=$\epsilon$=P= Rc=0, $Pr=0.7$, $S=3.0$ and $\lambda$ = -1 which focuses on the case of shrinking surface as presented in Table 3. We found a good agreement between the present and previously published results. This lends confidence to the accuracy of the numerical results presented in this study. Since there are two solutions, it is essential to analyze the stability of each to support the validity of the physical solution. When the smallest eigenvalue is positive and the disturbance in the early decay of the perturbation is present, the flow is said to be stable. Otherwise, it is declared unstable when the smallest eigenvalue is negative, and this is because of the disturbance in the perturbation’s initial growth. By solving Eqs. (21)–(31), the smallest eigenvalues $\gamma _1$ are presented in Tables 4 and 5 and Fig. 2. It can be observed in Fig. 2 that the upper half is related to the stable solution region and the lower half for the unstable solution region. Table 4 is a comparison table of the smallest eigenvalues $\gamma _1$ with the dual solution for different values of A and $\lambda$, which guarantee the technique used for stability analysis. For the first solution, the positive value of $\gamma _1$ denotes stability, but for the second solution, the negative sign denotes instability. Additionally, Fig. 2 and Table 5 corroborate the current stability study by showing that $\gamma _1\rightarrow 0$ is equivalent to $\lambda \rightarrow \lambda _{\text{c}}$. Actually, for several values of $\lambda$, Table 5 shows the smallest eigenvalue, $\gamma$. It is evident that the smallest eigenvalue for the lower branch solution was negative, indicating the emergence of disturbance in a steady flow and leading to the formation of an unstable lower branch solution. The smallest eigenvalue for the upper branch solution, however, showed positive values, indicating an initial reduction of the disturbance in the steady flow and a stable upper branch solution.

Moreover, the effects of specific parameters toward the skin friction coefficient $\text{Re}_{\text{x}}^{1/2}C_{\text{f}}$, local Nusselt number $\text{Re}_{\text{x}}^{-1/2}\text{Nu}_{\text{x}}$, and local Sherwood number $\text{Re}_{\text{x}}^{-1/2}\text{Sh}_{\text{x}}$ are portrayed in a graphical form as can be seen in Figs. 3–14, as well as the velocity $f'(\eta)$, temperature $\theta (\eta )$, and concentration $\Phi (\eta )$ profiles plots, are displayed in Figs. 15–22. All the figures contain dual solutions (first and second solutions), subject to the boundary conditions, for a specific range of shrinking surface parameter $\lambda$, which mainly depends on the strength of the suction parameter, S. The solutions bifurcate at $\lambda =\lambda _{\text{c}}$, where $\lambda _{\text{c}}$ denotes the critical value for $\lambda$ where there is no solutions for $\lambda <\lambda _{\text{c}}$. The dual solutions are joined by the critical value $\lambda _{\text{c}}$ that becomes the separation point of the solutions as well as the boundary layer with the surface. This critical point is the indicator point for the separation of the boundary layer from laminar to turbulent flow.

The variations of skin friction coefficient $\text{Re}_{\text{x}}^{1/2}C_{\text{f}}$, local Nusselt number $\text{Re}_{\text{x}}^{-1/2}\text{Nu}_{\text{x}}$, and local Sherwood number $\text{Re}_{\text{x}}^{-1/2}\text{Sh}_{\text{x}}$ with shrinking parameter $\lambda$ for $S=2.3, 2.4, 2.5$ for shrinking sheet are shown in Figs. 3–5, respectively. From Fig. 3, it is seen that when the value of the suction parameter S increases, the values of the skin friction coefficient upsurge for the first solution but for the second solution, it destroys. Figures 4 and 5 demonstrate that the local Nusselt number and local Sherwood number both are amplified with suction parameter S; meanwhile, the value of the local Sherwood number decreases for the second solution. Physically, the act of suction S allows the fluid molecules to fill the shrinking surface and triggers the heat from the surface to increase. Hence, the thinner thermal boundary layer thickness will affect the temperature gradient to be steeper as suction increases and hence supports the heat transfer enhancement. It can also be observed that more than one solution is obtained for a fixed value of $\lambda$. The dual solutions exist when $\lambda >\lambda _{\text{c}}$ where $\lambda _{\text{c}}$ indicates the critical value of $\lambda$. Further, when $\lambda$ is equal to a certain value of $\lambda _{\text{c}}$, there is only one solution that exists, and no solution exists for $\lambda <\lambda _{\text{c}}$. We found that by increasing the suction parameter S, the range of solutions widens where $\lambda _{\text{c1}}=-1.4747, \lambda _{\text{c2}}=-1.6047, \lambda _{\text{c3}}=-1.7417$ for $S=2.3, 2.4, 2.5$, respectively.

An essential physical parameter for determining how well nanoparticles affect mass, heat, and fluid flow is the nanoparticle volume fraction. Figures 6–8 accordingly show the variations of skin friction coefficient, local Nusselt number, and Sherwood number of $\text{Al}_2\text{O}_3-\text{Cu}$/water hybrid nanofluid with volume fraction of $\text{Al}_2\text{O}_3$ nanoparticle $\phi _1$ (=0.01,  0.05, 0.1) over the shrinking parameter $\lambda$. According to physical laws, the first solution’s fluid is physically dragged in the direction of the fluid motion of the nanoparticle, which is impacted by the hydrodynamic contact. Also, we know the thermal conductivity of hybrid nanofluids is enhanced due to a rise in the volume of nanoparticles. As a result, an increase in the thermal conductivity of hybrid nanofluids has a positive effect on the fluid temperature as it increases with an increase in the nanoparticle volume fraction. As a result, the skin friction coefficient and the local Nusselt number both increase with an increase in $\phi _1$, and for both solution branches, the Sherwood number is observed to decrease with an increase in $\phi _1$. Hence, from our computations, with the expansion of the critical value (indicator of the boundary layer separation) where $\lambda _{\text{c1}}=-1.7415, \lambda _{\text{c2}}=-1.7381, \lambda _{\text{c3}}=-1.7014$, for $\phi -1=0.01, 0.05, 0.1$ multiple solutions are available. This also implies that hybrid nanofluid provides a better heat performance than nanofluid.

From Figs. 9–11, the critical value of S for different values of $\lambda$ are numerically computed as $\text{Sc}_1=2.3198, \text{Sc}_2=2.4698, \text{Sc}_3=2.6760$ with $\lambda =-1.5,-1.7,-2.0$. It is shown from the figures that the skin friction coefficient is increasing, but the local Nusselt number is diminished as the value of $\lambda$ increasing for both the solutions at the shrinking region. Meanwhile, the Sherwood number decreases as the values of $\lambda$ rising for the first solution, but the opposite trend occurs for the second solution. The fluid is drawn closer to the surface as a result of mass suction, which stops the vorticity from diffusing. The variations of the skin friction coefficient, local Nusselt number, and Sherwood number with shrinking parameter $\lambda$ are provided in Figs. 12–14, for variation in the value of the magnetic parameter $M(=0.1,0.2, 0.3)$, respectively, when $S=2.5$ with existence of dual solutions. It is worth mentioning that the critical value of $\lambda _{\text{c}}$ is obtained as $\lambda _{\text{c1}}=-1.7421, \lambda _{\text{c2}}=-1.8234, \lambda _{\text{c3}}=-1.9060$, respectively. The observation is that on the expansion of magnetic parameter M, the critical value $\lambda _{\text{c}}$ (an indicator of the boundary layer separation) improves its magnitude value. The magnetic field creates a resistive Lorentz force that prevents fluid motion and raises the skin friction coefficient as a result. Additionally, it can be seen in Fig. 13 that the magnetic field exhibits a reversible tendency to lower the local Nusselt number by slowing down the fluid’s temperature. Figure 14, where the Sherwood number increases with the magnetic field parameter M, shows the opposite tendency. By adding a magnetic field to the boundary layer flow, it is possible, according to this observation, to postpone the boundary layer’s separation. The effect of the magnetic field’s presence broadens the range of solutions’ potential existence.

Figures 15–23 portray the velocity and temperature profiles of the $\text{Al}_2\text{O}_3-\text{Cu}$/water hybrid nanofluid with various parameters like porous/Darcy parameter P, thermal radiation parameter Nr, Eckert number Ec, chemical reaction parameter Rc, Schmidt number Sc, velocity slip parameter A, temperature slip parameter B, and variable thermal conductivity parameter $\epsilon$, respectively. All the figures approached asymptotically and fulfilled the boundary conditions. Figure 15 reveals the velocity profile for the various value porosity parameter P when S = 2.5 and $\lambda =-1.7$. Dual solutions are shown in this image, where the increment of P causes the velocity profile to rise for the first solution but fall for the second solution. Physically, the presence of a porous material in the initial solution allows the fluid to be dragged in the direction of motion and will enhance the velocity of the hybrid nanofluid. Figure 16 displays the distribution of the temperature profile of hybrid nanofluid for different values of thermal radiation parameter Nr. Further dual solution observations with increment trend in temperature profile are found in Fig. 16, which designates the active heat transfer operation when radiation parameter Nr is considered. Rosseland radiative absorptive $K^\star$ diminutions with higher thermal radiation and, consequently, the radiative heat flux results in the intensification in the thickness of the thermal boundary layer. Figure 17 presents the impact of Eckert Ec number on the temperature profile of the hybrid nanofluid. It is found that two types of solutions exist, and a small acceleration of Eckert numbers seems to boost the temperature profile for both dual solutions. As Ec grows, the friction between the fluid layer increase which consequently increases the heat transport rate. Further, the relationship between the kinetic energy and the heat enthalpy variation is called the Eckert number. So, the kinetic energy of the hybrid nano liquid increases with the increase in Ec which is justified in Fig. 17. Figure 18 highlights the impact of the chemical reaction parameter $R_{\text{c}}$ parameter on the concentration profile of hybrid nanofluid. The effect of $R_{\text{c}}$ is to decrease the concentration profile for the present two types of solutions. Physically, the fluid becomes thicker due to increasing value in $R_{\text{c}}$, which reduces the concentration profile. This is because the chemical is consumed as a result of the chemical reaction in this system, which lowers the concentration profile. Figure 19 portrays the effects of Schmidt number Sc on the concentration profile of the hybrid nanofluid. In both the solutions, rising in the values of Sc shows a decrement in the concentration profile. The shear component for diffusivity, viscosity/density, to the diffusivity for mass transfer ratio is known as the Schmidt number. Physically, as the Sc number rises, molecular diffusion reduces. Figures 20 and 21 indicate the velocity and temperature profile for hybrid nanofluid with an increment of velocity slip parameter A and thermal slip parameter B, respectively. Velocity slip means that the fluid velocity in the vicinity of the sheet is no longer equivalent to the shrinking sheet velocity. It is noticed in Fig. 20 that the velocity profile has to improve for the first solution, but it declines for the second solution. Dual solutions are depicted in this picture, where the increment of A results in an increase in the velocity profile for the first solution while a decrease in the velocity profile for the second solution. According to physical laws, the first solution’s porous media physically drags the fluid in the direction of motion, increasing the velocity of the hybrid nanofluid. The impact of the thermal slip parameter B over the temperature profile is reduced with B for the hybrid nanofluids, as observed in Fig. 21. Physically, increasing the slip parameter produces less friction at the surface, which, in turn, provides decreasing the fluid temperature. Moreover, the boundary layer thickness for the first solution (upper branch) is lower than that of the second solution (lower branch). The effects of the thermal conductivity parameter $\epsilon$ on the temperature profile of the hybrid nanofluid are shown in Fig. 22. As the fluid’s thermal conductivity increases, the fluid temperature rises. Physically, the transfer of heat from the surface into the fluid is sped up by an increase in thermal conductivity brought on by a rise in temperature. The flowchart to get the ultimate solution using MATLAB software is depicted in Fig. 23.

Fig. 3

Skin friction coefficient varies with $\lambda$ for varying S

Fig. 4

Local Nusselt number modification using $\lambda$ for various S

Fig. 5

Sherwood number modification using $\lambda$ for various S

Fig. 6

Skin friction coefficient varies with $\lambda$ with varying $\phi _1$

Fig. 7

Nusselt number variation for varying $\phi _1$ with local S

Fig. 8

Sherwood number variation for varying $\phi _1$ with S

Fig. 9

Skin friction coefficient variation with S for varied $\lambda$

Fig. 10

local Nusselt number variation with S for varied $\lambda$

Fig. 11

Sherwood number variation with S for varied $\lambda$

Fig. 12

Skin friction coefficient variation with $\lambda$ for varied M

Fig. 13

local Nusselt number variation with $\lambda$ for varied M

Fig. 14

Sherwood number variation with $\lambda$ for varied M

Fig. 15

Velocity profile variation for varied of P

Fig. 16

Temperature profile variation for varied Nr

Fig. 17

Temperature profile variation for varied Ec

Fig. 18

Concentration profile variation for varied Rc

Fig. 19

Concentration profile variation for varied Sc

Fig. 20

Velocity profile variation for varied A

Fig. 21

Temperature profile variation for varied B

Fig. 22

Temperature profile variation for varied $\epsilon$

Fig. 23

MATLAB way of solution

Conclusions

With simultaneous effects of velocity and thermal slip boundary condition, suction, variable thermal conductivity, Joule heating, and viscous dissipation, the current study aims to numerically solve the heat and mass transfer of radiative-magnetite flow of $\text{Al}_2\text{O}_3{-}\text{Cu}$/water-based hybrid nanofluid flow toward a shrinkable sheet. The distribution of skin friction coefficient, local Nusselt number, Sherwood number, velocity, temperature, and concentration profiles are displayed using the effective bvp4c solver in the Matlab software. Due to the emergence of the two solutions, the flow stability analysis is carried out to demonstrate the validity of the first solution. The results can be summed up as follows:

• 1. When a shrinking surface and the right amount of suction are present, dual solutions with critical/separation values are discovered, with the first solution being found to be stable and the other solution being found to be unstable. The two branch solutions merged with one another at a critical value for a hybrid nanofluid.

• 2. Positive minimum eigenvalues $\gamma _1>0$ are produced by the first solution branch, whereas negative minimum eigenvalues $\gamma _1<0$ are produced by the second.

• 3. The first solution branch yields positive minimum eigenvalues $\gamma _1>0$ while the second yields negative minimum eigenvalues $\gamma _1<0$. For hybrid nanofluid, the critical value is extended by increasing the alumina volume fraction $\phi _1$ and decreasing the sheet parameter $\lambda$; nevertheless, it is decreased by the suction parameter S and magnetic parameter M.

• 4. For the first solution branch, the velocity increases with the addition of the porous parameter and the velocity slip parameter, whereas it drops for the second solution branch in the region of the shrinking surface.

• 5. The increment of the thermal radiation parameter, Eckert number, and variable thermal conductivity parameter enhance, but the thermal slip parameter drops the temperature of hybrid nanofluid for both the solution branch for shrinking sheet.

• 6. The concentration profile can be diminished by the chemical reaction parameter and Schmidt number for both the first and second solutions in the shrinking surface region.

• 7. In the future, this work can be continued to assess the impact of variable viscosity, variable diffusivity, presence of Riga plate, convective boundary conditions, etc. Different combinations of dual nanoparticles or triple nanoparticles can be used in this model. Other than these impacts, it can be extended for three-dimensional boundary layer flows by conserving various possible effects.