Introduction

The researchers are taking interested in energy transfer with fluid flow across a curved surface due to its practical significance in various manufacturing sectors including the aerodynamics of vehicles, extraction of polymeric sheets, turbine blades, glass fiber, ship design, heat exchangers, hot rolling, paper production, wind turbines sports equipment, and biomedical applications. Ullah et al. [1] examined thermal transfer in hybrid nanofluid Darcy–Forchheimer flows subjected to various shape impact across a curved stretching surface (CSS). Incorporating carbon nanotubes and iron ferrite nanoparticles (NPs), Gohar et al. [2] investigated the movement of Casson Hnf (hybrid nanofluid) across a CSS. The flow of Hnf across a porous exponential CSS with thermal slip and suction/ injunction effect was assessed by Abbas et al. [3]. According to the outcomes, the positive coefficient of curvature factor increased the velocity field for both the injection and suction scenarios. Raza et al. [4] examined the thermal transportation characteristics of a radiative Hnf flow over a CSS. The findings revealed that the curvature factor has a moderating effect on the velocity field. Ahmed et al. [5] described the dynamics of magnetohydrodynamic (MHD) steady 2D flow of Hnf across a CSS with the homogeneous–heterogeneous reactions. Xiong et al. [6] investigated the magnetized Darcy laminar flow of viscous fluid over a CSS with the effects of second-order slip. Ali and Jubair [7] explored the rheological features of Hnf flow with heat source and thermal emission across a CSS. The outcome demonstrates that the velocity field is raised but the energy is decreased for greater curvature coefficient. Hayat et al. [8] reported the flow of radiative hybrid nanomaterials via a porous curving surface with Joule heating and inertial features. The results indicated that the velocity curve is enhances when the curvature factor rises; while, the opposite tendency is found concerning the magnetic parameters. Using a stretchable curved oscillatory surface, Imran et al. [9] considered the impact of Soret and Dufour on the MHD flow of unsteady couple stress fluid. Employing joule heating and viscous dissipation effect, Haq and Ashraf [10] evaluated the entropy generation of MHD convective flow of Carreau fluid on a CSS. Recently several authors have reported on curved stretching surface [11,12,13,14].

As the world's population continues to expand at a rapid rate, there will be an ever-increasing demand for energy consumption that is more efficient. Efficient and rapid heat transfer inside a thermal system necessitates the use of high-performance thermal management systems due to the elevated temperatures concerned. Nanofluids have garnered significant interest in recent times, especially regarding their use in renewable energy systems and techniques to enhance heat transfer. Nanofluids are considered to comprise particles with diameters of nanometers suspended in base fluids, such as water or motor oil, creating a completely new class of fluids called nanofluids. Metal or carbon are the most common materials for nanoparticles utilized in nanofluids. There are numerous applications for nanofluid as a coolant in the engineering, automotive industry, nuclear coolant, renewable energy and healthcare sectors. The term "nanofluid" (NF) was 1st used by Choi and Eastman [15] in 1995 and Buongiorno [16] demonstrated that NF are formed by combining nanoparticles with base fluids. The effects of MHD convective free stream NF flow across a stretching cylinder were studied by Makkar et al. [17]. Hnf and Thnf exhibit enhanced thermal properties when compared to standard NF. A base fluid is used to synthesize Thnfs and Hnfs, respectively, by incorporating two or more distinct NPs into the base fluid. The numerical analysis emphasizes the flow of a nano-liquid containing hybrid nanoparticles (AA7072, AA7075) via an endless disc was performed by Ullah et al. [18]. With the use of aluminum alloys, Hanif et al. [19] examined the two-dimensional water-based Hnf flow through an inclined sheet with suction and Joule heating effect. A 3-D Hnf flow of methanol and AA7072–AA7075 with slip effect was studied by Tlili et al. [20] on an irregular surface. Archana et al. [21] considered the effect of radiative heat transfer on the mobility of ternary alloys consisting of Nimonic 80A and aluminum alloys (AA7072–AA7075) over a melting surface. Manjunatha et al. [22] investigated the Thnf flow across a two-dimensional enlarging surface. Recently significant results are presented by Ref. [23,24,25,26,27,28,29].

Understanding a system's irreversibility factor in heat transfer processes requires an understanding of entropy generation, especially in conventional industrial sectors where fluid fluxes and heat transmission are involved. The formation of entropy is a significant feature of thermodynamics. In a thermal system that is isolated from other systems, the second law of thermodynamics asserts that entropy does not diminish. Total entropy is continually increasing in irreversible phenonium; whereas, it is always remaining identical in reversible processes. The entropy formation is the idea that plays an essential role in comprehending and increasing the efficiency of a wide variety of systems and procedures including air conditioning, heat transfer devices, air conditioning units, combustion, vehicle engines, reactors, chillers, and desert coolers [30]. Khan and Alzahrani [31] and Naveed [32] used the Joule heating, thermophoresis and Brownian motion effect for Blasius flow on a curving surface to analyze the entropy formation of a chemically reactive nanofluid. Ibrahim and Gizewu [33] investigated the bioconvective formation of entropy and gyrotactic microbes incompressible, viscous flow over a curving extended surface. The entropy formation in MHD Hnf flow with variable porosity was investigated by Hayat et al. [34]. Employing Arrhenius activation energy and entropy optimization, Alsallami et al. [35] simulated the Marangoni Maxwell nanofluid flowing on a spinning disc. Murtaza et al. [36] addressed the numerical simulation for entropy formation and thermal transport through tri-hybrid nanoliquid. Sakkaravarthi and Reddy [37] employed blood as the base fluid to assess the formation of entropy in MHD Hnf flow comprised of silver and aluminum oxide NPs across a porous surface with Joule heating and convective boundary circumstances. The references [38,39,40,41] provide some of the additional investigations that are associated with the entropy formation of a fluid flow over a curving extended surface.

Based on the above literature, no one has described the C–C heat flux model using Thnf flow with viscous dissipation across a porous curved surface. In order to fill such gap, the current research work focuses on the Thnf flow encompassed of aluminum alloys (Ti6Al4V, AA7072 and AA7075) across curved stretching surface. The flow has been numerically assessed under the consequences of heat radiation, Joule heating and C–C theory, viscous dissipation, and exponential heat source. Some core novelties are:

  • To investigate the heat transfer subject to C–C heat flux, viscous dissipation, thermal radiation and EHS.

  • To study the Thnf flow across a permeable curved surface.

  • To examine the consequences of Ti6Al4V, AA7072 and AA7075-NPs on the fluid velocity and heat transfer rate.

  • What is the impact of thermal time relaxation factor on temperature?

  • What is the effect of Darcy medium with varying porosity and permeability has on the flow of the Thnf?

Mathematical modeling

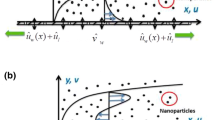
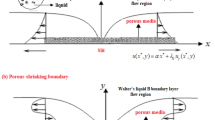
The 2D incompressible Thnf flow across a porous CSS of radius R is considered. Variations on the Darcy–Forchheimer relation are employed to characterize the flow in permeable surface. The addition of C–C heat flux, radiation and Joule heating to the energy expression contributes to the enhancement of the thermal field. The velocity of stretching surface along the s-axis is denoted by \(u_{{\text{w}}} = \frac{{{\text{bs}}}}{{\left( {1 - \alpha^{*} t} \right)}}\) where \(b > 0\) (see Fig. 1). Here \(b = 0\) correspond to static sheet and \(b > 0\) describes the stretching of curved surface. In r-direction, a magnetic field with intensity \(\overrightarrow {{B_{0} }}\) is integrated. The surface's temperature is described as \(T_{{\text{w}}} .\) Entropy generation is also computed using the 2nd law of thermodynamics. The following equations are based on the above assumptions [34, 42]:

$$ \frac{{\partial \rho }}{{\partial t}} + {\mkern 1mu} {\mkern 1mu} \mathop \nabla \limits^{ \rightharpoonup } \cdot\; (\rho \mathop V\limits^{ \rightharpoonup } ) = 0,$$
(1)
Fig. 1
figure 1

Physical visualization of the flow

Full size image

For incompressible fluid \(\rho\) is constant so \(\frac{\partial \rho }{{\partial t}} = 0,\) Eq. (1) become

$$ \mathop{\nabla }\limits^{\rightharpoonup} \cdot \mathop{V}\limits^{\rightharpoonup} = 0, $$
(2)

In a curvilinear coordinate the continuity equation become,

$$ \left( { - R\frac{\partial u}{{\partial s}}} \right) = \frac{{\partial \left( {\left( {r + R} \right)v} \right)}}{\partial r}, $$
(3)
$$ \frac{\partial p}{{\partial r}} = \rho_{{{\text{Thnf}}}} \left( {\frac{{u^{2} }}{r + R}} \right), $$
(4)
$$ \begin{aligned} & \frac{\partial u}{{\partial t}} + v\left( {\frac{\partial u}{{\partial r}}} \right) + \left( {\frac{u}{r + R}} \right)\left( {R\left( {\frac{\partial u}{{\partial s}}} \right) + v} \right) \\ = & \frac{ - R}{{\rho_{{{\text{Thnf}}}} \left( {R + r} \right)}}\left( {\frac{\partial P}{{\partial s}}} \right) - \frac{{C_{{\text{b}}} \varepsilon^{2} (r)}}{{\left( {k^{*} (r)} \right)^{\frac{1}{2}} }}u^{2} \\ \quad & + \nu_{{{\text{Thnf}}}} \left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + u\frac{1}{{\left( {R + r} \right)}}\left( {\frac{\partial u}{{\partial r}} - \frac{u}{(R + r)}} \right) - \frac{\varepsilon (r)}{{k^{*} (r)}}} \right) - \frac{{\sigma_{{{\text{Thnf}}}} }}{{\rho_{{{\text{Thnf}}}} }}B_{0}^{2} u, \\ \end{aligned} $$
(5)
$$ \begin{aligned} & \frac{\partial T}{{\partial t}} + u\left( {\frac{R}{R + r}} \right)\frac{\partial T}{{\partial s}} + \lambda_{{\text{E}}} \Phi_{{\text{E}}} + v\left( {\frac{\partial T}{{\partial r}}} \right) \\ = & \frac{{k_{{{\text{Thnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{Thnf}}}} }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} - \frac{1}{{\left( {R + r} \right)}}\frac{\partial T}{{\partial r}}} \right) + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \left( {\rho C_{{\text{p}}} } \right)_{{{\text{Thnf}}}} }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} - \frac{1}{{\left( {R + r} \right)}}\frac{\partial T}{{\partial r}}} \right) \\ \quad & + \frac{Q}{{\left( {\rho C_{p} } \right)_{{{\text{Thnf}}}} }}(T - T_{\infty } ){\text{e}}^{{ - r\sqrt {\left( {\frac{{u_{{\text{w}}} }}{{\nu_{{\text{f}}} }}} \right)} }} + \frac{{\sigma_{{{\text{Thnf}}}} B_{0}^{2} u^{2} }}{{\left( {\rho C_{p} } \right)_{{{\text{Thnf}}}} }} + \frac{{\mu_{{{\text{Thnf}}}} }}{{(\rho C_{p} )_{{{\text{Thnf}}}} }}\frac{\varepsilon (r)}{{k^{*} (r)}}u^{2} + \frac{{\rho_{{{\text{Thnf}}}} }}{{(\rho C_{{\text{p}}} )_{{{\text{Thnf}}}} }}\frac{{C_{b} \varepsilon^{2} (r)}}{{\left( {k^{*} (r)} \right)^{\frac{1}{2}} }}u^{3} , \\ \end{aligned} $$
(6)

where

$$ \begin{aligned} \Phi_{E} = & \frac{{\partial^{2} T}}{{\partial t^{2} }} + \frac{\partial v}{{\partial t}}\frac{\partial T}{{\partial r}} + 2v\frac{\partial }{\partial r}\left( {\frac{\partial T}{{\partial t}}} \right) + \left( {\frac{R}{R + r}} \right)\left( {2u\frac{\partial }{\partial s}\left( {\frac{\partial T}{{\partial t}}} \right) + \frac{\partial T}{{\partial s}}\frac{\partial u}{{\partial t}} + u^{2} \left( {\frac{R}{r + R}} \right)\left( {\frac{{\partial^{2} T}}{{\partial s^{2} }}} \right)} \right) \\ \quad & + v^{2} \frac{{\partial^{2} T}}{{\partial r^{2} }} + \left( {\frac{uR}{{r + R}}\left( {2v\left( {\frac{\partial T}{{\partial s}}} \right) + \frac{\partial v}{{\partial s}}} \right) + v\left( {\frac{\partial v}{{\partial r}}} \right)} \right)\frac{\partial T}{{\partial r}} + \left( {v\frac{\partial u}{{\partial r}} + u\left( {\frac{\partial u}{{\partial s}} - v} \right)\left( {\frac{R}{R + r}} \right)} \right)\left( {\frac{R}{R + r}} \right)\frac{\partial T}{{\partial s}}, \\ \end{aligned} $$
(7)
$$ \varepsilon \left( r \right) = \left( {1 + d_{2} {e}^{{ - \left( {\frac{\text{r}}{\upgamma }} \right)}} } \right)\varepsilon_{\infty } ,\,\,\,\,\frac{{k^{*} \left( r \right)}}{{k_{\infty } }} = \left( {1 + d_{1} {e}^{{^{{ - \left( {\frac{\text{r}}{\upgamma }} \right)}} }} } \right). $$
(8)

In the above equations, \((\rho C_{{\text{p}}} )_{{{\text{Thnf}}}}\) is the volumetric heat capacity, k* demonstrates the porosity term, \(\left( {u,v} \right)\) are the component of the velocity, \(\gamma\) is the constant length of dimension, \(\varepsilon_{\infty }\) is the surface porosity, \(\lambda_{{\text{E}}}\) is the time relaxation heat flux, \(k_{\infty }\) is the surface permeability, \(B_{0}\) is the magnetic field strength, \(\alpha^{*}\) is the thermal diffusivity, \(C_{{\text{b}}}\) is the drag coefficient, \(d_{1}\) is the variable permeability \(k_{{{\text{Thnf}}}}\) demonstrates the thermal conductivity, \(d_{2}\) is the variable porosity, \(\rho_{{{\text{Thnf}}}}\) is the density, \(\sigma_{{{\text{Thnf}}}}\) is the electrical conductivity, \(\sigma^{*}\) is the Stefan Boltzmann coefficient and \(\nu_{{{\text{Thnf}}}}\) is the kinematic viscosity as show in Table 1.

Table 1 Numerical values of thermophysical characteristics of base fluid and NPs \( /{\phi_{1} = \phi_{{{\text{AA7075}}}} ,\,\phi_{2} = \phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} } /\) [20, 43, 44]
Full size table

The appropriate boundary conditions (BCs) are:

$$ \left. {\begin{array}{*{20}l} {u\left( r \right) = \frac{{u_{w} }}{{\left( {1 - \alpha^{*} t} \right)}},\quad T\left( r \right) = T_{w} ,\quad v\left( r \right) = 0,\;{\text{at}}\;r{ = 0,}} \hfill \\ {u\left( r \right) \to 0,\quad T\left( r \right) \to T_{\infty } ,\quad v\left( r \right) \to 0,\;{\text{when}}\;r \to \infty .} \hfill \\ \end{array} } \right\} $$
(9)

The thermal characteristics of the tri-hybrid nanofluid are \(\left( {\phi_{1} = \phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} ,\,\,\phi_{2} = \phi_{{{\text{AA7072}}}} ,\,\phi_{3} = \phi_{{{\text{AA7075}}}} } \right)\):

Viscosity

$$ \frac{{\mu_{{{\text{Thnf}}}} }}{{\mu_{{\text{f}}} }} = \frac{1}{{(1 - \phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} )^{2.5} (1 - \phi_{{{\text{AA7072}}}} )^{2.5} (1 - \phi_{{{\text{AA7075}}}} )^{2.5} }}, $$

Density

$$ \frac{{\rho_{{{\text{Thnf}}}} }}{{\rho_{{\text{f}}} }} = \left( {1 - \phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} } \right)\left[ {\left( {1 - \phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} } \right)\left\{ {\left( {1 - \phi_{{{\text{AA7072}}}} } \right) + \phi_{{{\text{AA7075}}}} \frac{{\rho_{{{\text{AA7072}}}} }}{{\rho_{{\text{f}}} }}} \right\} + \phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} \frac{{\rho_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} }}{{\rho_{{\text{f}}} }}} \right] + \phi_{{{\text{AA7075}}}} \frac{{\rho_{{{\text{AA7075}}}} }}{{\rho_{{\text{f}}} }}, $$

Specific heat

$$ {\frac{{(\rho c{\text{p}})_{{{\text{Thnf}}}} }}{{\left( {\rho c{\text{p}}} \right)_{{\text{f}}} }} = \phi _{{AA7075}} \frac{{\left( {\rho c{\text{p}}} \right)_{{{\text{AA7075}}}} }}{{\left( {\rho c{\text{p}}} \right)_{{\text{f}}} }} + \left( {1 - \phi _{{{\text{AA7075}}}} } \right)\left[ {\left( {1 - \phi _{{{\text{Ti}}_{{\text{6}}} {\text{Al}}_{{\text{4}}} {\text{V}}}} } \right)\left\{ {\left( {1 - \phi _{{{\text{AA7072}}}} } \right) + \phi _{{{\text{AA7072}}}} \frac{{\left( {\rho c{\text{p}}} \right)_{{{\text{AA7072}}}} }}{{\left( {\rho c{\text{p}}} \right)_{{\text{f}}} }}} \right\} + \phi _{{{\text{Ti}}_{{\text{6}}} {\text{Al}}_{{\text{4}}} {\text{V}}}} \frac{{\left( {\rho cp} \right)_{{{\text{Ti}}_{{\text{6}}} {\text{Al}}_{{\text{4}}} {\text{V}}}} }}{{\left( {\rho c{\text{p}}} \right)_{f} }}} \right]} $$

Thermal conduction

$$ \left. \begin{aligned} \frac{{k_{{{\text{Thnf}}}} }}{{k_{{{\text{hnf}}}} }} = & \left( {\frac{{k_{{{\text{AA7072}}}} + 2k_{{{\text{hnf}}}} - 2\phi_{{{\text{AA7072}}}} \left( {k_{{{\text{hnf}}}} - k_{{{\text{AA7072}}}} } \right)}}{{k_{{{\text{AA7072}}}} + 2k_{{{\text{hnf}}}} + \phi_{{{\text{AA7072}}}} \left( {k_{{{\text{hnf}}}} - k_{{{\text{AA7072}}}} } \right)}}} \right), \\ \frac{{k_{{{\text{hnf}}}} }}{{k_{{{\text{nf}}}} }} = & \left( {\frac{{k_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} + 2k_{{{\text{nf}}}} - 2\phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} \left( {k_{{{\text{nf}}}} - k_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} } \right)}}{{k_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} + 2k_{{{\text{nf}}}} + \phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} \left( {k_{{{\text{nf}}}} - k_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} } \right)}}} \right), \\ \frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }} = & \left( {\frac{{k_{{{\text{AA7075}}}} + 2k_{{\text{f}}} - 2\phi_{{{\text{AA7075}}}} \left( {k_{{\text{f}}} - k_{{{\text{AA7075}}}} } \right)}}{{k_{{{\text{AA7075}}}} + 2k_{{\text{f}}} + \phi_{{{\text{AA7075}}}} \left( {k_{{\text{f}}} - k_{{{\text{AA7075}}}} } \right)}}} \right), \\ \end{aligned} \right\} $$

Electrical conductivity

$$ \begin{aligned} \frac{{\sigma_{{{\text{Thnf}}}} }}{{\sigma_{{{\text{hnf}}}} }} = & \left( {1 + \frac{{3\left( {\frac{{\sigma_{{{\text{AA7072}}}} }}{{\sigma_{{{\text{hnf}}}} }} - 1} \right)\phi_{{{\text{AA7072}}}} }}{{\left( {\frac{{\sigma_{{{\text{AA7072}}}} }}{{\sigma_{{{\text{hnf}}}} }} + 2} \right) - \left( {\frac{{\sigma_{{{\text{AA7072}}}} }}{{\sigma_{{{\text{hnf}}}} }} - 1} \right)\phi_{{{\text{AA7072}}}} }}} \right), \\ \frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{{{\text{nf}}}} }} = & \left( {1 + \frac{{3\left( {\frac{{\sigma_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} }}{{\sigma_{{{\text{nf}}}} }} - 1} \right)\phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} }}{{\left( {\frac{{\sigma_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} }}{{\sigma_{{{\text{nf}}}} }} + 2} \right) - \left( {\frac{{\sigma_{{Ti_{6} Al_{4} V}} }}{{\sigma_{{{\text{nf}}}} }} - 1} \right)\phi_{{{\text{Ti}}_{{6}} {\text{Al}}_{{4}} {\text{V}}}} }}} \right), \\ \frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{{\text{f}}} }} = & \left( {1 + \frac{{3\left( {\frac{{\sigma_{{{\text{AA7075}}}} }}{{\sigma_{{\text{f}}} }} - 1} \right)\phi_{{{\text{AA7075}}}} }}{{\left( {\frac{{\sigma_{{{\text{AA7075}}}} }}{{\sigma_{{\text{f}}} }} + 2} \right) - \left( {\frac{{\sigma_{{{\text{AA7075}}}} }}{{\sigma_{{\text{f}}} }} - 1} \right)\phi_{{{\text{AA7075}}}} }}} \right) \\ \end{aligned} $$

Considering the variables

$$ \left. \begin{aligned} u = & \frac{bs}{{\left( {1 - \alpha^{*} t} \right)}}F^{\prime}(\eta ),\,\,\,\,p = \frac{{\rho_{{\text{f}}} \left( {bs} \right)^{2} }}{{\left( {1 - \alpha^{*} t} \right)^{2} }}P(\eta ), \\ v = & - \left( {\frac{R}{R + r}} \right)\left( {\frac{{b\nu_{{\text{f}}} }}{{1 - \alpha^{*} t}}} \right)^{\frac{1}{2}} F(\eta ), \\ T =\; & T_{\infty } + (T_{w} - T_{\infty } )\theta (\eta ),\quad \eta = \sqrt {\frac{{u_{{\text{w}}} }}{{\nu_{{\text{f}}} s\left( {1 - \alpha^{*} t} \right)}}} r. \\ \end{aligned} \right\} $$
(10)

Using Eq. (10), Eq. (3) is satisfied, whereas Eqs. (4)–(6) are converted into:

$$ \left. {F^{\prime 2} = \frac{{\left( {K + \eta } \right)}}{{A_{1} }}P^{\prime},} \right\} $$
(11)
$$ \left. {\begin{array}{*{20}l} {\frac{K}{{\left( {\eta + K} \right)}}\left( {\frac{2P}{{A_{1} }}} \right) = \frac{1}{{A_{1} A_{2} }}\left( {F^{\prime \prime \prime } \frac{1}{{\left( {K + \eta } \right)}}\left( {F^{\prime } - F^{\prime \prime } } \right)} \right) + \frac{K}{(K + \eta )}\left( {F\left( {F^{\prime \prime } + \frac{{F^{\prime } }}{{\left( {K + \eta } \right)}}} \right) - F^{\prime 2} } \right)} \hfill \\ { - {\mathbf{C}}F^{\prime } - \frac{{A_{3} A_{31} }}{{A_{1} }}{\text{M}}F^{\prime } - \frac{1}{{\alpha A_{1} A_{2} }}\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)}}{{\left( {1 + d_{1} e^{ - \eta } } \right)}}F^{\prime } - \beta \frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{1}{2}} }}F^{\prime 2} - {\mathbf{C}}\frac{\eta }{2}F^{\prime \prime } .} \hfill \\ \end{array} } \right\} $$
(12)

Putting Eq. (12) into Eq. (11) we have

$$ \left. {\begin{array}{*{20}l} {F^{\prime \prime \prime \prime } + 2\frac{{F^{\prime \prime \prime } }}{{\left( {\eta + K} \right)}} + A_{1} A_{2} \left[ {F\left( {F^{\prime \prime \prime } + \frac{{F^{\prime \prime } }}{{\left( {K + \eta } \right)}}} \right) - \left( {F^{\prime \prime } - \frac{{F^{\prime}}}{{\left( {\eta + K} \right)}}\left( {F^{\prime} - \frac{F}{{\left( {\eta + K} \right)}}} \right)} \right)} \right]\left( {\frac{K}{K + \eta }} \right) + \frac{{F^{\prime}}}{{\left( {\eta + K} \right)^{3} }}} \hfill \\ { - A_{2} A_{3} A_{31} A_{32} \left( {{\text{M}}F^{\prime \prime } + \frac{1}{(K + \eta )}{\text{M}}F^{\prime } } \right) - \frac{{A_{1} A_{2} {\mathbf{C}}}}{2(K + \eta )}\left( {2F^{\prime } + (K + \eta )\left( {3F^{\prime \prime } + \eta F^{\prime \prime \prime } } \right) + \eta F^{\prime \prime } } \right)} \hfill \\ { + \frac{{KF^{\prime \prime } }}{{\alpha \left( {K + \eta } \right)^{2} }}\left( {e^{ - \eta } d_{2} - F^{\prime } \left( {\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)}}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{2} }}e^{ - \eta } d_{1} } \right)\left( {\frac{{1 + d_{2} e^{ - \eta } }}{{1 + d_{1} e^{ - \eta } }}} \right)} \right) - \frac{{F^{\prime \prime } }}{{\left( {\eta + K} \right)^{3} }}} \hfill \\ { - \frac{\beta K}{{\left( {K + \eta } \right)^{2} }}\left( {2F^{\prime } F^{\prime \prime } \left( {\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{1}{2}} }}} \right) + \left( {\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{2\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{3}{2}} }}d_{1} e^{ - \eta } - 2d_{2} e^{ - \eta } \left( {1 + d_{2} e^{ - \eta } } \right)^{2} } \right)F^{\prime 2} } \right) = 0,} \hfill \\ \end{array} } \right\} $$
(13)
$$ \left. {\begin{array}{*{20}l} {\theta^{\prime \prime } + \frac{{A_{5} {\text{Pr}}K}}{{A_{4} \times A_{41} \times A_{42} + {\text{Ra}}(\eta + K)}}F\theta^{\prime } + \frac{{A_{3} \times A_{31} \times A_{32} }}{{A_{4} \times A_{41} \times A_{42} + {\text{Ra}}}}{\text{BrM}}F^{\prime 2} + \frac{{{\text{Pr}}S}}{{A_{4} \times A_{41} \times A_{42} + {\text{Ra}}}}\theta } \hfill \\ { + \frac{{\theta^{\prime } }}{\eta + K} + \frac{1}{{A_{4} \times A_{41} \times A_{42} + {\text{Ra}}}}\left( {{\text{Ec}}\left( {\left( {F^{\prime \prime } + \frac{1}{\eta + K}F^{\prime } } \right)^{2} } \right)} \right) + \frac{{{\text{Br}}}}{{A_{2} A_{5} \alpha {\text{Re}}_{{\text{s}}} }}\left( {\frac{{1 + d_{2} e^{ - \eta } }}{{1 + d_{1} e^{\eta } }}F^{\prime 2} } \right)} \hfill \\ { + {\text{Qe}}\left( {e^{ - n\,\eta } } \right)\theta + \frac{{A_{1} \beta }}{{A_{5} }}\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{1}{2}} }}F^{\prime 3} - \frac{\mathbf{C}}{2}\eta \left( {\eta + K} \right)^{3} \theta^{\prime } } \hfill \\ { + \beta_{1} \left( \begin{gathered} + K\left( {\eta + K} \right)^{2} \left( {\frac{1}{2}f^{\prime } \theta^{\prime } + f\theta^{\prime \prime } } \right)\eta {\mathbf{C}} - \frac{3}{4}{\mathbf{C}}^{2} \eta \left( {\eta + K} \right)^{3} \theta^{\prime} - \frac{1}{4}{\mathbf{C}}^{2} \eta^{2} \left( {\eta + K} \right)^{3} \theta^{\prime \prime } \hfill \\ + \frac{3K}{2}{\mathbf{C}}\left( {\eta + K} \right)^{2} f\theta^{\prime } - K^{2} \left( {\eta + K} \right)f^{2} \theta^{\prime \prime } - K^{2} \left( {\left( {\eta + K} \right)ff^{\prime } - f^{2} } \right)\theta^{\prime } \hfill \\ \end{gathered} \right) = 0,} \hfill \\ \end{array} } \right\} $$
(14)

The following are transformed boundary conditions:

$$ \left. {\begin{array}{*{20}l} {{\text{when}}\,\,\,\,\eta = 0,\,\,\,F = 0,\,\,\,F^{\prime } = \theta = 1,} \hfill \\ {{\text{when}}\,\,\,\,\eta \to \infty ,\,\,\,F^{\prime \prime } = \,\,\,F^{\prime } = \theta \to 0.} \hfill \\ \end{array} } \right\} $$
(15)

In above expressions

$$ \left. \begin{aligned} A_{1} = & \frac{{\rho_{{{\text{Thnf}}}} }}{{\rho_{{\text{f}}} }},\,\,\,A_{2} = \frac{{\mu_{{{\text{Thnf}}}} }}{{\mu_{{\text{f}}} }},\,\,\,A_{31} = \frac{{\sigma_{{{\text{Thnf}}}} }}{{\sigma_{{{\text{hnf}}}} }},\,\,\,A_{32} = \frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{{{\text{nf}}}} }},\,\,\,A_{3} = \frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{{\text{f}}} }}, \\ A_{41} = & \frac{{k_{{{\text{Thnf}}}} }}{{k_{{{\text{hnf}}}} }},\,\,\,A_{42} = \frac{{k_{{{\text{hnf}}}} }}{{k_{{{\text{nf}}}} }},\,\,\,A_{4} = \frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }},\,\,\,A_{5} = \frac{{(\rho c_{{\text{p}}} )_{{{\text{Thnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}. \\ \end{aligned} \right\} $$
(16)

The dimensionless variables are:

Parameters

Symbols

Expression

Magnetic factor

 

\(M = \frac{{\sigma B_{0}^{2} }}{{b\rho_{{\text{f}}} }}\)

Radiation parameter

\({\text{Ra}}\)

\({\text{Ra}} = \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3kk^{ * } }}\)

Eckert number

\({\text{Ec}}\)

\({\text{Ec}} = \frac{{u_{{\text{w}}}^{2} }}{{(T_{{\text{w}}} - T_{\infty } )(C_{{\text{p}}} )_{{\text{f}}} }}\)

Permeability term

\(\alpha\)

\(\alpha = \frac{{k_{\infty } }}{{\varepsilon_{\infty } }}\frac{{\rho_{{\text{f}}} u_{{\text{w}}} \left( {1 - \alpha^{*} t} \right)}}{{\mu_{{\text{f}}} }}\)

Unsteadiness parameter

\({\mathbf{C}}\)

\({\mathbf{C}} = \frac{{\alpha^{*} }}{b}\)

Non-uniform inertia factor

\(\beta\)

\(\beta = \frac{1}{{k_{\infty }^{1/2} }}C_{{\text{b}}} r\varepsilon_{\infty }\)

Exponential heat source

\({\text{Qe}}\)

\({\text{Qe}} = \frac{Q}{{u_{{\text{w}}} (C_{{\text{p}}} )_{{\text{f}}} }}\)

Prandtl number

\({\text{Pr}}\)

\({\text{Pr}} = \frac{{(\mu C_{{\text{p}}} )_{{\text{f}}} }}{{k_{{\text{f}}} }}\)

Curvature parameter

\(K\)

\(K = R\sqrt {\frac{b}{{\nu \left( {1 - \alpha^{*} t} \right)}}}\)

Thermal relaxation parameter

\(\beta_{1}\)

\(\beta_{1} = \frac{{b\lambda_{{\text{E}}} }}{{\left( {1 - \alpha^{*} t} \right)}}\)

Brinkman number

\({\text{Br}}\)

\({\text{Br}} = \frac{{\mu_{{\text{f}}} \left( {bs} \right)^{2} }}{{(T_{{\text{w}}} - T_{\infty } )k_{{\text{f}}} }}\)

Rate of entropy generation

\(N_{{{\text{EG}}}}\)

\(N_{{{\text{EG}}}} = \frac{{S_{{{\text{gen}}}} \nu_{{\text{f}}} T_{\infty } }}{{k_{{\text{f}}} b\left( {T_{{\text{w}}} - T_{\infty } } \right)}}\)

Temperature ratio parameter

\(\gamma_{1}\)

\(\gamma_{1} = \frac{{T_{{\text{f}}} - T_{\infty } }}{{T_{\infty } }}\)

The required skin friction and Nusselt number values are as follows:

$$ Cf_{{\text{s}}} = \frac{1}{{\rho_{{\text{f}}} }}\left( {\frac{{\tau_{{{\text{rs}}}} }}{{u_{{\text{w}}}^{2} }}} \right),\,\,\,\,\,{\text{Nu}}_{{\text{s}}} = \frac{1}{{k_{{\text{f}}} }}\left( {\frac{{sq_{{\text{w}}} }}{{(T_{{\text{w}}} - T_{\infty } )}}} \right), $$
(17)

In Eq. (17) heat flux \(q_{{\text{w}}}\) and wall shear stress \(\tau_{{{\text{rs}}}}\) are given as:

$$ q_{{\text{w}}} = \left. { - k_{{{\text{Thnf}}}} \left( {\frac{\partial T}{{\partial r}}} \right)\left( {\frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k_{{\text{f}}} k^{*} }}\frac{{k_{{\text{f}}} }}{{k_{{{\text{Thnf}}}} }} + 1} \right)} \right|_{{{\text{r}} = 0}} ,\,\,\,\,\tau_{{{\text{rs}}}} = \left. { - \mu_{{{\text{Thnf}}}} \left( {\frac{u}{r + R} - \frac{\partial u}{{\partial r}}} \right)} \right|_{{{\text{r}} = 0}} , $$
(18)

By using Eq. (9), the above equations become:

$$ \left( {{\text{Re}}_{{\text{s}}} } \right)^{{\frac{ - 1}{2}}} {\text{Nu}}_{{\text{s}}} = A_{41} A_{4} \left( {1 + \frac{{{\text{Ra}}}}{{A_{41} A_{4} }}} \right)\theta^{\prime } \left( 0 \right),\,\,\,\,\,\,\left( {{\text{Re}}_{{\text{s}}} } \right)^{\frac{1}{2}} C_{{{\text{fs}}}} = \frac{ - 1}{{A_{2} }}\left( {\frac{1}{K}f^{\prime } \left( 0 \right) - f^{\prime \prime } \left( 0 \right)} \right), $$
(19)

where Reynolds’s number \({\text{Re}}_{{\text{s}}} = \frac{{{\text{bs}}^{2} }}{{\nu_{{\text{f}}} }}.\)

Entropy optimization

The present problem's entropy development is defined as [34]:

$$ \begin{aligned} S_{{{\text{gen}}}} = & \frac{{k_{{{\text{Thnf}}}} }}{{T_{\infty }^{2} }}\left( {\frac{\partial T}{{\partial r}}} \right)^{2} + \frac{{k_{{{\text{Thnf}}}} }}{{T_{\infty }^{2} }}\frac{{16\sigma^{*} T_{\infty }^{3} }}{{3kk^{*} }}\left( {\frac{\partial T}{{\partial r}}} \right)^{2} + \frac{{\mu_{{{\text{Thnf}}}} }}{{T_{\infty }^{{}} }}\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \frac{{\sigma_{{{\text{Thnf}}}} B_{0}^{2} }}{{T_{\infty } }}u^{2} \\ \quad & + \frac{{Q^{*} e}}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{Thnf}}}} }}(T - T_{\infty } )\exp \left( { - \left( {\frac{{u_{{\text{w}}} }}{{\nu_{{\text{f}}} }}} \right)^{\frac{1}{2}} r} \right) + \frac{{\mu_{{{\text{Thnf}}}} }}{{(\rho C_{{\text{p}}} )_{{{\text{Thnf}}}} }}\frac{\varepsilon (r)}{{k^{*} (r)}}u^{2} + \frac{{\rho_{{{\text{Thnf}}}} }}{{(\rho C_{{\text{p}}} )_{{{\text{Thnf}}}} }}\frac{\varepsilon (r)}{{\left( {k^{*} (r)} \right)^{\frac{1}{2}} }}u^{3} . \\ \end{aligned} $$
(20)

Equation (20) can be modified as follows with the use of Eq. (9):

$$ \begin{aligned} N_{{{\text{EG}}}} =\; & A_{4} A_{41} \gamma_{1} \theta^{\prime 2} + A_{4} A_{41} \gamma_{1} {\text{Ra}}\theta^{\prime 2} + \frac{{{\text{Br}}}}{{A_{2} }}f^{\prime \prime 2} + A_{3} A_{31} {\text{BrM}}F^{\prime 2} + {\text{Pr}}S\theta \\ \quad & + \frac{{{\text{PrQe}}}}{{A_{5} }}\text{e}^{ - \text{n}\upeta } \theta + \frac{{{\text{Br}}}}{{A_{2} A_{5} \alpha {\text{Re}}_{\text{s}} }}\left( {\frac{{1 + d_{2} {e}^{ - \upeta } }}{{1 + d_{1} {e}^{\upeta } }}F^{\prime 2} } \right) + \frac{{A_{1} \beta }}{{A_{5} }}\frac{{\left( {1 + d_{2} \text{e}^{ - \upeta } } \right)^{2} }}{{\left( {1 + d_{1} \text{e}^{ - \upeta } } \right)^{\frac{1}{2}} }}F^{\prime 3} . \\ \end{aligned} $$
(21)

Numerical technique and problem validation

The numerical technique PCM is employed for the solution of the proposed model [11, 45, 46]. Scientific study often experiences challenging nonlinear boundary value problems (BVPs) that are challenging to resolve. Many problems, usually addressed by the Newton–Raphson linearization technique, have numerical convergence that depends on differential topology, initial guesses and relaxation variables. In this work, the alternative approach-known as the parametric continuation method—is emphasized. The methodology is consisting of the following steps:

Step 1: simplifications of ODEs to lowest order

The system of Eqs. (13, 14 and 22) along with Eq. (15), is further reset into the lowest order by selecting the following variables:

$$ \begin{aligned} F = & \Im_{1} , F^{\prime } = \Im_{2} , \,F^{\prime \prime } = \Im_{3} , \,\,F^{\prime \prime \prime } = \Im_{4} , \\ \theta = & \Im_{5} , \,\theta^{\prime } = \Im_{6} ,\,\,\, N_{\text{EG}} = \Im_{7} . \\ \end{aligned} $$
(22)

By incorporating Eq. (22) in Eqs. (13, 14 and 22), we get:

$$ \left. {\begin{array}{*{20}l} {\Im_{4}^{\prime } + 2\frac{{\Im_{4} }}{{\left( {\eta + K} \right)}} + A_{1} A_{2} \left[ {\Im_{1} \left( {\Im_{4} + \frac{{\Im_{3} }}{{\left( {K + \eta } \right)}}} \right) - \left( {\Im_{3} - \frac{{\Im_{2} }}{{\left( {\eta + K} \right)}}\left( {\Im_{2} - \frac{{\Im_{1} }}{{\left( {\eta + K} \right)}}} \right)} \right)} \right]\left( {\frac{K}{K + \eta }} \right)} \hfill \\ { + \frac{{\Im_{2} }}{{\left( {\eta + K} \right)^{3} }} - A_{2} A_{3} A_{31} A_{32} \left( {M\Im_{3} + \frac{1}{(K + \eta )}M\Im_{2} } \right) - \frac{{A_{1} A_{2} {\mathbf{C}}}}{2(K + \eta )}\left( \begin{gathered} 2\Im_{2} + (K + \eta ) \hfill \\ \left( {3\Im_{3} + \eta \Im_{4} } \right) + \eta \Im_{3} \hfill \\ \end{gathered} \right)} \hfill \\ { + \frac{{K\Im_{3} }}{{\alpha \left( {K + \eta } \right)^{2} }}\left( {e^{ - \eta } d_{2} - \Im_{2} \left( {\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)}}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{2} }}e^{ - \eta } d_{1} } \right)\left( {\frac{{1 + d_{2} e^{ - \eta } }}{{1 + d_{1} e^{ - \eta } }}} \right)} \right) - \frac{{\Im_{3} }}{{\left( {\eta + K} \right)^{3} }}} \hfill \\ { - \frac{\beta K}{{\left( {K + \eta } \right)^{2} }}\left( {2\Im_{1} \Im_{3} \left( {\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{1}{2}} }}} \right) + \left( {\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{2\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{3}{2}} }}d_{1} e^{ - \eta } - 2d_{2} e^{ - \eta } \left( {1 + d_{2} e^{ - \eta } } \right)^{2} } \right)\Im_{2}^{2} } \right) = 0,} \hfill \\ \end{array} } \right\} $$
(23)
$$ \left. {\begin{array}{*{20}l} {\Im_{6}^{\prime } + \frac{{A_{5} {\text{Pr}}K}}{{A_{4} A_{41} A_{42} + {\text{Ra}}(\eta + K)}}\Im_{1} \Im_{6} + \frac{{A_{3} A_{31} A_{32} }}{{A_{4} A_{41} A_{42} + {\text{Ra}}}}{\text{Br}}M\Im_{2}^{2} + \frac{{{\text{Pr}}S}}{{A_{4} A_{41} A_{42} + {\text{Ra}}}}\Im_{5} } \hfill \\ {\Im_{6}^{\prime } + \frac{{\Im_{5} }}{\eta + K} + \frac{1}{{A_{4} A_{41} A_{42} + {\text{Ra}}}}\left( {{\text{Ec}}\left( {\left( {\Im_{3} + \frac{1}{\eta + K}\Im_{2} } \right)^{2} } \right)} \right) + \frac{{{\text{Br}}}}{{A_{2} A_{5} \alpha {\text{Re}}_{s} }}\left( {\frac{{1 + d_{2} e^{ - \eta } }}{{1 + d_{1} e^{\eta } }}\Im_{3}^{2} } \right)} \hfill \\ { + {\text{Qe}}\left( {e^{ - n\,\eta } } \right)\Im_{5} + \frac{{A_{1} \beta }}{{A_{5} }}\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{1}{2}} }}\Im_{2}^{3} - \frac{\mathbf{C}}{2}\eta \left( {\eta + K} \right)^{3} \Im_{6} } \hfill \\ { + \beta_{1} \left( \begin{gathered} + K\left( {\eta + K} \right)^{2} \left( {\frac{1}{2}\Im_{2} \theta^{\prime} + \Im_{1} \Im_{6}^{\prime } } \right)\eta {\mathbf{C}} - \frac{3}{4}{\mathbf{C}}^{2} \eta \left( {\eta + K} \right)^{3} \Im_{6} - \frac{1}{4}{\mathbf{C}}^{2} \eta^{2} \left( {\eta + K} \right)^{3} \Im_{6}^{\prime } \hfill \\ + \frac{3K}{2}{\mathbf{C}}\left( {\eta + K} \right)^{2} \Im_{1} \Im_{6} - K^{2} \left( {\eta + K} \right)\Im_{1}^{2} \Im_{6}^{\prime } - K^{2} \left( {\left( {\eta + K} \right)\Im_{1} \Im_{2} - \Im_{1}^{2} } \right)\Im_{6} \hfill \\ \end{gathered} \right) = 0,} \hfill \\ \end{array} } \right\} $$
(24)

The transformed boundary conditions for the first-order fractional differential equations are as:

$$ \left. {\begin{array}{*{20}l} {\Im_{1} \left( 0 \right) = 0,\,\,\,\,\,\,\,\Im_{2} \left( 0 \right) = 0,\,\,\,\Im_{5} \left( 0 \right) = 1,\,\,\,} \hfill \\ {\Im_{3} \left( \infty \right) \to 0,\,\,\,\,\,\Im_{2} \left( \infty \right) \to 0,\,\,\,\Im_{5} \left( \infty \right) \to 0.} \hfill \\ \end{array} } \right\} $$
(25)

Step 2: introducing continuation parameter “p”

$$ \left. {\begin{array}{*{20}l} {\Im_{4}^{\prime } + \left( {\frac{2}{{\left( {\eta + K} \right)}} + A_{1} A_{2} \Im_{1} - \frac{{A_{1} A_{2} {\mathbf{C}}}}{2}\eta } \right)\left( {\Im_{4} - 1} \right)p + A_{1} A_{2} \left[ { - \left( {\Im_{3} - \frac{{\Im_{2} }}{{\left( {\eta + K} \right)}}\left( {\Im_{2} - \frac{{\Im_{1} }}{{\left( {\eta + K} \right)}}} \right)} \right)} \right]} \hfill \\ {\left( {\frac{K}{K + \eta }} \right) - A_{2} A_{3} A_{31} A_{32} \left( {M\Im_{3} + \frac{1}{(K + \eta )}M\Im_{2} } \right) + \frac{{\Im_{2} }}{{\left( {\eta + K} \right)^{3} }} - \frac{{A_{1} A_{2} {\mathbf{C}}}}{2(K + \eta )}\left( \begin{gathered} 2\Im_{2} + 3\Im_{3} \hfill \\ (K + \eta ) + \eta \Im_{3} \hfill \\ \end{gathered} \right)} \hfill \\ { + \frac{{K\Im_{3} }}{{\alpha \left( {K + \eta } \right)^{2} }}\left( {e^{ - \eta } d_{2} - \Im_{2} \left( {\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)}}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{2} }}e^{ - \eta } d_{1} } \right)\left( {\frac{{1 + d_{2} e^{ - \eta } }}{{1 + d_{1} e^{ - \eta } }}} \right)} \right) - \frac{{\Im_{3} }}{{\left( {\eta + K} \right)^{3} }} + A_{1} A_{2} K\frac{{\Im_{1} \Im_{3} }}{{\left( {K + \eta } \right)^{2} }}} \hfill \\ { - \frac{\beta K}{{\left( {K + \eta } \right)^{2} }}\left( {2\Im_{1} \Im_{3} \left( {\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{1}{2}} }}} \right) + \left( {\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{2\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{3}{2}} }}d_{1} e^{ - \eta } - 2d_{2} e^{ - \eta } \left( {1 + d_{2} e^{ - \eta } } \right)^{2} } \right)\Im_{2}^{2} } \right) = 0,} \hfill \\ \end{array} } \right\} $$
(26)
$$ \left. {\begin{array}{*{20}l} {\Im_{6}^{\prime } + \left( {\frac{{A_{5} {\text{Pr}}K}}{{A_{4} A_{41} A_{42} + {\text{Ra}}(\eta + K)}}\Im_{1} - \frac{\mathbf{C}}{2}\eta \left( {\eta + K} \right)^{3} - \frac{3}{4}\beta_{1} {\mathbf{C}}^{2} \eta \left( {\eta + K} \right)^{3} + \frac{3K}{2}\beta_{1} {\mathbf{C}}\left( {\eta + K} \right)^{2} \Im_{1} } \right)} \hfill \\ {\left( {\Im_{6} - 1} \right)p + \Im_{6}^{\prime } + \frac{{\Im_{5} }}{\eta + K} + \frac{1}{{A_{4} A_{41} A_{42} + {\text{Ra}}}}\left( {{\text{Ec}}\left( {\left( {\Im_{3} + \frac{1}{\eta + K}\Im_{2} } \right)^{2} } \right)} \right) + \frac{{{\text{Br}}}}{{A_{2} A_{5} \alpha {\text{Re}}_{s} }}\left( {\frac{{1 + d_{2} e^{ - \eta } }}{{1 + d_{1} e^{\eta } }}\Im_{3}^{2} } \right)} \hfill \\ { + {\text{Qe}}\left( {e^{ - n\,\eta } } \right)\Im_{5} + \frac{{A_{1} \beta }}{{A_{5} }}\frac{{\left( {1 + d_{2} e^{ - \eta } } \right)^{2} }}{{\left( {1 + d_{1} e^{ - \eta } } \right)^{\frac{1}{2}} }}\Im_{2}^{3} + \frac{{{\text{Pr}}S}}{{A_{4} A_{41} A_{42} + Ra}}\Im_{5} + \frac{{A_{3} A_{31} A_{32} }}{{A_{4} A_{41} A_{42} + Ra}}{\text{Br}}M\Im_{2}^{2} } \hfill \\ { + \beta_{1} \left( \begin{gathered} + K\left( {\eta + K} \right)^{2} \left( {\frac{1}{2}\Im_{2} \theta^{\prime} + \Im_{1} \Im_{6}^{\prime } } \right)\eta {\mathbf{C}} - \frac{1}{4}{\mathbf{C}}^{2} \eta^{2} \left( {\eta + K} \right)^{3} \Im_{6}^{\prime } \hfill \\ - K^{2} \left( {\eta + K} \right)\Im_{1}^{2} \Im_{6}^{\prime } - K^{2} \left( {\left( {\eta + K} \right)\Im_{1} \Im_{2} - \Im_{1}^{2} } \right)\Im_{6} \hfill \\ \end{gathered} \right) = 0,} \hfill \\ \end{array} } \right\} $$
(27)

Step 3: solving the Cauchy problems

By employing the implicit numerical scheme as:

$$ \frac{{U^\text{i + 1} - U^{\text{i}} }}{\Delta \eta } = AU^\text{i + 1} \,\,\,{\text{and}}\,\,\,\,\frac{{W^\text{i + 1} - W^\text{i} }}{\Delta \eta } = AW^\text{i + 1} . $$
(28)

The final iterative form is obtained as:

$$ U^{i + 1} = \frac{{U^{i} }}{(I - \Delta \eta A)}\,\,\,\,\,{\text{and}}\,\,\,\,\,W^{i + 1} = \frac{{(W^{i} + \Delta \eta R)}}{(I - \Delta \eta A)}. $$
(29)

Validation of results

Comparing the present results to previously published work for m = 1 and numerous values of K is illustrated in Table 2. It can be noticed that the both results show remarkable similarity.

Table 2 Comparative analysis of current results with the published work
Full size table

Discussion and graphical results

This section examines the variances in entropy generation, velocity, temperature gradient, and skin friction, concerning various physical features. The entropy formation in a Thnf flow through a CSS under the influence of exponential heat source/sink is assessed in the current investigation. The results are obtained through PCM. In these illustrations, solid lines represent the Thnf, dashed lines reflect the Hnf, and dot lines indicate the NF. The primary findings are addressed as follows:

Figures 2–5 demonstrate the outcome of volume fraction \(\left( {\phi_{1} ,\,\,\phi_{2} ,\,\,\phi_{3} } \right)\) inertia coefficient \(\beta ,\) unsteadiness parameter \({\mathbf{C}},\) permeability parameter \(\alpha\) on the fluid velocity. The outcome of the volume fraction on the velocity is extensively represented in Fig. 2. As the numbers of NPs rises, the fluid velocity falls due to the intensified fluid resistance. In addition, Fig. 2 demonstrates that the ternary hybrid nanofluid has a greater impact on reducing velocity compared to the binary and conventional nanofluids. Figure 3 depicts the effect of \(\beta\) on velocity. An improved internal force is produced by a higher value of \(\beta ,\) which elevates velocity. Figure 4 shows an illustration of the velocity curve \(F^{\prime}\left( \eta \right)\) against the unsteadiness factor \({\mathbf{C}}\). There is a correlation between higher values of the unsteadiness parameter \({\mathbf{C}}\) and an increase in velocity \(F^{\prime}\left( \eta \right)\). Figure 4 shows that ternary hybrid nanofluid boosted the velocity more than hybrid and nano-fluids. The consequences of permeability parameter \(\alpha\) on velocity \(F^{\prime}\left( \eta \right)\) are illustrated in Fig. 5. Rising values of \(\alpha\) led to a corresponding increase in velocity. Higher permeability coefficient enables fluid to flow more effortlessly, leading to increased velocities and flow rates. As seen in Fig. 5 Thnf exhibits a greater impact on the increase in velocity when compared to both NF and Hnf.

Fig. 2
figure 2

Impact of volume friction parameters on \(F^{\prime}\left( \eta \right)\)

Full size image
Fig. 3
figure 3

Impact of inertia coefficient \(\beta\) on \(F^{\prime}\left( \eta \right)\)

Full size image
Fig. 4
figure 4

Impact of unsteadiness parameter \({\mathbf{C}}\) on \(F^{\prime}\left( \eta \right)\)

Full size image
Fig. 5
figure 5

Impact of permeability parameter on \(F^{\prime}\left( \eta \right)\)

Full size image

The effects of the unsteadiness parameter \({\mathbf{C}},\) variable permeability \(d_{1} ,\) variable porosity \(d_{2} ,\) and curvature parameter K on the temperature distribution are illustrated in Figs. 6–9. Figure 6 describes the upshot of \({\mathbf{C}}\) on the temperature field \(\theta \left( \eta \right)\). Greater values of the unsteadiness parameter \({\mathbf{C}}\) result in a more intense temperature field \(\theta \left( \eta \right)\) and an increased thickness of the thermal layer. As the unsteadiness variable \({\mathbf{C}}\) increases, there is a decrease in the amount of heat that flows from the surface to the fluid, consequently, the temperature \(\theta \left( \eta \right)\) falls. Variable permeability and porosity factors effect on temperature \(\theta \left( \eta \right)\) is seen in Figs. 7 and 8. The ability of a substance or substrate to permit fluids or substances to pass through it is called its variable permeability. An decline in \(\theta \left( \eta \right)\) is reported for higher values of \(d_{1}\). Fluids with higher permeability \(d_{1}\) can move relatively easily which reduce the convective heat transfer. Figure 8 exhibit the behavior of temperature \(\theta \left( \eta \right)\) against different values of \(d_{2} .\) Lower flow resistance is usually the result of higher number of variable porosity \(d_{2} ,\) which increases the number of pores for fluid flow which boosts the flow rate of the fluid and consequently accelerates the heat transfer rates. The influence of the curvature parameter on \(\theta \left( \eta \right)\) is addressed in Fig. 9.

Fig. 6
figure 6

Impact of unsteadiness parameter \({\mathbf{C}}\) on \(\theta \left( \eta \right)\)

Full size image
Fig. 7
figure 7

Impact of variable permeability \(d_{1}\) on \(\theta \left( \eta \right)\)

Full size image
Fig. 8
figure 8

Impact of variable porosity \(d_{2}\) on \(\theta \left( \eta \right)\)

Full size image
Fig. 9
figure 9

Impact of curvature parameter K on \(\theta \left( \eta \right)\)

Full size image

Figures 10–12 discussed the generation of entropy against variable porosity \(d_{2}\) unsteadiness parameter \({\mathbf{C}}\) and curvature parameter \(K.\) The influence of variable porosity \(d_{2}\) is depicted in Fig. 10. A rise in variable porosity \(d_{2}\) causes an upsurge in entropy production. As a result of the variation in variable porosity, non-uniform flow patterns emerge, or flow instabilities are induced. Additionally, the amount of entropy generation increased. A graphic representation of entropy formation for varying values of \({\mathbf{C}}\) is shown in Fig. 11. Higher entropy formation is observed with larger values of the unsteadiness parameter. Figure 12 discussed the entropy generation against curvature parameter \(K.\) A spike in entropy production is caused by a rise in the curvature parameter. Due to the radial boundary's configuration, Fig. 12 revealed that an increase in the radius's curvature parameter will result in a decrease in the entropy profile. Furthermore, it is noted that ternary hybrid nanofluid improves entropy optimization noticeably more than hybrid and nano-fluid.

Fig. 10
figure 10

Impact of variable porosity \(d_{2}\) versus \(N_{{\text{G}}} (\eta )\)

Full size image
Fig. 11
figure 11

Impact of unsteadiness parameter \({\mathbf{C}}\) versus \(N_{{\text{G}}} (\eta )\)

Full size image
Fig. 12
figure 12

Impact of curvature parameter \(K\) versus \(N_{{\text{G}}} (\eta )\)

Full size image

Table 3 demonstrates the numerical outcomes of \(\sqrt {{\text{Re}}} {\text{Cf}}_{{\text{r}}}\). As the variable permeability, and magnetic parameter \(M\) increases, the coefficient of skin friction diminishes, while increase in permeability parameter \(\alpha ,\) variable unsteadiness parameter \({\mathbf{C}}\) and variable porosity improved the skin friction of the fluid. Table 4 illustrates the variation of the \({\text{Nu}}_{{\text{r}}}\) as a function of the various physical parameters. \({\text{Nu}}_{{\text{r}}}\) boosts as there is more heat owing to variable permeability \(d_{1} ,\) and Brinkman number and decline with increase in inertia coefficient \(\beta_{1}\), variable porosity, unsteadiness parameter \({\mathbf{C}}\) and Exponential heat source.

Table 3 Numerical results for skin friction \({\text{Cf}}_{{\text{s}}}\)
Full size table
Table 4 Numerical outputs for Nusselt number \({\text{Nu}}_{{\text{s}}}\)
Full size table

Conclusions

Optimizing the entropy production of magnetized Darcy–Forchheimer ternary hybrid flow of nanoliquid on a porous curved stretched surface is the focus of this study. In order to synthesize the modified hybrid nanofluid, Ti6Al4V, AA7072 and AA7075-NPs are added to water and ethylene glycol (50% + 50%). The need to speed up heat transfer for industrial and engineering applications inspired the present study. The novel findings are as follows:

  • In comparison with NF and Hnf, the Thnf exhibits dominant behavior.

  • Combining ethylene glycol and water improves efficiency of heat transfer.

  • Heat transmission in base fluid is positively influenced by the addition of Ti6Al4V, AA7072 and AA7075-NPs.

  • The inertia coefficient has a negative effect on the velocity distribution; while, larger values of the permeability parameter have a positive effect on the distribution of velocity.

  • Strengthening curvature parameter and fluctuating porosity increased temperature.

  • Improvements in the unsteadiness parameter and varying porosity lead to increases in Entropy production.

  • Skin friction declines as the variable porosity increases.

  • Higher \({\text{Br}}\) values result in a higher Nusselt number; while, low \({\text{Ra}}\) and \({\text{Qe}}{.}\) values result in a smaller Nusselt number.